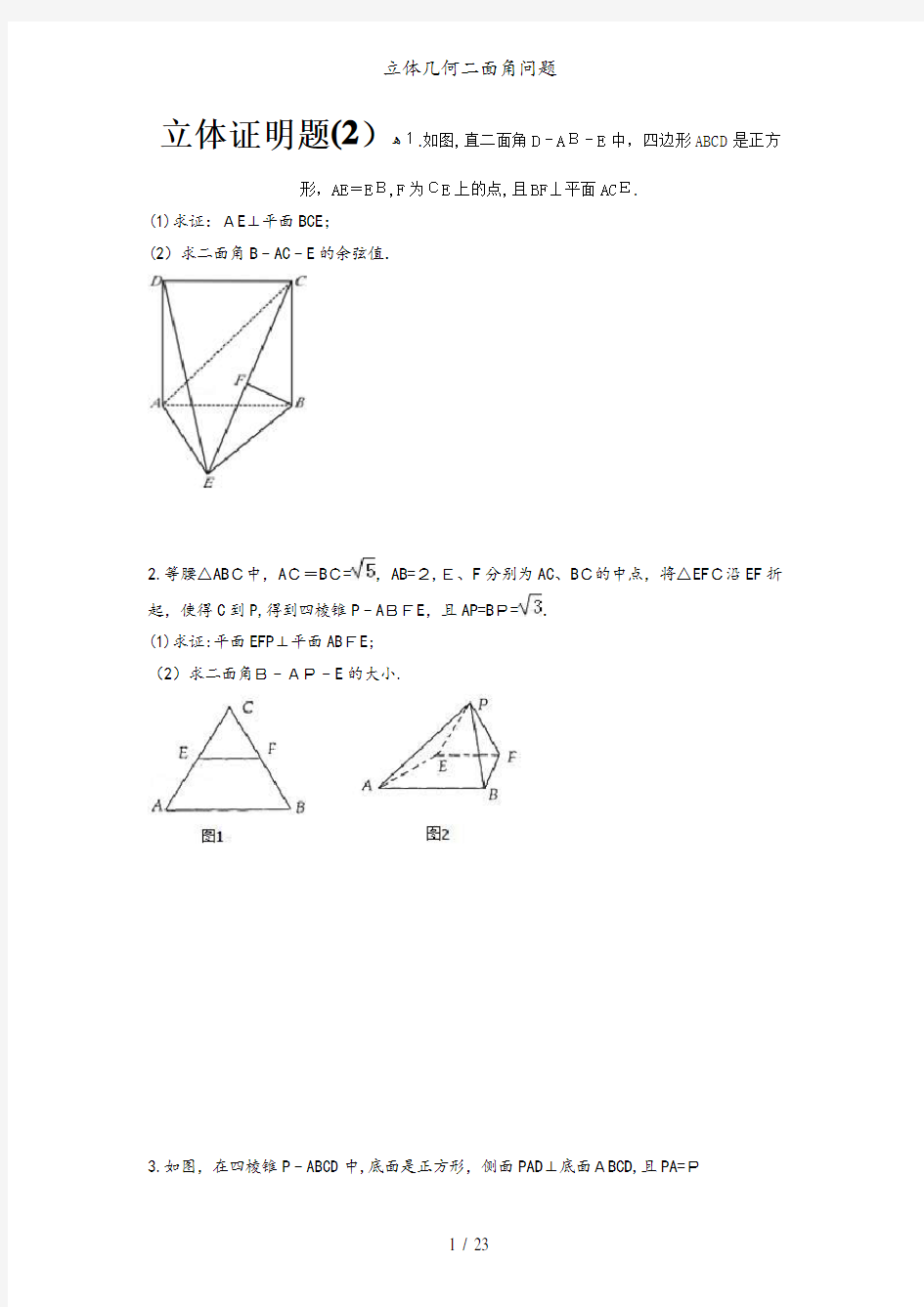
立体证明题(2)?1.如图,直二面角D﹣AB﹣E中,四边形ABCD是正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求二面角B﹣AC﹣E的余弦值.
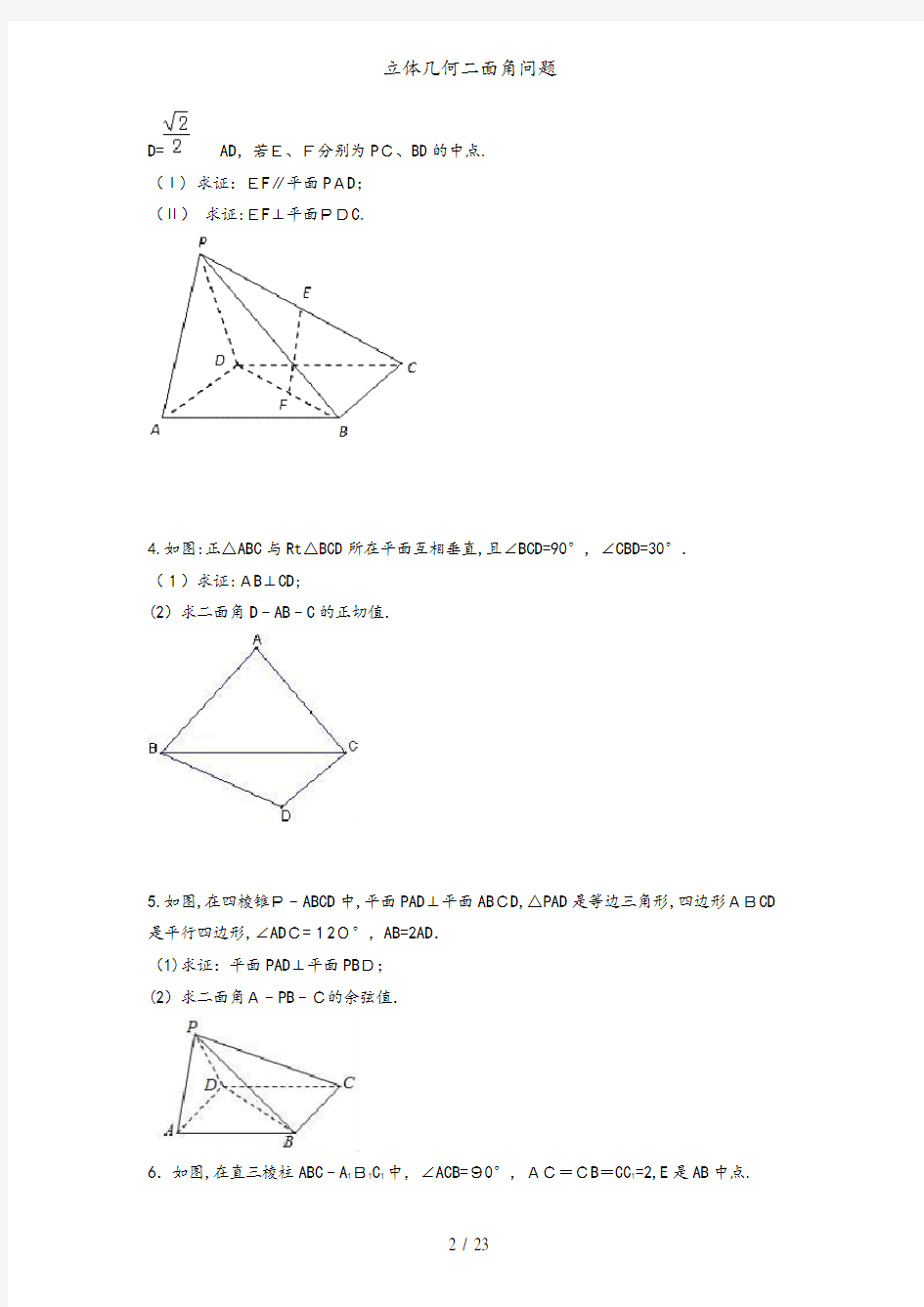
2.等腰△ABC中,AC=BC=,AB=2,E、F分别为AC、BC的中点,将△EFC沿EF折起,使得C到P,得到四棱锥P﹣ABFE,且AP=BP=.
(1)求证:平面EFP⊥平面ABFE;
(2)求二面角B﹣AP﹣E的大小.
3.如图,在四棱锥P﹣ABCD中,底面是正方形,侧面PAD⊥底面ABCD,且PA=P
D=AD,若E、F分别为PC、BD的中点.
(Ⅰ) 求证:EF∥平面PAD;
(Ⅱ)求证:EF⊥平面PDC.
4.如图:正△ABC与Rt△BCD所在平面互相垂直,且∠BCD=90°,∠CBD=30°.
(1)求证:AB⊥CD;
(2)求二面角D﹣AB﹣C的正切值.
5.如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,四边形ABCD 是平行四边形,∠ADC=120°,AB=2AD.
(1)求证:平面PAD⊥平面PBD;
(2)求二面角A﹣PB﹣C的余弦值.
6.如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.
(Ⅰ)求证:AB1⊥平面A1CE ;
(Ⅱ)求直线A 1C1与平面A 1C E所成角的正弦值.
7.如图,在四棱锥P ﹣ABC D中,PA ⊥平面A BCD,∠DAB 为直角,AB∥C D,AD=CD=2AB =2,E,F分别为PC,CD 的中点.
(Ⅰ)证明:AB ⊥平面BEF;
(Ⅱ)若PA=,求二面角E ﹣BD ﹣C.
8.如图,在四棱锥P ﹣ABCD 中,PA⊥平面AB CD,PA=AB=A D=2,四边形ABCD 满足AB⊥AD,BC∥AD 且BC=4,点M 为PC 中点.
(1)求证:DM⊥平面PBC;
(2)若点E 为BC边上的动点,且
λ=EC BE ,是否存在实数λ,使得二面角P ﹣DE ﹣B 的余弦值为3
2?若存在,求出实数λ的值;若不存在,请说明理由.
9.如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点(Ⅰ)求证:AM⊥平面BEC;
(Ⅱ)求三棱锥B﹣ACE的体积;
(Ⅲ)若点Q是线段AD上的一点,且平面QEC⊥平面BEC,求线段AQ的长.
10.如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB
(1)求证:EA⊥平面EBC
(2)求二面角C﹣BE﹣D的余弦值.
11.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD中点,M是棱PC上的点,AD=2BC.
(1)求证:平面POB⊥平面PAD;
12.如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E、F分别是CC1,BC的中点.
(1)求证:平面AB1F⊥平面AEF;
(2)求二面角B1﹣AE﹣F的余弦值.
13.如图,在菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=AE=2.
( I)求证:BD⊥平面ACFE;
( II)当直线FO与平面BDE所成的角为45°时,求二面角B﹣EF﹣D的余弦角.
14.如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2.
(1)证明:平面PAD⊥平面ABFE;
(2)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是.
15.如图,已知斜三棱柱ABC一A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.
(Ⅰ)求证:AC1⊥平面A1BC;
(Ⅱ)求二面角A﹣A1B﹣C的平面角的余弦值.
试卷答案
1.
【考点】与二面角有关的立体几何综合题;直线与平面垂直的判定.
【分析】(1)由已知中直二面角D﹣AB﹣E中,四边形ABCD是正方形,且BF⊥平面ACE,我们可以证得BF⊥AE,CB⊥AE,进而由线面垂直的判定定理可得AE⊥平面BCE.
(2)连接BD与AC交于G,连接FG,设正方形ABCD的边长为2,由三垂线定理及二面角的平面角的定义,可得∠BGF是二面角B﹣AC﹣E的平面角,解Rt△BFG即可得到答案.【解答】证明:(1)∵BF⊥平面ACE
∴BF⊥AE…
∵二面角D﹣AB﹣E为直二面角,且CB⊥AB,
∴CB⊥平面ABE
∴CB⊥AE…
∴AE⊥平面BCE.…
解:(2)连接BD与AC交于G,连接FG,设正方形ABCD的边长为2,
∴BG⊥AC,BG=,…
∵BF垂直于平面ACE,由三垂线定理逆定理得FG⊥AC
∴∠BGF是二面角B﹣AC﹣E的平面角…
由(1)AE⊥平面BCE,得AE⊥EB,
∵AE=EB,BE=.
∴在Rt△BCE中,EC==,…
由等面积法求得,
则
∴在Rt△BFG中,
故二面角B﹣AC﹣E的余弦值为.…
2.
【考点】二面角的平面角及求法;平面与平面垂直的判定.
【分析】(1)用分析法找思路,用综合法证明.取EF中点O,连接OP、OC.等腰三角形CEF中有CO⊥EF,即OP⊥EF.根据两平面垂直的性质定理,平面PEF和平面ABFE的交线是EF,且PO⊥EF,分析得PO⊥平面ABFE.故只需根据题中条件证出PO⊥平面ABFE,即可利用面面垂直的判定定理证得平面EFP⊥平面ABFE.
(2)根据第一问分析空间位置关系,可建立空间直角坐标线求得平面ABP和平面AEP的法向量的所成角,利用向量角和二面角关系,确定二面角大小.
【解答】解:(1)证明:在△ABC中,D为AB中点,O为EF中点.
由AC=BC=,AB=2.
∵E、F分别为AC、BC的中点,
∴EF为中位线,得CO=OD=1,CO⊥EF
∴四棱锥P﹣ABFE中,PO⊥EF,…2分
∵OD⊥AB,AD=OD=1,∴AO=,
又AP=,OP=1,
∴四棱锥P﹣ABFE中,有AP2=AO2+OP2,即OP⊥AO,…4分
又AO∩EF=O,EF、AO?平面ABFE,
∴OP⊥平面ABFE,…5分
又OP?平面EFP,
∴平面EFP⊥平面ABFE.…6分
(2)由(1)知OD,OF,OP两两垂直,以O为原点,建立空间直角坐标系(如图):
则A(1,﹣1,0),B(1,1,0),E(0,,0),P(0,0,1)…7分
∴,,
设,分别为平面AEP、平面ABP的一个法向量,
则?取x=1,得y=2,z=﹣1
∴. …9分
同理可得,…11分
由于=0,
所以二面角B﹣AP﹣E为90°. (2)
3.
【考点】空间中直线与平面之间的位置关系.
【专题】证明题.
【分析】对于(Ⅰ),要证EF∥平面PAD,只需证明EF平行于平面PAD内的一条直线即可,而E、F分别为PC、BD的中点,所以连接AC,EF为中位线,从而得证;
对于(Ⅱ)要证明EF⊥平面PDC,由第一问的结论,EF∥PA,只需证PA⊥平面PDC即可,
已知PA=PD=AD,可得PA⊥PD,只需再证明PA⊥CD,而这需要再证明CD⊥平
面PAD,
由于ABCD是正方形,面PAD⊥底面ABCD,由面面垂直的性质可以证明,从而得证.
【解答】证明:(Ⅰ)连接AC,则F是AC的中点,在△CPA中,EF∥PA(3分)
且PA?平面PAD,EF?平面PAD,
∴EF∥平面PAD(6分)
(Ⅱ)因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
又CD⊥AD,所以CD⊥平面PAD,
∴CD⊥PA(9分)
又PA=PD=AD,
所以△PAD是等腰直角三角形,且∠APD=,即PA⊥PD(12分)
而CD∩PD=D,
∴PA⊥平面PDC,又EF∥PA,所以EF⊥平面PDC(14分)
【点评】本题考查线面平行的判定及线面垂直的判定,而其中的转化思想的应用值得注意,将线面平行转化为线线平行;证明线面垂直,转化为线线垂直,在证明线线垂直时,往往还要通过线面垂直来进行.
4.
【考点】与二面角有关的立体几何综合题;空间中直线与直线之间的位置关系.
【分析】(1)利用平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,可得DC⊥平面ABC,利用线面垂直的性质,可得DC⊥AB;
(2)过C作CE⊥AB于E,连接ED,可证∠CED是二面角D﹣AB﹣C的平面角.设CD=a,则B C==,从而EC=BCsin60°=,在Rt△DEC中,可求tan∠DEC.
【解答】(1)证明:∵DC⊥BC,且平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,
∴DC⊥平面ABC,
又AB?平面ABC,
∴DC⊥AB.…
(2)解:过C作CE⊥AB于E,连接ED,
∵AB⊥CD,AB⊥EC,CD∩EC=C,
∴AB⊥平面ECD,
又DE?平面ECD,∴AB⊥ED,
∴∠CED是二面角D﹣AB﹣C的平面角,…
设CD=a,则BC==,
∵△ABC是正三角形,
∴EC=BCsin60°=,
在Rt△DEC中,tan∠DEC=.…
5.
【考点】MT:二面角的平面角及求法;LY:平面与平面垂直的判定.
【分析】(1)令AD=1,求出BD=,从而AD⊥BD,进而BD⊥平面PAD,由此能证明平面PAD⊥平面PBD.
(2)以D为坐标原点,DA为x轴,DC为y轴,过D作垂直于平面ABCD的直线为z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣PB﹣C的余弦值.
【解答】证明:(1)在平行四边形ABCD中,令AD=1,
则BD==,
在△ABD中,AD2+BD2=AB2,∴AD⊥BD,
又平面PAD⊥平面ABCD,
∴BD⊥平面PAD,BD?平面PBD,
∴平面PAD⊥平面PBD.
解:(2)由(1)得AD⊥BD,以D为坐标原点,DA为x轴,DC为y轴,
过D作垂直于平面ABCD的直线为z轴,建立空间直角坐标系,
令AD=1,则A(1,0,0),B(0,,0),C(﹣1,,0),P(,0,),