
数形结合思想在高中数学中的应用
灵宝实验高中王少辉
一、什么是“数形结合思想”
数形结合是一种数学思考方法;是数学研究和学习中的重要思想;也是解决数学问题的有效方法。“以形助数”可以使复杂问题简单化、抽象问题具体化;能够把抽象的数学语言变为直观的图形语言、把抽象的数学思维变为直观的形象思维;“以数助形”有助于把握数学问题的本质。
二、什么类型的题可以用“数形结合思想”解决
“数”和“形”是数学研究的两个基本对象。
数,通俗地说一般是指文字语言、数学符号语言、代数式等;
形,通俗地说一般指图形语言、函数图象、代数式的几何意义等。
既能用“数”表示,又能用“形”表示的知识就可以用数形结合思想解决。
数形结合的思想方法是数学教学内容的主线之一,应用数形结合思想,可以解决以下问题:
①集合问题②函数问题③方程与不等式问题④三角函数问题⑤向量问题⑥数列问题⑦线性规划问题⑧解析几何问题⑨立体几何问题⑩绝对值问题
三、数形结合思想应用举例
(一)在集合中的应用
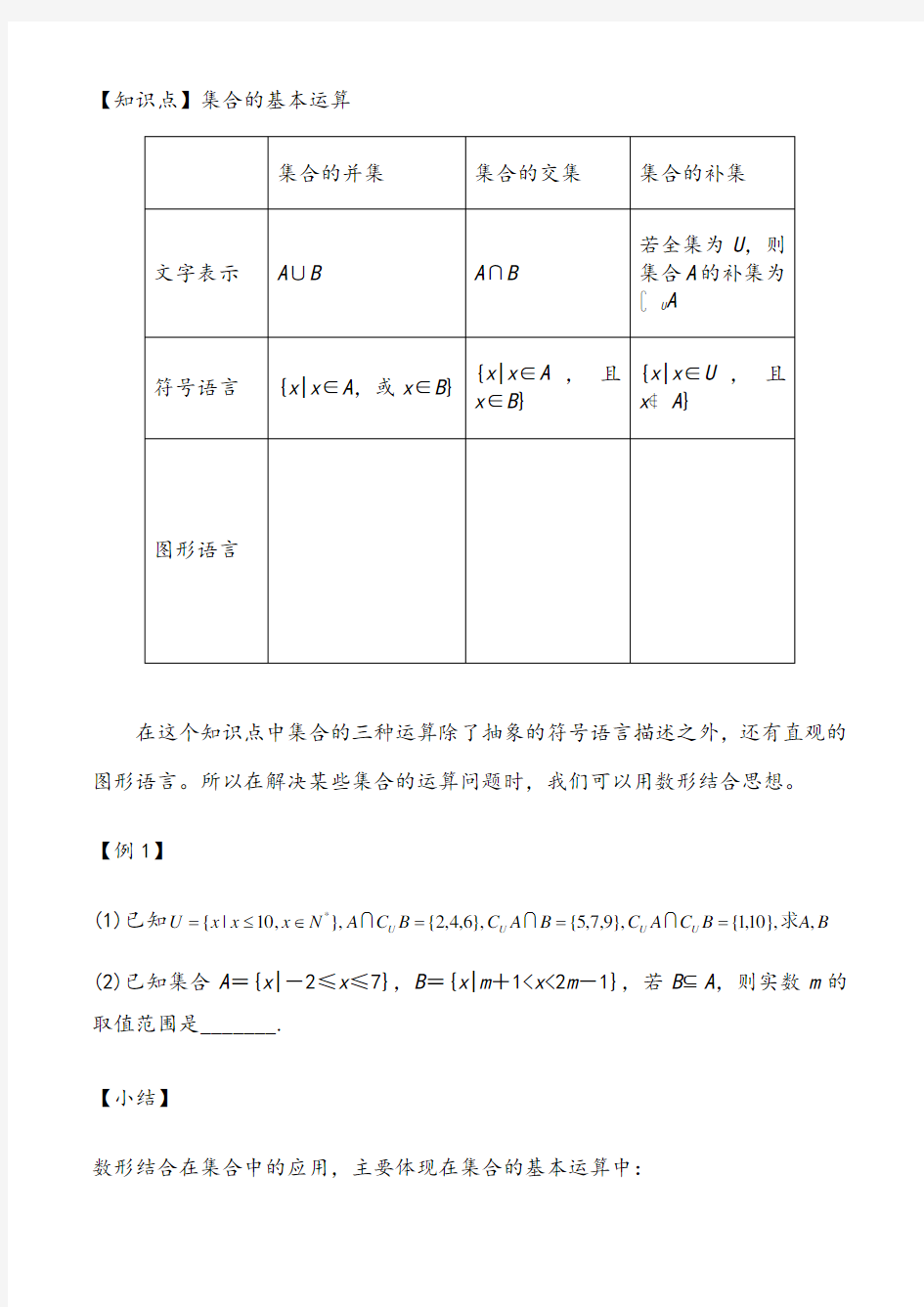
【知识点】集合的基本运算
在这个知识点中集合的三种运算除了抽象的符号语言描述之外,还有直观的图形语言。所以在解决某些集合的运算问题时,我们可以用数形结合思想。
【例1】
(1)已知B A B C A C B A C B C A N x x x U U U U U ,},10,1{},9,7,5{},6,4,2{},,10|{*求===∈≤=
(2)已知集合A ={x |-2≤x ≤7},B ={x |m +1 【小结】 数形结合在集合中的应用,主要体现在集合的基本运算中: (1)离散的集合用Venn 图表示 (2)连续的数集用数轴表示,注意端点 (二)在函数中的应用 1.二次函数区间求值问题 二次函数的图象我们都很熟悉,所以在解决二次函数的相关问题时,我们就可以借助图象来进行。 【例2】已知12)(2+-=ax x x f ,求f (x )在[1,2]上的最小值 【跟踪训练】已知12)(2+-=x x x f ,求f (x )在[t,t+2]上的最小值 2.函数性质综合应用 函数的性质在图象上都有直观的反应,所以在利用函数性质解决某些问题时,我们就可以借助图象来进行。 【例3】设函数???>≤+-=4 ,log 4,4)(22x x x x x x f ,若函数y =f (x )在区间(a ,a +1)上单调递增,则实数a 的取值范围是________. 【例4】已知函数?? ?<+-≥=0,20,2)(x x x x f ,则满足不等式)2()3(2x f x f <-的x 的取值范 围为 3.函数零点个数问题 函数零点、方程的根与函数图象的交点密切相关,所以在解决函数零点个数问题,方程根的个数问题时,常使用数形结合思想。 【例5】已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2-2x,如果函数g(x)=f(x)-m(m∈R)恰有4个零点,则m的取值范围是________. 【例6】已知定义在R上的偶函数f(x)满足f(x-4)=f(x),且在区间[0,2]上f(x)=x,若关于x的方程f(x)=log a x有三个不同的实根,求a的取值范围. 【小结】 数形结合在函数中的应用,主要体现在函数图象的应用中 (1)二次函数求给定区间上的最值问题 ①轴动区间定②轴定区间动 (2)函数性质(奇偶性、单调性、周期性)的综合应用 ①求范围②解不等式 (3)函数零点个数、方程根的个数 转化为图象交点个数问题 【跟踪训练1】函数f(x)=|x-2|-ln x在定义域内的零点的个数为( ) 解析由题意可知f(x)的定义域为(0,+∞).在同一 直角坐标系中画出函数y1=|x-2|(x>0),y2=ln x(x >0)的图象,如图所示: 由图可知函数f(x)在定义域内的零点个数为2. 答案C 【跟踪训练2】若关于x 的方程|x |=a -x 只有一个解,则实数a 的取值范围是________. 解析 在同一个坐标系中画出函数y =|x |与y =a -x 的图象, 如图所示.由图象知当a >0时,方程|x |=a -x 只有一个解. 答案 (0,+∞) 【跟踪训练3】已知函数???>-≤+=0 ,130,)(x x x a e x f x (a ∈R ),若函数f (x )在R 上有两个零点, 则a 的取值范围是( ) A.(-∞,-1) B.(-∞,0) C.(-1,0) D.[-1,0) 解析 当x >0时,f (x )=3x -1有一个零点x =13 . 因此当x ≤0时,f (x )=e x +a =0只有一个实根, ∴a =-e x (x ≤0),则-1≤a <0. 答案 D 【跟踪训练4】(2016·山东卷)已知函数???>+-≤=m x m mx x m x x x f ,42|,|)(2,其中m >0.若存在实数b ,使得关于x 的方程f (x )=b 有三个不同的根,则m 的取值范围是________. 解析 在同一坐标系中,作y =f (x )与y =b 的图象. 当x >m 时,x 2-2mx +4m =(x -m )2+4m -m 2, ∴要使方程f(x)=b有三个不同的根,则有4m-m2 即m2-3m>0.又m>0,解得m>3. 答案(3,+∞) 四、作函数图象的常用方法 数形结合的关键在于准确作出函数的图象,那么如何作函数图象就是最关键的步骤,同学们一定要掌握。下面介绍两种高中数学中最常用的方法。 1.利用描点法作函数的图象 步骤:(1)确定函数的定义域;(2)化简函数解析式;(3)讨论函数的性质(奇偶性、单调性、周期性、对称性等);(4)列表(尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等),描点,连线. 2.利用图象变换法作函数的图象 (1)平移变换 ①y=f(x+a)(a>0)的图象把y=f(x)的图象向左平移a个单位即可; ②y=f(x -a)(a>0)的图象把y=f(x)的图象向右平移a个单位即可; ③y=f(x)+b(b>0)的图象把y=f(x)的图象向上平移b个单位即可; ④y=f(x) -b(b>0)的图象把y=f(x)的图象向下平移b个单位即可; 即我们通常所说的左加右减,上加下减。 【练习1】作出下列函数的图象 (1)2 1-=x y (2)2)1(+=x y (3)12-=x y (2)对称变换 ①y =-f(x) 的图象把y =f(x)的图象关于 x 轴对称即可 ; ②y =f(-x) 的图象把y =f(x)的图象关于 y 轴对称即可 ; ③y =-f(-x) 的图象把y =f(x)的图象关于原点对称即可 ; 【练习2】作出下列函数的图象 (1)x y 2-= (2))ln(x y -= (3)x e y --= (3)伸缩变换 ①y =f(ax)(a>0)的图象 把y =f(x)的图象纵坐标不变,各点的横坐标变为原来的a 1倍即可 ; 相当于以y 轴为中心,把图象往左右伸长或压缩;a<1时伸长,a>1时压缩. ②y =Af(x)(A>0)的图象 把y =f(x)的图象横坐标不变,各点的纵坐标变为原来的 A 倍即可 ; 相当于以x 轴为中心,把图象上下伸长或压缩;A>1时伸长,A<1时压缩. (4)翻转变换 ①y =|f(x)|的图象,把y =f(x)的图象位于x 轴下方的部分翻到x 轴上方即可; 函数值为负数的变为其相反数,函数值为正数的不变,图象全部在x轴上方。 ②y=f(|x|)的图象,把y=f(x)的图象位于y轴左边的部分去掉,然后把右边的对称到左边即可. 自变量为负数时,与其相反数对应的函数值一样,所以是偶函数。 【练习3】作出下列函数的图象 (1)| | y= ln x ln |x y=(2)| 【练习4】作出下列函数的图象 (1)|)1 ln+ =x | y |+ ln( =x y(2)|1