模糊控制器设计实验报告

课程名称：智能控制实验名称：模糊控制一、实验目的：（1）了解在Simulink 仿真环境下建立控制系统方框图的方法，熟悉Matlab 和Simulink 仿真环境（2）掌握模糊控制器的设计方法。

（3）比较PID 控制和模糊控制的特点。

二、实验内容和步骤 已知s e s s s G 2.0214820)(-++=，分别设计PID 控制与模糊控制，使系统达到较好性能，并比较两种方法的结果。

结构如下图。

（1）模糊控制规则设计针对该定位系统，设计二维模糊控制规则，使性能达到最佳。

模糊控制规则如下：（2）设计未加PID或FUZZY控制器时，设计系统如下：输入阶跃信号，观测与分析仿真结果。

（3）加入PID控制器如下：对应的仿真结构图为：调整参数，观测与分析仿真结果。

PID控制的仿真曲线如下：（4）设计FUZZY控制器在simulink仿真环境下，设计模糊控制系统，包括模糊控制规则、隶属函数、比例因子、量化因子、论域等参数设计。

FUZZY控制仿真结构图如下：其中黄色部分具体为：利用simulink设计的模糊控制的仿真结构图为：其中对于模糊控制器的设计：E=[-6 6] EC=[-6 6] U=[-6 6]，并且其隶属函数分别为：E的隶属函数EC的隶属函数U的隶属函数再将其中一个学生的比较好的实验结果作为参考实例：首先仿真图如下：模糊控制器的设计：E=[-6 6] EC=[-6 6] U=[-6 6]，并且其隶属函数分别为：E和EC的隶属函数U的隶属函数控制规则：ECNB NM NS ZE PS PM PB ENB PB PB PB PB PM ZE ZENM PB PB PB PB PM ZE ZENS PM PM PM PM ZE NS NSZE PM PM PS ZE NS NM NMPS PS PS ZE NM NM NM NMPM ZE ZE NM NB NB NB NBPB ZE ZE NM NB NB NB NB设计好模糊控制器后，运行仿真图形，得到的仿真曲线如下（step time＝1）：模糊控制的仿真曲线由仿真可知，通过选择合适的PID参数可以达到较好的控制性能。

模糊控制系统的仿真实验实验目的：现有被控对象一：G(s)=1/(s2+2s+1)被控对象二：G(s)=K /【(T1s+1)(T2s+1) 】试设计一个模糊控制系统来实现对它的控制，并完成以下任务：任务一：通过仿真分析模糊控制器的参数的变化（主要讨论控制器解模方法和量化因子的变化）对系统性能的影响。

任务二：在控制器参数一定的情况下改变被控对象的参数，分析对象参数变化时fuzzy controller的适应能力。

任务三：在控制器参数一定的情况下改变被控对象的结构，分析对象结构变化时fuzzy controller的适应能力。

实验分析：要完成以上任务应分两个步骤：一设计模糊控制器，二用matlab的模糊逻辑工具箱建立模糊推理系统，并在simulink中实现对模糊系统的仿真。

接下来就以对象一为例说明模糊控制系统的仿真。

一、模糊控制器的设计模糊控制器的设计步骤为：1、选择控制器的输入输出：选择误差e及误差变化量ec为输入，u作为输出用于控制对象，这样模糊控制器具有二输入一输出的结构。

2、模糊集及论域的定义：z输入e的模糊子集为{NB NM NS NO PO PS PM PB}z输入ec和输出u的模糊子集均为{NB NM NS ZO PS PM PB}z e的论域为{-6 -5 -4 -3 -2 -1 －0 ＋0 1 2 3 4 5 6 }z ec的论域为{-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 }z u的论域为{-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 }我们选择三角形作为隶属度函数的形状，e的隶属度函数如下图所示：图1－1 ec的隶属度函数如下图所示：图1－2 u的隶属度函数如下图所示图1-3表1-14、选择输入输出变量的量化因子：这里暂时选定输入输出的量化因子Ke＝Kc＝Ku＝1，接下来的仿真过程还可以调整。

5、择模糊规则前提交的方法为min，模糊推理方法为min，而反模糊化方法可以在仿真过程中设置。

实验一：洗衣机的模糊控制实验目的：用MATLAB实现模糊控制器的设计实验步骤：（1）模糊控制器的结构设计选用单变量二维模糊控制器。

控制器的输入为衣物的污泥和油脂，输出为洗涤时间。

（2）定义输入输出模糊集将污泥分为三个模糊集：SD（污泥少），MD（污泥中），LD（污泥多），取值范围为[0，100]。

（3）定义隶属函数选用如下隶属函数：采用三角形隶属函数实现污泥的模糊化，采用三角形隶属函数实现污泥的模糊化，如图1-1所示。

图1-1 污泥隶属函数采用Matlab仿真，可实现污泥隶属函数的设计，仿真程序为：附录一将油脂分为三个模糊集：NG（无油脂），MG（油脂中），LG（油脂多），取值范围为[0，100]。

选用如下隶属函数：采用三角形隶属函数实现污泥的模糊化，如下图1-2所示。

仿真程序同污泥隶属函数（附录一）。

图1-2 油脂隶属函数将洗涤时间分为三个模糊集：VS（很短），S（短），M（中等），L （长），VL （很长），取值范围为[0，60]。

选用如下隶属函数：采用三角形隶属函数实现洗涤时间的模糊化，如图1-3所示。

图1-3 洗涤时间隶属函数采用Matlab 仿真，可实现洗涤时间隶属函数的设计，仿真程序为：模糊一（4）建立模糊控制规则根据人的操作经验设计模糊规则，模糊规则设计的标准为：“污泥越多，油脂越多，洗涤时间越长”；“污泥适中，油脂适中，洗涤时间适中”；“污泥越少，油脂越少，洗涤时间越短”。

（5）建立模糊控制表根据模糊规则的设计标准，建立模糊规则表1-1。

表1-1 模糊洗衣机的洗涤规则第*条规则为：“IF 衣物污泥少 且 没有油脂 THEN 洗涤时间很短”。

（6）模糊推理分以下几步进行：① 规则匹配。

假定当前传感器测得的信息为：x0(污泥)=60，y0(油脂)=70，分别带入所属的隶属函数中求隶属度：通过上述四种隶属度，可得到四条相匹配的模糊规则，如表1-2所示： 表1-2 模糊推理结果② 规则触发。

中南大学模糊控制课程实验报告学生姓名：彭雄威_____________ 指导教师： ________________ m _______ 学院：信息科学与工程学院学号：114611167 ______________实验一：本系统设计基于MATLAB图形模糊推理系统，设计步骤如下：打开MATLAB,输入指令fuzzy,打开模糊逻辑工具箱的图形用户界面窗口，新建一个Mamdani模糊推理系统。

(1) 增加一个输入变量，将输入变量命名为E、Ec,将输出变量命名U。

这样就建立了一个两输入单输出的模糊推理系统。

如图1.1所示。

图1.1增加一个输入变量(2) 设计模糊化模块：设计隶属度函数论域范围图3.2设计水位误差E模块3.3设计水位误差EC模块图3.4设计水位输出U模块（4）模糊控制器的规则设计le Editor: fuzzf（5）通过观察器观察规则情况在菜单view中的rules和surface选项分别对应得是规则观测器和曲而观测器。

123 4567891011121314151617181920212223242526272829”Input: 20】Plot points: ioi Move: [ left 11 rg ] |down] ( up ]Opened system tuzzf, 49 rules| 5 Close |图3.7规则观测器图3.6曲面观测器(6)保存编辑好的FIS文件实验二利用MATLAB软件的M文件编辑器和实验一所生成的fuzzf.FIS文件，在M 文件编辑器中输入：a=readfis('fuzzf');evalfis([・0.5广0.07;-0.5,0;・0.5,0.07; 0,・0.07;0,0;0,0.07;0.5广0.07;0.5,0;0.5,0.07],a)便可得fuzzf.FIS文件的模糊控制査询表，其中的数据在水位误差E的论域为[・ 1 1], 误差变化EC的论域为[.0.1 0.1]内可以任意取值。

模糊控制实验报告本实验通过使用模糊控制器来控制直流电机的转速。

模糊控制是一种基于模糊推理的控制方法，该方法可以处理一些无法准确数学建模的系统控制。

模糊控制的输入和输出都是模糊变量，这样可以考虑到系统存在的不确定性和模糊性。

实验装置包括模糊控制器、直流电机、转速测量装置、实验板等。

模糊控制器由模糊推理机、偏差和变化率输入模糊化模块、输出反模糊化模块、规则库组成。

实验板可通过控制开关选择转速和方向。

在实验中，通过设置转速值和方向，记录电机的真实转速和输出控制信号，来验证模糊控制器的控制效果。

通过不同的控制变量和规则库来对比不同的控制方案。

实验结果表明，模糊控制器对于直流电机转速的控制具有较好的效果。

当控制变量为偏差和变化率时，规则库中的设定合理，输出控制信号的变化平稳，电机转速较为稳定。

当增加控制变量或修改规则库时，控制效果也发生了变化。

同时，实验还验证了模糊控制的重要性和优越性，可以解决一些无法准确建模的系统控制问题。

在实验中，还需要注意一些实验细节，例如校准直流电机转速传感器的准确度，保证实验板电路的正常工作和实验数据的准确性，减少误差的影响。

总之，本实验通过实际操作验证了模糊控制器在直流电机转速控制中的应用，对于学习模糊控制的控制方法和实验操作具有很好的参考意义。

同时，本实验也展示了模糊控制对于处理模糊问题的效果。

在直流电机转速控制中，存在许多因素的影响导致控制过程不确定和模糊，例如负载的变化、外部干扰的存在等等。

而模糊控制可以将这些不确定因素转化为模糊变量进行处理，从而提高控制精度和鲁棒性。

此外，本实验也强调了规则库的重要性。

规则库是模糊控制中很关键的一部分，其中包含了专家经验和数学模型的映射关系。

规则库中的设定需要充分考虑被控对象的特性，才能够保证模糊控制器的控制效果。

而实验中不同的规则库设计对于控制效果的影响也展现了模糊控制的灵活性和可定制性。

最后，本实验的数据记录和实验结果分析也为后续工程实际应用提供了很好的参考。

中南大学模糊控制课程实验报告学生姓名：彭雄威指导教师：袁艳学院：信息科学与工程学院学号：114611167实验一：本系统设计基于MATLAB图形模糊推理系统，设计步骤如下：打开MATLAB，输入指令fuzzy，打开模糊逻辑工具箱的图形用户界面窗口，新建一个Mamdani模糊推理系统。

（1）增加一个输入变量，将输入变量命名为E、Ec，将输出变量命名U。

这样就建立了一个两输入单输出的模糊推理系统。

如图1.1所示。

图1.1增加一个输入变量(2) 设计模糊化模块：设计隶属度函数论域范围图3.2设计水位误差E模块3.3设计水位误差Ec模块图3.4设计水位输出U模块（4）模糊控制器的规则设计（5）通过观察器观察规则情况在菜单view中的rules和surface选项分别对应得是规则观测器和曲面观测器。

图 3.7 规则观测器图 3.6 曲面观测器 (6) 保存编辑好的FIS文件实验二：利用MATLAB软件的M文件编辑器和实验一所生成的fuzzf.FIS文件，在M 文件编辑器中输入：a=readfis('fuzzf');evalfis([-0.5,-0.07;-0.5,0;-0.5,0.07; 0, -0.07;0,0;0,0.07;0.5,-0.07;0.5,0;0.5,0.07],a)便可得fuzzf.FIS文件的模糊控制查询表，其中的数据在水位误差E的论域为[-1 1]，误差变化Ec的论域为[-0.1 0.1]内可以任意取值。

a=readfis(' fuzzf ')a =name: ' fuzzf 'type: 'mamdani'andMethod: 'min'orMethod: 'max'defuzzMethod: 'centroid'impMethod: 'min'aggMethod: 'max'input: [1x2 struct]output: [1x1 struct]rule: [1x5 struct]a=readfis(' fuzzf ');evalfis([-0.5,-0.07;-0.5,0;-0.5,0.07; 0, -0.07;0,0;0,0.07;0.5,-0.07;0.5,0;0.5,0.07],a)ans =-0.2000-0.4444-0.46670.1363-0.0014-0.22710.40000.44120.1333实验三利用MATLAB软件的M文件编辑器（也可选择C语言）完成模糊控制查询表的计算。

模糊控制实例及simulink仿真实验报告
一、背景介绍
模糊控制是一种基于模糊逻辑的控制方法，其优点在于可以很好地处理复杂的非线性和不确定性系统，而且不需要精确的数学模型和计算，能够快速实现控制的优化。

二、实例介绍
本次实例采用一个双轮小车为对象，实现小车在平面上向指定位置运动的控制。

通过小车的速度和转向角两个输入变量，输出一个模糊控制信号，控制小车前进和转向。

三、实验过程
1. 建立模糊控制系统模型
打开Simulink软件，建立一个新模型，模型中包括输入变量、输出变量和控制器。

2. 设计输入变量和输出变量
（1）设计输入变量
本实例选择小车速度和转向角两个输入变量，每个变量包含三个模糊集合，速度变量分别为“慢速”、“中速”、“快速”，转向角变量分别为“左转”、“直行”、“右转”。

（2）设计输出变量
模糊控制信号输出变量选择小车的前进和转向，每个变量包含三个模糊集合，分别为“慢行”、“中行”、“快行”、“左转”、“直行”、“右转”。

3. 建立控制器
建立模糊控制器，包含输入变量和输出变量的关系，建立控制规则库和模糊关系。

4. 仿真实验
在Simulink下进行仿真实验，调整控制器参数，观察小车运动状态，对比试验。

四、实验结果
经过多次试验和调整，得到最优的小车模糊控制参数，可以实现小车的平滑运动
和准确转向。

五、实验结论
本实验通过建立一个小车的模糊控制系统，可以有效实现小车的平滑运动和准确转向，控制效果优于传统的PID控制方法。

模糊控制可以很好地处理非线性、不确定性和模糊性的系统，适合许多需要快速优化控制的场合。

clear all;close all;T=0; %ʱ¼ä³£Êýa=newfis('fuzz_temperatrue');a=addvar(a,'input','e',[-3,3]); %Parameter e a=addmf(a,'input',1,'NB','zmf',[-3,-1]);a=addmf(a,'input',1,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);a=addmf(a,'input',1,'PM','trimf',[0,2,3]);a=addmf(a,'input',1,'PB','smf',[1,3]);a=addvar(a,'output','u',[72,78]); %Parameter u a=addmf(a,'output',1,'NB','zmf',[72,74]);a=addmf(a,'output',1,'NM','trimf',[72,73,75]);a=addmf(a,'output',1,'NS','trimf',[73,74,75]);a=addmf(a,'output',1,'Z','trimf',[74,75,76]);a=addmf(a,'output',1,'PS','trimf',[75,76,77]);a=addmf(a,'output',1,'PM','trimf',[75,77,78]);a=addmf(a,'output',1,'PB','smf',[76,78]);rulelist=[1 1 1 1; %Edit rule base2 2 1 1;3 3 1 1;4 4 1 1;5 5 1 1;6 6 1 1;7 7 1 1];a=addrule(a,rulelist);a1=setfis(a,'DefuzzMethod','mom'); %Defuzzywritefis(a1,'temperatrue'); %Save to fuzzy file "tank.fis" a2=readfis('temperatrue');figure(1);plotfis(a2);figure(2);plotmf(a,'input',1);figure(3);plotmf(a,'output',1);flag=1;if flag==1showrule(a) %Show fuzzy rule baseruleview('temperatrue'); %Dynamic Simulationenddisp('-------------------------------------------------------');disp(' fuzzy controller table:e=[-3,+3],u=[-4,+4] ');disp('-------------------------------------------------------');for i=1:1:7e(i)=i-4;Ulist(i)=evalfis([e(i)],a2);endUlist=round(Ulist)e=-3; % Erroru=evalfis([e],a2) %Using fuzzy inference四、Simulink仿真模型五、实验结果令T=0;1、模糊控制器为一维控制器，输入输出变量的量化等级为7级，取5个模糊集。

智能控制实验报告学院：电气工程学院班级：电气F1104姓名：***学号：************老师：***时间：2014.11.6模糊控制器设计一.实验目的1.了解模糊控制的原理2.学习Matlab模糊逻辑工具箱的使用3.使用工具箱进行模糊控制器的仿真二.实验设备1.计算机2.Matlab软件三.实验内容和步骤1.在Matlab命令窗口输入fuzzy，如图1所示，并按回车键，弹出如图2所示的FIS Editor界面，即模糊推理系统编辑器。

图1 Matlab命令窗口图2 FIS Editor界面2.本设计包含两个输入变量，在FIS编辑器界面上，执行菜单命令“Edit”→“Add Variable”→“Input”,即可成为二维模糊推理系统，并在变量窗口将变量名称修改为“temp-input”、“mag-input”、“dryness”，结果显示如图3所示。

图3 二维模糊推理系统3.执行菜单命令“File”→“Export”→“To File”，在弹出的“Save FIS”对话框中输入FIS系统名称后，即可实现对FIS的名称编辑。

用鼠标左键双击输入变量temp-input，弹出如图4所示的输入变量temp-input的隶属函数编辑器。

图4 隶属函数编辑器4.执行菜单命令“Edit”→“Remove All MFs”,然后执行菜单命令“Edit”→“Add MFs”,弹出“Membership Function”对话框，将隶属度函数设置为三角形。

将输入变量temp-input中的三个三角形函数的名称分别设置为“it”、“mt”、“ht”,取值范围和显示范围均设置为[0 9]，结果如图5所示。

将输入变量mag-input中的三个三角形函数的名称分别设置为“lm”、“mm”、“hm”,取值范围和显示范围均设置为[0 9]，结果如图6所示。

将输出变量dryness中的七个三角形函数的名称分别设置为“nw”、“lw”、“sh”“nh”、“hd”、“nd”、“od”“sd”、“sd”,取值范围和显示范围均设置为[0 14]，参数按[0 1 2]、[1 2 3]、[2 3 4]这样的规律设置，结果如图7所示。

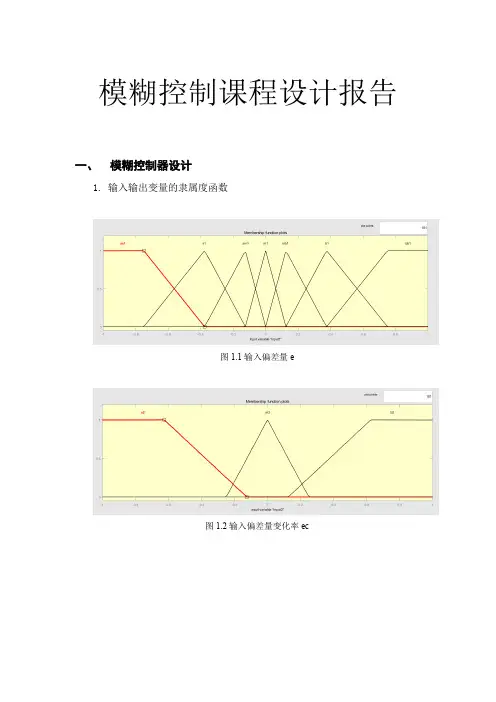
模糊控制课程设计报告一、模糊控制器设计1.输入输出变量的隶属度函数图1.1输入偏差量e图1.2输入偏差量变化率ec图1.3输出控制量u2.模糊规则设置1.if(input1 is ss1 ) and (input2 is s2)then (output1is b3)2.if(input1 is ss1 )and (input2 is m2)then (output1 is b3)3.if(input1 is ss1 )and (input2 is b2)then (output1 is mb3)4.if(input1 is s1 ) and (input2 is s2)then (output1 is b3)5.if(input1 is s1 )and (input2 is m2)then (output1 is mb3)6.if(input1 is s1 ) and (input2 is b2)then (output1 is m3)7.if(input1 is sm1) and (input2 is s2)then (output1 is mb3)8.if(input1 is sm1)and (input2 is m2)then (output1 is mb3)9.if(input1 is sm1)and (input2 is b2)then (output1 is m3)10.if(input1 is bb1)and (input2 is b2)then (output1 is s3)11.if(input1 is bb1)and (input2 is m2)then (output1 is s3)12.if(input1 is bb1)and (input2 is s2)then (output1 is sm3)13.if(input1 is b1) and (input2 is b2)then (output1 is s3)14.if(input1 is b1)and (input2 is m2)then (output1 is sm3)15.if(input1 is b1)and (input2 is s2)then (output1 is m3)16.if(input1 is mb1)and (input2 is b2)then (output1 is sm3)17.if(input1 is mb1)and (input2 is m2)then (output1 is sm3)18.if(input1 is mb1)and (input2 is s2)then (output1 is m3)19.if(input1 is m1)and (input2 is m2)then (output1 is m3)20.if(input1 is m1)and (input2 is s2)then (output1 is mb3)21.if(input1 is m1)and (input2 is b2)then (output1 is sm3)二、Simulink回路设计1.设计思路按照书中所示的基本结构将偏差、控制器、被控对象连接成一个回路，通过将偏差和偏差变化率输入模糊控制器，得到输出控制力矩u输入到被控对象中，最终得到理想的控制结果。