Model-independent Constraints on Topcolor from $R_b$
- 格式:pdf
- 大小:147.79 KB
- 文档页数:12


进行mechanical分析的步骤:1)建立几何模型:在Pro/ENGINEER中创建几何模型。
2)识别模型类型:将几何模型由Pro/ENGINEER导入Pro/MECHANICA中,此步需要用户确定模型的类型,默认的模型类型是实体模型。
我们为了减小模型规模、提高计算速度,一般用面的形式建模。
3)定义模型的材料物性。
包括材料、质量密度、弹性模量、泊松比等4)定义模型的约束。
5)定义模型的载荷。
6)有限元网格的划分:由Pro/MECHANICA中的Auto GEM(自动网格划分器)工具完成有限元网格的自动划分。
7)定义分析任务,运行分析。
8)根据设计变量计算需要的项目。
9)图形显示计算结果。
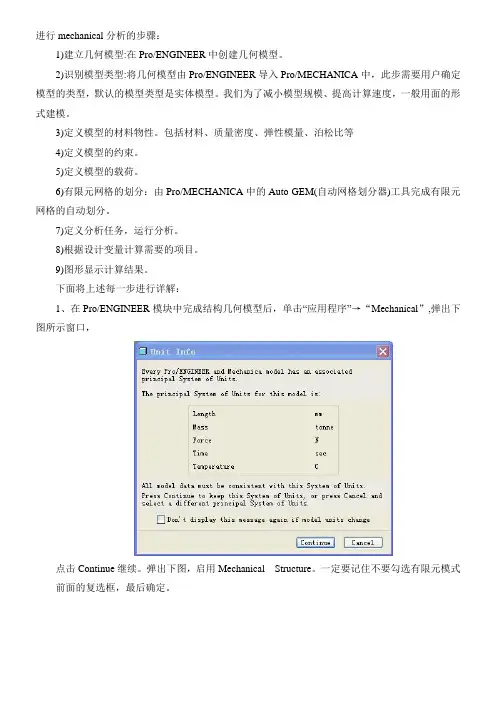
下面将上述每一步进行详解:1、在Pro/ENGINEER模块中完成结构几何模型后,单击“应用程序”→“Mechanical”,弹出下图所示窗口,点击Continue继续。
弹出下图,启用Mechanical Structure。
一定要记住不要勾选有限元模式前面的复选框,最后确定。
2、添加材料属性单击“材料”,进入下图对话框,选取“More”进入材料库,选取材料Name---------为材料的名称;References-----参照Parrt(Component)-----零件/组件/元件V olumes-------------------体积/容积/容量;Properties-------属性Material-----材料;点选后面的More就可以选择材料的类型Material Orientation------材料方向,金属材料或许不具有方向性,但是某些复合材料是纤维就具有方向性,可以根据需要进行设置方向及其转角。
点选OK,材料分配结束。
3、定义约束1):位移约束点击,出现下图所示对话框,Name 约束名称Number of Set 约束集名称,点击New可以新建约束集的名称。
Reference 施加约束时的参照,可以是surfaces(面)、edges/curves(边或曲面)、points(点)等Coordinate System 选择坐标系,默认为全局坐标系Translation 平动约束(Free为自由,fixed为固定,Prescribed为指定范围)Rotation 旋转约束单位为度Individual--------------单独的、孤立的Surf Options----------面选项Part Boundary---------零件的选择。

a r X i v :a s t r o -p h /0604217v 1 11 A p r 2006Mon.Not.R.Astron.Soc.000,000–000(2005)Printed 5February 2008(MN L A T E X style file v2.2)Redshift-Space Distortions with the Halo OccupationDistribution II:Analytic ModelJeremy L.Tinker 1⋆1KavliInsitute for Cosmological Physics,University of Chicago,933E.56th St.,Chicago,IL 60637ABSTRACTWe present an analytic model for the galaxy two-point correlation function in redshift space.The cosmological parameters of the model are the matter density Ωm ,power spectrum normalization σ8,and velocity bias of galaxies αv ,circumventing the linear theory distortion parameter βand eliminating nuisance parameters for non-linearities.The model is constructed within the framework of the Halo Occupation Distribution (HOD),which quantifies galaxy bias on linear and non-linear scales.We model one-halo pairwise velocities by assuming that satellite galaxy velocities follow a Gaussian distribution with dispersion proportional to the virial dispersion of the host halo.Two-halo velocity statistics are a combination of virial motions and host halo motions.The velocity distribution function (DF)of halo pairs is a complex function with skewness and kurtosis that vary substantially with ing a series of col-lisionless N-body simulations,we demonstrate that the shape of the velocity DF is determined primarily by the distribution of local densities around a halo pair,and at fixed density the velocity DF is close to Gaussian and nearly independent of halo mass.We calibrate a model for the conditional probability function of densities around halo pairs on these simulations.With this model,the full shape of the halo velocity DF can be accurately calculated as a function of halo mass,radial separation,angle,and cosmology.The HOD approach to redshift-space distortions utilizes clustering data from linear to non-linear scales to break the standard degeneracies inherent in pre-vious models of redshift-space clustering.The parameters of the occupation function are well constrained by real-space clustering alone,separating constraints on bias and cosmology.We demonstrate the ability of the model to separately constrain Ωm ,σ8,and αv in models that are constructed to have the same value of βat large scales as well as the same finger of god distortions at small scales.Key words:cosmology:theory —galaxies:clustering —large-scale structure of universe1INTRODUCTIONThe growth of structure through gravity creates peculiar velocities with respect to the smooth Hubble flow,mak-ing the line of sight a preferred direction when redshift is used as a measure of distance.The systematic differ-ences between the distribution of structure in real and red-shift space contain information about both the cosmology of the universe and the bias of galaxies observed (see,e.g.,Peebles 1976;Sargent &Turner 1977;Kaiser 1987).In Pa-⋆E-mail:tinker@per I (Tinker et al.2006a),we used numerical simulations to develop a blueprint for determining cosmological parameters from redshift-space distortions.In this paper,we use those simulations to calibrate an analytic model for redshift-space galaxy clustering that has the necessary accuracy to inter-pret high-precision measurements from large-scale galaxy redshift surveys,like the Two-Degree Field Galaxy Redshift Survey (2dFGRS;Colless et al.2001)and the Sloan Digital Sky Survey (SDSS;York et al.2000).The effect of redshift-space distortions is most apparent at small scales,where the internal motions of galaxies in groups and clusters spread out close pairs along the line ofc2005RAS2J.L.Tinkersight,creating the so-called“fingers-of-god”(FOGs).This picture of clustering in redshift space can be expressed as a convolution of the real-space two-point correlation function ξR(r)with the probability distribution function(PDF)of galaxy pairwise velocities P(v z),i.e.,1+ξ(rσ,rπ)= ∞−∞[1+ξR(r)]P(v z)dv z,(1)whereξR(r)is the real-space correlation function,rσis the projected separation,rπis the line-of-sight separation, r2=r2σ+z2,and v z=H(rπ−z),where H is the Hubble constant.Equation(1)is often referred to as the“stream-ing model”(Peebles1980).Although this approach has been used primarily to model observations of small-scale distor-tions(e.g.,Peebles1979;Davis&Peebles1983;Bean et al. 1983),equation(1)is valid in the linear regime as well (Fisher1995).Scoccimarro(2004)demonstrated that,pro-vided P(v z)is correct,the streaming“model”is a valid de-scription of the relation between the real-and redshift-space correlation functions on all scales.As presented,equation(1)contains no cosmology.The aforementioned investigations utilized the streaming model to estimate the velocity dispersion of galaxy pairs,which was used to estimate the matter density parameterΩm through a“cosmic virial theorem”.More recent studies of redshift-space distortions have utilized a modified linear the-ory model of anisotropies that,when applied to the real-space galaxy power spectrum P R(k),takes the formP Z(k,µ)=P R(k)(1+βµ2)2(1+k2σ2kµ2/2)−1,(2) whereβ=Ω0.6m/b g,b g is the linear bias parameter,andµis the cosine of the angle between the wavevector k and the line of sight.The term(1+βµ2)2,derived from linear the-ory by Kaiser(1987),models the coherentflow of matter out of underdense regions and into overdense regions.The last term on the right hand side represents an exponential dis-tribution of random,uncorrelated peculiar velocities,which dominates P Z on small scales and is meant to encapsulate the FOG effect described above.Equation(2),commonly re-ferred to as the“dispersion model”,has two free parameters,βand the galaxy velocity dispersionσk.Scoccimarro(2004) points out several deficiencies in this model,both in the inability of linear theory to properly describe anisotropies even in the large-scale limit,and in the oversimplification of using a single parameterσk,which has no clear physi-cal definition,to model small-scale velocities.Consequently, equation(2)introduces a10−15%systematic error in the determination ofβ(Hatton&Cole1999;Paper I),a level of error significant compared with the precision achievable with SDSS and the2dFGRS.The goal of this paper is to create an analytic model for the redshift-space correlation function by combining the streaming model of equation(1)with the Halo Oc-cupation Distribution(HOD;see, e.g.,Jing et al.1998; Ma&Fry2000;Peacock&Smith2000;Seljak2000;Benson 2001;Scoccimarro et al.2001;Berlind&Weinberg2002; Cooray&Sheth2002).The HOD quantifies bias on both linear and non-linear scales for a given galaxy sample by specifying the probability P(N|M)that a halo of mass M contains N galaxies of a given type,together with any spa-tial and velocity biases between galaxies and dark mat-ter within individual halos.The HOD has been utilized to model the real-space clustering of galaxies in the SDSS (Zehavi et al.2004,2005;Tinker et al.2005)and the2dF-GRS(Tinker et al.2006b;see also Yang et al.2003).In this paper we extend the HOD model from real space to redshift space by providing a model for P(v z)which is physically motivated and empirically calibrated on numerical simula-tions.Several recent papers have presented calculations of redshift-space distortions using halo models of dark matter and galaxy clustering(Seljak2001;White2001;Kang et al. 2002;Cooray2004;Skibba et al.2005;Slosar et al.2006), providing insight into the role of non-linear dynamics and non-linear bias in shaping clustering and anisotropy.How-ever,these studies rely on the same linear theory compo-nent of equation(2)for large-scale anisotropies.Kang et al. (2002)show that their model only reproduces the dark mat-ter P Z(k,µ)from N-body simulations after introducing a σk parameter for the halos,even after the virial motions of particles within halos were taken into account.Skibba et al. (2005)demonstrate the difficulty is modeling redshift-space galaxy clustering in the transition region between quasi-linear and fully non-linear regimes using a linear theory de-scription of halo velocities.Other recent papers have used the halo approach to model galaxy and dark matter ve-locity statistics(Sheth et al.2001a;Sheth&Diaferio2001; Sheth et al.2001b).While the model outlined in these pa-pers is derived fromfirst principles,in contrast to the cali-brated model presented here,it is still based on linear theory, which does not provide the required accuracy for a robust implementation of equation(1).The purpose of our model is less as afirst-principles derivation of P(v z)than as a tool to extract information from forthcoming observational data. In this context,the accuracy of the model is the paramount concern.In the course of developing the model,we will also gain new insight into the physics that determines P(v z),es-pecially the role of environment in producing a non-Gaussian velocity distribution.An accurate model forξ(rσ,rπ)with the HOD must properly incorporate halo motions.A proper model for halo pairwise velocities P h(v)must correctly describe the distri-bution function for an arbitrary pair of halo masses,at any angle with respect to the line of sight,and as a function of separation.In the large-scale limit,linear theory is ade-quate for describing the mean infall velocities of halos(see, e.g.,Juszkiewicz et al.1999;Sheth et al.2001a).However, the applicability of linear theory is problematic at scales where the observational data are robust.At all scales,linear theory does not accurately predict the pairwise dispersion (Scoccimarro2004).Higher order moments also play an im-portant role in P h(v).N-body results have shown that the radial velocity PDF of dark matter halos exhibits significant skewness and kurtosis(Zurek et al.1994;Juszkiewicz et al. 1998).1The skewness arises from the infall of matter into overdense regions(Juszkiewicz et al.1998).The kurtosis, 1In this paper we use the convention of radial being the directionc 2005RAS,MNRAS000,000–000Redshift-Space Distortions with the HOD3manifesting as exponential wings in both the radial and tan-gential velocities,is due to local non-linear effects for each halo in the pair.Scoccimarro(2004)concludes that a Gaus-sian is never a good description of velocities,even at the largest scales.Scoccimarro(2004)focuses on velocity statis-tics of dark matter,but local non-linear effects apply to halos as well(Kang et al.2002),and P h(v)from simulations are non-Gaussian at all scales.It is not sufficient for P h(v)to describe thefirst two moments of the velocity distribution. To accurately modelξ(rσ,rπ),P h(v)must reasonably de-scribe higher order moments of the distribution as well(see, e.g.,Fisher et al.1994).As stated in Paper I,our method for analyzing redshift-space distortions is tofirst use measurements of the pro-jected correlation function w p(r p)to determine the param-eters of the HOD for a given cosmology.If HOD parameters cannot be found that allow the cosmological model to re-produce the observed w p(r p)then that model is ruled out. Once the HOD has been determined,the redshift-space clus-tering is investigated by the analytic model presented here or the N-body approach of Paper I.The cosmological param-eters that most directly influence redshift-space clustering are the matter density parameterΩm,the amplitude of the linear matter power spectrum,defined here byσ8,the rms linear-theory massfluctuation in8h−1Mpc spheres(where h≡H0/100km s−1Mpc−1),and the velocity bias of the galaxy sample,which we parameterize byαv,the ratio be-tween the satellite galaxy velocity dispersion and the virial velocity dispersion of the dark matter halo.One can con-sider models in which the velocities of central galaxies are biased with respect to mean motion of the host halo.In Pa-per I we considered the shape of the linear matter power spectrum P lin(k)to be determined by measurements of the cosmic microwave background(CMB)anisotropies and the large-scale galaxy power spectrum(e.g.,Percival et al.2002; Spergel et al.2003;Tegmark et al.2004a).An advantage of the analytic model forξ(rσ,rπ)is that it allows for marginal-ization over P lin(k)without the cumbersome process of run-ning multiple N-body simulations.The redshift-space ob-servables explored here and in Paper I are largely indepen-dent of P lin(k),thus the constraints on HOD parameters come primarily from w p(r p)and to a small degree the as-sumed P lin(k),and the constraints on our cosmological pa-rameter space ofΩm,σ8,andαv come from the redshift-space data.Any degeneracies between cosmology and HOD parameters can be identified and marginalized over as well.In§2we outline the analytic model,presenting analytic expressions forξ(rσ,rπ)by combining the HOD model for real-space clustering with the streaming model of equation (1).In§3we detail the model for halo pairwise velocities, the key ingredient in the two-halo term,and calibrate it on the N-body simulations.§4tests the model against the mock galaxy samples of Paper I,demonstrating that the model can recover the correct cosmological parameters from a wide va-connecting the halo pair,tangential being in a direction orthog-onal to the radial,and line-of-sight to be the direction from the observer.Velocities in these directions will be referred to as v r, v t,and v z,respectively.Figure1.A slice through one simulation showing the locations of halos of different rge open circles are halos of mass M>3×1013.Smallfilled circles are halos of mass∼2×1012 h−1M⊙.The inset box plots the probability distribution function (PDF)of radial velocities for the lower-mass halo pairs in the slice.The shaded regions of the histogram highlights the skewness toward high-velocity pairs.All halo pairs within the shaded region of the histogram are connected in the slice plot.riety of cosmologies which produce significant degeneracies in redshift-space clustering.In§5we summarize and discuss prospects for applying the model to current data sets.2MODELING THE CORRELATIONFUNCTION IN REAL AND REDSHIFTSPACEThe real-space galaxy correlation functionξR(r)can be cal-culated analytically with the HOD for a given galaxy sample and cosmology.In the HOD framework,galaxy clustering is separated into two distinct parts;pairs of galaxies within a single halo and those from two separate halos.The total correlation function is the sum of these two contributions (see,e.g.,Berlind&Weinberg2002;Cooray&Sheth2002; Zheng2004;and Tinker et al.2005for details on calculating the real-space correlation function).The real-space one-halo term is written as1+ξ1h(r)=1dMN(N−1) M2R vir(M)F′ r4J.L.TinkerIn practice,F′(x)is different for galaxy pairs which involve the central galaxy and those between two satellite galaxies, and the calculation is separated into these two terms.In real space,one-halo pairs dominateξR(r)at small scales.In redshift space,these pairs have large relative mo-tions due to the virial dispersion of the halos they oc-cupy,spreading these pairs out along the line of sight. We model the velocity distribution within each halo as an isotropic,isothermal Gaussian distribution,an approx-imation supported by numerical hydrodynamic simulations (Faltenbacher et al.2004)and observational analysis of rich SDSS clusters(McKay et al.,in preparation).The satellite galaxy velocity dispersion in a halo of mass M is propor-tional to the virial dispersion,σ2sat=α2vσ2vir=α2vG M h2σsat.For central galaxies,a natural as-sumption is that these galaxies are at rest with respect to the center of mass of the halo,orαvc=0.In Paper I we tested this assumption,demonstrating thatαvc=0.2has a negligible effect on redshift-space observables.We define σcen=αvcσvir,so the dispersion of central-satellite pairs is σcs=(α2v+α2vc)1/2σvir.Deviations from isotropy have lit-tle effect onξ(rσ,rπ)for any physically reasonable value of the anisotropy,while non-isothermality resulting from spa-tial bias or unrelaxed systems can be modeled as an“effec-tive”velocity bias parameter(Paper I).In equation(3),the total number of one-halo pairs in-volves an integral over the halo mass function.At a given separation,the velocity PDF for one-halo pairs is a super-position of Gaussians weighted by the relative number of galaxy pairs from each halo of mass M.This superposi-tion of Gaussians of varying dispersion makes the overall pairwise galaxy velocity dispersion approximately exponen-tial(Sheth1996),in accord with observational inferences (Davis&Peebles1983;Hawkins et al.2003).The combination of equations(1)and(3)for central-satellite pairs isξ(cs) 1h (rσ,rπ)=1dMN sat M N cen Mr2σ+z2√2σ2cs dz2π¯n2g ∞0dM dn4R vir∞−∞F′ss √2R vir 1π2σsat×exp −(rπ−z)2(r2σ+z2),(6)where N sat(N sat−1) is the second moment of the satelliteoccupation function,and F′ss(x)is the fraction of satellite-satellite pairs(see Sheth et al.2001a for a derivation ofF cs(x)and F ss(x)for the NFW profile).The full one-halocorrelation function isξ1h(rσ,rπ)=ξ(cs)1h+ξ(ss)1h.The two halo term is most straightforward to calculatethrough a direct implementation of the equation(1),1+ξ2h(rσ,rπ)= ∞−∞[1+ξR2h(r)]P2h(v z|r,φ)dv z.(7)whereξR2h(r)is the two-halo contribution to the real-spacecorrelation function,P2h(v z|r,φ)is the line-of-sight velocityPDF of galaxy pairs from two distinct halos,and cosφ=rσ/r.This PDF is a convolution of the line of sight PDFof halo pairwise velocities with the Gaussian distributionfor galaxy velocities within each halo.P2h(v z|r,φ)is a pair-weighted average integrated over all possible combinationsof halos;P2h(v z|r,φ)=2(¯n′g)−2 M lim,10dM1dndM2 N M2P g+h(v z|r,φ,M1,M2),(8)where P g+h is the velocity PDF for galaxy pairs from ha-los of masses M1and M2.P g+h includes both the internalmotions of the galaxies within each halo and the relativemotions of the halo centers of mass.The limits on each inte-gral in equation(8)are determined by halo exclusion;halopairs cannot be closer than the sum of their virial radii(i.e.,R vir,1+R vir,2 r).At large separation,this effect is neg-ligible because the largest collapsed objects have radii∼2h−1Mpc,and the limits of equation(8)approach infinitywhen r is large.At small scales,halo exclusion strongly in-fluences the number of pairs.In equation(8),M lim,1is themaximum halo mass such that R vir(M lim,1)=r−R vir(M min)and M lim,2is related to M1by R vir(M lim,2)=r−R vir(M1),where M min is the minimum mass halo that can host agalaxy.The restricted number density,¯n′g,is the total num-ber of two-halo galaxy pairs at separation r,also calculatedusing halo exclusion by¯n′g2= M lim,10dM1dn dM2 N M2.(9)We denote the velocity PDF of halo pairs asP h(v z|r,φ,M1,M2).This represents the center-of-massmotions only.Once the relative motions of the dark matterhalos are determined,P g+h is calculated by convolving P hc 2005RAS,MNRAS000,000–000Redshift-Space Distortions with the HOD5Figure 2.Velocity PDFs for halo pairs at different local densities.The top four panels plot PDFs as a function of local environment for low-mass halos (solid histograms)and high-mass halos (filled circles connected with dotted lines).The local density is calculated by a top-hat smoothing kernel centered on the midpoint between the halo pair,with radius equal to the halo separation.The bottom panel shows the unconditional velocity PDF for the same halos.with the Gaussian describing the internal motions of the galaxies within the halos.The model for P h (v z |r,φ,M 1,M 2)is important both for capturing the behavior of the redshift-space correlation function in the transition region between the one-and two-halo terms and for correctly modeling dis-tortions between quasi-linear to linear scales.We describe it in detail in the next section.3THE HALO VELOCITY MODEL 3.1Conditional matter PDFIn §1we listed the requirements an accurate model of P h (v )must satisfy.To meet these requirements,we use the N-body simulations from Paper I to explore halo velocity statistics.Our simulation set consists of five realizations of an inflationary ΛCDM cosmology with Ωm =0.1andσ8=0.95at z =0,using the public N-body code GAD-GET (Springel,Yoshida,&White 2001).We utilize outputs at higher redshifts to represent models at different values of σ8and Ωm .Each simulation is 3603particles in a cubic volume 253h −1Mpc on a side,yielding a mass resolution of 9.6410×Ωm h −1M ⊙.The simulations have a power spec-trum shape parameter Γ=0.2in the parameterization of Efstathiou et al.(1992),and a spectral index n s =1.See Paper I for further details regarding the simulations.Our fiducial cosmology is Ωm =0.3,σ8=0.8,corresponding to z =0.55.Unless otherwise stated,N-body results will be using this output.Figure 1elucidates the complexity of P h (v |r,φ,M 1,M 2).The inset box shows the PDF of radial velocities of halo pairs of mass M 1=M 2≈2×1012h −1M ⊙at a separation of r ∼10h −1Mpc.Negative radial velocities are defined as the halos going toward one another.The PDF is not well described by either a Gaussian or anc2005RAS,MNRAS 000,000–0006J.L.TinkerFigure parison between the conditional matter PDFs measured from the simulations (solid histograms )and the model of Equation (11)(dotted lines ).Top row:P m (δ|r,M 1,M 2)for fixed mass (1012h −1M ⊙)and σ8=0.8,but changing radius.Middle row:P m (δ|r,M 1,M 2)for fixed radius (10h −1Mpc)and σ8=0.8,but increasing halo mass.Bottom row:P m (δ|r,M 1,M 2)for fixed mass (1012.3h −1M ⊙)and radius (10h −1Mpc),but changing σ8.exponential.The shaded regions of the PDF highlights the skewed tail of halo pairs rapidly approaching each other.The outer panel plots the positions of these halos in a 40h −1Mpc slice through one realization.Small,filled circles indicate the 2×1012h −1M ⊙halos of the inset histogram.The open circles in the plot represent high mass halos,M >3×1013h −1M ⊙.All pairs inside the shaded region of the histogram have been connected with a line.These high-velocity pairs are almost exclusively in regions that include a high mass halo.Because high mass halos prefer-entially occupy dense regions,we recover the well-known result that the non-linear halo velocity field is coupled to the non-linear density field.However,Figure 1leads us to investigate the velocity PDF as a function of environment.In Figure 2,the lower panel plots the same PDF from Figure 1for 1012h −1M ⊙halos at r ∼10h −1Mpc.This panel also plots the PDF for 3×1013h −1M ⊙at the same separation.The width of these mass bins is a factor oftwo.The PDF for high-mass halos is noisier due to lower statistics,but it is apparent that the PDF for high-mass halos peaks at v ∼−150km s −1,while the mode of the low-mass PDF is at zero.It is unlikely to find high-mass halos moving away from one another at this scale,while that probability is nearly 40%for low-mass halos.The upper panels of Figure 2show the PDFs for the same halos,now binned by local overdensity,δ≡ρ/¯ρ−1.We calculate δinside spheres of radius equal to the separation of the halo pairs,centered on the midpoint between the two halos.Setting the radius of the smoothing kernel equal to the halo separation allows for cleaner determination of the pair’s environment.The four top panels span a range in mean local density of δ ∼0to 3.From these data the origin of the high-velocity tail is clear;the negative skewness arises from halo pairs which lie in dense environments.At δ=0,the velocity distribution is narrow and peaked at v ≈0km s −1.As δincreases,both the mean velocity and the dispersionc2005RAS,MNRAS 000,000–000Redshift-Space Distortions with the HOD7Figure 4.The scale and mass dependence of parameters of the two-halo velocity model.Each line represents of halo pair with mass ratio M 2/M 1=4i ,with i =0−3and M 1=1012h −1M ⊙.Panel (a):cutoffdensity scale for the 2-halo conditional mat-ter PDF (Eq.[13]).Panel (b):Power-law index for the density-dependence of the pairwise velocity dispersion (Eq.[19]).There is only one line in this panel because there is no dependence on mass.Panel (c):Normalization of the density dependence of the pairwise radial velocity dispersion (Eq.[21]).Panel (d):Normal-ization of the density dependence of the pairwise tangential ve-locity dispersion (Eq.[22]).increase as well.At fixed δ,the PDFs no longer show strong skewness or kurtosis;a Gaussian is a good approximation.Therefore the total distribution in the bottom panel can be modeled as a superposition of Gaussians weighted by the probability of finding a halo pair at a given δ.At a given density,Figure 2also demonstrates that the PDFs for high-and low-mass halos are very similar.It is the different distributions of local environments which leads to the differences in the total PDFs in the lower panel.We therefore propose the ansatz P h (v [r,t ]|r,M 1,M 2)=P G (v [r,t ]|r,δ,M 1,M 2)P m (δ|r,M 1,M 2)dδ,(10)to model the radial and tangential pairwise motions of ha-los.In equation (10)P G is a Gaussian,and P m (δ|r,M 1,M 2)is the conditional matter density PDF in spheres of radius r centered on a halo pair of masses M 1and M 2.An ansatz of this type has been used to model one-point velocity statistics of halos and galaxies (Sheth &Diaferio 2001;Hamana et al.2003).Although the PDFs in the upper panels of Figure 2appear independent of halo mass,P G varies moderately with mass at small scales because at small r the halos themselves contribute a large fraction of the total local mass.At scalessignificantly larger than the halo radii,P G becomes inde-pendent of mass.The PDF for the unconditional matter distribution P m (δ|r )is well fit by a lognormal distribution function with dispersion that varies with smoothing scale (e.g.,Coles &Jones 1991;Kofman et al.1994).The relationship between the halo mass function and the large-scale den-sity field can also be quantified (e.g.,Bond et al.1991;Sheth &Tormen 2002;Pavlidou &Fields 2005).The con-ditional mass function can be roughly approximated as n (M |δ)≈[1+b (M )δ]n (M )(Mo &White 1996),where b (M )is the large-scale bias factor for halos of mass M (here we use the halo bias formula in Appendix A of Tinker et al.2005).The distribution of densities at which a halo of a given mass can be found is roughly P m (δ|r,M )≈[1+b (M )δ]P m (δ|r )(Hamana et al.2003).The term [1+b (M )δ]effectively shifts the matter PDF to higher densities by an amount which depends on the bias of the halo.The density distribution around pairs of halos,de-noted as P m (δ|r,M 1,M 2),is a murky theoretical prob-lem with no obvious straightforward approach.To model P m (δ|r,M 1,M 2)we truncate the unconditional matter dis-tribution with an exponential cutoffat low densities,i.e.,P m (δ|r,M 1,M 2)=A exp−˜ρ0(r,M 1,M 2)2πσ21exp−[ln(1+δ)+σ21/2]21+δ,(12)where σ21(r )=ln[1+σ2m (r )]and σm (r )is the mass vari-ance in top-hat spheres of radius r (e.g.,Coles &Jones 1991;Kofman et al.1994).To calculate σm (r ),we use the non-linear matter power spectrum of Smith et al.(2003).The cutoffdensity scale ˜ρ0is˜ρ0=˜ρ1[b (M 1)+b (M 2)]+r8J.L.TinkerFigure parison between the velocity statistics of N-body halos and the velocity model integrated over all halo masses.In all panels the solid line plots the N-body results and the open circles connected by dotted lines plots the model.The top four panels present the first four moments of the radial velocity PDFs as a function of scale:mean µ,dispersion σr ,skewness µ3/σ3,and kurtosis κ.The bottom two panels show the dispersion σt and kurtosis κof the tangential PDFs.For proper comparison,the integrals over velocity for the moments are binned in the same manner as the N-body results and are truncated at the high and low velocities of the N-body statistics.of Tinker et al.(2005).Equation (11)accurately tracks thechange in P m (δ|r,M 1,M 2)with smoothing scale.The middle row of panels in Figure 3compares the model to the N-body results for different halo masses at the same smoothing scale of 10h −1Mpc.N-body halo pairs of mass ∼2×1012h −1M ⊙,which have large-scale bias of ∼0.8in our fiducial cosmology,reside on average in overdense re-gions,with δ =0.80.As the mass increases by factors of 4and 16(with b ∼1.1and 1.5,respectively), δ increases to 1.00and 1.36.The mean density calculated from equa-tion (11)for each halo mass is 0.82,1.02,and 1.32,in good agreement with the numerical results.The bottom panel in Figure 3isolates the effect of changing σ8on P m (δ|r,M 1,M 2).The three panels present numerical results for M ∼5×1012h −1M ⊙halos at r ∼10h −1Mpc for σ8=0.6,0.8,and 0.95.In equation (12),the dependence of the matter distribution on the power spec-trum is through the parameter σm (r ),which is proportional to σ8.As σ8increases,the dispersion in the unconditional P m (δ|r )from equation (12)increases.The same is true for P m (δ|r,M 1,M 2);the N-body results broaden substantially from σ8=0.6to 0.95.The results from equation (11),plot-ted once again with the dotted lines,model the changes of P m (δ|r,M 1,M 2)with σ8accurately.With three adjustable parameters,the quantities ˜ρ1,α0and r 0of equation (13),our model for the conditional matter PDF P m (δ|r,M 1,M 2)reproduces the distinct effects of varying halo mass,smooth-ing scale,and power spectrum normalization.3.2Parameters of the GaussianFor a halo pair at separation r and density δ,we approximate the radial velocity PDF as a distribution of the form P (v r |δ,r,M 1,M 2)=12πσrexp−(v −µr )23.(15)At small scales,µr is approximated by the non-linear spher-ical collapse model (see,e.g.,Peacock 1999).In this model,the dependence of the velocity perturbation on density is expressed parametrically as δ=9(γ−sin γ)2(1−cos γ)2−1.(17)The mean radial velocity isµsc (δ,r )=H r Ω0.6m u (δ)exp[−(4.5/r ˜ρ)2],(18)where the exponential term is added to better match the N-body results at the smallest scales but has little influ-ence on the overall behavior of µsc .Investigation of our N-body results shows that the spherical collapse model best describes the N-body simulations at r 4h −1Mpc,while linear theory is an excellent description of the results for r 20h −1Mpc.In the transition region,we express µr as a weighted mean of equations (15)and (18),which smoothly transitions between the two regimes.The weighting fac-tor,w µincreases linearly from 0to 1in ln(r )in the range 4 r 20h −1Mpc,with µr =wµsc +(1−w )µlin .Recalling Figure 2,the skewness of the radial veloc-ity PDF arises from the combination of halo pairs in high-density regions,which have a large streaming velocity and high dispersion,with halo pairs in mean-to low-density re-gions,which have low mean streaming velocity (relative to Hubble flow)and small dispersion.In our N-body simula-tions,the skewness of the radial velocity distribution does not monotonically increase as halo separation decreases.As halo pairs become close,of order twice the sum of their virial radii,the skewness decreases and the PDF becomes more symmetric.Because µsc diverges rapidly as δbecomes large,the skewness of the model will always increase with decreasing r .To compensate for this effect,we enforce the condition that at r =4R vir ,1,µr is held constant for all δat the value of the most probable δfor that separation,remov-ing the skewness entirely.In the full halo+galaxy PDF,this change from skewed to symmetric distribution functions isc2005RAS,MNRAS 000,000–000。

即以此功德,庄严佛净土。
上报四重恩,下救三道苦。
惟愿见闻者,悉发菩提心。
在世富贵全,往生极乐国。
(一)优化模型的组成优化模型包括以下3部分:l Objective Function:目标函数是一个能准确表达所要优化问题的公式。
l Variables:Decision variables(决策变量),在模型中所使用的变量。
l Constraints:约束条件。
(二)Lingo软件使用的注意事项(1)LINGO中不区分大小写字母,变量(和行名)可以使用不超过32个字符表示,且必须以字母开头。
(2)在命令方式下(Command Window中),必须先输入MODEL:表示开始输入模型。
LINGO中模型以“MODEL:”开始,以“END”结束。
对简单的模型,这两个语句也可以省略。
(3)LINGO中的语句的顺序是不重要的,因为LINGO总是根据“MAX=”或“MIN=”语句寻找目标函数,而其它语句都是约束条件(当然注释语句和TITLE除外)。
(4)LINGO模型是由一系列语句组成,每个语句以分号“;”结束。
(5)LINGO中以感叹号“!”开始的是说明语句(说明语句也需要以分号“;”结束)。
(6)LINGO中解优化模型时假定所有变量非负(除非用限定变量取值范围的函数@free或@sub或slb另行说明)。
(7)当您要判断表达式输入是否有错误时,也可以使用菜单“Lingo“的”Picture“选项。
(8) 用命令"@BND(下界, 变量名, 上界)"设置变量的上界和下界(9) 用命令"@free(x1)"取消变量x1的非负限制,x1可以取正实数和负实数(10)一般整数变量可以用"@GIN(变量名)"来标识,0-1型变量可以用"@BIN(变量名)"来标识(三)Solution Report各项的含义例1 将以下模型粘贴到Lingo中求解,其中第一行MODEL和最后一行END在Lingo Model 窗口下可以不要。


gkmodel 公式和 stmodel 公式下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!介绍在现代科学研究中,模型在理论和实践中扮演着重要角色。

3DSHU SUHVHQWHG DW WKH 0RGHOLFD :RUNVKRS 2FW /XQG 6ZHGHQ $OO SDSHUV RI WKLV ZRUNVKRS FDQ EH GRZQORDGHG IURP KWWS ZZZ 0RGHOLFD RUJ PRGHOLFD SURFHHGLQJV KWPO:RUNVKRS 3URJUDP &RPPLWWHH3HWHU )ULW]VRQ 3(/$% 'HSDUWPHQW RI &RPSXWHU DQG ,QIRUPDWLRQ 6FLHQFH /LQN|SLQJ 8QLYHUVLW\ 6ZHGHQ FKDLUPDQ RI WKH SURJUDP FRPPLWWHH0DUWLQ 2WWHU *HUPDQ $HURVSDFH &HQWHU ,QVWLWXWH RI 5RERWLFV DQG 0HFKDWURQLFV 2EHUSIDIIHQKRIHQ *HUPDQ\+LOGLQJ (OPTYLVW '\QDVLP $% /XQG 6ZHGHQ+XEHUWXV 7XPPHVFKHLW 'HSDUWPHQW RI $XWRPDWLF &RQWURO /XQG 8QLYHUVLW\ 6ZHGHQ :RUNVKRS 2UJDQL]LQJ &RPPLWWHH+XEHUWXV 7XPPHVFKHLW 'HSDUWPHQW RI $XWRPDWLF &RQWURO /XQG 8QLYHUVLW\ 6ZHGHQ 9DGLP (QJHOVRQ 'HSDUWPHQW RI &RPSXWHU DQG ,QIRUPDWLRQ 6FLHQFH /LQN|SLQJ8QLYHUVLW\ 6ZHGHQ. /XQGH2EMHFW 2ULHQWHG 0RGHOLQJ LQ 0RGHO %DVHG 'LDJQRVLV0RGHOLFD :RUNVKRS 3URFHHGLQJV SSObject-Oriented Modeling in Model-BasedDiagnosisKarin Lundermatik GmbH,Schloßstr.34,D-89518HeidenheimOctober13,20001IntroductionIn the life cycle of a product,engineers have toperform many analysis tasks,from design lay-out,over system simulation and risk analysis,todiagnosis during product operation.Most anal-ysis tools are specialized for just a few of theseanalysis tasks.This forces the engineer to workwith a whole tool suite using various model for-mats(often even different models)for the sameproduct.But modeling a technical system is akind of art—it requires both expert domainknowledge and the ability to structure a problemand tofind out the appropriate level of abstrac-tion for it.It is a creative,time-consuming andexpensive task.To increase efficiency in prod-uct development,it would be desirable to haveanalysis tools which reduce the modeling effortas far as possible,by providing means to reuseexisting models,and by offering multiple ana-lyzes of a product on the base of a single prod-uct model.For programming languages like Java orSmalltalk,the advantages of object-orientedconcepts are well-known.They can be em-ployed to support hierarchical structuring ofproblems,to allow wide reuse of code,andmaintenance of large and evolving software sys-tems.The same applies to object-oriented mod-eling languages.They are especially well-suitedto model complex and multi-domain systems.Avery promising attempt to introduce a coherentobject-oriented modeling language based on theexperience of previous languages is Modelica[Mod99].Figure2:An automatically generated decision tree for model-supported diagnostics by the service.methods with AI technology(see[Sei97]).It provides the following analyzes using the same knowledge base:requirements analysis(design layout)design verificationrisk analysis–fault tree analysis–failure mode and effect analysis–sneak circuit analysis–tolerance analysisprocess monitoringmodel-supported diagnosis–decision trees–diagnostic rulesmodel-based diagnosis(on or off board) 2.1Declarative modelingTo build the necessary knowledge base,a tech-nical system is mapped to a hierarchical model consisting of a number of functional units which are connected with each other.The behavior of each functional unit(component)is described in terms of physical laws,in the form of con-straints.A constraint defines a relation between model variables.Thus,the component behavior is formulated declaratively,in contrast to many conventional simulation tools like Simulink or Matrix X,where all system equations are es-sentially assignments,and all component ports have to be either inputs or outputs.The declar-ative(or non-causal)modeling concept allows to model component behavior independently of the context where the component shall be used.This leads to more simple andflexible model libraries,which are reusable in many contexts. At the same time,it remains possible to formu-late certain constraints as assignments if neces-sary,for instance in subsystems where a behav-ior description by signalflow is an appropriate abstraction.A declarative modeling approach reflects also the fact that in physical systems,a steady state is an equilibrium determined by the interaction between all components.For instance,model-ing a complex electrical circuit by signalflow is nearly impossible.Moreover,if the behav-ior of one component in the circuit changes (e.g.in case of a defect),the model had to be re-designed because of the different signalflow. This shows that for model-based diagnosis,a declarative formulation of model behavior is es-sential.Risk analyzes as well as diagnostics bene-fit from the definition of additional behavioral modes modeling the component behavior in typical failure states.How behavior modes can be used in model-based diagnosis will be de-scribed in Section2.3.2.2Simulation in RODONIn real technical systems,some model parame-ters may be subject to manufacturing tolerances, others may be inaccurate because of measure-ment errors.For diagnostic purposes,it is es-pecially important that the simulation results of a model match the behavior of the real system, because discrepancies are interpreted as defec-tive behavior.Hence,it is dangerous to define those uncertain parameters by sharp real num-Figure3:A diagnosis:in case that gr-node-2is disconnect,a leakage current causes the high beam lamps to shine dimmed,although they are switched off.bers,more or less arbitrarily,as is usually done with conventional simulation tools.To reflect these uncertainties,in RODON the basic value type is not the real number but the interval.More precisely,since interval opera-tions may result in multiple intervals,the values of RODON variables are represented by interval sets,and all operations are carried out by inter-val arithmetics(see[HHKR95],[AH74]). Since product specifications often contain tol-erances or ranges,this value representation also suggests the use of RODON as a tool in require-ments analysis or design verification.The simulation algorithm of RODON seeks to constrict the values of all model variables as far as possible,without losing any solution.It bases on a local constraint propagation tech-nique which was adapted for interval constraint propagation by E.Hyv¨o nen(see[Hyv91]).The iterative algorithm starts by assigning undeter-mined values to all variables except for those whose values are given by the user(or in case of diagnosis:where input from the real system is available).An agenda mechanism is initialized with a list of all constraints.Now,the problem solver takes the constraints from the agenda one by one and evaluates them.If the value of some variable changes after evaluation,the problem solver collects all constraints which depend on this variable and puts them on the agenda again. They have to be evaluated anew,to propagate the new value through the system.This itera-tive process does not stop while the agenda con-tains constraints,that means,while some values keep changing(with respect to some accuracy, which is adjustable by the user).This algorithm is called local constraint propagation because changes are propagated through the system by passing them to the immediate neighbors in the constraint net.Local constraint propagation has a number of advantages.For instance,it allows to solve con-straint systems which are under-or overdeter-mined.This is especially important in model-based diagnosis,where a system has to be overdetermined in order to allow conclusions about defective components.2.3Model-based diagnosis Suppose one is given a description of a system, together with an observation of the system’s be-havior which conflicts with the way the sys-tem is meant to behave.The diagnostic prob-lem is to determine those components of the system which,when assumed to behave abnor-mally,will explain the discrepancy between the observed and correct system behavior[Rei87]. The observed system behavior is given by pro-cess data,i.e.by a set of values measured by the real system in operation.A diagnosis starts with a simulation of the nominal system behav-ior together with the given process data.The resulting equation system has to be overdeter-mined.If it has no solution,a conflict occurs during local propagation,which means that one or more components must be defect(i.e.behave abnormally).In case of a conflict,RODON analyzes the conflict and generates hypotheses(candidates) which may explain the abnormal system be-havior.A candidate is a minimal set of vi-olated assumptions,where an assumption can have a form like”the component XY behaves normally”.For the efficient generation of hypotheses it is not sufficient to know that a simulation ended with a conflict.Without additional information about where the conflict occured candidate gen-eration would be a search in a gigantic search space.Simulation by local constraint propaga-tion provides us with this information.With each value set,RODON manages the assump-tions the value set depends on.This is done by means of a truth-maintenance system(TMS).If a conflict occurs,RODON is able to backtrack the assumptions corresponding to the conflict-ing values.They can be used to narrow the search space to candidates containing these as-sumptions.This diagnostic approach is based on the GDE (general diagnostic engine)introduced by de Kleer([dKW87],[dKW89]).It is characterized byan incremental diagnostic procedureuse of behavioral modes for candidate ver-ificationa truth-maintenance system(TMS)toreuse knowledge in multiple contextsa scalable candidate generatorthe ability to diagnose multiple faults aswell as unspecified faults 3Object-Oriented Modeling in RODONThe tool goes back to ideas of W.Seibold [Sei92]in the early80’s,and has developed over the past10years.From the very begin-ning,an object-oriented modeling approach was used to define hierarchies of model component classes.It agrees with the Modelica philosophy [Mod99]in central points,namelyhierarchical modelingcomponent-oriented modelingdeclarative modelingquantitative modelingmulti-domain modelingsupport by object-oriented model libraries This remarkable similarity suggests the idea to support Modelica as a modeling language in RODON.To gain experience for the integra-tion of Modelica into RODON,we implemented a prototype of a model representation module, and combined it with a new version of the RODON diagnostic engine.While structure and topology representation of Modelica models could be adopted without any changes,the behavior representation had to be slightly modified.In the following subsections,we will explain the alterations made for our application.All exam-ples are written in the Modelica dialect we cur-rently use with our prototype implementation. Its behavior section isfitted to our special needs. Note that the language specification is notfixed entirely.3.1Modeling behavior modesLet us start with a simple example model-ing an electrical wire class with two behav-ioral modes:the nominal behavior,and the most common failure modes disconnect,and shortT oGround.An appropriate class hierar-chy could be the following.package Rose.Electricalconnector Porttype Current=Interval(unit="A",quantity="current");type Resistance=Interval(unit="Ohm",quantity="resistance"); type Voltage=Interval(unit="V",quantity="voltage");type FM=Discrete(min=0,quantity="failure mode");Figure4:Type definitions in RODON.Voltage u;flow Current i;end Port;partial model TwoPortPort p,n;FM fm(max=1);behaviorif(fm==0|fm==1)Kirchhoff(p.i,n.i);if(fm==1)p.i=0;end TwoPort;model IdealWire2extends TwoPort(fm(max=2)); protected Interval iGnd;behaviorif(fm==0|fm==2)p.u=n.u;if(fm==2)p.i+n.i+iGnd=0; if(fm==2)p.u=0;end Wire2;end Rose.Electrical;The model TwoPort is a general electri-cal component providing basic physical laws for the current in case of nominal behavior (fm==0)and the failure mode disconnect (fm==1).The alternative behavior for dif-ferent behavioral modes is defined using con-ditional constraints,where the discrete failure mode variable fm serves as a kind of switch. The model IdealWire2extends this base class by adding a constraint for the voltage(it is an ideal wire without resistance)as well as constraints defining the behavioral mode short-T oGround(fm==2).Recall that all variables in a RODON model are represented by sets of values.This is reflected by the type definitions in Fig.4.The basic type Interval has all attributes of the Modelica type Real,but its value attribute is a set of in-tervals.Accordingly,the value attribute of the basic type Discrete is a set of integer values. An important semantic difference to the equa-tion section in Modelica is that in our be-havior section,any variable can participate in any number of constraints.Our iterative simu-lation algorithm does not rely on the fact that the equation system contains exactly the same number of state variables and equations.It can handle over-or underdetermined equation sys-tems easily.3.2Modeling alternatives3.2.1if-clauses in RODONThe example above illustrated one way to model alternative behavior by means of a syntacti-cal element known from Modelica—the if-clause.However,there are some semantic dif-ferences between if-clauses in RODON and Modelica.In RODON,the clauseif(<condition>)<relation> means that when the problem solver takes this constraint from the agenda,it checksfirst the condition.Only if the condition is decidable and true,the relation is evaluated,and the con-sequent value changes are propagated as usual. This approach allows the use of many if-clauses in a model without slowing down the simulation process significantly.For set-valued variables,logical expressions have not merely two possible values,but three: true,false,or undecidable.A condition is de-cidable if it is either true or false for all combi-nations of values out of the variable’s value sets. For instance,consider the constraintif(2<x&x<5)<relation>If x has the value set[04],there are some elements of the set for which the condition is true,but there are other elements in the value set of x for which it is false.During the itera-tive propagation process,the value set of x may be further constricted so that at some moment in the propagation process,the condition will have a unique logical value.But at the present moment,the problem solver cannot know whichlogical value that will be.Note that for set-valued variables,there are some subtleties when defining correct seman-tics for conditions.Conditions have to be evalu-able monotonly,i.e.if a condition has been de-cided to be true or false once,it must not change this logical value during propagation.This is due to the fact that if a condition has once been true,the corresponding relation has been evalu-ated,and the resulting value changes have been propagated further.If later on the condition be-comes false,we would have to withdraw all val-ues which depend on the earlier evaluation of that relation.To keep track of all these depen-dencies requires a huge effort.Therefore,only monotonously evaluable condi-tions are allowed.That means that a condition like(x subset y),where x and y are in-terval variables,is not permissible,because it is true for x=[010]and y=[-1020],but during the iterative propagation process y may be constricted to y=[-102],which renders the condition undecidable.An overview of all permissible logical relations for set-valued vari-ables is shown in Fig.5.Interval x,y;Real a;constant Interval s;x==ax!=a x!=yx<=a x<=yx<a x<yx>=a x>=yx>a x>yFigure5:Permissible logical relations for value sets.Another topic is the negation of logical expres-sions,which have a slightly different mean-ing for sets than for real values.For instance, the negation of the condition(x==a)is not (x!=a)but(a x).In general,the relation x!=y has to be interpreted as x y==/0.3.2.2The or-clauseThere are situations where it is desirable to have another kind of alternative behavior.Consider the following definition of a piecewise linearx yf xconstraint MyQuadraticSplineInterval x,y;extends Spline(final degree=2,periodic=true,final values=0.5,1,1,1.5, 1.5,3); end MyQuadraticSpline;model UseSplineInterval a,b;behaviorMyQuadraticSpline(a,b)(periodic=false,boundary= 1.3); end UseSpline;Figure7:An example of a simple constraint class.value based on a continuous variable.Consider the following model of an electrical light bulb.model Bulb extends TwoPort;Discrete light(max=2); parameter Current pNom=20; parameter Voltage uNom=12.0; protectedResistance r;Power pc;constant Power pLow=[-0.10.1];constant Power pMedium=[-0.3-0.1][0.10.3];constant Power pHigh=[-2-0.3][0.32];behaviorr=uNom*uNom/pNom;pc=p.i*(p.u-n.u)/pNom;if(fm==0)Ohm(p.u,n.u,p.i,r); if(fm==1)light=0;if(fm==0)or p.i=0;light=0;pc=pLow;light=0;pc=pMedium;light=1;pc=pHigh;light=2;end Bulb;The variable light is an indicator for the mechanic whether the bulb is off(light=0), is dimmed(light=1)or bright(light=2). If by some reason the constraint net is un-derdetermined so that the consumed power of the bulb pc=[0.21],the mechanic gets the information light=0,1,i.e.the bulb is off or dimmed,which may be an impor-tant indication.An analogous definition by means of conditional constraints would result in light=0,1,2,i.e.the whole range of this variable.3.3Defining constraint classes Very much like function classes in Modelica, RODON allows the user to define constraint classes.This may be useful for constraints which are used very often,like Ohm’s law or Kirchhoff’s law in the electrical domain.But it is also convenient for constraints which are laborious to define,e.g.characteristic curves of engines which are given in table form rather than in closed form.As for the function classes in Modelica,constraint classes define an argu-ment list and provide type checking when the constraint class is used.In the example shown in Fig.7,the constraint class Spline is a basic constraint class pro-vided by the RODON modeling language.It has pre-defined attributes degree,peri-odic,boundary and values.There are some other basic constraint classes.Constraint classes may be parameterized by means of the usual modification mechanism.4ConclusionThe striking correspondence of the modeling philosophies in Modelica and RODON as well as the neat class model of Modelica are strong arguments in favour of Modelica as the future modeling language of RODON.But there are some additional requirements caused by our dif-ferent simulation algorithm and the diagnostic approach,namelybasic data type:interval setmultiple behavioral modesalternative behavior:disjunctionsalternative behavior:conditional con-straints,semantics of conditions for set-valued variablesconstraint classescoping with over-or underdetermined con-straint netssimulation by local constraint propagation A few of them can possibly be met by provid-ing special libraries.However,our experience shows that there are features which require an extension of the Modelica language,or the defi-nition of a separate dialect for behavior descrip-tion.References[AH74]G.Alefeld and J.Herzberger.Einf¨u hrung in die Intervallarith-metik.Bibliographisches InstitutAG,Z¨u rich,1974.[dKW87]J.de Kleer and B.Williams.Di-agnosing multiple faults.ArtificialIntelligence,32:1297–1307,1987. [dKW89]J.de Kleer and B.Williams.Di-agnosis with behavioral modes.InProceedings of the IJCAI’89,pages1324–1330,1989.[HHKR95]R.Hammer,M.Hocks,U.Kulisch,and D.Ratz.C++Toolbox for Ver-ified Computing.Springer,1995. [Hyv91] E.Hyv¨o nen.Constraint Reasoningwith Incomplete Knowledge.PhDthesis,Helsinki University,1991. [Mod99]Modelica Association.Modelica-Language Specification,December1999.[Rei87]R.Reiter.A theory of diagnosisfromfirst principles.Artificial In-telligence,32:57–95,1987. [Sei92]W.Seibold.Grundlage der Diag-nose technischer Systeme—sechsThesen.ist–Intelligente Software-Technologien,2(3),1992.[Sei97]W.Seibold.First time right fromlayout to repair.In Proceedingsof the30th ISATA Symposium,Flo-rence(Italy),pages483–492,June1997.。


缩写中文解释3C3个关键零件(缸体、缸盖、曲轴)4 VDP四阶段的汽车发展过程A/D/V分析/发展/验证AA审批体系ABS防抱死制动系统ACD实际完成日期AI人工智能AIAG汽车工业产业群ALBS装配线平衡系统AP提前采购API先进的产品信息APM汽车加工模型APQP先进的产品质量计划AR拨款申请ARP拨款申请过程ARR建筑必要性检查ASA船运最初协议ASB船运第二个协议ASI建筑研究启动ASP船运标准协议ASR建筑选择审查B&U土建公用BCC品牌特征中心BEC基础设计内容BI开始冒气泡B-I-S最佳分节段BIW白车身BOD设计清单BOM原料清单BOP过程清单CAD计算机辅助设计CAE计算机辅助工程(软件)CAFÉ公司的平均燃油经济CAM计算机辅助制造CAMIP持续汽车市场信息项目CARE用户接受度审查和评估CAS概念可改变的选择CDD成分数据图CGS公司图形系统CI提出概念CIT隔间融合为组CKD完全拆缷CMM坐标测量仪CMOP结构管理工作计划CPP关键途径CPP关键途径CR&W 控制/机器人技术和焊接CRIT中心新产品展示执行组CS合同签订CTS零件技术规格D/EC设计工程学会DAP设计分析过程DCAR设计中心工作申请DDP决策讨论步骤DES设计中心DFA装配设计DFM装配设计DLT设计领导技术DMA经销商市场协会DMG模具管理小组DOE试验设计DOL冲模业务排行DQV设计质量验证DRE设计发布工程师DSC决策支持中心DVM三维变化管理DVT动态汽车实验E/M进化的EAR工程行为要求ECD计划完成日期EGM工程组经理ELPO电极底漆ENG工程技术、工程学EOA停止加速EPC&L工程生产控制和后勤EPL工程零件清单ETSD对外的技术说明图EWO工程工作次序FA最终认可FE功能评估FEDR功能评估部署报告FFF自由形态制造FIN金融的FMEA失效形式及结果分析FTP文件传送协议GA总装GD&T几何尺寸及精度GM通用汽车GME通用汽车欧洲GMIO通用汽车国际运作GMIQ通用汽车初始质量GMPTG通用汽车动力组GP通用程序GSB全球战略部HVAC加热、通风及空调I/P仪表板IC初始租约ICD界面控制文件IE工业工程IEMA国际出口市场分析ILRS间接劳动报告系统IO国际业务IPC国际产品中心IPTV每千辆车的故障率IQS初始质量调查IR事故报告ISP综合计划ITP综合培训方法ITSD内部技术规范图IUVA国际统一车辆审核KCC关键控制特性KCDS关键特性标识系统KO Meeting启动会议KPC关键产品特性LLPRLOI意向书M&E机器设备MDD成熟的数据图MFD金属预制件区MFG制造过程MIC市场信息中心MIE制造综合工程师MKT营销MLBS物化劳动平衡系统MMSTS制造重要子系统技术说明书MNG制造工程MPG试验场MPI主程序索引MPL主零件列表MPS原料计划系统MRD物料需求日期MRD物料需求时间MSDSMSE制造系统工程MSS市场分割规范MTBF平均故障时间MTS生产技术规范MVSS汽车发动机安全标准NAMA北美市场分析NAO北美业务NAOC NAO货柜运输NC用数字控制NGMBP新一代基于数学的方法NOA授权书NSB北美业务部OED组织和员工发展P.O采购订单PA生产结果PAA产品行动授权PAC绩效评估委员会PACE项目评估和控制条件PAD产品装配文件PARTS零件准备跟踪系统PC问题信息PCL生产控制和支持PDC证券发展中心PDM产品资料管理PDS产品说明系统PDT产品发展小组PED产品工程部PEP产品评估程序PER人员PET项目执行小组PGM项目管理PIMREP事故方案跟踪和解决过程PLP生产启动程序PMI加工建模一体化PMM项目制造经理PMR产品制造能要求PMT产品车管理小组POMS产品指令管理小组POP采购点PPAP生产零部件批准程序PPAP生产件批准程序PPH百分之PPM百万分之PR绩效评估PR采购需求PR/R问题报告和解决PSA潜在供应商评估PSC部长职务策略委员会PTO第一次试验PUR采购PVM可设计的汽车模型PVT生产汽车发展QAP质量评估过程QBC质量体系构建关系QC质量特性QFD质量功能配置QRD质量、可靠性和耐久力QS质量体系QUA质量RC评估特许RCD必须完成日期RFQ报价请求RFQ报价要求书RONA净资产评估RPO正式产品选项RQA程序安排质量评定RT&TM严格跟踪和全程管理SDC战略决策中心SF造型冻结SIU电子求和结束SL系统规划SMBP理论同步过程SMT系统管理小组SOP生产启动,正式生产SOR要求陈述SOR要求说明书SOW工作说明SPE表面及原型工程SPO配件组织SPT专一任务小组SQC供方质量控制SQIP供应商质量改进程序SSF开始系统供应SSLT子系统领导组SSTS技术参数子系统STO二级试验SUW标准工作单位TA 技术评估TAG定时分析组TBD下决定TCS牵引控制系统TDMF文本数据管理设备TIMS试验事件管理系统TIR试验事件报告TLA 技术转让协议TMIE总的制造综合工程TOE总的物主体验TSM贸易研究方法TVDE整车外型尺寸工程师TVIE整车综合工程师TWS轮胎和车轮系统UAW班组UCL统一的标准表UDR未经核对的资料发布UPC统一零件分级VAPIR汽车发展综合评审小组VASTD汽车数据标准时间数据VCD汽车首席设计师VCE汽车总工程师VCRI确认交叉引用索引VDP汽车发展过程VDPP汽车发展生产过程VDR核实数据发布VDS汽车描述概要VDT汽车发展组VDTO汽车发展技术工作VEC汽车工程中心VIE汽车综合工程师VIS汽车信息系统VLE总装线主管,平台工程师VLM汽车创办经理VMRR汽车制造必要条件评审VOC顾客的意见VOD设计意见VSAS汽车综合、分析和仿真VSE汽车系统工程师VTS汽车技术说明书WBBA全球基准和商业分析WOT压制广泛开放WWP全球采购PC项目启动CA方案批准PA项目批准ER工程发布PPV产品和工艺验证PP预试生产P试生产EP工程样车Descriptions3 Critical Parts(Cylinder-block, Cylinder-head, Crankshaft) Four Phase Vehicle Development ProcessAnalysis/Development/ValidationApprove ArchitectureAnti-lock Braking SystemActual Completion DateArtificial IntelligenceAutomotive Industry Action GroupAssembly Line Balance SystemAdvanced PurchasingAdvanced Product InformationAutomotive Process ModelAdvanced Product Quality PlanningAppropriation RequestAppropriation Request ProcessArchitectural Requirements ReviewAgreement to Ship AlphaAgreement to Ship BetaArchitecture Studies InitiationAgreement to Ship PrototypeArchitecture Selection ReviewBuilding & UtilityBrand Character CenterBase Engineered ContentBubble Up InitiationBest-In-SegmentBody In WhiteBill of DesignBill of MaterialBill of ProcessComputer-Aided DesignComputer-Aided EngineeringCorporate Average Fuel EconomyComputer-Aided ManufacturingContinuous Automotive Marketing Information Program Customer Acceptance Review and EvaluationConcept Alternative SelectionComponent Datum DrawingsCorporate Graphic SystemConcept InitiationCompartment Integration TeamComplete KnockdownCoordinate Measuring MachinesConfiguration Management Operating PlanCorporate Product PorefolioCritical Path PlanControls/Robotics & WeldingCenter Rollout Implementation Team Contract SigningComponent Technical SpecificationDesign and Engineering CouncilDesign Analysis ProcessDesign Center Action RequestDecision Dialog ProcessDesign CenterDesign for AssemblyDesign For ManufacturabilityDesign leader TechnicalDealer Market AssociationDie Management GroupDesign Of ExperimentsDie Operation Line-UpDesign Quality VerificationDesign Release EngineerDecision Support CenterDimensional Variation ManagementDynamic Vehicle TestEvolutionary/MajorEngineering Action RequestEstimated Completion DateEngineering Group ManagerElectrode position PrimerEngineeringEnd of AccelerationEngineering Production Cntrol &Logistics Engineering Parts ListExterior Technical Specification Drawing Engineering Work OrderFinal ApprovalFunctional EvaluationFunctional Evaluation Disposition Report Free Form FabricationFinancialFailure Mode and Effects AnalysisFile Transfer ProtocolGeneral AssemblyGeometric Dimensioning & Tolerancing General MotorsGeneral Motors EuropeGeneral Motors International Operations General Motors Initial QualityGeneral Motors Powertrain GroupGeneral ProcedureGlobal Strategy BoardHeating, Ventilation ,and Air ConditioningInstrument PanelInitiate CharterInterface Control DocumentIndustrial EngineeringInternational Export Market AnalysisIndirect Labor Reporting SystemInternational OperationsInternational Product CenterIncidents Per Thousand VehiclesInitial Quality SurveyIncident ReportIntegrated Scheduling ProjectIntegrated Training ProcessInterior Technical Specification DrawingInternational Uniform Vehicle AuditKey Control CharacteristicsKey Characteristics Designation SystemKick-off MeetingKey product CharacteristicLing Lead P ReleaseLetter of IntentMachine & EquipmentMaster Datum DrawingsMetal Fabrication DivisionManufacturing OperationsMarketing Information CenterManufacturing Integration EngineerMarketingMaterial Labor Balance SystemManufacturing Major Subsystem Technical Specifications Manufacturing EngineeringMilford Proving GroundMaster Process IndexMaster Parts ListMaterial Planning SystemMaterial Required DateMaterial Required DateMaterial Safery Data SheetsManufacturing System EngineerMarket Segment SpecificationMean Time Between FailuresManufacturing Technical SpecificationMotor Vehicle Safety StandardsNorth American Market AnalysisNorth American OperationsNAO ContainerizationNumerically ControlledNext Generation Math-Based ProcessNotice of AuthorizationNAO Strategy BoardOrganization and Employee DevelopmentPurchasing OrderProduction AchievementProduction Action AuthorizationPerformance Assessment CommitteeProgram Assessment and Control EnvironmentProduct Assembly DocumentPart Readiness Tracking SystemProblem CommunicationProduction Control and LogisticsPortfolio Development CenterProduct Data ManagementProduct Description SystemProduct Development TeamProduction Engineering DepartmentProduct Evaluation ProgramPersonnelProgram Execution TeamProgram ManagementProject Incident Monitoring and Resolution Process Production Launch ProcessProcess Modeling IntegrationProgram Manufacturing ManagerProduct Manufacturability RequirementsProduct Management TeamProduction Order Management SystemPoint of PurchaseProduction Part Approval ProcessProduction Parts Approval ProcessProblems Per HundredProblems Per MillionPerformance ReviewPurchase RequirementProblem Reporting and ResolutionPotential Supplier AssessmentPortfolio Strategy CouncilPrimary TryoutPurchasingProgrammable Vehicle ModelProduction Vehicle DevelopmentQuality Assessment ProcessQuality Build ConcernQuality CharacteristicQuality Function DeploymentQuality, Reliability,andDurabilityQuality SystemQualityReview CharterRequired Completion DateRequest For QuotationRequirement for QuotationReturn on Net AssetsRegular Production OptionRouting Quality AssessmentRigorous Tracking and Throughout Managment Strategic Decision CenterStyling FreezeSumming It All UpSystem LayoutsSynchronous Math-Based ProcessSystems Management TeamStart of ProductionStatement of RequirementsStatement of RequirementsStatement of WorkSurface and Prototype EngineeringService Parts OperationsSingle Point TeamStatistical Quality ControlSupplier Quality Improvement ProcessStart of System FillSubsystem Leadership TeamSubsystem Technical Specification Secondary TryoutStandard Unit of WorkTechnology AssessmentTiming Analysis GroupTo Be DeterminedTraction Control SystemText Data Management FacilityTest Incident Management SystemTest Incident ReportTechnology License AgreementTotal Manufacturing Integration Engineer Total Ownership ExperienceTrade Study MethodologyTotal Vehicle Dimensional EngineerTotal Vehicle Integration EngineerTire and Wheel SystemUnited Auto WorkersUniform Criteria ListUnverified Data ReleaseUniform Parts ClassificationVehicle & Progress Integration Review TeamVehicle Assembly Standard Time DataVehicle Chief DesignerVehicle Chief EngineerValidation Cross-Reference IndexVehicle Development ProcessVehicle Development Production Process Verified Data ReleaseVehicle Description SummaryVehicle Development TeamVehicle Development Technical Operations Vehicle Engineering CenterVehicle Integration EngineerVehicle Information SystemVehicle Line ExecutiveVehicle Launch ManagerVehicle and Manufacturing Requirements Review Voice of CustomerVoice of DesignVehicle Synthesis,Analysis,and Simulation Vehicle System EngineerVehicle Technical SpecificationWorldwide Benchmarking and Business Analysis Wide Open ThrottleWorldwide PurchasingProgram CommencementConcept ApprovalPrograme ApprovalEngineering ReleaseProduct & Process ValidationPre-PilotPilot。

附录Ⅱ工具箱数学词汇英汉对照表Ⅱ.1 概率论与数理统计词汇英汉对照表Aabsolute value 绝对值accept 接受acceptable region 接受域additivity 可加性adjusted 调整的alternative hypothesis 对立假设analysis 分析analysis of covariance 协方差分析analysis of variance 方差分析arithmetic mean 算术平均值association 相关性assumption 假设assumption checking 假设检验availability 有效度average 均值Bbalanced 平衡的band 带宽bar chart 条形图beta-distribution 贝塔分布between groups 组间的bias 偏倚binomial distribution 二项分布binomial test 二项检验Ccalculate 计算case 个案category 类别center of gravity 重心central tendency 中心趋势chi-square distribution 卡方分布chi-square test 卡方检验classify 分类cluster analysis 聚类分析coefficient 系数coefficient of correlation 相关系数collinearity 共线性column 列compare 比较comparison 对照components 构成,分量compound 复合的confidence interval 置信区间consistency 一致性constant 常数continuous variable 连续变量control charts 控制图correlation 相关covariance 协方差covariance matrix 协方差矩阵critical point 临界点critical value 临界值crosstab 列联表cubic 三次的,立方的cubic term 三次项cumulative distribution function 累加分布函数curve estimation 曲线估计Ddata 数据default 默认的definition 定义deleted residual 剔除残差density function 密度函数dependent variable 因变量description 描述附录II 工具箱数学词汇英汉对照表·535·design of experiment 试验设计deviations 差异df.(degree of freedom) 自由度diagnostic 诊断dimension 维discrete variable 离散变量discriminant function 判别函数discriminatory analysis 判别分析distance 距离distribution 分布D-optimal design D-优化设计Eeaqual 相等effects of interaction 交互效应efficiency 有效性eigenvalue 特征值equal size 等含量equation 方程error 误差estimate 估计estimation of parameters 参数估计estimations 估计量evaluate 衡量exact value 精确值expectation 期望expected value 期望值exponential 指数的exponential distributon 指数分布extreme value 极值Ffactor 因素,因子factor analysis 因子分析factor score 因子得分factorial designs 析因设计factorial experiment 析因试验fit 拟合fitted line 拟合线fitted value 拟合值fixed model 固定模型fixed variable 固定变量fractional factorial design 部分析因设计frequency 频数F-test F检验full factorial design 完全析因设计function 函数Ggamma distribution 伽玛分布geometric mean 几何均值group 组Hharmomic mean 调和均值heterogeneity 不齐性histogram 直方图homogeneity 齐性homogeneity of variance 方差齐性hypothesis 假设hypothesis test 假设检验Iindependence 独立independent variable 自变量independent-samples 独立样本index 指数index of correlation 相关指数interaction 交互作用interclass correlation 组内相关interval estimate 区间估计intraclass correlation 组间相关inverse 倒数的iterate 迭代Kkernal 核Kolmogorov-Smirnov test柯尔莫哥洛夫-斯米诺夫检验kurtosis 峰度MATLAB 6.1与工程数学应用指南(下册)·536·Llarge sample problem 大样本问题layer 层least-significant difference 最小显著差数least-square estimation 最小二乘估计least-square method 最小二乘法level 水平level of significance 显著性水平leverage value 中心化杠杆值life 寿命life test 寿命试验likelihood function 似然函数likelihood ratio test 似然比检验linear 线性的linear estimator 线性估计linear model 线性模型linear regression 线性回归linear relation 线性关系linear term 线性项logarithmic 对数的logarithms 对数logistic 逻辑的lost function 损失函数Mmain effect 主效应matrix 矩阵maximum 最大值maximum likelihood estimation 极大似然估计mean squared deviation(MSD) 均方差mean sum of square 均方和measure 衡量media 中位数M-estimator M估计minimum 最小值missing values 缺失值mixed model 混合模型mode 众数model 模型Monte Carle method 蒙特卡罗法moving average 移动平均值multicollinearity 多元共线性multiple comparison 多重比较multiple correlation 多重相关multiple correlation coefficient 复相关系数multiple correlation coefficient 多元相关系数multiple regression analysis 多元回归分析multiple regression equation 多元回归方程multiple response 多响应multivariate analysis 多元分析Nnegative relationship 负相关nonadditively 不可加性nonlinear 非线性nonlinear regression 非线性回归noparametric tests 非参数检验normal distribution 正态分布null hypothesis 零假设number of cases 个案数Oone-sample 单样本one-tailed test 单侧检验one-way ANOVA 单向方差分析one-way classification 单向分类optimal 优化的optimum allocation 最优配制order 排序order statistics 次序统计量origin 原点orthogonal 正交的outliers 异常值Ppaired observations 成对观测数据paired-sample 成对样本parameter 参数parameter estimation 参数估计附录II 工具箱数学词汇英汉对照表·537·partial correlation 偏相关partial correlation coefficient 偏相关系数partial regression coefficient 偏回归系数percent 百分数percentiles 百分位数pie chart 饼图point estimate 点估计poisson distribution 泊松分布polynomial curve 多项式曲线polynomial regression 多项式回归polynomials 多项式positive relationship 正相关power 幂P-P plot P-P概率图predict 预测predicted value 预测值prediction intervals 预测区间principal component analysis 主成分分析proability 概率probability density function 概率密度函数probit analysis 概率分析proportion 比例Qqadratic 二次的Q-Q plot Q-Q概率图quadratic term 二次项quality control 质量控制quantitative 数量的,度量的quartiles 四分位数Rrandom 随机的random number 随机数random number 随机数random sampling 随机取样random seed 随机数种子random variable 随机变量randomization 随机化range 极差rank 秩rank correlation 秩相关rank statistic 秩统计量regression analysis 回归分析regression coefficient 回归系数regression line 回归线reject 拒绝rejection region 拒绝域relationship 关系reliability 可靠性repeated 重复的report 报告,报表residual 残差residual sum of squares 剩余平方和response 响应risk function 风险函数robustness 稳健性root mean square 标准差row 行run 游程run test 游程检验Ssample 样本sample size 样本容量sample space 样本空间sampling 取样sampling inspection 抽样检验scatter chart 散点图S-curve S形曲线separately 单独地sets 集合sign test 符号检验significance 显著性significance level 显著性水平significance testing 显著性检验significant 显著的,有效的significant digits 有效数字skewed distribution 偏态分布skewness 偏度MATLAB 6.1与工程数学应用指南(下册)·538·small sample problem 小样本问题smooth 平滑sort 排序soruces of variation 方差来源space 空间spread 扩展square 平方standard deviation 标准离差standard error of mean 均值的标准误差standardization 标准化standardize 标准化statistic 统计量statistical quality control 统计质量控制std. residual 标准残差stepwise regression analysis 逐步回归stimulus 刺激strong assumption 强假设stud. deleted residual 学生化剔除残差stud. residual 学生化残差subsamples 次级样本sufficient statistic 充分统计量sum 和sum of squares 平方和summary 概括,综述Ttable 表t-distribution t分布test 检验test criterion 检验判据test for linearity 线性检验test of goodness of fit 拟合优度检验test of homogeneity 齐性检验test of independence 独立性检验test rules 检验法则test statistics 检验统计量testing function 检验函数time series 时间序列tolerance limits 容许限total 总共,和transformation 转换treatment 处理trimmed mean 截尾均值true value 真值t-test t检验two-tailed test 双侧检验Uunbalanced 不平衡的unbiased estimation 无偏估计unbiasedness 无偏性uniform distribution 均匀分布Vvalue of estimator 估计值variable 变量variance 方差variance components 方差分量variance ratio 方差比various 不同的vector 向量Wweight 加权,权重weighted average 加权平均值within groups 组内的ZZ score Z分数附录II 工具箱数学词汇英汉对照表·539·Ⅱ.2 最优化方法词汇英汉对照表Aactive constraint 活动约束active set method 活动集法analytic gradient 解析梯度approximate 近似arbitrary 强制性的argument 变量attainment factor 达到因子Bbandwidth 带宽be equivalent to 等价于best-fit 最佳拟合bound 边界Ccoefficient 系数complex-value 复数值component 分量constant 常数constrained 有约束的constraint 约束constraint function 约束函数continuous 连续的converge 收敛cubic polynomial interpolation method三次多项式插值法curve-fitting 曲线拟合Ddata-fitting 数据拟合default 默认的,默认的define 定义diagonal 对角的direct search method 直接搜索法direction of search 搜索方向discontinuous 不连续Eeigenvalue 特征值empty matrix 空矩阵equality 等式exceeded 溢出的Ffeasible 可行的feasible solution 可行解finite-difference 有限差分first-order 一阶GGauss-Newton method 高斯-牛顿法goal attainment problem 目标达到问题gradient 梯度gradient method 梯度法Hhandle 句柄Hessian matrix 海色矩阵Iindependent variables 独立变量inequality 不等式infeasibility 不可行性infeasible 不可行的initial feasible solution 初始可行解initialize 初始化inverse 逆invoke 激活iteration 迭代iteration 迭代MATLAB 6.1与工程数学应用指南(下册)·540·JJacobian 雅可比矩阵LLagrange multiplier 拉格朗日乘子large-scale 大型的least square 最小二乘least squares sense 最小二乘意义上的Levenberg-Marquardt method列文伯格-马夸尔特法line search 一维搜索linear 线性的linear equality constraints 线性等式约束linear programming problem 线性规划问题local solution 局部解Mmedium-scale 中型的minimize 最小化mixed quadratic and cubic polynomial interpolation and extrapolation method混合二次、三次多项式内插、外插法multiobjective 多目标的Nnonlinear 非线性的norm 范数Oobjective function 目标函数observed data 测量数据optimization routine 优化过程optimize 优化optimizer 求解器over-determined system 超定系统Pparameter 参数partial derivatives 偏导数polynomial interpolation method多项式插值法Qquadratic 二次的quadratic interpolation method 二次内插法quadratic programming 二次规划Rreal-value 实数值residuals 残差robust 稳健的robustness 稳健性,鲁棒性Sscalar 标量semi-infinitely problem 半无限问题Sequential Quadratic Programming method序列二次规划法simplex search method 单纯形法solution 解sparse matrix 稀疏矩阵sparsity pattern 稀疏模式sparsity structure 稀疏结构starting point 初始点step length 步长subspace trust region method 子空间置信域法sum-of-squares 平方和symmetric matrix 对称矩阵Ttermination message 终止信息termination tolerance 终止容限the exit condition 退出条件the method of steepest descent 最速下降法transpose 转置Uunconstrained 无约束的under-determined system 负定系统附录II 工具箱数学词汇英汉对照表·541·Vvariable 变量vector 矢量Wweighting matrix 加权矩阵Ⅱ.3 样条词汇英汉对照表Aapproximation 逼近array 数组a spline in b-form/b-spline b样条a spline of polynomial piece /ppform spline分段多项式样条Bbivariate spline function 二元样条函数break/breaks 断点Ccoefficient/coefficients 系数cubic interpolation 三次插值/三次内插cubic polynomial 三次多项式cubic smoothing spline 三次平滑样条cubic spline 三次样条cubic spline interpolation三次样条插值/三次样条内插curve 曲线Ddegree of freedom 自由度dimension 维数Eend conditions 约束条件Iinput argument 输入参数interpolation 插值/内插interval 取值区间Kknot/knots 节点Lleast-squares approximation 最小二乘拟合Mmultiplicity 重次multivariate function 多元函数Ooptional argument 可选参数order 阶次output argument 输出参数Ppoint/points 数据点Rrational spline 有理样条rounding error 舍入误差(相对误差)Sscalar 标量sequence 数列(数组)spline 样条spline approximation 样条逼近/样条拟合spline function 样条函数spline curve 样条曲线spline interpolation 样条插值/样条内插spline surface 样条曲面smoothing spline 平滑样条MATLAB 6.1与工程数学应用指南(下册)·542·T tolerance 允许精度U univariate function 一元函数V vector 向量W weight/weights 权重Ⅱ.4 偏微分方程数值解词汇英汉对照表Aabsolute error 绝对误差absolute tolerance 绝对容限adaptive mesh 适应性网格Bboundary condition 边界条件Ccontour plot 等值线图converge 收敛coordinate 坐标系Ddecomposed 分解的decomposed geometry matrix 分解几何矩阵diagonal matrix 对角矩阵Dirichlet boundary conditionsDirichlet边界条件Eeigenvalue 特征值elliptic 椭圆形的error estimate 误差估计exact solution 精确解Ggeneralized Neumann boundary condition推广的Neumann边界条件geometry 几何形状geometry description matrix 几何描述矩阵geometry matrix 几何矩阵graphical user interface(GUI)图形用户界面Hhyperbolic 双曲线的Iinitial mesh 初始网格Jjiggle 微调LLagrange multipliers 拉格朗日乘子Laplace equation 拉普拉斯方程linear interpolation 线性插值loop 循环Mmachine precision 机器精度mixed boundary condition 混合边界条件NNeuman boundary condition Neuman边界条件node point 节点nonlinear solver 非线性求解器normal vector 法向量附录II 工具箱数学词汇英汉对照表·543·PParabolic 抛物线型的partial differential equation 偏微分方程plane strain 平面应变plane stress 平面应力Poisson's equation 泊松方程polygon 多边形positive definite 正定Qquality 质量Rrefined triangular mesh 加密的三角形网格relative tolerance 相对容限relative tolerance 相对容限residual 残差residual norm 残差范数Ssingular 奇异的sparce matrix 稀疏矩阵stiffness matrix 刚度矩阵subregion 子域Ttriangular mesh 三角形网格Uundetermined 未定的uniform refinement 均匀加密uniform triangle net 均匀三角形网络Wwave equation 波动方程。
workbench中topology optimization详解Topology optimization is a technique used in engineering design to determine the optimal distribution of material within a given design space in order to meet specific performance objectives. This technique is commonly used in various industries, including aerospace, automotive, and manufacturing.In Workbench, topology optimization can be performed using the Topology Optimization tool. This tool is part of the DesignModeler module and allows engineers to define design criteria and constraints, run optimization simulations, and analyze the results.Here is a step-by-step guide to performing topology optimization in Workbench:1. Create a geometric model: Start by creating a CAD model of the part or structure you want to optimize. This can be done using the DesignModeler module in Workbench. Import or create the geometry and define the necessary details such as dimensions, features, and boundary conditions.2. Define design criteria: Next, you need to define the design criteria or performance objectives for the optimization. This includes specifying the stiffness, weight, or other characteristics that you want to achieve. You can also define constraints such as minimum and maximum volume fractions, or allowable displacement limits.3. Assign material properties: Specify the material properties forthe model. This includes properties such as Young's modulus, Poisson's ratio, and density. You can either choose from a predefined material library or enter custom values.4. Set up the optimization study: In the Workbench Project Schematic, add the Topology Optimization tool to the project and connect it to other required modules such as Meshing and Analysis. Define the optimization objectives, constraints, and study parameters such as maximum iterations and convergence criteria.5. Generate mesh: Generate a finite element mesh for the model using the Meshing tool. Optimal mesh density is crucial for accurate results.6. Run the optimization simulation: Once the mesh is generated, start the optimization simulation. The Topology Optimization tool will iteratively modify the material distribution within the design space to optimize the performance objectives while satisfying the defined constraints. The simulation may take several iterations to converge, depending on the complexity of the problem.7. Analyze the results: Once the simulation is complete, analyze the optimized results. Workbench provides various visualization tools to observe the distribution of material within the optimized design, as well as other metrics such as displacement, stress, and strain. You can evaluate whether the performance objectives and constraints are met and make any necessary refinements to the design.8. Refine and finalize the design: Based on the optimization results,refine the design if needed. This may involve modifying the geometry, adjusting the optimization criteria, or rerunning the simulation with different settings. Iterate this process until you achieve the desired design performance.Overall, topology optimization in Workbench allows engineers to explore a wide range of design possibilities and discover optimized solutions with improved performance and reduced weight. It helps optimize the use of material, reduce development time, and improve the overall efficiency of the design process.。
基于Optistruct脱模约束函数的悬架控制臂拓扑设计潘尚君;苏小平;陈亚林【摘要】以麦弗逊悬架下控制臂为研究对象,将Adams/car提供的悬架参数为基础在CATIA中建立控制臂原始几何模型并在Hyperworks中建立有限元模型.进行了转向及制动工况中控制臂的受载分析,并在此基础上进行了以最小加权应变能为目标基于脱模方向约束的拓扑优化.根据对优化结果的解读对控制臂进行了重新建模,并进行了模态分析验证.结果表明,该结构能有效地减少控制臂材料,保证刚度,并避免了悬架系统的共振,为控制臂设计提供了一套新的系统化设计方法,具有一定工程指导意义.【期刊名称】《科学技术与工程》【年(卷),期】2014(014)032【总页数】5页(P94-98)【关键词】麦弗逊悬架;下控制臂;拓扑优化;脱模方向约束【作者】潘尚君;苏小平;陈亚林【作者单位】南京工业大学机械与动力工程学院,南京211816;南京工业大学机械与动力工程学院,南京211816;南京工业大学机械与动力工程学院,南京211816【正文语种】中文【中图分类】U463.33麦弗逊悬架是大多数中小型轿车前悬架的首选,其下控制臂则是负责导向及传力的主要部件,同时由于现代车辆的高速化发展,乘车舒适性要求大大提高,而根据车辆平顺性特性的研究,影响车辆振动特性的一大因素即是非簧载质量。
作为非簧载质量的主要承担者之一,下控制臂的轻量化设计非常紧要。
传统的设计方法主要基于物理样机结合经验公式来开展,已经很难适应日益严格的设计要求。
目前解决这一问题的主要途径是采用拓扑优化技术,寻求材料的最优分布,设计出轻量化高强度的产品。
文献[1]研究了以悬架静态柔度和振动低阶频率为目标的控制臂拓扑结构优化,并且给出了优化后控制臂的结构;文献[2—4]均对悬架控制臂进行了结构拓扑优化,给出了优化后的控制臂结构,并对优化后的控制臂进行了强度、刚度、模态分析,在各自关心的领域阐明了优化结构的合理性。
ߜ1⁄4DIN SizeߜDual Loop Control ߜPID, Proportional or On/Off ControlߜField Selectable Relay or dc Pulse OutputsߜTimer, 2 SegmentRamp/ Soak and Idle/Run FunctionsߜAutotuning StandardߜOptional RS-232, RS-422, RS-485 Communications ߜ102 mm (4")Mounting DepthߜAluminum Housing ApplicationsߜPlatens and PressesߜFurnaces and OvensߜTemperature ControlPanelsߜExtrudersߜFood ProcessingTimer and EventInput FeaturesIncorporated into the CN3240’sprogrammed control features is abasic timer, configurable inhour/minute increments. The CN3240timer can be used to enable theprocess at a preset time, or disablethe process after a specified amountof time, avoiding the additionalexpense, space requirements andinstallation costs of a separate timer.Most importantly, the CN3240 timerassures you of total compatibility withthe CN3240 process controllerfunctions, requiring only initial setupand minimal operator attention.SpecificationsControl Modes:On/Off,Proportional, and PID-proportionalwith automatic reset (integral)and/or rate (derivative)Control Adjustments:Allparameters independentlyadjustable for each loopModel CN3240$625Basic UnitThe OMEGA®CN3240 Seriestemperature controllerspack the sophisticationand flexibility of twomicroprocessor-basedcontrollers into onecompact 1⁄4DIN package.Two Flexible LoopsEach of the two independent controlloops can be field programmed:Loop #1Loop #2PID T emp. Control PID T emp. ControlPID T emp. Control Overtemp. ControlAlarm/Overtemp Alarm/OvertempTwo sensor inputs (one per loop)can be field programmed as J or Kthermocouple or RTD. The controloutputs are 8 amp relays, fieldchangeable to dc pulse. The relayoutput can be used to directly drivesmall heater loads. In addition, athird 10 Amp relay can be used foralarm control.Dual Input TemperatureControllersWith Timer,Ramp/Soakand Idle/Run FunctionsGKQSS-14U-12thermocoupleprobe, $33,sold separately.See page A-54.P-73Shown smaller than actual size(Specify Model Number)Model Number Price Descriptionyour sales representative for full details when placing an order. OMEGACARE SM covers parts,labor, and equivalent loaners. Comes with complete operator’s manual.Ordering Example: CN3240-4, dual loop temperature controller with digital communications,$625 + 105 = $730. OCW-3 OMEGACARE SM extends standard 1-year warranty toa total of 4 years ($182), $730 + 182 = $912.Pt-129 to 538°C (-200 to 1000°F)±0.10% + 1 digitCN3240 shownwith open doorDual Set Points:Instrument sensorrange, °F or °C, with Ramp/Soakand timer capabilitiesSet Point Limits:Instrumentsensor rangeDeadband:1 to 99°F/1 to 55°CProportional Band:0.1 to 999.9%Automatic Reset:0.00 to 99.99repeats/minuteRate:0 to 500 secondsOutput Cycle Time:0.1 to 60.0 secondsOutput Limit:0 to 100 %Control Outputs:One individualoutput per channelRelay:N.O. contact rated 8 A at120/250 Vac or 5 A at 30 Vdcdc Pulse:Transistor output of20 Vdc at 40 mA, jumper selectableAuxiliary Alarm Output:Non-Latching, normally-energizedor normally de-energized,power-up inhibit featureSetpoint:Sensor spanModes:High or Low AlarmInput Sensor:Channel #1 sensor,channel #2 sensor or both.Relay:N.O. contact rated 10 A at120/250 Vac or 10 A at 30 VdcAuxiliary Event Input:One digitalinput accepts momentary orsustained contact closure, requiringminimum 100 millisecondclosure/openingTimers:00.00 to 99.99 hours,minutes with a “continuous” settingfor soak intervals000.0 to 999.9 Hrs., 0000 to 9999 Hrs.Input Update Rate:600 msec/updateReadout Stability:±1.0°F maximum for every±10°F change ambientInstrument Power:120/230 Vac,50/60 Hz, nominal powerconsumption 10 VA power failuredetection circuitry, watchdog timersOperating environment:0 to 55°C (30 to 130°F) ambienttemperature with relative humidityless than 95%, non-condensingDimensions:Overall:96 x 96 x 121 mm(3.78 x 3.78 x 4.75")Depth Behind Panel:102 mm (4.0")Front Panel Projection:19 mm (0.75")Panel Cutout:92 x 92 mm (3.6 x 3.6")Weight:1.1 kg (2.5 lb)Influence of Line Voltage Variation:±1°F maximum change in readout for±10% nominal line voltageNoise RejectionCommon Mode:Less than ±1°C(2°F) with 230 Vac, 60 Hz appliedfrom sensor input to instrumentcase (with digital filter enabled)Series Mode:Less than ±1°C (2°F)with 100 mV peak to peak. 60Hzseries mode noiseRadio-Frequency Interference(RFI):Typically less than 0.5% ofsensor span at 1 m (3.1') from atransmitter (4 W at 464 MHz)Fieldselectable°F or °CTwo-segmentramp/soakprogramAVAILABLE FORFAST DELIVERY!Open Sensor and Out-of-RangeConditions:Control output adjustablefrom 0 to 100%Digital Communications OptionRS-232-C:Single-drop, IsolatedRS-422, RS-485:Multi-drop, IsolatedCASS-18G-12-DUAL, Dual Element ThermocoupleProbe, $57.50. See page A-76.Female connectorincluded with probe.CANADA www.omega.ca Laval(Quebec) 1-800-TC-OMEGA UNITED KINGDOM www. Manchester, England0800-488-488GERMANY www.omega.deDeckenpfronn, Germany************FRANCE www.omega.frGuyancourt, France088-466-342BENELUX www.omega.nl Amstelveen, NL 0800-099-33-44UNITED STATES 1-800-TC-OMEGA Stamford, CT.CZECH REPUBLIC www.omegaeng.cz Karviná, Czech Republic596-311-899TemperatureCalibrators, Connectors, General Test and MeasurementInstruments, Glass Bulb Thermometers, Handheld Instruments for Temperature Measurement, Ice Point References,Indicating Labels, Crayons, Cements and Lacquers, Infrared Temperature Measurement Instruments, Recorders Relative Humidity Measurement Instruments, RTD Probes, Elements and Assemblies, Temperature & Process Meters, Timers and Counters, Temperature and Process Controllers and Power Switching Devices, Thermistor Elements, Probes andAssemblies,Thermocouples Thermowells and Head and Well Assemblies, Transmitters, WirePressure, Strain and ForceDisplacement Transducers, Dynamic Measurement Force Sensors, Instrumentation for Pressure and Strain Measurements, Load Cells, Pressure Gauges, PressureReference Section, Pressure Switches, Pressure Transducers, Proximity Transducers, Regulators,Strain Gages, Torque Transducers, ValvespH and ConductivityConductivity Instrumentation, Dissolved OxygenInstrumentation, Environmental Instrumentation, pH Electrodes and Instruments, Water and Soil Analysis InstrumentationHeatersBand Heaters, Cartridge Heaters, Circulation Heaters, Comfort Heaters, Controllers, Meters and SwitchingDevices, Flexible Heaters, General Test and Measurement Instruments, Heater Hook-up Wire, Heating Cable Systems, Immersion Heaters, Process Air and Duct, Heaters, Radiant Heaters, Strip Heaters, Tubular HeatersFlow and LevelAir Velocity Indicators, Doppler Flowmeters, LevelMeasurement, Magnetic Flowmeters, Mass Flowmeters,Pitot Tubes, Pumps, Rotameters, Turbine and Paddle Wheel Flowmeters, Ultrasonic Flowmeters, Valves, Variable Area Flowmeters, Vortex Shedding FlowmetersData AcquisitionAuto-Dialers and Alarm Monitoring Systems, Communication Products and Converters, Data Acquisition and Analysis Software, Data LoggersPlug-in Cards, Signal Conditioners, USB, RS232, RS485 and Parallel Port Data Acquisition Systems, Wireless Transmitters and Receivers。
Validating Mechanical ModelsChecking Model Validity Simulink can simulate a SimMechanics model only if it is valid. A model is valid if it satisfies the following rules:Each machine in the model contains at least one Ground, and exactly one Ground in each machine is connected to a MachineEnvironment block. Each submachine connected to a full machine by a Shared Environment block must have at least one Ground.See Representing Machines with Models in this chapter.Every machine in the model is topologically valid. See Checking Model Topology .The model contains at least one degree of freedom. See Counting Model Degrees of Freedom .Any machine in the model interfaced to Simscape mechanical circuits satisfies both SimMechanics and Simscape modeling rules. See Combining One-and Three-Dimensional Mechanical Elements in this chapter.Checking Model TopologyTo avoid simulation failures, you must ensure that the topology of your block diagram is valid. A block diagram is topologically valid if each machine that it contains is valid. A machine is valid if its spanning tree is valid. Thus to determine if your model is valid, first determine the spanning tree of each machine that it contains and then the validity of each resulting tree.Machine Topology and SubsystemsWhen examining your model's topology, be sure to inspect all its subsystems, including masked subsystems, down to the bottom of the model's subsystem hierarchy.Determining a Machine's Spanning TreeYou can think of a machine as a graph with elements (bodies) and connectors (joints, constraints, and drivers). A spanning tree is a reduced graph with bodies connected only by joints and all closed loops cut once.To determine the spanning tree of a machine, remove all blocks from the machine except Body and Joint blocks and open every closed loop in the resulting reduced machine. To open a closed loop, follow the loop-cutting rules in Cutting Machine Diagram Loops .For example, here is a machine with two closed loops.Cutting the top loop at the Disassembled Prismatic and removing the Parallel Constraint block (thus simultaneously cutting the bottom loop) yields the machine's spanning tree, as shown here.On this page…Checking Model ValidityChecking Model TopologyCounting Model Degrees of FreedomDetermining the Validity of a Spanning TreeTo be valid, a spanning tree must meet these requirements:The spanning tree must have at least one Ground block to serve as a reference to World.Every Joint block must be connected to exactly two Body blocks.Every non-Ground Body block must have a unique path to a Ground block. (This need not be true of the whole machine.) This ensures that, while each body moves via joints relative to other bodies, the simulation can resolve all bodies' motions relative to one another into absolute motions with respect to World.Every non-Ground Body block at an end of a chain of Bodies must have nonzero inertia (mass or inertial moment) associated with all joint primitives that can move. Each translational DoF must carry a nonzero mass, and each rotational DoF a nonzero inertial moment. This prevents infinite accelerations when forces and torques are applied.Examples of Invalid Machine TopologiesHere are some examples of invalid topologies:This one-loop machine lacks a Ground block.This open machine has a dangling Joint block.Another open machine features a zero-mass body at one end of a chain of bodies.The last two invalid examples are dynamically (but not topologically) equivalent, because a zero-mass body is dynamically no body at all.Counting Model Degrees of FreedomIdentifying and counting the independent degrees of freedom (DoFs) of a machine are important for trimming and linearizing SimMechanics models (see Trimming Mechanical Models and Linearizing Mechanical Models in the Analyzing Motion chapter) and for correcting simulation errors (see Troubleshooting Simulation Errors in the Running Mechanical Models chapter).Your SimMechanics model must have at least one DoF to be valid. A free physical body has six DoFs: three translational and three rotational. But in a machine, connections between bodies by joints, constraints, and drivers, and motion actuation by joint and body actuators reduce the machine's independent DoFs to a smaller number. You also reduce a body's DoFs if you confine the machine's motion to one or two spatial dimensions.A SimMechanics Body block has no DoFs. Connecting Joints to a Body adds DoFs to the machine. The joint primitives represent the Body's DoFs relative to other connected Bodies or Grounds. Connecting Constraint and Driver blocks to Bodies or motion-actuating joint primitives in Joints removes DoFs from the machine. A locked Joint Stiction Actuator also removes a DoF.Degrees of Freedom in SubsystemsWhen you examine your model to identify and count its DoFs, be sure to open and inspect all its subsystems, including masked subsystems, to the bottom of the model's subsystem hierarchy.Finding Independent Degrees of FreedomHere is the formula for determining the number of independent DoFs your model has:# of independent DoFs = # of body DoFs + # of primitive DoFs -# of motion restrictionsThe following three steps define each term on the right side:1.Calculate the number of body DoFs from the number of Body and Joint blocks in your model:# of body DoFs = 6 * (number of Bodies - number of Joints)If you have confined the machine to move in only two dimensions, replace the 6 by 3. If you have confined the machine to move in only one dimension, replace the 6 by 1.2.Calculate the number of primitive DoFs by adding up the primitive DoFs from the Joint dialog boxes:Count one for each prismatic (P) or revolute (R) primitive.Count three for each spherical (S) primitive.Count zero for each weld (W) primitive.Do not count a primitive DoF that is motion-actuated by a Joint Actuator.3.Calculate the number of motion restrictions by adding up the motion restrictions of each Constraint and Driver block andfrom each locked Joint Stiction Actuator. Different blocks from the Constraints & Drivers library impose different numbers of motion restrictions. Stiction actuators apply to individual joint primitives.Be sure not to count redundant motion restrictions. These are restrictions that forbid the motion of joint primitives that couldnot move anyway even if the constraint were removed, because of how the joints are configured.Example: A body is connected to a ground by a single prismatic. You place a constraint on the body that prevents it from moving perpendicularly to the prismatic axis. The body could not move in that direction even if you removed the constraint.So the constraint is redundant, and you would not count it as a motion restriction.The Role of Joint Stiction ActuatorsA Joint Stiction Actuator can remove or restore a DoF during a simulation. It is the only block that can change the number of independent DoFs after you start simulating. You must count an additional motion restriction during the period when a stiction-actuated primitive is locked. The primitive counts as another DoF if it is unlocked.DoF Example: Double PendulumThe mech_dpen model from the Demos library represents planar double pendulum motion actuated by a Joint Actuator.The double pendulum has two rigid bodies, such as two rods, confined to move in two dimensions. Ignoring the Joint Actuator temporarily, there are two bodies, two joints, and two revolute primitives, and thus 3 * (2 - 2) + 2 = 2 independent DoFs. There are many ways to represent these two DoFs, but the two revolute primitives are the simplest way.Including the Joint Actuator in the DoF count removes the revolute primitive in the Revolute block as an independent DoF. So this model actually only has one independent DoF, the revolute primitive in the Revolute1 block.DoF Example: Four Bar MechanismThe Modeling and Simulating a Closed-Loop Machine example in the Modeling, Simulating, and Visualizing Simple Machines chapter has four revolutes. You can establish that only 3 * (3 - 4) + 4 = 1 of these DoFs is actually independent and arrive at the same result obtained in the example.© 1984-2011-The MathWorks, Inc. -Site Help-Patents-Trademarks-Privacy Policy-Preventing Piracy-RSS。
a rXiv:h ep-ph/972265v28May1997MADPH-97-984TUM-HEP-267/97hep-ph/9702265Model-independent Constraints on Topcolor from R b Gustavo Burdman ∗Department of Physics,University of Wisconsin,Madison,WI 53706,USA and Dimitris Kominis †Institut f¨u r Theoretische Physik,Technische Universit¨a t M¨u nchen,James-Franck-Straße,85748Garching,Germany Abstract We identify and compute the main corrections to R b in Topcolor theories.Theyare due to the top-pions,the pseudo-Goldstone bosons associated with the chiral symmetry breaking responsible for the top quark mass,and amount to −(1−4)%,independent of the details of the Topcolor model.We show that the cancellation of this effect against the contributions from Topcolor vector and scalar resonances is unlikely,given the inherently distinct character of the two scales governing the potentially cancelling terms.The resulting value of R b leads to severe constraints on Topcolor theories.1IntroductionThe large value of the top-quark mass has led to speculation that the properties of the top quark may be fundamentally different from those of the other known fermions.In theories of top condensation,for example,a new strong gauge interaction(Topcolor), which couples to the t-quark and perhaps to other fermions as well,drives the formation of a ¯t t condensate and imparts a large dynamical mass to the top quark.In the process, the chiral symmetries associated with the strongly interacting fermions are spontaneously broken and at least three Goldstone bosons emerge.In the earliest incarnation of this idea [1],these Goldstone bosons were identified with the longitudinal components of the W and Z in an attempt to simultaneously resolve the puzzle of electroweak symmetry breaking. The Goldstone boson decay constant fπis approximately given in terms of the dynamical top mass m t and the scaleΛ,at which Topcolor is assumed to break spontaneously to the Standard Model gauge group,by the Pagels-Stokar formula[2]f2π≈N C m2(1)twhere N C is the number of colors.If fπis to be identified with the weak scale v w≈175GeV,thenΛmust be of the order of1015GeV.This,in turn,requires an extreme fine-tuning of the Topcolor gauge coupling in order to achieve a hierarchy of thirteen orders of magnitude between m t andΛ.Alternatively,one may wish to construct top-condensate theories which do not suffer from such unnatural hierarchies[3].This means that the scaleΛof the new gauge interactions should be brought down to a few TeV or so,depending on the amount offine-tuning one is prepared to tolerate.From eq.(1)we then deduce that the Goldstone boson decay constant is fπ≈60GeV,a value insufficient to account for the observed W and Z masses.Consequently a separate mechanism,such as Technicolor(along with Extended Technicolor(ETC))[4],must be invoked to supply the remainder of the weak gauge boson masses and give mass to the lighter fermions.The second major consequence of this approach is that the Goldstone bosons associated with the formation of the ¯t t condensate(“top-pions”)are now physical degrees of freedom1.Along with the light fermions,the top quark is expected to acquire itself a small hard mass of approximately1GeV or so,from ETC interactions.This breaks the top chiral symmetries explicitly and turns the top-pions into massive pseudo-Goldstone bosons.A simple estimate gives[3]M2˜π≈N C f2Λ2γ(2)πwhereγis a radiative correction factor which can be rather large because of the strength of Topcolor interactions.For m ET C∼1GeV,this yields M˜π∼(100−300)GeV.Note that,because of its dependence on the parameter m ET C,the top-pion mass represents an energy scale which is largely independent from,and much lower than the Topcolor scale Λ.In this note we wish to point out that the presence of physical top-pions in the low-energy spectrum is an inevitable feature of any Topcolor model that purports to avoid fine-tuning.The effects of top-pions on low-energy observables are governed by the scale M˜π(not the topcolor scaleΛ),while the top-pion couplings to third generation quarks and to gauge bosons are to a large degree model-independent.Therefore,a study of top-pion effects at low energies can be used to test the Topcolor idea as a whole,rather than constrain particular implementations of it.With these comments in mind we investigate the impact of top-pions on R b,the ratio of the Z boson decay rate to b¯b pairs to its total hadronic width.This observable is expected to be sensitive to the Topcolor dynamics because of the non-trivial Topcolor interactions of the left-handed b-quark.Wefind that the top-pions lead to a substantial reduction of R b relative to the Standard Model prediction.While competing contributions are expected to arise in general[5],they are governed by the Topcolor scaleΛand cannot compensate fully for the top-pion effects,despite the fact that they are formally leading in a1/N C expansion.The crucial observation here is that,in addition to1/N C,the theory possesses another small parameter,namely M2˜π/Λ2,which on symmetry grounds must vanish as m ET C→0independently of the model or the number of colors.In Sec.2 we derive the top-pion couplings to quarks in the effective Lagrangian approach.Their effect on R b is discussed in Sec.3.Here we also take into account the possible effects of Topcolor vector mesons as well as those of additional scalar resonances present in specific models.We close with some concluding remarks in Sec.4.2Low-energy LagrangianThe Topcolor gauge group is assumed to contain an SU(3)1×SU(3)2subgroup,which is spontaneously broken at an energy scaleΛdown to the SU(3)of QCD.The doublet ψL=(t L b L)T as well as t R couple to SU(3)1,which is the strongest of the two SU(3) groups.The representation assignment of the remaining fermions is a model-dependent issue.However it should be made in such a way as to cancel gauge anomalies and ensure that no condensate of known quarks forms other than ¯t t .Additional fermions may be enlisted in order for these requirements to be fulfilled.In this section we restrict attention only to the interactions ofψL and t R which are common to all models.The quantitative study of this theory[3]begins with the simplifying assumption that, at energies below the scaleΛthe leading effects of the Topcolor dynamics are adequately described by a contact termL=−2πκ2ψL+¯t RγµλAΛ2¯ψLt R¯t RψL(4)Calculations with this effective lagrangian are usually carried out in the so-called Nambu–Jona-Lasinio(NJL)approximation[6],which consists in resumming diagrams involving chains of fermion bubbles(but not loops of such chains).This approximation is justified in the limit where the number of colors N C becomes large.Alternatively,one may introduce collective variables in the form of an auxiliary doublet fieldφ0[7].The Lagrangian(4)is equivalent toL scalar=−λ¯ψLφ0t R+h.c.−Λ2φ†0φ0(5) whereλ2=4πκ.The renormalization group evolution of this Lagrangian to low energy scales generates a gauge-invariant kinetic term as well as self-interactions forφ0.In terms of the properly renormalizedfieldφthe effective Lagrangian readsL eff=|Dµφ|2−˜λ¯ψLφt R+h.c.−V(φ)(6) whereDµ=∂µ−igW aµτa−ig′Ygeneral Lagrangian describing a SU(2)×U(1)→U(1)symmetry breaking pattern and involving as the sole degrees of freedom(apart from the quarks and gauge bosons)an en-tire2scalar doubletφ.The details of the potential V(φ)are irrelevant to our discussion, except that it is such as to causeφto develop a nonzero vacuum expectation value,fπ. Since the top quark acquires the bulk of its mass through this mechanism,its Yukawa coupling to the scalar doublet isfixed:˜λ=m t/fπ.The remaining couplings are deter-mined by gauge invariance.As far as the effective theory is concerned,the value of fπis a free parameter.In the numerical estimates of the following sections we take fπ=60GeV as suggested by the NJL approximation to the Pagels-Stokar formula(eq.(1)).The soft dependence on the generally unknown cutoffΛindicates that sharp deviations from this value are unlikely.In terms of the componentfields of the scalar doublet,defined by,(8)φ= fπ+12(h+i˜π0)˜π−the Lagrangian(6)is given byL eff=|Dµφ|2−m t¯t t−m t√M2h h2+(scalar self−interactions)(9)2where M h is the mass of the scalar state h.As explained above,the ETC interactions explicitly break the chiral symmetries and cause the states˜πto acquire masses M˜π±,M˜π0. These are not necessarily equal in general,because of the lack of an SU(2)custodial symmetry.Finally,note that the mixing of˜π±,0with the Goldstone bosons of electroweak symmetry breaking introduces a factor of cosθto the fermion couplings of the physical top-pions,where sinθ=fπ/v w,and generates a coupling between the top-pions and the right-handed b-quark.The latter is proportional to m b and will be neglected.Correcting for the former effect and keeping only the terms which are relevant to the calculation of the next section,wefinally obtainL eff=|Dµφ|2−m t¯t t−m t√M2˜π0˜π02+ (10)2150300450600750900M top-pion (GeV)0.000.010.020.030.040.05-δR b /Rb Figure 1:Fractional change in R b induced by the top-pions of a generic Topcolor model.Notice that the quantity plotted is the negative of the correction to R b .3R b in TopcolorIn Fig.1we plot the relative correction to R b due to top-pion exchange as a function of the mass of the charged top-pion.The calculation has been carried out to one loop with the Lagrangian (10)and follows closely the corresponding computation in the Two-Higgs-Doublet model [8],as it can be seen in Fig.2.The contributions of the neutral states˜π0and h are suppressed at this level by a factor of order (m 2b /m 2t )and are ignored.Thearguments of the previous section imply that the only uncertainty in this result resides in the value of f π.Of course,due to the strong couplings of the top-pions,higher-order corrections are expected to be substantial.We therefore regard our results only as rough estimates.The collaborations at LEP have recently reported a measured value of 0.2178±0.0011for R b [9]to be compared with the Standard Model prediction of 0.2158.This allows negative deviations relative to the Standard Model of only 0.6%at 3σ,and im-poses very severe constraints on Topcolor models,unless there exist further contributions to R b ,which can naturally neutralize the top-pion effects.Candidates for such contribu-tions include the exchange of Topcolor vector mesons or of additional light scalars which sometimes occur in specific models.We now turn to the study of these states and of their influence on R b ,adopting the NJL approximation as our calculational framework.t b bZ π∼−π∼+Z t tbb π∼+Figure 2:Corrections to the Z ¯bb vertex due to top-pions.Not shown are the corresponding corrections to the fermion lines.As mentioned in Section 2,a Topcolor model is specified when the anomaly-free as-signment of all fermions is chosen so as to ensure that no SM fermion other than the top quark acquires a large dynamical mass.In particular,the b quark will get a large mass if b R couples to the Topcolor interaction in the same way as t R does.This need for explicit isospin breaking has been addressed in various ways,all of which result in the presence of additional scalars in the spectrum.Here we show the effects of this model-dependent aspect of Topcolor on electroweak observables in the two scenarios described in [10].First,let us consider the case where the condensation is tilted in the top direction by the presence of an extra U (1)interaction embedded in the weak hypercharge group such that,at the scale Λ,U (1)1×U (1)2→U (1)Y .Here the U (1)1is strongly coupled to the third generation fermions.The fermions have U (1)1×U (1)2assignments such that the couplings of the remnant Z ′to fermions are analogous to those of the Z .Thus the effect of the Z ′in the top channel adds to that of the Topcolor interaction,whereas it is repulsive in the b quark channel.This defines a region in the coupling parameter space where only the coupling in the top channel is super-critical,leading to the breaking of the top chiral symmetry and to the scalar doublet in (8).In addition,in this region the effective interaction in the b channel,although sub-critical,is strong enough to form rather deeply bound scalar states [11].These make up the doubletφb = H +12(H 0+iA 0) (11)Their masses can be estimated within the NJL approximation to be [11]M H 0,A ≃(150−350)GeV ,(12)whereas the mass of the charged states is determined by the relationM 2H ±=M 2H 0,A +2m 2t .(13)The presence of this doublet adds the term−˜λ¯ψLφb b R+h.c.(14) to the effective Lagrangian(6),where as before˜λ=m t/fπ.Therefore the charged scalarsH±couple to b R with strength˜λ,whereas the neutrals H0,A0have the same strong coupling to¯b L b R.This results in additional contributions to R b.The overall effect ofthe“b-pions”H±and H0,A0is to further decrease R b by a small amount,making the deviation from the experimental result even larger.For instance,for M H0=350GeV andM˜π=300GeV,the value of R b is reduced by about3.3%.In the absence of the b-pions theeffect is≃2.8%.In these estimates we used the relation(13)for the b-pion masses,whichhowever does not have to be taken literally.It is well-known[12]that the charged scalarsinφb tend to reduce R b while the contribution from the neutrals is positive.The lattercan only become dominant,however,if M H0,A≪M H±,in drastic departure from the NJL estimate(13).To reverse the top-pion effect one would further need M H0,A≪M˜π, which is counterintuitive.The relatively mild effect of the“b-pions”can be traced to thefact that the Z boson decays predominantly into left-handed b-quarks,while in the limitof negligible m b the scalars H±couple exclusively to b R.One can further study the effects of vector and axial-vector mesons in Topcolor byessentially repeating the steps outlined at the beginning of Section2for the scalar doubletφ.The methods employed have been extensively discussed in different contexts by variousauthors[13].A vector or axial-vector resonance composed of b-quarks would contribute toR b by virtue of its mixing with the Z.In fact,taking into account this mixing amounts tosumming all leading1/N C contributions to the Zb¯b vertex.However,an estimate in theNJL approximation shows that these resonances are very loosely bound,that is,they havea mass of the order of the Topcolor scaleΛ,and consequently the resummation hardlyimproves on the one-loop result of Ref.[5],according to which R b receives a positivecorrection ofδR b/R b≈2.5×10−3forΛ=2TeV falling toδR b/R b≈5.8×10−4for Λ=5TeV.This correction cannot compensate for the top-pion effects(cf.Fig.1)which are governed by the–presumably much lower–scale M˜π.Another way to avoid the formation of a ¯b L b R condensate is to have the b R trans-forming as a SU(3)1singlet,so that it does not feel the Topcolor interaction.Following ref.[10],we notice that the cancelation of anomalies requires the introduction of a new set of fermionfields,Q a L,R,with a=1,...,N Q.There is a new interaction,SU(N Q).For instance for N Q=3the following assignments under SU(3)Q×SU(3)1×SU(3)2are anomaly-free:(t,b)L(c,s)L≃(1,3,1)t R≃(1,3,1)Q R≃(3,3,1)(u,d)L≃(1,1,3)(u,d)R(c,s)R≃(1,1,3)b R≃(1,1,3)Q L≃(3,1,3).The fact that(c,s)L transforms as a triplet under SU(3)1,in addition to(t,b)L,implies that the chiral symmetry is now SU(4)L×U(1).The breaking of this global symmetry by the Topcolor interactions now leads not only to the scalar doubletφdefined in Section2 but also to the presence of an extra doublet of Goldstone bosons,the“charm-top-pions”:(15)C= 12(h c+iπc)π−cAlthough in principle massless,they acquire a mass generated by the same explicit chiral symmetry breaking responsible for M˜πand thus of similar value.Their coupling to the right-handed top quark is equal to that of the top-pions:−˜λ(¯c¯s)L C t R+h.c.(16) This Topcolor model not only suffers from large deviations from the measured value of R b, but in addition,the couplings in(16)imply large corrections to R c.In Fig.3we plot the relative corrections to R b and to R c in this model as a function of the pseudo-Goldstone boson mass.Also shown is the3σLEP result.Although the determination of R c is more uncertain,it can be seen that it can potentially pose an important additional constraint on these type of models.Notefinally that the decay width of the Z to light hadrons is also affected because R s is reduced by the same amount as R b.In sum,this particular Topcolor model presents a lot of difficulties when confronted with observables at the Z pole.In general,it is likely that other specific models will give rise to large deviations not only in R b but also in R c and the Z hadronic width due to the ubiquitous presence of additional scalars in the spectrum.4ConclusionsWe have seen that it is possible to constrain top condensation theories in general and Topcolor models in particular by concentrating on the effects due to the presence of top-pions in the spectrum.Not only are these the minimal scalar content of any Topcolor model,but they also have a largely model-independent coupling to quarks,˜λ=m t/fπ, allowing for rather general predictions.As it can be seen from(2),their masses are150300450600750900M top-pion (GeV)0.000.020.040.060.080.10δR c /R c -δR b /R b 3σ bound on R c 3σ bound on R b Figure 3:Fractional change in R b and R c in the Topcolor model with strongly coupled (c,s )L relative to the Standard Model value.The horizontal lines represent the experi-mental 3σupper bounds to these corrections.Note that,as in Fig.1,the R b correction is negative.expected to be well below the Topcolor scale Λ.This,together with the fact that their decay constant is expected to lie in the range f π=(50−70)GeV in order to avoid fine-tuning,brings about the potential for strong effects,governed by the scale M ˜πof a few hundred GeV rather than by the Topcolor scale itself.We computed the effect of top-pions in R b and found it to be a large and negative shift with respect to the SM,as shown in Fig.1.For typical values of M ˜πthis result is particularly constraining when compared to the experimental measurements at LEP [9],which at present point to a positive shift.The effects of other Topcolor states were taken into account in order to investigate the possibility of cancellations.As noted in ref.[5],the contribution of the heavy topcolor gauge bosons,or “top-gluons”,to R b is positive and small (less then 1%for realistic Topcolor scales).We considered the positive contributions of vector and axial-vector states and found that they are not enough to compensate for the negative shift due to the top-pions.We remark that,although the precise quantitative results depend on the approximation used,the contributions of these states are controlled by the scale Λ.Thus,a cancellation as large as the one required seems unlikely given the two different scales entering.Attempts to involve some of the other standard quarks in the strong Topcolor interac-tions typically lead to additional light scalars which exacerbate the effect.We calculated the contributions to R b from these states in two specific realizations.In the model withan extra U(1)we observe that the shift in R b is slightly more negative than in the sole presence of top-pions.The other model considered requires(c s)L to be a triplet under the strong SU(3)1,i.e.to couple to the top-gluon.Here,in addition to the top-pions which modify the Zb¯b vertex in the same way as in the previous model,there is a new set of pseudo-Goldstone bosons,the charm-top-pions,which induce a very large positive shift to R c.This also conflicts with experiment,but the discrepancy is milder than in the case of R b.The situation is summarized in Fig.3.There is also a large negative shift in R s,of the same order as the one in R b.We conclude that a large and negative correction to R b is present in Topcolor models with minimal fermionic structure,and that there are no natural sources of cancellation, at least in the cases examined.Our quantitative conclusions are of course valid only to the extent that the approxi-mations we use are justified.Were fπ,for instance,allowed tofloat upwards by a factor of two relative to the Pagels-Stokar estimate,the correction to R b would be about6.7 times smaller than the one presented in Fig.1.Similarly,larger values of M˜πcannot be excluded given the uncertainty in the radiative correction factorγin eq.(2).The top-pion mass can also be enhanced by allowing larger values of m ET C,but this option is rather unattractive.A possible way out could in principle be provided by an extended fermionic content of the theory.If the top quark mixes with a new strongly interacting fermion of electric charge2/3,but possibly of“exotic”electroweak quantum numbers,then the correction to R b could be naturally smaller than in the case of no mixing.The challenge is to achieve this while avoiding the proliferation of pseudo-Goldstone bosons which will emerge from the breaking of a necessarily larger chiral symmetry group.Although the simplest models with additional fermions do not give rise to the desired symmetry breaking pattern,this remains perhaps an avenue to pursue further.It should be remarked that other electroweak observables are also affected by the presence of light strongly interacting top-pions.For instance,theρparameter receives a two-loop contribution from the latter in addition to the one from top-gluon exchange considered in ref.[14].Any proposed mechanism introducing delicate cancellations in order to bring R b in line with experiment should also have a counterpart in the case of all other observables which are sensitive to the presence of pseudo-Goldstone bosons. AcknowledgementsWe thank Chris Hill for helpful discussions and a careful reading of the manuscript.DK thanks the Fermilab Theory Group for their warm hospitality during the initial stages of this work.His work was supported in part by the German DFG under contract numberLi519/2-1.The work of GB was supported by the U.S.Department of Energy under Grant No.DE-FG02-95ER40896and the University of Wisconsin Research Committee with funds granted by the Wisconsin Alumni Research Foundation.References[1]Y.Nambu,in New Theories in Physics,Proceedings of the XI International Sympo-sium on Elementary Particle Physics,Kazimierz,Poland,1988,edited by Z.Ad-juk,S.Pokorski and A.Trautmann(World Scientific,Singapore,1989);Enrico Fermi Institute Report EFI89-08(unpublished);V.A.Miransky,M.Tanabashi and K.Yamawaki,Phys.Lett.221B,(1989)177;Mod.Phys.Lett.A4(1989)1043;W.A.Bardeen,C.T.Hill and M.Lindner,Phys.Rev.D41,(1990)1647.[2]H.Pagels and S.Stokar,Phys.Rev.D20(1979)2947.[3]C.T.Hill,Phys.Lett.B345(1995)483.[4]S.Weinberg,Phys.Rev.D19(1979)1277;L.Susskind,Phys.Rev.D20(1979)2619;S.Dimopoulos and L.Susskind,Nucl.Phys.B155(1979)237;E.Eichten and ne,Phys.Lett.B90(1980)125.[5]C.T.Hill and X.Zhang,Phys.Rev.D51(1995)3563.[6]Y.Nambu and G.Jona-Lasinio,Phys.Rev.122(1961)345;124(1961)246.[7]T.Eguchi,Phys.Rev.D14(1976)2755.[8]A.Denner,R.Guth,W.Hollik and J.H.K¨u hn,Z.Phys.C51(1991)695.[9]A.Blondel,Plenary talk at the28th International Conf.on High Energy Physics,Warsaw,July1996.[10]G.Buchalla,G.Burdman,C.T.Hill and D.Kominis,Phys.Rev.D53(1996)5185.[11]D.Kominis,Phys.Lett.B358(1995)312.[12]P.Bamert et al.,Phys.Rev.D54(1996)4275.[13]V.Bernard and U.-G.Meissner,Nucl.Phys.A489(1988)647;J.Bijnens,C.Brunoand E.de Rafael,Nucl.Phys.B390(1993)501;J.Bijnens,E.de Rafael and H.Zheng, Z.Phys.C62(1994)437;J.Bijnens,Phys.Rep.265(1996)369.[14]R.S.Chivukula,B.A.Dobrescu and J.Terning,Phys.Lett.B353(1995)289.。