
极值点偏移问题(2)
——函数的选取(操作细节)
杨春波(高新区枫杨街 郑州外国语学校,河南 郑州 450001)
例4 已知函数()x f x e ax =-有两个不同的零点12,x x ,其极值点为0x .
(1)求a 的取值范围;(2)求证:1202x x x +<;(3)求证:122x x +>;(4)求证:
121x x <.
解:(1)()x f x e a '=-,若0a ≤,则()0f x '>,()f x 在R 上单增,()f x 至多有1个零点,舍去;故必有0a >,易得()f x 在(),ln a -∞上单减,在()ln ,a +∞上单增,要使()f x 有两个不同的零点,则有()ln 0f a a e (严格来讲,还需补充两处变化趋势的说明:当x →-∞时,()f x →+∞;当x →+∞时,()f x →+∞).
(2)由所证结论知这是()f x 的极值点偏移问题,选取函数()f x 来做.下面按对称化构造的三个步骤来写,其中0ln x a =.
①由(1)知()f x 在()0,x -∞上单减,在()0,x +∞上单增,可设102x x x <<; ②构造函数()()()02F x f x f x x =--,则
()()()02022x x x F x f x f x x e e a -'''=+-=+-,
当0x x <时,有()20F x a '>-=,则()F x 在()0,x -∞上单增,得
()()00F x F x <=,即()()()002f x f x x x x <-<;
③将1x 代入②中不等式得()()()12012f x f x f x x =<-,又20x x >,0102x x x ->,
()f x 在()0,x +∞上单增,故2012x x x <-,1202x x x +<.
(3)由所证结论可以看出,这已不再是()f x 的极值点偏移问题.谁的极值点会是1
x =呢?回到题设条件:()0x x
x
e f x e ax e ax a x =-=?=?=,记函数()x
e g x x
=,则有
()()12g x g x a ==.求导得()()
2
1x e x g x x -'=
,则1x =是()g x 的极小值点,我们选取函
数()g x 来证(3)中结论122x x +>,也可证(4)中结论121x x <.
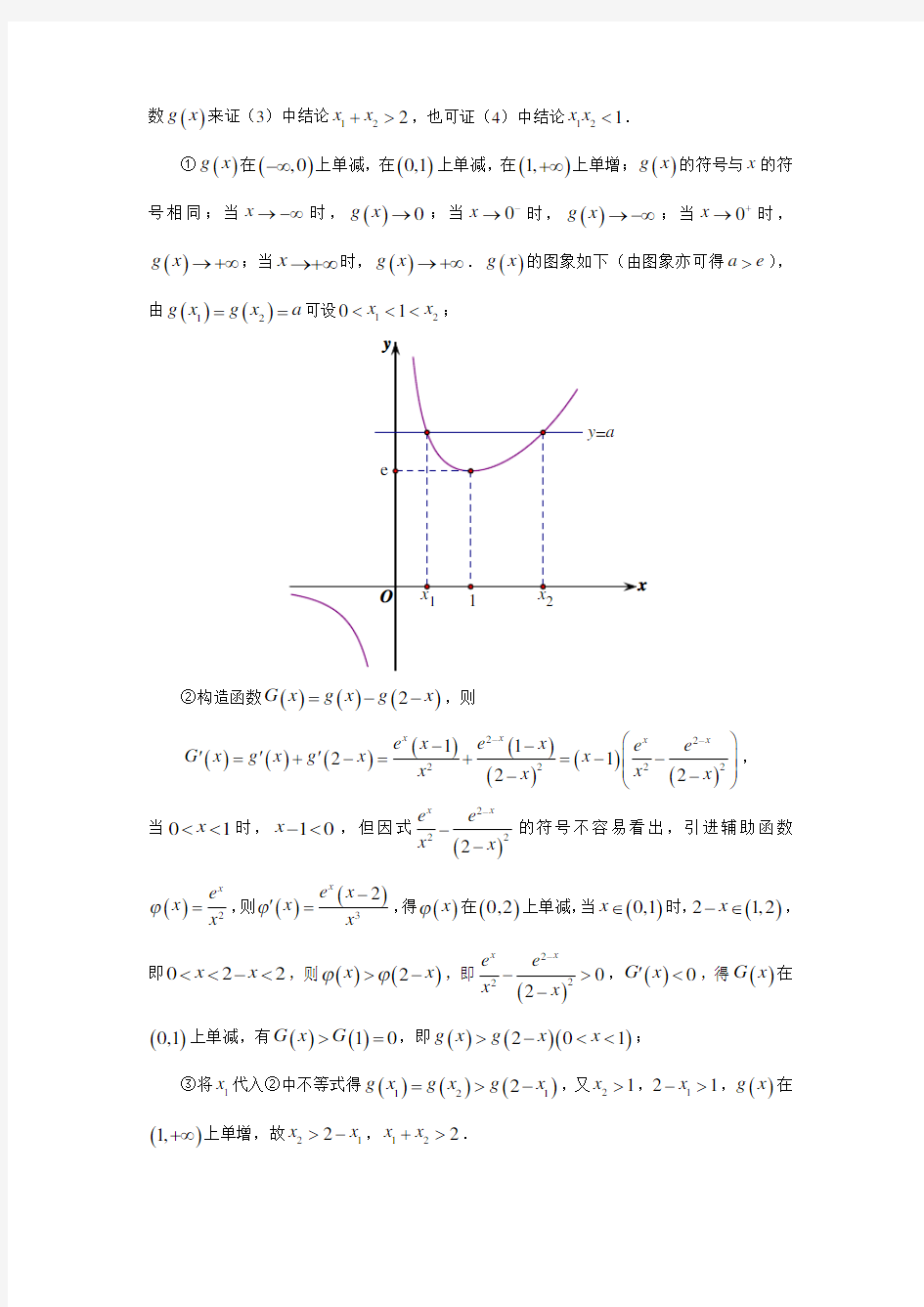
①()g x 在(),0-∞上单减,在()0,1上单减,在()1,+∞上单增;()g x 的符号与x 的符
号相同;当x →-∞时,()0g x →;当0x -→时,()g x →-∞;当0x +
→时,
()g x →+∞;当x →+∞时,()g x →+∞.()g x 的图象如下(由图象亦可得a e >),由()()12g x g x a ==可设1201x x <<<;
②构造函数()()()2G x g x g x =--,则
()()()()()()()()22222
2112122x x x x e x e x e e G x g x g x x x x x x --??
--'''=+-=+=-- ? ?--??
, 当01x <<时,10x -<,但因式()2222x x
e e x x ---的符号不容易看出,引进辅助函数
()2x
e x x
?=,则()()3
2x e x x x ?-'=,得()x ?在()0,2上单减,当()0,1x ∈时,()21,2x -∈,即022x x <<-<,则()()2x x ??>-,即()
22
202x x
e e x x -->-,()0G x '<,得()G x 在()0,1上单减,有()()10G x G >=,即()()()201g x g x x >-<<;
③将1x 代入②中不等式得()()()1212g x g x g x =>-,又21x >,121x ->,()g x 在
()1,+∞上单增,故212x x >-,122x x +>.
(4)①同上;
②构造函数()()1G x g x g x ??
=-
???
,则 ()()()()1
122222
11111111x x x
x
x e xe e e x x G x g x g x x x x x x ??
??--- ? ?-??????'''=+=+= ?????
???
g ,
当01x <<时,10x -<,但因式1x
x
e xe -的符号不容易看出,引进辅助函数
()1
x
x
x e xe ?=-,
则()1
11x
x x e e x ???
'=+- ???
,当()0,1x ∈时,()0x ?'>,得()x ?在()0,1上单增,有()()10x ??<=,则()0G x '>,得()G x 在()0,1上单增,有()()10G x G <=,即()()101g x g x x ??
<<<
???
; ③将1x 代入②中不等式得()()1211g x g x g x ??=< ???
,又21x >,11
1x >,()g x 在()1,+∞上单增,故21
1
x x <
,121x x <. 点评:结论虽已证出,但判定因式()
22
22x x e e x x ---及1
x
x e xe -的正负时,均需辅助函数的介入,费了一番功夫.虽然()g x 的极值点是1,理论上可以用来做(3)(4)两问,但实践发现略显麻烦,我们还没有找到理想的函数.
再次回到题设条件:
()()0,0ln ln ln ln x f x e ax a e x x a x x x a =?=>>?=+?-=,
记函数()ln h x x x =-,则有()()12ln h x h x a ==.接下来我们选取函数()h x 再证(3)(4)两问.
(3)①()1
1h x x
'=-
,得()h x 在()0,1上单减,在()1,+∞上单增,有极小值()11h =;又当0x +
→时,()h x →+∞;当x →+∞时,()h x →+∞.故()h x 的图象如下(由图象得ln 1a >,亦得a e >),由()()12ln h x h x a ==可设1201x x <<<.
x
②构造函数(2H x h x h x =--,则
()()()()111
1211122H x h x h x x x x x x ??????'''=+-=-+-=-- ? ? ?--??????
,
当01x <<时,10x -<,
1102x x
->-,则()0H x '<,得()H x 在()0,1上单减,有()()10H x H >=,即()()()201h x h x x >-<<;
③将1x 代入②中不等式得()()()1212h x h x h x =>-,又21x >,121x ->,()h x 在
()1,+∞上单调递增,故212x x >-,122x x +>.
(4)①同上;
②构造函数()()1H x h x h x ??
=-
???
,则 ()()()2
2211111111H x h x h x x x x x x ??????
'''=+=-+-=- ? ? ???????
,
当01x <<时,()0H x '>,得()H x 在()0,1上单增,有()()10H x H <=,即
()()101h x h x x ??
<<< ???
;
③将1x 代入②中不等式得()()1211h x h x h x ??=<
???
,又2
1x >,11
1x >,()h x 在()1,+∞上单调递增,故21
1
x x <
,121x x <. 点评:用函数ln y x x =-来做(3)(4)两问,过程如行云流水般,格外顺畅.这说明
在极值点偏移问题中,若函数选取得当,可简化过程,降低难度.
注1:第(2)问也可借助第(4)问来证:将11ln ln x x a =+,22ln ln x x a =+相加得
()12120ln 2ln 2ln 2x x x x a a x +=+<=;
注2:在第②步中,我们为什么总是给定1x 的范围?这是因为1x 的范围()0,1较2x 的范围()1,+∞小.以第(3)问为例,若给定()1,x ∈+∞,因为所构造的函数为
()()()2H x h x h x =--,这里0x >,且20x ->,得02x <<,则当2x ≥时,()
H x 无意义,需要分为两类:(1)若22x ≥,则1222x x x +>≥,结论成立;(2)当()1,2x ∈时,同原解答.而给定()0,1x ∈,则不会遇到上述问题.当然第(4)问中给定1x 或2x 的范围均可,请读者自己体会其中差别.
思考:上一讲中练习1应该用哪一个函数来做呢?
提示:ln 1ln 00,x x ax a x e ??-=?=
∈ ???,用函数ln x y x
=来做2
12x x e >;或用函数ln y x ax =-来做2122
x x e a
+>
>.