第二章复变函数的积分
- 格式:pdf
- 大小:795.49 KB
- 文档页数:36




第二章 复变函数的积分在微积分学中,微分法与积分法是研究函数性质的重要方法。
同样,在复变函数中,积分法也跟微分法一样是研究复变函数性质十分重要的方法和解决实际问题的有力工具。
§2.1 复变函数积分的概念一、复变函数的积分设C 为平面上给定的一条光滑(或按段光滑)曲线。
若选定C 的两个可能方向中的一个作为正方向,那么就把C 理解为带有方向的曲线,称为有向曲线。
设曲线C 的两个端点为A 与B ,如果从A 到B 的方向作为C 的正方向,那么从B 到A 的方向就是C 的负方向,并把它记作-C 。
在今后的讨论中,常把两个端点中的一个作为起点,另一个作为终点。
除特殊声明外,正方向总是指从起点到终点的方向。
关于简单闭曲线的正方向是指当曲线上的点P 顺此方向沿该曲线前进时,临近P 点的曲线内部始终位于P 点的左方。
与之相反的方向就是曲线的负方向。
若光滑或逐段光滑的曲线C 的参数方程为)()()(t iy t x t z z +==,)(βα≤≤t (2.1) t 为实参数,则规定t 增加的方向为正方向,即由)(αz a =到)(βz b =的方向为正方向。
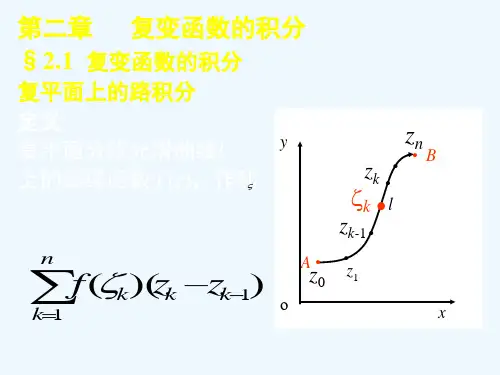
定义2.1 设函数)(z f w =定义在区域D 内,C 为区域D 内起点为A 终点为B 的一条光滑有向曲线,把曲线C 任意分成n 个弧段,设分点为:B z z z z z A n n ==-,...,,,1210 在每个小弧段上任取一点k ζ(图3.1),作和∑=∆=nk k k n z f S 1)(ζ其中1--=∆k k k z z z ,记=∆k s 的长度,}Δ{max 1k nk s δ≤≤=。
当n 无限增加,且δ趋于零时,如果不论对C 的分法及k ζ的取法如何,当n S 有唯一极限,那么称这个极限值为函数)(z f 沿曲线C 的积分,记作∑⎰=→=nk k kδCz ζf dz z f 1Δ)(lim )( (2.2)图2.1C 称为积分路径,⎰Cdz z f )(表示沿C 的正方向的积分,⎰-C dz z f )(表示沿C的负方向的积分。






第二章 复变函数的积分2-1 复变函数的积分一、复变函数的路径积分()()()11lim -=∞→-≡∑⎰k k n k kn l z z f dz z f ξ()()()()()⎰⎰⎰++-=l ll dy y x u dx y x v i dy y x v dx y x u dz z f .,., 二、复变函数的路径积分的简单性质()29p2-2 科希定理一、单连通区域上的科希定理若()z f 是闭合回路l 所围区域上的解析函数,则 ()0=⎰dz z f l或()()()1221Z F Z F dz z f z z -=⎰2.复连通区域上的科希定理若()z f 是闭合回路l 所围区域上的解析函数,则 ()()021=+⎰⎰dz z f dz z f l l ()()dz z f dz z f l l ⎰⎰'=21 例1 计算回路积分dz a z l ⎰-1解:(1)回路l 不包围a 的情况 根据科希定理01=-⎰d z a z l (2)回路l 包围a 的情况根据复连通区域上的科希定理,有dz a z dz a z C l ⎰⎰-=-11令 ϕi a z Re =-,则()i id a d dz a z dz a z i i C l 2Re Re 112020πϕππϕϕ==+=-=-⎰⎰⎰⎰ 例2 计算回路积分()dz a z l n ⎰-, (1-≠n )解:(1)0≥n 的情况()z f 是闭合回路l 所围区域上的解析函数,根据科希定理 ()0=-⎰dz a z ln(2)1-<n 的情况仿例2,有()01120)1(1)1(201=+==-++++⎰⎰πϕϕπϕn i n n i n l n e R n d e iR dz a z 2-4 科希公式()()dz a z z f i a f l ⎰-=21π 或()()ξξξπd z f i z f l ⎰-= 21 解析函数的两个重要性质● 解析函数在任一内点z 的值()z f 等于包围点z 的任一境界线的回路积分。