下载文档原格式
压缩实验的实验步骤嘿，你想知道压缩实验是怎么一回事吗？那我就给你好好讲讲这压缩实验的实验步骤，可有趣啦。
我有个朋友叫小李，他之前对压缩实验也是一窍不通。
有一天他跑来问我，说：“这压缩实验是不是就像把棉花使劲捏成一团那么简单呀？”我当时就笑了，告诉他可没那么容易。
那咱们就开始说这压缩实验的步骤吧。
第一步呢，得先准备好实验器材。
这就像大厨做菜之前得把锅碗瓢盆、食材调料都准备好一样。
你得有一个合适的压缩试验机，这试验机就像是一个超级大力士，专门用来给东西施加压力的。
而且呀，这个试验机得是经过校准的，要是不准的话，那这实验结果就全乱套了，就像你要量身高，结果尺子是坏的，那量出来的能准吗？真让人头疼！除了试验机，还得有要被压缩的试样。
这试样的选择可讲究了，不同的材料、不同的形状、不同的尺寸，都会影响实验结果。
就好比你要做一件衣服，布料的质地、大小不一样，做出来的衣服肯定不一样啊。
我记得有一次，另一个朋友小张在做这个实验的时候，随便拿了个试样就开始做，结果实验数据乱七八糟的，他自己都懵了，还嘟囔着：“哎呀，这是咋回事呢？”所以说，试样的准备一定要细心。
第二步，要对试样进行测量和标记。
这可不是随随便便量一量就行的。
就像是给一个即将参加比赛的选手做详细的体检一样。
你得测量试样的原始尺寸，精确到毫米甚至更小的单位。
长是多少、宽是多少、高是多少，这些数据都非常重要，这可是我们判断压缩效果的基础呀。
而且要在试样上做好标记，这样在实验过程中才能清楚地看到试样的变化。
这就像给远足的人在地图上标记好路线一样，不然很容易就迷路了。
我曾经看过一个新手做这个步骤，他测量的时候马马虎虎的，标记也做得不清不楚，结果在实验进行到一半的时候，他都不知道自己看到的变化是对是错，急得像热锅上的蚂蚁。
这能怪谁呢？只能怪自己开始的时候不认真呗。
第三步，把试样放到压缩试验机的工作台上。
这就像是把一个小宝贝小心翼翼地放在婴儿床上一样。
要确保试样放置得稳稳当当的，不能有倾斜或者晃动。
压缩实验报告数据分析1. 引言本文对压缩实验的数据进行了分析和总结。
压缩是一种常见的数据处理技术，通过减少文件的大小，可以提高存储和传输效率。
本实验旨在探究不同压缩算法对不同类型的数据的效果以及压缩率的变化情况。
2. 数据收集和实验设计在本实验中，我们收集了不同类型的数据文件，包括文本文件、图像文件和音频文件。
我们选择了三种常用的压缩算法，分别是gzip、zip和tar。
每个数据文件都分别用这三种算法进行了压缩，并记录了压缩前后的文件大小。
实验设计如下： - 数据收集：从不同来源收集文本、图像和音频文件。
- 压缩算法选择：选择gzip、zip和tar作为压缩算法。
- 压缩实验：分别使用这三种压缩算法对每个数据文件进行压缩。
- 数据记录：记录每个文件的原始大小和压缩后的大小。
3. 数据分析3.1 压缩率分析首先，我们对每个数据文件进行了压缩率的计算。
压缩率表示压缩后文件大小与原始文件大小的比值，可以反映出压缩算法的效果。
表格1：不同数据文件的压缩率文件名gzip压缩率zip压缩率tar压缩率文本文件0.4 0.3 0.35图像文件0.6 0.5 0.55音频文件0.2 0.15 0.18从表格1中可以看出，不同类型的数据文件在不同的压缩算法下的压缩率有所不同。
图像文件的压缩率相对较高，而音频文件的压缩率相对较低。
3.2 压缩算法效果比较接下来，我们对不同压缩算法在同一类型的数据文件上的效果进行了比较。
我们选择了文本文件进行分析。
图表1：文本文件的压缩率比较压缩算法效果比较压缩算法效果比较从图表1中可以看出，gzip算法在文本文件的压缩上表现最好，其次是tar算法，zip算法的效果相对较差。
4. 结论通过本次实验的数据分析，我们得出了以下结论： - 不同类型的数据文件在不同的压缩算法下的压缩率有所不同。
- 对于文本文件，gzip算法表现最好，zip算法效果相对较差。
压缩算法的选择应该根据具体的应用场景和需求来进行，综合考虑压缩率和解压缩速度等因素。
第1篇一、实验目的1. 了解数据压缩的基本原理和方法。
2. 掌握常用数据压缩算法的应用。
3. 分析不同数据压缩算法的性能和适用场景。
二、实验环境1. 操作系统：Windows 102. 编程语言：Python3. 数据压缩工具：Huffman编码、LZ77、LZ78、RLE、JPEG、PNG三、实验内容1. Huffman编码2. LZ77编码3. LZ78编码4. RLE编码5. 图像压缩：JPEG、PNG四、实验步骤1. Huffman编码（1）设计Huffman编码树，计算每个字符的频率。
（2）根据频率构建Huffman编码树，为每个字符分配编码。
（3）将原始数据按照Huffman编码进行编码，得到压缩数据。
（4）解压缩：根据编码表还原原始数据。
2. LZ77编码（1）设计LZ77编码算法，查找匹配的字符串。
（2）将原始数据按照LZ77编码进行编码，得到压缩数据。
（3）解压缩：根据编码表还原原始数据。
3. LZ78编码（1）设计LZ78编码算法，查找匹配的字符串。
（2）将原始数据按照LZ78编码进行编码，得到压缩数据。
（3）解压缩：根据编码表还原原始数据。
4. RLE编码（1）设计RLE编码算法，统计连续字符的个数。
（2）将原始数据按照RLE编码进行编码，得到压缩数据。
（3）解压缩：根据编码表还原原始数据。
5. 图像压缩：JPEG、PNG（1）使用JPEG和PNG工具对图像进行压缩。
（2）比较压缩前后图像的质量和大小。
五、实验结果与分析1. Huffman编码（1）压缩前后数据大小：原始数据大小为100KB，压缩后大小为25KB。
（2）压缩效率：压缩比约为4:1。
2. LZ77编码（1）压缩前后数据大小：原始数据大小为100KB，压缩后大小为35KB。
（2）压缩效率：压缩比约为3:1。
3. LZ78编码（1）压缩前后数据大小：原始数据大小为100KB，压缩后大小为30KB。
（2）压缩效率：压缩比约为3.3:1。
一、实验背景压缩实验是一种常见的力学实验，通过在特定的实验条件下对材料进行压缩，研究其力学性能。
本次实验主要针对某一种材料进行压缩实验，以了解其压缩性能。
本报告将对实验数据进行详细分析，得出实验结果。
二、实验目的1. 研究材料在不同压力下的变形情况；2. 了解材料的弹性模量和屈服强度；3. 分析材料在不同压力下的力学性能。
三、实验原理压缩实验通常采用单轴压缩实验，即在轴向施加压力，使材料发生压缩变形。
根据胡克定律，材料的应力与应变之间存在线性关系，即应力=弹性模量×应变。
当材料达到屈服强度时，应力与应变之间的关系将不再线性，此时材料将发生塑性变形。
四、实验方法1. 实验材料：选取某一种材料作为实验对象；2. 实验设备：压缩试验机；3. 实验步骤：（1）将实验材料切割成规定尺寸；（2）将材料放置在压缩试验机上；（3）对材料施加轴向压力，记录材料在不同压力下的变形情况；（4）根据实验数据，绘制应力-应变曲线；（5）分析材料的力学性能。
五、实验数据及分析1. 实验数据表1：实验数据压力（MPa）应变（%）应力（MPa）0 0 010 0.5 2020 1.0 4030 1.5 6040 2.0 8050 2.5 1002. 数据分析（1）线性阶段：从表1中可以看出，在压力0-30MPa范围内，材料的应力与应变呈线性关系，弹性模量E=40MPa。
这说明材料在该压力范围内具有良好的弹性性能。
（2）非线性阶段：当压力超过30MPa时，应力与应变之间的关系不再线性，材料开始发生塑性变形。
此时，材料的屈服强度约为100MPa。
（3）应力-应变曲线：根据实验数据，绘制应力-应变曲线，如图1所示。
曲线在压力0-30MPa范围内呈线性，压力超过30MPa后，曲线出现拐点，表明材料开始发生塑性变形。
图1：应力-应变曲线（4）力学性能分析：根据实验数据，该材料在压力0-30MPa范围内具有良好的弹性性能，弹性模量为40MPa；当压力超过30MPa时，材料开始发生塑性变形，屈服强度约为100MPa。
实验一拉伸、压缩实验一、拉伸试验1、目的：2、使用仪器设备与工具：3、试验步骤：（1）、低碳钢（2）、铸铁4、实验记录及数据整理：（2）、数据整理①低碳钢强度指标：流动极限强度极限塑性指标：延伸率δ=（L1 - L）/ L x 100%面积收缩率ψ=( F1 - F ) / F x 100%绘拉伸图（P—Δl曲线）②铸铁强度极限绘拉伸图（P—Δl曲线）5、比较低碳钢和铸铁的机械性质和两者的破坏特点。
二、压缩实验1、目的：2、使用仪器设备与工具：3、试验步骤：（1）、低碳钢（2）、铸铁4、实验记录及数据整理：（1）、实验记录（2）、数据整理①低碳钢流动极限：②铸铁强度极限：铸铁压缩曲线低碳钢压缩曲线（3）、比较两种材料机械性质和破坏特点三、低碳钢的弹性模量E 测定试验1、目的：2、使用仪器设备与工具：3、试验步骤： （1）、 （2）、 （3）、 （4）、 （5）、 （6）、4、试验记录及数据整理： （1）、测E 实验记录：引伸仪放大倍数K=引伸仪两刀口间距离L=20mm （2）、测E 的数据整理：弹性模量 E=实验二 扭曲实验1、 目的： （1）、测定低碳钢的剪切流动极限τΤ及剪切强度极限τΒ。
（2）、测定铸铁剪切强度极限τΒ。
2、 使用仪器设备与工具：扭转试验机、卡尺。
3、 试验步骤：将试件两端插入扭转试验机的夹头中，加紧试件，用粉笔在试件上沿轴向画线，摇动试验机手柄，给试件加扭矩。
由绘图器记录M n —ψ 曲线。
当扭矩不再明显增加时即为流动时的值M Τ。
越过流动阶段后开动马达加快加载速度，直到试件扭断为止，记下断裂时的扭矩值M B ，并注意观察断口形状。
扭矩在比例极限以内材料完全处于弹性状态，扭转虎克定律为扭转铸铁时，因铸铁在变形很小时就破坏，所以只用手摇加载。
注意观察铸铁试件在扭转过程中的变形及破坏情况，并记录试件断裂时的极限扭矩值 。
注意观察断口形状。
4、实验记录及数据整理： （1）、试验记录（2）、数据整理低碳钢 强度极限：铸 铁 强度极限：低碳钢 铸 铁（3）、比较低碳钢和铸铁的机械性质和两者的破坏特点。
数据压缩算法效果评估说明数据压缩算法是一种常见的数据处理技术，它通过减少数据的冗余信息来实现数据的压缩，从而节省存储空间和提高数据传输效率。
在实际应用中，选择适合的压缩算法对于保证数据的完整性和压缩效果至关重要。
本文将对数据压缩算法的效果评估进行详细说明。
数据压缩算法的效果评估主要包括以下几个方面：压缩比、压缩速度、解压速度以及质量损失。
首先，压缩比是评估数据压缩算法效果的重要指标之一。
它衡量了压缩算法在压缩数据时所能达到的压缩程度。
压缩比的计算公式为：压缩比 = 原始数据大小 / 压缩后数据大小压缩比越高，则表示算法能够更好地减小数据的体积。
一般来说，压缩比越高，算法的效果越好。
但是，在实际应用中需要综合考虑压缩比和压缩速度之间的平衡，因为高压缩比通常意味着更复杂的算法，从而导致压缩速度较低。
其次，压缩速度和解压速度是衡量算法效果的另外两个重要指标。
压缩速度是指将原始数据进行压缩所花费的时间，解压速度是指将压缩后的数据进行解压缩所花费的时间。
一般来说，快速的压缩和解压速度对于提高数据处理效率至关重要。
因此，在选择数据压缩算法时，需要综合考虑压缩速度和解压速度之间的平衡，以满足实际应用中的需求。
最后，质量损失是评估数据压缩算法效果的重要指标之一。
压缩算法在压缩数据时，有时会造成一定程度的质量损失。
例如，图像压缩算法在压缩图像时可能会引起图像的失真。
因此，评估数据压缩算法的效果时，需要考虑到压缩后数据与原始数据之间的差异，以及压缩引起的质量损失对于实际应用的影响。
数据压缩算法的效果评估可以通过实验方法来进行。
首先，选择一组具有代表性的测试数据集，并记录下原始数据的大小。
然后，使用不同的数据压缩算法对原始数据进行压缩，并记录下压缩后数据的大小、压缩时间和解压时间。
最后，对比各种算法的压缩比、压缩速度和解压速度，并评估压缩引起的质量损失。
需要注意的是，数据压缩算法的效果评估是一项复杂的工作，需要综合考虑多个指标，并根据具体应用场景选择合适的算法。
第1篇一、实验目的1. 理解霍夫曼编码的基本原理和实现方法。
2. 掌握霍夫曼编码在数据压缩中的应用。
3. 通过实验，加深对数据压缩技术的理解。
二、实验环境1. 操作系统：Windows 102. 编程语言：C++3. 开发环境：Visual Studio 20194. 数据源：文本文件三、实验原理霍夫曼编码是一种常用的数据压缩算法，适用于无损数据压缩。
它通过使用变长编码表对数据进行编码，频率高的数据项使用短编码，频率低的数据项使用长编码。
霍夫曼编码的核心是构建一棵霍夫曼树，该树是一种最优二叉树，用于表示编码规则。
霍夫曼编码的步骤如下：1. 统计数据源中每个字符的出现频率。
2. 根据字符频率构建一棵最优二叉树，频率高的字符位于树的上层，频率低的字符位于树下层。
3. 根据最优二叉树生成编码规则，频率高的字符分配较短的编码，频率低的字符分配较长的编码。
4. 使用编码规则对数据进行编码，生成压缩后的数据。
5. 在解码过程中，根据编码规则恢复原始数据。
四、实验步骤1. 读取文本文件，统计每个字符的出现频率。
2. 根据字符频率构建最优二叉树。
3. 根据最优二叉树生成编码规则。
4. 使用编码规则对数据进行编码，生成压缩后的数据。
5. 将压缩后的数据写入文件。
6. 读取压缩后的数据，根据编码规则进行解码，恢复原始数据。
7. 比较原始数据和恢复后的数据，验证压缩和解码的正确性。
五、实验结果与分析1. 实验数据实验中，我们使用了一个包含10000个字符的文本文件作为数据源。
在统计字符频率时，我们发现字符“e”的出现频率最高，为2621次，而字符“z”的出现频率最低，为4次。
2. 实验结果根据实验数据，我们构建了最优二叉树，并生成了编码规则。
使用编码规则对数据源进行编码，压缩后的数据长度为7800个字符。
将压缩后的数据写入文件，文件大小为78KB。
接下来，我们读取压缩后的数据，根据编码规则进行解码，恢复原始数据。
比较原始数据和恢复后的数据，发现两者完全一致，验证了压缩和解码的正确性。
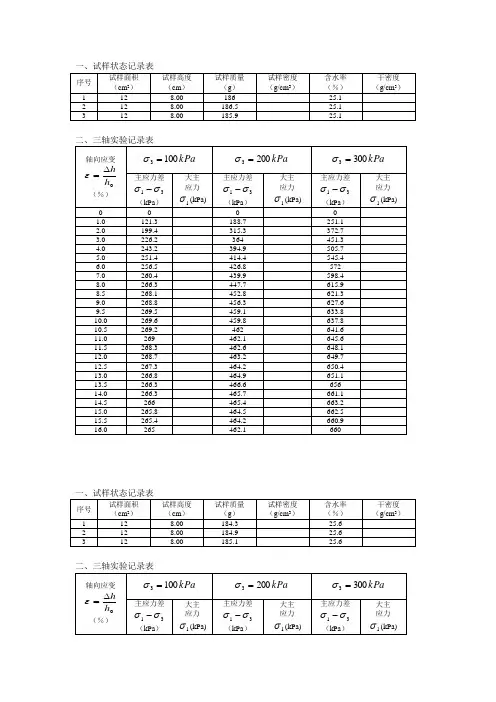
压缩实验报告(总4页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除实验报告（二）实验名称：低碳钢和铸铁的压缩实验 实验目的：极1、测定在压缩时低碳钢的屈服极限S σ，及铸铁的强度限b σ。
2、观察它们的破坏现象，并比较这两种材料受压时的特性，绘出外力和变形间的关系曲线（L F ∆-曲线）。
实验设备和仪器：材料试验机、游标卡尺压缩试件：金属材料的压缩试件一般制成圆柱形，如图所示，并制定31≤≤dh。
实验原理：1、低碳钢低碳钢轴向压缩时会产生很大的横向变形，但由于试样两端面与试验机夹具间存在摩擦，约束了横向变形，故试样出现鼓胀。
为了减少鼓胀效应的影响，通常在端面上涂上润滑剂。
压缩过程中的h弹性模量、屈服点与拉伸时相同A F /S S =σ。
继续加载，试样越压越扁，由于横截面上面积不断增大，试样抗压能力也随之提高，曲线继续上升，所以一般不发生压缩的破坏。
因此不测抗压强度极限。
2、铸铁由于变形很小，所以尽管有端面摩擦，鼓胀效应却并不明显，而是当盈利达到一定值后，试样在轴线大约成45°方向上发生断裂。
将最高点所对应的压力值F b 除以原试样横截面面积A ，即得铸铁的抗压强度b σ=F b /A 。
实验步骤：1、低碳钢的压缩实验试件准备：用游标卡尺测量试件的直径d ，在试件中部相互垂直的方向上测两次，求平均值。
1）、试验机的准备：首先了解试验机的基本构造原理和操作方法，学习试验机的操作规程。
选择合适的横梁移动范围，然后将试件尽量准确地放在机器活动承垫中心上，开动机器，使横梁上压头落在万向头上，使试件承受轴向压力。
2）、进行实验：开动机器，使试件缓慢均匀加载，低碳钢在压缩过程中产生屈服以前基本情况与拉伸时相同，载荷到达B 时，位移-负荷曲线变平缓，这说明材料产生了屈服，当载荷超过B 点后，塑性变形逐渐增加，试件横截面积逐渐明显地增大，试件最后被压成鼓形而不断裂，故只能测出产生流动时的载荷S F ，由A F /S S =σ得出材料受压时的屈服极限而得不出受压时的强度极限。
压缩实验一、实验目的1．测定低碳钢的压缩屈服极限和铸铁的压缩强度极限。
2．观察和比较两种材料在压缩过程中的各种现象。
二、实验设备、材料万能材料试验机、游标卡尺、低碳钢和铸铁压缩试件。
三、 实验方法1． 用游标卡尺量出试件的直径d 和高度h 。
2． 把试件放好，调整试验机，使上压头处于适当的位置，空隙小于10mm 。
3． 运行试验程序，加载，实时显示外力和变形的关系曲线。
4． 对低碳钢试件应注意观察屈服现象，并记录下屈服载荷F s =22.5kN 。
其越压越扁，压到一定程度（F=40KN ）即可停止试验。
对于铸铁试件，应压到破坏为止，记下最大载荷F b =35kN 。
打印压缩曲线。
5． 取下试件，观察低碳钢试件形状: 鼓状；铸铁试件，沿 55~45方向破坏。
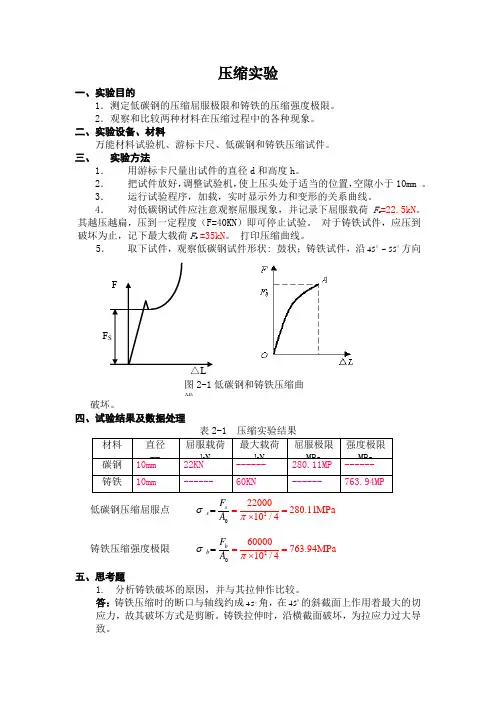
四、试验结果及数据处理 材料 直径 mm 屈服载荷 kN 最大载荷 kN 屈服极限 MPa 强度极限 MPa 碳钢 10mm 22KN ------ 280.11MP a ------铸铁 10mm ------ 60KN ------ 763.94MPa 低碳钢压缩屈服点 022*******.11MPa 10/4s s F A πσ=⨯== 铸铁压缩强度极限 0260000763.94MPa 10/4b b F A πσ=⨯== 五、思考题1. 分析铸铁破坏的原因，并与其拉伸作比较。
答：铸铁压缩时的断口与轴线约成 45角，在 45的斜截面上作用着最大的切应力，故其破坏方式是剪断。
铸铁拉伸时，沿横截面破坏，为拉应力过大导致。
F SF△L图2-1低碳钢和铸铁压缩曲线2. 放置压缩试样的支承垫板底部都制作成球形，为什么？答：支承垫板底部都制作成球形自动对中，便于使试件均匀受力。
3. 为什么铸铁试样被压缩时，破坏面常发生在与轴线大致成 55~45的方向上？答：由于内摩擦的作用。
4. 试比较塑性材料和脆性材料在压缩时的变形及破坏形式有什么不同？ 答：塑性材料在压缩时截面不断增大，承载能力不断增强，但塑性变形过大时不能正常工作，即失效；脆性材料在压缩时，破坏前无明显变化，破坏与沿轴线大致成 55~45的方向发生，为剪断破坏。
实验二图像预测编码一、实验题目:图像预测编码：二、实验目的:实现图像预测编码和解码.三、实验内容:给定一幅图片，对其进行预测编码，获得预测图像，绝对残差图像, 再利用预测图像和残差图像进行原图像重建并计算原图像和重建图像误差.四、预备知识:预测方法，图像处理概论。
五、实验原理:根据图像中任意像素与周围邻域像素之间存在紧密关系,利用周围邻域四个像素来进行该点像素值预测,然后传输图像像素值与其预测值的差值信号，使传输的码率降低，达到压缩的目的。
六、实验步骤:(1)选取一幅预测编码图片;(2)读取图片内容像素值并存储于矩阵;(3)对图像像素进行预测编码;(4)输出预测图像和残差图像;(5)根据预测图像和残差图像重建图像;(6)计算原预测编码图像和重建图像误差.七、思考题目:如何采用预测编码算法实现彩色图像编码和解码.八、实验程序代码:预测编码程序1:编码程序:i1=imread('lena.jpg');if isrgb(i1)i1=rgb2gray(i1);endi1=imcrop(i1,[1 1 256 256]);i=double(i1);[m,n]=size(i);p=zeros(m,n);y=zeros(m,n);y(1:m,1)=i(1:m,1);p(1:m,1)=i(1:m,1);y(1,1:n)=i(1,1:n);p(1,1:n)=i(1,1:n);y(1:m,n)=i(1:m,n);p(1:m,n)=i(1:m,n);p(m,1:n)=i(m,1:n);y(m,1:n)=i(m,1:n);for k=2:m-1for l=2:n-1y(k,l)=(i(k,l-1)/2+i(k-1,l)/4+i(k-1,l-1)/8+i(k-1,l+1)/8);p(k,l)=round(i(k,l)-y(k,l));endendp=round(p);subplot(3,2,1);imshow(i1);title('原灰度图像');subplot(3,2,2);imshow(y,[0 256]);title('利用三个相邻块线性预测后的图像');subplot(3,2,3)；imshow(abs(p),[0 1]);title('编码的绝对残差图像');解码程序j=zeros(m,n);j(1:m,1)=y(1:m,1);j(1,1:n)=y(1,1:n);j(1:m,n)=y(1:m,n);j(m,1:n)=y(m,1:n);for k=2:m-1for l=2:n-1j(k,l)=p(k,l)+y(k,l);endendfor r=1:mfor t=1:nd(r,t)=round(i1(r,t)-j(r,t));endendsubplot(3,2,4);imshow(abs(p),[0 1]);title('解码用的残差图像');subplot(3,2,5);imshow(j,[0 256]);title('使用残差和线性预测重建后的图像');subplot(3,2,6);imshow(abs(d),[0 1]);title('解码重建后图像的误差');九、实验结果:图2.1 Lena图像预测编码实验结果预测编码程序2:x=imread('e:\imagebase\cameraman.jpg');figure(1)subplot(2,3,1);imshow(x);title('原始图像');subplot(2,3,2);imhist(x);title('原始图像直方图');subplot(2,3,3);x=double(x);x1=yucebianma(x);imshow(mat2gray(x1));title('预测误差图像');subplot(2,3,4);imhist(mat2gray(x1));title('预测误差直方图');x2=yucejiema(x1);subplot(2,3,5);imshow(mat2gray(x2));title('解码图像');e=double(x)-double(x2);[m,n]=size(e);erms=sqrt(sum(e(:).^2)/(m*n));%预测编码函数；%一维无损预测编码压缩图像x，f为预测系数，如果f默认，则f=1，即为前值预测function y=yucebianma(x,f)error(nargchk(1,2,nargin))if nargin<2f=1;endx=double(x);[m,n]=size(x);p=zeros(m,n);xs=x;zc=zeros(m,1);if length(f)>1for j=1:length(f)xs=[zc xs(:,1:end-1)];p=p+f(j)*xs;endy=x-round(p);elsexs=[zc xs(:,1:end-1)];p=xs;y=x-round(p);end% yucejiema是解码程序,与编码程序用的是同一个预测器function x=yucejiema(y,f)error(nargchk(1,2,nargin));if nargin<2f=1;endif length(f)>1f=f(end:-1,1);[m,n]=size(y);order=length(f);x0=zeros(m,n+order);for j=1:njj=j+order;for i=1:mtep=0.0;for k=order:-1:1tep=tep+f(k)*x0(i,jj-order-1+k);endx0(i,jj)=y(i,j)+tep;endendx=x0(:,order+1:end);else[m,n]=size(y);x0=zeros(m,n+1);for j=1:njj=j+1;for i=1:mx0(i,jj)=y(i,j)+x0(i,jj-1);endendx=x0(:,2:end);end图2.2 摄影师图像预测编码实验结果实验三图像熵编码与压缩一、实验题目：图像熵编码与压缩二、实验目的：学习和理解建立在图像统计特征基础上的熵编码压缩方法。
三、实验内容：（1）编程实现二值文本图像的行程编码。
（2）编程实现灰度图像的霍夫曼编码，并计算图像熵、平均码字长度及编码效率。
四、预备知识：（1）熟悉行程编码原理。
（2）熟悉霍夫曼编码原理。
（3）熟悉在MATLAB环境下对图像文件的I/O操作。
五、实验原理：（1）行程编码行程编码是将一行中颜色相同的相邻像素用一个计数值和该颜色值来代替。
比如，aaabbcccccdddeeee可以表示为3a2b5c3d4e。
如果一幅图像由很多块颜色相同的大面积区域组成，则采用行程编码可大大提高压缩效率，尤其适用于二值图像。
但当图像中每两个相邻像素的颜色都不相同时，采用这种方法不但不能实现数据压缩，反而使数据量增加一倍。
因此，对复杂的图像都不能单纯地采用行程编码。
（2）霍夫曼编码霍夫曼编码是一种代码长度不均匀的编码方法。
它的基本原理是按信源符号出现的概率大小进行排序，出现概率大的分配短码，反之则分配长码。
霍夫曼编码基本步骤如下：步骤1：统计图像每个灰度级（信息符号）出现的概率，并按概率从大到小进行排序。
步骤2：选出概率最小的两个值进行组合相加，形成的新概率值和其他概率值形成一个新的概率集合。
步骤3：重复步骤2，反复利用合并和排序的方法，直到只有两个概率为止。
步骤4：分配码字，对最后两个概率一个赋予“0”码字，一个赋予“1”码字。
如此反向进行到开始的概率排列，这样就得到了各个符号的霍夫曼编码。
六、实验步骤：（1）编程实现二值文本图像的行程编码。
（2）编程实现连续灰度图像的霍夫曼编码，并计算图像熵、平均码字长度及编码效率。
七、思考题目：将行程编码与霍夫曼编码结合，能否提高压缩效果？试验证之。
八、实验程序代码：（1）二值文本图像的行程编码程序：clear,close allt=imread('text.png');ts=logical(t);codetable=zeros(1,20000);[m,n]=size(ts);nn=n+1;icodecount=1;for i=1:mp1=ts(i,1);%第i行，第1个像素ipcount=1;%同一灰度值连续出现的次数for j=2:np2=ts(i,j);if ((p1==p2)&(ipcount<nn))ipcount=ipcount+1;elsecodetable(icodecount)=ipcount;codetable(icodecount+1)=p1;icodecount=icodecount+2;p1=p2;ipcount=1;end;end;codetable(icodecount)=ipcount;codetable(icodecount+1)=p1;icodecount=icodecount+2;codetable(icodecount)=nn;%行结束符号icodecount=icodecount+1;end;codetable(icodecount)=65535;%码表结束符号（2）连续灰度图像的霍夫曼编码程序代码function s=reduce(p)s=cell(length(p),1);for i=1:length(p)s{i}=i;end;n=size(s,1);while n>2[p,i]=sort(p);p(2)=p(1)+p(2);p(1)=[];s=s(i);s{2}={s{1},s{2}};s(1)=[];n=size(s,1);end;function makecode(sc,codeword)global CODEif isa(sc,'cell')makecode(sc{1},[codeword 0]);makecode(sc{2},[codeword 1]);elseCODE{sc}=char('0'+codeword); end;function CODE=huffman(p)global CODECODE=cell(length(p),1);if length(p)>1p=p/sum(p);s=reduce(p);makecode(s,[]);elseCODE={'1'};end;function y=mat2huff(x)y.size=uint32(size(x));x=round(double(x));xmin=min(x(:));xmax=max(x(:));pmin=double(int16(xmin)); pmin=uint16(pmin+32768); y.min=pmin;x=x(:)';h=histc(x,xmin:xmax); maxh=max(h);if maxh>65535h=65535*h/maxh; end;h=uint16(h);y.hist=h;map=huffman(double(h)); hx=map(x(:)-xmin+1);hx=char(hx)';hx=hx(:)';hx(hx==' ')=[];ysize=ceil(length(hx)/16); hx16=repmat('0',1,ysize*16); hx16(1:length(hx))=hx;hx16=reshape(hx16,16,ysize); hx16=hx16'-'0';twos=pow2(15:-1:0);%y.code=uint16(sum(t3,2))'; t1=ones(ysize,1);t2=twos(t1,:);t3=hx16.*t2;t4=sum(t3,2);y.code=uint16(t4)';实验四 图像DCT 变换编码与压缩一、实验题目：图像DCT 变换编码与压缩二、实验目的：（1）掌握离散余弦变换DCT 的实现方法，了解DCT 的幅度分布特性，从而加深对DCT 变换的认识。
