ii c ○ Koninklijke Philips Electronics N.V. 2006 Philips Restricted TN-PR-TN 200600495 Tit
- 格式:pdf
- 大小:903.34 KB
- 文档页数:43

PhilipsLCD Monitor with Digital TV tuner55 cm (21.5") w T-line1920x1080 Full HD221T1SB1Digital Full HD TV monitor in a stylish packageExperience brilliant multimedia performance with this stylish, glossy and stunning Full HD 1080p display with Digital TV tuner! Combined with HDMI and AV inputs along with powerful sound the 221T1 takes entertainment to a new height!Best picture quality•Full HD LCD display, with a 1920x1080p resolution •SmartContrast 50000:1 for incredible rich black details•Smart mode selects a perfect mode for what you are watching •Up to 5ms response time for clear, fast moving action Experience true multimedia•SmartSound selects a perfect mode for audio performance •HDMI-ready for top quality, multimedia experience •Incredible Surround for enhanced audio enjoyment Ready for digital•MPEG4 HDTV reception via DVBT tunerGreat convenience•Built-in TV tuner for viewing TV programs on your PC monitor •Remote control for TV functionsHighlightsSmartContrast ratio 50000:1You want the LCD flat display with the highest contrast and most vibrant images. Philips advanced video processing combined with unique extreme dimming and backlightboosting technology results in vibrant images. SmartContrast will increase the contrast with excellent blacklevel and accurate rendition of dark shades and colors. It gives a bright, lifelike picture with high contrast and vibrant colorsHDMI ReadyA HDMI-ready device has all the required hardware to accept High-DefinitionMultimedia Interface (HDMI) input, high quality digital video and audio signals all transmitted over a single cable from a PC or any number of AV sources including set-top boxes, DVD players and A/V receivers and video cameras.MPEG4 HDTVHDTV allows you to watch High Definition TV in the best picture and sound quality without additional set-top box. With the built in DVBT tuner that can handle state-of-the-art MPEG-4 formats, you can now receive and watch High Definition TV programs and other rich multimedia contents in Digital Quality Incredible SurroundIncredible Surround is an audio technology from Philips that dramatically magnifies the sound field to immerse you in the audio. Using state-of-the-art electronic phase shifting, Incredible Surround mixes sounds from left and right in such a way that it expands the virtual distance between the two speakers. This wider spread greatly enhances the stereo effect and creates a more natural sounddimension. Incredible Surround allows you to experience total surround with greater depth and width of sound, without the use of additional speakers.5ms response timeResponse time measures signal reaction speed in milliseconds. Faster response time is better as it eliminates visible image artifacts that could dampen your experience when viewing fast moving images or objects. In this case, thisLCD panel gives you 5ms response time so that you can watch your LCD TV with a clear, fast moving action.Full HD LCD display 1920x1080pThe Full HD screen has the widescreenresolution of 1920 x 1080p. This is the highest resolution of HD sources for the best possible picture quality. It is fully future proof as it supports 1080p signals from all sources, including the most recent like Blu-ray and advanced HD game consoles. The signalprocessing is extensively upgraded to support this much higher signal quality and resolution. It produces brilliant flicker-free progressive scan pictures with superb brightness and colors.Smart modeThe optimum picture and sound depends on various aspects like the video source, content type, surroundings of the room, type of display device etc. Smart Mode has predefined picture and sound settings conveniently preset by the way you use your TV. The ‘Personal’ setting, allows you to define the picture settingsaccording to your preference, store it and gain easy access for future selection. All these conveniently built into your TV for optimalsettings.®Issue date 2011-06-07Version: 1.0.112 NC: 8670 000 66737EAN: 87 12581 55904 5© 2011 Koninklijke Philips Electronics N.V.All Rights reserved.Specifications are subject to change without notice. Trademarks are the property of Koninklijke Philips Electronics N.V. or their respective owners.SpecificationsPicture/Display•Aspect ratio: 16:9, Widescreen •Brightness: 250 cd/m²•SmartContrast: 50000:1•Contrast ratio (typical): 1000:1•Response time (typical): 5 ms •Panel resolution: 1920 x 1080•Viewing angle: 170º (H) / 160º (V)•Picture enhancement: Progressive scan, TrueVision•Screen enhancement: Anti-Reflection coated screen•Diagonal screen size: 21.5 inch / 54.61 cmSound•Output power (RMS): 2 x 3W•Sound Enhancement: Incredible Surround, Smart Sound•Sound System: Mono, StereoTuner/Reception/Transmission•TV system: PAL I, PAL B/G, PAL D/K, SECAM B/G, SECAM D/K, SECAM L/L'•Video Playback: NTSC, PAL, SECAM •Aerial Input: 75 ohm coaxial (IEC75)•Tuner bands: Hyperband, S-Channel, UHF, VHF •Digital TV: DVB Terrestrial *•Tuner Display:PLLConnectivity•Signal Input: VGA (Analog ), HDMI, PC Audio in •Ext 1:SCART in•Ext 2: YPbPr in, Audio L/R in •Ext 3: CVBS out, Audio L/R out•Other connections: Audio L/R in, CVBS in, S/PDIF out (coaxial), USB Service port, Common InterfaceConvenience•Other convenience: VESA mount (100x100mm)•Screen Format Adjustments: Widescreen, Normal, Zoom 1, Zoom 2•Smart mode: Movie, Personal, Standard, Vivid, Eco •SmartSound: Music, Speech, Personal •Teletext: 1000 page Smart Text•Ease of Use: Program List, Side Control•Ease of Installation: Plug & Play, Automatic Tuning System (ATS)•On-Screen Display languages: Bulgarian, Croatian, Czech, Danish, Dutch, English, Finnish, French, German, Greek, Hungarian, Italian, Norwegian, Polish, Portuguese, Russian, Serbian, Slovakian, Slovenian, Spanish, Swedish, Simplified Chinese, Turkish•Remote control: 221T1 Remote controlPower•On mode: 31W (Typ.@monitor mode)•Off mode: <0.3W•Mains power: 100-240V, 50/60Hz •Ambient temperature: 0 °C to 40 °CDimensions•Product with stand (mm): 382 x 528 x 176 mm •Product without stand (mm): 347 x 528 x 65 mm •Packaging in mm (WxHxD): 451 x 620 x 160 mmWeight•Product with stand (kg): 4.6 kg •Product without stand (kg): 4.5 kg •Product with packaging (kg): 6.5 kgAccessories•Included accessories: Power cord, RemoteControl, Batteries for remote control, Quick start guide, User Manual, Table top standSupported Display Resolution•Computer formats Resolution Refresh rate 1920 x 1080 60Hz •Video formats Resolution Refresh rate 480i 60Hz 480p 60Hz 576i 50Hz 576p 50Hz 720p 50, 60Hz 1080i 50, 60Hz 1080p 50, 60Hz。

飛利浦 GoGear MP4 播放機配備 FullSound™ 功能ViBE8GB*SA2VBE08K優異的音效體驗體積小巧,娛樂無限這款超小型、超耐用的 GoGear Vibe 與飛利浦 FullSound™ 技術琴瑟和鳴、合作無間,共同強化音效體驗,並有 Songbird 供您探索並同步處理最酷的音樂。
不僅如此,舒適的耳機更完美了您的娛樂體驗。
優異音效•FullSound™ 重現 MP3 音樂優異音質•柔軟橡膠耳塞讓您舒適地聆聽音樂豐富您的生活• 以數位有聲書及其他商品為主要特色•1.5 吋全彩顯示,方便進行瀏覽和觀賞專輯藝術封面•鋁合金機身,堅固又耐用•FM 收音機內含 RDS 和 20 組預設電台,讓您的音樂選擇多更多•語音錄音功能讓您隨時隨地紀錄任何點滴簡單直覺•飛利浦 Songbird :一套簡單易用的程式,讓您探索、播放、同步處理音樂•利用 Smart Shuffle 功能選擇您最想先聽的音樂•搭配全彩專輯藝術封面,簡單直覺的使用者介面•資料夾檢視功能可以整理和檢視媒體檔案,就像在電腦操作一樣FullSound™飛利浦創新的 FullSound 技術能精準而忠實的恢復 MP3 壓縮音樂的聲音細膩度,大幅的豐富並提昇音質,讓您完全體驗 CD 音效,絕不失真。
FullSound 以音訊後製處理演算技術為基礎,結合飛利浦最為人稱道的原音重現技術和最新一代數位訊號處理器 (DSP),帶給您更深沈飽滿、寬廣震撼的低音、大幅強化人聲與樂器清晰度以及豐富的細節。
讓直達靈魂深處、令人不禁舞動的逼真音效,引領您重新認識 MP3 壓縮音樂。
飛利浦 Songbird您的 GoGear 播放器隨附飛利浦 Songbird ,是一套簡單易用的程式,能讓您探索和播放所有的媒體,並與您的飛利浦 GoGear 完整同步。
其直覺式與強大的音樂管理功能,能讓您透過音樂與媒體商店、服務和網站,直接在程式中探索新的演唱者和音樂風格。

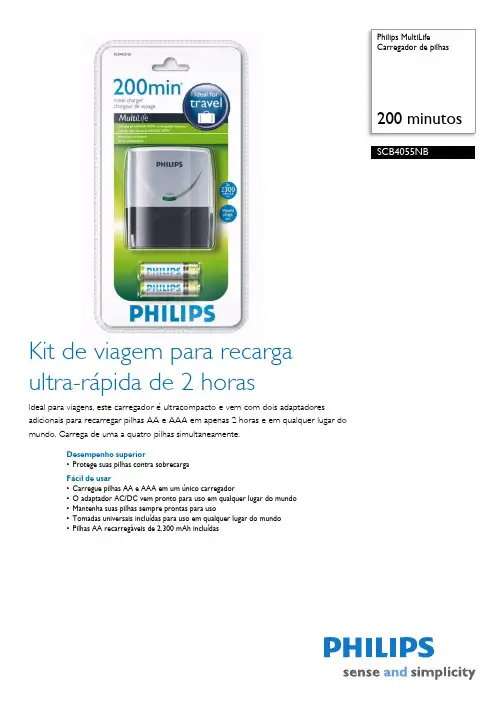
Philips MultiLifeCarregador de pilhas200 minutosSCB4055NB Kit de viagem para recargaultra-rápida de 2 horasIdeal para viagens, este carregador é ultracompacto e vem com dois adaptadoresadicionais para recarregar pilhas AA e AAA em apenas 2 horas e em qualquer lugar domundo. Carrega de uma a quatro pilhas simultaneamente.Desempenho superior•Protege suas pilhas contra sobrecargaFácil de usar•Carregue pilhas AA e AAA em um único carregador•O adaptador AC/DC vem pronto para uso em qualquer lugar do mundo•Mantenha suas pilhas sempre prontas para uso•Tomadas universais incluídas para uso em qualquer lugar do mundo•Pilhas AA recarregáveis de 2.300 mAh incluídasData de emissão2009-11-11Versão: 1.0.612 NC: 8670 000 37762EAN: 87 12581 40135 1© 2009 Koninklijke Philips Electronics N.V.Todos os direitos reservados.As especificações estão sujeitas a alterações sem aviso prévio. As marcas registradas são de responsabilidade da Koninklijke Philips Electronics N.V. ou de seus representantes legais Especificações Carregador de pilhas 200 minutosDestaques Carregue AA e AAA O carregador foi projetado para carregar pilhas AA e AAA.Pronto para uso em qualquer lugar do mundo O adaptador AC/DC funciona com voltagens de entrada de 100 a 240 V. Basta conectar o conversor de tomada adequado para o país e usar o carregador em qualquer lugar do mundo.Proteção inteligente de recarga O sensor especial detecta quando as pilhas estão totalmente carregadas e passa para o modo de recarga lenta para mantê-las carregadas e prontas para uso. A proteção contra sobrecarga estende a vida das pilhas evitando danos causados por sobrecarga.Carga lenta Todas as baterias recarregáveis estão sujeitas ao autodescarregamento com o passar do tempo. O carregamento lento automático mantém suas pilhas carregadas e prontas para uso quando estão no carregador conectado à eletricidade.Tomadas universais incluídas Os dois adaptadores incluídos podem ser conectados à tomada original para que você use o carregador em países onde são usadas tomadas padrão do Reino Unido ou dos EUA.AA MultiLife de 2.300 mAh incluída Os 2.300 mAh de energia fazem com que seu audio player ou sua câmera digital funcionem por mais tempo.Alimentação •Pilhas incluídas •Capacidade da bateria: 2.300 mAh •Fonte de alimentação: 100-240 VAC, 50/60 Hz Especificações técnicas •Material da estrutura: ABSEspecificações ambientais •Metais pesados: Sem Cd, Sem Hg, Sem Pb •Material de embalagem: PET •Tipo da embalagem: Blister em concha Dimensões do produto •Comprimento do cabo: 0 cm •Dimensões do produto (L x A x P): 0 x 0 x 0 cm •Peso:0 kgDimensões da embalagem •Dimensões da embalagem (L x A x P): 13,1 x 25 x 8,5 cm •Peso líquido: 0.24 kg •Peso bruto: 0,298 kg •Peso da embalagem: 0,058 kg •EAN: 87 12581 40135 1•Número de produtos inclusos: 1•Tipo da embalagem: Blister Embalagem externa •Embalagem externa (L x L x A): 32,7 x 20 x 16 cm •Peso líquido: 0,96 kg •Peso bruto: 1,5 kg •Peso da embalagem: 0,54 kg •EAN: 87 12581 40137 5•Número de embalagens para o cliente: 4。



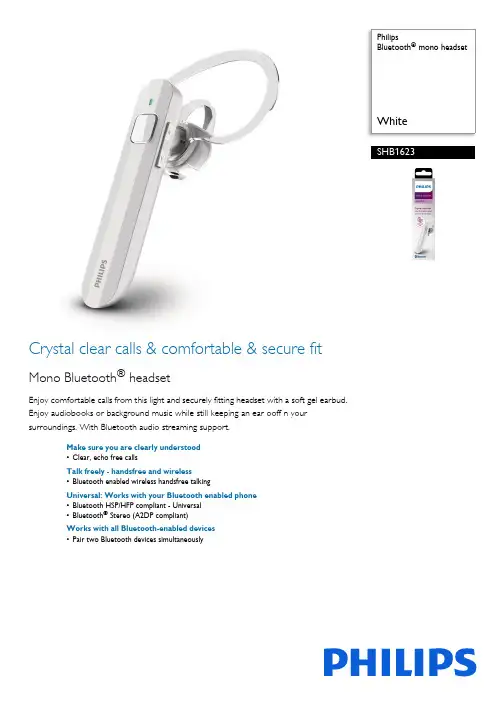
PhilipsBluetooth® mono headsetWhiteSHB1623Crystal clear calls & comfortable & secure fitMono Bluetooth® headsetEnjoy comfortable calls from this light and securely fitting headset with a soft gel earbud.Enjoy audiobooks or background music while still keeping an ear ooff n yoursurroundings. With Bluetooth audio streaming support.Make sure you are clearly understood•Clear, echo free callsTalk freely - handsfree and wireless•Bluetooth enabled wireless handsfree talkingUniversal: Works with your Bluetooth enabled phone•Bluetooth HSP/HFP compliant - Universal•Bluetooth® Stereo (A2DP compliant)Works with all Bluetooth-enabled devices•Pair two Bluetooth devices simultaneouslyIssue date 2022-04-24Version: 4.1.412 NC: 8670 001 45832EAN: 69 59033 84276 4© 2022 Koninklijke Philips N.V.All Rights reserved.Specifications are subject to change without notice. Trademarks are the property of Koninklijke Philips N.V. or their respective SpecificationsBluetooth® mono headsetWhiteHighlightsClear, echo free callsEnjoy clear, echo free calls with the headsets' highly sensitive microphone and smart acoustic design.Wireless handsfree talkingUsing your cellphone without a headset can be inconvenient and unsafe. In many locations it is also illegal while driving. Wired handsfree kits add the hassle of a cable. A Bluetooth headset replaces the cable with a short range wireless Bluetooth connection, so your hands are free and your freedom to move is not hampered by a cable.Because the transmitted energy close to your head is much lower than that radiated from your mobile phone Bluetooth also decreases potential risks associated with cellphone radiation.Bluetooth HSP/HFP compliantBluetooth is a cable replacement technology.Bluetooth is a global standard, so Bluetooth devices of different manufacturers can interoperate using shared Bluetooth profiles. HSP (Handset Profile) and HFP (Handsfree Profile) are the profiles required for typical Bluetooth headset operations. If your mobile phone is compliant to HSP or HFP (like virtually any Bluetooth enabled phone) this headset will work with it. The Bluetooth word mark and logos are owned by the Bluetooth SIG, Inc. and any use of such marks by Koninklijke Philips Electronics N.V. is under license.Pair two Bluetooth devices Pair two Bluetooth devices simultaneously Bluetooth ® StereoBluetooth ® Stereo (A2DP compliant)Connectivity•Bluetooth profiles: handsfree, headset •Bluetooth version: 3.0+EDR•Maximum range: up to 33 feet / 10 mConvenience•Call management: Switch between call and music, Answer / End call, Reject call, Last number redial, Call transferPower•Talk time:up to 5 hour(s)•Battery Type:Li-polymer •Rechargeable•Power supply headset: via USB adapter •Standby time: up to 120 hour(s)Accessories•Included: Quick start guide, USB charging cableInner Carton•Gross weight: 0.38 kg•GTIN: 2 48 95185 63017 9•Inner carton (L x W x H): 22.3 x 20.7 x 6.7 cm •Nett weight: 0.042 kg•Number of consumer packagings: 6•Tare weight: 0.338 kg Outer Carton•Gross weight: 2.71 kg•GTIN: 1 48 95185 63017 2•Outer carton (L x W x H): 63.9 x 23.7 x 16 cm •Nett weight: 0.252 kg•Number of consumer packagings: 36•Tare weight: 2.458 kgPackaging dimensions•Packaging dimensions (W x H x D): 9.5 x 17.5 x 3.5 cm•EAN: 48 95185 63017 5•Gross weight: 0.05 kg •Nett weight: 0.007 kg•Number of products included: 1•Packaging type: Carton •Tare weight: 0.043 kg•Type of shelf placement: BothProduct dimensions•Product dimensions (W x H x D): 1.28 x 5.88 x 1.98 cm •Weight: 0.007 kg。

揭秘飞利浦最初二十年:从灯泡工房到欧洲第三大照企张焜杰【摘要】闻名天下的荷兰皇家飞利浦电子公司(Koninklijke Philips ElectronicsN.V.),成立超过120年,是当今世界上最大的电子公司之一.在过去,与美国的通用电气(GE)、德国的西门子(Siemens)、日本的东芝(Toshiba)并称全球四大电子集团.【期刊名称】《中国照明》【年(卷),期】2016(000)003【总页数】5页(P38-42)【关键词】荷兰皇家飞利浦电子公司 Philips 欧洲工房灯泡初二通用电气西门子【作者】张焜杰【作者单位】【正文语种】中文【中图分类】TN873.93闻名天下的荷兰皇家飞利浦电子公司(Koninklij ke Philips Electronics N.V.),成立超过120年,是当今世界上最大的电子公司之一。
在过去,与美国的通用电气(GE)、德国的西门子(Siemens)、日本的东芝(Toshiba)并称全球四大电子集团。
四大集团,共同的特色都是从电灯泡这个改变人类历史的科技产品开始发迹,进而拓展了真空管技术,开发出了医疗用的X光管、收音机与电视的真空管,最后投入半导体产业,成为全方位的电子王国;不同的是,飞利浦的竞争者们,得天独厚地拥有母国庞大的内需市场,而飞利浦的母国荷兰,至今仍然只是个拥有区区1600万人(比台湾还少)的低地小国。
创业之初,飞利浦在美国与德国的专利诉讼夹杀之下求生,从一个位于安荷芬(Eindhoven)小小的红砖工房开始,在短短20年间成长为欧洲第三大的照明公司;接着,随着第一次世界大战的爆发,抓住了千载能逢的机会,借着各国抵制德国产品而垄断了欧洲;更一举打下无线电收音机市场,发展自有专利技术,将竞争对手抛诸脑后。
时间拉回到1895年1月,新年刚过,深锁眉头的安东‧飞利浦(Anton Philips)背着行囊,从繁华的阿姆斯特丹来到了南方乡下的小村庄安荷芬。

electronic user's manualSafety & Troubleshooting安全与故障排除信息安全注意事项与维护 •故障排除 •监管信息 •其他有关信息安全注意事项与维护警告:不遵循本文规定执行控制、调整或程序有可能导致电击、电及/或机械危险。
连接与使用计算机显示器前请阅读并遵循以下说明:● 如果在一段时期内不会使用显示器,将显示器电源插头拔下。
● 切勿尝试拆除背板,否则可能遭受电击。
仅限合格维护人员拆除背板。
● 请勿将物体放置在显示器顶部,物体可能跌入通风口,或遮蔽通风口,影响显示器电子装置正常冷却。
● 为避免电击风险或永久性损坏机器,切勿将显示器暴露在雨中或使之接触高湿度。
● 切勿使用酒精或氨基液体清洁显示器。
必要时用稍微粘湿的布清洁。
清洁前将显示器电源插头拔下。
● 放置此显示器时, 请确认电源线和插座是容易接上的。
如果遵循本手册说明操作,但显示器不正常运转,请与维护人员接洽。
返回页首关于本电子用户手册关于本指南 •您可能需要的其它文件 •符号说明关于本指南本电子用户指南适用于任何飞利浦彩色显示器用户。
它描述了该显示器特征、设定、操作和其它信息,该资料与印刷版本完全相同。
指南中包含以下章节:● 安全与故障排除信息提供排除常见故障的提示和方法以及您可能需要的其它有关信息。
● “关于本电子用户手册”简要介绍了手册内容、符号说明以及您可能需要参考的其它文件。
● 产品信息简要介绍了本显示器的特征及其技术规格。
● 安装显示器阐述了首次设定过程,简要介绍了显示器使用方法。
● 屏幕显示提供了调整显示器设定值的信息。
● 客户服务与保修列举了世界各地飞利浦消费者信息中心、服务台电话号码以及有关产品保修信息。
● 术语表对技术用语作了更详细的解释。
● 下载选项允许您在硬盘中保存一份完整的手册。
● 常问问题 。
返回页首您可能需要的其它文件除本电子用户指南外,您可能还需要参考以下文件:● 飞利浦彩色显示器快速入门指南总结了显示器设定步骤。
Congratulations on your purchase, and welcome to Philips!T o fully benefit from the support that Philips offers, register your product at /welcome.1 ImportantSafetyRead this user manual carefully before you use this juicer and save it for future reference.Electromagnetic fields (EMF)This Philips appliance complies with all standards regarding electromagnetic fields (EMF). If handled properly andaccording to the instructions in this user manual, the appliance is safe to use based on scientific evidence available today.Built-in safety lockThis feature ensures that you can only switch on the appliance if lid, the blade unit are assembled on the motor unit properly.If lid, blade unit are correctly assembled, the built-in safety lock will be unlocked.2 Overviewa Pusher h Pulp containerb Feeding tube i Switchc Lid j Motor unitd Sieve k Juice container (HR1811 only)e Juice collector l Juice container cover (HR1811 only)f Locking clips m Spoutg Driving shaft3 Before first use1 T ake out all the accessories.2 Clean the parts of the juicer thoroughly before using the juicer for the first time (see chapter ‘Cleaning’).3 Make sure all parts are completely dry before you start using the juicer.4Using the juicerExtracting JuiceThe juicer can be used for preparing fresh fruit juices. Pulp, pips and skins will be separated.Make sure the control switch is off. Then, connect to the power socket.1 Clean and cut large ingredients into pieces that fit into the feeding tube.2 T urn the control switch to the suggested speed.3 Put your ingredients through the feeding tube.4 Push the ingredients gently down with the pusher.5 CleaningIt is easiest to clean the juicer,its parts and accessories immediately after use.1 After you unplug the juicer, detach the used accessories, parts and clean them in lukewarm washing up liquid.2 Rinse all accessories and parts under a tap.3 For better cleaning, you can use the brush to clean.6 Storage1 Keep it in dry places to avoid the sieve, blades get rusty.2 Plug could be inserted into the main unit for storage.7 RecipesWith Juicer, you can experiment endlessly and try out all kind of recipes. Y ou can make delicious juices, shakes, soups, and sauces in no time at all. T o give you an idea of the possibilities, you can go to .For Juicing IngredientsWeight Speed Cucumbers/ Spinach/ Melons/ T omatoes/ Oranges/ Lemon/ Grapes/ Berries500g 1Apples/ Carrots/ Pineapples/ Beetroots/ Celery/ Pear 500g2Ginger juice recipeJuice 60g ginger for 10 seconds. You have to exert a higher pressing force (of up to 2kg) on the pusher.8 EnvironmentDo not throw away the appliance with normal household waste at the end of its life, but hand it in at an official collection point for recycling. By doing this, you can help to preserve the environment.9 T roubleshootingIf you encounter problems when using this juicer, check the following points before requesting service. If you cannot solve the problem, contact the Philips Consumer Care Center in your country.ProblemSolutionThe juicer does not work.The juicer is equipped with a safety system. If the accessories are not properly connected with the motor unit, the juicer does not work. Check whether the accessories have been connected in the right way (see the various sections). Turn off the juicer first!The motor unit is blocked.T urn off the juicer and process a smaller quantity.The motor unit gives an unpleasant smell during the first few times of use.This is normal for the first few applications. If the smelling continues, check the quantity you are processing, the application time, or used speed.The sieve of the juicer makes contact with the feeding tube or shows a high vibration during processing.T urn off the juicer. Check if the sieve is properly connected. The ribs on the bottom of the sieve should fit properly on the motor coupling opening.Check if the sieve is not damaged. Cracks, fissures, loose grater disc or any other irregularity may cause malfunction.ENUser manualZH-CN 用户手册注册您的产品并在以下网站链接中了解详情HR1811HR1824/welcome技术规格如有变更,恕不另行通知© 2012 Koninklijke Philips Electronics N.V .保留所有权利HR1811_HR1824_UM_V3.03140 035 32063内置安全锁此功能可确保您只有将杯盖和刀片组件正确安装在马达装置上,才可以打开产品。
飞利浦,是世界上最大的电子公司之一,1891年成立于荷兰,主要生产照明、家庭电器、医疗系统。
飞利浦现已发展成为一家大型跨国公司,2007年全球员工已达128,100人,在28个国家设有生产基地,在150个国家设有销售机构,拥有8万项专利,实力超群。
2011年7月11日,飞利浦宣布收购奔腾电器(上海)有限公司,金额可能约25亿元。
2011年10月17日,飞利浦电子发布了第三季度财报,第三季度净利润同比下滑85.9%;同时宣布,飞利浦将在全球范围内裁员4500人。
公司类型:公开(NYSE: PHG)公司口号:精于心,简于形(sense and simplicity)成立时间:1891年总部地点:荷兰阿姆斯特丹(Amsterdam)重要人物:万豪敦(Frans van Houton)总裁兼首席执行官何孟阳,首席财政官郝爱德,执行副总裁兼首席技术官主营产业:消费电子主营产品:照明、家庭电器、医疗系统、IT市场份额飞利浦在Interbrand全球最高价值品牌排行榜中公布调查显示:飞利浦2011年全球品牌价值排名第41位,达到86.5亿美元。
世界品牌500强企业2011年排名第85位[1]世界品牌500强企业2008年排名第197位全球30强电子公司中名列第二飞利浦在Interbrand 2008年全球最有价值品牌排名中位居第43位。
[2]飞利浦名列Ethisphere研究院季刊“Ethisphere杂志”2008年度全球最具责任感企业。
[2]全球第一大液晶电视生产商(2008)全球第一大医疗系统公司(2010)全球第二大申请国际专利公司(2009)全球第一大电动剃须刀品牌(2010)全球第一大照明公司(2010)蓝光DVD的主要支持者全球第三大电话公司全球第一大小家电公司全球十大IT公司飞利浦手机飞利浦是全球主要手机品牌。
2006 年10月12日,飞利浦宣布已经签署了意向书,将其现有的移动电话业务转让给中国电子信息产业集团公司(CEC)。
十大品牌护眼台灯排行榜1、飞利浦PHILIPS(飞利浦电子公司是全球个人优质生活领域的领导者)荷兰皇家菲利浦电子公司(Euronext: PHIA, NYSE:PHG,荷兰语:KoninklijkePhilipsElectronicsN.V.,英语RoyalDutchPhilipsElectronics Ltd.),简称菲利浦公司,是世界上最大的电子公司之一。
2、欧司朗(欧司朗已成为世界两大光源制造商之一,十佳护眼台灯品牌)1906年4月17日,Deutsche Gasgluhlicht-Anstalt(德国煤气灯公司,也被称为Auer-Gesellschaft)注册了“OSRAM”商标。
不过官方资料表示欧司朗诞生于1919年。
因为在DeutscheGasgluhlicht-Anstalt注册“OSRAM”商标之后...3、明可达MKD(鹤山市明可达实业有限公司,为国内最早的灯具制造企业之一)创始于1984年,为国内最早的灯具制造企业之一;23年专心专注,成就国内书写台灯顶级品牌;2000多万台精品灯具,畅销国内及全球50多个国家和地区;1000多万学子在明可达灯光的照耀下勤奋苦读,学业有成;800万社会精英在...4、德贝斯DEBASE(德贝斯是全球护眼台灯企业的领航者)德贝斯公司座落于有“家电之乡”美誉的佛山市。
是一家集开发、生产、销售、服务于一体的专业灯饰生产企业,企业拥有自主出口经营权。
“德贝斯”品牌拥有三大系列产品:启蒙系列儿童护眼台灯、扬帆系列时尚护眼台灯、睿智系列办公护眼台灯。
产品以其新颖时尚、健康护眼、品质过硬的绝对优势,深受欧美消费者喜爱,多年来占据了国内护眼台灯领域50%以上的消费群体。
5、良亮(知名品牌,宁波良亮灯饰总厂,十佳护眼台灯品牌)宁波良亮灯饰总厂位于浙江省宁波市镇海区骆驼街道,紧靠329国道,周边有铁路、机场、北仑码头等,交通十分便利。
本厂属股份制企业,占地面积一万多平方米,现有员工近200名。
Technical note TN-PR-TN2006/00495Issued:07/2006Weighting in fuzzy subsumption discoveryRisto GligorovPhilips Research EindhovenPhilips Restrictedc Koninklijke Philips Electronics N.V.2006TN-PR-TN2006/00495Philips RestrictedPhilips Restricted TN-PR-TN2006/00495 Keywords:semantic web,concept hierarchy,music,subsumption discovery,weigh-ing,normalized google distanceAbstract:We address the problem of discovering fuzzy subsumption relations between concepts from different concept hierarchies.We investigatetwo approximate reasoning schemes which aim at improving of thefuzzy subsumption relation assessment.Thefirst scheme utilizes thestructure of a concept hierarchy and the second takes advantage of aGoogle-based dissimilarity measure.We present the results of experi-ments with several music concept hierarchies from actual sites on theInternet.TN-PR-TN2006/00495Philips Restricted Conclusions:In this study,we have addressed the problem of discovering fuzzy sub-sumption relations between concepts from different concept hierarchies.We have examined two weighting schemes.Thefirst exploits the struc-ture of the CH and the second the NGD dissimilarity measure.Fromthe evidence provided in section1.4we can conclude that weightingimproves the accuracy of the fuzzy subsumption relation assessment.The structure-based weighting as it is,depends solely on the struc-ture of the CH.Hence,if the CH’s structure does not preserve theactual supergenre-subgenre relations then the weight values can be mis-leading.Unfortunately,in reality this is the case.ADN,for instance,evenly disperse the classified music genres into a tree-like structure ofdepth2.In order to achieve this artificial structure the designers ofADN music metaschema had to sacrifice some supergenre-subgenre re-lations;Metal and rock are siblings in ADN classification even thoughmetal is a subgenre of rock.Google-based weighting,on the other hand,utilizes the NGD which takes advantage of the vast knowledge available on the web today.Con-sequently,it should provide a more accurate assessment of the weightvalues.Therefore,we are inclined to believe that the Google-basedweighting is a better method.iv c Koninklijke Philips Electronics N.V.2006Philips Restricted TN-PR-TN2006/00495 Contents1Fuzzy subsumption discovery11.1Introduction (1)1.1.1Internet Music Schemas (2)1.1.2Terminology and definitions (3)1.1.3Matching (5)1.1.4Approximate subsumption algorithm (5)1.1.5Weighting (6)1.2Structure-based weighting (8)1.2.1The two-phase method (8)1.2.2Equal cardinality weighting (10)1.2.3Path length weighting (11)1.3Google-based weighting (12)1.3.1Normalized Google Distance (12)1.3.2The weighting scheme (12)1.4Experiments (17)1.4.1Structure-based weighting experiments (18)1.4.2Google-based weighting experiments (19)1.5Conclusion (19)1.6Appendix A (21)1.7Appendix B (26)1.8Appendix C (29)1.9Appendix D (33)c Koninklijke Philips Electronics N.V.2006vPhilips Restricted TN-PR-TN2006/00495Section1Fuzzy subsumption discovery1.1IntroductionThe progress of information technology has made it possible to store and access large amounts of data.However,since people think in different ways and use different termi-nologies to store information,it becomes hard to search each other’s data stores.With the advent of the Internet,which has enabled the integrated access of an ever-increasing number of such data stores,the problem becomes even more serious.The music domain is no exception.(We restrict to legal distribution.)The variety and size of offered con-tent makes it difficult tofind music of interest.It is often cumbersome to retrieve even a known piece of music.Our goal is to improve this Internet music search.We aim to use semantics in the retrieval process,which is conveyed in the Semantic Web.In this context we study the problem of semantic integration over different music provider’s schemas.More specific, the problem is tofind pairs of concepts(genres,styles,classes...)from different metadata schemas that have an equivalent meaning.It is not sufficient to use the concept labels only,since,for example,their position in the schemas influences their meaning as well. Figure1.1illustrates with an example from existing music schemas.Although the labels are equivalent(“Experimental”),they represent different classes.Figure1.1:Two music genres:Although the labels are equivalent,Experimental,they represent different classes.The problem offinding the right music thatfits a user preferences is similar to the problem of matching the schemas of two different providers.The main problem when matching different schemas is the discovery of concept pairs across the schemas that c Koninklijke Philips Electronics N.V.20061TN-PR-TN2006/00495Philips RestrictedFigure1.2:The extracted music schemas.have an equivalent meaning,orfinding a concept with the closest meaning in the other schema when an equivalent one does not exist.The discovery of such similar concepts requires mechanisms that are able tofind fuzzy correspondences rather than the exact ones.In this study,we explore the problem of discovering fuzzy subsumption relations across schemas,and in particular the improvement of the accuracy when assessing fuzzy relations.We develop weighting schemes that emphasize the more important parts of the fuzzy subsumption problem at hand.The document is structured as follows.In the rest of section1.1we explain the problem we are addressing in more detail and introduce the terminology used in this document.In section1.2we present a weighting scheme that utilizes the structure of the metadata schema.In section1.3we lay out a Google-based weighting scheme and in section1.4we present results from the experiments on the effect of weighting.1.1.1Internet Music SchemasOn the Internet,music metadata schemas mostly exist in the form of a navigation path through the music offered.A metadata schema isn’t always offered next to the music,but a visitor can interactively navigate through different pages that list the music. We consider this structure of navigation paths together with the labeling on the links and pages as the metadata schema of that provider.After considering several music provision sites,we selected seven of them and extracted the schema(navigation path): CDNOW()1,MusicMoz2,CD Baby3,ARTIST direct Network4,allmusic 5,LAUNCH cast on Yahoo6and 7.Also,we have extracted the music schema present in the free online encyclopaedia Wikipedia8.In Figure1.2we present a general overview of the data.Philips Restricted TN-PR-TN2006/00495Music classifications and stylesMusic content providers usually classify the music they offer into classes for easy ac-cess.These classes are organized in a hierarchy.We refer to the classified entities as ually these are artists,albums,compilations,other kinds of releases,songs, and etc.The majority of the terms used to identify a class of music entities are music genres and styles,for example Blues,Jazz,....They can be associated with various kinds of attributes that make a further distinction,for example Americal Blues,Electronic Jazz,....Music genres and styles on their own are intrinsically ill-defined,there is no single authority that can decide for a music entity which genre or style it belongs to.For example,it’s becoming increasingly dificult to categorize the newly emerging musical styles that incorporate features from multiple genres.Also,the attempts to clasify particular musicians in a single genre are sometimes ill-founded as they may produce music in a variety of genres over time or even within a single piece.In general,however, two definitions are accepted:intrinsic-a set of rules that decide when an entity belongs to the genre or not,and extrinsic-a set of all possible music entities that belong to the genre.For our purpose,we use the second one and account for the genres and styles as sets of music entities.Consequently,music classification is a collection of music classes described with english language terms,where instances are being classified.It can be modelled as a concept hierarchy.Fuzziness in music classificationThere are no objective criteria that sharply define music classes.Genre is not precisely defined.As a result,different providers often classify the same music entities(artists, albums,songs...)differently.Widely used terms like Pop and Rock do not denote the same sets of artists at different portals.That is also the case for even more specific styles of music like Speed Metal.In our experiments when testing with instance data,we restricted to the artists shared by Music Moz and Artist Direct Network,i.e.artists that are present and classified in both portals.In the sequel we refer to them as MM and ADN,respectively.From the class named Rock(including its subclasses)in MM there are471shared classified artists, in ADN there are245,and196shared artists are classified under Rock in both of them. Hence,from all the artists classified under Rock in at least one of the two portals,only about38%is classified under Rock in both portals,figure1.3.This example shows that there is a high degree of fuzziness present in the music domain.Therefore we expect that exact reasoning methods to create matching are not useful,and approximate methods are more appropriate.1.1.2Terminology and definitionsIn this section we will introduce several terms used in the rest of the text.Definition1(Concept hierarchy)A Concept Hierarchy(CH)is a triple(N,E,l), where N is a set of nodes,E⊆N×N is a set of edges among the nodes,and l:N→L is a function that assigns a label from the set of all labels L to every node.The graph structure underlying the CH represents a directed acyclic graph.c Koninklijke Philips Electronics N.V.20063TN-PR-TN2006/00495Philips RestrictedFigure1.3:Equivalence testing between ADN and MM.Figure1.4:Part of MusicMoz CHIn our case the classifications and the corresponding CHs have tree-like structure. Figures1.4depicts part of the CH used within MuzicMoz electronic catalogue of music. We extracted the CH using the navigation paths and the labeling of the pages that list the music offered by several providers.In the problem of integration,besides the node’s labels in a CH,we can also use the structure implied by the edges.We carry out this idea by introducing the notions of node concept and extension concept of a node.Definition2(Node Concept)Given CH(N,E,l)and n∈N,the node concept of n,designated with C(n),is the concept denoted by the label l(n)attached to n.For instance,the label Alternative attached to node5from MusicMoz CH(figure1.4)reffers to the concept C Alternative which is the node concept for this node i.e.C(5)≡C Alternative.According to[1]and[2]we define the extension concept of a node as follows:Definition3(Extension concept of node)If n1,n2,···,n is the path leading from 4c Koninklijke Philips Electronics N.V.2006the root node n1to the node n in CH(N,E,l)then the extension concept of the node n is the concept given with Ext(n)=C(n1)∩C(n2)∩···∩C(n)Example1C Rock and C Alternative represent the node concepts of nodes3and5, respectively(figure1.4).Extension concept of node5is given with Ext(5)≡C Rock∩C Alternative.The extended concept of a node takes into consideration not only the node label of that node but also the node’s position in the graph.By using the extended concept in-stead of the node concept we capture more semantics.We will clarify this using example 1.Clearly,if looking at the CH(figure1.4)one would deduce that node5semantically coincides with the set of rock music entities that are also members of alternative music genre,which is the exact meaning of Ext(5).Node concept of node5(C Alternative), on the other hand,includes non-rock music entities(members of alternative hip-hop, an altenative music subgenre that has no connection with rock music).Therefore it is semantically inacurate just to consider the node concept.In the rest of the text we will use the terms concept and node concept interchangeably.1.1.3MatchingIn this section we will state the problem of matching different CHs.A CH can be represented as a graph.Therefore the problem of matching CHs can be phrased as a problem of matching graphs.According to[2]we can define graph matching as follows:Mapping element is a4-tuple<m ID,N i1,N j2,R>,i=1,···,h;j=1,···,k;where m ID is a unique identifier of the given mapping element;N i1is the i-th node of thefirst graph, h is the number of nodes in thefirst graph;N j2is the j-th node of the second graph,k is the number of nodes in the second graph;and R specifies a similarity relation of the given nodes.A mapping is a set of mapping elements.Matching is the process of discovering mappings between two graphs through the application of a matching algorithm.In the sequel we will adapt the above definition to better suite our purpose of matching terminologies.We have two concept hierarchies A=(N A,E A,l A)and B= (N B,E B,l B)with the corresponding label sets L A and L B that represent two different terminologies.Let n∈N A be a node from A and m∈N B a node from B.With Ext A(n) and Ext B(m)we will denote the extension concepts of the nodes n and m,respectively. As we have said previously we focus our attention on the problem of discovering fuzzy subsumption relations across CHs,therefore the similarity relation R will be a sumsump-tion relation quantified by a coefficient on[0,1]interval.R measures by what extent the fuzzy subsumption relation between Ext A(n)and Ext B(m)holds.Mapping elements are computed as4-tuples<m ID,Ext A(n),Ext B(m),R>where Ext A(n)and Ext B(m)are extension concepts of nodes n and m,respectively and R is a coefficient that measures by what extent the fuzzy subsumption relation between Ext A(n)and Ext B(m)holds.The algorithm that computes the fuzzy subsumption relation is stated in the next section.1.1.4Approximate subsumption algorithmWe utilize the algorithm stated in[3]that addresses the problem of subsumption test between two propositional logic formulas used to represent classes(concepts).We briefly explain the algorithm.c Koninklijke Philips Electronics N.V.20065The subsumption check between classes can be split into a set of subproblems,each checking if one(left)disjunct is a subclass of a(right)conjunct.If all the subproblems are satisfied,the original problem is also satisfied.In our approximation,we allow a few of the subproblems to be unsatisfiable,while still declaring the original problem satisfiable.The(relative)number of satisfiable subproblems is a measure of how strongly the subclass relation between the two given formulas hold.Below,we explain the approach in a more formal way.In our notion we use the inter-pretation of the concepts as sets and consequently we replace conjunction by intersection relation,and implication by a subset relation.We want to check ifA⊆B(1.1) where A≡A n1∩A n2∩···∩A n I and B≡B m1∩B m2∩···∩B m J,holds.It can be easily seen that(1.1)is true if and only ifA⊆B m(1.2)jholds for all j=1,2,···,J.We refer to the expresions(1.2)as subproblems.Now we introduce the idea of approximation:The relation(1.1)holds ifffor all subproblems the subclass relation(1.2)holds.If for only a few of the subproblems the relation(1.2)doesn’t hold,we may say that the relation(1.1)almost holds.Even more, we can express the strength at which the relation(1)holds as the ratio between the number of false subproblems(subproblems for which the subclass relation doesn’t hold) and the total number of subproblems.We call this ratio the sloppiness and we use the letter s to denote its value:|{j:A⊆B m j|}s(A⊆B)=For this purpose we can“weight”the subproblems to determine their contribution in the end result.In the remainder of this report we address the problem of improving the accuracy when assessing fuzzy subsumption relations by subproblem weighting.We investigate two different approaches to obtain the weighting coefficients.Thefirst ap-proach uses the graph structure of the CH and the second one takes advantage of the vast knowledge available on the web today by using a google-based dissimilarity measure. Both approaches are described in detail in the subsequent sections.c Koninklijke Philips Electronics N.V.20067Figure1.5:Example1.2Structure-based weightingIn structure-based weighting we exploit the graph structure of the concept hierarchy to derive the weights.The approach we take is based on the following two assumptions.•Generally,the greater the distance from the root of the graph the more specific the node concept of the node.•Both,more specific and less specific node concepts are relevant for the sumsumption relation discovery.Figure1.1suggests that when there is high level of agreement between the more specific concepts,thefinal outcome should be mainly influenced by the less specific concepts.Figure1.5,on the other hand,indicates the opposite.The subsumption relation assessment should be mainly influenced by the more specific concepts when there is high level of agreement between the less specific concepts.In-line with these assumptions we investigate aflexible subsumption relation dis-covery method comprised of two phases.In thefirst phase we assign more importance (weight)to less specific concepts,and in the second phase we reverse the situation, more specific concepts receive more importance(weight).From each phase we obtain a sloppiness value.Thefinal sloppiness value is a combination of these two sloppiness values.1.2.1The two-phase methodIn this subsection we will present the aforementioned method.We are given the con-cept hierachies(N A,E A,l A)and(N B,E B,l B).n I and m J are nodes from N A and N B respectively.We want to check the validity ofExt A(n I)≡A n1∩···∩A n I⊆B m1∩···∩B m J≡Ext B(m J)where n1,···,n I is the path leading from root node n1to node n I in CH(N A,E A,l A), m1,···,m J is the path leading from root node m1to node m J in CH(N B,E B,l B),8c Koninklijke Philips Electronics N.V.2006A ni≡C(n i)i=1,···,I and B m j≡C(m j)j=1,···,J.According to the algorithm destribed in section1.1.4we have the following subproblems to solveA⊆B mj(1.4)where A≡A n1∩···∩A n I,j=1,···,J.As said,in thefirst(second)phase more (less)importance is assigned to the more(less)general concepts.Therefore the level of“generality”of a concept plays a central role in our method.In the subsequent sections we will introduce(graph)structure based measures for quantifying this notion of concept “generality”.But,for the time being,given a node concept B mjj=1···,J,we assumethat gen(B mj )measures the generality of the concept B mj.In the sequel we explain themethod in detail.Phase1:The“weight”assigned to the subproblem A⊆B mjin phase1is given byw j=gen(B mj)1.2.2Equal cardinality weightingAs stated previously,we define genre as a set of all music entities that belong to the genre.From a semantics viewpoint,node concepts and extended concepts represent musical genres.Therefore,we can think of node concepts and extended concepts as the set of all entities included in the genre they represent.We can use this interpretation to develop “generality”measure.We focus ourselves on the subproblems given by (1.4)in subsection 1.2.1.We will use the logarithm of cardinality ratio as a generality measure i.e.gen (B m j )=ln|B m j ||B 1∩B 2∩B 22|.From the CH we haveB 1=21 i =2(B 1∩B i )The sets (B 1∩B i ),i =2,···,21,represent different sibling nodes from the CH.Hence,they are pairwise disjoint.If we assume that these sets have equal cardinality we will get the following result |B 1|=20·|B 1∩B 2|.Furthermore,B 1∩B 2=41 i =22(B 1∩B 2∩B i )10cKoninklijke Philips Electronics N.V.2006and(B1∩B2∩B i),i=22,···,41represent different sibling nodes from the CH.There-fore,they are pairwise disjoint.If we again assume that these sets have equal cardinality we obtain the result|B1|=400·|B1∩B2∩B22|Next,we will try to approximately assess the value of|B2||B1∩B2∩B22|.The set B3is partitionedby the sets B1and B2into four disjoint sets,B3\(B1∩B2),(B3∩B1)\(B1∩B2∩B3), (B3∩B2)\(B1∩B2∩B3)and B1∩B2∩B3.We assume that|B3\(B1∩B2)|= |(B3∩B1)\(B1∩B2∩B3)|=|(B3∩B2)\(B1∩B2∩B3)|=|B1∩B2∩B3|.As a consequence we have|B3|=4·|B1∩B2∩B22|The type of partition of a set that we have used in the last two cases is formally defined in Appendix A.Also,in Appendix A we have proved that the number of disjoint sets in which a set A i is partitioned by a family of sets A1,···,A i−1,A i+1,···,A n is equal to2n−1(Appendix A,theorem3).Using this fact,we can deduce,just as we did in the example,thatgen(B mj)=(j−1)ln(2)+ J−1k=j ln(p m k)j=1,···,J−1gen(B mJ)=(J−1)ln(2)where p mj,j=1,···,J−1,is the branching factor(number of children)of the node m j. We reffer to the two-phase method that uses this generality measure as equal cardinality weighting.In Appendix B we state and prove several theorems regarding the maximal values of the weights used in equal cardinality weighting scheme.If we observe the cardinality ratios given in the example we notice that their values decrease exponentially.Consequently,if we substitute these values into(1.5)as generality measures,thefirst subproblem in thefirst phase will receive far more weight than the rest of the subproblems.This observation is also valid for the last subproblem in the second phase.Therefore,thefinal result will be mainly influenced by thefirst and the last subproblem.In order to alleviate this effect we consider the logarithm of the cardinality ratios rather than the actual cardinality ratios,as expressed in(1.7).1.2.3Path length weightingOnce again,we attach our attention to the subproblems given by(1.4)in subsection 1.2.1.We will use the lenght of the path in the graph representation of CH as a generality measure i.e.gen(B mj)=dist(m j,m J)(1.8)where m j and m J are the nodes to whom the node concepts B mj and B mJbelong,respectively.The measure given with(1.8)is calculated in respect to the node m J and it is defined only for the node concepts of the ancestors of m J.We call the two-phase method that uses(1.8)as generality measure path length weighting.c Koninklijke Philips Electronics N.V.2006111.3Google-based weightingThe weighting scheme we consider in this section takes advantage of the vast knowledge available on the web today by using a google-based dissimilarity measure described in the next section.1.3.1Normalized Google DistanceWe utilize a dissimilarity measure,called Normalized Google Distance(NGD),intro-duced in[4].According to[4]each web page indexed by the Google search engine can be observed as a set of index terms.A search for a particular index term returns a certain number of hits-web pages where this term occurred.NGD takes advantage of the number of hits returned by Google to compute the semantic distance between concepts. The concepts are represented with their labels which are fed to the Google search engine as search terms.Given two search terms x and y,the the normalized google distance between x and y,NGD(x,y),can be obtained as followsmax{log f(x),log f(y)}−log f(x,y)NGD(x,y)=to the subproblem A⊆B i,i=1,···,m,depends on how much information the concept B i provides about the concept B.The level of informativeness can be observed as a“semantic closeness”between the concepts B i and B.Intuitively,a concept that is semantically less distant should be more relevant than a concept that is semantically more distant.As a semantic distance measure we use the Normalized Google Distance. The procedure that assigns weights to the subproblems proceeds as follows: First,we compute the normalized google distances.d1=NGD(B1,B)...d m=NGD(B m,B)We normalize these values to the[0,1]intervald 1=d1m i=1d i(1.11)Subsequently,the normalized distance values are converted into similaritiess1=1−d 1...s m=1−d mFinally,from the similarity values the weights for the subproblems are derived.w1=s1mi=1s iAfter solving the subproblems we obtain the sloppiness value in the following manners(A⊆B)= A⊆B i w i(1.12) Google queriesAs said,concepts are represented with their labels.The concept labels are transformed into search queries and fed into the Google search engine.For instance,if we have to compute the NGD between the concepts C rock and C rock∩C alternative we have to gather three pieces of information:the number of hits for the term rock(label of C rock),the number of hits for the terms alternative and rock(labels of C alternative∩C rock)and the number of hits for the tuple of search terms rock and alternative rock(C rock,C alternative∩C rock).To get the number of web pages in which the search term rock occurs we use the query:rock music.Besides music style,the word rock has other senses.One of them is rock as a lump or mass of hard consolidated mineral matter(stone).Therefore,tofilter out the occurrences of the term rock in a non-musical context we add the search term music to the google query.c Koninklijke Philips Electronics N.V.200613Analogously,we retrieve the number of web pages where both search terms alternative and rock occur using the query:alternative rock music.Finally,we use the query: alternative rock music to retrieve the number of pages where the tuple of search terms rock and alternative rock occurs.In general,if we want to compute the NGD between the concepts B i and B,where the label L k denotes the concept B k,k=1,···,m,we proceed as follows: First,we obtain the number of hits for B i using the query:“L i”music.L i might be a multi-word,and by putting quotes around it we force Google to search for the exact occurrences of the word.Second,we obtain the number of hits for B using the query:“L1”···“L m”music. L k,k=1,···,m,might be a multi-word,and by putting quotes around it we force Google to search for the exact occurrences of the word.Finally,we obtain the number of hits for the tuple(B i,B)using the query:“L1”···“L m”music.L k,k=1,···,m,might be a multi-word,and by putting quotes around it we force Google to search for the exact occurrences of the word.L i∈{L1,···,L m}, therefore the last query coincides with the previous.Modified NGDAs said,we compute the NGD values using(1.9)d i=NGD(B i,B)=max{log f(B i),log f(B)}−log f(B i,B)log M−log f(B)(1.14) ord i=NGD(B i,B)=N iNN =N if(B)(1.16)where mNGD stands for modified Normalized Google Distance.14c Koninklijke Philips Electronics N.V.2006ExampleIn this section we explain the process of weighting when assessing fuzzy subsumption relation in detail.In our example we consider the subsumption relation between two styles from MusicMoz and ArtistDirectNetwork portals,seefigure1.11.Thefirst step is to transform the concepts into formulas.The formulas representing the meaning of Country from ADN and Bluegrass Gospel from MM are given as follows:CountryMM=Country∩Bluegrass∩Bluegrass GospelWe use these formulas to test for the subsumption relation between the two concepts Country MM(CountryMM).According to the algorithm described in section1.1.4we have to solve the following subproblems:Country⊆Country−true(Country is on both sides)Country⊆Bluegrass−false,Country⊆Bluegrass Gospel−falseFor this set of subproblems the uniform weighting scheme yields a sloppiness value of 66%.Next,we apply the google-based weighting scheme on the same set of subproblems. As described in section1.3.2we willfirst compute the NGD valuesd1=NGD(Country,Country∩Bluegrass∩Bluegrass Gospel)d2=NGD(Bluegrass,Country∩Bluegrass∩Bluegrass Gospel)d3=NGD(Bluegrass Gospel,Country∩Bluegrass∩Bluegrass Gospel)The google queries“Country”music,“Bluegrass”music,“Bluegrass Gospel”music and “Country”“Bluegrass”“Bluegrass Gospel”music return467000000,24000000,338000 and261000hits,respectively.Consequently,wefind the following mNGD distances:d1=7.44147d2=4.39942d3=0.164622As described in section1.3.2,using these values we derive the weights for the subproblemsw1=0.190081w2=0.336629w3=0.493144In this case the sloppiness value is81%.Compared to the66%sloppiness of the uniform weighting scheme,the google-based weighting scheme yields an accuracy gain of15%.c Koninklijke Philips Electronics N.V.200615。