LMS算法实验报告

LMS 算法自适应均衡器实验08S005073 房永奎一、实验目的1、掌握LMS 算法的计算过程，加深对LMS 算法的理解。

2、研究用LMS 算法自适应均衡引起失真的线性色散信道问题。

3、研究特征值扩散度()R χ和步长参数μ对学习曲线的影响。

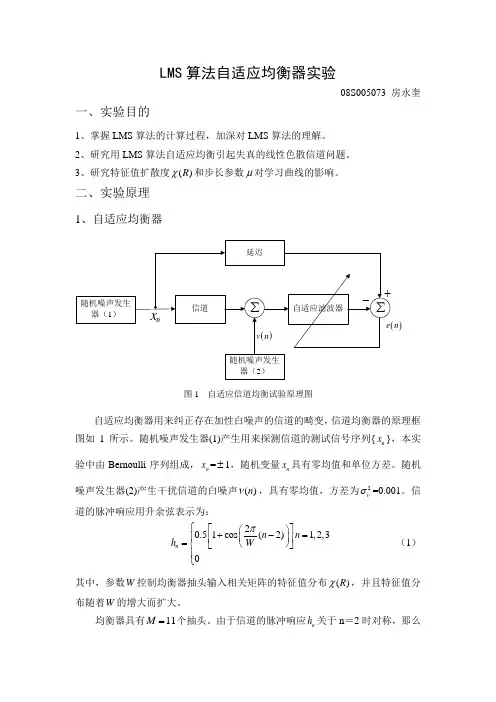
二、实验原理1、自适应均衡器)n图1 自适应信道均衡试验原理图自适应均衡器用来纠正存在加性白噪声的信道的畸变，信道均衡器的原理框图如1所示。

随机噪声发生器(1)产生用来探测信道的测试信号序列{n x }，本实验中由Bernoulli 序列组成，n x =±1，随机变量n x 具有零均值和单位方差。

随机噪声发生器(2)产生干扰信道的白噪声()n ν，具有零均值，方差为2νσ=0.001。

信道的脉冲响应用升余弦表示为：20.51cos (2)1,2,30n n n h W π⎧⎡⎤⎛⎫+-=⎪ ⎪⎢⎥=⎝⎭⎨⎣⎦⎪⎩（1） 其中，参数W 控制均衡器抽头输入相关矩阵的特征值分布()R χ，并且特征值分布随着W 的增大而扩大。

均衡器具有11M =个抽头。

由于信道的脉冲响应n h 关于n ＝2时对称，那么均衡器的最优抽头权值on ω在5n =时对称。

因此，信道的输入n x 被延时了257∆=+=个样值，以便提供均衡器的期望响应。

通过选择匹配横向均衡器中点的合适延时∆，LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。

2、均衡器输入相关矩阵在时刻n ，均衡器第1个抽头的输入为()()()31k k u n h x n k v n ==-+∑ （2）其中所有参数均为实数。

因此，均衡器输入的11个抽头(),(1),,(10)u n u n u n --的自相关矩阵R 为一个对称的1111⨯矩阵。

此外，因为脉冲响应n h 仅在1,2,3n =时为非零，且噪声过程()v n 是零均值、方差为2v σ的白噪声，因此相关矩阵R 是主对角线的，有以下特殊结构所示：()()()()()()()()()()()()()()()012001012021010021000000r r r r r r r r r r r r r r r ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦R （3） 其中()22221230v r h h h σ=+++ （4）()12231r h h h h =+ （5）()132r h h = （6）其中方差20.001v σ=。

音视频信号处理实验报告一、实验目地：1、掌握LMS算法的基本原理，了解自适应波器原理及性能分析的的方法。

2、利用改进LMS算法实现对一个含有噪声的信号的滤波。

二、实验内容：LMS算法的编程仿真。

三、实验原理：LMS算法是自适应滤波器中常用的一种算法，其系统的系数随输入序列而改变。

LMS算法则是对初始化的滤波器系数依据最小均方误差准则进行不断修正来实现的。

在系统进入稳定之前有一个调整的时间，这个时间受到算法步长因子u 的控制，在一定值范围内，增大u会减小调整时间，但超过这个值范围时系统不再收敛，u的最大取值为R的迹。

权系数更新公式为：W(n+1)=W(n)+2u*e(n)*X(n)。

对LMS算法的改进主要集中在对u的算法的改进。

通过对步长大小的控制来控制收敛速度。

本实验采用了u=1/(1+rho_max)算法来避免步长过大同时使补偿足够大来加快收敛速度。

四、实验程序及程序的分析：1、首先产生一个周期性余弦信号作为原始音频信号并输出其波形，如图1t=0:99;xs=10*cos(0.5*t);figure;subplot(2,1,1);plot(t,xs);grid;ylabel('幅值');title('输入周期性信号');2、然后生成一个随机噪声信号作为噪声干扰并输出其波形，如图1randn('state',sum(100*clock));xn=randn(1,100);subplot(2,1,2);plot(t,xn);grid;ylabel('幅值');xlabel('时间');title('随机噪声信号');图13、将其二者相加形成受干扰的音频信号4、利用滤波器权值计算的迭代式求滤波器权值系数并利用最优系数对受干扰信号进行滤波for k = M:N % 第k次迭代x = xn(k:-1:k-M+1); % 滤波器M个抽头的输入y = W(:,k-1).' * x; % 滤波器的输出en(k) = dn(k) - y ; % 第k次迭代的误差W(:,k) = W(:,k-1) + 2*u*en(k)*x;% 滤波器权值计算的迭代式endyn = inf * ones(size(xn));for k = M:length(xn)x = xn(k:-1:k-M+1);yn(k) = W(:,end).'* x;end5、最后分别输出滤波器的输入、输出信号的波形，并且输出两者之差，即误差波形如图2图2由图2我们不难看出，输出信号与原始信号基本吻合。

LMS算法的公式如下：
1 w(n 1) w(n) [ (n)] 2

w(n) e(n) x(n)
归一化LMS算法
归一化 LMS 算法可以看作是时变步长 参数的LMS算法。归一化 LMS 算法是通过 输入向量 x(n)的平方欧氏范数对步长μ进行 “归一化”。归一化 LMS算法的变步长μ的 公式为： μ(n)= 其中μ为算法所取的初始步长。
归一化LMS算法
报告人：王倩
LMS算法
最小均方算法（LMS）是一种以期望响应和滤波器 输出信号之间误差的均方最小为准则，依据输入信号在 迭代过程在估计梯度矢量，并更新权系数以达到最佳的 自适应迭代算法。LMS算法是一种用瞬时值估计梯度矢 量的方法，即 [e 2 (n)] (n) 2e(n) xMS算法公式：
w(n 1) w(n)

x(n)
T ( d ( n ) w (n) x(n))x(n) 2
归一化LMS算法
输入x(n)的平方欧氏范数即二范数去除 算法的初始步长μ，随着输入的增大，变步 长 μ(n)逐渐的减小，算法的稳态误差也相 应逐步减小，具有很好的跟踪收敛效果.可 见归一化 LMS 算法与变步长 LMS 算法相 比，具有更快的收敛速度与更小的稳态误 差。

实验报告实验名称：基于LMS算法的矩阵变换实验目的：本次实验主要是让大家对Widrow 和 Hoff 为 ADALINE 网络设计的 LMS 学习算法进一步了解和认识，熟悉ADALINE 网络，熟知LMS学习算法的原理以及其在MATLAB中的程序实现，在掌握这些基本原理的同时把LMS算法运用求解矩阵的实际问题中。

实验内容：在 Windows 环境中用 C 或MATLAB实现LMS学习算法，并实现X=AY的矩阵变换(矩阵A∈R n⨯m自选)实验步骤：1、熟读LMS算法，深知其原理，并求出其在MATLAB中的实现程序；2、在MATLAB中写出矩阵变换程序，并运行，查看结果是否正确；3、根据实验结果写出实验报告；实验原理：W-H 学习规则是由威德罗和霍夫提出的用来修正权矢量的学习规则，所以用他们两人姓氏的第一个字母来命名。

采用 W-H 学习规则可以用来训练一层网络的权值和偏差使之线性地逼近一个函数式而进行模式联想（Pattern Association）。

线性网络具有抛物线型误差函数所形成的误差表面，所以只有一个误差最小值。

通过W-H 学习规则来计算权值和偏差的变化，并使网络误差的平方和最小化，总能够训练一个网络的误差趋于这个最小值。

我们的目的是通过调节权矢量，使误差函数达到最小值。

所以在给定误差函数后，利用 W-H 学习规则修正权矢量和偏差矢量，使误差函数从误差空间的某一点开始，沿着函数的斜面向下滑行。

依梯度下降原理，以均方误差为性能函数，以搜寻最优点 *ew 使 mse (w e) 最小为目标，计算ADALINE 网络联接关系向量 w e 的梯度下降算法(Gradient Descent Algorithm)为：其中，σ 为学习率(Learning Rate)。

上式称为 W-H 学习规则，或为最小均方差算法(LMS) 。

注：在矩阵变换X=AY 中设Y 为输入量，X 为输出量，A 为权值矩阵，通过给定的A 以及运用LMS 算法找出接近给定矩阵的权值矩阵。

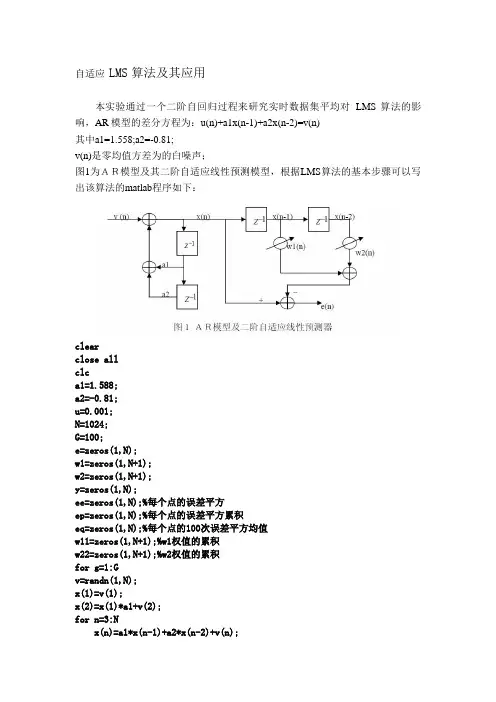
自适应LMS算法及其应用本实验通过一个二阶自回归过程来研究实时数据集平均对LMS算法的影响，AR模型的差分方程为：u(n)+a1x(n-1)+a2x(n-2)=v(n)其中a1=1.558;a2=-0.81;v(n)是零均值方差为的白噪声；图1为ＡＲ模型及其二阶自适应线性预测模型，根据LMS算法的基本步骤可以写出该算法的matlab程序如下：clearclose allclca1=1.588;a2=-0.81;u=0.001;N=1024;G=100;e=zeros(1,N);w1=zeros(1,N+1);w2=zeros(1,N+1);y=zeros(1,N);ee=zeros(1,N);%每个点的误差平方ep=zeros(1,N);%每个点的误差平方累积eq=zeros(1,N);%每个点的100次误差平方均值w11=zeros(1,N+1);%w1权值的累积w22=zeros(1,N+1);%w2权值的累积for g=1:Gv=randn(1,N);x(1)=v(1);x(2)=x(1)*a1+v(2);for n=3:Nx(n)=a1*x(n-1)+a2*x(n-2)+v(n);endfigure(1)plot(x)title('输入信号x')for n=3:Ny(n)=w1(n)*x(n-1)+w2(n)*x(n-2);e(n)=x(n)-y(n);w1(n+1)=w1(n)+2*u*e(n)*x(n-1);w2(n+1)=w2(n)+2*u*e(n)*x(n-2);ee(n)=e(n)^2;endw11=w1+w11;w22=w2+w22;ep=ep+ee;endeq=ep/G;W1=w11/G;W2=w22/G;figure(2)subplot(2,1,1)plot(w1)hold onsubplot(2,1,2)plot(W1)hold onsubplot(2,1,1)plot(w2,'r')title('w1与w2的收敛曲线,u=0.004')hold onsubplot(2,1,2)plot(W2,'r');title('100次平均后w1与w2的收敛曲线,u=0.004')figure(3)subplot(2,1,1)plot(e)title('误差曲线（学习曲线）u=0.004')subplot(2,1,2)plot(eq)title('100次平均误差曲线（学习曲线）u=0.004')下面对结果进行分析：图3为w1与w2的收敛曲线，比较平滑的为100次平均求得的收敛曲线，而另外一种起伏较大的为单次实现的收敛曲线，权初值为0。

包括： （a）计算线性滤波器输出对输入信号的响应； （b）通过比较输出结果与期望响应产生估计误差。 2）自适应过程 根据估计误差自动调整滤波器参数。 下面简单简绍下 LMS 算法的基本步骤： 1、设置变量和参量： x(n)为输入向量，或称为训练样本 w(n)为权值向量 b(n)为偏差 d(n)为期望输出 y(n)为实际输出 u 为步长因子 n 为迭代次数 2、初始化，赋给 w(0)一个较小的随机非零值，令 n=0 ； 3、对于一组输入样本 x(n)和对应的期望输出 d，计算 e(n)=d(n)-x(n)w(n) w(n+1)=w(n)+ux(n)e(n) 4、判断是否满足条件，若满足算法结束，若否 n 增加 1，转入第 3 步继续执行。 由上边的权值系数更新过程可以看出，上 LMS 算法具有算法简单、每步迭代 计算量小、所需存储量小等特点，但是 LMS 算法的收敛速度一般较慢。另外 LMS 算法还有一些改进算法如归一化 LMS (NLMS)算法等。
随机性，因而实验中需进行多次 LMS 算法迭代，最后取平均。这里取实验次 数 M 为 80。 本实验将分四个步骤完成。 首先， 实验开始先定义参变量 M、 N 和 w=zeros(M,N,3,2)与 f=zeros(M,N,3,2)， 括号里的 3 和 2 分别用来控制 3 种步长因子和 a 的两个不同参数。 然后，对不同的参数 a、不同的步长因子 u 和不同的试验次数 M 分别进行 N 次迭代来获得每个点的权值系数。 其次， 对于不同的参数 a 和步长因子分别计算它们的 M 次集平均权值特性和 均方误差特性。 最后， 分别绘出该一阶自适应预测器的权值和均方误差瞬时特性图与不同步 长因子下的学习曲线图。 本次实验的程序如下所示：
一、实验题目
For this computer experiment involving the LMS algorithm, use a first-order, autoregressive (AR) process to study the effects of ensemble averaging on the transient characteristics of the LMS algorithm for real data. Consider an AR process of order one, described by the difference equation

LMS算法实验报告LMS（Least Mean Squares）算法是一种基于梯度下降的自适应滤波算法，常用于信号处理、通信系统等领域。

本实验通过实现LMS算法并对其性能进行评估，探究其在自适应滤波中的应用。

1.实验背景自适应滤波在许多领域中被广泛应用，如信号降噪、语音增强、通信频谱感知等。

自适应滤波的核心思想是根据输入信号的特性自动调整滤波器的系数，以实现信号的最佳重构或增强。

2.实验目的本实验旨在通过实现LMS算法并对其性能进行评估，探究其在自适应滤波中的应用。

具体目的如下：1）了解LMS算法的基本原理和实现步骤；2）实现LMS算法，完成自适应滤波任务；3）评估LMS算法的性能，分析其在不同情况下的表现；4）对比LMS算法和其他自适应滤波算法的优缺点。

3.实验步骤本实验的实现步骤如下：1）理解LMS算法的基本原理和数学模型；2）根据LMS算法的更新规则，实现算法的代码；3）根据自适应滤波的具体任务需求，选择合适的输入信号和期望输出；4）根据实验需求，设置合适的参数（如学习率、滤波器长度等）；5）使用LMS算法对输入信号进行滤波，并计算输出信号的均方误差；6）根据实验结果，评估LMS算法的性能，并进行分析。

4.实验结果根据以上步骤，完成了LMS算法的实现和性能评估。

实验结果显示，LMS算法能够有效地调整滤波器的权值，实现输入信号的滤波和增强。

随着学习率的增加，LMS算法的收敛速度较快，但容易发生震荡现象。

而学习率过小，则会导致算法收敛速度慢，需要更多的迭代次数才能达到较小的均方误差。

此外，在不同噪声情况下，LMS算法的性能表现也有所差异。

在信噪比较低的情况下，LMS算法的滤波效果明显，能够有效抑制噪声并实现信号增强。

然而，在信噪比较高的情况下，LMS算法的性能受到一定影响，可能会出现性能下降或收敛困难的情况。

5.总结与分析通过本实验，深入了解了LMS算法的原理和实现步骤，并对其性能进行了评估。

μ的选择
对权系数向量更新公式（15）两边取数学期望，得
（17）
μ的选择
μ的选择
（18）
（19）
将式（19）代入式（18）后得：
（20）
μ的选择
（1）
（8-1-21a）
（8-1-21b） （8-1-21c） （8-1-21d）
（22）
μ的选择
或
（22）
LMS算法应用
LMS算法应用
LMS算法应用
MATLAB实验结果及分析
图4一阶自适应预测器的平方预测误差瞬时特性（u=0.05）
MATLAB实验结果及分析

由图4中所示的一阶自适应预测器的平方预测 误差瞬时特性曲线可以看出，LMS单一实现的 学习曲线呈现出严重的噪声存在形式，但经平 均处理以后得到了一条较稳定的曲线，即固定 u=0.05时的一阶自适应预测器的学习曲线。

自适应是指处理和分析过程中，根据处理数据的 数据特征自动调整处理方法、处理顺序、处理参 数、边界条件或约束条件，使其与所处理数据的 统计分布特征、结构特征相适应，以取得最佳的 处理效果 。
LMS算法推导：

LMS算法是自适应滤波器中常用的一种算法，与维纳 算法不同的是，其系统的系数随输入序列而改变。维 纳算法中截取输入序列自相关函数的一段构造系统的 最佳系数。而LMS算法则是对初始化的滤波器系数依 据最小均方误差准则进行不断修正来实现的。因此， 理论上讲LMS算法的性能在同等条件下要优于维纳算 法，但是LMS算法是在一个初始化值得基础上进行逐 步调整得到的，因此，在系统进入稳定之前有一个调 整的时间，这个时间受到算法步长因子u的控制，在一 定值范围内，增大u会减小调整时间，但超过这个值范 围时系统不再收敛，u的最大取值为R的迹。

基于LMS算法自适应滤波器的Matlab仿真学院(系)：计算机与通信学院年级专业：通信与信息系统学号：学生姓名：1 LMS算法的原理图1中，设x k为输入信号，它表示了连续时间信号x(t)在t=kT 时刻的离散采样值。

在数字信号处理中，我们一般采用x(kT)表示这一输入值，这里将其记为x k。

这个输入信号经过一个乘法器与权值w1，w2，…，w L相乘，把这些相乘结果相加，便形成了此时的输出信号y k。

系统的输出信号y k与期望信号d k相比较，产生一个误差信号e k=d k-y k，这个误差信号就成为自适应滤波器的控制信号。

自适应算法根据输入的误差信号e k，按照一定的算法和准则，去控制和调整各权值。

图1 自适应横向滤波器的结构定义输入矢量定义权矢量我们希望y k尽可能地逼近d k，即希望y k与d k之间的误差尽可能地小。

从统计意义上说，就是希望e k的均方误差越小越好。

定义R为下述方阵：这个方阵即为输入相关矩阵，其中主对角线上的各项是输入信号的诸元素的均方值，而其他项则是输入信号元素之间的互相关值。

根据梯度搜索法的基本思想，若权矢量W在k时刻值记为W k，为求得一个权向量使均方误差最小，可以从一组初始值W0开始，计算此时的梯度值，然后选一个新值W1，让它等于初值W0加上一个正比于负梯度负值的增量。

下一个新值W2是由计算W1的梯度用同样的方法导出。

这个过程重复进行直到最佳权被找到为止。

上述过程表示为：W k+1=W k+μ(-▽k)式中k是步数或迭代次数，参数μ是一个控制稳定度与收敛度的常数。

可以证明，迭代收敛的充要条件是：式中，λmax是的最大特征值。

实际应用中，有两个关键问题需要解决：①梯度值无法精确给出；②μ上限中的特征值依然是未知的。

LMS算法为这两个问题提供了一条简单的解决途径。

LMS 包含两个过程：①滤波过程，包括计算线性滤波器输出对信号输入的响应,通过比较输出结果与期待响应产生估计误差;②自适应过程，根据估计误差自动调整滤波器参数。

.Harbin Institute of Technology自适应平衡器计算机实验课程名称：自适应信号处理院系：电子与信息工程学院姓名：学号：授课教师：**哈尔滨工业大学一、实验目的：1. 深入掌握自适应平衡器的理论基础和以及它的可能用途。

2. 理解最小均方自适应算法的适用条件，以及最小均方自适应算法的理论推导。

3. 改变特征值扩散度）（R χ与步长参数μ，观察实验结果，深入理解理解这些参数对实验结果的重要性。

4. 探究在线性色散信道中使用最小均方自适应算法引起的失真问题。

二、实验内容：在此次实验中我们研究LMS 算法自适应均衡引起未知失真的线性色散信道问题。

假设数据是实数，图2.1表示用来进行该项研究的系统框图。

自适应均衡器用来纠正存在白噪声的信道的畸变。

通过随机数发生器1产生用来探测信道的测试信号n x ；通过随机数发生器2来产生干扰信道输出的白噪声源()v n 。

这两个发生器是相互独立的。

经过适当延迟，随机数发生器1页提供用作训练序列的自适应均衡器的期望相应。

加到信道输入的随机序列{}n x 由伯努利序列组成，其中1n x =±，随机变量n x 具有零均值和单位方差。

信道的单位脉冲响应应用升余弦表示为20.5[1cos((2))]1,2,30n n n h Wπ⎧+-=⎪=⎨⎪⎩，其他 (2-1)等价地，参数W 控制均衡器抽头输入的相关矩阵的特征值分布()χR ，并且特征值分布随着W 的增大而扩大。

随机数发生器2产生的序列是零均值，方差20.001v σ=。

随机噪声发生器(1)信道随机噪声发生器(2)延迟∑自适应横向滤波器∑nx nv +-ne图2.1 自适应均衡实验框图这里均衡器具有11M =个抽头。

由于信道的脉冲响应n h 关于2n =时对称，均衡器的最优抽头权值on w 在5n =时对称。

因此信道的输入n x 被延时了=∆2+5=7个样值，以便提供均衡器的期望响应。

通过选择匹配横向均衡器中点的合适延时Δ，LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。

目录一、绪论 (2)1.1 论文背景及研究意义 (2)1.2 音频简介 (2)1.3 自适应滤波理论的发展 (3)1.3.1 FIR滤波器的结构 (5)1.4 自适应滤波算法简介 (6)1.4.1 基于维纳滤波理论的算法 (6)1.4.2 基于卡尔曼滤波理论的算法 (7)1.4.3 基于最小二乘法的算法 (8)1.4.4 基于神经网络的算法 (8)1.5自适应LMS算法的发展 (9)1.5.1 LMS算法的历史 (9)1.5.2 LMS算法的发展现状 (10)1.5.3 LMS算法的发展前景 (10)1.6 变步长LMS算法 (11)二、最小均方算法 (12)2.1 LMS算法原理 (12)2.2 LMS算法性能分析 (13)2.2.1 收敛性 (13)2.2.2 收敛速度 (15)2.2.3 稳态误差 (16)2.2.4 计算复杂度 (17)2.3 变步长的LMS (17)三、实验过程 (19)3.1 LMS算法实现 (19)3.1.1 音频读取 (19)3.1.2 参考噪声及带噪信号的获得 (19)3.1.3 LMS算法 (21)3.1.4 代码实现 (23)3.2 VSSLMS算法实现 (25)3.2.1 VSSLMS算法 (25)3.2.2 代码实现 (27)3.3 本章总结 (29)四、总结与展望 (30)4.1 论文总结 (30)4.2 展望 (30)五、参考文献 (31)一、绪论1.1 论文背景及研究意义自适应信号处理是现代通信处理的一个重要分支学科。

与传输函数恒定的滤波器相比，自适应滤波器能根据环境自动调节抽头系数以达到最佳工作状态，被广泛应用于通信、雷达、系统控制和生物医学工程等领域。

自适应信号处理的主要应用有均衡、系统辨识、阵列信号的波束成形、噪声对消和预测编码等。

在音频降噪方面，自适应信号处理也应用诸多。

音频中降噪方法很多，按照是否有参考信号可以将降噪分为主动降噪和被动降噪。

基于MATLAB的最小均方算法（LMS）仿真与分析实验目地：掌握LMS算法的基本原理和算法中矩阵的构造方法，了解自适应波器原理及性能分析的的方法，对教材中理论知识有直观印象。

实验内容：LMS算法的编程仿真。

实验仪器：计算机及MATLAB软件。

实验时间：2010年12月1日。

一、实验原理：LMS算法是自适应滤波器中常用的一种算法，与维纳算法不同的是，其系统的系数随输入序列而改变。

维纳算法中截取输入序列自相关函数的一段构造系统的最佳系数。

而LMS算法则是对初始化的滤波器系数依据最小均方误差准则进行不断修正来实现的。

因此，理论上讲LMS算法的性能在同等条件下要优于维纳算法，但是LMS算法是在一个初始化值得基础上进行逐步调整得到的，因此，在系统进入稳定之前有一个调整的时间，这个时间受到算法步长因子u的控制，在一定值范围内，增大u会减小调整时间，但超过这个值范围时系统不再收敛，u的最大取值为R的迹。

权系数更新公式为：W i+1=W i+2ue i X i 依据上述算式，制定LMS滤波器设计实现方法为：（1）设计滤波器的初始化权系数W（0）=0，收敛因子u；（2）计算输入序列经过滤波器后的实际输出值：out(n)=WT(n)*X(n); （3）计算估计误差e(n)=xd(n)-out(n);（4）计算n+1阶的滤波器系数Wn+1=Wn+2*u*e(n)*X(n);（5）重复（2）--(4)过程；二、实验程序及程序的分析：（一）实验程序length=1024*16; %数长N=100; %滤波器的阶数u=0.00001; %步长常数t=0:2*pi/ (length-1):2*pi;xd=[sin(2*pi*t)+sin(10*pi*t)]/2; %期望信号for i=1:100 %假设信号输入以前，系统存储器中的值全为0xd(i)=0;endxnoise=sqrt(0.04)*randn(1, length);x=xd+xnoise; %叠加噪声的实际输入信号w=zeros(N,1); %初始化滤波器的权系数for i=1: lengthout(i)= x(i:i+N-1)*w; %输出序列在循环体内部实现，表明其自适应特性e(i)=xd(i)-out(i);w=w+2*u*e(i)*x(i:i+N-1)'; %权系数更新endsubplot(4,1,1)plot(out)title('滤波器输出')hold onsubplot(4,1,2)plot(xd)title('期望信号')subplot(4,1,3)plot(x,'r')title('输入信号')subplot(4,1,4)plot(e,'g')title('误差变化')（二）程序分析（1）由于滤波器的权系数必须是依据输入序列来更新的，当输入序列未达到X（N）时，由于部分存储器中没有数值或者造成滤波器输出误差只有longth- N个，系数更新达不到要求，因此要对输入前的存储器进行赋零初始化。

LMS算法收敛性能研究及应用共3篇LMS算法收敛性能研究及应用1LMS算法是一种常用的自适应滤波算法，它可以根据误差信号实时调整滤波器的权值，从而提高滤波的效果。

LMS算法在信号处理、通信系统和控制系统等领域被广泛应用，并且在实际应用中具有良好的性能。

一般来说，LMS算法的收敛性能是评价该算法性能的一个重要指标。

收敛性能的好坏直接影响算法的效率和准确性。

为了提高算法的收敛性能，需要对该算法的原理和性质进行深入研究，并且对不同情况下的应用场景进行探讨。

LMS算法的收敛性能主要受到以下几个因素的影响：（1）步长因子。

步长大小的选择直接影响了算法的收敛速度和稳定性。

如果步长太小，算法的收敛速度会很慢；如果步长太大，则算法可能会发散。

（2）滤波器长度。

滤波器长度的选择也会影响算法的性能。

一般来说，滤波器长度越长，滤波器的性能越好，但计算量也会增加。

（3）输入信号的特性。

输入信号的统计特性对算法的收敛性能也有一定的影响。

对于LMS算法的应用来说，既要考虑算法性能的问题，也要考虑算法的实现问题。

在具体应用中，可能存在算法实现的不确定性，如何在应用中使算法有更好的效果也是需要考虑的。

在数字信号处理中，LMS算法被广泛应用于去除噪声和回声等处理。

以降噪领域为例，针对算法的性能，可以通过实验来验证算法的性能，并且将实验的结果与理论结果进行比较。

通过实验可以得到滤波器长度和步长调节范围等参数的最佳取值。

针对算法实现的问题，需要从硬件和软件两个方面考虑。

在硬件实现上，可以通过使用专用的数字信号处理器来提高算法的处理速度；在软件实现上，可以使用相关软件库来简化算法的实现过程。

除了降噪应用之外，LMS算法还可以用于通信领域中的自适应均衡、PAPR约束等问题。

在这些应用场景中，LMS算法的性能也需要特别考虑。

总之，LMS算法是一种很有用的自适应滤波算法。

在应用中，需要考虑算法的收敛性能和实现问题，通过经验和理论研究，找到最佳的参数取值和实现方案。

LMS 自适应线性预测实验报告一、实验要求首先由二阶AR 模型产生自适应滤波器的输入信号)(n x ，公式如下：)()2()1()(21n v n u a n u a n u =-+-+其中)(n v 为方差为2v σ的零均值高斯白噪声，模型参数1a 与2a 满足2214a a <。

二阶AR 模型图如下：二阶AR 模型框图得到自适应滤波器的输入信号)(n x 后，通过二阶线性预测滤波器进行自适应线性预测，其框图如下：自适应线性滤波器采用LMS 算法进行自适应线性预测，设第n 次预测的权值向量Hn w n w n W )](),([)(21=，第n 次预测的输入数据向量H n x n x n X )]2(),1([)(--=，)(n x 的预测值)(n y 经滤波过程产生，其公式如下：)()1()(n X n W n y H -=误差信号计算公式如下：)()()(n y n x n e -=权值更迭公式如下：)()(2)1()(n X n e n W n W μ+-=其中μ为迭代因子。

实验要求如下：（1）令1,0965.0,95.0,195.02221===-=xv a a σσ，迭代因子μ、数据长度N 自定，给出LMS 自适应预测的仿真结果，结果用权值)(),(21n w n w 变化曲线以及误差平方)(2n e 变化曲线表示，观察其收敛情况，分别进行单次预测及100次预测取平均值两次实验。

（2）条件与（1）相同，改变迭代因子μ的值，分别进行单次预测及800次预测取平均值两次实验，观察其收敛情况。

（3）条件与（1）相同，但改变特征根扩散度min max /λλ，)1/()1(/2121min max a a a a +++-=λλ，可通过改变21,a a 的值实现，分别进行单次预测及100次预测取平均值两次实验，观察其收敛情况。

二、理论分析LMS 算法的收敛是统计意义下的收敛问题，分别讨论其均值收敛及最小均方误差收敛。

3.6检验
正确次数qbx=191 192 190
用权系数计算出实际输出后，对实际输出用对称型符号函数处理成-1和1。然后再去与原期望输出比较。用的是相减判零的方法。从统计可以看出，均方误差最小的那个确实正确次数多一些。
图15检验样本和3种算法结果
四、试验思考
1.如果想用硬限幅函数的单个神经元完成该分类任务，会出现什么样的现象？
else
wk=wk+2*u/P*sum([err(k:(k+P-1)).*xk(k:(k+P-1),1) err(k:(k+P-1)).*xk(k:(k+P-1),2) err(k:(k+P-1)).*xk(k:(k+P-1),3)]);
end
yk=xk*wk';
err=dk-yk;
averError(k)=sum(err.^2)/length(err);
gridon
boxoff
holdon
%srearchfor one circle's radius
qbx=dps(p1,[1 2]);
globalMAX=0;
globalI=1;
globalJ=2;
form=1:(length(qbx)-1)
forn=(m+1):length(qbx)
ifnorm(qbx(m,:)-qbx(n,:),2)>globalMAX
clear
loadlms_samp.mat;
Emin=0.2617;
xk=[samp(:,1:2) ones(length(samp),1)];dk=samp(:,3);wk=[0 0 rand];k=0;
yk=xk*wk';

实用Harbin Institute of Technology自适应平衡器计算机实验课程名称：自适应信号处理院系：电子与信息工程学院姓名：学号：授课教师：邹斌哈尔滨工业大学一、实验目的：1. 深入掌握自适应平衡器的理论基础和以及它的可能用途。

2. 理解最小均方自适应算法的适用条件，以及最小均方自适应算法的理论推导。

3. 改变特征值扩散度）（R χ与步长参数μ，观察实验结果，深入理解理解这些参数对实验结果的重要性。

4. 探究在线性色散信道中使用最小均方自适应算法引起的失真问题。

二、实验内容：在此次实验中我们研究LMS 算法自适应均衡引起未知失真的线性色散信道问题。

假设数据是实数，图2.1表示用来进行该项研究的系统框图。

自适应均衡器用来纠正存在白噪声的信道的畸变。

通过随机数发生器1产生用来探测信道的测试信号n x ；通过随机数发生器2来产生干扰信道输出的白噪声源()v n 。

这两个发生器是相互独立的。

经过适当延迟，随机数发生器1页提供用作训练序列的自适应均衡器的期望相应。

加到信道输入的随机序列{}n x 由伯努利序列组成，其中1n x =±，随机变量n x 具有零均值和单位方差。

信道的单位脉冲响应应用升余弦表示为20.5[1cos((2))]1,2,30n n n h Wπ⎧+-=⎪=⎨⎪⎩，其他 (2-1)等价地，参数W 控制均衡器抽头输入的相关矩阵的特征值分布()χR ，并且特征值分布随着W 的增大而扩大。

随机数发生器2产生的序列是零均值，方差20.001v σ=。

随机噪声发生器(1)信道随机噪声发生器(2)延迟∑自适应横向滤波器∑nx nv +-ne图2.1 自适应均衡实验框图这里均衡器具有11M =个抽头。

由于信道的脉冲响应n h 关于2n =时对称，均衡器的最优抽头权值on w 在5n =时对称。

因此信道的输入n x 被延时了=∆2+5=7个样值，以便提供均衡器的期望响应。

通过选择匹配横向均衡器中点的合适延时Δ，LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。

实验报告实验名称：基于LMS算法的自适应滤波实验报告实验名称：基于LMS算法的自适应滤波实验内容：最小均方算法即LMS是一种自适应滤波算法，这里的Matlab程序根据LMS对一个线性噪声系统进行滤波。

实验原理：最小均方算法是一种以期望响应和滤波器输出信号之间误差的均方值最小为原则，依据输入信号在迭代过程中估计梯度矢量，并更新权系数以达到最佳的自适应迭代算法。

实验程序：clear;clc;grid off;%周期信号的产生t=0:99;sn=10*sin(0.5*t);figure(1)subplot(2,1,1)plot(t,sn);title('原始的周期信号')grid on;%噪声信号的产生randn('state',sum(100*clock));noise=randn(1,100);subplot(2,1,2)plot(t,noise);title('噪声信号')grid on;%信号滤波xn=sn+noise;xn=xn.';dn=sn.';M=20;figure(2)subplot(2,1,1)plot(t,xn)title('加噪声后的信号波形')grid on;%初始化r_max=max(eig(xn*xn.'));mu=rand()/r_max;itr=length(xn);en=zeros(itr,1);w=zeros(M,itr);%LMSfor k=M:itrx=xn(k:-1:k-M+1);y=w(:,k-1).'*x;en(k)=dn(k)-y;%加权因子w(:,k)=w(:,k-1)+2*mu*en(k)*x;endyn=inf*ones(size(xn));for k=M:itrx=xn(k:-1:k-M+1);yn(k)=w(:,end).'*x;end%画图subplot(2,1,2)plot(t,yn)title('滤波器输出信号')grid on;figure(3)hold on;plot(t,dn,'g',t,yn,'b',t,dn-yn,'r'); grid on;legend('期望输出','滤波器输出','误差')实验结果仿真：实验总结：LMS算法是一种梯度最速下降算法，其显著特点是简单、计算量小、易于实现。