
2015-2016学年第一学期立体几何测试
高二理科数学
参考公式:
圆柱的表面积公式:rl r S ππ222
+=,圆锥的表面积公式:rl r S ππ+=2
台体的体积公式h S S S S V )(3
1''
++=
,球的表面积公式:24r S π= 圆台的表面积公式Rl rl R r S π+π+π+π=2
2,球的体积公式:33
4r V π=
一、选择题(每小题5分,共60分) 1.下列四个几何体中,是棱台的为( )
2.如图所示为一平面图形的直观图,则此平面图形可能是( )
3.给出下列命题:
①垂直于同一直线的两条直线互相平行; ②若直线a ,b ,c 满足a ∥b ,b ⊥c ,则a ⊥c ;
③若直线l 1,l 2是异面直线,则与l 1,l 2都相交的两条直线是异面直线. 其中假命题的个数是( )
A .1
B .2
C .3
D .4
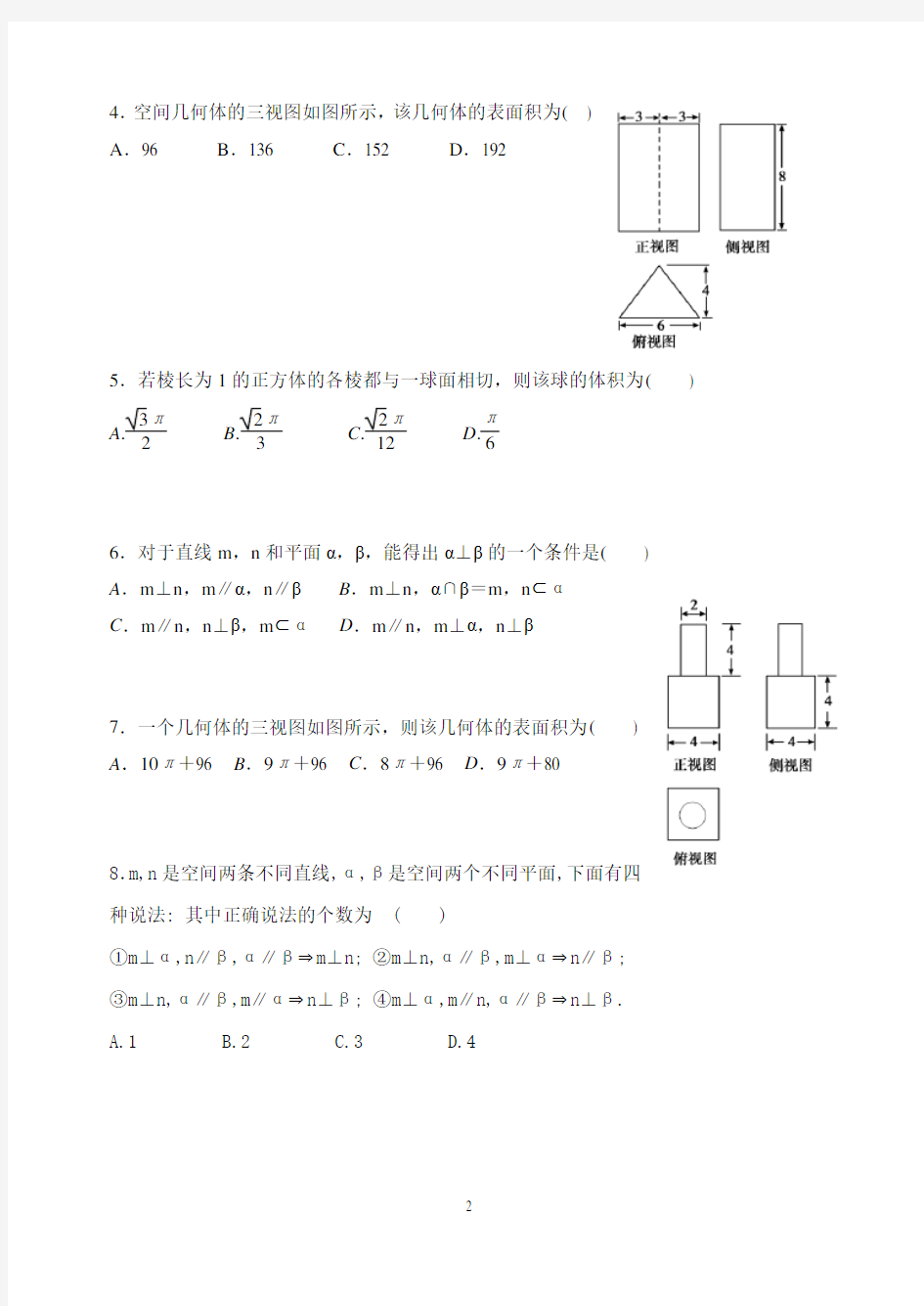
4.空间几何体的三视图如图所示,该几何体的表面积为()
A.96 B.136 C.152 D.192
5.若棱长为1的正方体的各棱都与一球面相切,则该球的体积为()
A.3π
2B.
2π
3C.
2π
12D.
π
6
6.对于直线m,n和平面α,β,能得出α⊥β的一个条件是() A.m⊥n,m∥α,n∥βB.m⊥n,α∩β=m,n?α
C.m∥n,n⊥β,m?αD.m∥n,m⊥α,n⊥β
7.一个几何体的三视图如图所示,则该几何体的表面积为() A.10π+96 B.9π+96 C.8π+96 D.9π+80
8.m,n是空间两条不同直线,α,β是空间两个不同平面,下面有四种说法: 其中正确说法的个数为( )
①m⊥α,n∥β,α∥β?m⊥n; ②m⊥n,α∥β,m⊥α?n∥β;
③m⊥n,α∥β,m∥α?n⊥β; ④m⊥α,m∥n,α∥β?n⊥β.
A.1
B.2
C.3
D.4
9、某几何体的三视图如图所示,则该几何体的体积为( )
3560.
A
3580
.
B 200.
C 240.D
10.如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )
A.1727
B.59
C.1027
D.13
11.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
A .62
B .42
C .6
D .4
12.已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ?是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( ) A.
26 B.36 C.23 D.2
2
二、填空题(每小题5分,共20分)
13.某一几何体的三视图如图所示,则该几何体的体积
为________.
14.正四棱台的上底为边长为2的正方形,下底为边长为4的正方形,侧面是全等的等腰梯形,侧棱长为3,则此四棱台的体积为,
15. 己知棱长为2,各面均为等边三角形的四面体S-ABC的四个顶点都在一个球面上,则该四面体的表面积为__________,该球的体积为___________
AH HB=,AB⊥平面α,H为垂足,α截16.已知H是球O的直径AB上一点,:1:2
球O所得截面的面积为π,则球O的表面积为______。
三、解答题(17题10分,其余各题12分,共70分)
17.已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图是一个底边长为6,高为4的等腰三角形.求: (1)该几何体的体积V ; (2)该几何体的侧面积S .
18、如图3,AB 是圆O的直径,C是圆周上一点,
PA ⊥平面ABC .
(1)求证:BC ⊥平面PAC
(2)若AE ⊥PC ,E为垂足,F是PB 上任意一点,求证:平面AEF ⊥平面PBC .
19.如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点。 (1)求证:1//A C 平面BDE 。
(2)求直线1A C 与平面D D AA 11所成角余弦值。
N
M
A
B
D
C
O
20.如图,在四棱锥O ABCD -中,底面ABCD 四边长为1的菱形,0
45=∠ABC ,
OA ABCD ⊥底面,2OA =,M 为OA 的中点,N 为BC 的中点。
(1)证明:直线MN OCD
平面‖;
(2)求异面直线AB 与MD 所成角的大小;
21. 如图,正方形ABCD 所在平面与三角形CDE 所在平面相交于CD ,AE ⊥平面CDE ,且
3AE =,6AB =.
(1)求证:AB ⊥平面ADE ; (2)求凸多面体ABCDE 的体积.
22.如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,PO 垂直于圆O 所在的平面,且1PO =OB =.
(Ⅰ)若D 为线段AC 的中点,求证:C A ⊥平面D P O ; (Ⅱ)求三棱锥P ABC -体积的最大值; (Ⅲ)若2BC =
,点E 在线段PB 上,
求CE OE +的最小值.
A
B
C
D E
参考答案
1-5:CCBCB 2-10:CCBCC 11-12:CA
10
.
.
.27
10
π54π34-π54π.342π944.2342π.
546π96321C v v 故选积之比削掉部分的体积与原体体积,高为径为,右半部为大圆柱,半,高为小圆柱,半径加工后的零件,左半部体积,,高加工前的零件半径为==
∴=?+?=∴=?=∴π 11.
12. 【解析】ABC ?的外接圆的半径3
3
r =
,点O 到面ABC 的距离2263
d R r =
-=
. SC 为球O 的直径?点S 到面ABC 的距离为26
2d =
此棱锥的体积为113262233ABC V S d ?=
?=??= 另:13
23ABC V S R ?<
?=排除,,B C D 13. 8-2π
3
14.7328
15. 34 ,π6 16.
17.由已知该几何体是一个四棱锥P -ABCD ,如图所示. 由已知,AB =8,BC =6,高h =4,
由俯视图知底面ABCD 是矩形,连接AC 、BD 交于点O ,连接PO ,则PO =4,即为棱锥的高.作OM ⊥AB 于M ,ON ⊥BC 于N ,连接PM 、PN ,则PM ⊥AB ,PN ⊥BC . ∴PM =PO 2+OM 2=42+32=5, PN =PO 2+ON 2=42+42=42.
(1)V =13Sh =1
3
×(8×6)×4=64.
(2)S 侧=2S △P AB +2S △PBC =AB ·PM +BC ·PN =8×5+6×42=40+242.
18、证:(1)∵PA ⊥平面ABC .BC ?平面ABC
∴BC ⊥PA
∵AB 是圆O的直径,C是圆周上一点 ∴BC⊥AC
又PA ?AC=A,PA?平面PAC,AC?平面PAC
∴BC ⊥平面PAC
(2) 由(1)知BC ⊥平面PAC ,又AE ?平面PAC
∴AE ⊥ BC 又∵AE ⊥PC
BC ?PC=C,BC ?平面PBC .PC ?平面PBC .∴平面AEF ⊥平面PBC . 19.证:(1)连接AC 交BD 于O,连接EO ∵AC 与BC 是正方形ABCD 的对角线 ∴点O 的AC 的中点,又E 的1AA 的中点, ∴OE //C A 1
又OE ?平面BDE ,C A 1?平面BDE
∴1//A C 平面BDE 。 (2)连接D A 1
∵CD ⊥平面11A ADD ,
∴D A 1是C A 1在平面11A ADD 的射影
∴D CA 1∠是直线D A 1与平面11A ADD 所成的角,
设正方体1111ABCD A B C D -的边长为a
在直角三角形D CA 1中,D A 1=a 2 ,C A 1=a 3,cos D CA 1∠=C A D A 11=36
32=a
a .. 20. (1)取OD 中点E ,连接ME ,CE 。
因为M 为OA 中点,
所以ME 是三角形OAD 的中位线
所以AD
ME
2
1//=
因为底面ABCD 是菱形,N 为BC 中点,
所以
AD
BN
2
1//=
所以ME
BN =//
所以四边形MNCE 是平行四边形
所以MN//CE
又因为OCD MN 面?,OCD CE 面?
所以OCD MN 面//。
(2)连接MC ,AC 因为AB//CD 所以CDM ∠为所求角或其补角。
在三角形ABC 中,
2
22
2
*
2112-=-+=AC , 232-=MC ,22=MD ,12=CD ,
所以
21
1
*2*22312cos =
+-+=
∠CDM , 所以060=∠CDM ,所以所求角为060
21. 证明:(1)∵AE ⊥平面CDE ,CD ?平面CDE ,∴AE ⊥CD .
在正方形ABCD 中,CD AD ⊥,∵AD
AE A =,∴CD ⊥平面ADE .
∵AB CD ,∴AB ⊥平面ADE .
(2)解法1:在Rt △ADE 中,3AE =,6AD =,
∴DE =.
过点E 作EF AD ⊥于点F ,
∵AB ⊥平面ADE ,EF ?平面ADE , ∴EF AB ⊥. ∵AD AB A =,
∴EF ⊥平面ABCD . ∵AD EF AE DE ?=?,
∴AE DE EF AD ?=== 又正方形ABCD 的面积36ABCD S =, ∴1
3
ABCDE E ABCD ABCD V V S EF -==
?
13632=??
= 故所求凸多面体ABCDE
的体积为
解法2:在Rt △ADE 中,3AE =,6AD =
,∴DE =.
连接BD ,则凸多面体ABCDE 分割为三棱锥B CDE -和三棱锥B ADE -. 由(1)知,CD ⊥DE
.∴11
622
CDE S CD DE ?=??=??= 又AB CD ,AB ?平面CDE ,CD ?平面
CDE ,
∴AB
平面CDE .
∴点B 到平面CDE 的距离为AE 的长度. ∴11
333
B CDE
CDE V S AE -?=?=?= ∵AB ⊥平面ADE ,∴116332
B ADE ADE V S AB -?=
?=?=. ∴ABCDE B CDE B ADE V V V --=+== 故所求凸多面体ABCDE 的体积为 22.(15年福建文科)
A B
C
D
E
F
A
B
C D
E
分析:(Ⅰ)要证明C A ⊥平面D P O ,只需证明AC 垂直于面D P O 内的两条相交直线.首先由PO 垂直于圆O 所在的平面,可证明C PO ⊥A ;又C OA =O ,D 为C A 的中点,可证明C D A ⊥O ,进而证明结论;(Ⅱ)三棱锥P ABC -中,高1PO =,要使得P ABC -体积最大,则底面ABC 面积最大,又2AB =是定值,故当AB 边上的高最大,此时高为半径,进而求三棱锥P ABC -体积;(Ⅲ)将侧面C B P 绕PB 旋转至平面C 'B P ,使之与平面ABP 共面,此时线段'
OC 的长度即为CE OE +的最小值. 证明:(I )在C ?AO 中,因为C OA =O ,D 为C A 的中点, 所以C D A ⊥O .
又PO 垂直于圆O 所在的平面,且ABC AC 面?, 所以C PO ⊥A . 因为D O
PO =O ,PDO DO ,O,面?
所以C A ⊥平面D P O . (II )因为点C 在圆O 上,
所以当C O ⊥AB 时,C 到AB 的距离最大,且最大值为1. 又2AB =,所以C ?AB 面积的最大值为1
2112??=. 又因为三棱锥C P -AB 的高1PO =, 故三棱锥C P -AB 体积的最大值为11113
3
??=
. (III )在?POB 中,1PO =OB =,90∠POB =,
所以22
112PB =+=
.
同理C 2P =,所以C C PB =P =B .
在三棱锥C P -AB 中,将侧面C B P 绕PB 旋转至平面C 'B P ,使之与平面ABP 共面,如图所示.当O ,E ,C '共线时,C E +OE 取得最小值. 又因为OP =OB ,C C ''P =B ,所以C 'O 垂直平分PB ,
即E 为PB 中点.从而C C ''O =OE +E =
=,
亦即C E +OE 的最小值为
2
. 解法二:(I )、(II )同解法一.
(III )在?POB 中,1PO =OB =,90∠POB =,
所以45∠OPB =,PB ==
.同理C P =
所以C C PB =P =B ,所以C 60∠PB =.
在三棱锥C P -AB 中,将侧面C B P 绕PB 旋转至平面C 'B P ,使之与平面ABP 共面,如图所示.
当O ,E ,C '共线时,C E +OE 取得最小值. 所以在C '?O P 中,由余弦定理得:
()
2C 1221cos 4560'O =+-?+
112222
2=+--??
2=
从而C 2
'O =
=
.
所以C E +OE 的最小值为2
.