深度优先搜索练习题

深度优先遍历例题摘要：一、深度优先遍历概念介绍1.定义2.特点二、深度优先遍历算法应用1.图形遍历2.搜索算法三、深度优先遍历例题解析1.题目一：二叉树的深度优先遍历1.分析2.算法实现3.答案解析2.题目二：链式广度优先遍历1.分析2.算法实现3.答案解析四、深度优先遍历实战技巧与优化1.避免回溯2.提高效率正文：一、深度优先遍历概念介绍1.定义深度优先遍历（Depth-First Traversal，简称DFT）是一种遍历树或图的算法。

它沿着一个路径一直向前，直到达到最深的节点，然后回溯到上一个节点，继续沿着另一个路径遍历。

2.特点深度优先遍历的特点是访问一个节点后，会沿着该节点的子节点继续遍历，直到没有未访问的子节点为止。

此时，遍历过程会回溯到上一个节点，继续访问其未访问的子节点。

二、深度优先遍历算法应用1.图形遍历深度优先遍历在图形处理领域有广泛应用，如图像处理中的边缘检测、图像分割等。

通过遍历图像像素点，可以发现像素点之间的关系，从而实现图像处理任务。

2.搜索算法深度优先搜索（DFS）是一种经典的搜索算法，它采用深度优先策略在树或图中寻找目标节点。

DFS算法常用于解决迷宫问题、八皇后问题等。

三、深度优先遍历例题解析1.题目一：二叉树的深度优先遍历1.分析二叉树的深度优先遍历通常采用递归或栈实现。

递归方法简单，但效率较低；栈方法效率较高，但实现较复杂。

2.算法实现（递归）```def dfs(root):if not root:returnprint(root.val, end=" ")dfs(root.left)dfs(root.right)```3.答案解析按照题目给定的二叉树，进行深度优先遍历，得到的序列为：1 2 4 5 3 6 8。

2.题目二：链式广度优先遍历1.分析链式广度优先遍历与树的同层遍历类似，采用队列实现。

队列中的元素依次为当前层的节点，每次遍历时，取出队首节点，将其相邻节点加入队列，并将其标记为已访问。

⼋数码难题（8puzzle）深度优先和深度优先算法1 搜索策略搜索策略是指在搜索过程中如何选择扩展节点的次序问题。

⼀般来说，搜索策略就是采⽤试探的⽅法。

它有两种类型：⼀类是回溯搜索，另⼀类是图搜索策略。

2 盲⽬的图搜索策略图搜索策略⼜可分为两种：⼀种称为盲⽬的图搜索策略，或称⽆信息图搜索策略；⽽另⼀种称为启发式搜索策略，⼜称为有信息的图搜索策略。

最常⽤的两种⽆信息图搜索策略是宽度优先搜索和深度优先搜索。

2.1 宽度优先搜索它是从根节点（起始节点）开始，按层进⾏搜索，也就是按层来扩展节点。

所谓按层扩展，就是前⼀层的节点扩展完毕后才进⾏下⼀层节点的扩展，直到得到⽬标节点为⽌。

这种搜索⽅式的优点是，只要存在有任何解答的话，它能保证最终找到由起始节点到⽬标节点的最短路径的解，但它的缺点是往往搜索过程很长。

2.2 深度优先搜索它是从根节点开始，⾸先扩展最新产⽣的节点，即沿着搜索树的深度发展下去，⼀直到没有后继结点处时再返回，换⼀条路径⾛下去。

就是在搜索树的每⼀层始终先只扩展⼀个⼦节点，不断地向纵深前进直到不能再前进（到达叶⼦节点或受到深度限制）时，才从当前节点返回到上⼀级节点，沿另⼀⽅向⼜继续前进。

这种⽅法的搜索树是从树根开始⼀枝⼀枝逐渐形成的。

由于⼀个有解的问题树可能含有⽆穷分枝，深度优先搜索如果误⼊⽆穷分枝（即深度⽆限），则不可能找到⽬标节点。

为了避免这种情况的出现，在实施这⼀⽅法时，定出⼀个深度界限，在搜索达到这⼀深度界限⽽且尚未找到⽬标时，即返回重找，所以，深度优先搜索策略是不完备的。

另外，应⽤此策略得到的解不⼀定是最佳解（最短路径）。

3 “⼋”数码难题的宽度优先搜索与深度优先搜索3.1“⼋”数码难题的宽度优先搜索步骤如下：1、判断初始节点是否为⽬标节点，若初始节点是⽬标节点则搜索过程结束；若不是则转到第2步；2、由初始节点向第1层扩展，得到3个节点：2、3、4；得到⼀个节点即判断该节点是否为⽬标节点，若是则搜索过程结束；若2、3、4节点均不是⽬标节点则转到第3步；3、从第1层的第1个节点向第2层扩展，得到节点5；从第1层的第2个节点向第2层扩展，得到3个节点：6、7、8；从第1层的第3个节点向第2层扩展得到节点9；得到⼀个节点即判断该节点是否为⽬标节点，若是则搜索过程结束；若6、7、8、9节点均不是⽬标节点则转到第4步；4、按照上述⽅法对下⼀层的节点进⾏扩展，搜索⽬标节点；直⾄搜索到⽬标节点为⽌。

深度优先搜索（深搜）——DeepFirstSearch【例题：迷宫】深度优先搜索 基本思想：先选择⼀种可能情况向前探索，在探索过程中，⼀点那发现原来的选择是错误的，就退回⼀步重新选择，继续向前探索，（回溯）反复进⾏。

【例题】迷宫问题思路：先随意选择⼀个⽅向，⼀步步向前试探，如果碰到死胡同说明该前进⽅向已经⽆路可⾛，这时⾸先看别的⽅向还是否有路可⾛，若有路可⾛，则该⽅向再次向前试探，若没有，则退回上⼀步，再看其他⽅向是否有路可⾛，，按此原则不断回溯和探索，知道找到⼊⼝为⽌。

框架：int search(int ......){for(i=1;i<=⽅向总数;i++)if(满⾜条件){保存结果;if(到达⽬的地)输出解;else search(k+1);恢复：保存结果之前的状态{回溯⼀步};}}具体代码实现如下：#include<iostream>#include<cstdio>#include<cstring>#define MAXN 20using namespace std;int map[MAXN][MAXN];//表⽰迷宫地图bool temp[MAXN][MAXN];//标记是否⾛过int dx[4]={0,0,1,-1};//横坐标的上下左右int dy[4]={-1,1,0,0};//纵坐标的上下左右int m,n,total,sx,sy,fx,fy,l,r,t;//m,n:地图的长宽，total：⽅案总数，sx,sy起点的横纵坐标，fx,fy：终点的横纵坐标，t:障碍总数，l,r:障碍坐标void search(int x,int y)//x,y:现在所在的点的坐标{if(x==fx&&y==fy)//到达终点{total++;//⽅案总数return; //返回继续寻找}for(int i=0;i<=3;i++)if(temp[x+dx[i]][y+dy[i]]==0&&map[x+dx[i]][y+dy[i]]==1)//判断下⾯要⾛的路是否有障碍if(x+dx[i]>=1&&y+dy[i]>=1&&x+dx[i]<=n&&y+dy[i]<=m)//判断是否超越迷宫边界{temp[x+dx[i]][y+dy[i]]=1;search(x+dx[i],y+dy[i]);temp[x+dx[i]][y+dy[i]]=0;//回溯⼀步}}int main(){cin>>n>>m>>t;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)map[i][j]=1;cin>>sx>>sy;cin>>fx>>fy;for(int i=1;i<=t;i++){cin>>l>>r;map[l][r]=0;}map[sx][sy]=0; search(sx,sy); printf("%d",total); return0;}。

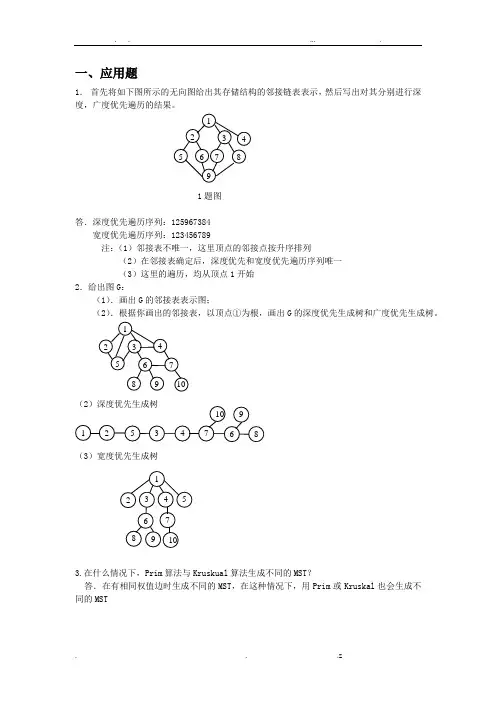
一、应用题1．首先将如下图所示的无向图给出其存储结构的邻接链表表示，然后写出对其分别进行深度，广度优先遍历的结果。

1题图答．深度优先遍历序列：125967384宽度优先遍历序列：123456789注：（1）邻接表不唯一，这里顶点的邻接点按升序排列（2）在邻接表确定后，深度优先和宽度优先遍历序列唯一（3）这里的遍历，均从顶点1开始2．给出图G：（1）．画出G的邻接表表示图；（2）．根据你画出的邻接表，以顶点①为根，画出G的深度优先生成树和广度优先生成树。

（3）宽度优先生成树3.在什么情况下，Prim算法与Kruskual算法生成不同的MST？答．在有相同权值边时生成不同的MST，在这种情况下，用Prim或Kruskal也会生成不同的MST4．已知一个无向图如下图所示，要求分别用Prim 和Kruskal 算法生成最小树（假设以①为起点，试画出构造过程）。

答．Prim 算法构造最小生成树的步骤如24题所示，为节省篇幅，这里仅用Kruskal 算法，构造最小生成树过程如下：（下图也可选(2,4)代替(3,4),(5,6)代替(1,5)）5．G=(V,E)是一个带有权的连通图,则：（1）．请回答什么是G 的最小生成树； （2）．G 为下图所示,请找出G 的所有最小生成树。

28题图答．（1）最小生成树的定义见上面26题 （2）最小生成树有两棵。

（限于篇幅，下面的生成树只给出顶点集合和边集合，边以三元组（Vi,Vj,W ）形式），其中W 代表权值。

V （G ）={1，2，3，4，5} E1(G)={(4，5，2)，（2，5，4），（2，3，5），（1，2，7）}；E2(G)={(4，5，2），（2，4，4），（2，3，5），（1，2，7）}6．请看下边的无向加权图。

（1）．写出它的邻接矩阵。

（2）．按Prim 算法求其最小生成树，并给出构造最小生成树过程中辅助数组的各分量值。

辅助数组各分量值：7．已知世界六大城市为:(Pe)、纽约(N)、巴黎(Pa)、伦敦(L) 、东京(T) 、墨西哥(M),下表给定了这六大城市之间的交通里程:世界六大城市交通里程表(单位:百公里)（1）．画出这六大城市的交通网络图;（2）．画出该图的邻接表表示法;（3）．画出该图按权值递增的顺序来构造的最小(代价)生成树.8．已知顶点1-6和输入边与权值的序列（如右图所示）：每行三个数表示一条边的两个端点和其权值，共11行。

深度优先和广度优先例题一、以下哪个图遍历算法会首先访问所有邻居节点，然后再深入下一层？A. 深度优先搜索B. 广度优先搜索C. Dijkstra算法D. A*搜索算法（答案：B）二、在深度优先搜索中，使用什么数据结构来跟踪访问节点？A. 队列B. 栈C. 链表D. 树（答案：B）三、给定一个无向图，如果从节点A开始广度优先搜索，下列哪个节点会最先被访问（假设所有边的权重相同）？A. 与A直接相连的节点BB. 与A距离两跳的节点CC. 与A距离三跳的节点DD. 无法确定（答案：A）四、在广度优先搜索中，如果某个节点被访问过，则其状态会被标记为？A. 已访问B. 未访问C. 正在访问D. 可访问（答案：A）五、深度优先搜索在处理哪种类型的问题时可能更有效？A. 查找最短路径B. 生成所有可能的解C. 计算最小生成树D. 求解线性方程组（答案：B）六、下列哪个选项不是深度优先搜索的特点？A. 易于实现递归版本B. 可能会陷入无限循环（在无终止条件的图中）C. 总是能找到最短路径D. 适用于解空间较大的问题（答案：C）七、在广度优先搜索中，节点的访问顺序是？A. 按照深度优先B. 按照宽度优先（即逐层访问）C. 随机访问D. 按照节点编号顺序（答案：B）八、给定一个有向图，如果从节点A到节点B存在多条路径，深度优先搜索找到的路径是？A. 一定是最短路径B. 一定是最长路径C. 可能是其中任意一条路径D. 总是找到权重和最小的路径（答案：C）九、在深度优先搜索中，当遇到一个新节点时，首先将其？A. 加入队列B. 压入栈C. 标记为已访问D. 忽略（答案：B）十、广度优先搜索和深度优先搜索在遍历图时的主要区别在于？A. 使用的数据结构不同B. 访问节点的顺序不同C. 适用于的图结构不同D. A和B都正确（答案：D）。

原题目：描述深度优先搜索算法的过程。

描述深度优先搜索算法的过程深度优先搜索（Depth-First Search，DFS）是一种用于遍历或搜索图的算法，它是一种递归算法，通过深度的方式探索图的节点以获得解决方案。

步骤使用深度优先搜索算法来遍历图的节点的步骤如下：1. 选择一个起始节点作为当前节点，并将其标记为已访问。

2. 检查当前节点是否是目标节点。

如果是目标节点，则算法结束。

3. 如果当前节点不是目标节点，则遍历当前节点的邻居节点。

4. 对于每个未访问的邻居节点，将其标记为已访问，并将其加入到待访问节点的列表中。

5. 从待访问节点的列表中选择一个节点作为新的当前节点，并重复步骤2-4，直到找到目标节点或所有节点都被访问。

6. 如果所有节点都被访问但没有找到目标节点，则算法结束。

递归实现深度优先搜索算法可以使用递归的方式来实现。

以下是一个递归实现深度优先搜索的示例代码：def dfs(graph, node, visited):visited.add(node)print(node)for neighbor in graph[node]:if neighbor not in visited:dfs(graph, neighbor, visited)在上述代码中，`graph` 是表示图的邻接表，`node` 是当前节点，`visited` 是已访问节点的集合。

算法以起始节点作为参数进行递归调用，并在访问每个节点时打印节点的值。

非递归实现除了递归方式，深度优先搜索算法还可以使用栈来实现非递归版本。

以下是一个非递归实现深度优先搜索的示例代码：def dfs(graph, start_node):visited = set()stack = [start_node]while stack:node = stack.pop()if node not in visited:visited.add(node)print(node)for neighbor in graph[node]:if neighbor not in visited:stack.append(neighbor)在上述代码中，`graph` 是表示图的邻接表，`start_node` 是起始节点。

深度优先搜索、广度优先搜索专题练习1.走迷宫（Maze）【问题描述】已知一N×N的迷宫，允许往上、下、左、右四个方向行走，现请你找出一条从左上角到右下角的最短路径。

【输入数据】输入数据有若干行，第一行有一个自然数N（N≤20），表示迷宫的大小，其后有N行数据，每行有N个0或1（数字之间没有空格，0表示可以通过，1表示不能通过），用以描述迷宫地图。

入口在左上角（1，1）处，出口在右下角（N，N）处。

所有迷宫保证存在从入口到出口的可行路径。

【输出数据】输出数据仅一行，为从入口到出口的最短路径（有多条路径时输出任意一条即可）。

路径格式参见样例。

【样例】maze.in40001010000100110maze.out(1,1)->(1,2)->(1,3)->(2,3)->(2,4)->(3,4)->(4,4)2.跳马（horse）【问题描述】象棋中马走“日”字，这是大家都知道的规则，也就是说，如下图所示，一个在“*”位置的马可以跳到1～8中的某一个位置。

【输入数据】第一行两个整数N，M表示棋盘的大小，左上角为（1，1），右下角为（N，M），其中N和M都不超过8。

第二行两个整数X，Y表示马出发时的位置。

【输出数据】N行，每行M个整数，为马跳到此格子时的步数（规定马的出发点这个值为0）。

如果有多种解，输出任意一种即可。

所有情况保证有解。

【样例】horse.in4 51 1horse.out0 19 6 15 25 14 1 10 718 9 12 3 1613 4 17 8 113.倒牛奶( milk.cpp )题目描述：农民约翰有三个容量分别是A,B,C升的桶，A,B,C分别是三个从1到20的整数，最初，A和B桶都是空的，而C桶是装满牛奶的。

有时，约翰把牛奶从一个桶倒到另一个桶中，直到被灌桶装满或原桶空了。

当然每一次灌注都是完全的。

由于节约，牛奶不会有丢失。

写一个程序去帮助约翰找出当A桶是空的时候，C桶中牛奶所剩量的所有可能性。

第五章搜索策略习题参考解答5.1 练习题5.1 什么是搜索？有哪两大类不同的搜索方法？两者的区别是什么？5.2 用状态空间法表示问题时，什么是问题的解？求解过程的本质是什么？什么是最优解？最优解唯一吗？5.3 请写出状态空间图的一般搜索过程。

在搜索过程中OPEN表和CLOSE表的作用分别是什么？有何区别？5.4 什么是盲目搜索？主要有几种盲目搜索策略？5.5 宽度优先搜索与深度优先搜索有何不同？在何种情况下，宽度优先搜索优于深度优先搜索？在何种情况下，深度优先搜索优于宽度优先搜索？5.6 用深度优先搜索和宽度优先搜索分别求图5.10所示的迷宫出路。

图5.10 习题5.6的图5.7 修道士和野人问题。

设有3个修道士和3个野人来到河边，打算用一条船从河的左岸渡到河的右岸去。

但该船每次只能装载两个人，在任何岸边野人的数目都不得超过修道士的人数，否则修道士就会被野人吃掉。

假设野人服从任何一种过河安排，请使用状态空间搜索法，规划一使全部6人安全过河的方案。

（提示：应用状态空间表示和搜索方法时，可用(N m,N c)来表示状态描述，其中N m和N c分别为传教士和野人的人数。

初始状态为(3,3)，而可能的中间状态为(0,1),(0,2),(0,3), (1,1),(2,1),(2,2),(3,0),(3,1),(3,2)等。

）5.8 用状态空间搜索法求解农夫、狐狸、鸡、小米问题。

农夫、狐狸、鸡、小米都在一条河的左岸，现在要把它们全部送到右岸去。

农夫有一条船，过河时，除农夫外，船上至多能载狐狸、鸡和小米中的一样。

狐狸要吃鸡，鸡要吃小米，除非农夫在那里。

试规划出一个确保全部安全的过河计划。

（提示：a.用四元组(农夫，狐狸，鸡，米)表示状态，其中每个元素都可为0或1，0表示在左岸，1表示在右岸；b.把每次过河的一种安排作为一个算符，每次过河都必须有农夫，因为只有他可以划船。

）5.9 设有三个大小不等的圆盘A 、B 、C 套在一根轴上，每个圆盘上都标有数字1、2、3、4，并且每个圆盘都可以独立地绕轴做逆时针转动，每次转动90°，初始状态S 0和目标状态S g 如图5.11所示，用宽度优先搜索法和深度优先搜索法求从S 0到S g 的路径。

【题目1】N皇后问题(八皇后问题的扩展)【题目2】排球队员站位问题【题目3】把自然数Ｎ分解为若干个自然数之和。

【题目4】把自然数Ｎ分解为若干个自然数之积。

【题目5】马的遍历问题。

【题目6】加法分式分解【题目7】地图着色问题【题目8】在n*n的正方形中放置长为2,宽为1的长条块,【题目9】找迷宫的最短路径。

（广度优先搜索算法）【题目10】火车调度问题【题目11】农夫过河【题目12】七段数码管问题。

【题目13】把1-8这8个数放入下图8个格中,要求相邻的格(横,竖,对角线)上填的数不连续.【题目14】在4×4的棋盘上放置8个棋,要求每一行,每一列上只能放置2个.【题目15】迷宫问题.求迷宫的路径.(深度优先搜索法)【题目16】一笔画问题【题目17】城市遍历问题.【题目18】棋子移动问题【题目19】求集合元素问题（1,2x+1,3X+1类)【题目】N皇后问题(含八皇后问题的扩展，规则同八皇后)：在N*N的棋盘上，放置N个皇后，要求每一横行每一列，每一对角线上均只能放置一个皇后，问可能的方案及方案数。

const max=8;var i,j:integer;a:array[1..max] of 0..max; {放皇后数组}b:array[2..2*max] of boolean; {/对角线标志数组}c:array[-(max-1)..max-1] of boolean; {\对角线标志数组}col:array[1..max] of boolean; {列标志数组}total:integer; {统计总数}procedure output; {输出}var i:integer;beginwrite('No.':4,'[',total+1:2,']');for i:=1 to max do write(a[i]:3);write(' ');if (total+1) mod 2 =0 then writeln; inc(total);end;function ok(i,dep:integer):boolean; {判断第dep行第i列可放否} beginok:=false;if ( b[i+dep]=true) and ( c[dep-i]=true) {and (a[dep]=0)} and (col[i]=true) then ok:=trueend;procedure try(dep:integer);var i,j:integer;beginfor i:=1 to max do {每一行均有max种放法}if ok(i,dep) then begina[dep]:=i;b[i+dep]:=false; {/对角线已放标志}c[dep-i]:=false; {\对角线已放标志}col[i]:=false; {列已放标志}if dep=max then outputelse try(dep+1); {递归下一层}a[dep]:=0; {取走皇后,回溯}b[i+dep]:=true; {恢复标志数组}c[dep-i]:=true;col[i]:=true;end;end;beginfor i:=1 to max do begin a[i]:=0;col[i]:=true;end;for i:=2 to 2*max do b[i]:=true;for i:=-(max-1) to max-1 do c[i]:=true;total:=0;try(1);writeln('total:',total);end.【测试数据】n=8 八皇后问题No.[ 1] 1 5 8 6 3 7 2 4 No.[ 2] 1 6 8 3 7 4 2 5 No.[ 3] 1 7 4 6 8 2 5 3 No.[ 4] 1 7 5 8 2 4 6 3 No.[ 5] 2 4 6 8 3 1 7 5 No.[ 6] 2 5 7 1 3 8 6 4 No.[ 7] 2 5 7 4 1 8 6 3 No.[ 8] 2 6 1 7 4 8 3 5 No.[ 9] 2 6 8 3 1 4 7 5 No.[10] 2 7 3 6 8 5 1 4 No.[11] 2 7 5 8 1 4 6 3 No.[12] 2 8 6 1 3 5 7 4 No.[13] 3 1 7 5 8 2 4 6 No.[14] 3 5 2 8 1 7 4 6 No.[15] 3 5 2 8 6 4 7 1 No.[16] 3 5 7 1 4 2 8 6 No.[17] 3 5 8 4 1 7 2 6 No.[18] 3 6 2 5 8 1 7 4 No.[19] 3 6 2 7 1 4 8 5 No.[20] 3 6 2 7 5 1 8 4 No.[21] 3 6 4 1 8 5 7 2 No.[22] 3 6 4 2 8 5 7 1 No.[23] 3 6 8 1 4 7 5 2 No.[24] 3 6 8 1 5 7 2 4 No.[25] 3 6 8 2 4 1 7 5 No.[26] 3 7 2 8 5 1 4 6 No.[27] 3 7 2 8 6 4 1 5 No.[28] 3 8 4 7 1 6 2 5 No.[29] 4 1 5 8 2 7 3 6 No.[30] 4 1 5 8 6 3 7 2 No.[31] 4 2 5 8 6 1 3 7 No.[32] 4 2 7 3 6 8 1 5 No.[33] 4 2 7 3 6 8 5 1 No.[34] 4 2 7 5 1 8 6 3 No.[35] 4 2 8 5 7 1 3 6 No.[36] 4 2 8 6 1 3 5 7 No.[37] 4 6 1 5 2 8 3 7 No.[38] 4 6 8 2 7 1 3 5 No.[39] 4 6 8 3 1 7 5 2 No.[40] 4 7 1 8 5 2 6 3 No.[41] 4 7 3 8 2 5 1 6 No.[42] 4 7 5 2 6 1 3 8 No.[43] 4 7 5 3 1 6 8 2 No.[44] 4 8 1 3 6 2 7 5 No.[45] 4 8 1 5 7 2 6 3 No.[46] 4 8 5 3 1 7 2 6 No.[47] 5 1 4 6 8 2 7 3 No.[48] 5 1 8 4 2 7 3 6 No.[49] 5 1 8 6 3 7 2 4 No.[50] 5 2 4 6 8 3 1 7 No.[51] 5 2 4 7 3 8 6 1 No.[52] 5 2 6 1 7 4 8 3 No.[53] 5 2 8 1 4 7 3 6 No.[54] 5 3 1 6 8 2 4 7 No.[55] 5 3 1 7 2 8 6 4 No.[56] 5 3 8 4 7 1 6 2 No.[57] 5 7 1 3 8 6 4 2 No.[58] 5 7 1 4 2 8 6 3 No.[59] 5 7 2 4 8 1 3 6 No.[60] 5 7 2 6 3 1 4 8 No.[61] 5 7 2 6 3 1 8 4 No.[62] 5 7 4 1 3 8 6 2No.[63] 5 8 4 1 3 6 2 7 No.[64] 5 8 4 1 7 2 6 3No.[65] 6 1 5 2 8 3 7 4 No.[66] 6 2 7 1 3 5 8 4No.[67] 6 2 7 1 4 8 5 3 No.[68] 6 3 1 7 5 8 2 4No.[69] 6 3 1 8 4 2 7 5 No.[70] 6 3 1 8 5 2 4 7No.[71] 6 3 5 7 1 4 2 8 No.[72] 6 3 5 8 1 4 2 7No.[73] 6 3 7 2 4 8 1 5 No.[74] 6 3 7 2 8 5 1 4No.[75] 6 3 7 4 1 8 2 5 No.[76] 6 4 1 5 8 2 7 3No.[77] 6 4 2 8 5 7 1 3 No.[78] 6 4 7 1 3 5 2 8No.[79] 6 4 7 1 8 2 5 3 No.[80] 6 8 2 4 1 7 5 3No.[81] 7 1 3 8 6 4 2 5 No.[82] 7 2 4 1 8 5 3 6No.[83] 7 2 6 3 1 4 8 5 No.[84] 7 3 1 6 8 5 2 4No.[85] 7 3 8 2 5 1 6 4 No.[86] 7 4 2 5 8 1 3 6No.[87] 7 4 2 8 6 1 3 5 No.[88] 7 5 3 1 6 8 2 4No.[89] 8 2 4 1 7 5 3 6 No.[90] 8 2 5 3 1 7 4 6No.[91] 8 3 1 6 2 5 7 4 No.[92] 8 4 1 3 6 2 7 5 total:92对于N皇后:┏━━━┯━━┯━━┯━━┯━━┯━━┯━━┯━━┓┃皇后N│4 │5 │6 │7 │8 │9 │10 ┃┠───┼──┼──┼──┼──┼──┼──┼──┨┃方案数│2 │10 │4 │40 │92 │352 │724 ┃┗━━━┷━━┷━━┷━━┷━━┷━━┷━━┷━━┛【题目】排球队员站位问题┏━━━━━━━━┓图为排球场的平面图，其中一、二、三、四、五、六为位置编号，┃┃二、三、四号位置为前排，一、六、五号位为后排。

解：启发函数h(n)=每个w左边B的个数，f(n)=d(n)+3*h(n)
W可以移到B右边的三种情况：
EBW
代价：2 B E W
代价：3
B WE
代价：2
f=1+3*4=13
B B WWE
f=0+3*4=12 f=1+3*4=13
B B WE W
B B E WW
f=2+3*4=14
f=2+3*3=11
(x)(C(x)→Easy(x))；
C(ds);
Q：Like(Li,ds)
3、某公司招聘工作人员，A，B，C三人应试。面试后，公司表示如下意见： （1）三人中至少录用一人； （2）如果录用A而不录用B，则一定录用C； （3）如果录用B，则一定录用C； 求证：公司一定录用C。
定义谓词：accept (x)：录用x 表示已知事实：
（1）三人中至少录用一人； accept (A) accept (B) accept (C)
（2）如果录用A而不录用B，则一定录用C； accept (A) accept (B) →accept (C)
（3）如果录用B，则一定录用C； accept (B) →accept (C)
结论Ｑ：accept (C)
B D
C
I
E
G
F
宽度优先
A
A
B
B
D
CD
C
I
I
E
E
OPEN
节父 深 点节 度 A 0 BA 1
CA 1
DA 1
I B2 CB 2
EC 2
G
G
GD 2
在OPEN表中调整C的父指针 G E 3 在OPEN表中调整G的父指针 F G 3

A、递归(DFS) 说白了还是循环，只是当3种循环不能做的时候的循环，我们用递归实现。

B、递归必须有终点，否则就会死递归，最后栈溢出202错误。

C、递归的实现，是按照层数优先搜索的方式实现的。

到底返回上一层看看有没有其他的路可以继续下去。

D、函数function的递归必须有返回值。

过程procedure到底就结束。

E、区分全局变量和局部变量的关系，全局一个子过程或函数里面动，全动，局部则互不影响，但会随着子过程或函数的消失而消失，子过程或函数的开始而开始。

F、四大法宝，剪枝（暗剪明剪）、迭代、回溯、*记忆化搜索。

在递归过程中，局部变量必须要赋初始值。

阶加普通for写法varn,i,s:longint;beginreadln(n);for i:=1 to n dos:=s+i;writeln(s);end.Procedure 递归写法varn,i,s:longint;procedure try(x:integer);beginif x=n thenbegins:=s+n;exit;end;s:=s+x;try(x+1);end;beginreadln(n);try(1);writeln(s);end.Function 递归写法varn:longint;function try(x:integer):longint;beginif x=n thenexit(n);exit(try(x+1)+x);end;beginreadln(n);writeln(try(1));end.那些三位数请你从小到大输出3位数，每一位的数字可以用1，2,3111112113。

333那些四位数请你从小到大输出4位数，每一位的数字可以用1，2,3，4Oj10911091: 【提高】那些n位数时间限制: 1 Sec 内存限制: 16 MB提交: 1379 解决: 706[提交][状态][讨论版]题目描述一个n位数，只由1，2，3，4...p这几个数字组成。

深度优先搜索算法教程[例1] 有A、B、C、D、E五本书，要分给张、王、刘、赵、钱五位同学，每人只能选一本。

事先让每个人将自己喜爱的书填写在下表中。

希望你设计一个程序，打印分书的所有可能方案，当然是让每个人都满意。

（如下图所示）[分析] 这个问题中喜爱的书是随机的，没有什么规律，所以用穷举法比较合适。

为编程方便，用1、2、3、4、5分别表示这五本书。

这五本书的一种全排列就是五本书的一种分法。

例如54321表示第5本书（即E）分给张，第4本书（即D 分给王，）……第1本书（即A分给钱）。

“喜爱书表”可以用二维数组来表示，1表示喜爱，0表示不喜爱。

[算法设计]：1、产生5个数字的一个全排列；2、检查是否符合“喜爱书表”的条件，如果符合就打印出来。

3、检查是否所有排列都产生了，如果没有产生完，则返回1。

4、结束。

[算法改进]：因为张只喜欢第3、4本书，这就是说，1* * * *一类的分法都不符合条件。

所以改进后的算法应当是：在产生排列时，每增加一个数，就检查该数是否符合条件，不符合，就立即换一个，符合条件后，再产生下一个数。

因为从第i本书到第i+1本书的寻找过程是相同的，所以可以用递归算法。

算法如下：procedure try(i); {给第I个同学发书}beginfor j:=1 to 5 dobeginif 第i个同学分给第j本书符合条件thenbegin记录第i个数; {即j值}if i=5 then 打印一个解else try(i+1);删去第i个数字endendend;具体如下：◆递归算法program zhaoshu;constlike:array[1..5,1..5] of 0..1=((0,0,1,1,0),(1,1,0,0,1),(0,1,1,0,0),(0,0,0,1,0),(0,1,0,0,1)); name:array[1..5] of string[5] =('zhang','wang','liu','zhao','qian'); varbook:array[1..5] of 0..5;flag:set of 1..5;c:integer;procedure print;var i:integer;begininc(c);writeln('answer',c,':');for i:=1 to 5 dowriteln(name[i]:10,':',chr(64+book[i]));end;procedure try(i:integer);var j:integer;beginfor j:=1 to 5 doif not(j in flag) and (like[i,j]>0) thenbeginflag:=flag+[j]; book[i]:=j;if i=5 then print else try(i+1);flag:=flag-[j]; book[i]:=0;end;end;{=====main====}beginflag:=[]; c:=0;try(1);readln;end.C语言代码：#include<stdio.h>#include<stdlib.h>int like[5][5]={0,0,1,1,0,1,1,0,0,1,0,1,1,0,0,0,0,0,1,0,0,1,0,0,1}; char name[5][10]={"zhang","wang","liu","zhao","qian"};int flag[5]={1,1,1,1,1};int book[5],c=0;void print(){ int i;printf("answer %d:",c);for(i=0;i<=4;i++)printf("%s:%c ",name[i],65+book[i]);printf("\n");}void dsf(int i){int j;for(j=0;j<=4;j++)if(flag[j]&&like[i][j]){ flag[j]=0;book[i]=j;if(i==4) print();else dsf(i+1);flag[j]=1;book[i]=0;}}int main(){ dsf(0);system("pause");return 0;}◆非递归算法program path;dep:=0; {dep为栈指针，也代表层次}repeatdep:=dep+1; r:=0; p:=false;repeat r:=r+1;if 子节点mr符合条件then产生新节点并存于dep指向的栈顶；if 子节点是目标then 输出并退出（或退栈）else p:=true;else if r>=maxr then 回溯else p:=flase;endif;until p:=true;until dep=0;其中回溯过程如下：procedure 回溯；dep:=dep-1;if dep=0 then p:=true else 取回栈顶元素（出栈）；具体如下：◆非递归算法program zhaoshu2;constlike:array[1..5,1..5] of 0..1=((0,0,1,1,0),(1,1,0,0,1),(0,1,1,0,0),(0,0,0,1,0),(0,1,0,0,1));name:array[1..5] of string[5]=('zhang','wang','liu','zhao','qian');var book:array[0..5] of 0..5;flag:set of 1..5;c,dep,r:longint;p:boolean;f:text;procedure print;var i:integer;begininc(c);writeln(f,'answer',c,':');for i:=1 to 5 dowriteln(f,name[i]:10,':',chr(64+book[i]));end;procedure back;begindep:=dep-1;if dep=0 then p:=trueelse begin r:=book[dep]; flag:=flag-[r]; end;end;{================================main======================= =}beginassign(f,'d:\wuren.pas');rewrite(f);clrscr;flag:=[]; c:=0;dep:=0;repeatdep:=dep+1; r:=0; p:=false;repeatr:=r+1;if not(r in flag) and (like[dep,r]>0)and (r<=5)thenbeginflag:=flag+[r]; book[dep]:=r;if dep=5 then begin print;inc(dep);back; endelse p:=true;endelseif r>=5 then back else p:=falseuntil p=true;until dep=0;end.上述程序运行产生结点的过程如下图所示：结点旁的编号是结点产生的先后顺序。

红与黑题目描述有一个矩形房间，覆盖正方形瓷砖。

每块瓷砖涂成了红色或黑色。

一名男子站在黑色的瓷砖上，由此出发，可以移到四个相邻瓷砖之一，但他不能移动到红砖上，只能移动到黑砖上。

编写一个程序，计算他通过重复上述移动所能经过的黑砖数。

输入开头行包含两个正整数W和H，W和H分别表示矩形房间的列数和行数，且都不超过20. 每个数据集有H行，其中每行包含W个字符。

每个字符的含义如下所示：'.'——黑砖'#'——红砖'@'——男子（仅出现一次）输出程序应该输出一行，包含男子从初始瓷砖出发可到达的瓷砖数样例输入样例输出迷宫问题题目描述设有一个N*N(2<=N<=10)方格的迷宫，入口和出口分别在左上角和右上角。

迷宫格子中分别放0和1,0表示可通，1表示不能，入口和出口处肯定是0.迷宫走的规则如下所示：即从某点开始，有八个方向可走，前进方格中数字为0时表示可通过，为1时表示不可通过，要另找路径。

找出所有从入口（左上角）到出口（右上角）的路径（不能重复），输出路径总数，如果无法到达，则输出0.输入第一行输入N,接下来输入N*N的矩阵输出输出路径总数样例输入样例输出单词接龙题目描述单词接龙是一个与我们经常玩的成语接龙相类似的游戏，现在我们已知一组单词，且给定一个开头的字母，要求出以这个字母开头的最长的“龙”（每个单词都最多在“龙”中出现两次），在两个单词相连时，其重合部分合为一部分，例如beast和astonish，如果接成一条龙则变为beastonish，另外相邻的两部分不能存在包含关系，例如at和atide间不能相连。

输入输入的第一行为一个单独的整数n(n<=20)表示单词数，以下n行每行有一个单词，输入的最后一行为一个单个字符，表示“龙”开头的字母。

你可以假定以此字母开头的“龙”一定存在.输出只需输出以此字母开头的最长的“龙”的长度样例输入样例输出选数题目描述已知 n 个整数x1,x2,…,xn，以及一个整数 k（k＜n）。

一、填空题1、产生式系统由三部分组成（综合数据库）、（知识库）和推理机，其中推理可分为（正向推理）和（反向推理）。

2、从已知事实出发，通过规则库求得结论的产生式系统的推理方式是（正向推理）。

3、在启发式搜索当中，通常用（ 启发函数 ）来表示启发性信息。

4、规则演绎系统根据推理方向可分为（规则正向演绎系统）、（规则逆向演绎系统）以及（规则双向演绎系统）等。

5、启发式搜索是一种利用（启发式信息）的搜索，估价函数在搜索过程中起的作用是（估计节点位于解路径上的希望）。

二、选择题1、如果问题存在最优解，则下面几种搜索算法中，（ A ）必然可以得到该最优解。

A 、广度优先搜索B 、深度优先搜索C 、有界深度优先搜索D 、启发式搜索2、如果问题存在最优解，则下面几种搜索算法中，（ D ）可以认为是“智能程度相对比较高”的算法。

A 、广度优先搜索B 、深度优先搜索C 、有界深度优先搜索D 、启发式搜索3、产生式系统的推理不包括（ D ）。

A 、正向推理B 、逆向推理C 、双向推理D 、简单推理4、下列搜索方法中不属于盲目搜索的是：（ D ）A 、等代价搜索B 、宽度优先搜索C 、深度优先搜索D 、有序搜索三、简答题1、广度优先搜索与深度优先搜索各有什么特点？ 答：广度优先搜索也称为宽度优先搜索，它是一种先生成的节点先扩展的策略；广度优先搜索是一种完备的策略，即只要问题有解，它就一定可以找到解。

并且，广度优先搜索找到的解，还不一定是路径最短的解。

广度优先搜索的缺点是盲目性较大，尤其是当目标节点距初始节点较远时，将产生许多无用的节点，因此其搜索效率较低。

深度优先搜索是一种非完备策略，即对某些本身有解的问题，采用深度优先搜索可能找不到最优解，也可能根本找不到解。

常用的解决方法是增加一个深度限制，当搜索达到一定深度但还没有找到解时，停止深度搜索，向宽度发展。

2、简述广度优先搜索算法，对下图给出广度优先搜索序列。

3、简述深度优先算法，对下图给出深度优先搜索序列。

第五章搜索策略习题参考解答5.1 练习题5.1 什么是搜索？有哪两大类不同的搜索方法？两者的区别是什么？5.2 用状态空间法表示问题时，什么是问题的解？求解过程的本质是什么？什么是最优解？最优解唯一吗？5.3 请写出状态空间图的一般搜索过程。

在搜索过程中OPEN表和CLOSE表的作用分别是什么？有何区别？5.4 什么是盲目搜索？主要有几种盲目搜索策略？5.5 宽度优先搜索与深度优先搜索有何不同？在何种情况下，宽度优先搜索优于深度优先搜索？在何种情况下，深度优先搜索优于宽度优先搜索？5.6 用深度优先搜索和宽度优先搜索分别求图5.10所示的迷宫出路。

图5.10 习题5.6的图5.7 修道士和野人问题。

设有3个修道士和3个野人来到河边，打算用一条船从河的左岸渡到河的右岸去。

但该船每次只能装载两个人，在任何岸边野人的数目都不得超过修道士的人数，否则修道士就会被野人吃掉。

假设野人服从任何一种过河安排，请使用状态空间搜索法，规划一使全部6人安全过河的方案。

（提示：应用状态空间表示和搜索方法时，可用(N m,N c)来表示状态描述，其中N m和N c分别为传教士和野人的人数。

初始状态为(3,3)，而可能的中间状态为(0,1),(0,2),(0,3), (1,1),(2,1),(2,2),(3,0),(3,1),(3,2)等。

）5.8 用状态空间搜索法求解农夫、狐狸、鸡、小米问题。

农夫、狐狸、鸡、小米都在一条河的左岸，现在要把它们全部送到右岸去。

农夫有一条船，过河时，除农夫外，船上至多能载狐狸、鸡和小米中的一样。

狐狸要吃鸡，鸡要吃小米，除非农夫在那里。

试规划出一个确保全部安全的过河计划。

（提示：a.用四元组(农夫，狐狸，鸡，米)表示状态，其中每个元素都可为0或1，0表示在左岸，1表示在右岸；b.把每次过河的一种安排作为一个算符，每次过河都必须有农夫，因为只有他可以划船。

）5.9 设有三个大小不等的圆盘A 、B 、C 套在一根轴上，每个圆盘上都标有数字1、2、3、4，并且每个圆盘都可以独立地绕轴做逆时针转动，每次转动90°，初始状态S 0和目标状态S g 如图5.11所示，用宽度优先搜索法和深度优先搜索法求从S 0到S g 的路径。

第3章作业题参考答案2.综述图搜索的方式和策略。

答：用计算机来实现图的搜索，有两种最基本的方式：树式搜索和线式搜索。

树式搜索就是在搜索过程中记录所经过的所有节点和边。

线式搜索就是在搜索过程中只记录那些当前认为是处在所找路径上的节点和边。

线式搜索的基本方式又可分为不回溯和可回溯的的两种。

图搜索的策略可分为：盲目搜索和启发式搜索。

盲目搜索就是无向导的搜索。

树式盲目搜索就是穷举式搜索。

而线式盲目搜索，对于不回溯的就是随机碰撞式搜索，对于回溯的则也是穷举式搜索。

启发式搜索则是利用“启发性信息”引导的搜索。

启发式搜索又可分为许多不同的策略，如全局择优、局部择优、最佳图搜索等。

5.（供参考）解：引入一个三元组(q0,q1,q2)来描述总状态，开状态为0，关状态为1，全部可能的状态为：Q0=(0,0,0) ; Q1=(0,0,1); Q2=(0,1,0)Q3=(0,1,1) ; Q4=(1,0,0); Q5=(1,0,1)Q6=(1,1,0) ; Q7=(1,1,1)。

翻动琴键的操作抽象为改变上述状态的算子，即F ＝{a, b, c} a:把第一个琴键q0翻转一次 b:把第二个琴键q1翻转一次 c:把第三个琴键q2翻转一次问题的状态空间为<{Q5},{Q0 Q7}, {a, b, c}>问题的状态空间图如下页所示：从状态空间图，我们可以找到Q5到Q7为3的两条路径，而找不到Q5到Q0为3的路径，因此，初始状态“关、开、关”连按三次琴键后只会出现“关、关、关”的状态。

6.解：用四元组(f 、w 、s 、g)表示状态， f 代表农夫，w 代表狼，s代表羊，g 代表菜，其中每个元素都可为0或1，用0表示在左（0，0，（1，0，（0，0，（0，1，（1，1，（1，0，（0，1，（1，1，acab ac abc bb c岸，用1表示在右岸。

初始状态S0：(0,0,0,0) 目标状态：(1,1,1,1)不合法的状态:(1,0,0,*),(1,*,0,0),(0,1,1,*),(0,*,1,1) 操作集F={P1，P2，P3，P4，Q1，Q2，Q3，Q4}方案有两种：p2→q0 →p3→q2 →p2 →q0 →p2p2→q0 →p1→q2 →p3→q0→p212 一棵解树由S0,A,D,t1,t2,t3组成；另一棵解树由S0,B,E,t4,t5组成。

DFS深度优先搜索（附例题）深度优先搜索，简称DFS，算是应⽤最⼴泛的搜索算法，属于图算法的⼀种,dfs按照深度优先的⽅式搜索，通俗说就是“⼀条路⾛到⿊”，dfs 是⼀种穷举，实质是将所有的可⾏⽅案列举出来，不断去试探，知道找到问题的解，其过程是对每⼀个可能的分⽀路径深⼊到不能再深⼊为⽌，且每个顶点只能访问⼀次。

dfs⼀般借助递归来实现例题：⾛迷宫#include <iostream>#include <string.h>using namespace std;int m,n;int sx,sy,ex,ey;//起点终点坐标int mp[20][20];//记录地图int cnt=0;//结果个数int ax[10]={0,0,-1,1};//x的四个⾛向int ay[10]={1,-1,0,0};//y的四个⾛向int vis[20][20];//记录是否来过int dfs(int x,int y){if((x>=0)&&(y>=0)&&(x<n)&&(y<m)&&(mp[x][y]==0)){//坐标合法性if(x==ex&&y==ey){//如果是终点cnt++;return0;}vis[x][y]=1;//将x，y设为已经来过if(vis[x][y]==1){//判断是否相邻顶点可⾛for(int i=0;i<4;i++){int tx=x+ax[i];int ty=y+ay[i];if((tx>=0)&&(ty>=0)&&(tx<n)&&(ty<m)&&(mp[tx][ty]==0)&&vis[tx][ty]==0)//相邻顶点可⾛条件dfs(tx,ty);//递归dfs此点}}vis[x][y]=0;return0;}}int main(){memset(vis,0,sizeof(vis));//将遍历数组全部置0cin>>n>>m;for(int i=0;i<n;i++){for(int j=0;j<m;j++){char c;cin>>c;if(c=='.'){//边输⼊边置mp的0或1，并设置起点坐标和终点坐标mp[i][j]=0;}else if(c=='S'){sx=i;sy=j;mp[i][j]=0;}else if(c=='T'){ex=i;ey=j;mp[i][j]=0;}elsemp[i][j]=1;//'#'为墙壁，⾛不通所以设为1}}dfs(sx,sy);//从起点开始遍历cout<<cnt<<endl;return0;}。