
浅谈微积分学的发展史
1 引言
提起微积分,人们自然会想到英国的牛顿(Newton,1642-1727)和德国的莱布尼茨(Leibniz,1646-1716),这主要是因为他们提出了微积分的基本概念和运算方法,发现了微积分的内在联系,建立了著名的牛顿——莱布尼茨公式.但是微积分的发展远不止这些,它的发展过程是数学家集体智慧的结晶.微积分的发展大致可分为以下五个阶段:早期萌芽、酝酿时期、创建期、发展期以及严密完善期.
2 早期萌芽
微积分的萌芽出现得比较早.中国战国时代庄周所著的《庄子·天下篇》中的“一尺之棰,日取其半,万世不竭”及三国时期刘徽在他的“割圆术”中提到的“割之弥细,所失弥少;割之又割,以至于不可割,则与圆周合体而无所失矣”,就都蕴涵了无穷小的思想.古希腊数学家、力学家阿基米德在公元前三世纪依据前人的穷竭法,用“切片”方法并借助杠杆原理建立了球体的体积公式,这其中就包含了定积分的思想.但在当时,微积分并没有受到人们的关注.
3 酝酿时期
从16世纪中叶开始,微积分正式进入了酝酿阶段.数学的发展与科学的进步紧密结合在一起,产生了以下有待解决的问题:
(1)已知物体移动的距离表示为时间的函数,求物体在任意时刻的速度和加速度;反之,已知物体的加速度表示为时间的函数,求速度和距离.
(2)求曲线的切线问题.一般人们把切线定义为与曲线只相交于一点且位于曲线的一边的这样一条直线足够了.显然,对于一些较复杂的曲线就不适用了.
(3)确定抛射体获得最大射程时的发射角及寻求行星离开太阳的最远和最近距离等涉及的函数最大值、最小值问题.
(4)求曲线的长、曲线围成的面积、曲面围成的体积、物体的重心以及一个体积相当大的物体(例如行星)作用于另一物体上的引力等.
为解决科学发展所带来的这一系列问题,17世纪上半叶被人们遗忘千年的微积分重又成为重点研究对象,几乎所有的科学大师都竭力寻求这些问题的解决方法,其中具有代表性成果的有:
3.1 笛卡尔“圆法”[1](P111)
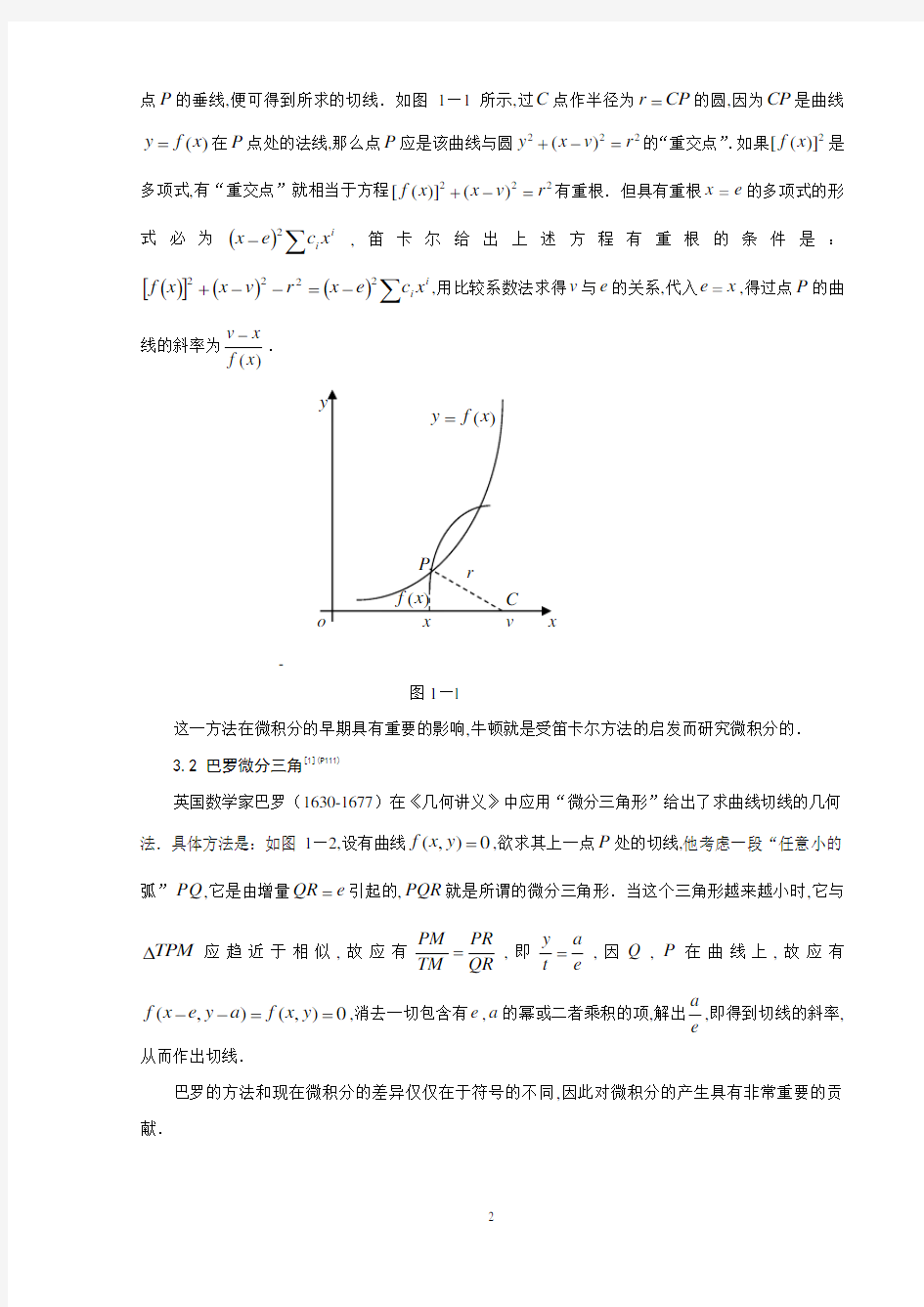
法国数学家笛卡尔(1596-1650)在《几何学》中提到了用代数方法求切线的所谓“圆法”,其方法是:首先确定曲线()y f x 在点(,())P x f x 处的法线与x 轴的交点C 的位置,然后作该法线的过
点P 的垂线,便可得到所求的切线.如图1—1所示,过C 点作半径为r CP =的圆,因为CP 是曲线
()y f x =在P 点处的法线,那么点P 应是该曲线与圆222()y x v r +-=的
“重交点”.如果2[()]f x 是多项式,有“重交点”就相当于方程222[()]()f x x v r +-=有重根.但具有重根e x =的多项式的形
式必为()i i x c e x ∑-2,笛卡尔给出上述方程有重根的条件是:()[]()()i i x c e x r v x x f ∑-=--+2222,用比较系数法求得v 与e 的关系,代入e x =,得过点P 的曲线的斜率为()
v x f x -. -
图1—1 这一方法在微积分的早期具有重要的影响,牛顿就是受笛卡尔方法的启发而研究微积分的.
3.2 巴罗微分三角[1](P111)
英国数学家巴罗(1630-1677)在《几何讲义》中应用“微分三角形”给出了求曲线切线的几何法.具体方法是:如图1—2,设有曲线(,)0f x y =,欲求其上一点P 处的切线,他考虑一段“任意小的弧”PQ ,它是由增量QR e =引起的,PQR 就是所谓的微分三角形.当这个三角形越来越小时,它与TPM ?应趋近于相似,故应有PM PR TM QR =,即y a t e
=,因Q ,P 在曲线上,故应有(,)(,)0f x e y a f x y --==,消去一切包含有e ,a 的幂或二者乘积的项,解出
a e
,即得到切线的斜率,从而作出切线. 巴罗的方法和现在微积分的差异仅仅在于符号的不同,因此对微积分的产生具有非常重要的贡献.
3.3 开普勒与旋转体体积 德国天文学家、数学家开普勒(1571-1630)发展了阿基米德求面积和体积的方法.在他1615年出版的《新空间几何》中,采用“用无数个同维的无限小元素之和来确定曲边形的面积及旋转体的体积”,给出了92个阿基米德未讨论过的体积问题,并研究了酒桶的最佳比例.
3.4 卡瓦列利不可分量原理
意大利数学家卡瓦列利(1598-1647)出版的《用新方法促进的连续不可分量的几何学》,影响巨大.他在其中提出了著名的“卡瓦列利原理”:“两个等高的立体,如果它们的平行于底面且离开底面有相等距离的截面面积之比为定值,那么这两个立体的体积之间也有同样的比”(当比为1︰1时,就是祖暅原理,只不过相差1000多年),他将面积的不可分量比作织成一块布的线,体积的不可分量比作一册书的各页,不可分量的个数为无穷多,且没有厚薄和宽窄.这已到达积分学的边缘并且他已发现公式101++=?n a a
n n dx x ,n 为正整数.
3.5 费马极大极小值
法国的大数学家费马(1601-1665)成就广泛,数论中费马定理尤著称于世.他在求极大极小值上的成功,为微积分的发展开辟了道路.
费马论证如下:
设()A x a x =-.今取x E +,则A '()()x E x a E =+--,作2(2)A A E a x E '-=-+(1),因极大值面积只有一个,故可认为0A A '-=,在(1)中约去E ,即得0(2)a x E =-+.然后令E 为0,得2x a =,即2a x =.E 相当于今天的x ?,费马正是从0A A E '-=中解出了2
a x =.[2](P282-283) 经过众多科学大师的探讨与研究,至此,微积分的诞生已经到了“万事俱备,只欠东风”的时刻. 4 微积分学的创建
十七世纪后半叶,牛顿和莱布尼茨分别独立创建了微积分.
图1—2
4.1 牛顿及其流数术
英国数学家牛顿对微积分问题的研究始于1664年.当时他反复阅读笛卡尔的《几何学》,对笛卡尔求切线所用的“圆法”产生了极大的兴趣,还试图寻找更好的求切线方法.1665年5月20日,在牛顿手写的一页文件中开始有“流数术”的记载.他称连续变量为“流动量”,流动量的导数为“流
动率”.x &表示流动量x 的流动率.关于牛顿流动率的求法举例如下,例:设给定函数20y x -=,时间
的刹那用0表示(即dt ),,x y 的刹那用0x &和0y &表示(即,dx dy dx dt dy dt dt dt
=?=?).以0x x +&及0y y +&替代,x y ,代入方程得:2220(200)0y y
x xx x +-++=&&&,因20y x -=,故有2202000y xx x -+=&&&.全式除以0,得2200y xx x -+=&&&,略去20,x &即得2.y xx =&&用现在的记号就是
x dx
dy 2=.牛顿在《流数术》一书中陈述了所研究的基本问题是“已知量的关系,要算出它们的流数;以及反过来.”正是这一点,使牛顿超过所有的微积分先驱者.牛顿完整地提出微分和积分是一对逆运算,并且得出了微积分学基本定理)()()(a F b F dx x f b a -=?.牛顿在1665年11月发明了“正流数
术”(微分法),1666年5月建立了“反流数术”(积分法).同年10月,牛顿将前两年的工作总结为《流数简论》,明确了现代微积分的基本方法,是历史上第一篇系统的微积分文献.牛顿关于微积分的著作大多写于1665—1676年间,但这些著作发表很迟.
4.2 莱布尼茨和微积分
德国数学家莱布尼茨是一位博学多才的学者,他平生所学的知识涉及数学、哲学、历史学、生物学、物理学、神学、法学等领域.1672年,莱布尼茨出使巴黎时深受法国数学家帕斯卡事迹的鼓舞,决心钻研高等数学.莱布尼茨是从巴罗的“微分三角形”切入微积分研究工作的,他在研究时认识到:“求曲线的切线依赖于纵坐标的差值与横坐标的差值在变成无限小时之比;求曲线的面积则依赖于无限小区间上的纵坐标之和”.1673年,莱布尼茨开始了对无穷小算法的研究,在1675年10月29日他的一份手稿中,他决定用sum 拉长的s ,?表示积分.1676年11月,莱布尼茨已经能够给出幂函数的微分与积分公式.1677年,莱布尼茨在一篇手稿中明确陈述了微积分基本定理.1684年,莱布尼茨在《学艺》杂志上发表了名为《一种求极大极小和切线的新方法,它也适用于分式和无理量,以及这种新方法的奇妙类型的计算》的论文,这是历史上最早公开发表的关于微分学的文章.1686年,他在该杂志上又发表的《潜在的几何与分析不可分和无限》是历史上第一篇关于积分学的文章.
4.3 优先权之争
牛顿与莱布尼茨关于“发明微积分”优先权的争论被称为“数学史上最不幸的一章”,并导致了英国与欧洲国家在数学发展上的分道扬镳.实际上,牛顿在微积分方面的研究虽早于莱布尼茨,但莱布
尼茨成果的发表则早于牛顿.他们是相互独立的创建微积分的.
5 微积分的发展
自从牛顿和莱布尼茨创立微积分以后,数学进入了生机勃勃的大革命时代.许多数学家利用微积分创立了辉煌的成就.其中以欧拉(L.Euler,1707-1783)最为著名,他用微积分工具解决了大量的天文、物理、力学等问题,开创了微分方程、无穷级数、变分学等诸多新学科.随后,拉格朗日(Lagrange,1736-1813),拉普拉斯(Laplace,1749-1827),勒让德(Legendre,1752-1833),傅里叶(Eourier,1768-1836)等许多数学家也对微积分的发展作出了重大的贡献.然而,初创时期的微积分存在一些漏洞,如逻辑基础不牢固、无穷小概念不够明确等,更曾就此爆发过一场大的争论.但由于这种基础不牢固的微积分用于天文、力学等科学上总能获得可喜的巨大成果,因此,数学家们无暇顾及其理论上的漏洞,微积分得以快速地发展并达到空前的辉煌.
6 微积分的严密完善期
数学学科要求它自身必须具有严密的逻辑性.十七世纪创立及十八世纪发展的空前灿烂的微积分仍没有建立起自己的严密的理论基础.十九世纪初,数学家开始转向微积分逻辑基础的建设.波尔查诺(Bolzano,1781-1848)是最早对无穷小概念进行审慎研究的先驱,他在论文“纯粹的分析证明”中首先给出了连续函数的定义并清楚表明:连续性概念的基础存在于极限概念之中.之后,法国著名数学家柯西(Cauchy,1789-1857)在重新定义了极限和无穷小后,进一步澄清了存在于连续、导数、微分、积分、无穷级数的和等概念上的模糊之处并创立了一系列判别法则,确立了较为严谨的极限理论.柯西认识到“无理数是有理数迫近的极限”,但极限又要用到实数,这是一个循环论证.柯西以后,分析学逻辑基础发展史上的重大事件就是实数理论的建立了.作出重要贡献的主要有:魏尔斯特拉斯(Weierstrass,1815-1897)、戴德金(Dedekind,1831-1916)和康托尔(Cantor,1845-1918)等人.德国数学家魏尔斯特拉斯认为实数系是解决极限与连续等概念的关键.要使分析严格化,必须使实数系严格化,最可靠的办法是按照严密的推理将实数归结为整数(有理数),这样,分析的所有概念便可由整数导出,从而使以往的漏洞和缺陷得以填补.这就是“分析算术化”纲领.魏尔斯特拉斯和他的学
ε-语言就是由他创造的,这生们为实现这一纲领付出了艰苦的努力并获得了很大的成功.现代的δ
为他博得了“现代分析之父”的称号.随着戴德金的实数理论和康托尔的集合理论的建立,微积分的严格基础体系宣告完成.这一阶段的微积分,通常被人们称为标准分析.至此,微积分的发展基本完善.但是,这并没有终止人们对微积分的探究.二十世纪以后,微积分仍在大步前进,如产生了复分析、泛函分析等微积分的重要分支,六十年代,美国逻辑学家鲁滨逊(Robinson)还创立了非标准分析,构成了微积分的一个组成部分.这都使得微积分跃上了新的高度.
但是,微积分仍需要发展,数学这门重要的学科仍需进步,人类才能走向更高的历史阶段.
定积分的发展史 起源 定积分的概念起源于求平面图形的面积和其他一些实际问题。定积分的思想在古代数学家的工作中,就已经有了萌芽。比如古希腊时期阿基米德在公 元前 240 年左右,就曾用求和的方法计算过抛物线弓形及其他图形的面积。 公元 263 年我国刘徽提出的割圆术,也是同一思想。在历史上,积分观念的 形成比微分要早。但是直到牛顿和莱布尼茨的工作出现之前( 17 世纪下半叶),有关定积分的种种结果还是孤立零散的,比较完整的定积分理论还未能形成, 直到牛顿 -- 莱布尼茨公式建立以后,计算问题得以解决,定积分才迅速建立 发展起来。 未来的重大进展,在微积分才开始出现,直到16 世纪。此时的卡瓦列利与 他的indivisibles方法,并通过费尔马工作,开始卡瓦列利计算度N = 9×N的积分奠定现代微积分的基础,卡瓦列利的正交公式。17世纪初巴罗提 供的第一个证明微积分基本定理。 牛顿和莱布尼茨 在一体化的重大进展是在 17 世纪独立发现的牛顿 ?? 和莱布尼茨的微积分 基本定理。定理演示了一个整合和分化之间的连接。这方面,分化比较容易 地结合起来,可以利用来计算积分。特别是微积分基本定理,允许一个要解决 的问题更广泛的类。同等重要的是,牛顿和莱布尼茨开发全面的数学
框架。由于名称的微积分,它允许精确的分析在连续域的功能。这个框架最终成为现代微积分符号积分是直接从莱布尼茨的工作。 正式积分 定积分概念的理论基础是极限。 人类得到比较明晰的极限概念,花了大约 2000 年的时间。在牛顿和莱布尼茨的时代,极限概念仍不明确。因此牛顿和莱布尼茨建立的微积分的理论基础还不十分牢靠,有些概念还比较模糊,由此引起了数学界甚至哲学界长达一个半世纪的争论,并引发了“第二次数学危机”。经过十八、十九世纪 一大批数学家的努力,特别是柯西首先成功地建立了极限理论,魏尔斯特拉斯进一步给出了现在通用的极限的定义,极限概念才完全确立,微积分才有 了坚实的基础,也才有了我们今天在教材中所见到的微积分。现代教科书 中有关定积分的定义是由黎曼给出的。 术语和符号 艾萨克牛顿以上的变量使用一个小竖线表示一体化,或放置在一个盒子里的变量,竖线是很容易混淆。或牛顿用来指示分化和方块符号打印机难以重现,所以这些符号没有被广泛采用。 1675 年戈特弗里德莱布尼茨改编的积分符号,∫,从字母S(“总结”或“总”)。 ∫符号表示的整合 ; A和 B 的下限和上限,分别一体化,定义域的融合 ; f是积,x 在区间 [a ,b] 上的变化进行评估;
微积分的应用 微积分是研究函数的微分、积分以及有关概念和应用的数学分支。微积分是建立在实数、函数和极限的基础上的。微积分学是微分学和积分学的总称。它是一种数学思想,‘无限细分’就是微分,‘无限求和’就是积分。无限就是极限,极限的思想是微积分的基础,它是用一种运动的思想看待问题。微积分最重要的思想就是用"微元"与"无限逼近",好像一个事物始终在变化你不好研究,但通过微元分割成一小块一小块,那就可以认为是常量处理,最终加起来就行。微积分是与实际应用联系着发展起来的,它在天文学、力学、化学、生物学、工程学、经济学等自然科学、社会科学及应用科学等多个分支中,有越来越广泛的应用。特别是计算机的发明更有助于这些应用的不断发展。客观世界的一切事物,小至粒子,大至宇宙,始终都在运动和变化着。因此在数学中引入了变量的概念后,就有可能把运动现象用数学来加以描述了。 微积分建立之初的应用:第一类是研究运动的时候直接出现的,也就是求即时速度的问题。第二类问题是求曲线的切线的问题。第三类问题是求函数的最大值和最小值问题。第四类问题是求曲线长、曲线围成的面积、曲面围成的体积、物体的重心、一个体积相当大的物体作用于另一物体上的引力。 微积分学极大的推动了数学的发展,同时也极大的推动了天文学、力学、物理学、化学、生物学、工程学、经济学等自然科学、社会科学及应用科学各个分支中的发展。并在这些学科中有越来越广泛
的应用,特别是计算机的出现更有助于这些应用的不断发展。 微积分作为一种实用性很强的数学方法和根据,在数学发展中的地位是十分重要的。例如,微分可以解决近似计算问题。比如:求sin29°的近似值,求不规则图形面积或几何体体积的近似值等。通过微积分求极限、利用微分中值定理,能够及时的放缩多项式,有利于不等式的化简和证明。极限求和、导数求和、积分求和也都是解决求数列前n项和的好方法。其次,数理化不分家。而且微积分在不等式中也有很大的运用,我们可以运用微积分中值定理,泰勒公式,函数的单调性,极值,最值,凸函数法等来证明不等式。在物理问题上,通过解微分方程研究物体运动问题、气体问题、电路问题也是非常普遍的。已知位移——时间函数计算速度,已知速度——时间函数计算加速度(即生活中交通管理方面的应用);运动学中的曲线轨迹求解(即生活中在篮球投篮训练中的应用);求不规则物体的重心;力学工程中计算变力和非恒力做功等等。在化学领域,用气相色谱仪和液相色谱仪做样品化学成分分析时,我们得到的并不是直观的数字结果,而是一张色谱图。色谱图是由一个一个的峰组成的,而我们进行定量计算的根据,就是这些峰的面积。而求这些峰的面积,就需要用到积分。现在的仪器里都集成了自动积分仪,只要选定某一个峰,它就能把积分计算出来。最终得到的成分含量就是基于积分原理计算出来的 微积分的应用不仅仅遍及各个学科,也渗透到了社会的各个行业,甚至深入人们日常生活和工作。利用微积分进行边际分析(经济函数的
第九章 多元函数微分学 内容复习 一、基本概念 1、知道:多元函数的一些基本概念(n 维空间,n 元函数,二重极限,连续等);理解:偏导数;全微分. 2、重要定理 (1)二元函数中,可导、连续、可微三者的关系 偏导数连续?可微???函数偏导数存在 ?连续 (2)(二元函数)极值的必要、充分条件 二、基本计算 (一) 偏导数的计算 1、 偏导数值的计算(计算),(00y x f x ') (1)先代后求法 ),(00y x f x '=0),(0x x y x f dx d = (2)先求后代法(),(00y x f x '=00),(y y x x x y x f ==') (3)定义法(),(00y x f x '=x y x f y x x f x ?-?+→?),(),(lim 00000)(分段函数在分段点处的偏导数) 2、偏导函数的计算(计算(,)x f x y ') (1) 简单的多元初等函数——将其他自变量固定,转化为一元函数求导 (2) 复杂的多元初等函数——多元复合函数求导的链式法则(画树形图,写求导公式) (3) 隐函数求导 求方程0),,(=z y x F 确定的隐函数),(y x f z =的一阶导数,z z x y ???? ,,,(),,y x z z F F z z x y z x F y F x y x y z ''???=-=-?''????? 公式法:(地位平等)直接法:方程两边同时对或求导(地位不平等) 注:若求隐函数的二阶导数,在一阶导数的基础上,用直接法求。 3、高阶导数的计算 注意记号表示,以及求导顺序 (二) 全微分的计算 1、 叠加原理
中国陶瓷发展史 中国是瓷器的故乡,中国瓷器的发明是中华民族对世界文明的伟大贡献,在英文中"瓷器"(china)一词也有"中国"的意思。大约在公元前16世纪的商代中期,中国就出现了早期的瓷器。因为其无论在胎体上,还是在釉层的烧制工艺上都尚显粗糙,烧制温度也较低,表现出原始性和过渡性,所以一般称其为"原始瓷"。 瓷器脱胎于陶器,它的发明是中国古代先民在烧制白陶器和印纹硬陶器的经验中,逐步探索出来的。烧制瓷器必须同时具备三个条件:一是制瓷原料必须是富含石英和绢云母等矿物质的瓷石、瓷土或高岭土。二是烧成温度须在1200℃以上。三是在器表施有高温下烧成的釉面。 原始瓷作为陶器向瓷器过渡时期的产物,与各种陶器相比,具有胎质致密、经久耐用、便于清洗、外观华美等特点,因此发展前景广阔。原始瓷烧造工艺水平和产量的不断提高,为后来瓷器逐渐取代陶器,成为中国人日常生活的主要用器奠定了基础。 中国瓷器是从陶器发展演变而成的,原始瓷器起源于3000多年前。至宋代时,名瓷名窑已遍及大半个中国,是瓷业最为繁荣的时期。当时的钧窑、哥窑、官窑、汝窑和定窑并称为五大名窑。被称为瓷都的江西景德镇在元代出产的青花瓷已成为瓷器的代表。青花瓷釉质透明如水,胎体质薄轻巧,洁白的瓷体上敷以蓝色纹饰,素雅清新,充满生机。青花瓷一经出现便风靡一时,成为景德镇的传
统名瓷之冠。与青花瓷共同并称四大名瓷的还有青花玲珑瓷、粉彩瓷和颜色釉瓷。另外,还有雕塑瓷、薄胎瓷、五彩胎瓷等,均精美非常,各有特色。 多姿多彩的瓷器是中国古代的伟大发明之一,"瓷器"与"中国"在英文中同为一词,充分说明中国瓷器的精美绝伦完全可以作为中国的代表。而各个时期的陶瓷文化展现着不同的风采。 夏、商、周朝时期的陶瓷文化 商朝殷虚的遗址中挖出的陶片、陶罐包括很多种款式,有灰陶、黑陶、红陶、彩陶、白陶,以及带釉的硬陶,这些陶器上的纹饰、符号、文字与殷商时代的甲骨文和青器有密切的关系。青器的成本高只能为贵族享用,广大民众的各种生活器皿只能采用陶器。因此可以了解商代制陶工艺也得到普遍的发展,带釉的硬陶在这个时期已经出现了,釉色青绿而带褐黄,胎质比较硬,呈灰白色。 陶器在此时已经不在局限於盛物器皿,应用范围较广,大略可分为日用品类、建筑类、殉葬类、祭祀礼器类。朝廷对於制陶工作也很重视。 秦汉时期陶瓷文化 秦汉-古代的建筑多采用木料来架构,不易久存,所以一些伟大的建筑,如秦代的阿房宫和汉代的未央宫,都无法完整保存下来,但仍可在残存的废墟中发现瓦当及汉砖等遗物,藉以略窥古代建筑的规模。
微积分发展史 摘要:本文将介绍微积分的由来以及发展过程以及他对于人类发展的重大意义。并且在文章中也会对微积分的一些基本内容和理论等进行说明和归纳 关键词:微积分,微分,积分,建立 一、微积分学的建立 微积分在如今的数学领域中占到了非常重要的地位,并且作为 一门学科,微积分是研究函数的微分、积分以及有关概念和应 用的数学分支。它的起源可以追溯到其诞生的2000多年前, 比如,古代的人用方砌圆,我国庄子的“一尺之棰,日取其半,万世不竭”,魏晋时刘徽的“割圆术”等等,都涉及到了以“直”代“曲” 的极限观念,属于微积分的朴素思想,阿基米德更可称为时微 积分学的先驱,他不仅成功地将“穷竭法”应用于求像抛物线弓 形那样复杂地曲边形地面积中,而且在求积时应用了各种微积 分学地思想。但微积分思想真正形成是在十七世纪,由牛顿总 结和发展了前人的工作,几乎同时建立了微积分的方法和理论 微积分的起源。牛顿是从物理角度建立了微积分的思想,而德 国数学家莱布尼兹从几何角度出发,独立地创立了微积分 (1675-1676)。这两位数学家总结出处理各种有关问题地一般 方法,并揭示出微分学和积分学之间的本质联系。两人各自建
立了微积分学基本定理,并给出微积分的概念、法则、公式及 其符号。这位日后的微积分学的进一步发展奠定了坚实而重要 的基础。微积分的创立,极大地推动了数学地发展,过去很多 初等数学束手无策地问题,通过运用微积分,往往引刃而解。 使得微积分学地创立成为数学发展地一个里程碑式的事件。二、微积分建立的重要意义 恩格斯曾经说过:“在一切理论成就中,未必再有什么像十七世 纪下半叶微积分的发现那样被看作人类精神的最高胜利了。如 果在某个地方我们看到人类精神的纯粹的和惟一的功绩,那就 正是在这里。”在微积分建立之前,人类基本还处于农耕文明时 期。但在微积分建立之后它为创立许多新的学科提供了源泉。 可以说微积分的建立是人类头脑最伟大的创造之一,是人类智 慧的结晶,它极大地推动了科学地进步,并且对社会也有深远 的影响。有了微积分,就有了工业革命,它是世界近代科学的 开端,同时也摧毁了笼罩在天体上的神秘主义、迷信和神学, 对社会产生了极大的影响,使人们进入了现代化的社会。这一 切都表面了微积分学的产生是人类历史上的一次空前飞跃。三、微积分理论的基本介绍和归纳 微积分学是微分学和积分学的总称。微积分学基本定理指出, 求不定积分与求导函数是互为逆运算的过程,而把上下限代入 不定积分即得到积分值,微分则是倒数值与自变量增量的乘积。 作为一种数学的思想微分就是“无限细分”,而积分就是“无限求
微积分在实际中的应用 一、微积分的发明历程 如果将整个数学比作一棵大树,那么初等数学是树的根,名目繁多的数学分支是树枝,而树干的主要部分就是微积分。微积分堪称是人类智慧最伟大的成就之一。微积分是微分学和积分学的总称。它是一种数学思想,“无限细分”就是微分,“无限求合”就是积分。微分学包括求导的运算,是一套关于变化的理论。它使得函数、速度、加速度和曲线的斜率等均可以用一套通用的符号进行讨论。积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法。微积分的产生一般分为三个阶段:极限概念、求面积的无限小方法、积分与微分的互逆关系。前两阶段的工作,欧洲及中国的大批数学家都做出了各自的贡献。 从17世纪开始,随着社会的进步和生产力的发展,以及如航海、天文、矿山建设等许多课题要解决,数学也开始研究变化着的量,数学进入了“变量数学”时代,即微积分不断完善成为一门学科。整个17世纪有数十位科学家为微积分的创立做了开创性的研究,但使微积分成为数学的一个重要分枝还是牛顿和莱布尼茨。 二、微积分的思想 从微积分成为一门学科来说,是在17世纪,但是,微分和积分的思想早在古代就已经产生了。公元前3世纪,古希腊的数学家、力学家阿基米德(公元前287~前212)的著作《圆的测量》和《论球与圆柱》中就已含有微积分的萌芽,他在研究解决抛物线下的弓形面积、球和球冠面积、螺线下的面积和旋转双曲线的体积的问题中就隐含着近代积分的思想。作为微积分的基础极限理论来说,早在我国的古代就有非常详尽的论述, 与此同时,战国时期庄子在《庄子·天下篇》中说“一尺之棰,日取其半,万世不竭”,体现了无限可分性及极限思想。公元3世纪,刘徽在《九章算术》中
龙源期刊网 https://www.doczj.com/doc/8314699943.html, 浅谈中国陶瓷艺术 作者:司忠辉 来源:《学习与科普》2019年第08期 从古到今,尽管世界各民族对美的鉴赏千差万别,但是,却都能以某种方式获得对美的享受。而在中国,陶瓷无疑是最受欢迎的艺术品之一。陶瓷艺术在中国的发展源远流长,种类繁多,在世界历史的进程中,中国的陶瓷艺术也一直是颇具代表性的艺术珍品,历经千年,仍盛而不衰。本文将从中国陶艺的发展历程,现当代陶艺发展所存在的问题等方面,来浅谈中国 的陶瓷艺术。 一、中国传统陶艺的发展历程 远在九千多年前,中国先民在从事渔猎、农业生产活动的同时,开始了最原始的活动。随着火的发明和使用,在改造大自然的长期劳动实践中,伴随着无数次失败与成功的体验,开始制造和使用成为中国古文化之一的艺术创造物——陶器,并揭开了人类发展史上的“新石器时代”。 新石器时代中期中国制陶业取得的最大成就就是彩陶艺术,各个地区文化彼此影响、相互交流、或继承发展,在中国历史长河中形成了共同又丰富多彩的艺术风格。以彩陶为文化的仰韶文化之后,以山东为中心的龙山文化的另一类文化遗存方式出现,那便是黑陶艺术。 进入商代,模仿同时期青铜器纹样与器型的白陶出现了,在当时它是比青铜器更为豪华的工艺,器形几乎全是礼器。尤其富有特点的是波状雷纹、勾连雷纹和一种怪异人形云雷纹,是人类文化上罕见的工艺美术品。尽管在商代制陶工艺没有明显进步,艺术性也没有明显提高,但是白陶的烧制成功对由陶器过度到瓷器起了十分重要的作用。在这一时期,也出现了瓷器的前身“原始青瓷”。 原始瓷从商代出现,经历了西周和春秋战国到东汉,逐渐的走向成熟,出现了青瓷。这些青瓷的加工精细,胎质坚硬,不吸水,表面施有一层青色玻璃质釉。而且它以瓷质细腻,线条明快流畅、造型端庄浑朴、色泽纯洁而斑斓著称于世。青瓷的出现标志着中国瓷器生产已进入一个新时代。同时,在秦汉时期,制陶业也得到了进一步的发展。秦朝时的陶俑造型逼真,深刻揭露了人物的内心世界。在彩陶方面,汉代彩陶一改奔放热烈的作风,转而崇尚凝重精雅的神韵,艺术表现力强。 到了隋唐时期,经济的高度发达,民族的大一统使得唐朝各个领域全面开花,空前繁荣。而在陶瓷艺术中,最能代表这种盛唐气息的便是唐三彩。它多用于陪葬,作为一种冥器,它的实用性远不如当时的青瓷、白瓷。萌发于南北朝时期的白瓷,到隋朝时,已发展到了成熟阶段,至唐朝更有新的发展瓷器烧成温度达到1200°C,瓷的白度也达到了70%以上,接近现代高级细瓷的标准。这一成就为釉下彩和釉上彩瓷器的发展打下基础。
《微积分》学习方法 来源:东财网院 很多同学都会认为,数学是一门比较难学的学科,有那么多的定义、公式、定理,还有图像以及各种曲线等等,总是让人头疼。所以同学们在接触微积分之前,可能就已经对它产生了心理恐惧,甚至是排斥心理。而事实并非如此,之所以会这样是因为你还没有掌握正确的学习方法。 首先,大家应该大致翻一下教科书,或者是看看目录和前言,了解学习这么课程所需具备的基础知识是什么。从第一章的内容中,大家可以了解到,微积分的起点是中学里的函数概念和解析几何。所以,如果以往的知识不牢固,或是没有接触过,那么最好找来中学的教科书复习一下。接下来,大家就接触到了极限,数列的极限以及函数的极限。大家可能会发现,极限的定义很难看懂。那是不是就能以此为借口,停顿在这里呢?当然不能,我们可以先把这个问题放一下,继续向下。实际上,极限的概念是很直观的,理解其思想即可,看不懂定义并不影响下面的学习。 接下来的部分就较为重要了,而且不能跳过。导数的概念其实也很简单,就是一个量关于另一个量的变化率。下面可能牵扯到很多导数的公式和运算技巧,很少有人会马上记住,这也不要紧,可以在平时的练习中慢慢掌握。可能有些同学喜欢解题,喜欢推导和运算,这固然是好事,但不要过度的沉浸在题海中。接触到微分,大家会发现,它和导数没有实质性的区别,只是在表达方式上有所不同,这是需要大家分清楚地。 下一个难点就是积分了。积分的数学定义可能较难理解,那么可以从图形下手,可以充分发挥想象力:为了求得曲线所围的面积,用无数小梯形去无限逼近,这也就是极限的思想。其实积分的本质就是极限。理解它的本质后,运算技巧可以暂放一下,在考试前可以集中解决运算技巧的问题。 对于多数同学来说,微积分的后半部分会更难些。对于无穷级数,同学们还是重在理解思想。多元函数微积分比前面的一元函数稍微复杂了些,但是基本的思路是一样的。最后一个难点,就是关于微分方程了。首先,要理解微分方程的有关概念以及微分方程的解,这样才能对微分方程有所识别。其次,对各种类型的微分方程,都要抓住其特征的本质,领会每一道例题中解题的方法和含义。 在学习数学的过程中,前后的连贯性较为重要,所以要注意知识点之间的衔接。但也不排除个别的情况,比如前文中说到的极限和级数。事实上很多人的亲身经历也证明了,微积分并不可怕,关键看你肯不肯下功夫。相信在大家的努力和老师的帮助下,微积分的难关是可以攻克的。 微 积 分》 的 学 习 方 法 读书好比走路。不知道去那里干什么,走起路来也没 劲儿。读书也是这样,没有目的,读起书来也没兴趣。 走路也得有方法,方法对走起路来才省劲儿。读书也 是这样,方法得当才能收到好效果。学生在校期间, 读书当然应以教科书为主,但是大学生与中小学生不
微积分发展史 微积分在数学发展史上可以认为是一个伟大的成就,由于微积分的创立不仅解决了当时的一些重要的科学问题,而且由此产生了数学的一些重要分支,如微分方程、无穷级数、微分几何、变分法、复变函数等。这个伟大的成就当然首先应该归功于牛顿(Newton)和莱布尼茨(Leibniz),但是在他们创立微积分之前,微积分问题至少被17世纪十几个大数学家和几十个小数学家探索过,得出了一些有价值的结论,且具有很大启发性。牛顿和莱布尼茨是在前人的基础上将微积分发展到了高峰。 17世纪遇到了哪些问题呢?主要有四类问题。第一类是速度和加速度问题。17世纪遇到的速度和加速度问题大都是变量问题,即变速与变加速。这与17世纪以前所遇到的大量常速问题所不同,如何求速度与加速度成为当时科学家们所关心的问题。第二类是切线问题。17世纪光学是一门重要的学科,例如透镜如何设计,这涉及切线与法线。切线问题在17世纪以前虽也解决过,但只限于圆锥曲线,而切线的定义是只与曲线接触一点的直线,这种情况不能适应17世纪所遇到的复杂的曲线的切线问题,另外物体运动时在它轨迹上的运动方向也涉及切线。第三类是最大值和最小值问题。炮弹的最大射程如何求,行星运行时离开太阳的最远和最近距离如何求,都是17世纪迫切要解决的。第四类是求曲线的长、曲线围成的面积和曲面围成的体积、物体的重心、引力等。这些问题在17世纪之前个别地解决过,但必须有较好的技巧,且方法缺乏一般性。 尝试解决这四类问题在牛顿、莱布尼茨之前已经有过不少经验,罗贝瓦尔(Roberval)从炮弹的水平速度与垂直速度构成矩形的对角线出发,认为这条对角线就是炮弹的轨迹切线。牛顿的老师巴罗(Barrow),也给出了求切线的方法。17世纪开普勒(Kepler)证明了所有内接于球的,具有正方形底的正平行四面体中立方体的容积最大。当越来越接近最大体积时,相应尺寸的变化对体积的变化越来越小(就是我们现在所说的极值处的导数为0)。费马(Fermat)在1629年已经找到与现在求最大值和最小值的方法实质相同的方法。卡瓦列利(Cavalieri)在他老师伽利略(Galileo)和开普勒的影响下,并在他老师的敦促下,考查了微积分,并且获得n为正整数时的积分公式(1639年) 1634年罗贝瓦尔求出了旋轮线x=R(t-s in t),y=R(1-c os t)一个拱下的面积。他还求出了正弦曲线一个拱下的面积及它绕底旋转的体积。一些图形的重心也计算出来了。格利哥利(Gregory)在1647年算出了 以上都是一些具体的结果,在原则性的问题上,如微积分的主要特征——积分与微分互逆,也早为人们所遇到。托里拆利(Torricelli)通过特殊的例子看到了变化率问题本质上是面积问题的反问题。费马同样也在特殊的例子中知道了面积与导数的关系。格利哥利1668年证明了切线问题是面积问题的逆问题。巴罗也看到了这种关系,但他们不是没有看到其普遍意义或一般性,就是没引起重视和看到其重要性。17世纪的前三分之二的时间内,微积分的工作被困拢在一些细节问题里,作用不大的细微末节的推理使数学家们精疲力竭了。
高等数学在实际生活中的应用 在学习高数之前,总是听学长、学姐提起,高数十分难学,我对高数的印象一直都是:高数是一门特别难、特别高深的学科。但在学习了高等数学之后,我发现了数学的美,同时我发现在实际生活中也时常可以看高数的身影。 高等数学在实际生活中的应用十分广泛,而且也特别有趣。我就简单的举几个生活中常见的,我所发现的高等数学在生活中的运用的例子分析一下。 首先,我发现在支付宝当中,有一个小功能,叫做蚂蚁森林,这个功能是模拟出了一颗树苗,当人们在生活中做出了一些绿色、低碳的行为时,对用户发放绿色能量进行奖励,当用户的绿色能量积累到一定的值时,支付宝模拟出的小树苗就会长成一颗大树,用户可以通过兑换,将这颗模拟出来的小树(电子数据)兑换成为一颗真实的、种植在沙漠里的树木,现在可以兑换的树木类型越来越丰富了,有梭梭树、沙柳、樟子松、胡杨树等一些树苗。 这个时候我就发现,不同的地区的树苗不尽相同,而且,肯定不同的树木类型各自的水土保持能力也不尽相同,因此,在什么地区选择什么样的树木类型、分别种植在哪里,可以起到最好的水土保持功能以及,每平方米需要种植几颗树苗,我相信,这些问题都离不开高等数学进行周密的计算。 首先,我们需要认真计算防护林需要种植多大面积、到底种植在哪里可以起到最佳的水土保持作用,我们需要了解到风沙的源地与我
们需要保护的地区的距离,同时量化考虑风沙的强度,将不同的树苗类型的水土保持力以及他们的防风沙能力量化考虑。我们所了解到的资料很少,因此只能做一下简单的模型的建立,以及一些较为简单的分析。当然,这只是我的个人想法,很不成熟,也很可能有错误。我是这样考虑的,比如:我们设距离风沙源地越远,风沙程度越弱,当风沙强度吹到我们所居住的地区时即为0,风沙的总强度为F,风沙源地与我们所居住地区的距离为f。因此可以得出结论,距离风沙源地越远,所需要的防护林面积就越小,设防护林种植地与风沙源地之间的距离为x,设所需要的防护林面积为y,同时将不同的树苗类型的水土保持能力量化:当种植了梭梭树之后,其每平米的水土保持力即可以阻挡的风沙的程度为a,沙柳为b,樟子松为c,胡杨树则为d。这时我们可以相应的依据量化关系列出一个方程式来:y=(F - F/f*x)/a(其中的a是指当所种的防护林是梭梭树时的方程式,相应的,当我们分析的是其他的树木,沙柳、樟子松以及胡杨树等,我们则可以将a替换为b、c以及d)。 根据上述所列的方程式,当我们了解了各种类型的树木的水土保持能力以及他们的防风沙的能力时,我们可以代入上述的方程式中进行计算,计算当距离风沙源地的距离不同时,所需要种植的防护林的面积也不尽相同。同时,我们可以分析得出,当x趋于无限小或者无穷大时,即防护林的种植地距离风沙源地极近或者极远时,这个方程式就转换为了一个极限问题的研究。 如果我们可以再多收集一些资料,具体了解到风沙强度与距离远
习题课:多元函数求偏导,多元函数微分的应用 多元复合函数、隐函数的求导法 (1) 多元复合函数 设二元函数),(v u f z =在点),(00v u 处偏导数连续,二元函数),(),,(y x v v y x u u ==在点 ),(00y x 处偏导数连续, 并且),(),,(000000y x v v y x u u ==, 则复合函数 )),(),,((y x v y x u f z = 在点),(00y x 处可微,且 ()()()() x y x v v v u f x y x u u v u f x z y x ?????+?????= 00000000) ,(,,,,00??()()()() y y x v v v u f y y x u u v u f y z y x ?????+?????= 00000000) ,(,,,,00?? 多元函数微分形式的不变性:设),(),,(),,(y x v v y x u u v u f z ===,均为连续可微, 则将z 看成y x ,的函数,有 dy y z dx x z dz ??+??= 计算 y v v f y u u f y z x v v f x u u f x z ????+????=??????+????=??,,代人, dv v f du u f dy y v dx x v v f dy y u dx x u u f dy y v v f y u u f dx x v v f x u u f dy y z dx x z dz ??+??= ???? ????+????+???? ????+????=???? ??????+????+??? ??????+????=??+??= 我们将dv v f du u f dy y z dx x z dz ??+??=??+??= 叫做微分形式不变性。 例1 设??? ??=x y xy f x z , 3 ,求y z x z ????,。
陶器的发明,是人类文明发展的重要标志,是人类第一次利用天然物,按照自己的意志,创造出来的一种崭新的东西。陶器的出现,标志着新石器时代的开端。陶器的发明,也大大改善了人类的生活条件。 其实在上古时代,先民们就开始制作一些陶器。陶器的发明是人类文明的重要进程,是人类第一次利用天然物,按照自己的意志创造出来的一种崭新的东西。从河北省阳原县泥河湾地区发现的旧石器时代晚期的陶片来看,在中国陶器的产生距今已有11700多年的悠久历史。 原始陶器的发展 裴李岗文化距今约8千年,是我国目前发现最早的新石器时代遗址。与此同时在河北武安县的磁山也发现同时期的文话遗址,而出土陶器带有一定原始性,是目前中国发现最早的陶器。 仰韶文化仰韶文化以半坡遗址的陶器为典型。主要纹饰有动物纹(包括鱼纹、蛙纹)、几何纹、陶器基本为手制,出现了慢轮修整技术;陶质以细泥红陶、夹砂红陶为主,灰陶、黑陶较少,出现白陶;陶质松软,烧成温度约900—1000℃。彩陶艺术是仰韶文化的杰出成就,烧前彩画,不易脱落,以黑彩为主、兼用红色。器型有碗、钵、杯、罐瓮、瓶、釜、甑、尖底瓶等。陶器常饰以线纹、绳纹、弦纹和附加堆文等。 马家窑文化范围可达青海、宁夏、四川等省区。器形仍以盆、钵、罐、壶为主,尖底器已基本消失。其纹饰有:①人物纹,②动物纹,有蝌蚪纹、蛙形纹;最具有时代特征的为旋涡纹和波浪纹,纹饰旋转、起伏,给人以强烈的运动感。 龙山文化继承仰韶文化因素发展起来。早期主要分布在关中、晋南、豫西一带。晚期主要分布于河南、和河北的南部。陶质以灰陶为主,也有少量红陶,1000℃左右。陶器常见手制轮修,晚期黑陶数量增加,出现少量蛋壳陶。温度. 可以见到的是轮制陶器以及模制陶器。器型有杯、盘、碗、盆、罐、鼎、甑、鬲、鬶、等。彩陶很少,常见纹饰有篮纹、绳纹、方格纹、附加堆纹等。 齐家文化是继马家窑文化而发展起来的。其主要分布于甘肃、青海、宁夏等地。它以泥质、加砂红陶为主,均用手制,烧成温度800—1100℃。器型有杯、盘、碗、盆、罐、豆、盉、斝、鬲、甑等。问世有篮纹、绳纹、划纹、弦纹、篦纹、锥刺纹等。彩陶数量下降,以黑陶彩绘为主,红色较少用,图案对称规整。 大汶口文化分布于山东、江苏北部、河南东部、安徽东北部。有泥质、加砂陶,早期红陶为主,晚期灰、黑比例上升,并出现白陶、蛋壳陶。手制为主,晚期发展为轮制陶器,烧成温900—1000℃。器型有鼎、鬶、盉、豆、尊、单耳杯、觚形杯、高领罐、背水壶等。许多陶器表面膜光,纹饰有划纹、弦纹、篮纹、圆圈纹、三角印纹、镂孔等。彩陶较少但富有特色,彩色有红、黑、白三种,纹样有圈点、几何、花叶等。 屈家岭文化主要分布于长江中游江汉地区。早期以黑陶为主,晚期灰陶为主,少量红陶。陶器以手制为主,少量轮修,烧成温度900℃左右。器型有高圈足杯、三足杯、圈足碗、长颈圈足壶、折盘豆、盂、扁凿形足鼎、甑、釜、缸等,蛋壳彩陶杯、碗最富代表性。陶器大部分素面,少量饰以弦纹、浅篮纹、刻划纹、镂孔等。由部分彩陶及彩绘陶,有黑、灰、褐等色彩,纹样以点、线状几何纹为主。
第一章 微积分的发展历史简介 1.1微积分的概念 微积分是高等数学中研究函数的微分、积分以及有关概念和应用的数学分支。它是数学的一个基础学科。内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算,是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。 基本定义 设函数0)(=x f 在],[b a 上有解,在],[b a 中任意插入若干个分点 n n x x x x x a <<<<<=-1210 把区间],[b a 分成n 个小区间 ].,[],,[],,[12110n n x x x x x x - 在每个小区间],[1i i x x -上任取一点)(1i i x i x i <<-ζζ,作函数值)(i f ζ与小区间长度的乘积x i f ?)(ζ并作出和如果不论对],[b a 怎样分法,也不论在小区间上的点i ζ怎样取法,只要当区间的长度趋于零时,和S 总趋于确定的极限I ,这时我们称这个极限I 为函数)(x f 在区间[a,b]上的定积分记作K 。 微积分的基本概念和内容包括微分学和积分学。 微分学的主要内容包括:极限理论、导数、微分等。 积分学的主要内容包括:定积分、不定积分等。 一元微分定义 设函数)(x f y =)在某区间内有定义,0x 及x x ?+0在此区间内。如果函数的增量)()(00x f x x f y -?+=?可表示为 0ox x A y +?=?(其中A 是不依赖于x ?的常数),而x o ?是比x ?高阶的无穷小,那么称函数)(x f 在点0x 是可微的,且x A ?称作函数在点0x 相应于自变量增量x ?的微分,记作dy ,即x A dy ?= 通常把自变量x 的增量x ?称为自变量的微分,记作dx ,即x dx ?=。于是函数)(x f y =的微分又可记作dx x f dy )('=。函数的微分与自变量的微分之商等于该函数的导数。因此,导数也叫做微商。 几何意义 设x ?是曲线)(x f y =上的点M 的在横坐标上的增量,y ?是曲线在点M 对
第8章 多元函数微分学及其应用 参考解答 1、设22 , y f x y x y x ??+=- ??? ,求(),f x y ,(),f x y xy -。 解:()()()()2 21, 1y y x y x f x y x y x y x y x y y x x y x - -??+=+-=+=+ ?+? ? + ,故得 ()2 1,1y f x y x y -=+,()()21,1xy f x y xy x y xy --=-+ 2、求下列各极限: 2242222 2220000 cos sin 1(1) lim lim lim sin 204x r r y x y r r x y r θθθ→→→→===+ 注意:在利用极坐标变换cos , sin x r y r θθ==来求极限时,θ也是变量。本题中,0r →时,2r 为无穷小量,而2 sin 2θ为有界变量,故所求极限为零。 ()00sin sin (2) lim lim 1x t y a xy t xy t →→→== 3、证明极限2 2400 lim x y xy x y →→+不存在。 证明:当2 y kx =时,()2242,1xy k f x y x y k ==++,故2 22420 lim 1y kx x xy k x y k =→=++与k 有关。可见,(),x y 沿不同的路径趋于()0,0时,函数极限不同,故极限不存在。(两路径判别法) 4、讨论下列函数在()0,0点处的连续性: (1)()()()222222 22 ln , 0 ,0, 0 x y x y x y f x y x y ?+++≠?=?+=?? 解: ()() ()()() ()()()2 222,0,0,0,0 lim ,lim ln lim ln 00,0x y x y t f x y x y x y t t f →→→= ++=== 故原函数在()0,0点处连续。
艺术随笔Art Essays CERAMICS SCIENCE & ART 【关键词】发展史;白瓷代表;发展前景 浅谈中国陶瓷发展史及现代陶瓷的发展前景 陈良瑜 1、新石器时代: 陶瓷的产生和发展,其实是同人们的生活和生产实践紧密相连的,在大约70万年以前的原始时代,人们就泥巴晾干后用火烧烤坚硬的盛器用于盛水,存放食物等等,这便是陶器产生的初始。最新的考古资料表明,我国境内目前发现最早的陶器遗址是位于江西万年县内的仙人洞遗址、广东英德青塘、灵山滑岩石洞、广西桂林甄皮皮岩。其主要品种有灰陶、彩陶、黑陶和几何印纹陶等,手法粗糙,构图新颖流畅,表现了当时制陶的技术水平。 2、夏至两晋时期:在商朝殷墟的遗址中,出土很多陶片、各种款式陶罐,这些陶器上的纹饰、符号、文字与殷商时代的甲骨文和青器有着密切的联系,陶器在此时已经不局限于盛物器皿,应用范围广泛,大致可分为日用品、建筑、殉葬、祭祀礼品类等。而后秦汉古代的建筑多用木料来架构,不易久存,所以一些伟大的建筑,如秦代的阿房宫和汉代的未央宫,都无法完整保存下来,但仍可在殘存的废墟中发现瓦当及汉砖等遗物,藉以略窥古代建筑的规模。两汉时期,釉陶大量替代铜质日用品,从而使陶器得到迅速 我是众多陶瓷艺术工作者中的一个,从事陶瓷行业多年,我热爱我的工作,我为之骄傲,我也为之努力,正是有老一辈的陶瓷人代代相传,才有今天陶瓷的发展,我愿尽绵簿之力为之传承。 一、中国陶瓷发展史 DOI:10.13212/https://www.doczj.com/doc/8314699943.html,ki.csa.2015.07.008
艺术随笔 Art Essays 发展,由于对于加工技巧的掌握,随之出现图案 及造型生动活泼的陶器装饰品,具有极高的艺术 价值,这是陶向瓷的过渡桥梁。两晋时期到南北朝陶瓷主要成就主要体现是越窑,以青瓷为主极尽装饰之能事,有较高的艺术水平。 3、隋唐五代时期:隋的朝代虽短,但在瓷器烧制上,却有了新的突破,不但有青瓷烧造,白瓷也有很好的发展 ,另外此时在装饰手法上也有了创新,如在器物上另外的泥片一贴花,就是一例。到了唐代,瓷器制作可为以蜕变到成熟的境界,而跨入真正的瓷器时代,因为陶与瓷的分开,在乎质白坚硬或半透明,而最大的关键在于火烧温度,汉代产有瓷器,但温度不高,质地脆弱只能算是原瓷,而发展到唐代,不但釉药发展成熟,火烧温度能达到摄氏一千度以上,所以我们说唐代是真正进入瓷器的代。 4、宋元时期:瓷业在宋代随各地新兴窑场不断出现而发展,涌现出不少驰名中外的瓷窑,所谓五大名窑——定、汝、官、哥、钧就是其中的代表,宋代形成品种丰富多彩、造型简洁优美、装饰方法多样化的特点。官私名窑名瓷风格各异,百花争艳,各现独特风格之美。元代时期也有新的发展,如青花和釉里红的兴起,彩瓷大量的流行,带动以后明清两代的瓷器发展。 5、明清时期:我国的陶艺发展到了明代又进入一个新的旅程,明代以前的瓷器以青瓷为主,而明代之后以白瓷为主特别是青花,五彩成明代白瓷的主要产品,此时瓷胎也趋向薄,细、白的需求,在坯身上记住款式也从此开始,年代、堂号、人名都有,使研究考据有更确实的辨认。 清朝中国瓷器可谓登峰造极,清初的瓷器制作技术高超,装饰精细华美,清代彩瓷在明代的基础上有了很大发展,工艺创新,分化出更多的彩色,墨彩、蓝彩、金彩也出现在五彩瓷器画面上,色彩淡雅是其特点,从而丰富了清代瓷器装饰。 从上述陶瓷在各个时期的发展历程看,它是辉煌的,璀璨的。美来自于生活,从业者是从表现生活的角度,有寓意地间接表现了人的思想和感情,或直接描绘了现实生活的风俗和风貌。不仅表明了我雕塑艺术现实主义传统的久远和我国古代陶瓷制作水平之高,并且还为世人展示了中华民族深沉雄大的民族风格。 宋代早期的产品主要是青白瓷,随着技术的 不断提高,逐渐发展为白釉瓷。明代白釉瓷瓷质 如脂似玉,创造了独具一格的"象牙白",被视为 中国白瓷代表。其装饰工艺主要有刻、画、印花 和堆贴印花装饰刻花也称画花。德化白瓷具有质 地洁白、细腻如玉、釉面光滑、击声如磬的特 点,故有"中国白"之称。其特制的薄胎产品,薄 如蝉翼,精美绝伦。德化民间雕塑艺人将雕塑与 瓷艺结合,擅长制作白瓷观音,所做白瓷观音仪 态生动,是举世公认的白瓷珍品。德化白瓷不求 色彩之华丽,而是追求单纯、素洁、典雅之美, 对所利用的材料有充分的认识,设计定位与取向 是准确的,充分显示着历代匠师们的创造智慧。 如果说景德镇窑的白瓷是以青白釉称著于世,德 化白瓷则是以乳白色为主,釉层腴润,光色如 玉,显示着冰清玉洁的特质,蕴涵着耐人寻味的 魅力,相比之下具有异曲同工之妙 1:从陶瓷本身而言 为使陶瓷艺术在现在这个社会生存下去,且 获得多姿多彩,首先要实现传统陶瓷向现代陶瓷 的转变。 陶瓷材质的转变和发展 在陶瓷艺术作品中,材料的运用可谓至关重 要,可以直接感受作品的力度及内在结构的审美 空间。从传统材料中可以看出青花、粉彩、古彩 等传统装饰,形成了景德镇传统陶瓷艺术特有的 面貌,决定了其题材风格的独特性,它承载着一 个时代的变迁,用自身的语言范式带给世人长久 的喜爱与眷顾 在现代陶艺的制作中,原料的取材是不拘一 格的。与多种材料的结合、并用、渗透,产生了 相得益彰的艺术效果,使现代陶艺既有丰富的表 现性又有充分的协调性,表面装饰和空间处理也 登上一个更高的层次。现代陶艺注重质地性能, 不讲究是粗糙还是精细的原料,取材也不再仅限 于瓷泥和陶泥,而是有意突破传统陶艺原料的使 用范围,利用泥料的不同特性,发挥各种材质的 潜在美感,只要能经窑烧的泥、沙等材料都可用 来为之服务。 现代陶瓷张扬个性和内涵 二、白瓷代表 三、陶瓷业的发展前景(解困之路) 17 CERAMICS SCIENCE & ART
学习微积分的感想和建议 班级:国际商务一班姓名:沈识宇学号:171400151 对于学习方面,以前我总觉得数学一直处于主心骨的位置,它是我从小的梦想、我的骄傲。可是自从大学以来的第一个学期,微积分却着实让我们倍受打击。成绩的不再拔尖,沉痛的打击了我的自信心。但是,通过和老师交流,与同学讨论,让我明白强中自有强中手, 而自己,并不是笨,只是有些方面自己做的不够,只要深切的去思考自己的学习方法,自己依旧有很大的进步空间。 首先我们觉得大学里的学习课后巩固很重要,光靠一周两次大课的学习,远远不够。并且,课上老师可能会因为进度问题而降得很快,很多时候我们会跟不上老师的速度,这时, 如果课后不再看老师局的例题,课上的疑问会永远得不到解答。在此情况下谈想进步是不可能的,然而课后的巩固应该从两方面着手,一方面是教学大纲上要求必须掌握的内容,这些是 考试必考内容,或许看似很简单的内容,确实解题目的最基本的基础。秋季学期的期末考,正是由于自己对基本知识忽略,在一些很简单的题目丢了分,惨痛的教训给了我们深刻的教 训,夯实基础知识,才能为考试打下良好的基础。 另一方面。是自己认为在内容掌握上的盲点和误区,这些事最容易忘记的,也是熟练度最差的。而考试不会因为这是自己认为的难点就会不考,所以认真钻研这些题目便可为自己在分数上的突破起决定性作用。
同时,复习一定要有耐心,要持之以恒。学习上最大的忌讳便是三天打鱼两天晒网,这 样的学习不会有任何收获。知识既然学习了,我们就要好好消化,不能让它成为太脑中的累赘。周期性的复习才不会使大脑一片空白,一周一次或两周一次,可以根据自己的记忆力而 定,以适合自己的为基准便可以。 复习的时候,第一,便是要克服浮躁的毛病,静心看课本。考试题目几乎都是从课本知识中发散来的,所以,复习中必须要看课本,反复看,细节很重要,特别是不被重视的基本概念和定理。力争课后复习参考题每题都过关。第二,是要制定好复习计划,针对自身情况 分配好时间,各个击破。第三,要理清知识结构网络图,从上学期到现在,我们已经学了极限、连续不连续、导数、定积分、不定积分等知识内容,然后根据知识结构网络图区发散、联想基础概念和基本定理和每个知识点的应用计算题,对本章节的内容有个清晰的思 路,这样就可以在整体上把我书本知识。从整体上把握书本知识有利于我们对于试卷中的一些基本的题目有一个宏观的把握。对于试卷中的问答题,可以从多角度去理解和把握,这样就能做到回答问题的严密性。第四,将课上老师所讲授的典型例题及做题过程中遇到的难题还有易错的题归纳整理,分析。数学中,我们很容易遇到同一个问题有不同方法的解决方法。第五,最好多看看往年真题,针对出现频率较高的题型,适当做些有针对性的模拟试题。对于自己认为薄弱的环节更要加强钻研,与同学和老师多交流,更要勇于舍弃那些偏题、怪题。