大学数学5课后习题答案(李丹衡版)
- 格式:pdf
- 大小:572.86 KB
- 文档页数:73


同济版 工程数学-线性代数第五版答案第一章 行列式1. 利用对角线法则计算下列三阶行列式:(1)381141102---;解381141102--- =2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4.(2)ba c a cbc b a ;解ba c a cbc b a =acb +bac +cba -bbb -aaa -ccc =3abc -a 3-b 3-c 3.(3)222111c b a cb a ;解222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).(4)yx y x x y x y yx y x +++.解yx y x x y x y y x y x +++ =x (x +y )y +yx (x +y )+(x +y )yx -y 3-(x +y )3-x 3 =3xy (x +y )-y 3-3x 2 y -x 3-y 3-x 3 =-2(x 3+y 3).2. 按自然数从小到大为标准次序, 求下列各排列的逆序数: (1)1 2 3 4; 解 逆序数为0 (2)4 1 3 2;解 逆序数为4: 41, 43, 42, 32. (3)3 4 2 1;解 逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1. (4)2 4 1 3;解 逆序数为3: 2 1, 4 1, 4 3. (5)1 3 ⋅ ⋅ ⋅ (2n -1) 2 4 ⋅ ⋅ ⋅ (2n ); 解 逆序数为2)1(-n n : 3 2 (1个) 5 2, 5 4(2个) 7 2, 7 4, 7 6(3个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n -1)2, (2n -1)4, (2n -1)6, ⋅ ⋅ ⋅, (2n -1)(2n -2) (n -1个)(6)1 3 ⋅ ⋅ ⋅ (2n -1) (2n ) (2n -2) ⋅ ⋅ ⋅ 2. 解 逆序数为n (n -1) : 3 2(1个) 5 2, 5 4 (2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n -1)2, (2n -1)4, (2n -1)6, ⋅ ⋅ ⋅, (2n -1)(2n -2) (n -1个) 4 2(1个) 6 2, 6 4(2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n )2, (2n )4, (2n )6, ⋅ ⋅ ⋅, (2n )(2n -2) (n -1个) 3. 写出四阶行列式中含有因子a 11a 23的项. 解 含因子a 11a 23的项的一般形式为(-1)t a 11a 23a 3r a 4s ,其中rs 是2和4构成的排列, 这种排列共有两个, 即24和42. 所以含因子a 11a 23的项分别是(-1)t a 11a 23a 32a 44=(-1)1a 11a 23a 32a 44=-a 11a 23a 32a 44, (-1)t a 11a 23a 34a 42=(-1)2a 11a 23a 34a 42=a 11a 23a 34a 42. 4. 计算下列各行列式:(1)71100251020214214; 解 7110025102021421410014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-; 解2605232112131412-26053212213041224--=====c c 041203212213041224--=====r r0000003212213041214=--=====r r . (3)efcf bf decd bd ae ac ab ---;解ef cf bf de cd bd ae ac ab ---ec b e c b e c b adf ---= a b cdef a d f b c e 4111111111=---=. (4)dc b a 100110011001---. 解d c b a100110011001---dc b a ab ar r 10011001101021---++===== d c a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ad a ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1.5. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 .(2)yx z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++ bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=yx z x z y zy x b a )(33+=.(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;证明2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2, c 2-c 1得) 5232125232125232125232122222++++++++++++=d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2得)022122212221222122222=++++=d d c c b b a a .(4)444422221111d c b a d c b a d c b a =(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d );证明444422221111d c b a d c b a d c b a )()()(0)()()(001111222222222a d d a c c a b b a d d a c c a b b ad a c a b ---------=)()()(111))()((222a d d a c c a b b d c b a d a c a b +++---= ))(())((00111))()((a b d b d d a b c b c c b d b c a d a c a b ++-++------=)()(11))()()()((a b d d a b c c b d b c a d a c a b ++++-----= =(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ).(5)12211 000 00 1000 01a x a a a a x x x n n n+⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--- =x n +a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n .证明 用数学归纳法证明.当n =2时,2121221a x a x a x a x D ++=+-=, 命题成立. 假设对于(n -1)阶行列式命题成立, 即 D n -1=x n -1+a 1 x n -2+ ⋅ ⋅ ⋅ +a n -2x +a n -1, 则D n 按第一列展开, 有11100 100 01)1(11-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--+=+-x x a xD D n n n n =xD n -1+a n =x n +a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n . 因此, 对于n 阶行列式命题成立.6. 设n 阶行列式D =det(a ij ), 把D 上下翻转、或逆时针旋转90︒、或依副对角线翻转, 依次得n nn n a a a a D 11111 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=, 11112 n nn n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= , 11113 a a a a D n nnn ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=,证明D D D n n 2)1(21)1(--==, D 3=D .证明 因为D =det(a ij ), 所以nnn n n n nnnn a a a a a a a a a a D 2211111111111 )1( ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=- ⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--=-- )1()1(331122111121nnn n nn n n a a a a a a a aD D n n n n 2)1()1()2( 21)1()1(--+-+⋅⋅⋅++-=-=.同理可证nnn n n n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=- )1(11112)1(2D D n n T n n 2)1(2)1()1()1(---=-=. D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(.7. 计算下列各行列式(D k 为k 阶行列式):(1)a aD n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0;解aa a a a D n 0 0010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 000 00 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a an n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1)1()1(=a n -a n -2=a n -2(a 2-1).(2)xa a a x a a a x D n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得ax x a ax x a a x x a aa a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0 , 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 0000 )1(=[x +(n -1)a ](x -a )n -1. (3)111 1 )( )1()( )1(1111⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅--⋅⋅⋅-=---+n a a a n a a a n a a a D n n n nn n n ; 解 根据第6题结果, 有nnn n n n n n n n a a a n a a a n a a aD )( )1()( )1( 1111)1(1112)1(1-⋅⋅⋅--⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=---++此行列式为范德蒙德行列式.∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏≥>≥++---=112)1()]([)1(j i n n n j i∏≥>≥++⋅⋅⋅+-++-⋅-⋅-=1121)1(2)1()()1()1(j i n n n n n j i∏≥>≥+-=11)(j i n j i .(4)n nnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112;解nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112(按第1行展开)nn n n n nd d c d c b a b a a 00011111111----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=0)1(1111111112c d c d c b a b a b nn n n n nn ----+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-+.再按最后一行展开得递推公式D 2n =a n d n D 2n -2-b n c n D 2n -2, 即D 2n =(a n d n -b n c n )D 2n -2. 于是∏=-=ni i i i i n D c b d a D 222)(.而111111112c b d a d c b a D -==, 所以∏=-=n i i i i i n c b d a D 12)(.(5) D =det(a ij ), 其中a ij =|i -j |; 解 a ij =|i -j |,4321 4 01233 10122 21011 3210)det(⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅==n n n n n n n n a D ij n43211 11111 11111 11111 1111 2132⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅--⋅⋅⋅-=====n n n n r r r r15242321 0 22210 02210 00210 0001 1213-⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅-+⋅⋅⋅+=====n n n n n c c c c =(-1)n -1(n -1)2n -2.(6)nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ⋅ ⋅ ⋅ a n≠0.解nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121nn n n a a a a a a a a a c c c c +-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=====--100001 000 100 0100 0100 0011332212132 11113121121110 00011 000 00 11000 01100 001 ------+-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅⋅⋅⋅=n n n a a a a a a a a∑=------+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n i i n n a a a a a a a a 1111131******** 000100 10000 01000 001)11)((121∑=+=ni in a a a a .8. 用克莱姆法则解下列方程组:(1)⎪⎩⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ;解 因为14211213513241211111-=----=D ,142112105132412211151-=------=D , 284112035122412111512-=-----=D ,426110135232422115113-=----=D , 14202132132212151114=-----=D , 所以 111==DD x , 222==D D x , 333==D D x , 144-==D D x .(2)⎪⎪⎩⎪⎪⎨⎧=+=++=++=++=+150650650651655454343232121x x x x x x x x x x x x x .解 因为665510006510006510065100065==D ,150751001651000651000650000611==D , 114551010651000650000601000152-==D ,70351100650000601000051001653==D , 395510601000051000651010654-==D ,2121105100065100651100655==D ,所以66515071=x ,66511452-=x ,6657033=x , 6653954-=x , 6652124=x .9. 问λ, μ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 系数行列式为μλμμμλ-==1211111D .令D =0, 得 μ=0或λ=1.于是, 当μ=0或λ=1时该齐次线性方程组有非零解.10. 问λ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解?解 系数行列式为λλλλλλλ--+--=----=101112431111132421D=(1-λ)3+(λ-3)-4(1-λ)-2(1-λ)(-3-λ) =(1-λ)3+2(1-λ)2+λ-3. 令D =0, 得λ=0, λ=2或λ=3.于是, 当λ=0, λ=2或λ=3时, 该齐次线性方程组有非零解.第二章 矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换. 解 由已知:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ,故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y , ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换. 解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A T B .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T.4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫ ⎝⎛=49635.(2)⎪⎪⎭⎫⎝⎛123)321(;解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛;解 )21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫ ⎝⎛---=632142.(4)⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ; 解 ⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876.(5)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ; 解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x =(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA . 因为⎪⎭⎫⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B )2=A 2+2AB +B 2吗? 解 (A +B )2≠A 2+2AB +B 2. 因为⎪⎭⎫⎝⎛=+5222B A ,⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148,但⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610,所以(A +B )2≠A 2+2AB +B 2. (3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2. 因为⎪⎭⎫⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A ,而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A , 故(A +B )(A -B )≠A 2-B 2.6. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0; 解 取⎪⎭⎫⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ; 解 取⎪⎭⎫⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y . 解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y . 7. 设⎪⎭⎫⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k .解⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k .8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k .解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ,⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫ ⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫ ⎝⎛=⋅=545345450050105λλλλλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA k k kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A ⎪⎪⎪⎪⎭⎫ ⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ, 由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵. 证明 因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA . 证明 充分性: 因为A T =A , B T =B , 且AB =BA , 所以 (AB )T =(BA )T =A T B T =AB , 即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB )T =AB , 所以 AB =(AB )T =B T A T =BA . 11. 求下列矩阵的逆矩阵: (1)⎪⎭⎫ ⎝⎛5221; 解⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故*||11A A A =-⎪⎭⎫ ⎝⎛--=1225.(2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ;解 ⎪⎭⎫⎝⎛-=θθθθc o s s in s in c o s A . |A |=1≠0, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A ,所以*||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos .(3)⎪⎪⎭⎫⎝⎛---145243121;解 ⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A , 所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012. (4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程: (1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛12643152X ;解⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232.(2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311111012112X ;解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X ⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫⎝⎛---=32538122. (3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ; 解11110210132141--⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111. (4)⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X .解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012.13. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解 方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x , 故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A )-1(E -A ). 另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1. 证明 由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或E E A A =-⋅)(21, 由定理2推论知A 可逆, 且)(211E A A-=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E ⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-, 又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1,)3(41)2(1A E E A -=+-.16. 设A 为3阶矩阵, 21||=A , 求|(2A )-1-5A *|. 解 因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |2521|11---=A A=|-2A -1|=(-2)3|A -1|=-8|A |-1=-8⨯2=-16. 17. 设矩阵A 可逆, 证明其伴随阵A *也可逆, 且(A *)-1=(A -1)*. 证明 由*||11A A A =-, 得A *=|A |A -1, 所以当A 可逆时, 有|A *|=|A |n |A -1|=|A |n -1≠0, 从而A *也可逆.因为A *=|A |A -1, 所以 (A *)-1=|A |-1A . 又*)(||)*(||1111---==A A A A A , 所以 (A *)-1=|A |-1A =|A |-1|A |(A -1)*=(A -1)*. 18. 设n 阶矩阵A 的伴随矩阵为A *, 证明: (1)若|A |=0, 则|A *|=0; (2)|A *|=|A |n -1. 证明(1)用反证法证明. 假设|A *|≠0, 则有A *(A *)-1=E , 由此得 A =A A *(A *)-1=|A |E (A *)-1=O ,所以A *=O , 这与|A *|≠0矛盾,故当|A |=0时, 有|A *|=0. (2)由于*||11A A A =-, 则AA *=|A |E , 取行列式得到 |A ||A *|=|A |n . 若|A |≠0, 则|A *|=|A |n -1;若|A |=0, 由(1)知|A *|=0, 此时命题也成立. 因此|A *|=|A |n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解 由AB =A +2E 可得(A -2E )B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫⎝⎛-=011321330.20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解 由AB +E =A 2+B 得 (A -E )B =A 2-E , 即 (A -E )B =(A -E )(A +E ).因为01001010100||≠-==-E A , 所以(A -E )可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A *BA =2BA -8E , 求B . 解 由A *BA =2BA -8E 得 (A *-2E )BA =-8E , B =-8(A *-2E )-1A -1 =-8[A (A *-2E )]-1 =-8(AA *-2A )-1 =-8(|A |E -2A )-1 =-8(-2E -2A )-1 =4(E +A )-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-= =2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B . 解 由|A *|=|A |3=8, 得|A |=2. 由ABA -1=BA -1+3E 得 AB =B +3A ,B =3(A -E )-1A =3[A (E -A -1)]-1A11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3,⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731.24. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511,求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明 因为A -1(A +B )B -1=B -1+A -1=A -1+B -1,而A -1(A +B )B -1是三个可逆矩阵的乘积, 所以A -1(A +B )B -1可逆, 即A -1+B -1可逆. (A -1+B -1)-1=[A -1(A +B )B -1]-1=B (A +B )-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121. 解 设⎪⎭⎫⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B , 则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ,而⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A , 所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠. 解4100120021010*********0021010010110100101==--=--=D C B A ,而01111|||||||| ==D C B A , 故|||||||| D C B A D C B A ≠. 28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4. 解 令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A , 则 ⎪⎭⎫ ⎝⎛=21A O O A A ,故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A ,1682818281810||||||||||===A A A A A .⎪⎪⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求(1)1-⎪⎭⎫ ⎝⎛O B A O ;解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143.由此得 ⎪⎩⎪⎨⎧====s n E BC O BC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C O C A C , 所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A .解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321. 由此得 ⎪⎩⎪⎨⎧=+=+==s n E BD CD O BD CD O AD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D , 所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫ ⎝⎛2500380000120025; 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则 ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--853*******B .于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛----850032000052002125003800001200251111B A B A . (2)⎪⎪⎪⎭⎫ ⎝⎛4121031200210001. 解 设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛------1111114121031200210001B CA B O A B C O A ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----=411212458103161210021210001.第三章 矩阵的初等变换与线性方程组1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫⎝⎛--340313021201;解 ⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. ) ~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). ) ~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. ) ~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. ) ~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. ) ~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. ) ~⎪⎪⎭⎫⎝⎛100001000001. (2)⎪⎪⎭⎫⎝⎛----174034301320; 解 ⎪⎪⎭⎫⎝⎛----174034301320(下一步: r 2⨯2+(-3)r 1, r 3+(-2)r 1. ) ~⎪⎪⎭⎫ ⎝⎛---310031001320(下一步: r 3+r 2, r 1+3r 2. )~⎪⎪⎭⎫⎝⎛0000310010020(下一步: r 1÷2. ) ~⎪⎪⎭⎫⎝⎛000031005010. (3)⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311; 解 ⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. ) ~⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). ) ~⎪⎪⎪⎭⎫ ⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. ) ~⎪⎪⎪⎭⎫ ⎝⎛---00000000002210032011. (4)⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132.解 ⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132(下一步: r 1-2r 2, r 3-3r 2, r 4-2r 2. ) ~⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110(下一步: r 2+2r 1, r 3-8r 1, r 4-7r 1. ) ~⎪⎪⎪⎭⎫ ⎝⎛--41000410002020111110(下一步: r 1↔r 2, r 2⨯(-1), r 4-r 3. ) ~⎪⎪⎪⎭⎫ ⎝⎛----00000410001111020201(下一步: r 2+r 3. ) ~⎪⎪⎪⎭⎫ ⎝⎛--00000410003011020201. 2. 设⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A , 求A . 解 ⎪⎪⎭⎫⎝⎛100001010是初等矩阵E (1, 2), 其逆矩阵就是其本身. ⎪⎪⎭⎫⎝⎛100010101是初等矩阵E (1, 2(1)), 其逆矩阵是 E (1, 2(-1)) ⎪⎪⎭⎫⎝⎛-=100010101.⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=100010101987654321100001010A ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=287221254100010101987321654. 3. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫⎝⎛323513123; 解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫ ⎝⎛---101011001200410123 ~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫ ⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001 故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267. (2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解 ⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023 ~⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321 ~⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321 ~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫ ⎝⎛----------10612631110`1022111000010000100021 ~⎪⎪⎪⎭⎫ ⎝⎛-------106126311101042111000010000100001 故逆矩阵为⎪⎪⎪⎭⎫ ⎝⎛-------10612631110104211. 4. (1)设⎪⎪⎭⎫ ⎝⎛--=113122214A , ⎪⎪⎭⎫ ⎝⎛--=132231B , 求X 使AX =B ; 解 因为⎪⎪⎭⎫ ⎝⎛----=132231 113122214) ,(B A ⎪⎪⎭⎫⎝⎛--412315210 100010001 ~r , 所以 ⎪⎪⎭⎫ ⎝⎛--==-4123152101B A X . (2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B , 求X 使XA =B . 解 考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫⎝⎛---411007101042001 ~r , 所以 ⎪⎪⎭⎫ ⎝⎛---==-417142)(1T T T B A X , 从而 ⎪⎭⎫ ⎝⎛---==-4741121BA X . 5. 设⎪⎪⎭⎫⎝⎛---=101110011A , AX =2X +A , 求X . 解 原方程化为(A -2E )X =A . 因为⎪⎪⎭⎫⎝⎛---------=-101101110110011011) ,2(A E A ⎪⎪⎭⎫⎝⎛---011100101010110001~, 所以 ⎪⎪⎭⎫ ⎝⎛---=-=-011101110)2(1A E A X . 6. 在秩是r 的矩阵中,有没有等于0的r -1阶子式? 有没有等于0的r 阶子式?解 在秩是r 的矩阵中, 可能存在等于0的r -1阶子式, 也可能存在等于0的r 阶子式.例如, ⎪⎪⎭⎫⎝⎛=010*********A , R (A )=3. 0000是等于0的2阶子式, 010001000是等于0的3阶子式. 7. 从矩阵A 中划去一行得到矩阵B , 问A , B 的秩的关系怎样?解 R (A )≥R (B ).这是因为B 的非零子式必是A 的非零子式, 故A 的秩不会小于B 的秩.8. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.9. 求下列矩阵的秩, 并求一个最高阶非零子式:(1)⎪⎪⎭⎫⎝⎛---443112112013; 解 ⎪⎪⎭⎫⎝⎛---443112112013(下一步: r 1↔r 2. ) ~⎪⎪⎭⎫⎝⎛---443120131211(下一步: r 2-3r 1, r 3-r 1. )~⎪⎪⎭⎫⎝⎛----564056401211(下一步: r 3-r 2. ) ~⎪⎭⎫ ⎝⎛---000056401211, 矩阵的2秩为, 41113-=-是一个最高阶非零子式. (2)⎪⎪⎭⎫⎝⎛-------815073*********; 解 ⎪⎪⎭⎫⎝⎛-------815073*********(下一步: r 1-r 2, r 2-2r 1, r 3-7r 1. ) ~⎪⎭⎫ ⎝⎛------15273321059117014431(下一步: r 3-3r 2. ) ~⎪⎭⎫ ⎝⎛----0000059117014431, 矩阵的秩是2,71223-=-是一个最高阶非零子式. (3)⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812. 解 ⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812(下一步: r 1-2r 4, r 2-2r 4, r 3-3r 4. )~⎪⎪⎪⎭⎫ ⎝⎛------02301024205363071210(下一步: r 2+3r 1, r 3+2r 1. ) ~⎪⎪⎪⎭⎫ ⎝⎛-0230114000016000071210(下一步: r 2÷16r 4, r 3-16r 2. ) ~⎪⎪⎪⎭⎫ ⎝⎛-02301000001000071210 ~⎪⎪⎪⎭⎫ ⎝⎛-00000100007121002301, 矩阵的秩为3, 070023085570≠=-是一个最高阶非零子式.10. 设A 、B 都是m ⨯n 矩阵, 证明A ~B 的充分必要条件是R (A )=R (B ). 证明 根据定理3, 必要性是成立的.充分性. 设R (A )=R (B ), 则A 与B 的标准形是相同的. 设A 与B 的标准形为D , 则有A ~D , D ~B .由等价关系的传递性, 有A ~B .11. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使 (1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 ⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1;(2)当k =-2且k ≠1时, R (A )=2;(3)当k ≠1且k ≠-2时, R (A )=3.12. 求解下列齐次线性方程组:(1)⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛--212211121211~⎪⎪⎭⎫ ⎝⎛---3/410013100101, 于是 ⎪⎪⎩⎪⎪⎨⎧==-==4443424134334x x x x x x x x , 故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x (k 为任意常数). (2)⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛----5110531631121~⎪⎪⎭⎫⎝⎛-000001001021,于是 ⎪⎩⎪⎨⎧===+-=4432242102x x x x x x x x , 故方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛10010012214321k k x x x x (k 1, k 2为任意常数). (3)⎪⎩⎪⎨⎧=-+-=+-+=-++=+-+07420634072305324321432143214321x x x x x x x x x x x x x x x x ; 解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎪⎭⎫ ⎝⎛-----7421631472135132~⎪⎪⎪⎭⎫ ⎝⎛1000010000100001,于是 ⎪⎩⎪⎨⎧====00004321x x x x , 故方程组的解为⎪⎩⎪⎨⎧====00004321x x x x . (4)⎪⎩⎪⎨⎧=++-=+-+=-+-=+-+03270161311402332075434321432143214321x x x x x x x x x x x x x x x x . 解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎪⎭⎫ ⎝⎛-----3127161311423327543~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000000001720171910171317301,于是 ⎪⎪⎩⎪⎪⎨⎧==-=-=4433432431172017191713173x x x x x x x x x x , 故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛1017201713011719173214321k k x x x x (k 1, k 2为任意常数).13. 求解下列非齐次线性方程组:(1)⎪⎩⎪⎨⎧=+=+-=-+83111021322421321321x x x x x x x x ;解 对增广矩阵B 进行初等行变换, 有B =⎪⎪⎭⎫ ⎝⎛--80311102132124~⎪⎭⎫ ⎝⎛----600034111008331, 于是R (A )=2, 而R (B )=3, 故方程组无解.(2)⎪⎩⎪⎨⎧-=+-=-+-=+-=++69413283542432z y x z y x z y x z y x ;解 对增广矩阵B 进行初等行变换, 有B =⎪⎪⎪⎭⎫ ⎝⎛-----69141328354214132~⎪⎪⎪⎭⎫ ⎝⎛--0000000021101201, 于是 ⎪⎩⎪⎨⎧=+=--=zz z y z x 212,即 ⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛021112k z y x (k 为任意常数). (3)⎪⎩⎪⎨⎧=--+=+-+=+-+12222412w z y x w z y x w z y x ;解 对增广矩阵B 进行初等行变换, 有B =⎪⎪⎭⎫ ⎝⎛----111122122411112~⎪⎪⎭⎫⎝⎛-00000010002/102/12/11, 于是 ⎪⎪⎩⎪⎪⎨⎧===++-=0212121w z z y y z y x ,即 ⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛00021010210012121k k w z y x (k 1, k 2为任意常数). (4)⎪⎩⎪⎨⎧-=+-+=-+-=+-+2534432312w z y x w z y x w z y x .解 对增广矩阵B 进行初等行变换, 有。

习题5-11. 利用定积分定义计算由抛物线y =x 2+1, 两直线x =a 、x =b (b >a )及横轴所围成的图形的面积.解 第一步: 在区间[a , b ]内插入n -1个分点i n a b a x i -+=(i =1,2, ⋅⋅⋅, n -1), 把区间[a , b ]分成n 个长度相等的小区间, 各个小区间的长度为: na b x i -=∆(i =1, 2, ⋅⋅⋅, n ).第二步: 在第i 个小区间[x i -1, x i ] (i =1, 2, ⋅⋅⋅, n )上取右端点i n a b a x i i -+==ξ, 作和n a b i n a b a x f S ni i i n i n -⋅+-+=∆=∑∑==]1)[()(211ξ∑=+-+-+-=ni i na b i n a b a a n a b 12222]1)()(2[ ]6)12)(1()(2)1()(2[)(222n n n n n a b n n n a b a na n a b +++⋅-++⋅-+-= ]16)12)(1()()1)(()[(222+++-++-+-=nn n a b n n a b a a a b . 第三步: 令λ=max{∆x 1, ∆x 2, ⋅⋅⋅, ∆x n }na b -=, 取极限得所求面积∑⎰=→∆==ni i i ba x f dx x f S 1)(lim )(ξλ]16)12)(1()()1)(()[(lim 222+++-++-+-=∞→nn n a b n n a b a a a b n a b a b a b a b a a a b -+-=+-+-+-=)(31]1)(31)()[(3322.2. 利用定积分定义计算下列积分:(1)xdx ba⎰(a <b );解 取分点为i na b a x i -+=(i =1, 2, ⋅⋅⋅, n -1), 则n a b x i -=∆(i =1, 2,⋅⋅⋅, n ). 在第i 个小区间上取右端点i na b a x i i -+==ξ(i =1, 2, ⋅⋅⋅, n ). 于是∑∑⎰=∞→=∞→-⋅-+=∆=ni n n i i i n ba n ab i n a b a x xdx 11)(lim lim ξ )(21]2)1()()([lim )(22222a b n n n a b a b a a b n -=+-+--=∞→. (2)dx e x ⎰10.解 取分点为n i x i =(i =1, 2, ⋅⋅⋅, n -1), 则nx i 1=∆(i =1, 2, ⋅⋅⋅, n ). 在第i 个小区间上取右端点ni x i i ==ξ(i =1, 2, ⋅⋅⋅, n ). 于是) (1lim 1lim 21110n n n n n n i n i n xe e e n n e dx e +⋅⋅⋅++==∞→=∞→∑⎰1)1(]1[lim1])(1[1lim 11111-=--=--⋅=∞→∞→e e n e e ee e nnnn nnn n n .3. 利用定积分的几何意义, 说明下列等式: (1)1210=⎰xdx ;解⎰12xdx 表示由直线y =2x 、x 轴及直线x =1所围成的面积,显然面积为1. (2)41102π=-⎰dx x ;解⎰-121dx x 表示由曲线21x y -=、x 轴及y 轴所围成的四分之一圆的面积, 即圆x 2+y 2=1的面积的41:414112102ππ=⋅⋅=-⎰dx x .(3)⎰-=ππ0sin xdx ;解 由于y =sin x 为奇函数, 在关于原点的对称区间[-π, π]上与x 轴所夹的面积的代数和为零, 即⎰-=ππ0sin xdx .(4)⎰⎰=-2022cos 2cos πππxdx xdx .解⎰-22cos ππxdx 表示由曲线y =cos x 与x 轴上]2,2[ππ-一段所围成的图形的面积. 因为cos x 为偶函数, 所以此图形关于y 轴对称. 因此图形面积的一半为⎰20cos πxdx , 即⎰⎰=-2022cos 2cos πππxdx xdx .4. 水利工程中要计算拦水闸门所受的水压力, 已知闸门上水的压强p (单位面积上的压力大小)是水深h 的函数, 且有p =9⋅8h (kN/m 2). 若闸门高H =3m , 宽L =2m , 求水面与闸门顶相齐时闸门所受的水压力P .解 建立坐标系如图. 用分点i nH x i =(i =1, 2, ⋅⋅⋅, n -1)将区间[0,H ]分为n 分个小区间, 各小区间的长为n H x i =∆(i =1, 2, ⋅⋅⋅, n ).在第i 个小区间[x i -1, x i ]上, 闸门相应部分所受的水压力近似为∆P i =9.8x i L ⋅∆x i . 闸门所受的水压力为∑∑=∞→=∞→⋅=∆⋅⋅=ni n ni i i n n H i n H L x L x P 11lim 8.98.9lim 228.42)1(lim 8.9H L nn n H L n ⋅=+⋅=∞→.将L =2, H =3代入上式得P =88.2(千牛). 5. 证明定积分性质: (1)⎰⎰=babadx x f k dx x kf )()(;证明∑⎰=→∆=n i iibax kf dx x kf 1)(lim )(ξλ⎰∑=∆==→bani iidx x f k x f k )()(lim 1ξλ.(2)a b dx dx baba-==⋅⎰⎰1.证明a b a b x x dx ni in i iba-=-=∆=∆⋅=⋅→=→=→∑∑⎰)(lim lim 1lim 1011λλλ. 6. 估计下列各积分的值: (1)⎰+412)1(dx x ;解 因为当1≤x ≤4时, 2≤x 2+1≤17, 所以 )14(17)1()14(2412-⋅≤+≤-⋅⎰dx x ,即 51)1(6412≤+≤⎰dx x .(2)⎰+ππ4542)sin 1(dx x ;解 因为当ππ454≤≤x 时, 1≤1+sin 2x ≤2, 所以)445(2)sin 1()445(14542ππππππ-⋅≤+≤-⋅⎰dx x , 即 ππππ2)sin 1(4542≤+≤⎰dx x .(3)⎰331arctan xdx x ;解 先求函数f (x )=x arctan x 在区间]3 ,31[上的最大值M 与最小值m .21arctan )(x x x x f ++='. 因为当331≤≤x 时, f '(x )>0, 所以函数f (x )=x arctan x 在区间]3 ,31[上单调增加. 于是3631arctan 31)31(π===f m ,33arctan 3)3(π===f M .因此 )313(3arctan )313(36331-≤≤-⎰ππxdx x ,即 32arctan 9331ππ≤≤⎰xdx x .(4)⎰-022dx e xx.解 先求函数xxe xf -=2)(在区间[0, 2]上的最大值M 与最小值m . )12()(2-='-x e x f xx, 驻点为21=x .比较f (0)=1, f (2)=e 2, 41)21(-=e f , 得41-=e m , M =e 2. 于是)02()02(22412-⋅≤≤-⎰--e dx e e xx,即 41022222---≤≤-⎰e dx dx ee xx .7. 设f (x )及g (x )在[a , b ]上连续, 证明:(1)若在[a , b ]上, f (x )≥0, 且0)(=⎰ba dx x f , 则在[a ,b ]上f (x )≡0;证明 假如0/)(≡x f , 则必有f (x )>0. 根据f (x )在[a , b ]上的连续性, 在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时,2)()(0x f x f >. 于是⎰⎰⎰⎰++=bdd cc abadx x f dx x f dx x f dx x f )()()()(0)(2)()(0>-≥≥⎰c d x f dx x f dc. 这与条件0)(=⎰badx x f 相矛盾. 因此在[a , b ]上f (x )≡0.(2)若在[a , b ]上, f (x )≥0, 且0/)(≡x f , 则0)(>⎰badx x f ;证明 证法一 因为f (x )在[a , b ]上连续, 所以在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时,2)()(0x f x f >. 于是 ⎰⎰>-≥≥b a d c c d x f dx x f dx x f 0)(2)()()(0.证法二 因为f (x )≥0, 所以0)(≥⎰badx x f . 假如0)(>⎰badx x f 不成立. 则只有0)(=⎰badx x f ,根据结论(1), f (x )≡0, 矛盾. 因此0)(>⎰badx x f .(3)若在[a , b ]上, f (x )≤g (x ), 且⎰⎰=bab adx x g dx x f )()(, 则在[a , b ]上f (x )≡g (x ).证明 令F (x )=g (x )-f (x ), 则在[a , b ]上F (x )≥0且0)()()]()([)(=-=-=⎰⎰⎰⎰bab ab ab adx x f dx x g dx x f x g dx x F ,由结论(1), 在[a , b ]上F (x )≡0, 即f (x )≡g (x ).4. 根据定积分的性质及第7题的结论, 说明下列积分哪一个的值较大:(1)⎰12dx x 还是⎰13dx x ?解 因为当0≤x ≤1时, x 2≥x 3, 所以⎰⎰≥13102dx x dx x .又当0<x <1时, x 2>x 3, 所以⎰⎰>13102dx x dx x .(2)⎰212dx x 还是⎰213dx x ?解 因为当1≤x ≤2时, x 2≤x 3, 所以⎰⎰≤213212dx x dx x .又因为当1<x ≤2时, x 2<x 3, 所以⎰⎰<213212dx x dx x .(3)⎰21ln xdx 还是⎰212)(ln dx x ?解 因为当1≤x ≤2时, 0≤ln x <1, ln x ≥(ln x )2, 所以⎰⎰≥21221)(ln ln dx x xdx .又因为当1<x ≤2时, 0<ln x <1, ln x >(ln x )2, 所以⎰⎰>21221)(ln ln dx x xdx .(4)⎰1xdx 还是⎰+1)1ln(dx x ?解 因为当0≤x ≤1时, x ≥ln(1+x ), 所以⎰⎰+≥11)1ln(dx x xdx .又因为当0<x ≤1时, x >ln(1+x ), 所以⎰⎰+>110)1ln(dx x xdx .(5)⎰10dx e x 还是⎰+1)1(dx x ?解 设f (x )=e x -1-x , 则当0≤x ≤1时f '(x ) =e x -1>0, f (x )=e x -1-x 是单调增加的. 因此当0≤x ≤1时, f (x )≥f (0)=0, 即e x ≥1+x , 所以⎰⎰+≥110)1(dx x dx e x .又因为当0<x ≤1时, e x>1+x , 所以⎰⎰+>110)1(dx x dx e x .习题5-21. 试求函数⎰=xtdt y 0sin 当x =0及4π=x 时的导数.解 x tdt dx dy x sin sin 0=='⎰, 当x =0时, y '=sin0=0;当4π=x 时, 224sin =='πy . 2. 求由参数表示式⎰=t udu x 0sin , ⎰=tudu y 0cos 所给定的函数y对x 的导数.解 x '(t )=sin t , y '(t )=cos t , t t x t y dx dy cos )()(=''=.3. 求由⎰⎰=+xyt tdt dt e 00cos 所决定的隐函数y 对x 的导数dxdy. 解 方程两对x 求导得 0cos =+'x y e y ,于是 y ex dx dy cos -=. 4. 当x 为何值时, 函数⎰-=xt dt te x I 02)(有极值?解 2)(x xe x I -=', 令I '(x )=0, 得x =0.因为当x <0时, I '(x )<0; 当x >0时, I '(x )>0, 所以x =0是函数I (x )的极小值点. 5. 计算下列各导数: (1)⎰+2021x dtt dxd ;解 dx du dt t du d dt t dx d u ux x ⋅+====+⎰⎰=02021122令421221x x x u +=⋅+=.(2)⎰+32411x x dt tdx d ; 解 ⎰⎰⎰+++=+323204044111111x x x x dt t dx d dt t dx d dt t dx d ⎰⎰+++-=3204041111x x dt t dx d dt t dx d )()(11)()(11343242'⋅++'⋅+-=x x x x 12281312x x x x +++-=. (3)⎰x xdt t dx d cos sin 2)cos(π. 解⎰⎰⎰+-=x x x x dt t dx d dt t dx d dt t dx d cos 02sin 02cos sin 2)cos()cos()cos(πππ))(cos cos cos())(sin sin cos(22'+'-=x x x x ππ )cos cos(sin )sin cos(cos 22x x x x ππ⋅-⋅-= )sin cos(sin )sin cos(cos 22x x x x πππ-⋅-⋅-= )sin cos(sin )sin cos(cos 22x x x x ππ⋅+⋅-= )sin cos()cos (sin 2x x x π-=6. 计算下列各定积分: (1)⎰+-adx x x 02)13(;解a a a x x x dx x x a a+-=+-=+-⎰230230221|)21()13(. (2)⎰+2142)1(dx x x ;解 852)11(31)22(31|)3131()1(333321332142=---=-=+---⎰x x dx x x . (3)⎰+94)1(dx x x ;解 94223942194|)2132()()1(x x dx x x dx x x +=+=+⎰⎰ 6145)421432()921932(223223=+-+=.(4)⎰+33121x dx; 解 66331arctan 3arctan arctan 13313312πππ=-=-==+⎰x x dx . (5)⎰--212121x dx ; 解3)6(6)21arcsin(21arcsin arcsin 1212121212πππ=--=--==---⎰x x dx .(6)⎰+ax a dx3022; 解 aa a axa x a dx a a 30arctan 13arctan 1arctan 1303022π=-==+⎰.(7)⎰-1024x dx ; 解 60arcsin 21arcsin 2arcsin 410102π=-==-⎰x x dx . (8)dx x x x ⎰-+++012241133; 解 013012201224|)arctan ()113(1133---+=++=+++⎰⎰x x dx x x dx x x x 41)1arctan()1(3π+=----=.(9)⎰---+211e x dx;解 1ln 1ln ||1|ln 12121-=-=+=+------⎰e x x dx e e . (10)⎰402tan πθθd ;解4144tan )(tan )1(sec tan 4040242πππθθθθθθπππ-=-=-=-=⎰⎰d d .(11)dx x ⎰π20|sin |;解⎰⎰⎰-=ππππ2020sin sin |sin |xdx xdx dx xπππ20cos cos x x +-==-cos π +cos0+cos2π-cos π=4.(12)⎰2)(dx x f , 其中⎩⎨⎧>≤+=12111)(2x x x x x f .解 38|)61(|)21(21)1()(2131022121020=++=++=⎰⎰⎰x x x dx x dx x dx x f . 7. 设k 为正整数. 试证下列各题: (1)⎰-=ππ0cos kxdx ;证明⎰--=--==ππππππ0)(sin 1sin 1|sin 1cos k kk k kx k kxdx . (2)⎰-=ππ0sin kxdx ;证明 )(cos 1cos 1cos 1sin ππππππ-+-=-=--⎰k kk k x k k kxdx0cos 1cos 1=+-=ππk k k k .(3)⎰-=πππkxdx 2cos ;证明 πππππππ=+=+=---⎰⎰|)2sin 21(21)2cos 1(21cos 2kx kx dx kx kxdx . (4)⎰-=πππkxdx 2sin .证明 πππππππ=-=-=---⎰⎰|)2sin 21(21)2cos 1(21sin 2kx kx dx kx kxdx . 8. 设k 及l 为正整数, 且k ≠l . 试证下列各题: (1)⎰-=ππ0sin cos lxdx kx ;证明 ⎰⎰----+=ππππdx x l k x l k lxdx kx ])sin()[sin(21sin cos0])cos()(21[])cos()(21[=----++-=--ππππx l k l k x l k l k . (2)⎰-=ππ0cos cos lxdx kx ;证明 ⎰⎰---++=ππππdx x l k x l k lxdx kx ])cos()[cos(21cos cos 0])sin()(21[])sin()(21[=--+++=--ππππx l k l k x l k l k . (3)⎰-=ππ0sin sin lxdx kx .证明 ⎰⎰----+-=ππππdx x l k x l k lxdx kx ])cos()[cos(21sin sin . 0])sin()(21[])sin()(21[=--+++-=--ππππx l k l k x l k l k . 9. 求下列极限: (1)xdt t xx ⎰→020cos lim ;解 11cos lim cos lim20020==→→⎰x xdt t x xx .(2)⎰⎰→xt xt x dttedt e 0220022)(lim.解 22222202200)(2lim )(limx xt x t x xt xt x xedt e dt e dtte dt e '⋅=⎰⎰⎰⎰→→222220202lim 2lim x x t x x x x t x xe dte xe edt e ⎰⎰→→=⋅=2212lim 22lim 2020222=+=+=→→xe x e e x x x x x .10. 设⎩⎨⎧∈∈=]2 ,1[]1 ,0[)(2x x x x x f . 求⎰=x dt t f x 0)()(ϕ在[0, 2]上的表达式, 并讨论ϕ(x )在(0, 2)内的连续性.解 当0≤x ≤1时, 302031)()(x dt t dt t f x xx ===⎰⎰ϕ;当1<x ≤2时,6121212131)()(2211020-=-+=+==⎰⎰⎰x x tdt dt t dt t f x xxϕ.因此 ⎪⎩⎪⎨⎧≤<-≤≤=21 612110 31)(23x x x x x ϕ.因为31)1(=ϕ, 3131lim )(lim 30101==-→-→x x x x ϕ, 316121)6121(lim )(lim 20101=-=-=+→+→x x x x ϕ, 所以ϕ(x )在x =1处连续, 从而在(0, 2)内连续.11. 设⎩⎨⎧><≤≤=ππx x x x x f 或000sin 21)(. 求⎰=xdt t f x 0)()(ϕ在(-∞, +∞)内的表达式. 解 当x <0时,00)()(0===⎰⎰xxdt dt t f x ϕ;当0≤x ≤π时,21cos 21|cos 21sin 21)()(000+-=-===⎰⎰x t tdt dt t f x xxxϕ;当x >π时, πππϕ000|cos 210sin 21)()(t dt tdt dt t f x x x-=+==⎰⎰⎰10cos 21cos 21=+-=π.因此 ⎪⎩⎪⎨⎧≥≤≤-<=ππϕx x x x x 10)cos 1(2100)(.12. 设f (x )在[a , b ]上连续, 在(a , b )内可导且f '(x )≤0,⎰-=x a dt t f ax x F )(1)(. 证明在(a , b )内有F '(x )≤0.证明 根据积分中值定理, 存在∈[a , x ], 使))(()(a x f dt t f xa-=⎰ξ.于是有)(1)()(1)(2x f ax dt t f a x x F x a -+--='⎰ ))(()(1)(12a x f a x x f a x ----=ξ )]()([1ξf x f ax --=. 由f '(x )≤0可知f (x )在[a , b ]上是单调减少的, 而a ≤ξ≤x , 所以f (x )-f (ξ)≤0. 又在(a , b )内, x -a >0, 所以在(a , b )内 0)]()([1)(≤--='ξf x f ax x F .习题5-31. 计算下列定积分: (1)⎰+πππ2)3sin(dx x ;解0212132cos 34cos )3cos()3sin(22=-=+-=+-=+⎰ππππππππx dx x . (2)⎰-+123)511(x dx ;解51251110116101)511(2151)511(22122123=⋅+⋅-=+-⋅=+-----⎰x x dx . (3)⎰203cos sin πϕϕϕd ;解⎰⎰-=20323sin cos cos sin ππϕϕϕϕϕd s d410cos 412cos 41cos 4144204=+-=-=πϕπ. (4)⎰-πθθ03)sin 1(d ;解⎰⎰⎰+=-πππθθθθθ0203cos sin )sin 1(d d d⎰-+=ππθθθ020cos )cos 1(d34)cos 31(cos 03-=-+=πθθππ.(5)⎰262cos ππudu ;解 22262622sin 4121)2cos 1(21cos ππππππππu u du u udu +=+=⎰⎰ 836)3sin (sin 41)62(21-=-+-=πππππ.(6)dx x ⎰-2022;解tdt t dx x t x cos 2cos 2 220sin 222⎰⎰⋅======-=π令dt t ⎰+=2)2cos 1(π2)2sin 21(20ππ=+=t t . (7)dy y ⎰--22228;解dy y dy y ⎰⎰---=-2222224228⎰-=⋅=====44sin 2cos 2cos 22ππxdx x x y 令⎰-+=44)2cos 1(22ππdx x)2(2)2sin 21(224+=+=-πππy x . (8)⎰-121221dx x x ; 解⎰⎰⋅=====-=242sin 12122cos sin cos 1ππtdt tt dx x x tx 令 41)cot ()1sin 1(2422πππππ-=--=-=⎰t t dt t. (9)⎰-adx x a x 0222;解⎰⎰⋅⋅=====-=2022sin 0222cos cos sin πtdt a t a t a dx x a x t a x a令⎰=20242sin 4πtdt a 164sin 328)4cos 1(84204204204ππππa t a t a dt t a =-=-=⎰. (10)⎰+31221xx dx ;解⎰⎰⋅⋅=====+=3422tan 3122sec sec tan 11ππtdt t t x x dx tx 令 3322sin 1sin cos 3432-=-==⎰ππππt dt t t .(11)⎰--1145xxdx ; 解 61)315(81)5(81451313324511=--=-======-⎰⎰=--u u du u x xdx u x 令. (12) ⎰+411xdx;解 221112141=⋅+=====+⎰⎰=udu u x dx u x 令 )32ln 1(2)|1|ln (2)111(2121+=+-=+-⎰u u du u .(13)⎰--14311x dx ; 解du u u x dx u x )2(11110211143-⋅-======--⎰⎰=-令 2ln 21)|1|ln (2)111(221021-=-+=-+=⎰u u du u . (14)⎰-a x a xdx 20223; 解 ⎰⎰---=-a a x a d xa x a xdx 2022222022)3(31213 )13(32022-=--=a x a a .(15)dt te t ⎰-1022;解 2110102221021)2(222-----=-=--=⎰⎰e e t d e dt te t tt .(16)⎰+21ln 1e x x dx ; 解 )13(2ln 12ln ln 11ln 1222111-=+=+=+⎰⎰e e e x x d x x x dx . (17)⎰-++02222x x dx ;解 ⎰⎰--++=++022022)1(1122dx x x x dx 2)1arctan(1arctan )1arctan(02π=--=+=-x .(18)⎰-222cos cos ππxdx x ;解 32)sin 32(sin sin )sin 21(2cos cos 2322222=-=-=---⎰⎰ππππππx x x d x xdx x . (19)⎰--223cos cos ππdx x x ;解⎰⎰---=-222223cos 1cos cos cos ππππdx x x dx x x⎰⎰+-=-202sin cos )sin (cos ππxdx x dx x x34cos 32cos 3220230223=-=-ππx x . (20)⎰+π2cos 1dx x .解22cos 2sin 22cos 100=-==+⎰⎰πππx xdx dx x .2. 利用函数的奇偶性计算下列积分: (1)⎰-ππxdx x sin 4;解 因为x 4sin x 在区间[-π, π]上是奇函数, 所以0sin 4=⎰-ππxdx x .(2)⎰-224cos 4ππθθd ;解⎰⎰⎰+==-202204224)22cos 1(8cos 42cos 4ππππθθθθθd x d d ⎰++=202)2cos 2cos 21(2πθd x x⎰++=20)4cos 212cos 223(2πθd x x 23)4sin 412sin 23(20πθπ=++=x x . (3)⎰--2121221)(arcsin dx x x ; 解⎰⎰-=--210222121221)(arcsin 21)(arcsin dx xx dx x x ⎰=2102)(arcsin )(arcsin 2x d x324)(arcsin 3232103π==x .(4)⎰-++55242312sin dx x x xx .解 因为函数12sin 2423++x x x x 是奇函数, 所以012sin 552423=++⎰-dx x x x x . 3. 证明:⎰⎰-=aaadx x dx x 022)(2)(ϕϕ, 其中ϕ(u )为连续函数.证明 因为被积函数ϕ(x 2)是x 的偶函数, 且积分区间[-a , a ]关于原点对称, 所以有⎰⎰-=aaadx x dx x 022)(2)(ϕϕ.4. 设f (x )在[-b , b ]上连续, 证明⎰⎰---=bbbbdx x f dx x f )()(. 证明 令x =-t , 则dx =-dt , 当x =-b 时t =b , 当x =b 时t =-b , 于是 ⎰⎰⎰----=--=bb bbb bdt t f dt t f dx x f )()1)(()(,而 ⎰⎰---=-bbbb dx x f dt t f )()(,所以⎰⎰---=bbbbdx x f dx x f )()(.5. 设f (x )在[a , b ]上连续., 证明⎰⎰-+=babadx x b a f dx x f )()(. 证明 令x =a +b -t , 则dx =d t , 当x =a 时t =b , 当x =b 时t =a , 于是 ⎰⎰⎰-+=--+=ba baa bdt t b a f dt t b a f dx x f )()1)(()(,而 ⎰⎰-+=-+baba dx xb a f dt t b a f )()(,所以⎰⎰-+=babadx x b a f dx x f )()(.6. 证明: ⎰⎰>+=+11122)0(11x x x x dx x dx . 证明 令t x 1=, 则dt t dx 21-=, 当x =x 时xt 1=, 当x =1时t =1, 于是⎰⎰⎰+=-⋅+=+11121122211)1(1111x x x dt t dt t t x dx ,而 ⎰⎰+=+x xdx x dt t 1121121111, 所以 ⎰⎰+=+1112211x x x dx x dx .7. 证明:⎰⎰-=-110)1()1(dx x x dx x x m n nm.证明 令1-x =t , 则 ⎰⎰⎰⎰-=-=--=-11110)1()1()1()1(dx x x dt t t dt t t dx x x m n nm nm nm,即⎰⎰-=-11)1()1(dx x x dx x x m n nm.8. 证明: ⎰⎰=ππ020sin 2sin xdx xdx n n .证明 ⎰⎰⎰+=ππππ22sin sin sin xdx xdx xdx n nn,而 ⎰⎰⎰⎰==--=====-=202022sin sin ))((sin sin πππππππxdx tdt dt t xdx nn n tx n 令,所以⎰⎰=ππ20sin 2sin xdx xdx n n.9. 设f (x )是以l 为周期的连续函数, 证明⎰+1)(a adx x f 的值与a无关.证明 已知f (x +l )=f (x ).⎰⎰⎰⎰++++=la ll aa a dx x f dx x f dx x f dx x f )()()()(001⎰⎰⎰-+=+ala lldx x f dx x f dx x f 00)()()(,而 ⎰⎰⎰⎰=+=+=====+=+aaalt x la l dx x f dx l x f dt l t f dx x f 0)()()()(令, 所以 ⎰⎰=+la adx x f dx x f 01)()(.因此⎰+1)(a adx x f 的值与a 无关.10. 若f (t )是连续函数且为奇函数, 证明⎰xdt t f 0)(是偶函数;若f (t )是连续函数且为偶函数, 证明⎰xdt t f 0)(是奇函数.证明 设⎰=xdt t f x F 0)()(.若f (t )是连续函数且为奇函数, 则f (-t )=-f (t ), 从而 ⎰⎰--======--=-xut xdu u f dt t f x F 0)1)(()()(令)()()(0x F dx x f dx u f xx ===⎰⎰,即⎰=xdt t f x F 0)()(是偶函数.若f (t )是连续函数且为偶函数, 则f (-t )=f (t ), 从而 ⎰⎰--======--=-xut xdu u f dt t f x F 0)1)(()()(令)()()(0x F dx x f dx u f xx -=-=-=⎰⎰,即⎰=xdt t f x F 0)()(是奇函数.11. 计算下列定积分: (1)⎰-10dx xe x ;解11011101121--------=--=+-=-=⎰⎰⎰e ee dx e xexde dx xe x xx xx.(2)⎰e xdx x 1ln ;解 ⎰⎰⎰⋅-==e e e edx xx x x xdx xdx x 0212121121ln 21ln 21ln)1(4141212122+=-=e x e e.(3)⎰ωπω20sin tdt t (ω为常数);解⎰⎰-=ωπωπωωω2020cos 1sin t td tdt t⎰+-=ωπωπωωωω2020cos 1cos 1tdt t t220222sin 12ωπωωωπωπ-=+-=t . (4)⎰342sin ππdx xx ; 解 ⎰⎰⎰+-=-=34334342cot cot cot sin ππππππππxdx x x x xd dx x x 34sin ln 4313ππππx ++⋅-=23ln 21)9341(+-=π. (5)⎰41ln dx x x;解 ⎰⎰⎰⋅-==4141414112ln 2ln 2ln dx x x x x x xd dx xx)12ln 2(442ln 8122ln 84141-=-=-=⎰x dx x.(6)⎰1arctan xdx x ;解 ⎰⎰=1021arctan 21arctan xdx xdx x x d xx x x ⎰+⋅-=10221021121arctan 21 10102)arctan (218)111(218x x x d x --=+--=⎰ππ214)41(218-=--=πππ. (7)⎰202cos πxdx e x ;解⎰⎰⎰-==202202202202sin 2sin sin cos ππππxdx e x e x d e xdx e x xxx⎰⎰-+=+=202202202cos 4cos 2cos 2πππππxdx e x e e x d e e x x x ⎰-+=202cos 42ππxdx e e x所以)2(51cos 202-=⎰ππe xdx e x.(8)⎰212log xdx x ;解 ⎰⎰=2122212log 21log xdx xdx x⎰⋅-=21221222ln 121log 21dx x x x x2ln 432212ln 212212-=⋅-=x . (9)⎰π2)sin (dx x x ;解 ⎰⎰⎰-=-=ππππ20302022sin 4161)2cos 1(21)sin (x d x x dx x x dx x x ⎰⎰-=⋅+-=πππππππ03000332cos 41622sin 412sin 416x xd x xd x x x 462sin 81462cos 412cos 416303003ππππππππ-=+-=+-=⎰x xdx x x . (10)⎰edx x 1)sin(ln ;解法一 ⎰⎰⋅======1ln 1sin )sin(ln dt e t dx x t tx e令.因为⎰⎰⎰-==⋅11011cos sin sin sin tdt e t e tde dt e t t ttt⎰⎰--⋅=-⋅=1101sin cos 1sin cos 1sin tdt e t e e tde e t tt⎰-+⋅-⋅=10sin 11cos 1sin tdt e e e t ,所以)11cos 1sin (21sin 1+⋅-⋅=⎰e e tdt e t . 因此 )11cos 1sin (21)sin(ln 1+⋅-⋅=⎰e e dx x e.解法二⎰⎰⋅⋅-⋅=eeedx xx x x x dx x 1111)cos(ln )sin(ln )sin(ln ⎰-⋅=edx x e 1)cos(ln 1sin⎰⋅⋅-⋅-⋅=eedx xx x x x e 111)sin(ln )cos(ln 1sin⎰-+⋅-⋅=edx x e e 0)sin(ln 11cos 1sin ,故)11cos 1sin (21)sin(ln 1+⋅-⋅=⎰e e dx x e. (11)dx x ee⎰1|ln |;解dx x dx x dx x eee e⎰⎰⎰+-=1111ln ln |ln |⎰⎰-++-=eeeedx dx x x x x 111111ln ln )11(2)1()11(1e e e e e -=---++-=.(12)⎰-1022)1(dx x m(m 为自然数);解⎰⎰+======-201sin 122cos )1(πtdt dx x m t x m令. 根据递推公式⎰⎰--=20220cos 1cos ππxdx n n xdx n n,⎪⎩⎪⎨⎧⋅⋅⋅⋅⋅--⋅--⋅+⋅⋅⋅⋅⋅⋅--⋅--⋅+=-⎰. ,325476 34121, ,2214365 34121)1(1022为偶数为奇数m m m m m m m m m m m m m m dx x m π(13)⎰=πsin xdx x J m m (m 为自然数).解 因为⎰⎰---=====-=0)1)((sin )(sin πππππdt t t xdx x m tx m令⎰⎰-=πππ0sin sin tdt t tdt m m,所以 ⎰⎰==πππ0sin 2sin xdx xdx x J m mm⎰⎰=⋅=2020sin sin 22ππππxdx xdx m m (用第8题结果).根据递推公式⎰⎰--=20220sin 1sin ππxdx n n xdx n n ,⎪⎩⎪⎨⎧⋅⋅⋅⋅⋅--⋅--⋅-⋅⋅⋅⋅⋅⋅--⋅--⋅-=. ,325476 45231, ,2214365 452312为奇数为偶数m m m m m m m m m m m m m m J m ππ习题5-41. 判别下列各反常积分的收敛性, 如果收敛, 计算反常积分的值: (1)⎰∞+14x dx ; 解 因为3131)31(lim 3131314=+-=-=-+∞→∞+-∞+⎰x x x dx x , 所以反常积分⎰∞+14x dx 收敛, 且3114=⎰∞+x dx . (2)⎰∞+1xdx;解 因为+∞=-==+∞→∞+∞+⎰22lim 211x x x dx x , 所以反常积分⎰∞+1x dx发散.(3)dx e ax ⎰∞+-0(a >0);解 因为aa e a e a dx e ax x ax ax11)1(lim 100=+-=-=-+∞→∞+-∞+-⎰, 所以反常积分dx e ax⎰∞+-0收敛, 且adx e ax 10=⎰∞+-.(4)⎰∞+-0ch tdt e pt (p >1);解 因为⎰⎰∞++--∞+-+=0)1()1(0][21ch dt e e tdt e t p t p pt1]1111[2120)1()1(-=+--=∞++--p pe p e p t p t p ,所以反常积分⎰∞+-0ch tdt e pt收敛, 且1ch 20-=⎰∞+-p ptdt e pt .(5)⎰∞+-0sin tdt e pt ω(p >0, ω>0);解 ⎰⎰∞+-∞+--=0cos 1sin t d e tdt ept ptωωω⎰∞+-∞+--⋅+-=00)(cos 1cos 1dt pe t t e pt ptωωωω ⎰∞+--=02sin 1t d e p pt ωωω ⎰∞+-∞+--⋅+-=0202)(sin sin 1dt pe t p t e p pt pt ωωωωω⎰∞+--=022sin 1tdt e p pt ωωω, 所以220sin w p tdt e pt +=⎰∞+-ωω. (6)⎰+∞∞-++222x x dx ;解 πππ=--=+=++=++⎰⎰∞+∞-∞+∞-+∞∞-)2(2)1arctan()1(12222x x dx x x dx . (7)dx x x ⎰-121; 解 这是无界函数的反常积分, x =1是被积函数的瑕点.11)1(lim 1121102102=+--=--=--→⎰x x dx x x x . (8)⎰-202)1(x dx;解 这是无界函数的反常积分, x =1是被积函数的瑕点. 因为⎰⎰⎰-+-=-212102202)1()1()1(x dx x dx x dx , 而+∞=--=-=--→⎰111lim 11)1(110102xx x dx x ,所以反常积分⎰-202)1(x dx 发散. (9)⎰-211x xdx ; 解 这是无界函数的反常积分, x =1是被积函数的瑕点.21232121]12)1(32[)111(1-+-=-+-=-⎰⎰x x dx x x x xdx 322]12)1(32[lim 38231=-+--=+→x x x . (10)⎰-e x x dx 12)(ln 1. 解 这是无界函数的反常积分, x =e 是被积函数的瑕点.x d x x x dx e eln )(ln 11)(ln 11212⎰⎰-=- 2)arcsin(ln lim )arcsin(ln 1π===-→x x e x e. 2. 当k 为何值时, 反常积分⎰∞+0)(ln kx x dx 收敛? 当k 为何值时, 这反常积分发散? 又当k 为何值时, 这反常积分取得最小值?解 当k <1时,+∞=-==∞++-∞+∞+⎰⎰2122)(ln 11ln )(ln 1)(ln k k k x kx d x x x dx ;当k =1时,+∞===∞+∞+∞+⎰⎰222)ln(ln ln ln 1)(ln x x d xx x dx k ;当k >1时,k k k k k x k x d x x x dx -∞++-∞+∞+-=-==⎰⎰12122)2(ln 11)(ln 11ln )(ln 1)(ln .因此当k >1时, 反常积分⎰∞+0)(ln kx x dx 收敛; 当k ≤1时, 反常积分⎰∞+0)(ln kx x dx 发散.当k >1时, 令k k k x x dx k f -∞+-==⎰10)2(ln 11)(ln )(, 则 2ln ln )2(ln 11)2(ln )1(1)(112k k k k k f ------=' )2ln ln 11()1(2ln ln )2(ln 21+---=-k k k . 令f '(k )=0得唯一驻点2ln ln 11-=k .因为当2ln ln 111-<<k 时f '(k )<0, 当2ln ln 11->k 时f '(k )>0, 所以2ln ln 11-=k 为极小值点, 同时也是最小值点, 即当2ln ln 11-=k 时, 这反常积分取得最小值3. 利用递推公式计算反常积分⎰∞+-=0dx e x I x n n .解 因为⎰⎰∞+-∞+--==0x n x n n de x dx e x I1010-∞+--∞+-=+-=⎰n x n x n nI dx e x n ex ,所以 I n = n ⋅(n -1)⋅(n -2)⋅⋅⋅2⋅I 1. 又因为 1001=-=+-=-==∞+-∞+-∞+-∞+-∞+-⎰⎰⎰x x x xxe dx e xexde dx xe I ,所以 I n = n ⋅(n -1)⋅(n -2)⋅ ⋅ ⋅2⋅I 1=n !.总习题五1. 填空:(1)函数f (x )在[a , b ]上(常义)有界是f (x )在[a , b ]上可积的______条件, 而f (x )在[a , b ]上连续是f (x )在[a , b ]上可积______的条件;解 函数f (x )在[a , b ]上(常义)有界是f (x )在[a , b ]上可积的___必要___条件, 而f (x )在[a , b ]上连续是f (x )在[a , b ]上可积___充分___的条件;(2)对[a , +∞)上非负、连续的函数f (x ), 它的变上限积分⎰xa dx x f )(在[a , +∞)上有界是反常积分⎰+∞a dx x f )(收敛的______条件;解 对[a , +∞)上非负、连续的函数f (x ), 它的变上限积分⎰xa dx x f )(在[a , +∞)上有界是反常积分⎰+∞a dx x f )(收敛的___充分___条件;(3)绝对收敛的反常积分⎰+∞a dx x f )(一定______; 解 绝对收敛的反常积分⎰+∞a dx x f )(一定___收敛___;(4)函数f (x )在[a , b ]上有定义且|f (x )|在[a , b ]上可积, 此时积分⎰ba dx x f )(______存在. 解 函数f (x )在[a ,b ]上有定义且|f (x )|在[a , b ]上可积, 此时积分⎰ba dx x f )(___不一定___存在.2. 计算下列极限: (1)∑=∞→+n i n nin 111lim ;解 )122(32)1(32111lim 103101-=+=+=+⎰∑=∞→x dx x n i n n i n . (2)121lim+∞→+⋅⋅⋅++p pp p n nn (p >0);解 11111])( )2()1[(lim 21lim101101+=+==⋅⋅⋅⋅++=+⋅⋅⋅+++∞→+∞→⎰p x p dx x n n n n n nn p p p p p n p p p p n . (3)nn nn !lnlim ∞→; 解 ]ln 1)ln 2ln 1(ln 1[lim !lnlim n n nn n n n n nn ⋅-+⋅⋅⋅++=∞→∞→nn n n n n 1)]ln (ln )ln 2(ln )ln 1[(ln lim ⋅-+⋅⋅⋅+-+-=∞→⎰=⋅+⋅⋅⋅++=∞→10ln 1)ln 2ln 1(ln lim xdx n n n n n n1)ln ()ln (10101010-=-=-=⎰xx x dx x x .(4)⎰-→xaa x dt t f a x x )(lim, 其中f (x )连续; 解法一 )()(lim )(lima af xf dt t f a x x a xa a x ==-→→⎰ξξ (用的是积分中值定理). 解法二 )(1)()(lim)(lim )(lim a af x xf dt t f ax dt t f x dt t f a x x xa ax xa ax xa a x =+=-=-⎰⎰⎰→→→ (用的是洛必达法则). (5)1)(arctan lim202+⎰+∞→x dtt xx .解 4)(arctan 1lim 1)(arctan lim 1)(arctan lim22222202π=+=+=+∞→+∞→+∞→⎰x x x x x x x dtt x x xx . 3. 下列计算是否正确, 试说明理由: (1)⎰⎰----=-=+-=+111111222)1arctan ()1(1)1(1πx xx d x dx ;解 计算不正确, 因为x 1在[-1, 1]上不连续. (2)因为⎰⎰--++-=++111122111t t dt tx x x dx , 所以⎰-=++11201x x dx .解 计算不正确, 因为t1在[-1, 1]上不连续.(3)01lim 122=+=+⎰⎰-∞→+∞∞-A A A dx x xdx x x . 解 不正确, 因为⎰⎰⎰⎰-+∞→+∞→+∞∞--∞→+≠+++=+A A A b b a a dx x xdx x x dx x x dx x x 2020221lim 1lim 1lim 1. 4. 设p >0, 证明⎰<+<+10111px dx p p. 证明 p pp pp p px xx x x x x->+-=+-+=+>11111111. 因为⎰⎰⎰<+<-1010101)1(dx x dxdx x pp,而 110=⎰dx , pp p x x dx x p p+=+-=-+⎰1)1()1(10110, 所以⎰<+<+10111p xdx p p. 5. 设f (x )、g (x )在区间[a , b ]上均连续, 证明: (1)⎰⎰⎰⋅≤ba ba ba dx x g dx x f dx x g x f )()(])()([222;证明 因为[f (x )-λg (x )]2≥0, 所以λ2g 2(x )-2λ f (x )g (x )+f 2(x )≥0, 从而 0)()()(2)(222≥+-⎰⎰⎰ba ba ba dx x f dx x g x f dx x g λλ.上式的左端可视为关于λ的二次三项式, 因为此二次三项式大于等于0, 所以其判别式小于等于0, 即0)()(4])()([4222≤⋅-⎰⎰⎰ba b a b a dx x g dx x f dx x g x f ,亦即 ⎰⎰⎰⋅≤ba ba ba dx x g dx x f dx x g x f )()(])()([222. (2)()()()212212212)()()]()([⎰⎰⎰+≤+b ab a b a dx x g dx x f dx x g x f , 证明⎰⎰⎰⎰++=+ba b a b a b a dx x g x f dx x g dx x f dx x g x f )()(2)()()]()([222 212222])()([2)()(⎰⎰⎰⎰⋅++≤ba ba ba ba dx x g dx x f dx x g dx x f ,又()2212212212222])([])([])()([2)()(⎰⎰⎰⎰⎰⎰+=⋅++ba ba ba ba ba ba dx x gdx x fdx x gdx x f dx x g dx x f,所以()()()212212212)()()]()([⎰⎰⎰+≤+b ab a b a dx x g dx x f dx x g x f . 6. 设f (x )在区间[a , b ]上连续, 且f (x )>0. 证明⎰⎰-≥⋅b a baa b x f dxdx x f 2)()()(. 证明 已知有不等式⎰⎰⎰⋅≤ba ba ba dx x g dx x f dx x g x f )()(])()([222, 在此不等式中, 取)(1)(x f x f =, )()(x f x g =, 则有⎰⎰⎰⋅≥⋅⋅ba ba ba dx x f x f dx x f dx x f 222])(1)([])(1[])([,即⎰⎰-≥⋅ba baa b x f dxdx x f 2)()()(. 7. 计算下列积分: (1)⎰++2cos 1sin πdx xxx ;解 20202020220)cos 1ln()2(tan cos 1)cos 1(2cos2cos 1sin πππππ⎰⎰⎰⎰+-=++-=++x xxd x x d dx x x dx xxx⎰=++=+-=2022022ln 2cos ln 222ln 2tan )2tan (πππππx dx x xx .(2)⎰+40)tan 1ln(πdx x ;解 ⎰⎰+=+4040cos )4sin(2ln)tan 1ln(πππdx xx dx x ⎰⎰⎰-++=404040cos ln )4sin(ln 2ln ππππxdx dx x dx .令,4u x =-π则。
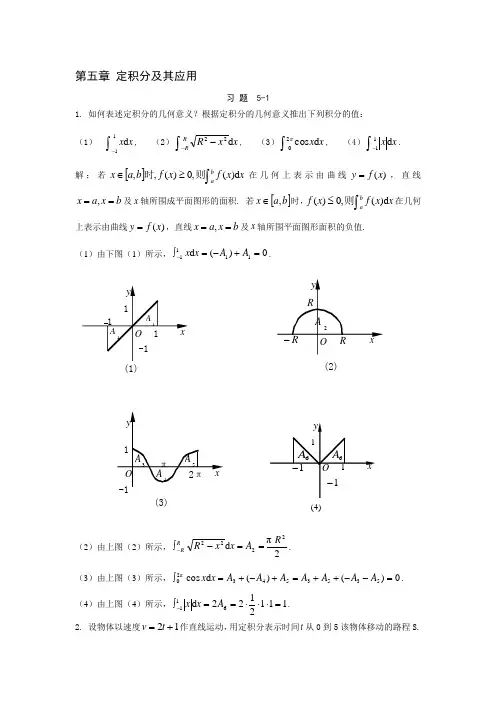
第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义?根据定积分的几何意义推出下列积分的值: (1)⎰-x x d 11, (2)⎰--x x R R R d 22, (3)⎰x x d cos 02π, (4)⎰-x x d 11.解:若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时,⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围平面图形面积的负值. (1)由下图(1)所示,0)(d 1111=+-=⎰-A A x x .(2)由上图(2)所示,2πd 2222R A x x R R R==-⎰-.(3)由上图(3)所示,0)()(d cos 5353543π20=--++=+-+=⎰A A AA A A A x x . (4)由上图(4)所示,1112122d 611=⋅⋅⋅==⎰-A x x . 2. 设物体以速度12+=t v 作直线运动,用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解:=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解:任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =,小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式:∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解:上在]1,0[)(2x x f =连续函数,故可积,因此为方便计算,我们可以对[]0,1 n 等分,分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点,故 ∑∑∑===∆=∆=∆ni i i ni i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ(即时∞→n ),由定积分的定义得: 120d x x ⎰=31.5. 利用定积分的估值公式,估计定积分⎰-+-1134)524(x x x d 的值.解:先求524)(34+-=x x x f 在[]1,1-上的最值,由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小,知min max 5093,111024f f ==,由定积分的估值公式,得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ,哪个积分值较大?解:在[]0,1区间内:22xx x x e e ≥⇒≥ 由性质定理知道:⎰1d xe x≥⎰1d 2x e x7. 证明:⎰---<<2121212d 22x e ex 。





word 完美格式第八章 多元函数微分法及其应用第一节 多元函数的基本概念本节主要概念,定理,公式和重要结论理解多元函数的概念,会表达函数,会求定义域; 理解二重极限概念,注意A y x f y x y x =→),(lim ),(),(00是点),(y x 以任何方式趋于),(00y x ;注意理解本节中相关概念与一元函数中相应内容的区分与联系。
习题 8-11.求下列函数表达式:(1)xy y x y x f +=),(,求),(y x xy f +解:(,)()x yxy f xy x y xyx y ++=++(2)22),(y x y x y x f -=-+,求),(y x f解:(,)()()(,)f x y x y x y x y f x y xy +-=-+⇒= 2.求下列函数的定义域,并绘出定义域的图形: (1)221)1ln(yx x y x z --+-+=解:22221011010x y x y x y x y x +->⎧+>⎧⎪-->⇒⎨⎨+<⎩⎪≥⎩(2))12ln(2+-=y x z 解:2210x y -+>(3) |)|||1ln(),(y x y x f --= 解:1||||0||||1x y x y -->⇒+< 3.求下列极限:(1)22)1,0(),(1limy x xyx y x ++-→解:22(,)(0,1)1lim1x y x xyx y →-+=+ (2)xy xy y x 42lim)0,0(),(+-→解一:(,)(0,0)(,)(0,0)(,)(0,0)18lim2lim2lim 4x y x y x y xyxy →→→=-=-=-(3)yxy x y x )sin()2(lim )0,1(),(+→(4)2222011limy x y x y x +-+→→解一:(,)(1,0)(,)(1,0)sin()sin()lim (2)lim [(2)]3x y x y xy xy x x x y xy→→+=+=解二:(,)(1,0)(,)(1,0)(,)(1,0)sin()lim (2)lim (2)lim (2)3x y x y x y xy xyx x x x y y →→→+=+=+= (4)22220011limyx y x y x +-+→→解一:2222222200000011lim lim()022x x x y y y x y y x x y x y →→→→→→==⋅=++解二:222222000000x x x y y y y x y →→→→→→===+ 4.证明下列函数当)0,0(),(→y x 时极限不存在:(1)2222),(yx y x y x f +-=解:222222222222001lim lim 1x x y kxx y x k x k x y x k x k →→=---==+++ (2)22222)(),(y x y x y x y x f -+= 解:224222400lim lim 1()x x y x x y x x y x y x →→===+- 2222200lim 0()x y x y x y x y →==+- 5.下列函数在何处是间断的? (1) yx z -=1解:x y =(2)x y xy z 2222-+=解:22y x =第二节 偏导数word 完美格式本节主要概念,定理,公式和重要结论1.偏导数:设),(y x f z =在),(00y x 的某一邻域有定义,则xy x f y x x f y x f x x ∆∆∆),(),(lim),(0000000-+=→, yy x f y y x f y x f y y ∆∆∆),(),(lim ),(0000000-+=→. ),(00y x f x 的几何意义为曲线⎩⎨⎧==0),(y y y x f z 在点)),(,,(0000y x f y x M 处的切线对x 轴的斜率.),(y x f 在任意点),(y x 处的偏导数),(y x f x 、),(y x f y 称为偏导函数,简称偏导数.求),(y x f x 时,只需把y 视为常数,对x 求导即可. 2.高阶偏导数),(y x f z =的偏导数),(),,(y x f y x f y x 的偏导数称为二阶偏导数,二阶偏导数的偏导数称为三阶偏导数,如此类推. 二阶偏导数依求导次序不同,有如下4个:xy zy x z y z x z ∂∂∂∂∂∂∂∂∂∂222222,,,,其中后两个称为混合偏导数. 若两个混合偏导数皆为连续函数,则它们相等,即可交换求偏导数的次序.高阶混合偏导数也有类似结果.习题 8-21.求下列函数的一阶偏导数:(1)xy y xz +=解:21,z z xy x x y y y∂∂=+=-+∂∂ (2)xyz arctan =解:2222222111,1()1()z y y z x y y x x x y y x x y x x∂--∂=⋅==⋅=∂+∂+++ (3))ln(22y x x z ++=解:(1z x ∂=+=∂z y ∂==∂ (4))ln(222z y x u ++=解:222222222222,,u x u y u z x x y z y x y z z x y z∂∂∂===∂++∂++∂++ (5)⎰=yzxzt dt e u 2解:22222222,,x z y z y z x z u u u ze ze ye xe x y z∂∂∂=-==-∂∂∂ (6)x y y x z cos sin = 解:2211cos cos sin sin ,cos cos sin sin z x y y x y u x x y x y x y y x x y x y y y x x y x ∂∂=+=--∂∂ (7)y x xy z ++=)1( (8))cos(ϕθϕθ-=+e u解:(1)[ln(1)],(1)[ln(1)]11x y x y z x y u x y xy xy y xy xy x x xy y xy ++∂+∂+=+++=+++∂+∂+ (8))cos(ϕθϕθ-=+e u解:[cos()sin()],[cos()sin()]u u e e θϕθϕθϕθϕθϕθϕθϕ++∂∂=---=-+-∂∂ 2.求下列函数在指定点处的一阶偏导数: (1)yxy x z arcsin)1(2-+=,求)1,0(x z 解:20(0,1)lim0x x x z x∆→∆==∆ (2)xyx e x z yarctan)1(2-+=,求)0,1(y z 解:01(1,0)lim1y y y e z y∆∆→-==-∆ 3.求下列函数的高阶偏导数:(1))ln(xy x z =, 求22x z ∂∂,22yz ∂∂,y x z∂∂∂2解:ln()1,z z x xy x y y∂∂=+=∂∂ 22222211,,z z x z x x y y x y y∂∂∂==-=∂∂∂∂ (2))2(cos 2y x z +=,求22x z ∂∂,22yz ∂∂,y x z ∂∂∂2,x y z ∂∂∂2解:2cos(2)sin(2)sin 2(2)z x y x y x y x∂=-++=-+∂word 完美格式4cos(2)sin(2)2sin 2(2)zx y x y x y y∂=-++=-+∂ 222222cos 2(2),8cos 2(2),4cos 2(2)z z zx y x y x y x y x y∂∂∂=-+=-+=-+∂∂∂∂ (3)⎰+=22 y x xtdt e z , 求22x z ∂∂, yx z∂∂∂2解:22222222222,2(12),4x y x x y x x y z z z xe e x e e xye x x x y+++∂∂∂=-=+-=∂∂∂∂ 4.设⎪⎩⎪⎨⎧=+≠++-=0 00),(22222233y x y x y x xy y x y x f ,求)0,0(xy f 和)0,0(yx f .解:00(0)(0,0)00(0,0)lim lim 0x x x f x f f x x ∆→∆→∆--===∆∆,00(0,)(0,0)00(0,0)lim lim 0y y y f y f f y y ∆→∆→∆--===∆∆4224222224(,),0()x x x y y f x y y x y x y +-=+≠+ 4224222224(,),0()y x x y y f x y x x y x y --=+≠+ 54000(0,)(0,0)(0,0)lim lim 1x x xy y y y f y f y f y y∆→∆→-∆-∆-∆===-∆∆54000(,0)(0,0)(0,0)lim lim 1x x yx x x x f x f x f x x ∆→∆→∆-∆-∆===∆∆5.设)11(y x e z +-=, 求证z y z y x z x222=∂∂+∂∂ 解: 1111()()2211,x y x y z z e ex x y y-+-+∂∂==∂∂ 111111()()()2222221122x yx y x y z z x y x e y e e z x y x y -+-+-+∂∂+=⋅+⋅==∂∂ 6.设222z y x r ++=, 证明r zr y r x r 2222222=∂∂+∂∂+∂∂证明: 22222223,r x r x r r x r r x x r x r x r r r ∂--∂∂-∂=====∂∂由轮换对称性, 2222222323,r r y r r z y r z r∂-∂-==∂∂ 222222222223321r r r r x y z r x y z r r r∂∂∂---++===∂∂∂ 第三节 全微分本节主要概念,定理,公式和重要结论1.全微分的定义若函数),(y x f z =在点),(00y x 处的全增量z ∆表示成22),(y x o y B x A z ∆+∆=+∆+∆=∆ρρ则称),(y x f z =在点),(00y x 可微,并称Bdy Adx y B x A +=+∆∆为),(y x f z =在点),(00y x 的全微分,记作dz .2.可微的必要条件:若),(y x f z =在),(00y x 可微,则 (1)),(y x f 在),(00y x 处连续;(2)),(y x f 在),(00y x 处可偏导,且),(),,(0000y x f B y x f A y x ==,从而dy y x f dx y x f dz y x ),(),(0000+=.一般地,对于区域D 内可微函数, dy y x f dx y x f dz y x ),(),(+=.3.可微的充分条件:若),(y x f z =在),(00y x 的某邻域内可偏导,且偏导数在),(00y x 处连续,则),(y x f z =在),(00y x 可微。

Page216向量空间7.证明对于任意正整数n 和任意向量α,都有个n ααα+⋯+=n(提示)利用数学归纳法4.设V 是一个向量空间,且V ≠{0}.证明:V 不可能表示成它的两个真子空间的并集。
证:设 W 1、W 2都是V 的真子集,且V ={}0,则至少有一个V 的非零向量W α∉1且至少有一个V 的非零向量W β∉2 ,(1)若W α∉2 则 因为W α∉1 ⇒Wα∉1W 2 命题得证. (2)若1W β∉则 因为W β∉2 ,⇒Wβ∉1W 2命题得证.(3)若W α∈2 ,而1W β∈,在这种情况下,我们考虑向量V αβ+∈.以下证明1W αβ+∉,且2W αβ+∉.(ị)若1W αβ+∈,则有1W γαβ=+∈,因为1W 是子空间⇒1W αγβ=-∈,这与W α∉1矛盾,所以1W αβ+∉,(ịị)若2W αβ+∈,则有2W δαβ=+∈,因为2W 是子空间⇒2W βδα=-∈,这与W β∉2矛盾.所以2W αβ+∉,于是有V αβ+∈,但Wαβ+∉1W 2综上表明12V W W ≠+.5.设W ,W 1,W 2都是向量空间V 的子空间,其中W 1⊆W 2,且W ∩W 1=W ∩W 2,W+W 1=W+W 2.证明W 1=W 2。
证:22W α∀∈因为2W ⊆W W +2W =W +1 ,所以21ααα=+,(W α∈,11W α∈)那么21ααα=-,又因为12W W ⊆,故212Wααα=-∈,所以21W W WW α∈=,因而1W α∈⇒11W αα+∈⇒21W α∈,即21W W ⊆,又12W W ⊆,故12W W =Page2276.3 向量的线性相关性3.令12(,,,),1,2,,.ni i i in a a a F i n α=∈=证明12,,,n a αα线性相关必要且只要行列1112121222120n n n n nna a a a a a a a a =证:1,,,na a 线性相关⇔有不全为零的数1,,,nk k 使10ni ii k a==⇔∑齐次11nnij ij i a k==∑∑有非零解⇔系数行列式ij a =.5.设,,,αβγ线性无关.证明,,αββγγα+++也线性无关.证:令123()()()0k k k αβγβαγ+++++=得齐次线性方程组121332000k k k k k k +=⎧⎪+=⎨⎪+=⎩ 而它只有零解.6.设向量组{}12,,,(2)r r ααα≥线性无关.任取121,,,.r k k k F -∈证明,向量组111222111,,,,r r r r r r r k k k a βααβααβαα---=+=+=+线性无关.证:令1ri ii k β==∑把1,,,rββ的表示代入上式,用1,,,rk k 的线性相关证明1,0r k k ===.6.4 基和维数2.求下列子空间的维数:(i)3((2,3,1),(1,4,2),(5,2,4));L R --⊆ (ii)22(1,1,)();L x x x x F x ---⊆ (iii)23(,,)[,].x x xL e e e C a b ⊆ 提示:12(,,,)n L ααα的维数为12,,,n ααα的极大无关组所含向量的个数.(ị)维数为2,因为2353420124--=,即它们线性相关,而其中任意两个都线性无关.(ịị)维数为2.(ịịị)维数为3.3.把向量组{}(2,1,1,3),(1,0,1,2)--扩充为4R 的一个基.提示:1(2,1,1,3)α=-2(1,0,1,2)α=-线性无关(不成比例)而1(1,0,0,0)ε=,2(0,1,0,0)ε=,3(0,0,1,0)ε=,4(0,0,0,1)ε=是4R 的一个基,所以1α,2α可由1ε,2ε,3ε,4ε表示,而1α,2α,1ε,2ε线性无关,故1α,2α,1ε,2ε是4R 的一个基.4.令S 是数域F 上一切数满足条件/A A =的n 阶矩阵A 所成的向量空间.求S 的维数.提示:因为S 是数域F 上一切满足'A A =的n 解矩阵A 所称的向量空间.令i j E 表示第i 行第j列交叉处是1 而其它元素全为零的n 解方阵,(i j E +')ji E =i j E +j iE , S 的一组基为: 11E ,22E ,,nn E ;12E +21E ,,1n E +1n E ;23E +32E ,,2n E +2n E ; ,1n n E -+1nn E -,故(1)dim (1)212n n S n n -=+-+++=.5.证明,复数域C 作为实数域R 上向量空间,维数是2.如果C 看成它本身上的向量空间的话,维数是几? 提示:1,i 在实数域R 上线性无关,且C 中任意复数均可由它们线性表示,故C 作为R 上的向量空间,维数为2.C 作为C 上的向量空间,维数为1.(任一非零复数均为它的基)6.5坐标1.设{}12,,,n a a a 是V的一个基.求由这个基到{}21,,,n a a a 的过渡矩阵.结果: 000110000100010⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭(提示:线性表示可得).2.证明,{}332,,1,1x xx x x +++是3()F x (数域F上一切次数3≤的多项式及零)的一个基.求下列多项式关于这个基的坐标:(i) 223x x ++; (ii) 3;x (iii) 4; (iv) 2x x -.结果:(i) (0,0,1,2); (ii) (1,0,0,0); (iii) (4,-4,0,4); (iv) (0,0,1,1) (提示:利用246P 公式(6)(取3[]F x 的基{}231,,,x x x )即得由{}231,,,x x x 到{}332,,1,1x x x x x +++的过渡矩阵.)4.设123123(1,2,1),(0,1,3),(1,1,0);(2,1,5),(2,3,1),(1,3,2).αααβββ=-=-=-==-=证明{}123,,ααα和{}1,23,βββ都是3R 的基,求前者到后者的过渡矩阵.结果:717422915424153424⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎪⎝⎭提示:取3R 的标准基,且求出123(,,)(ααα=123,,)A εεε,123(,,)(βββ=123,,)B εεε,并,A B 都可逆,即证得123(,,)ααα,123(,,)βββ都是3R 的基,从而有123(,,)βββ=1123(,,)A B ααα-,即1A B -为由123{,,}ααα到123{,,}βββ的过渡矩阵.5.设{}12,,,n a αα是F 上n 维向量空间V 的一个基.A 是F 上一个n s ⨯矩阵.令.1211(,,,)(,,,)s n A βββααα=.证明:12dim (,,,)s L βββ=秩A .证:设 秩A r =,则存在F 上n 阶可逆矩阵P 和Q ,使000rI A P Q ⎛⎫= ⎪⎝⎭(r I 为单位矩阵).1212(,,,)(,,,)n n P r r r ααα=,即12,,,nr r r 线性无关.于是有12(,,,)s βββ=12(,,,)n P ααα000r I Q⎛⎫ ⎪⎝⎭12(,,,)n r r r =000r I Q⎛⎫ ⎪⎝⎭12(,,,,0,,0)r r r r Q =,从而12,,,sβββ与12,,,,r r r r 等价,故有dim L 12(,,,)s βββdim L =12(,,,)r r r r r ==秩A .6.6向量空间2.设:f V W →是向量空间V 到W 的一个同构映射,1V 是V 的一个子空间.证明1()f V 是W 的一个子空间.证10V ∈,而1(0)0()f f V =∈,∴1()f V 是W 的一个非空子集.设,αβ∈1()f V ,所以存在11,αβ∈1V ,使得1()f αα=,1()f ββ=, ,a b F ∀∈, 有 a b αβ+=1()af α1()bf β+ =()f a b αβ+, 111a b V αβ+∈,a b αβ+∈1()f V ,故1()f V 是W 的子空间.6.7矩阵的秩 齐次线性方程组的解空间1.证明:行列式等于零的充分且必要条件是它的行(或列)线性相关. 证:设()i j n nA a ⨯=,0A =⇔秩A n <⇔行(列)空间的维数n <⇔A 的行(列)线性相关.2.证明,秩()A B +≤秩A +秩B提示:1W ,2W 是V 的子空间,由维数公式知,dim(1W +2W )=秩1W +秩2W ,令1W =A 的行空间,2W =B 的行空间,比较维数,结论得证.3.设A 是一个m 行的矩阵,秩A r =,从A 中任取出s 行,作一个s 行的矩阵B .证明,秩B r s m ≥+-. 证明:11S S m A αααα+⎛⎫⎪ ⎪ ⎪= ⎪⎪⎪ ⎪ ⎪⎝⎭(i α为A 的第i 行),1S B αα⎛⎫ ⎪= ⎪⎪⎝⎭,100S A αα⎛⎫⎪ ⎪ ⎪=+⎪ ⎪ ⎪ ⎪ ⎪⎝⎭100S m αα+⎛⎫⎪⎪⎪⎪⎪⎪⎪ ⎪⎝⎭据第2题,得,秩A ≤秩100S αα⎛⎫ ⎪ ⎪ ⎪+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭秩100S m αα+⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭,即r ≤秩B +秩100S m αα+⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭,因m ≥秩100S m αα+⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭+S ,所以秩B r ≥-秩100S m αα+⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭()r m s r s m ≥--=+-5.求齐次线性方程组 12345123451234523450323054330220x x x x x x x x x x x x x x x x x x x ++++=⎧⎪+++-=⎪⎨+++-=⎪⎪+++=⎩的一个基础解系.解:对系数矩阵施行初等行变换后,得 10110012200000100000--⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭1342345220x x x x x x x =+⎧⎪∴=--⎨⎪=⎩, 基础解系为()'12100-, ()'12010-.6.证明定理6.7.3的逆命题:nF 的任意一个子空间都是某一含n 个未知量的齐次线性方程组的解空间.证明:设W 是nF 的任一子空间,而且dim W r =,令1111(,)n a a α=,1(,)r r r n a a α=是W 的一个基,以12,,,r ααα为行构成矩阵r n A ⨯,经初等行变换(必要时交换列)将化为111212110010001r n r n r r rn c c c c c c +++⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭,因此111(1r r r c c ++ 00),()1001nr n cc 是100n x A x ⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭的基础解系,而12,,,r ααα正是111110001r n r nr nc c c c ++⎛⎫ ⎪ ⎪ ⎪⎝⎭1n y y ⎛⎫ ⎪= ⎪ ⎪⎝⎭00⎛⎫⎪ ⎪ ⎪⎝⎭ (*)的基础解系,所以(*)的解空间为W .第七章 线性变换7.1线性映射2.设V 是数域F 上一个一维向量空间,证明V 到自身的一个映射σ是线性映射的充要条件是:对于任意V ξ∈,都有()a σξξ=,这里a 是F 中一个定数.证: 必要性:设0α≠是V 的一个基,由σ是V 到自身的线性映射,有()V σα∈.设()a σαα=(a 是F 中的一个定数).所以,V ξ∀∈,有()V σξ∈,而k ξα=(k 是F 中的任意数),则有()()k σξσα=()k σα=()k a α==()a k α=a ξ.充分性a 是F 中的一个定数,∴V ξ∀∈,都有唯一确定的V 中的向量a ξ,使得()σξ=a ξ.12,Vξξ∀∈及12,a a F ∈,1122()a a σξξ+=a 1122()a a ξξ+=1a 1()a ξ+22()a a ξ=11()a σξ+ 22()a σξ.∴σ是V 到自身的线性映像.4.令4F 表示数域F 上四元列空间.取 1151112331811397A --⎛⎫ ⎪- ⎪=⎪- ⎪-⎝⎭对于4F ξ∈,令()A σξξ=.求线性映射σ的核和像的维数.解:先求k e r ()σ的维数.1234x x x x ξ⎛⎫ ⎪ ⎪∀=∈⎪ ⎪⎝⎭k e r ()σ,由核的定义,有()σξ=0A ξ=.即1151112331811397--⎛⎫⎪- ⎪ ⎪-⎪-⎝⎭12340000x x x x ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,因此,()Ker σ就是齐次线性方程组的解空间,由解空间的维数定理,得dim ()Ker σ=解空间的维数=4-秩A =4-2=2,再求Im()σ的维数.4F ξ∀∈,取4F 的标准基1,ε2,ε3,ε4,ε有:1k ξ=12k ε+23k ε+34k ε+4,ε()σξ=A ξ=A 1(k 122k εε+3k +34k ε+4)ε=1k (A 12)k ε+(A 23)k ε+(A34)k ε+(A 4),ε∴Im()σ=1234(,,,)L A A A A εεεε1234(,,,)L A A A A =, (i A 是A 的第i 列),故dim Im()σ=秩A =2.7.2线性变换的运算3.设V 是数域F 上一个有限维向量空间.证明,对于V 的线性变换σ来说,下列三个条件是等价的: (i)σ是满射;(ii)ker()0σ=;(iii)σ非奇异. 当V 不是有限维时,(i),(ii)是否等价?提示:参照7.1习题第6题中充分性的证明.7.3线性变换和矩阵1.令[]n F x 表示一切次数不大于n 的多项式连同零多项式所成的向量空间,:()'()f x f x σ.求σ关于以下两个基的矩阵:(1) 21,,,,n x x x ,(2)2()()1,,,,2!!nx c x c x c n ---.解(1)(1)0100nx x σ=⋅+⋅++⋅,()1100nx x x σ=⋅+⋅++⋅,,1()0100nn n x x nx x σ-=⋅+⋅++⋅∴σ关于基1,,,n x x 的矩阵为010********00000000n ⎛⎫⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭(它的阶数为1n +).(2)同理,σ关于基2()()1,,,2!!nx c x c x c n ---的矩阵为010000000001000⎛⎫⎪ ⎪⎪⎪ ⎪⎪⎝⎭2.设F 上三维向量空间的线性变换σ关于基123{,,}ααα的矩阵是1511520158876-⎛⎫⎪- ⎪ ⎪-⎝⎭.求σ关于基112321233123233422βαααβαααβααα=++⎧⎪=++⎨⎪=++⎩ 的矩阵.设1232ξααα=+-.求()σξ关于基123,,βββ的坐标.解:已知σ关于基123{,,}ααα的矩阵为1511520158876A -⎛⎫⎪=- ⎪⎪-⎝⎭,由基123,,ααα到基123,,βββ的过渡矩阵为231342112T ⎛⎫ ⎪= ⎪ ⎪⎝⎭,1652431111T ---⎛⎫ ⎪=- ⎪⎪-⎝⎭,设σ关于基123,,βββ的矩阵为B ,则有1B T AT -==100020003⎛⎫⎪ ⎪ ⎪⎝⎭,设ξ关于123,,βββ的坐标为123(,,)x x x ,()σξ关于123,,βββ的坐标为123(,,)y y y ,则有112233y x y B x y x ⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,ξ关于123,,ααα的坐标为(2,1,1)-,所以123x x x ⎛⎫ ⎪ ⎪ ⎪⎝⎭1211T -⎛⎫ ⎪= ⎪ ⎪-⎝⎭,所以123y y y ⎛⎫ ⎪= ⎪ ⎪⎝⎭1211BT -⎛⎫ ⎪ ⎪ ⎪-⎝⎭580-⎛⎫ ⎪= ⎪⎪⎝⎭. 3.设12{,,,}n γγγ是n 维向量空间V 的一个基11,,1,2,,nnj ij i j ij i i i a b j nαγβγ=====∑∑并且12,,,n ααα线性无关,又设σ是V 的一个线性变换,使得(),1,2,,j j j nσαβ==.求σ关于基12{,,,}n γγγ的矩阵.解 :由已知,有12(,,,)n ααα12(,,,)n r r r A =(A 可逆), 12(,,,)n βββ12(,,,)n r r r B =,12((),(),,())n r r r σσσ=112((),(),,())n A σασασα-=112(,,,)n A βββ-112(,,,)n r r r BA -=,故σ关于基12,,,n r r r 的矩阵为1BA -.4.设,A B 是n 阶矩阵,且A 可逆,证明,AB 与BA 相似. 证:11111()()()()AB AB AA A BA A A BA A -----===,∴BA 与AB 相似.5.设A 是数域F 上一个n 阶矩阵.证明,存在F 上一个非零多项式()f x 使得()0f A =.证:F 上所有n 阶矩阵作成F 上的向量空间()n M F ,其维数是2n .所以,0I A =,22,,,n A A A 一定线性相关,∴存在不全为零的数:2012,,,n a a a a F∈,使得222012n n a I a A a A a A ++++0=,设()f x 222012n n a a x a x a x=++++,因系数不全为零,∴()0f x ≠且有()0f A =.。
