初三——二次函数归类复习一、二次函数与面积
面积的求法:①公式法:S=1/2*底*高②分割法/拼凑法
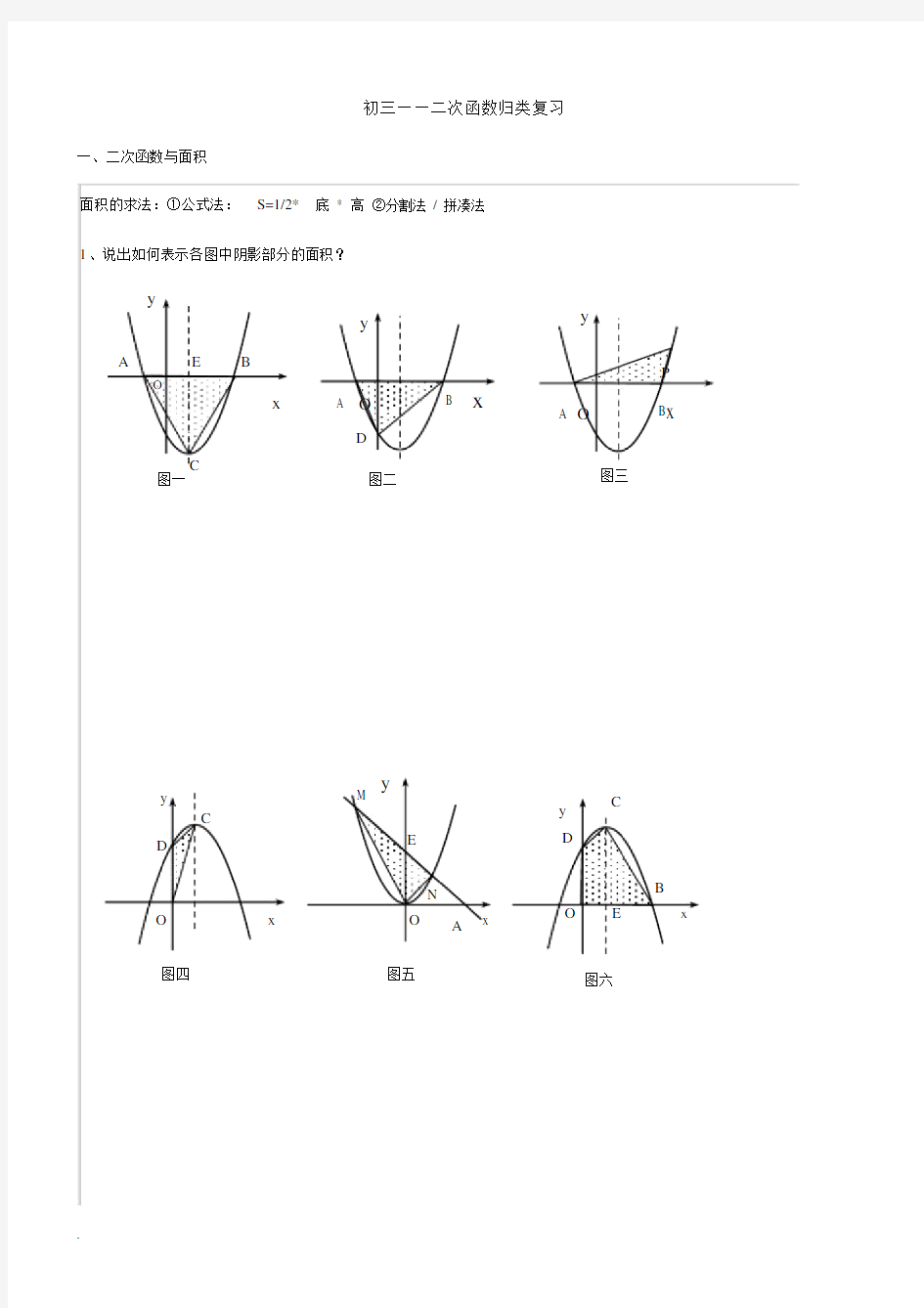
1、说出如何表示各图中阴影部分的面积?
y
y
A E B
O
x A O B x
D
C
图一图二
y
A O
P
B x
图三
y M
y
C
D E
N y
D
C
B
O x O A x 图四图五O E x 图六
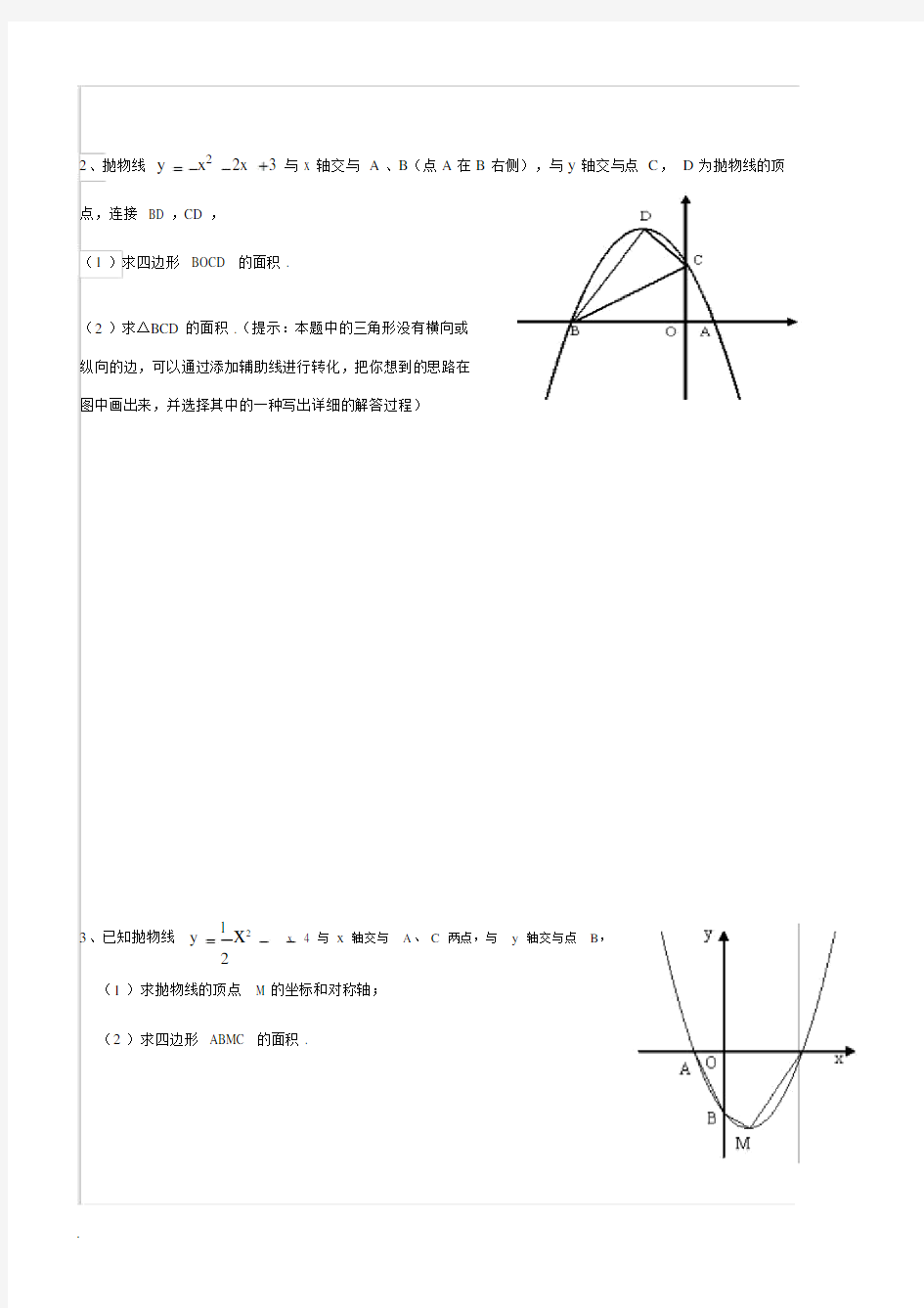
2、抛物线y x22x 3 与 x 轴交与A、B(点A在B右侧),与y轴交与点C,D为抛物线的顶点,连接 BD ,CD ,
(1)求四边形 BOCD 的面积 .
(2)求△BCD 的面积 .(提示:本题中的三角形没有横向或
纵向的边,可以通过添加辅助线进行转化,把你想到的思路在
图中画出来,并选择其中的一种写出详细的解答过程)
1 x2x 4与x轴交与A、C两点,与y轴交与点B,
3、已知抛物线y
2
(1)求抛物线的顶点 M 的坐标和对称轴;
(2)求四边形 ABMC 的面积 .
4、已二次函数y x 22x 3与x轴交于A、B两点(A在B的左边),与y轴交于点C,顶点为P.(1)结合图形,提出几个面积问题,并思考解法;
(2)求 A 、B、 C、P 的坐标,并求出一个刚刚提出的图形面积;
(3 )在抛物线上(除点 C 外),是否存在点N ,使得S NAB S ABC,
y
若存在,请写出点N 的坐标;若不存在,请说明理由。
A B
O x
C
P
变式一:在抛物线的对称轴上是否存点N ,使得S NAB S ABC,若存在直接写出N 的坐标;若不存
y
在,请说明理由.
A B
O x
C
变式一图
变式二:在双曲线 y 3
N ,使得S NAB S ABC,若存在直接写出N 的坐标;若不存上是否存在点
x
在,请说明理由 .
y
A B
O x
C
变式二图
5、抛物线y x 22x 3 与 x 轴交与A、B(点A在B右侧),与y轴交与点C,若点E为第二象限抛
物线上一动点,点 E运动到什么位置时,△ EBC的面积最大 ,并求出此时点 E的坐标和△ EBC的最大面
积.
【模拟题训练】
1.( 2015? 三亚三模)如图,直线y= ﹣x+2与x轴交于点B,与 y 轴交于点C,已知二次函数的图象经过点 B、C 和点 A (﹣ 1, 0).
(1)求 B、 C 两点坐标;
(2)求该二次函数的关系式;
(3 )若抛物线的对称轴与x 轴的交点为点 D ,则在抛物线的对称轴上是否存在点P,使△PCD是以CD 为腰的等腰三角形?如果存在,直接写出P 点的坐标;如果不存在,请说明理由;
(4 )点 E 是线段 BC 上的一个动点,过点 E 作 x 轴的垂线与抛物线相交于点F,当点 E 运动到什么位置时,四边形CDBF 的面积最大?求出四边形CDBF 的最大面积及此时 E 点的坐标.
二、二次函数与相似
【相似知识梳理】
二次函数为背景即在平面直角坐标系中,通常是用待定系数法求二次函数的解析式,在求点的坐
标过程中需要用到相似三角形的一些性质,如何利用条件找到合适相似三角形是需要重点突破的难点。
其实破解难点以后不难发现,若是直角三角形相似无非是如图1-1的几种基本型。
若是非直角三角形有如图1-2 的几种基本型。
利用几何定理和性质或者代数方法建议方程求解都是常用的方法。
【例题点拨】
【例 1 】如图 1-3 ,二次函数y ax2bx 2的图像与 x 轴相交于点A、B,与 y 轴相交于点C,经过
点 A 的直线y kx 2 与y轴相交于点D,与直线BC垂直于点E,已知AB=3,求这个二次函数的解
y
析式。
C
E
O A
x B
D
图1-3
【例 2 】如图 1-4 ,直角坐标平面内,二次函数图象的顶点坐标为 C 4, 3 ,且在x轴上截得的线段AB 的长为 6.
(1)求二次函数解析式;
(2)在x轴上方的抛物线上,是否存在点 D ,使得以 A 、 B、 D 三点为顶点的三角形与△ ABC 相似?若存在,求出点 D 的坐标,若不存在,请说明理由。
D1Y
D2
H
E O A
B X
C
【例 3 】如图 1-6 ,在平面直角坐标系中,二次函数y 1 x 2bx c-的图像经过点A(4,0),C(0,2)。
4
(1 )试求这个二次函数的解析式,并判断点B( -2,0 )是否在该函数的图像上;
(2 )设所求函数图像的对称轴与x 轴交于点D,点E在对称轴上,若以点C、D 、 E 为顶点的三角形与△ABC 相似,试求点 E 的坐标。
y
C
1A x
O
图1-6
【模拟题训练】
2.( 2015? 崇明县一模)如图,已知抛物线 y= x 2
+bx+c 经过直线 y= ﹣ +1 与坐标轴的两个交点
A 、
B ,点
C 为抛物线上的一点,且∠ ABC=90 °.
( 1 )求抛物线的解析式; ( 2 )求点 C 坐标;
(3 )直线 y= ﹣ x+1 上是否存在点 P ,使得△ BCP 与△ OAB 相似?若存在,请
直接写出 P 点的坐标;
若不存在,请说明理由.
三、二次函数与垂直
【方法总结】
①应用勾股定理证明或利用垂直
②三垂直模型
【例 1 】:如图,直线 l 过等腰直角三角形ABC 顶点
B,A 、C 两点到直线l 的距离分别是 2 和 3 ,则 AB
的长是()
【例 2 】:在平面直角坐标系中,抛物线 y=ax 2 +bx+c
与x 轴的两个交点分别为 A ( -3 , 0)、 B(1 ,0 ),
过顶点 C 作 CH ⊥x 轴于点 H.
(1)直接填写: a=,b=,顶点 C 的坐标为;
(2)在 y 轴上是否存在点 D ,使得△ACD 是以 AC 为斜边的直角三角形?若存在,求出点 D 的坐标;若不存在,说明理由;
【例 3 】、( 2011山东烟台)如图,已知抛物线y=x2+bx-3a过
y
C O A x
B
(第26题图 )
七、二次函数与图形转换
常见图像变换:①平移(上加下减,左加右减)②轴对称(折叠)
【模拟题训练】
8 .( 2014? 西城区一模)抛物线 y=x 2
﹣ kx ﹣ 3 与 x 轴交于点 A ,B,与 y 轴交于点C,其中
点 B 的坐标为( 1+k ,
0 ).
( 1)求抛物线对应的函数表达式;
( 2)将( 1 )中的抛物线沿对称轴向上平移,使其顶点M 落在线段BC 上,记该抛物线为G,求抛物线G 所对应的函数表达式;
( 3)将线段BC 平移得到线段B′ C′B(的对应点为B′,C 的对应点为C′,)使其经过( 2 )中所得抛物线G 的
顶点 M ,且与抛物线G 另有一个交点N,求点 B′到直线OC′的距离 h 的取值范围.
.
模拟训练题参考答案
1考点:二次函数综合题.
分析:(1
)分别令解析式 y= ﹣x+2 中 x=0 和 y=0 ,求出点 B、点 C 的坐标;
( 2)设二次函数的解析式为y=ax
2
+bx+c ,将点 A 、 B、 C 的坐标代入解析式,求出 a 、 b 、 c 的值,进而求得解析式;
( 3)由( 2 )的解析式求出顶点坐标,再由勾股定理求出CD 的值,再以点 C 为圆心, CD 为半径作弧交对称轴于 P1,以点 D 为圆心 CD 为半径作圆交对称轴于点P2, P3,作 CE 垂直于对称轴与点 E,由等腰三角形的性质及勾股定理就可以求出结论;
( 4)设出 E 点的坐标为( a,﹣ a+2 ),就可以表示出 F 的坐标,由四边形 CDBF 的面积
=S △BCD+S △CEF+S △BEF求出 S 与 a 的关系式,由二次函数的性质就可以求出结论.
解答: 解:(1 )令 x=0 ,可得 y=2 ,
令 y=0 ,可得 x=4 ,
即点 B ( 4, 0), C (0 ,2);
( 2 )设二次函数的解析式为 y=ax 2
+bx+c ,
将点 A 、B 、 C 的坐标代入解析式得,
,
解得:
,
即该二次函数的关系式为
y= ﹣ x 2
+ x+2 ;
( 3 )∵ y= ﹣x 2
+ x+2 ,
∴ y= ﹣ ( x ﹣ ) 2
+ ,
∴抛物线的对称轴是 x= .
∴ OD= .
∵ C (0 ,2), ∴ OC=2 .
在 Rt △ OCD 中,由勾股定理,得
CD= .
∵△ CDP 是以 CD 为腰的等腰三角形,
∴ CP 1=DP 2 =DP 3 =CD .
如图 1 所示,作 CH ⊥x 对称轴于 H ,
∴ HP 1=HD=2 ,
∴ DP 1=4 .
∴P 1( , 4),P 2( , ), P 3( ,﹣
);
( 4 )当 y=0 时, 0= ﹣ x 2
+ x+2
∴x 1= ﹣ 1 ,x 2=4 ,
∴ B (4, 0).
∵直线 BC 的解析式为: y= ﹣ x+2 .
如图 2 ,过点 C 作 CM ⊥ EF 于 M ,设 E ( a ,﹣
a+2 ), F ( a ,﹣ a 2
+ a+2 ),
∴ EF= ﹣ a 2
+ a+2 ﹣(﹣
a+2 )= ﹣ a 2 +2a ( 0 ≤ x ≤ .4)
∵S 四边形
CDBF =S
+S
+S = BD?OC+ EF?CM+ EF?BN ,
△ BCD
△ CEF △ BEF
= + a (﹣ a 2
+2a ) + ( 4 ﹣a )(﹣
a 2
+2a ),
= ﹣a 2
+4a+ ( 0 ≤ x ≤ .4)
= ﹣( a ﹣ 2 ) 2
+
∴ a=2 时, S 四边形 CDBF 的面积最大 =
,
∴ E (2 ,1).
点评: 本题考查了二次函数的综合运用,
涉及了待定系数法求二次函数的解析式的运用, 勾股定理的运用, 等
腰三角形的性质的运用,四边形的面积的运用,解答时求出函数的解析式是关键.
2 .
考点 : 二次函数综合题.
分析: ( 1 )根据直线的解析式求得 A 、 B 的坐标,然后根据待定系数法即可求得抛物线的解析式;
( 2 )作 CD ⊥x 轴于 D ,根据题意求得∠ OAB= ∠ CBD ,然后求得△ AOB ∽△ BDC ,根据相似三角形对应
边成比例求得 CD=2BD ,从而设 BD=m ,则 C ( 2+m , 2m ),代入抛物线的解析式即可求得; ( 3 )分两种情况分别讨论即可求得.
解答: 解:(1 )把 x=0
代入 y= ﹣ x+1 得, y=1 ,
∴ A (0, 1),
把 y=0 代入 y= ﹣ x+1 得, x=2 ,
∴ B (2, 0),
把 A ( 0, 1 ), B ( 2, 0)代入 y= x 2
+bx+c 得,
,解得 ,
∴抛物线的解析式 y= x 2
﹣ x+1 ,
( 2 )如图,作 CD ⊥x 轴于 D , ∵∠ ABC=90 °,
∴∠ ABO+ ∠ CBD=90 °, ∴∠ OAB= ∠ CBD ,
∵∠ AOB= ∠ BDC ,
∴△ AOB ∽△ BDC ,
∴ = =2,
∴ CD=2BD , 设 BD=m ,
∴ C (2+m , 2m ),
代入 y=
x 2﹣ x+1 得, 2m= ( m+2 ) 2 ﹣
(m+2 ) +1 ,解得, m=2 或
m=0 (舍去),
∴ C (4 ,4);
( 3 )∵ OA=1 ,OB=2 ,
.
∴AB=,
∵ B(2,0),C(4,4),
∴BC=2 ,
①当△AOB∽△PBC时,则=
∴=,解得,PB=,
作 PE⊥x轴于 E,则△AOB∽△PEB ,
∴=,即=,
∴PE=1 ,
∴P的纵坐标为±1,代y=入﹣x+1 得, x=0或 x=4 ,
∴ P(0, 1)或( 4,﹣ 1);
②当△AOB∽△ CBP时,则=,
即=,解得, PB=4,
作 PE⊥x轴于 E,则△AOB∽△ PEB ,
∴=,即=,
∴PE=4 ,
∴P的纵坐标为± 4 ,代y=入﹣x+1得,x=﹣6或x=10,
∴ P(﹣6 ,4 )或( 10 ,﹣ 4);
综上, P 的坐标为( 0, 1)或( 4,﹣ 1)或(﹣ 6, 4)或( 10 ,﹣ 4).
点评:本题是二次函数和一次函数的综合题,考查了待定系数法、三角形相似的判定和性质,数形结合运用是解题的关键.
3.
考点:二次函数综合题.
分析: (1 )分类讨论:△ BOC ∽△ BOA ,△ BOC ∽△ AOB ,根据相似三角形的性质,可得答案;
( 2 )根据全等三角形的性质,可得
C 点坐标,根据待定系数法,可得函数解析式;
( 3 )根据相似三角形的性质, 可得关于 a 的方程, 根据解方程, 可得 a 的值可得 p 点坐标, 分类讨论:
当点 P 的坐标为(
, 1 )时,根据正弦函数据,可得∠
的度COP 数,根据等腰三角形得到性质,可
得答案; 当点 P 的坐标为(﹣
, 1 )时,根据正弦函数据,可得∠
的度AOP 数,根据三角形外角的
性质,可得答案.
解答: 解:(1 )点 C 的坐标为( m , 0 )或( 4m , 0 ).或(﹣ 4m , 0 );
( 2 )当△ BOC 与△
AOB 全等时,点 C 的坐标为( m ,0 ),
二次函数 y= ﹣ x 2
+bx+c 的图象经过 A 、B 、 C 三点,
,解得
.
二次函数解析式为
y= ﹣ x 2
+4 ,点 C 的坐标为( 2 ,0 );
( 3 )作 PH ⊥ AC 于 H ,设点 P 的坐标为( a ,﹣ a 2
+4 ),
∵∠ AHP= ∠ PHC=90 °,∠
APH= ∠ PCH=90 °﹣∠ CPH ,
∴△ APH ∽△ PCH ,∴= ,
即 PH 2
=AH?CH ,
(﹣ a 2 +4 ) 2
= (a+2 )( 2﹣ a ).
解得 a= ,或 a= ﹣ ,即 P ( ,1 )或(﹣ ,1),
如图:
当点 P 1 的坐标为(
, 1)时, OP 1=2=OC , sin ∠P 1OE= = ∴∠ COP=30 °,
∴∠ ACP=
=75 °
当点 P 的坐标为(﹣,1)时,sin∠P2OF==,
∠P2OF=30°.
由三角形外角的性质,得∠P 2 OF=2∠ACP,即
∠ACP=15 °.
点评:本题考查了二次函数综合题,(1)利用了相似三角形的性质,分类讨论是解题关键;(2)利用全等三角形的性质,解三元一次方程组;(3)利用了相似三角形的性质,分类讨论是解题关键,正弦函数及等
腰三角形的性质,三角形外角的性质.
4 .
考点:二次函数综合题.
分析:(1)由抛物线的解析式可知OA=OB=OM=1,得出∠AMO=∠ MAO=∠ BMO=∠ MBO=45 °从而得出△ MAB是等腰直角三角形.
( 2 )分别过 C 点, D 点作 y 轴的平行线,交x 轴于 E、F,过 M 点作 x 轴的平行线交EC 于 G,交 DF
于 H ,设 D( m ,m 2
﹣1 ), C(n ,n
2
﹣ 1 ),通过 EG∥ DH,得出=,从而求得m 、 n 的关系,根
据 m 、n 的关系,得出△CGM∽△MHD,利用对应角相等得出∠CMG+∠ DMH=90 °,即可求得结论.解答:解:(1)△MAB是等腰直角三角形.理由如下:
由抛物线的解析式为:y=x 2
﹣1 可知 A (﹣ 1 , 0 ),B( 1 , 0 ),
∴ OA=OB=OM=1 ,
∴∠AMO=∠ MAO=∠ BMO=∠ MBO=45 °,∴∠AMB=∠ AMO+∠ BMO=90 °,AM=BM,∴△MAB是等腰直角三角形.
( 2 ) MC⊥ MD.理由如下: