关于多重序列比对距离矩阵的一点注记
- 格式:pdf
- 大小:417.56 KB
- 文档页数:8
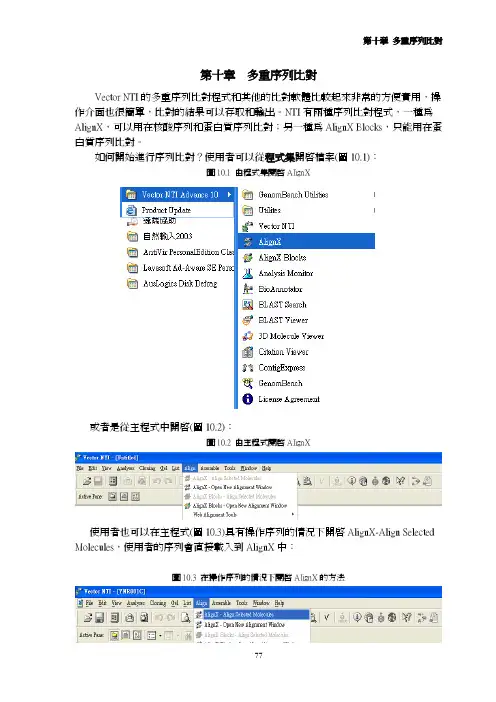
第十章 多重序列比對 Vector NTI的多重序列比對程式和其他的比對軟體比較起來非常的方便實用,操作介面也很簡單,比對的結果可以存取和輸出。
NTI有兩種序列比對程式,一種為AlignX,可以用在核酸序列和蛋白質序列比對;另一種為AlignX Blocks,只能用在蛋白質序列比對。
如何開始進行序列比對?使用者可以從程式集開啟檔案(圖10.1):圖10.1 由程式集開啟AlignX 或者是從主程式中開啟(圖10.2):圖10.2 由主程式開啟AlignX 使用者也可以在主程式(圖10.3)具有操作序列的情況下開啟AlignX-Align Selected Molecules,使用者的序列會直接載入到AlignX中:圖10.3 在操作序列的情況下開啟AlignX的方法 開啟AlignX之後,使用者會見到圖10.4的畫面:圖10.4在操作序列的情況下開啟AlignX首先使用者要把序列載入Vector NTI程式中,可以點選或者從左上方的Project→Add Files把序列檔案載入,請注意檔案名不可以過長,檔名過長會造成程式進行比對時無法完全顯示檔名(圖10.5):圖10.5 輸入的檔名注意不可過長 選取檔案後按下開啟就可以載入程式中,若比對的序列很多時可以用滑鼠圈選欲分析的序列後選擇開啟。
序列檔案載入的時候程式會詢問該序列為核酸序列或是蛋白質序列,點選好以後再點選Import就可以了(圖10.6):圖10.6 載入時,會詢問序列的性質,核酸序列或蛋白質序列接下來程式的左上方會出現使用者載入的序列(圖10.7),序列載入完成以後就可以開始進行比對的操作:圖10.7 成功載入序列的畫面進行比對前,先把欲比對的序列用滑鼠進行圈選(圖10.8):圖10.8 選取欲比對之序列只要按下或是從上方Align→Align Selected Sequence(圖10.9)就會進行比對運算:圖10.9按下Align→Align Selected Sequence進行比對運算好以後就會出現下面的畫面(圖10.10);圖10.10 比對完的結果 分析完成後畫面(圖10.11)會出現比對的相關結果,最下方是序列比對的圖形,左邊中間的區塊所顯示的圖形為導引樹(Guide tree),用來表示序列之間的關連性。

生物信息学中的多重序列比对算法生物信息学是一门交叉学科,主要研究生物体内的相关信息,如基因、蛋白质等,与计算机科学相结合,开发相应的算法和软件来处理这些信息。
多重序列比对是生物信息学中一个基本的、重要的问题,在基因组学和系统生物学研究中有着广泛的应用。
本文将会介绍多重序列比对的背景和意义,并着重讨论多种常见的多重序列比对算法。
一、多重序列比对的背景和意义DNA序列中的每一个碱基都是遵循特定的规律排列而成的,对于同一物种不同个体的DNA序列中,虽然具有相同的碱基种类,但在具体的分布和数量上,还是会存在一定的差异。
这些差异可能涉及到基因的表达、蛋白质的功能以及遗传变异等方面。
因此,通过对多个DNA序列进行比对,可以发现它们之间的差异和联系,从而深入了解物种的演化路径和生物功能等方面。
多重序列比对的具体过程是将多条序列进行比对,找出它们之间的共同区域和不同之处。
而这个过程并不是一件轻松的事情,因为序列长度的不同和存在的错配等现象,这个比对过程难点很多。
因此,多重序列比对算法的研究和发展也成为了生物信息学研究的前沿领域之一。
二、多重序列比对算法概述多重序列比对算法根据方法不同,可以分为两类,一种是基于全局比对的算法,另一种则是基于局部比对的算法。
在全局比对中,整条序列被视为一个整体进行比对;而在局部比对中,仅比对序列中的一部分区域,这个区域通常是各个序列中比较相似的地方。
下面分别介绍几个常见的多重序列比对算法:1. ClustalWClustalW是一种全局比对算法,它是一种基于序列之间的距离矩阵进行序列比对的方法。
在ClustalW中,首先将多个序列之间的距离计算出来,然后根据距离矩阵的结果进行多序列比对。
ClustalW算法具有速度快、易于使用的特点。
但是,它的精确度不高,适合处理比较简单的序列之间的比对。
2. MuscleMuscle是一种全局比对算法,其特点是能够使用多种方法来计算序列之间的距离矩阵,常见的包括kmer覆盖率、Poisson模型等。

多序列比对距离矩阵引言多序列比对是生物信息学领域中常用的一种分析方法,用于比较多个生物序列之间的相似性和差异性。
在多序列比对中,距离矩阵是一种常用的表示方法,用于衡量序列之间的相似程度。
本文将介绍多序列比对距离矩阵的概念、计算方法以及在生物信息学中的应用。
距离矩阵的定义距离矩阵是一个对称的矩阵,用于表示多个序列之间的距离或相似度。
在多序列比对中,距离通常是通过计算序列之间的差异性来得到的。
距离矩阵中的每个元素表示对应序列之间的距离或相似度值。
距离矩阵的计算方法计算距离矩阵的方法有很多种,常见的方法包括: 1. 序列相似度计算:可以使用基于编辑距离的方法(如Levenshtein距离)或基于相似性矩阵的方法(如BLOSUM矩阵)来计算序列之间的相似度。
2. 多序列比对算法:多序列比对算法(如ClustalW、MUSCLE等)可以直接计算序列之间的距离矩阵。
这些算法通常采用动态规划或迭代优化的方法来找到最优的序列比对结果。
3. 基于特征的方法:可以使用序列的特征(如氨基酸组成、二级结构等)来计算序列之间的距离矩阵。
这种方法适用于序列之间存在明显特征差异的情况。
距离矩阵的应用距离矩阵在生物信息学中有广泛的应用,包括以下几个方面: 1. 进化关系分析:距离矩阵可以用于构建进化树(phylogenetic tree),从而揭示不同物种或序列之间的进化关系。
通过计算不同物种或序列之间的距离,可以构建一个进化树,用于研究物种的亲缘关系或序列的进化历程。
2. 功能预测:距离矩阵可以用于预测序列的功能。
通过比较未知序列与已知功能序列之间的距离,可以推测未知序列的功能。
这种方法适用于序列之间存在一定的功能相关性的情况。
3. 物种分类:距离矩阵可以用于物种分类的研究。
通过计算不同物种之间的距离,可以将它们划分为不同的分类群。
这种方法可以帮助研究者理解物种之间的差异性和相似性,并为物种分类提供参考依据。
4. 蛋白质结构预测:距离矩阵可以用于预测蛋白质的二级结构。




实验六:多序列比对- Clustal、MUSCLE西北农林科技大学生物信息学中心实验目的:学会使用Clustal 和MUSCLE 进行多序列比对分析。
实验内容:多序列比对是将多条序列同时比对,使尽可能多的相同(或相似)字符出现在同一列中。
多序列比对的目标是发现多条序列的共性。
如果说序列两两比对主要用于建立两条序列的同源关系,从而推测它们的结构和功能,那么,同时比对多条序列对于研究分子结构、功能及进化关系更为有用。
例如,某些在生物学上有重要意义的相似区域只能通过将多个序列同时比对才能识别。
只有在多序列比对之后,才能发现与结构域或功能相关的保守序列片段,而两两序列比对是无法满足这样的要求的。
多序列比对对于系统发育分析、蛋白质家族成员鉴定、蛋白质结构预测、保守motif 的搜寻等具有非常重要的作用。
我们这节课主要学习两个广泛使用的多序列比对软件-Clustal、MUSCLE。
一、Clustal/Clustal 是一种利用渐近法(progressive alignment)进行多条序列比对的软件。
即先将多个序列两两比较构建距离矩阵,反应序列之间的两两关系;随后根据距离矩阵利用邻接法构建引导树(guide tree);然后从多条序列中最相似(距离最近)的两条序列开始比对,按照各个序列在引导树上的位置,由近及远的逐步引入其它序列重新构建比对,直到所有序列都被加入形成最终的比对结果为止(Figure 6.1)。
Clustal 软件有多个版本。
其中Clustalw 采用命令行的形式在DOS 下运行;Clustalx 是可视化界面的程序,方便在windows 环境下运行;Clustal omega 是最新的版本,优点是比对速度很快,可以在短短数小时内比对成百上千的序列,同时由于采用了新的HMM 比对引擎,它的比对准确性也有了极大的提高,有DOS 命令行和网页服务器版。
我们今天主要学习clustalx 的使用。
范例1. 采用clustalx 进行多序列比对。

一种新的DNA序列进化距离的修正方法邢林林;郭茂祖;王娟【摘要】进化树是推演生命历史的一个重要工具.在构建进化树的所有算法中,基于进化距离的算法是其中研究的重点.但是,这一方法较为严重地依赖着距离矩阵的质量.人们开发了多种基于生物事实的进化模型来改进距离矩阵的构建过程,很大程度上提高了进化距离的准确性.同时,也提出了许多方法来检测距离矩阵的质量.文中提出了基于模型的距离以及p距离,采用一种组合的新距离的方式来构建距离矩阵.同时采用直接检测距离矩阵的统计学计分方法以及构建进化树,对比实验结果表明文中的方法实用且有效.【期刊名称】《智能计算机与应用》【年(卷),期】2012(002)004【总页数】6页(P35-39,43)【关键词】距离矩阵;核苷酸替换模型;组合距离;进化距离【作者】邢林林;郭茂祖;王娟【作者单位】哈尔滨工业大学计算机科学与技术学院,哈尔滨150001;哈尔滨工业大学计算机科学与技术学院,哈尔滨150001;哈尔滨工业大学计算机科学与技术学院,哈尔滨150001【正文语种】中文【中图分类】TP3910 引言在系统发育分析中,推演一棵系统发生树是一个很重要的内容[1]。
在这一领域,基于距离的方法拥有大量忠实的拥趸,因其表现了较快的速度和不俗的准确性。
同时该方法的准确度亦在不断地改进中。
在众多基于距离的方法中,邻接法[2,3]是构建进化树的一个很好的选择。
只是作为一种基于距离的方法,邻接法的算法性能同样依赖于进化距离以及距离矩阵的质量。
通常,从两个方面来改进邻接法的性能,一种是采用更准确,真实的进化距离[4]。
另一种是修改算法,更快速、高效地推演一棵进化树[5]。
最初,人们使用位点差异比例来表示序列的进化距离,这个距离被称为p距离或者海明距离。
p距离只能反映原始序列的直接差异,不能正确反映进化时间内核苷酸替换数目的准确值,然而在过去的几十年中,又相继提出了多种核苷酸代替模型[6,7],用于距离矩阵的构建,这些核苷酸替换模型用来生成替换p距离的距离矩阵。

实习四:多序列⽐对(Multiplealignment)实习四:多序列⽐对(Multiple alignment)学号姓名专业年级实验时间提交报告时间实验⽬的:1. 学会利⽤MegAlign进⾏多条序列⽐对2. 学会使⽤ClustalX、MUSCLE 和T-COFFEE进⾏多条序列⽐对分析3. 学会使⽤HMMER进⾏HMM模型构建,数据库搜索和序列⽐对实验内容:多序列⽐对是将多条序列同时⽐对,使尽可能多的相同(或相似)字符出现在同⼀列中。
多序列⽐对的⽬标是发现多条序列的共性。
如果说序列两两⽐对主要⽤于建⽴两条序列的同源关系,从⽽推测它们的结构和功能,那么,同时⽐对多条序列对于研究分⼦结构、功能及进化关系更为有⽤。
例如,某些在⽣物学上有重要意义的相似区域只能通过将多个序列同时⽐对才能识别。
只有在多序列⽐之后,才能发现与结构域或功能相关的保守序列⽚段,⽽两两序列⽐对是⽆法满⾜这样的要求的。
多序列⽐对对于系统发育分析、蛋⽩质家族成员鉴定、蛋⽩质结构预测、保守模块的搜寻以及PCR引物设计等具有⾮常重要的作⽤。
作业:1.Align the orthologous nucleotide and protein sequences from 5 organisms you found from first practice with MegAlign. Describe the sequences you used (the title of each sequence), explain whether the phylogenetic tree is consistent with the species tree from NCBI taxonomy database. Set the alignment report to show consensus strength and decorate the residues different from consensus with green shade.(Hint: use the taxonomy common tree from NCBI to get the evolutionary relationship among the organisms. Save your organism name in a text file with each organism name in a line, and upload the file, choose Add from file, and you will see the relationship among the specified organisms) /doc/ea500ac1c1c708a1284a4449.html /Taxonomy/CommonTree/wwwcmt.cgi Hint 2:Change the accession number in your fasta or genPept format sequence file to organism name, so that the phylogenetic tree can be easily understood.⽅法与结果:打开Megalign,选择FILE下的Enter sequence ,打开之前保存的来⾃于五个物种的蛋⽩(或核酸)序列;⾸先选择打分矩阵,点击“Align”,选择Set residue Weight Table 选择矩阵:PAM100(核酸则设为weighted),通过“method parameters”查看参数,使⽤Clustal V的默认值;其次进⾏序列的⽐对,选择Align下的“by Clustal V Method”开始⽐对,再次待其结束后,进⾏⽐对结果的显⽰,选择view下的“Phylogenetic Tree”,显⽰出树形图;(图)与NCBI上找到的树形图进⾏对⽐(图);接下来点击View 下的“Alignment reports ”,选择OPTIONS下的“Alignment report contents”勾中“show consensus strength”,即在序列中显⽰出相似性条块;在OPTIONS下选择“New decorations”对decoration parameters 下选“shade—residues differing from—the consensus”把字符选择现实的颜⾊为绿⾊,结果显⽰如下:(图)同法可以得到核酸的树形图:(图)分析:系统发育树与NCBI上的物种树有很⼤的差异,因为可能这些物种间含有很多同源序列,我们不能单凭⼏条相似序列的同源关系来判断物种的亲缘关系,⽽应该考虑到物种更多相似序列的同源关系。


Alignment空间的几点注记卢国祥【摘要】Alignment空间是一种由度量空间产生的度量空间,其中的度量函数称为Alignment距离.本文首先利用扩张结构的方法直接证明了Alignment距离是度量空间中的度量函数.接下来讨论了Alignment空间中逆序列和子序列的Alignment 距离之间的关系,给出了关于Alignment距离的一系列不等式.%Alignment space is a metric space generated from a given metric space. The distance function in it is called Alignment distance. Using the extension structure method, it is first theoretically proved that Alignment distance is a distance function in the Alignment space. Next, the relationship between the different Alignment distances of inverse sequences and subsequences in the Alignment space is discussed. A series of inequalities for these distances are further proposed.【期刊名称】《工程数学学报》【年(卷),期】2012(029)001【总页数】8页(P47-54)【关键词】Alignment空间;Alignment距离;扩张结构;逆序列;子序列【作者】卢国祥【作者单位】中南财经政法大学统计与数学学院,武汉430073【正文语种】中文【中图分类】O17;O2361 引言在信息科学、生命科学中经常会遇到离散或连续数据的比较,如接收信号和发送信号的对比[1]、对模拟或数字信号的广义差错纠错[2,3]、不同图象间的比对[4]、生物序列(DNA、RNA和蛋白质等)的比对[5,6]等等.在通信以及计算机领域,产生广义差错的信道模型与纠错码理论得到了大量研究[7-9],文献[10]给出了一个综述介绍,并把具有广义差错的网络搜索问题列为重要的应用问题.以上讨论涉及的基本问题主要是序列间的关系,关键在于确定不同集合之间的度量以及讨论度量的合理性.从这些应用问题出发,沈世镒在文献[11,12]中初步讨论了它们当中度量的数学模型,提出离散数据集产生的Alignment空间的概念.随后文献[13]讨论了在一般的度量空间中广义差错的度量问题,对文献[11,12]作出推广,并证明一般的度量空间可以产生新的度量空间,称为由一般度量空间产生的Alignment空间,也简记为Alignment空间.因为Alignment空间不具有Hamming空间[14]中分量距离的叠加性,是一种非线性度量空间,所以其结构十分复杂,有关的数学讨论较Euclid空间、Hamming空间等困难.而Euclid空间、Hamming空间中的许多问题都可以在Alignment空间中讨论,许多有关广义差错信息处理的难点都与Alignment空间的结构有关,因此对其中任何理论的研究进展都会很有意义.本文在文献[13]的基础上对Alignment空间进行进一步讨论.在第2节利用扩张结构的方法对Alignment距离是度量空间中的度量函数给出了另外一种直观的证明,这是文献[13]结果的重要补充.在第3节给出了Alignment空间中的一些特殊序列Alignment距离大小关系的几个上界,并且说明了由不同度量空间产生的Alignment空间的一点区别.2 Alignment空间的相关定义为了下面的讨论,首先回顾一下Alignment空间的相关定义.设(V,d)是一个度量空间,相应的度量函数为d(a,b),其中a,b∈V.记分别是在V上取值的有限长序列,na,nb,nc分别是这些序列的长度,它们不一定相等,序列的下标简称为位点.记V+=V∪{−},其中“−”是一虚拟符号,它不在集合V中.如果(V+,d)是一个度量空间,V是它的子空间,那么称V+是V的扩张度量空间,相应的度量函数还是记为d(a,b),此时对a或b取值为“−”时要单独定义d(a,b)的值.记分别是在V+上取值的有限长序列.定义2.1 1) 称A′是A的扩张序列,如果序列A中插入一些虚拟符号后就变为序列A′;2) 称(A′,B′)是(A,B)的比对序列,如果A′,B′序列分别是A,B的扩张序列,在同一位点上不同时取“−”,而且它们的长度相同,记为n′.这时定义3)称是(A,B)的最优比对序列,如果是(A,B)的比对序列,而且对(A,B)的其他比对序列(A′,B′)总有d(A′0,B′0)≤d(A′,B′)成立;4) 记是空间V上的全体有限长序列,其中V(n)={(x1,x2,···,xn):xi∈V,1≤ i≤ n}.如果A,B∈V∗,而且它们的最优比对序列为(A′0,B′0),那么定义dA(A,B)=d(A′0,B′0).定义2.2 记是空间V+上的全体有限长序列,其中:xi∈V+,1≤ i≤ n}.如果是由序列A′插入一些虚拟符号“−”得到的序列,那么插入A′中的虚拟符号可用以下集合表示其中:1)为序列A′的长度,而ka表示从A′到A′′发生插入的次数,把插入的连续不间断的“−−···−”看作一次插入;2) 在H中,ik表示在紧挨A′的位点ik后有虚拟符号,ℓk表示紧挨位点ik后插入一个长度为ℓk且取值为虚拟符号“−”的向量;3) 在K中,γi表示在紧挨A′的位点i后插入虚拟符号“−”的数目.由上可知,.但当ik=0或γ0̸=0时也是有意义的,这表示在序列A′的第1个位点前有虚拟符号,于是实际上应有称H与K为序列A′′关于A′的扩张结构,而称I={ik,k=1,2,···,ka}为扩张位点的集合.易见H与K相互确定,由H确定K的表达式为反之,由K确定H的方式为:取I={i:γi>0},并将其中元素按从小到大的次序排列,而ℓk= γik,ik ∈ I.如果记序列A′的所有扩张结构为HA′,那么当K,K′∈HA′时,可以定义它们的交、并、差运算其中容易验证,扩张结构集合HA′对以上的交、并、差运算满足结合率与分配率,因此HA′构成一布尔代数.扩张结构集合HA′的意义可以扩充为所有与序列A′长度相等的序列的扩张结构集合,此时A′为其中的一个代表元.以下定理保证了dA是度量空间中的度量函数.定理2.1 (V∗,dA)构成一度量空间,称为Alignment空间,dA称为Alignment 距离.也就是说dA满足度量函数的非负性、对称性与三角不等式三个条件.证明 dA(A,B)的非负性与对称性是显然的,下面证明三角不等式成立.记A,B,C是V∗中的任意三序列,它们的两两最优比对序列分别记为:(A′,B′),(A∗,C∗),(Bo,Co).于是可以知道,序列A′,A∗是序列A的扩张序列,序列B′,Bo是序列B的扩张序列,序列C∗,Co是序列C的扩张序列,利用(1)式记相应的扩张结构分别为H′A,H∗A,H′B,HoB,H∗C,HoC.依据扩张结构运算,可以构造新的扩张结构:H′′A=H′A∨H∗A,并由扩张结构H′′A生成A的扩张序列A′′.同样A′′也是序列A′,A∗的扩张序列,此时得到两组扩张关系因|B′|=|A′|,|C∗|=|A∗|,故可由扩张结构HA′将序列B′变为扩张序列B′′,由扩张结构HA∗将序列C∗变为扩张序列C′′.扩张关系为易见|A′′|=|B′′|=|C′′|≡ n,d(−,−)=0,于是(Bo,Co)是(B,C)的最优比对序列,而(B′′,C′′)是(B,C)的比对序列,故再由扩张关系(2)和(3),便有d(A′,B′)=d(A′′,B′′),d(A∗,C∗)=d(A′′,C′′),所以d(A′,B′)+d(A∗,C∗)≥d(Bo,Co).最后利用Alignment距离的定义和(4)式,就可以得到结论dA(A,B)+dA(A,C)≥dA(B,C).至此,定理得证.在文献[13]中,通过dA与一种Levenshtein距离等价的结论证明了定理2.1,而本文现在通过序列扩张的方法直接证明了这个定理.3 序列的Alignment距离之间的关系定义3.1 设W=(w1,w2,···,wnw)是有限长序列,对序列W的一个逆序操作是将W变成序列,序列称作W的逆序列.定理3.1 记序列A的逆序列是A,序列B逆序列是,那么证明如果序列(A,B)的最优比对序列为(A′,B′),那么就是的比对序列,这样由Alignment距离的定义便有反之,如果的最优比对序列为就是(A,B)的比对序列,这样由Alignment距离的定义便有定义3.2 设X=(x1,x2,···,xnx),Y=(y1,y2,···,yny)是有限长序列,nx≥ ny.如果有一组1≤i1<i2<···<iny≤nx,使得xij=yj,j=1,2,···,ny成立,那么称序列Y是X的子序列.记A,B∈V∗,序列A,B分别删掉最后一位后所得序列为A−,B−,即如果那么A− =(a1,···,ana−1),B− =(b1,···,bnb−1).由定义3.2知序列A−,B−分别是A,B的子序列,并且以下定理成立.定理3.2 dA(A−,B−)≤ dA(A,B)+d(ana,bnb).证明由文献[13]中的Alignment距离与Levenshtein距离的等价性可知dA(A,B)=min{dA(A−,B−)+d(ana,bnb),dA(A−,B)+d(ana,−),dA(A,B−)+d(−,bnb )}.下面分3种情况讨论:1) 如果dA(A,B)=dA(A−,B−)+d(ana,bnb),显然就有dA(A−,B−)≤dA(A,B).2) 如果dA(A,B)=dA(A−,B)+d(ana,−),设序列(A−,B)的最优比对序列为(A⋄,B⋄),由对称性可不妨设bnb的位点不大于ana−1的位点,则比对序列(A⋄,B⋄)必满足A⋄中与bnb对齐的位点取值不能为“−”.若不然,将(A⋄,B⋄)从该位点开始截到末尾得到的序列对记为其中k≤na−1.再记,由Alignment距离的定义便有现在定义其中k≤na−1.那么序列,也是(A−,B)的比对序列,并且满足又(V+,d)是一个度量空间,ak ̸= −,bnb ̸= −,于是d(ak,bnb)<d(−,bnb)+d(ak,−).从而d(A⋄⋄,B⋄⋄)<dA(A−,B),这与Alignment距离的定义矛盾.现在可以知道最优比对序列(A⋄,B⋄)的形式应为记B⋄中的bnb换为“−”后B⋄变为B⋆,那么序列(A⋄,B⋆)为(A−,B−)的比对序列,并且注意到(V+,d)是一个度量空间,便有由Alignment距离的定义有dA(A−,B−)≤ d(A⋄,B⋆),从而3) 如果dA(A−,B−)=dA(A,B−)+d(−,bnb),注意到序列A,B地位的对称性,由类似情况2的讨论同样可以得到dA(A−,B−)≤dA(A,B)+d(ana,bnb).由定理3.2可以发现子序列的Alignment距离有可能比原来序列的Alignment距离大,以下是一个例子.例设V={0,1,2},其中的度量函数定义为d(a,b)=|a−b|,a,b∈V,那么(V,d)是一个度量空间.V的扩张度量空间V+中的度量函数定义如下对于序列A=11120,B=1111,可以得到它们最优比对序列是Alignment距离.而对于序列A−=1112,A−=111,可以得到它们最优比对序列是Alignment距离可以看出上面的例子恰好满足dA(A−,B−)=dA(A,B)+d(ana,bnb),所以这个上界是能够达到的.记A,B∈V∗,序列A,B分别删掉第一位后所得序列为−A,−B,即如果A=(a1,a2,···,ana),B=(b1,b2,···,bnb),那么−A=(a2,···,ana), −B=(b2,···,bnb).由定义3.2知序列−A,−B分别是A,B的子序列,并且以下定理成立.定理3.3 dA(−A,−B)≤ dA(A,B)+d(a1,b1).证明由定理3.1和定理3.2易得.推论3.1 A,B的任意连续子序列满足证明由定理3.2和定理3.3,可以得到对于特殊的度量空间(V,d),以上定理和推论的上界还可以减小.如果定义V=Fq是一个有限域其中u,v∈Fq,那么(Fq,dH)是一个度量空间.记表示Fq上的n维向量空间则就是在信息论与编码理论中经常遇到的Hamming度量空间[14].现在对(Fq,dH)的扩张度量空间(Fq+1,dH)定义如下:其中u,v∈Fq+1.容易验证(Fq+1,dH)也是一个度量空间,通过第2节中的构造方法可以定义任意两条Fq上的有限长序列的Alignment距离dA,得到是一个度量空间.此时以下定理成立.定理3.4在Alignment空间中,有证明证明方法与定理3.2的类似.先证dA(A−,B−)≤dA(A,B).注意到此时那么对于定理3.2的证明方法中的3种情况,第1种的讨论没有变化,dA(A−,B−)≤dA(A,B)成立.而第2种和第3种的讨论稍有不同.在第2种情况中,因为dA(A,B)=dA(A−,B)+1,同样可以得到序列(A−,B)的最优比对序列(A⋄,B⋄)的形式应为记B⋄中的bnb换为“−”后B⋄变为B⋆,那么序列(A⋄,B⋆)为(A−,B−)的比对序列,并且此时有由Alignment距离的定义便有dA(A−,B−)≤dA(A,B).再利用序列A,B地位的对称性可以得到在第3种情况中仍然有dA(A−,B−)≤d A(A,B),所以定理的前一个公式成立.由定理3.1,可得dA(−A,−B)≤ dA(A,B)成立.4 结束语本文只是讨论了Alignment空间中序列关系最简单的情况,可见对其处理是非常复杂的.弄清这些序列Alignment距离的大小关系可以深化我们对该空间的认识.由于Alignment空间在多个学科中,如计算机、网络、编码、密码与生物信息[15]等领域有着广泛而重要应用,而其中很多问题都是与它的数学结构有关,因此希望更多的数学家能够关注这个空间的理论,深入讨论其中的数学问题.致谢:作者感谢南开大学数学科学学院的导师沈世镒教授对此类问题的介绍及对本文的精心指导,感谢中南财经政法大学引进人才科研启动金项目(31140911216)的资助,并对审稿人表示衷心感谢!参考文献:[1]Diggavi S N,Grossglauser M.On transmission over deletionchannels[C]//Allerton Conference,Monticello,Illinois,October 2001[2]Bours A H.Construction of f i xed-length insertion/deletion correcting runlength-limited codes[J].IEEE Transactions on InformationTheory,1994,40(6):1841-1856[3]Helberg A S J,Ferreira H C.On multiple insertion/deletion codes[J].IEEE Transactions on Information Theory,2002,48(1):305-308[4]吴忠华,沈世镒.基于动态规划算法的人脸比对[J].计算机工程与应用,2006,42(33):53-55 Wu Z H,Shen S Y.Dynamic programming on face alignment[J].Computer Engineering and Applications,2006,42(33):53-55 [5]Smith T F,Waterman M S,Fitch W parative biosequence metrics[J].Journal of Molecular Biology,1981,18(1):38-46[6]Mount D W.Bioinformatics:sequence and Genome Analysis[M].New York:Cold Spring Harbor Laboratory Press,2001[7]Levenshtein V I.Binary coded capable of correcting deletions,insertions and reversals[J].Soviet Physics-Doklady,1966,10(8):707-710[8]Klein A.On perfect deletion-correcting codes[J].Journal of Combinatorial Designs,2004,12(1):72-77[9]Wang J.Some combinatorial constructions for optimal perfect deletion-correcting codes[J].Designs,Codes and Cryptography,2008,48(3):331-337 [10]Navarro G.A guided tour to approximate string matching[J].ACM Compuing Surveys,2001,33(1):31-88[11]Shen S Y,Wang K,Hu G,et al.On the alignment space[C]//Proceedings of the 2005 27th Annual International Conference of the Engineering in Medicine and Biology Society,IEEE-EMBS 2005,2005:244-247[12]沈世镒.多重序列比对Alignment的信息度量准则[J].工程数学学报,2002,19(4):1-10 Shen S rmation measure criteria of multiple sequences Alignment[J].Chinese Journal of Engineering Mathematics,2002,19(4):1-10[13]卢国祥,沈世镒.由一般拓扑度量空间所产生的Alignment空间[J].工程数学学报,2008,25(6):1097-1101 Lu G X,Shen S Y.The Alignment space generated by general metric spaces[J].Chinese Journal of Engineering Mathematics,2008,25(6):1097-1101[14]Hamming R W.Error detecting and error correcting codes[J].Bell System Technical Journal,1950,29(2):147-160[15]卢国祥.利用Alignment空间理论分析蛋白质的结构[J].计算机工程与应用,2011,47(23):54-56 Lu G ing Alignment space theory for protein structure analysis[J].Computer Engineering andApplications,2011,47(23):54-56。
r语言多序列比对后计算距离
在R语言中进行多序列比对后计算距离涉及到多个步骤和方法。
首先,进行多序列比对通常会使用一些包如Biostrings、msa、DECIPHER等。
这些包提供了多种函数和方法来进行多序列比对。
比
对完成后,可以使用不同的方法来计算序列之间的距离。
一种常见的方法是使用序列的相异性来计算距离。
这可以通过
计算序列之间的差异或者相似性来实现。
常见的方法包括计算序列
的编辑距离(如Hamming距离、Levenshtein距离等)或者计算序
列的相似性得分(如百分比相似性、相关系数等)。
这些方法可以
通过R语言中的一些包如ape、phangorn等来实现。
另一种常见的方法是基于多序列比对结果构建进化树,然后根
据进化树的拓扑结构和分支长度来计算序列之间的距离。
这可以通
过使用R语言中的包如ape、phangorn等来实现。
这些包提供了用
于构建和操作进化树的函数和方法,可以帮助计算序列之间的距离。
除了上述方法,还可以使用一些其他的方法来计算序列之间的
距离,比如基于序列特征的距离计算方法,或者基于序列间的相互
作用关系来计算距离等。
在R语言中,也有一些包可以提供这些方
法的实现。
总之,R语言提供了丰富的工具和包来进行多序列比对后的距离计算,研究人员可以根据自己的需求和数据特点选择合适的方法和工具来进行分析。
希望以上信息能够对你有所帮助。