Long Phase Coherence Time and Number Squeezing of two Bose-Einstein Condensates on an Atom

《JournalofLightwaveTechnology》期刊第2页50条数据《Journal of Lightwave Technology》期刊第2页50条数据https:///doc/8514081923.html,academic-journal-foreign_journal-lightwave-technology_info_11_1/1.《Dynamic Provisioning of Self-Organized Consumer Grid Services Over Integrated OBS/WSON Networks》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020417921.html2.《Experimental Demonstration of Highly Resilient Wavelength-Switched Optical Networks With a Multivendor Interoperable GMPLS Control Plane》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020417922.html3.《Overlapped-Subcarrier Multiplexing for WDM Passive Optical Networks: Experimental Verification and Mathematical Analysis》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020417923.html4.《A Highly Efficient Computational Model for FDTD Simulations of Ultrafast Electromagnetic Interactions With Semiconductor Media With CarrierHeating/Cooling Dynamics》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020417924.html5.《Demonstration of Wireless Backhauling Over Long-Reach PONs》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020417925.html6.《All Single-Mode Fiber Mach–Zehnder Interferometer Based on Two Peanut-Shape Structures》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020417926.html7.《Cross-Diabolo Nanoantenna for Localizing and Enhancing Magnetic Field With Arbitrary Polarization》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418029.html8.《A 25 Gbit/s Transmitter Optical Sub-Assembly Package Employing Cost-Effective TO-CAN Materials and Processes》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418030.html9.《Reconfigurable All-Optical OTDM-to-WDM ConversionUsing a Multiwavelength Ultrashort Pulse Source Based on Raman Compression》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418031.html10.《A General Characterizing Method for Ring Resonators Based on Low Coherence Measurement》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418032.html11.《Network-Coding-Based Energy Management for Next-Generation Passive Optical Networks》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418033.html12.《Green Packet Optical Transport Networks (P-OTNs) Based on Photonic PBB-TE Switches and Minimized EEE Overhead》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418034.html13.《PMD Vector Estimation Through Time-Resolved Waveform Analysis Basedon Ultrafast xy-Field Sampling》原文链接:https:///doc/8514081923.html,/academic-technology_thesis/020418035.html14.《End-to-End Multicore Multimode Fiber Optic Link Operating up to 120 Gb/s》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418036.html15.《Modal Birefringence Analysis of Strained Buried-Core Waveguides》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418037.html16.《Investigation on the Phase Noise and EVM of Digitally Modulated Millimeter Wave Signal in WDM Optical Heterodyning System》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418038.html17.《Mode Classification and Calculation in All-Solid Photonic Bandgap Fibers》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418039.html18.《Synergetic Effects of Humidity and Temperature on PMMA Based Fiber Bragg Gratings》原文链接:https:///doc/8514081923.html,/academic-technology_thesis/020418040.html19.《Broadband Chromium-Doped Fiber Amplifiers for Next-Generation Optical Communication Systems》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418041.html20.《Resonant Fiber Optic Gyroscope Using an Air-Core Fiber》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418091.html21.《Auto Bias Control Technique Based on Asymmetric Bias Dithering for Optical QPSK Modulation》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418092.html22.《Broadband Mach–Zehnder Switch for Photonic Networks on Chip》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418093.html23.《Ferroelectric Liquid Crystal Mixture Integrated Into Optical Waveguides》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418094.html24.《Fabrication of High Glass Transition Temperature Graded-Index Plastic Optical Fiber: Part 2—Fiber Fabrication and Characterizations》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418095.html25.《Demonstration of a Remotely Dual-Pumped Long-Reach PON for Flexible Deployment》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418096.html26.《Performance Analysis for Optical OFDM Transmission in Short-Range IM/DD Systems》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418097.html27.《Simultaneous Measurement of Strain and Temperature by Using a Micro-T apered Fiber Grating》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418145.html28.《Extending the Sensing Range of Brillouin Optical Time-Domain Analysis Combining Frequency-Division Multiplexing and In-Line EDFAs》原文链journal-foreign_journal-lightwave-technology_thesis/020418146.html29.《Experimental Research of an All-Polarization-Maintaining Optical Fiber Vector Hydrophone》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418147.html30.《Photonic Crystal Fiber Interferometer for Dew Detection》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418148.html31.《Impact of Loss Variations on Double-Ended Distributed Temperature Sensors Based on Raman Anti-Stokes Signal Only》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418149.html32.《Brillouin Spectrum in LEAF and Simultaneous Temperature and Strain Measurement》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418150.html33.《Reduction in the Number of Averages Required in BOTDA Sensors Using Wavelet Denoising Techniques》原文链journal-foreign_journal-lightwave-technology_thesis/020418151.html34.《Raman-Assisted Brillouin Distributed Temperature Sensor Over 100 km Featuring 2 m Resolution and 1.2 C Uncertainty》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418152.html35.《Lab-on-a-Fiber Device for Trace Vapor TNT Explosive Detection: Comprehensive Performance Evaluation》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418153.html36.《Hybrid TDM/WDM-Based Fiber-Optic Sensor Network for Perimeter Intrusion Detection》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418154.html37.《The Use of a Fiber Comb Filter Fabricated by a CO Laser Irradiation to Improve the Resolution of a Ratiometric Wavelength Measurement System》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418155.html38.《Index Guiding Photonic Liquid Crystal Fibers forPractical Applications》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418156.html39.《Etched-Core Fiber Bragg Grating Sensors Integrated With Microfluidic Channels》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418157.html40.《Superstructure Fiber Gratings Via Single Step Femtosecond Laser Inscription》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418158.html41.《Inspection T echnique for Cleaved Optical Fiber Ends Based on Fabry–Perot Interferometer》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418159.html42.《Temperature Fiber Laser Sensor Based on a Hybrid Cavity and a Random Mirror》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418160.html43.《High-Sensitivity Coherent Optical Time DomainReflectometry Employing Frequency-Division Multiplexing》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418161.html44.《Refractive-Index Sensing With Inline Core-Cladding Intermodal Interferometer Based on Silicon Nitride Nano-Coated Photonic Crystal Fiber》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418162.html45.《Miniaturized Long-Period Fiber Grating Assisted Surface Plasmon Resonance Sensor》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418163.html46.《Polarization-Dependent In-Line Mach–Zehnder Interferometer for Discrimination of Temperature and Ambient Index Sensitivities》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418164.html47.《Long-Range Coherent OFDR With Light Source Phase Noise Compensation》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418165.html48.《Polarization Mode Coupling Involved in a Capillary Optical Fiber Sensor: Modeling and Experimental Validation》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418166.html49.《Metrological Evaluation of Optical Fiber Grating-Based Sensors: An Approach Towards the Standardization》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418167.html50.《Optical Intensity-Type Refractometer for Remote Measurements Via Fiber-Optic Cables》原文链接:https:///doc/8514081923.html,/academic-journal-foreign_journal-lightwave-technology_thesis/020418168.html。

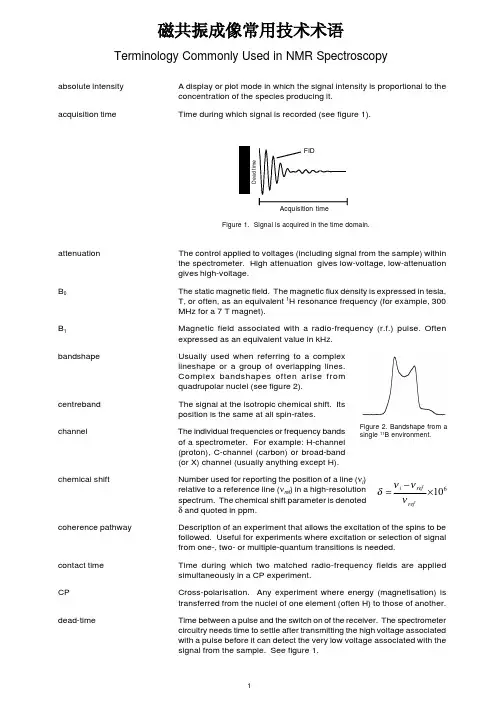
absolute intensityA display or plot mode in which the signal intensity is proportional to theacquisition timeattenuationThe control applied to voltages (including signal from the sample) within the spectrometer. High attenuation gives low-voltage, low-attenuation gives high-voltage.B 0The static magnetic field. The magnetic flux density is expressed in tesla,T, or often, as an equivalent 1H resonance frequency (for example, 300MHz for a 7 T magnet).B 1Magnetic field associated with a radio-frequency (r.f.) pulse. Often expressed as an equivalent value in kHz.bandshapeUsually used when referring to a complex lineshape or a group of overlapping plex bandshapes often arise from quadrupolar nuclei (see figure 2).centrebandThe signal at the isotropic chemical shift. Its position is the same at all spin-rates.channelThe individual frequencies or frequency bands of a spectrometer. For example: H-channel (proton), C-channel (carbon) or broad-band (or X) channel (usually anything except H).chemical shiftNumber used for reporting the position of a line (νi )relative to a reference line (νref ) in a high-resolution spectrum. The chemical shift parameter is denoted δ and quoted in ppm.coherence pathwayDescription of an experiment that allows the excitation of the spins to be followed. Useful for experiments where excitation or selection of signal from one-, two- or multiple-quantum transitions is needed.contact timeTime during which two matched radio-frequency fields are applied simultaneously in a CP experiment.CPCross-polarisation. Any experiment where energy (magnetisation) is transferred from the nuclei of one element (often H) to those of another.dead-time Time between a pulse and the switch on of the receiver. The spectrometercircuitry needs time to settle after transmitting the high voltage associatedwith a pulse before it can detect the very low voltage associated with thesignal from the sample. See figure 1.610×−=ref ref i νννδTerminology Commonly Used in NMR SpectroscopyFigure 2. Bandshape from a single 11B environment.磁共振成像常用技术术语d.c. offset Constant-value offset occurring in the FID (see “Problems”). Results ina central (zero-frequency) “spike” artefact in the spectrum whentransformed.deconvolution Mathematical process used to determine the intensities of overlappinglines.digital resolution This depends on the Fourier number. The bigger the Fourier number thegreater the number of data points per Hz of the spectrum and the higherthe digital resolution. See “Processing”.DP Direct-polarisation. An experiment in which the nuclei to be observedare excited directly.duty cycle A value used to assess whether anexperiment might damage thespectrometer (or the sample). Theduty cycle should never exceed 20 %(see “How to Choose a RecycleDelay”)dwell Spacing between data points in the time-domain. Can depend on theway acquisition is implemented but, commonly, dwell = 1/spectral width. endcap Open rotors have to be closed with endcaps before they can be spun. FID Free Induction Decay (see figure 1).field Magnetic field, with flux density quoted in T (Tesla) for the static magneticfield (B). For the magnetic field associated with an r.f. pulse the fluxdensity is given in mT or, more usually, expressed as a kHz equivalent(see “Matching”).flip-back Experimental procedure for shortening recycle times (see “How to Choosea Recycle”).Fourier number The number of points used in the FT. Always a power of 2.frequency domain Where information is displayed as a function of frequency - the spectrum FT Fourier Transform. Mathematical process to convert time-domain tofrequency-domain. Designed to work with 2n (n = integer) data points. gain Amplification applied to the received signal.Gauss Non-SI unit of magnetic field flux density. The SI equivalent is Tesla (T),1 T = 10,000 Gintensity On its own - the height of a line. Integrated-intensity is the area under theline.linebroadening Spectra can be artificially linebroadened to improve their appearance.This involves multiplying the FID with a decaying function prior to the FT.See “Processing”.lineshape The shape of individual lines in a spectrum. Commonly, Gaussian orLorentzian (figure 3) or a mixture of the two, are encounteredexperimentally.linewidth This is usually the full width at half-height (δν½)r.f. on-timer.f. on-time + r.f. off-timeduty cycle =magic-angle54.7° or 54° 44´magnetisation when described classically (non-quantum mechanically) an ensemble ofspins at equilibrium in an external magnetic field has a net magnetisationprecessing about an axis aligned along that field.magnetogyric ratio Symbol γ . A fundamental physical constant of elements with non-zerospin. For example γH is 2.675x108 rads -1T -1.matchShort for Hartmann-Hahn match (see “Matching”)noisenormalised intensity Signal intensity can be multiplied by an arbitrary factor to give a particularheight to the highest (often) line or the integrated intensity. Opposite ofabsolute intensity.nuclear spin quantum number Symbol I . A fundamental property of a nucleus. Only nuclei with I > 0are said to be NMR “active”.phase (1)The phase of a pulse relates to its position in the xy plane of the rotating frame.phase (2)The phase of a spectral line comes from the way in which the real and imaginary components of a complex FT are combined (see “Processing”).phase cycling The way in which the phase of a pulse (or the receiver) is changed duringsuccessive repetitions of a pulse sequence. Used to suppress artefactsand select specific coherence pathways.ppm Parts per million. Usual way of reporting a chemical shift. A frequencydifference ∆ Hz 610×∆≈n observatio ν ppm precession“Movement of the axis of a spinning body around another axis” (as a gyroscope)probeThe business end of the spectrometer, where the sample goes.pulse angle When described in the rotating frame a pulse rotates the magnetisationthrough an angle θ. A pulse that rotates the magnetisation though 90° iscalled a 90° pulse.pulse duration Time for which a pulse occurs.quadrupole Any nucleus with I > ½.recycle (time)Or pulse delay or relaxation delay. Time between the end of dataacquisition and the start of excitation in successive repetitions of a pulsesequence. (See “How to Choose a Recycle”).referenceThe material giving the signal which defines the zero position in a high-heightresolution spectrum.repetitionsThe number of times a pulse sequence is repeated in an experiment.resolutionThe ability to separate closely spaced lines (see figure 4). As a rule of thumb,a pair of lines will be resolved if their linewidth is less than their separation.resolution enhancementThe opposite of linebroadening. An FID multiplied by an appropriate combination of increasing and decaying functions can yield extra resolution in a spectrum. See “Processing”.rotary echoA feature of an FID that occurs at intervals of 1/spin-rate (see “How to Set the Magic-angle”). They give rise to spinning sidebands in the spectrum.rotating frameA mathematical tool to make the effect of a pulse easy to visualise.Magnetisation precessing at ν Hz in a laboratory-based xyz axis system appears static in an axis system (frame) rotating at ν Hz.rotorThe container that holds the sample. Often referred to in terms of its outside diameter (for example, 5 mm).saturationCondition that arises when there is no population difference between excited and ground states. No signal is observable under such conditions.sidebandsOr spinning sidebands. Under some circumstances sidebands appear in a spectrum. They can occur on both sides of a centreband and separated from it by a frequency equal to the spin-rate. A spectrum may contain a manifold of sidebands and the centreband is not necessarily more intense than all of the sidebands.signalThe FID or one or more of the lines in a spectrum.signal-to-noise ratio (S/N)Ratio of the height of a line or signal (usually the largest) to the noise.Definitions of the measurement of noise vary. Signal increases as n (the number of repetitions) but noise only increases by √n so S/N increases by √n.spectral widthDifference in frequency of the two ends of the full spectrum. Not to be confused with the now largely obsolete term sweep width.spinA property of a nucleus with non-zero nuclear spin-quantum number (I ),as in spin-½. Or, simply, a nucleus with a magnetic moment.spin-lockIf, after a 90°x pulse a second, long-duration (spin-lock) r.f. field is applied along the y-axis the magnetisation is said to be spin-locked.spin-rateThe rate at which the sample is spun.spin-temperature inversionA manipulation carried out within the phase cycling of a CP experiment to remove magnetisation originating directly from the X-channel contact pulse.standard Any sample used to set-up the spectrometer and/or to define the zeroposition in the spectrum.Figure 4. Two lines of constant spacing but different linewidth.T 1Spin-lattice relaxation time-constant. Relates to the time taken for excited spins, in the presence of B 0, to loose energy to their surroundings and return to their equilibrium state.T 1ρSpin-lattice relaxation time-constant in the rotating frame. As for T 1 but this time in the presence of an applied radio-frequency field B 1.T 2Spin-spin relaxation time-constant. Relates to the time for a conserved exchange of energy between spins.T 2*A time-constant sometimes used to describe the decay of the observed time-domain signal (T 2* ≤ T 2). The shorter T 2* the broader the associated signal(s) in the spectrum.time-domainWhere information is recorded or displayed as a function of time (see figure 1).transmitter offsetThis allows fine control of the position of a transmitter (carrier frequency).With an appropriate offset, signals can be put exactly on-resonance or a specific amount off-resonance. Can be applied to any spectrometer channel.truncationIf the acquisition time is shorter than the FID then truncation of the FID is said to have occurred (See “Problems”).zero filling If the number of data points is not a power of two then zeroes are addedto the acquired data so that the total number of points Fourier transformedis 2n . Zero filling adds no signal to the spectrum but it can improveresolution (see “Processing”).。

物理专业英语第6章翻译光波的干涉The light intensity distribution generated when several light waves (member waves) meet does not equal to the sum of the light intensity distribution caused by each member wave alone, and the phenomenon of alternating light and dark appears.For example, in Young's double-hole interference (see Young's interference experiment), the subwave out of each small hole H1 or H2 is a member wave. When the hole is small, the light intensity distribution I1 (x) caused by the member wave from the hole H1 alone is roughly uniform in a considerable range; so is the light intensity distribution I2 (x) caused by the member wave from the hole H2 alone.The sum of the two is still roughly evenly distributed.In the light intensity distribution I (x) caused by the two member waves together, the change of light and shade with position x is very significant, which is obviously not equal to.Each member wave alone causes a roughly uniform distribution of light intensity, which is equivalent to requiring that each member wave itself has no obvious diffraction, because the diffraction alsocauses alternating light and dark stripes (see diffraction of light).Therefore, when a number of member waves meet in a certain region of space and the interference occurs, it should mean that the diffraction of each member wave can not be considered in that region.Note that the aforementioned light intensity is not the instantaneous value of the light field intensity (proportional to the amplitude square), but the average or integral value of the light field intensity within a certain time interval t; t depends on the performance of the detection means or device.For example, during human eye observation, t is the visual retention time; while shooting on film, t is the exposure time. The interference phenomenon usually shows a fairly steady stripe distribution of the light field intensity in space; sometimes, when the certain parameter of the interference device changes with time, the light intensity received at a certain fixed point changes alternately. The discovery of the interference phenomenon of light has historically played an indelible role in the evolution from the particle of light to the fluctuation of light.In 1801, T. Young proposed the principle of interference and first made adouble-slit interference experiment, and also explained the color of the film formation.In 1811, the D.F.J. Arago first studied the interference phenomenon of polarized light.Modern times, light interference has been widely used in precision measurement, astronomical observation, photoelastic stress analysis, automatic control in optical precision machining and many other fields.Generate conditions Only the two columns of light waves of the same frequency, the phase difference is constant, the vibration direction of the same direction of the coherent light source, can produce light interference.The light emitted by two ordinary independent light sources can not have the same frequency, let alone have a fixed difference, so, the interference phenomenon cannot produce. Specific methods In order to stabilize the light intensity distribution of the synthetic wave field over a time interval t, the frequency of each ① member wave v (and hence the wavelength) is the same; the initial phase difference between the two member wa ves of ② remains constant within t.Conditional ② means that several usually independent light sources meet without interference, even if they emit light at the same frequency.Thereason is that usually the light emitted by the light source is a large number of waves distributed irregularly in the initial phase, and each wave lasts no more than 10 seconds, that is, every 10 seconds or so, the initial phase of the wave is a random change.Moreover, the initial phase of the wave column emitted by any two independent light sources is again statistically independent.You can imagine that when these independent light source wave meet, only in a very short time to produce a certain stripe pattern, and every 10 seconds or so, with another pattern, so far not any detection or recording device can keep up with such sharp changes, thus observed the average effect of the large number of patterns, namely uniform light intensity distribution rather than light and dark stripes.However, modern special lasers have produced tens of kilometers of waves, even lasting on the order of 10 seconds.Therefore, it can be said that if a detector with the time-resolution ability t is shorter than 10 seconds (which is possible), the interference of the light waves emitted by two independent lasers of the same frequency can also be observed.In addition, taking the two-wave interference as an example also requires that: the amplitude of the ③ two waves mustnot differ greatly; the polarization surface of the ④ two waves at the superposition point must be roughly consistent. When the condition ③ is not satisfied, although the interference stripes can still arise in principle, but the light and dark difference of the stripes is very little, and the interference phenomenon is not obvious.Conditiona l ④ is necessary because when the polarization surface of the two optical waves is perpendicular to each other, the light intensity of the synthetic field is the same value and does not show alternating light and shade (to observe the light alternation, you must use the polarization element). The above four points are commonly known as coherence conditions.Two or more light sources or light waves that satisfy these conditions are called coherent light sources or coherent light waves.若干个光波（成员波）相遇时产生的光强分布不等于由各个成员波单独造成的光强分布之和，而出现明暗相间的现象。

Chapter 5 Syntax 句法I. Multiple Choices:1.D. Immediate Constituent2. B. semantic3. A. concord4. A. the future is not expressed by morphological change5. D. substitutability6. C. co-occurrence7. B. Predicate 8.B. syntactic 9. C. self-control10. D. Government 11. D. coordinateII. Fill in the blanks with the most suitable words:1. Cohesion refers to ties and connections which exist within texts. They are also called formal links between sentences and between clauses.2. A sentence structure that is made up of layers of word groups is called a hierarchical structure.3. Sentences are traditionally assumed to be made up of words in _linear___ direction.4. Provide linguistic terms for the following descriptions.1) a type of relation holding with each other at aparticular place in a structure:2) an operation that moves a phrase category from its original position generated byPS rules to another within a structure: transformation3) the branch of linguistics which studies the rules governing the combination ofwords into sentences: syntaxIII. Decide whether the following statements are true or false. Write T for true and F for false in the bracket before each of them:T 1. It is characteristic of Halliday’s theory that more attention is paid to paradigmatic relations than to syntagmatic relations, which is the main concern of Chomsky.F2. Tense and aspect are two important categories of the verb, and they were separated in traditional grammar. (they were not separated in traditional grammar)F 3. Paradigmatic relation in syntax is alternatively called horizontal relation.(Paradigmatic relation is also called vertical relation; horizontal relation is a term for syntagmatic relation.)T 4. All human languages utilize a finite set of discrete units to form an infinite set of possible sentences.F 5. The English sentence "If only I could fly!" is in imperative mood. subjunctivemoodF 6. GOVERNMENT may be defined as the requirement that the form of two or morewords in a syntactic relationship should agree with each other. concordT 7. The SYNTAGMATIC RELATION is a relation between one item and others in a sequence, or between elements which are all present.T 8. The deep structure may be defined the abstract representation of the syntactic properties of a construction, i.e. the underlying level of structural relations between its different constituents, such as the relation between the underlying subject and its verbs, or a verb and its object.F 9. Categorization is the process of classifying our experiences into same categoriesbased on commonalities and differences. As a major ingredient in the creation of human knowledge, it allows us to relate present experiences to past ones.different categoriesF 10. The syntagmatic relation is also known as vertical relation. horizontal relationF 11. "Singing an English song" is an exocentric construction. endocentricconstructionT 12. Single words and clauses can both be constituents.IV. Define the following terms:1. IC analysisIC analysis. IC analysis (immediate constituent analysis) refers to the analysis of a sentence in terms of its immediate constituents ---- word groups ( or phrases), which are in turn analyzed into the immediate constituents of their own, and the process goes on until the ultimate constituents are reached. In practice, for the sake of convenience, we usually stop at the level of word.2. paradigmatic relationparadigmatic relation: Saussure originally called associative, is a relation holding between elements replaceable with each other at a particular place in a structure, or between one element present and the others absent.3. Lexical ambiguityLexical ambiguity: It refers to ambiguity explained by reference to lexical meanings. For example, “I went to the bank” is lexically ambiguous in the sense that “bank” in this sentence could refer to a business establishment or a slop of landing adjoining a river.4. Grammatical ambiguityGrammatical ambiguity: Grammatical ambiguity occurs when the grammatical structure of a sentence allows two different interpretations, each of which gives rise toa different meaning.5. Concord (or: Agreement)Concord (or: Agreement) could be defined as the requirement that the forms of two or more words in a syntactic relationship should agree with each other in terms of some categories. For example, in English the determiner and the noun it precedes should concord in number as in “this man”, “these men”; “book”, “same books”.6. endocentric constructionEndocentric construction is one kind of syntactic constructions whose distribution is functionally equivalent to that of one or more of its constituents, i.e., a word or a group of words, which serves as a definable centre or head. An endocentric construction is also known as a headed construction, for example, in the noun phrase “all these last few days”, days is the head. And this phrase is an endocentric construction.V. Questions:1. What is the aim of IC analysis? Make an IC analysis of the following sentence bymeans of either brackets or a tree diagram.北外2010My brother said Mary liked the handbag.The aim of IC analysis is to discover and demonstrate the interrelationships of the words in a linguistic structure—the sentence or the word-combination. The IC analysis views the sentence not just as a linear sequence of elements but as sequence made up of “layers”of immediate constituents, each lower-level constituent being part of a higher-level constituent.Though IC analysis, the internal structure of a sentence may be demonstrated clearly and ambiguities, if any, will be revealed.We can analyze the sentence like this:SNP VPVSˈNP VPN V NPDet N Det NMy mother said Mary liked the handbag. OrMy mother said Mary liked the handbag. 2. Why did Chomsky make the distinction between Deep and Surface structures?人大2006In generative grammar, deep structure is the abstract syntactic representation of a sentence, the underlying level of structural organization which specifies all the factors governing the way the sentence should be interpreted. On the other hand, surface structure is the final stage in the syntactic representation of a sentence, which provides the input to the phonological component of the grammar, and which thus most closely corresponds to the structure we articulate and hear.According to Chomsky, it is necessary to make the distinction, since it is helpful to differentiate and analyze syntactic structures such as "John is easy to please" and"John is eager to please", and also to disambiguate structures like "the shooting of the hunters". More importantly, it reflects two of the stages of how the language is processed through the generative grammar: the deep structure, which is an underlying structure, has to be transformed to the surface structure via a set of transformational rules.3.Try to identify the possible paradigmatic relation between any items in thefollowing poem by Lu Xun (i.e. tell if there is such a relation between which and which items).岂有豪情似旧时，花开花落两由之。

Faraday Discuss .,1997,108,469È471Concluding RemarksR.M.Hochstrasser a and J.P.Simons ba Department of Chemistry ,University of Pennsylvania ,Philadelphia ,PA 19104,USAb Physical and T heoretical Chemistry L aboratory ,University of Oxford ,Oxford ,UK OX13QZThere are several Golden Rules associated with the presentation of Concluding Remarks at Faraday Discussions.The Ðrst of these,“ask someone else to give themÏhas,sadly,been obeyed because of Prof.HochstrasserÏs enforced immobility,occasioned by a prol-apsed disc.We wish him a speedy recovery.The second Rule,“if you have nothing to say,say nothingÏhas been compensated,fortunately,by Prof.HochstrasserÏs provision of the outline notes of some of the remarks he would have made,had it been possible.They are presented below.The third Rule,“say some nice thingsÏis the easiest of all to obey since Prof.Whitehead has organised so imaginative and timely a Discussion,which has been introduced with all of Prof.JortnerÏs customary dynamism.It has addressed many issues.How do we monitor and interpret the dynamics of photon-induced processes in clusters and condensed media?What is the nature of the chromophore when it is no longer isolated in the gas phase?How does it “communicateÏwith its environment?How does the environment inÑuence electronic motions,e .g .in atomic or molecular Rydberg states;or nuclear motions,e .g .through caging or chap-eroning of atomic or molecular fragments;or their coupling,through non-adiabatic dynamics?How does photon absorption lead to nuclear motion in the neighbouring environment?How do the interactions of the chromophore with the environment depend upon the nature of the environment,and the way it is coupled to it,e .g .through space or through bonds?What are the characteristic timescales of the interactions;are they separable?Can we trace the pathway from the initial energy localisation,through its delocalisation to its eventual dissipation?What is the nature of the “molecular and intermolecular circuitryÏthat governs this evolution?Most pertinently,as Prof.Hochstrasser asks:How do the structural and dynamical results obtained from simple systems help us to understand the behaviour of more complex materials?What do clusters,for example,teach us about liquid structure?What do we learn about the dynamic behaviour in liquids and solids,from the study of Ðnite-sized assemblies?What conditions require statistical as opposed to discrete (level by level)models of dynamics?What is reasonable (or unreasonable)about seeking a microscopic quantum mechanical description of liquids?Investigations of small molecules teach us about chemical bonding and the charac-teristics of accurate potential energy surfaces.Weaker interactions are often evaluated from studies of van der Waals complexes and Ðnite clusters.The dynamics in such systems are determined by forces obtained from these potentials.While the properties of molecules in large clusters,liquids or extended aggregates might,in some cases,be framed in terms of isolated molecule potentials there will be cases where this is not possible.The most appropriate description of the dynamics of complex systems depends upon how the energy is partitioned.Typically,for a solution phase problem,the Hamiltonian involves the molecular part,and the solvent part which are separately solved either exactly or approx-H M H S ,imately,and a coupling part,that slightly mixes them.This partitioning yields a V MS ,useful representation when the molecular or solvent states are only slightly modiÐed by469470Concluding Remarkstheir interactions.The molecular potential is especially valuable in this case and may dominate the motion of the molecular nuclei even though the dynamics may be in a statistical limit.The intermolecular perturbations cause irreversible relaxation corre-sponding to transitions between the molecular states,accompanied by energy transfer to and from the solvent bath.In order that energy can be transferred to it,the solvent must have unoccupied states.Energy transfer to the molecule requires occupied states of the bath.A fully worked out example where this approach is nearly exact is the coupling of an atom or molecule to a very weak radiation Ðeld.Another example would be molecu-lar dynamics in very weakly interacting solvents.Quantum dynamics in this limit can be handled along the lines of RedÐeld theory,in which the reduced molecular density matrix is expanded to second order in This approach gives rise to spectral shifts V MS .and to coherence transfer along with relaxation of both the population and the phase of the molecular levels.The nuclear motions are largely governed by a slightly modiÐed version of the molecular potential.In stochastic dynamics,the solvent e†ect is estimated from correlation functions of where the Ñuctuations in the interaction potential V MS (t ),due to the motion of very large numbers of solvent nuclei and electrons are modelled by statistical forms or calculated from molecular dynamics simulations.There are situations where the molecular potential is so severely modiÐed by the solvent Èsolute interaction that an alternative representation is more realistic.In such cases it may be that the system of interest is a supermolecule or cluster,consisting of the solute and strongly interacting solvent molecules.The Hamiltonian could then be parti-tioned to yield a term for the energy states of the cluster,and the surrounding bath,comprising those solvent molecules that do not interact strongly with the solute.The dynamics can be determined from one of the perturbation approaches mentioned earlier.In examples of this type the relevant nuclear dynamics are controlled by the potential surface of the cluster but the irreversible relaxation is caused by the weak coupling between the supermolecule and the solvent.Measurements and calculations of potential energy surfaces of solute Èsolvent clusters are sorely needed for this approach.Such a picture assumes that the long-range forces are weak and that the interactions between the solvent molecules are not much inÑuenced by the presence of the solute.These assumptions would surely be inappropriate in accounting for the dynamics and struc-ture of polar molecules or ions in water,to give just one example.When Coulombic forces are important in determining structure,and their Ñuctuations determine the dynamics,we can imagine that long-range interactions will have to be included.As chemical reactions take place and charges redistribute,there may be large changes in the energy from interactions with moving solvent molecules.The solvent nuclear dynamics have been measured by time-resolved Kerr e†ects in transparent media,by dynamic Stokes shifts and by three pulse photon echoes in dye systems and in proteins (see the paper by Fleming and co-workers in this Discussion 1).In the cases that were examined theoretically,the major part of the solvent reorganisation energy around charges appears to originate from the Ðrst solvation shell.While the experiments charac-terise correlation functions of the solvent,they usually do not provide a microscopic picture of the motions that cause the energy changes other than to classify them broadly,as vibrational,librational or di†usive.On the other hand we would like to know when there are changes in the solute potential surfaces as a result of solvation and when solvation can inÑuence reactive motions.Equally important is the experimental charac-terisation of the solvent structures as the solvation dynamics evolve.Simulations are able to predict the answers to all these questions so some experimental results will allow the theory to be tested.In experiments on the photodissociation of changes HgBr 2,2in the potential energy function of the released HgBr occur on the timescale of the solvation.They can be followed through the changes in the vibrational frequency.The fast process involves the breaking up of the solvent structure associated with the tri-atomic molecule and a slower process involves the construction of the equilibriumR .M .Hochstrasser and J .P .Simons 471solvent structure around the HgBr fragment.Similar results for solvent structure changes were seen for ClO ~.3These structures should be accessible to spectroscopic experiments.As shown in the paper by Neumark and co-workers,4the cage reaction of I and I ~in a cluster of induces slow solvent evaporation and fast vibrational relax-CO 2ation.These experiments show details of the solvent involvement in the reactive motions that have proved difficult to obtain in solution phase experiments.Of course,it is known from experiment that the energy of a solution phase reaction is used to heat up the surrounding solvent molecules,and that the rate of reaction can be altered if the heat di†usion is very slow compared with the reaction rate.However,at conventional liquid densities (10M )the number of solvent molecules over which the released energy is dis-tributed grows to approximately 25in 10ps,by classical heat di†usion.The task of Ðnding a microscopic level description of solvent e†ects on relaxation and chemical processes is daunting.Nuclear motions can be extremely complex even for relatively small molecules in the absence of intermolecular interactions.When the solvent Èsolute interactions are strong the solvent forces can introduce additional anhar-monicity into the “soluteÏmotions thereby causing nuclear trajectories that are e†ec-tively absent in the isolated solvent molecule.For example,in the gas phase IR spectrum of the asymmetric stretch region shows no sign of any perturbations.In aqueous N 3~,solution,however,the mode relaxes in ca .1ps due to very strong coupling between solute modes;the motion is a combined solvent Èsolute displacement.5Such motions could be characterised through IR and Raman studies of clusters.There are many things (of course)that we have not heard about at this Discussion.One of the most important is single molecule spectroscopy,which can reveal the dis-tribution of molecular properties associated with Ñuctuations in their environment.When the observation time is shorter than the Ñuctuation timescale,the ensemble average is no longer equal to the time average.Not much has been heard about mol-ecules at interfaces,which is where much chemistry and biochemistry actually takes place.Not much has been heard about optical control of reaction rates in condensed phases;can we tune the solvent response to the lifetime of the transition state?We have not heard much about self-assembled supramolecular systems where the dynamics of photon-induced processes may be controlled by synthetic designÈmuch as it is in a photosynthetic centre.Perhaps these will feature in a future Faraday Discussion.References1Y.Nagasawa,J-Y.Yu,M.Cho and G.R.Fleming,Faraday Discuss .,1997,108,23.2M.Lim,M.Wo†ord,P.Hamm and R.M.Hochstrasser,Chem .Phys .L ett .,1998,in press.3M.Lim,S.Gnanakaran and R.M.Hochstrasser,J .Chem .Phys .,1997,106,3485.4B.J.Greenblatt,M.T.Zanni and M.Neumark,Faraday Discuss .,1997,108,101.5J.C.Owrutsky,D.Raftery and R.M.Hochstrasser,Ann .Rev .Phys .Chem .,1994,45,519.。

Phase Congruency Detects Corners and EdgesPeter KovesiSchool of Computer Science&Software EngineeringThe University of Western AustraliaCrawley,W.A.6009pk@.auAbstract.There are many applications such as stereo matching,mo-tion tracking and image registration that require so called‘corners’tobe detected across image sequences in a reliable manner.The Harris cor-ner detector is widely used for this purpose.However,the response fromthe Harris operator,and other corner operators,varies considerably withimage contrast.This makes the setting of thresholds that are appropri-ate for extended image sequences difficult,if not impossible.This paperdescribes a new corner and edge detector developed from the phase con-gruency model of feature detection.The new operator uses the principalmoments of the phase congruency information to determine corner andedge information.The resulting corner and edge operator is highly local-ized and has responses that are invariant to image contrast.This resultsin reliable feature detection under varying illumination conditions withfixed thresholds.An additional feature of the operator is that the cornermap is a strict subset of the edge map.This facilitates the cooperativeuse of corner and edge information.1IntroductionWith the impressive reconstruction results that have been achieved by those working in projective geometry(see for example Hartley and Zisserman[1])there has been a renewed interest in the detection of so called‘corners’,or‘interest points’.The success of these reconstructions depend very much on the reliable and accurate detection of these points across image sequences.The definition of a corner is typically taken to be a location in the image where the local autocorrelation function has a distinct peak.A variety of op-erators have been devised to detect corners.These include those developed by Moravec[2],Harris and Stephens[3],Beaudet[4],Kitchen and Rosenfeld[5], and Cooper et al.[6].Corner detectors based on the local energy model of fea-ture perception have been developed by Rosenthaler et al.[7],and Robbins and Owens[8].More recently the SUSAN operator has been proposed by Smith and Brady[9].Of these the Harris operator probably remains the most widely used.A common problem with all these operators,except the SUSAN operator, is that the corner response varies considerably with image contrast.This makes the setting of thresholds difficult.Typically we are interested in tracking fea-tures over increasingly extended image sequences.The longer the sequence the309greater the variations in illumination conditions one can expect,and the set-ting of appropriate thresholds becomes increasingly difficult,if not impossible. Inevitably thresholds have to be set at levels lower than ideal because detecting too many features is a lesser evil than detecting not enough.Stereo and motion reconstruction algorithms are then faced with the problem of dealing with very large clouds of noisy corner points,often greatly compromising their operation. Matching operations,which usually have rapidly increasing running time as a function of input size,suffer greatly in these conditions.Typically,considerable effort has to be devoted to the cleaning up of the output of the corner detector and to the elimination of outliers.The success of this cleaning up and outlier elimination process is usually crucial to the success of the reconstruction algo-rithm.Indeed,a very significant proportion of Hartley and Zisserman’s book[1] is devoted to robust estimation techniques.Another difficulty many of these operators have is that the Gaussian smooth-ing that is employed to reduce the influence of noise can corrupt the location of corners,sometimes considerably.The SUSAN operator deserves some special comment here because it does not suffer from these problems outlined above. It identifies features by determining what fraction of a circular mask has values the same,or similar,to the value at the centre point.Thresholds are therefore defined in terms of the size of the mask and no image smoothing is required. However,the SUSAN operator assumes that edges and corners are formed by the junctions of regions having constant,or near constant,intensity,and this limits the junction types that can be modeled.To address the many problems outlined above this paper describes a new corner and edge detector developed from the phase congruency model of feature detection.The new operator uses the principal moments of the phase congruency information to determine corner and edge information.Phase congruency is a dimensionless quantity and provides information that is invariant to image con-trast.This allows the magnitudes of the principal moments of phase congruency to be used directly to determine the edge and corner strength.The minimum and maximum moments provide feature information in their own right;one does not have to look at their ratios.If the maximum moment of phase congruency at a point is large then that point should be marked as an edge.If the mini-mum moment of phase congruency is also large then that point should also be marked as a‘corner’.The hypothesis being that a large minimum moment of phase congruency indicates there is significant phase congruency in more than one orientation,making it a corner.The resulting corner and edge operator is highly localized and the invariance of the response to image contrast results in reliable feature detection under varying illumination conditions withfixed thresholds.An additional feature of the operator is that the corner map is a strict subset of the edge map.This facilitates the cooperative use of corner and edge information.This paper is organized as follows:first the phase congruency model of feature perception is reviewed.We then examine how the phase congruency responses over several orientations can be analyzed in terms of moments to provide both310edge and corner information.Finally the performance is assessed relative to thecommonly used Harris operator.2The Phase Congruency Model of Feature DetectionRather than assume a gradient,the LocalEnergy Model in an image wherethe Fourier in Figure 1[10].NoticeFig.1.Fourier first four terms.how the Fourier the step in the squarewave.Congruency of perceived feature [11].The angle at which the congruency occurs dictates the feature type,for example,step or delta.The Local Energy Model model was developed by Morrone et al.[10]andMorrone and Owens [12].Other work on this model of feature perception can befound in Morrone and Burr [13],Owens et al.[14],Venkatesh and Owens [15],and Kovesi [16–20,11].The work of Morrone and Burr [13]has shown that thismodel successfully explains a number of psychophysical effects in human featureperception.The measurement of phase congruency at a point in a signal can be seengeometrically in Figure 2.The local,complex valued,Fourier components at alocation x in the signal will each have an amplitude A n (x )and a phase angleφn (x ).Figure 2plots these local Fourier components as complex vectors adding head to tail.The magnitude of the vector from the origin to the end point is theLocal Energy ,|E (x )|.The measure of phase congruency developed by Morrone et al.[10]isP C 1(x )=|E (x )|n A n (x ).(1)Under this definition phase congruency is the ratio of |E (x )|to the overall pathlength taken by the local Fourier components in reaching the end point.If allthe Fourier components are in phase all the complex vectors would be alignedand the ratio of |E (x )|/ n A n (x )would be 1.If there is no coherence of phase311RealaxisImaginaryaxisE(x)φφ(x)nA n (x)_noise circleFig.2.Polar diagram showing the Fourier components at a location in the signal plottedhead to tail.The weighted mean phase angle is given by (x ).The noise circle representsthe level of E (x )one can expect just from the noise in the signal.the ratio falls to a minimum of 0.Phase congruency provides a measure that isindependent of the overall magnitude of the signal making it invariant to vari-ations in image illumination and/or contrast.Fixed threshold values of featuresignificance can then be used over wide classes of images.It can be shown that this measure of phase congruency is a function of thecosine of the deviation of each phase component from the meanP C 1(x )= n A n (cos(φ(x )−φ(x )) nA n (x ).(2)This measure of phase congruency does not provide good localization and it isalso sensitive to noise.Kovesi [18,19]developed a modified measure consisting ofthe cosine minus the magnitude of the sine of the phase deviation;this produces amore localized response.This new measure also incorporates noise compensation:P C 2(x )=n W (x ) A n (x )(cos(φn (x )−φ(x ))−|sin (φn (x )−φ(x ))|)−T n A n (x )+ε.(3)The term W (x )is a factor that weights for frequency spread (congruency overmany frequencies is more significant than congruency over a few frequencies).Asmall constant,εis incorporated to avoid division by zero.Only energy valuesthat exceed T ,the estimated noise influence,are counted in the result.Thesymbols denote that the enclosed quantity is equal to itself when its value ispositive,and zero otherwise.In practice local frequency information is obtainedvia banks of Gabor wavelets tuned to different spatial frequencies,rather than viathe Fourier transform.The appropriate noise threshold,T is readily determinedfrom the statistics of the filter responses to the image.For details of this phasecongruency measure and its implementation see Kovesi [19–21].3123Combining Phase Congruency Information over many OrientationsA weakness of previous implementations of phase congruency has been the way in which information over many orientations is used and combined.The defini-tion of phase congruency outlined above only applies to1D signals.To obtain an overall measure of phase congruency in2D local energy isfirst calculated in several orientations,typically six,using data from oriented2D Gabor wavelets. Equation3is modified so that the numerator is the weighted and noise com-pensated local energy summed over all orientations,and the denominator is the total sum offilter response amplitudes over all orientations and scales.While this approach produces a phase congruency measure that results in a very good edge map it ignores information about the way phase congruency varies with orientation at each point in the image.To include information about the way phase congruency varies with orienta-tion we can proceed as follows:calculate phase congruency independently in each orientation using equation3,compute moments of phase congruency and look at the variation of the moments with orientation.The principal axis,corresponding to the axis about which the moment is minimized,provides an indication of the orientation of the feature.The magnitude of the maximum moment,correspond-ing to the moment about an axis perpendicular to the principal axis,gives an indication of the significance of the feature.If the minimum moment is also large we have an indication that the feature point has a strong2D component to it, and should therefore be additionally classified as a‘corner’.Following the classical moment analysis equations[22]we compute the fol-lowing at each point in the image:a=(P C(θ)cos(θ))2(4)b=2(P C(θ)cos(θ)).(P C(θ)sin(θ))(5)c=(P C(θ)sin(θ))2,(6)where P C(θ)refers to the phase congruency value determined at orientationθ, and the sum is performed over the discrete set of orientations used(typically six).The angle of the principal axisΦis given byΦ=12atan2bb22,a−cb22.(7)The maximum and minimum moments,M and m respectively,are given byM=12(c+a+b2+(a−c)2)(8)m=12(c+a−b2+(a−c)2).(9) 313This calculation of the maximum and minimum moments,along with the prin-cipal axis,corresponds to preforming a singular value decomposition on a phasecongruency covariance matrix.The moments correspond to the singular values.3.1Comparison with the Harris OperatorA comparison with the Harris operator is appropriate given its widespreaduse.The analysis described above is similar to that adopted by Harris andStephens [3].However they consider the minimum and maximum eigenvalues,αand β,of the image gradient covariance matrix in developing their corner detector.The gradient covariance matrix is given by G = I 2x I x I y I x I y I 2y(10)where I x and I y denote the image gradients in the x and y directions.A ‘corner’is said to occur when the two eigenvalues are large and similar in magnitude.Toavoid an explicit eigenvalue decomposition Harris and Stephens devise a measureusing the determinant and trace of the gradient covariance matrixR =det(G )−k (tr (G ))2,(11)where det(G )=αβand tr (G )=α+β,the parameter k is traditionally set to0.04.This produces a measure that is large when both αand βare large.Howeverwe have the problem of determining what is large.Noting that elements of theimage gradient covariance matrix have units of intensity gradient squared we cansee that the determinant,and hence the measure R will have units of intensitygradient to the fourth.This explains why the Harris operator is highly sensitiveto image contrast variations which,in turn,makes the setting of thresholdsexceedingly difficult.Some kind of sensitivity to image contrast is common to allcorner operators that are based on the local autocorrelation of image intensityvalues and/or image gradient values.Unlike image intensity gradient values phase congruency values are normal-ized quantities that have no units associated with them.If the moments arenormalized for the number of orientations considered we end up with phase con-gruency moment values that range between 0and 1.Being moments these valuescorrespond to phase congruency squared.Accordingly we can use the maximumand minimum phase congruency moments directly to establish whether we have asignificant edge and/or corner point.It should be emphasized that the minimumand maximum moments provide feature information in their own right;one doesnot have to look at their ratios.We can define a priori what a significant valueof phase congruency moment is,and this value is independent of image contrast.4ResultsThe performance of the phase congruency operator was compared to the Har-ris operator on a synthetic test image,and on a real scene containing strong314shadows.The results are shown infigures3and4.Raw Harris corner strength and raw phase congruency corner and edge strength images are displayed for comparison.It should be noted that the Harris corner strength values varied by many orders of magnitude across the image depending on contrast.To facilitate the display of the Harris corner strength image what is actually shown here is the fourth root of the image.Even after this transformation large variations are still evident.In contrast the phase congruency edge and corner strength images are minimally affected by image contrast and are readily thresholded(in this case with a value of0.4on both images)to produce a clear set of features.In applying the Harris operator to the synthetic image the standard deviation of the smoothing Gaussian was deliberately set to a large value of3pixels to illustrate the problem the operator has in localizing‘T’junctions.Notice how the detected Harris corners are displaced inwards on the left hand grey scale, note also the double response where the line intersects the circle.The phase congruency operator,on the other hand,locates‘T’junctions precisely.Changing the number offilter scales used to compute phase congruency does not affect the localization,it only affects the relative significance of features at different scales. For the real scene the standard deviation of the smoothing Gaussian for the Harris operator was1pixel.For both images phase congruency was computed using Gaborfilters over4scales(wavelengths of4,8,16and32pixels)and over 6orientations.Another important point to note is that the phase congruency edge map includes the corner map,this is unusual for an edge detector!The fact that the phase congruency corner map is a strict subset of the phase congruency edge map greatly simplifies the integration of data computed from edge and corner information.This facilitates the process of building a model of the scene from point and edge data matched over two or more views.In contrast,if the edge and corner information is computed via separate means,say the Canny and Harris operators respectively,the edge data is unlikely to include the corner data.The Gaussian smoothing that is applied to reduce the influence of noise results in the Canny edges being weakened in strength,and rounded at corner locations.MATLAB code is available for those wishing to replicate the results presented here[21].5ConclusionPhase congruency provides a contrast invariant way of identifying features within images.By combining phase congruency information over multiple orientations into a covariance matrix,and calculating the minimum and maximum moments we produce a highly localized operator that can be used to identify both edges and corners in a contrast invariant way.The contrast invariance facilitates the tracking of features over extended image sequences under varying lighting con-ditions.An additional advantage of the operator is that the phase congruency corner map is a strict subset of the phase congruency edge map.This simplifies the integration of data computed from edge and corner information.315Originalimage.Fourth root of Harris cornerstrength image(σ=3).Phase congruency edge strengthimage.Phase congruency corner strengthimage.Harris corners with threshold107(maximum corner strength was3.4x109).Phase congruency corners withthreshold0.4(maximum possiblephase congruency value is1).parison of the Harris and phase congruency operators on a test image.316Original image.Fourth root of Harris corner strength im-age (σ=1).Phase congruency edge strength image.Phase congruency corner strength image.Harris corners with threshold 108(maxi-mum corner strength was 1.25x 1010).Phase congruency corners with threshold 0.4(maximum possible phase congruencyvalue is 1).parison of the Harris and phase congruency operators on an image withstrong shadows.317References1.Hartley,R.,Zisserman,A.:Multiple View Geometry in Computer Vision.Cam-bridge University Press(2000)2.Moravec,H.P.:Robot rover visual navigation.UMI Research Press(1981)3.Harris,C.,Stephens,M.:A combined corner and edge detector.In:Proceedings,4th Alvey Vision Conference.(1988)147–151Manchester.4.Beaudet,P.R.:Rotationally invariant image operators.In:International JointConference on Artificial Intelligence.(1987)579–5835.Kitchen,L.,Rosenfeld,A.:Grey-level corner detection.Pattern Recognition Let-ters(1982)95–1026.Cooper,J.,Venkatesh,S.,Kitchen,L.:Early jump-out corner detectors.PAMI15(1993)823–8287.Rosenthaler,L.,Heitger,F.,Kubler,O.,Heydt,R.v.:Detection of general edgesand keypoints.In:ECCV92,Springer-Verlag Lecture Notes in Computer Science.Volume588.,Springer-Verlag(1992)78–86Santa Margherita Ligure,Italy.8.Robbins,B.,Owens,R.:2D feature detection via local energy.Image and VisionComputing15(1997)353–3689.Smith,S.M.,Brady,J.M.:SUSAN-a new approach to low level image processing.International Journal of Computer Vision23(1997)45–7810.Morrone,M.C.,Ross,J.R.,Burr,D.C.,Owens,R.A.:Mach bands are phase de-pendent.Nature324(1986)250–25311.Kovesi,P.D.:Edges are not just steps.In:Proceedings of the Fifth Asian Confer-ence on Computer Vision.(2002)822–827Melbourne.12.Morrone,M.C.,Owens,R.A.:Feature detection from local energy.Pattern Recog-nition Letters6(1987)303–31313.Morrone,M.C.,Burr,D.C.:Feature detection in human vision:A phase-dependentenergy model.Proc.R.Soc.Lond.B235(1988)221–24514.Owens,R.A.,Venkatesh,S.,Ross,J.:Edge detection is a projection.PatternRecognition Letters9(1989)223–24415.Venkatesh,S.,Owens,R.:On the classification of image features.Pattern Recog-nition Letters11(1990)339–34916.Kovesi,P.D.:A dimensionless measure of edge significance.In:The AustralianPattern Recognition Society,Conference on Digital Image Computing:Techniques and Applications.(1991)281–288Melbourne.17.Kovesi,P.D.:A dimensionless measure of edge significance from phase congruencycalculated via wavelets.In:First New Zealand Conference on Image and Vision Computing.(1993)87–94Auckland.18.Kovesi,P.D.:Invariant Measures of Image Features From Phase Information.PhDthesis,The University of Western Australia(1996)19.Kovesi,P.D.:Image features from phase congruency.Videre:Journal of ComputerVision Research1(1999)1–26/e-journals/Videre/.20.Kovesi,P.D.:Phase congruency:A low-level image invariant.Psychological Re-search64(2000)136–14821.Kovesi,P.D.:MATLAB functions for computer vision and image analysis(1996-2003).au/∼pk/Research/MatlabFns/.22.Horn,B.K.P.:Robot Vision.McGraw-Hill(1986)New York.318。

Two-dimensional data acquisition
• MR data acquired as a complex, composite frequency waveform • With methodical variations of the PEG during each acquisition, the k-space matrix is filled to produce the desired variations across the frequency and phase encmensional inverse Fourier transform decodes the frequency domain information piecewise along the rows and then along the columns of k-space 8. Final image is a spatial representation of the proton density, T1, T2, and flow characteristics of the tissue using a grayscale range
K-space matrix (cont.)
• Frequency domain data are encoded in the kx direction by the frequency encode gradient (FEG), and in the ky direction by the phase encode gradient (PEG) in most image sequences • Lowest spatial frequency increment is the bandwidth across each pixel

2011年技术物理学院08级（激光方向）专业英语翻译重点！！！作者：邵晨宇Electromagnetic电磁的principle原则principal主要的macroscopic宏观的microscopic微观的differential微分vector矢量scalar标量permittivity介电常数photons光子oscillation振动density of states态密度dimensionality维数transverse wave横波dipole moment偶极矩diode 二极管mono-chromatic单色temporal时间的spatial空间的velocity速度wave packet波包be perpendicular to线垂直be nomal to线面垂直isotropic各向同性的anistropic各向异性的vacuum真空assumption假设semiconductor半导体nonmagnetic非磁性的considerable大量的ultraviolet紫外的diamagnetic抗磁的paramagnetic顺磁的antiparamagnetic反铁磁的ferro-magnetic铁磁的negligible可忽略的conductivity电导率intrinsic本征的inequality不等式infrared红外的weakly doped弱掺杂heavily doped重掺杂a second derivative in time对时间二阶导数vanish消失tensor张量refractive index折射率crucial主要的quantum mechanics 量子力学transition probability跃迁几率delve研究infinite无限的relevant相关的thermodynamic equilibrium热力学平衡（动态热平衡）fermions费米子bosons波色子potential barrier势垒standing wave驻波travelling wave行波degeneracy简并converge收敛diverge发散phonons声子singularity奇点（奇异值）vector potential向量式partical-wave dualism波粒二象性homogeneous均匀的elliptic椭圆的reasonable公平的合理的reflector反射器characteristic特性prerequisite必要条件quadratic二次的predominantly最重要的gaussian beams高斯光束azimuth方位角evolve推到spot size光斑尺寸radius of curvature曲率半径convention管理hyperbole双曲线hyperboloid双曲面radii半径asymptote渐近线apex顶点rigorous精确地manifestation体现表明wave diffraction波衍射aperture孔径complex beam radius复光束半径lenslike medium类透镜介质be adjacent to与之相邻confocal beam共焦光束a unity determinant单位行列式waveguide波导illustration说明induction归纳symmetric 对称的steady-state稳态be consistent with与之一致solid curves实线dashed curves虚线be identical to相同eigenvalue本征值noteworthy关注的counteract抵消reinforce加强the modal dispersion模式色散the group velocity dispersion群速度色散channel波段repetition rate重复率overlap重叠intuition直觉material dispersion材料色散information capacity信息量feed into 注入derive from由之产生semi-intuitive半直觉intermode mixing模式混合pulse duration脉宽mechanism原理dissipate损耗designate by命名为to a large extent在很大程度上etalon 标准具archetype圆形interferometer干涉计be attributed to归因于roundtrip一个往返infinite geometric progression无穷几何级数conservation of energy能量守恒free spectral range自由光谱区reflection coefficient（fraction of the intensity reflected）反射系数transmission coefficient（fraction of the intensity transmitted）透射系数optical resonator光学谐振腔unity 归一optical spectrum analyzer光谱分析grequency separations频率间隔scanning interferometer扫描干涉仪sweep移动replica复制品ambiguity不确定simultaneous同步的longitudinal laser mode纵模denominator分母finesse精细度the limiting resolution极限分辨率the width of a transmission bandpass透射带宽collimated beam线性光束noncollimated beam非线性光束transient condition瞬态情况spherical mirror 球面镜locus（loci）轨迹exponential factor指数因子radian弧度configuration不举intercept截断back and forth反复spatical mode空间模式algebra代数in practice在实际中symmetrical对称的a symmetrical conforal resonator对称共焦谐振腔criteria准则concentric同心的biperiodic lens sequence双周期透镜组序列stable solution稳态解equivalent lens等效透镜verge 边缘self-consistent自洽reference plane参考平面off-axis离轴shaded area阴影区clear area空白区perturbation扰动evolution渐变decay减弱unimodual matrix单位矩阵discrepancy相位差longitudinal mode index纵模指数resonance共振quantum electronics量子电子学phenomenon现象exploit利用spontaneous emission自发辐射initial初始的thermodynamic热力学inphase同相位的population inversion粒子数反转transparent透明的threshold阈值predominate over占主导地位的monochromaticity单色性spatical and temporal coherence时空相干性by virtue of利用directionality方向性superposition叠加pump rate泵浦速率shunt分流corona breakdown电晕击穿audacity畅通无阻versatile用途广泛的photoelectric effect光电效应quantum detector 量子探测器quantum efficiency量子效率vacuum photodiode真空光电二极管photoelectric work function光电功函数cathode阴极anode阳极formidable苛刻的恶光的irrespective无关的impinge撞击in turn依次capacitance电容photomultiplier光电信增管photoconductor光敏电阻junction photodiode结型光电二极管avalanche photodiode雪崩二极管shot noise 散粒噪声thermal noise热噪声1.In this chapter we consider Maxwell’s equations and what they reveal about the propagation of light in vacuum and in matter. We introduce the concept of photons and present their density of states.Since the density of states is a rather important property，not only for photons，we approach this quantity in a rather general way. We will use the density of states later also for other(quasi-) particles including systems of reduced dimensionality.In addition,we introduce the occupation probability of these states for various groups of particles.在本章中，我们讨论麦克斯韦方程和他们显示的有关光在真空中传播的问题。

Ornstein–Uhlenbeck process - Wikipedia,the f...Ornstein–Uhlenbeck process undefinedundefinedFrom Wikipedia, the free encyclopediaJump to: navigation, searchNot to be confused with Ornstein–Uhlenbeck operator.In mathematics, the Ornstein–Uhlenbeck process (named after LeonardOrnstein and George Eugene Uhlenbeck), is a stochastic process that, roughly speaking, describes the velocity of a massive Brownian particle under the influence of friction. The process is stationary, Gaussian, and Markov, and is the only nontrivial process that satisfies these three conditions, up to allowing linear transformations of the space and time variables.[1] Over time, the process tends to drift towards its long-term mean: such a process is called mean-reverting.The process x t satisfies the following stochastic differential equation:where θ> 0, μ and σ> 0 are parameters and W t denotes the Wiener process. Contents[hide]1 Application in physical sciences2 Application in financialmathematics3 Mathematical properties4 Solution5 Alternative representation6 Scaling limit interpretation7 Fokker–Planck equationrepresentation8 Generalizations9 See also10 References11 External links[edit] Application in physical sciencesThe Ornstein–Uhlenbeck process is a prototype of a noisy relaxation process. Consider for example a Hookean spring with spring constant k whose dynamics is highly overdamped with friction coefficient γ. In the presence of thermal fluctuations with temperature T, the length x(t) of the spring will fluctuate stochastically around the spring rest length x0; its stochastic dynamic is described by an Ornstein–Uhlenbeck process with:where σ is derived from the Stokes-Einstein equation D = σ2 / 2 = k B T / γ for theeffective diffusion constant.In physical sciences, the stochastic differential equation of an Ornstein–Uhlenbeck process is rewritten as a Langevin equationwhere ξ(t) is white Gaussian noise with .At equilibrium, the spring stores an averageenergy in accordance with the equipartition theorem.[edit] Application in financial mathematicsThe Ornstein–Uhlenbeck process is one of several approaches used to model (with modifications) interest rates, currency exchange rates, and commodity prices stochastically. The parameter μ represents the equilibrium or mean value supported by fundamentals; σ the degree of volatility around it caused by shocks, and θ the rate by which these shocks dissipate and the variable reverts towards the mean. One application of the process is a trading strategy pairs trade.[2][3][edit] Mathematical propertiesThe Ornstein–Uhlenbeck process is an example of a Gaussian process that has a bounded variance and admits a stationary probability distribution, in contrast tothe Wiener process; the difference between the two is in their "drift" term. For the Wiener process the drift term is constant, whereas for the Ornstein–Uhlenbeck process it is dependent on the current value of the process: if the current value of the process is less than the (long-term) mean, the drift will be positive; if the current valueof the process is greater than the (long-term) mean, the drift will be negative. In other words, the mean acts as an equilibrium level for the process. This gives the process its informative name, "mean-reverting." The stationary (long-term) variance is given byThe Ornstein–Uhlenbeck process is the continuous-time analogue ofthe discrete-time AR(1) process.three sample paths of different OU-processes with θ = 1, μ = 1.2, σ = 0.3:blue: initial value a = 0 (a.s.)green: initial value a = 2 (a.s.)red: initial value normally distributed so that the process has invariant measure [edit] SolutionThis equation is solved by variation of parameters. Apply Itō–Doeblin's formula to thefunctionto getIntegrating from 0 to t we getwhereupon we seeThus, the first moment is given by (assuming that x0 is a constant)We can use the Itōisometry to calculate the covariance function byThus if s < t (so that min(s, t) = s), then we have[edit] Alternative representationIt is also possible (and often convenient) to represent x t (unconditionally, i.e.as ) as a scaled time-transformed Wiener process:or conditionally (given x0) asThe time integral of this process can be used to generate noise with a 1/ƒpower spectrum.[edit] Scaling limit interpretationThe Ornstein–Uhlenbeck process can be interpreted as a scaling limit of a discrete process, in the same way that Brownian motion is a scaling limit of random walks. Consider an urn containing n blue and yellow balls. At each step a ball is chosen at random and replaced by a ball of the opposite colour. Let X n be the number of blueballs in the urn after n steps. Then converges to a Ornstein–Uhlenbeck process as n tends to infinity.[edit] Fokker–Planck equation representationThe probability density function ƒ(x, t) of the Ornstein–Uhlenbeck process satisfies the Fokker–Planck equationThe stationary solution of this equation is a Gaussian distribution with mean μ and variance σ2 / (2θ)[edit ] GeneralizationsIt is possible to extend the OU processes to processes where the background driving process is a L évy process . These processes are widely studied by OleBarndorff-Nielsen and Neil Shephard and others.In addition, processes are used in finance where the volatility increases for larger values of X . In particular, the CKLS (Chan-Karolyi-Longstaff-Sanders) process [4] with the volatility term replaced by can be solved in closed form for γ = 1 / 2 or 1, as well as for γ = 0, which corresponds to the conventional OU process.[edit ] See alsoThe Vasicek model of interest rates is an example of an Ornstein –Uhlenbeck process.Short rate model – contains more examples.This article includes a list of references , but its sources remain unclear because it has insufficient inline citations .Please help to improve this article by introducing more precise citations where appropriate . (January 2011)[edit ] References^ Doob 1942^ Advantages of Pair Trading: Market Neutrality^ An Ornstein-Uhlenbeck Framework for Pairs Trading ^ Chan et al. (1992)G.E.Uhlenbeck and L.S.Ornstein: "On the theory of Brownian Motion", Phys.Rev.36:823–41, 1930. doi:10.1103/PhysRev.36.823D.T.Gillespie: "Exact numerical simulation of the Ornstein–Uhlenbeck process and its integral", Phys.Rev.E 54:2084–91, 1996. PMID9965289doi:10.1103/PhysRevE.54.2084H. Risken: "The Fokker–Planck Equation: Method of Solution and Applications", Springer-Verlag, New York, 1989E. Bibbona, G. Panfilo and P. Tavella: "The Ornstein-Uhlenbeck process as a model of a low pass filtered white noise", Metrologia 45:S117-S126,2008 doi:10.1088/0026-1394/45/6/S17Chan. K. C., Karolyi, G. A., Longstaff, F. A. & Sanders, A. B.: "An empirical comparison of alternative models of the short-term interest rate", Journal of Finance 52:1209–27, 1992.Doob, J.L. (1942), "The Brownian movement and stochastic equations", Ann. of Math.43: 351–369.[edit] External linksA Stochastic Processes Toolkit for Risk Management, Damiano Brigo, Antonio Dalessandro, Matthias Neugebauer and Fares TrikiSimulating and Calibrating the Ornstein–Uhlenbeck process, M.A. van den Berg Calibrating the Ornstein-Uhlenbeck model, M.A. van den BergMaximum likelihood estimation of mean reverting processes, Jose Carlos Garcia FrancoRetrieved from ""。

Accuracy 准确度AGC: Automatic gain control. 自动增益控制。

Airy Hypothesis艾里假说alias:假频amplitude spectrum振幅谱antiroots反山根Bouguer anomaly布格异常Bouguer correction布格改正continuation延拓density密度density contrast密度差depth of compensation补偿深度dot chart布点量板double Bouguer correction双重布格改正downward continuation向下延拓elevation correction高程改正field continuation位场延拓figure of the earth大地水准面free-air anomaly自由空间异常free-air correction自由空间改正free oscillation of the earth:地球自由震荡gal伽geodesy:大地测量学geoid大地水准面gradiomanometer压差密度计：gradiometer梯度仪gravimeter重力仪gravitational constant万有引力常数gravity重力gravity anomaly:重力异常gravity meter比重计：gravity reduction:重力改正gravity survey重力调查gravity unit重力单位Gutenberg discontinuity:古登堡不连续面horizontal cylinder水平圆柱体isostasy:地壳均衡说：isostatic correction:均衡改正：latitude correction:纬度改正local gravity局部重力值normal gravity正常重力：Poisson's equation：泊松方程：Pratt hypothesis:普拉特假说second-derivative map:二次微商图：topographic correction地形改正torsion balance扭秤Worden:沃尔登重力仪aeromagnetic航空磁测Airborne magnetometer:航空磁力仪alternating-field demagnetization:交变场退磁：Curie point:居里点declination:磁偏角diurnal variation:日变ferrimagnetism:亚铁磁性：ferromagnetic:铁磁性的field intensity:场强fluxgate magnetometer:磁通门磁力仪gamma:伽马gauss:高斯：geomagnetic pole:地磁极geomagnetic reversal: 地磁极倒转：geomagnetic-variation method:地磁变化法：geometric sounding:电磁几何测深：inclination:倾角inductivity:感应率：local magnetic anomalies:局部磁异常magnetic basement:磁性基底：magnetic dip:磁倾角magnetic disturbance磁扰magnetic equator:地磁赤道magnetic field磁场magnetic flux:磁通量magnetic intensity:磁场强度：magnetic interpretation methods磁测资料解释法magnetic meridian:地磁子午线：magnetic moment:磁矩：magnetic permeability:磁导率：magnetic polarization:磁极化：Magnetic pole:磁极：magnetic storms:磁暴：magnetization:磁化强度magnetometer:磁力仪：nanotesla:纳特斯拉：normal magnetic field:正常磁场oersted:奥斯特paleomagnetism:古地磁学：paramagnetic: 顺磁性的：permeability:磁导率，渗透率：polarity:极性：polarization:极化度，极化，偏振：reduction to the pole化向地磁极归极法：secular variation:长期变化：tesla:特斯拉weber:韦伯apparent resistivity: 视电阻率：conductivity:电导率：current electrode:供电电极：dielectric constant:介电常数：dielectric polarization:电介质极化：dipole array:偶极排列dipole-dipole array:偶极-偶极排列：electrical profiling:电剖面法：electrical sounding电测深electrical survey电法勘探，电测井electric field:电场electric susceptibility:电极化率：electrochemical SP:电化学自然电位：electrode电极：electrode equilibrium potential:电极平衡电位：electrode polarization:电极极化：electrode potential:电极电位electrode resistance:电极电阻：electrolyte:电解质：electromagnetic method:电磁法：electromagnetic spectrum:电磁波谱：electronic电子的ELF:极低频：EM:电磁的：emu:电磁单位：equipotential-line method:等位线法equipotential surface:等位面：far-field:远场：fixed-source method:定源法：free-space field:自由空间场：galvanometer:电流计heat flow unit:热流单位HFU:热流单位：horizontal-dipole sounding水平偶极测深induced polarization:激发极化：infinite electrode:无穷远电极：NMR核磁共振permittivity:电容率：polarization ellipse:极化椭圆：pole-dipole array:单极-偶极排列：pole-pole array:单极-单极排列：Primary field: 一次场：secondary field:二次场：self-potential:自然电位self-potential method:自然电位法skin depth:趋肤深度skin effect:趋肤效应sky wave:天波：sky-wave interference:天波干扰：SP:自然电位：spontaneous potential:自然电位：transient electromagnetic method:瞬变电磁法：abnormal events:异常同相轴absorption:吸收作用：acoustic声学的，声的acoustic impedance:声阻抗，波阻抗：acoustic wave: 声波，地震波：air gun:空气枪：air wave:空气波：angle of incidence:入射角：apparent velocity:视速度：apparent wavelength:视波长：arrival:波至：arrival time波至时间：attenuation:衰减average velocity:平均速度azimuth:方位角binary gain:二进制增益blind zone: 盲区：body waves:体波：break:波跳：buried focus effect:地下焦点效应：cable:电缆：chirp:线性调频脉冲:coefficient of anisotropy:各向异性系数coherence:相干性coherent:相关的：common-depth-point:共深度点：common-depth-point stack:共深度点叠加：common-offset gather:共偏移距道集：common-offset stack:共炮检距叠加（同距叠加）：common-range gather:共炮检距道集（选排）：Common reflection point: 共反射点：compressional wave:压缩波：configuration:排列形式：converted wave:转换波critical angle:临界角critical reflection:临界反射：curved path:弯曲射线路径deconvolution:反褶积：deep seismic sounding: DSS.深地震测深：diffraction: 绕射：diffraction stack:绕射叠加：dilatational wave:膨胀波dispersion:扩散，频散display:显示：diving waves:弓形射线波：Dix formula:Dix公式DSS:深地震测深：dynamic corrections动校正：earthquake:天然地震：earthquake seismology: 天然地震测震学：elastic:弹性的：elastic constants:弹性常数：elastic impedance:弹性阻抗：elastic wave:弹性波：electrodynamic geophone:电动检波器：epicenter:震中：event:同相轴：expanding spread: 扩展排列：extended spread:纵排列fathometer:水深计：Fermat’s principle:费马原理：first arrival:初至：first break:初至波：floating datum: 浮动基准面flute槽focus:震源fold: 覆盖次数format:数据格式：Gardner method:加德纳法：gather:道集：geophone:地震检波器：geophone interval:检波距：ground roll:地滚波：group interval:组合间距：group velocity:群速度：guided wave:导波：hammer冲击锤：head wave:首波：：hodograph:矢端线：Hooke's law:虎克定律：horizontal stacking:水平叠加：Huygens principle:惠更斯原理：impedance:阻抗incident angle:入射角：interval velocity:层速度：Kirchoff diffraction equation:基尔霍夫绕射方程：law of reflection:反射定律：law of refraction:透射定律：least-time path:最短时程：Lg-wave: Lg-波：longitudinal wave:纵波：long-path multiple:全程多次反射波：long wave长波：love wave:勒夫波low-velocity layer:低速层：marker bed:标准层：migration: 偏移，运移：minimum-phase:最小相位：multiple:多次波：multiple coverage:多次覆盖：multiplex:多路传输，多倍仪multiplexed format:多路编排格式：mute:切除：NMO: Normal moveout.正常时差。

PMT Package - User GuideHow to Access PMT AppFrom the App Launcher, you have two options to access PMT:●●PMT Console - RECOMMENDED PMTPMT ArchitecturePMT AutomationsThe following automations have been built to facilitate project updatesON PROJECTS●○●Start and End Dates are rolling from PMT TasksInitial Start and End Dates fields set during project creation remain unchangedProject % of Completion is rolling from PMT Tasks using a weighted average based on the task duration ON PHASES●●Start and End dates are rolling from PMT TasksPhase % of completion is rolling from PMT Tasks using a weighted average based on the task duration ON PMT TASKS●○Setting a Task status to Completed will automatically set its % of completion to 100 and vice-versa.To reopen a Task, both the Status and % of Completion must be updated.PMT ObjectsUSERS - STANDARD OBJECT●●○This is the Salesforce standard User object, used to define the PMT records ownership, PMT Tasks and Resource Availability assignmentsCustom fields:Is PMT User consider for Availability: check this checkbox for the users who should be available as resources for resource planning.PROGRAMS - CUSTOM OBJECT●●Programs are used to group Projects under a common umbrella, allowing to track and report on Programs achievements and status.Recommendation: Even if linking a Project to a Program is not mandatory , to facilitate the reporting and enforce data coherence, we recommend to assign non-program related Projects to a default “Individual Projects” Program .Creating a Program1. a.b.c.2. a.b.c.Option 1 - From Program object:Open the Program objectFrom the List view, click NewEnter Program Name and update Program Health if neededOption 2 - From Project details:Edit the Program fieldFrom the lookup search dropdown menu, click New ProgramEnter Program Name and update Program Health if neededProgram Page●Tab Chatter : Program dedicated Chatter feed●Tab Details : Default landing Page, presenting Program details and related Projects within a Lightning Enhanced datatable.PROJECTS - CUSTOM OBJECTCreating a Project Template○○○○○○○○■■■■□□□Open the Project objectFrom the List view, click NewEnter Project Name + mandatory fields and other necessary information.Check the checkbox field IsTemplate to mark the project as template.Create the phases and tasks which will then be used for project creation.NOTE : Avoid adding any resources to templates as resources will not be cloned.These projects are excluded from the reports provided in this package. Any further reports created should consider adding the filter as per the requirements.Task object contain some new fields to allow date calculations Start Days Out - Used to calculate the start date from project start date.Duration in Days - Adds the number of days to the task start date to calculate task end date.These date calculations exclude weekends (Sat and Sun) by default, this setting can be changed by the admin.Example for the date calculation:Let’s assume a task with start days out as 7 and duration in days 10.The user selected 5th Dec 2022 as the start date for the project.Creating a Project●○○○●○○○○○Option 1 : From Project object:Open the Project objectFrom the List view, click NewEnter Project Name + mandatory fields and other necessary information.Option 2 : From Project Template:Open the Project objectFrom the List view called 'All Templates ', select the template you want to use.Click on the button ‘Use This Template ’Enter Project Name and Start Date > Click NextSelect Phases and Tasks to clone on the next screens.Project Page●○○○■■■Tab Project Summary , Default landing pagepresenting:Project key informationsHealth, Status and Path to GreenPhase Table displaying:Phase status and completionTasks with an end date in Currentand Next periodsOngoing Tasks with an end dateafter Next period ●○○○Tips: All Icons are clickable and will open the related record in Edit mode for quick updates.The right corner buttons allows toswitch from a weekly to a monthly orquarterly viewThe Milestone List button will displayKey Milestones tasks in a popup.●○○Tab Chatter & ActivityProject dedicated Chatter feedProject Activity (emails + events) loggedfrom Salesforce Gmail/Outlookapplication●○○Tab Project DetailsProject record detailsInclude all the project information andfields used to document or report on theproject.●○■■■■■○■■■■Tab TasksSub-tab TasksDisplay PMT Tasks in a table UIUse picklists at the top to filterInline editing on Task Name, %compl., Start, End dates andDescriptionStandard mass change on abovefields by using the row checkboxesMass change via flow on Statusand Assigned To fields by usingrows checkbox + Changed buttonat the top of the table.Subtab Gantt ChartUse ‘Expand Al l’ button to see allphases and tasks.The colours representation for thegantt is mentioned on the rightside of the filters.Y ou can use the ‘View By ’dropdown to change thetimeframeGantt will not show anything forthe template type project.●○○○○Tab CasesDisplay the Cases in datatable UIUse picklists at the top to filter the tableClick on Case Number to open the CaserecordUse the row drop-down menu toOpen/Edit the case●○○Tab ResourcesDisplay Allocated Resources in a table UIClick Edit Allocations to switch to Edit○○ModeOnce in Edit mode, Click Save to validatechangesClick on the Resources Green Icon toupdate an assignment.●○■■■Tab FilesPresent the Files component, allowing toadd documentation to the project from:User computerGoogle Drive (if setup by admin)Quip (if setup by admin)PHASES - CUSTOM OBJECTThe phase object is used to give Projects a structure and group related PMT Tasks.Create Phases●○○○○●○○○○ Option 1 : From the Project Summary > Create PhasesButton:Click on theCreate Phases buttonA popup will appear allowing multiplephases to be created at onceClick the +Add Row button to addmultiple PhasesTips: Phases will be sorted based on thestart date on the Summary Page.Option 2 : From the Project Summary > ClonePhases/Tasks Button:Click on the Clone Phases/Tasks buttonSearch for a project to clone from andclick next.Select the phases to clone and click next.Select the tasks to clone and click next.Phase Page●○Tab DetailsDefault landing page providing the Phaserecord details○●○Present an enhanced list of related PMTTasksTab ChatterPhase dedicated Chatter feed.PMT TASKS - CUSTOM OBJECTThe PMT Tasks object represent the Project deliverables and work items and define the project timeline .Create PMT Tasks●○○○○ From the Project Summary or Tasks Tabs:Click on the Create Tasks buttonA popup will appear allowing multiplePMT Tasks to be created at once Click the +Add Row button to addmultiple TasksTips: To better identify Tasks relatedPhase and order them in the list andtable, a best practice is to number them,first with the Phase number and then asyou wish (1.01, 1.102...)PMT Task Page●○○Tab DetailsDefault PMT Tasks landing pagePresent record details●○○○Tab Chatter & ActivityPMT Tasks related Chatter FeedSend email from ActivityLog emails and Event with the GoogleSalesforce add-on●○Tab FilesDocument your Tasks by addingdocuments from your computer, GoogleDrive or Quip based on the integrationsdone using files connect.CASES - STANDARD OBJECTCases in PMT represent the Project RAID Log: Risks, Actions, Issues, Decisions. Salesforce Case feature allows to collaborate, document, share and quickly solved Project open items.Create PMT Tasks●○From Project Summary or Cases TabsClick New Case buttonCase Page●○■○○○○●●●Right PanelCase CommentsStatus update on the CaseCase HistoryRelated CasesFollowersEmails and Files attachedTab Details : Case informationsTab Chatter : Dedicated Chatter FeedTab Activity : Logged emails and EventRESOURCES ALLOCA TIONS - CUSTOM OBJECT●●●The Resource Allocation object records people allocated on Projects with their monthly % of allocations.One record per person and Fiscal year is created on the project.To manage Project Allocations, see Tab ResourcesRESOURCES A VAILABILITY - CUSTOM OBJECTOptional object: Only to be used if you plan to track your team resource capacity .Create Resource Availability●●Resource Availability records are automatically created based on the configuration done by the admin.Please get in touch with your admin for more details.Resource Availability Page●○■□□□■□□●○Tab DetailsDefault landing pageAllocation summaryCapacityAllocatedRemaining AvailabilityAssigned ProjectsEnhanced list presentedassigned projectsInline editing to quicklyupdate project allocations.Tab ChatterDedicated Chatter feedGlobal Custom TabsRESOURCE MANAGEMENT●●●●This view allows you to see the global resourcing at the org level.Filters are provided to filter on any specific resourcing needs.Inline editing is allowed ‘Resource Capacity’ and ‘Project Allocations ’ tabPMT GANTT VIEW●This shows the gantt chart at the org level, allowing users to filter and see the gantt view for multiple projects.●●●This view is limited to 30 projects at a time to keep the performance better, filter further to see any specific projects. Templates are excluded from this view.For any additional queries, please reach out to us atF********************************************。

全文分为作者个人简介和正文两个部分：作者个人简介：Hello everyone, I am an author dedicated to creating and sharing high-quality document templates. In this era of information overload, accurate and efficient communication has become especially important. I firmly believe that good communication can build bridges between people, playing an indispensable role in academia, career, and daily life. Therefore, I decided to invest my knowledge and skills into creating valuable documents to help people find inspiration and direction when needed.正文：陶大高中英语作文最简单三个步骤全文共3篇示例，供读者参考篇1The Easiest 3 Steps to Write a High School English CompositionAs a high school student, writing compositions can be a daunting task, especially in English class. We often find ourselvesstaring at a blank page, unsure of where to begin or how to organize our thoughts. However, fear not! With a few simple steps, you can conquer the art of essay writing and impress your English teacher.Step 1: Understand the Prompt and Brainstorm IdeasThe first and most crucial step in writing a successful composition is to thoroughly understand the prompt or question you're being asked to address. Read it carefully, underline or highlight key words, and make sure you grasp the crux of the task at hand.Once you've deciphered the prompt, it's time to unleash the power of brainstorming. This step is like a warm-up exercise for your brain, allowing you to generate as many ideas as possible without judging or censoring them. You can use mind maps, bullet points, or even good old-fashioned free writing to get those creative juices flowing.During the brainstorming process, don't hold back – let your thoughts run wild! Jot down anything that comes to mind, no matter how random or seemingly irrelevant it may seem. You never know which idea might spark an insightful connection or lead you down an unexpected yet compelling path.Step 2: Organize Your Thoughts and Create an OutlineAfter you've amassed a treasure trove of ideas, it's time to bring order to the chaos. This is where an outline comes into play, serving as the blueprint for your composition.Start by grouping your ideas into main points or topics, and arrange them in a logical sequence that flows smoothly from one point to the next. This structure will not only help you stay focused but also make it easier for your reader to follow your train of thought.Once you've established your main points, flesh them out with supporting details, examples, or evidence that reinforce your arguments. Remember, a well-crafted outline is like a roadmap – it guides you through the writing process and ensures that you don't get lost along the way.Step 3: Write, Revise, and PolishWith your outline in hand, it's time to embark on the writing journey. Don't worry about perfection just yet; focus on getting your thoughts down on paper (or screen) in a clear and coherent manner.As you write, refer back to your outline to ensure that you're staying on track and addressing all the necessary points. Don'tbe afraid to deviate from your initial plan if you come across a brilliant idea that enhances your argument – flexibility is key!Once you've completed your first draft, it's time for the revising and polishing phase. This is where you'll fine-tune your composition, checking for logical flow, clarity, and coherence. Read your work aloud to catch any awkward phrasing or clunky sentences, and don't hesitate to rearrange or rewrite sections if needed.Pay close attention to grammar, spelling, and punctuation errors – they can detract from the overall quality of your work. Consider having a friend, family member, or classmate review your composition and provide feedback; fresh eyes can often spot mistakes or areas for improvement that you may have missed.Remember, writing is an iterative process, and even the most accomplished authors go through multiple rounds of revisions. Embrace the editing process and strive for continuous improvement – your dedication will shine through in the final product.In ConclusionWriting a high school English composition may seem like a formidable task, but by following these three simple steps –understanding the prompt, creating an outline, and revising your work – you'll be well on your way to crafting a compelling and well-written piece.Embrace the writing process, stay organized, and don't be afraid to seek feedback or guidance when needed. With practice and perseverance, you'll not only improve your writing skills but also gain confidence in expressing your thoughts and ideas effectively.So, the next time you're faced with a composition assignment, take a deep breath, roll up your sleeves, and follow these steps – you've got this!篇2The Three Simplest Steps to Write an English Essay for Tao High SchoolHey everyone! As a current senior at Tao High, I know how stressful it can be to write those English essays we're always getting assigned. I've had so many panic attacks and all-nighters trying to crank those things out at the last minute. But over the years, I've figured out a few simple steps that have really helpedme get through the essay writing process without wanting to pull my hair out. I'm sharing my secrets with you today in the hope that they'll make your essay writing life a bit easier too!Step 1: Understand the Prompt/QuestionThis first step is crucial and sets the foundation for your entire essay. You need to make sure you fully understand what the prompt or question is asking you to do. Read it over very carefully, and if anything is unclear, ask your teacher to explain further.For example, let's say the prompt is: "Should high schools require students to perform community service? Present arguments from both sides and state your position." You need to identify a few key things:You must discuss arguments both for and against mandatory community service in high school. So you can't just pick a side and run with it.You need to state your own position/opinion on the issue after presenting the arguments.The prompt is not asking you to summarize what community service is - it assumes you already know that concept.Once you understand all the components the prompt is asking for, you're ready to start planning your essay structure. But skipping this critical first step of fully comprehending the prompt will put you on the wrong path from the start.Step 2: Create a Solid OutlineI know what you're thinking - making an outline is so boring and unnecessary, right? Wrong! An outline is going to be your best friend when writing any decent essay. It helps organize your thoughts into a logical sequence and ensures you don't miss any important points. Trust me, it's better than just winging it.So for our sample community service prompt, here's what a basic outline might look like:I. IntroductionHook/Background InfoThesis StatementII. Body Paragraph 1- Argument FOR mandatory community service- Supporting evidence/examplesIII. Body Paragraph 2- Argument AGAINST mandatory community service- Supporting evidence/examplesIV. Body Paragraph 3- Your position/opinion- Reasons for your stanceV. Conclusion- Restate thesis- Call to action/Concluding thoughtsWithin this structure, you can easily plug in the actual points and evidence you'll use under each section. The outline acts as a roadmap to follow so your essay flows logically rather than being all over the place.Having this outline allows you to ensure you've hit all the components the prompt asked for - presenting both sides, giving your opinion, using relevant support, etc. It makes the actual writing process much simpler when you can follow this guide instead of trying to organize your thoughts as you go.Step 3: Write, Revise, PolishNow for the part we all dread - actually writing the essay itself. But if you've followed the first two steps, it really shouldn't be horrible!For each section, take the notes from your outline and expand them into full, detailed paragraphs. Don't worry about making it perfect at first - just get all your thoughts down into paragraph form following the outline structure.You may find that some paragraphs are longer than others, and that's fine. The body paragraphs that present your evidence and examples will likely be the meatiest parts. Just make sure to fully explain and support the points you're making.Once you have all your paragraphs written out, go back through and revise. Look for any spots that seem unclear, choppy, or lacking evidence, and smooth those out. Make sure your transitions between paragraphs flow well. Check that you introduced your arguments properly and aren't just jumping right into them.Finally, do one last polish of the whole thing - cleaning up grammar, tweaking word choices, ensuring your essay still fully answers the prompt, etc. Give it a snazzy title too if you'd like. Proofread carefully before declaring it complete.And that's it! Three simple, straightforward steps to help you tackle any essay. I'm not saying this will make writing essays fun and exciting all of a sudden. It's still a process that requires effort. But these steps at least provide a clear framework to follow so you don't feel so overwhelmed and lost.Remember, any time you get stuck, refer back to the prompt to re-orient yourself. As long as you fully understand what it's asking and create an outline to organize your thoughts, the rest is really just filling in the blanks.So don't stress too much, Tao High fam! Writing essays doesn't have to be panic-inducing if you break it down into these straightforward steps. Go forth and scribbleyour hearts out! You've got this.篇3The Three Simplest Steps for English Writing at Tao High SchoolAs a high school student, writing in English can seem like an intimidating task. We're expected to craft well-structured essays, use sophisticated vocabulary, and express complex ideas – all in a language that isn't our native tongue. However, over the past few years at Tao High, I've discovered that effective Englishwriting can be boiled down to three simple steps: planning, drafting, and revising. By following these steps diligently, even the most daunting writing assignments can become manageable.Step 1: PlanningThe first and arguably most crucial step in the writing process is planning. Before putting pen to paper (or fingers to keyboard), it's essential to have a clear understanding of the assignment prompt, the purpose of your writing, and your intended audience. At Tao High, our English teachers emphasize the importance of brainstorming and organizing our thoughts before diving into the actual writing.One effective planning technique is mind mapping. Start with the central topic or prompt in the middle of a blank page, and then branch out with related ideas, supporting details, and examples. This visual representation of your thoughts can help you identify connections and hierarchies within your ideas, making it easier to structure your essay later on.Another valuable planning tool is an outline. After brainstorming, organize your ideas into a logical sequence, with main points and supporting details clearly delineated. This stephelps ensure that your essay will have a coherent flow and that each point will be adequately supported.During the planning stage, it's also crucial to consider your audience and purpose. Are you writing to inform, persuade, or entertain? Tailoring your language, tone, and approach to your specific audience and purpose will make your writing more effective and engaging.Step 2: DraftingOnce you've planned your essay, it's time to start drafting. This is where the actual writing happens, and it's essential to approach this step with an open mind and a willingness to let your ideas flow freely.At Tao High, we're taught to start with a strong introduction that captures the reader's attention and clearly states the main thesis or argument of our essay. From there, we build upon our outline, crafting well-developed body paragraphs that support our thesis with relevant evidence, examples, and analysis.During the drafting stage, it's important to focus on getting your ideas down on paper (or screen) without getting too bogged down in perfecting every sentence or worrying about minor errors. The goal is to get your thoughts organized andexpressed in a coherent manner – the polishing and refining will come later.One crucial aspect of effective drafting is the use of transitions. These words and phrases (such as "furthermore," "however," "in addition," etc.) help guide the reader smoothly from one idea to the next, creating a sense of cohesion and flow within your essay.Step 3: RevisingAfter completing your initial draft, it's time for theoften-dreaded but absolutely essential step of revising. This is where you critically evaluate your work, identify areas for improvement, and refine your writing to ensure clarity, coherence, and impact.At Tao High, our English teachers emphasize the importance of stepping away from our drafts for a period of time before revising. This allows us to approach our work with a fresh perspective, making it easier to spot areas that need improvement or clarification.During the revision process, we focus on several key areas:Content and organization: Does your essay effectively address the prompt or central idea? Are your points logicallystructured and supported with strong evidence? Are there any gaps or redundancies that need to be addressed?Clarity and conciseness: Have you expressed your ideas clearly and concisely, without unnecessary wordiness or ambiguity? Are there any confusing or awkward phrasing that needs to be revised?Grammar, spelling, and punctuation: While these technical aspects may seem less important than content, they are crucial for ensuring that your writing is polished and professional. Take the time to carefully proofread your work and correct any errors.Style and tone: Does your writing style and tone effectively engage your intended audience? Are you maintaining a consistent voice throughout the essay?Revising is an iterative process, and it's not uncommon to go through multiple rounds of revisions before achieving a final draft that you're truly satisfied with. At Tao High, we're encouraged to seek feedback from our peers and teachers, as fresh perspectives can often help identify areas for improvement that we may have overlooked.By following these three simple steps – planning, drafting, and revising – even the most daunting English writingassignments can become manageable and even enjoyable. With practice and perseverance, you'll develop the skills and confidence to express your ideas effectively in written English, a valuable asset for academic success and beyond.。

transistor n 晶体管diode n 二极管semiconductor n 半导体resistor n 电阻器capacitor n 电容器alternating adj 交互的amplifier n 扩音器，放大器integrated circuit 集成电路linear time invariant systems 线性时不变系统voltage n 电压，伏特数tolerance n 公差；宽容；容忍condenser n 电容器；冷凝器dielectric n 绝缘体；电解质electromagnetic adj 电磁的adj 非传导性的deflection n偏斜；偏转；偏差linear device 线性器件the insulation resistance 绝缘电阻anode n 阳极，正极cathode n 阴极breakdown n 故障；崩溃terminal n 终点站；终端，接线端emitter n 发射器collect v 收集，集聚，集中insulator n 绝缘体，绝热器oscilloscope n 示波镜；示波器gain n 增益，放大倍数forward biased 正向偏置reverse biased 反向偏置P-N junction PN结MOS（metal-oxide semiconductor）金属氧化物半导体enhancement and exhausted 增强型和耗尽型integrated circuits 集成电路analog n 模拟digital adj 数字的，数位的horizontal adj, 水平的，地平线的vertical adj 垂直的，顶点的amplitude n 振幅，广阔，丰富attenuation n衰减；变薄；稀薄化multimeter n 万用表frequency n 频率，周率the cathode-ray tube 阴极射线管dual-trace oscilloscope 双踪示波器signal generating device 信号发生器peak-to-peak output voltage 输出电压峰峰值sine wave 正弦波triangle wave 三角波square wave 方波amplifier 放大器，扩音器oscillator n 振荡器feedback n 反馈，回应phase n 相，阶段，状态filter n 滤波器，过滤器rectifier n整流器；纠正者band-stop filter 带阻滤波器band-pass filter 带通滤波器decimal adj 十进制的，小数的hexadecimal adj/n十六进制的binary adj 二进制的；二元的octal adj 八进制的domain n 域；领域code n代码，密码，编码v编码the Fourier transform 傅里叶变换Fast Fourier Transform 快速傅里叶变换microcontroller n 微处理器；微控制器assembly language instrucions n 汇编语言指令chip n 芯片，碎片modular adj 模块化的；模数的sensor n 传感器plug vt堵，塞，插上n塞子，插头，插销relay contact 继电接触器single instruction programmer 单指令编程器dedicated manufactures programming unit 专供制造厂用的编程单元beam n （光线的）束，柱，梁polarize v（使）偏振，（使）极化Cathode Ray Tube（CRT）阴极射线管neuron n神经元；神经细胞fuzzy adj 模糊的Artificial Intelligence Shell 人工智能外壳程序Expert Systems 专家系统Artificial Intelligence 人工智能Perceptive Systems 感知系统neural network 神经网络fuzzy logic 模糊逻辑intelligent agent 智能代理electromagnetic adj 电磁的coaxial adj 同轴的，共轴的microwave n 微波charge v充电，使充电insulator n 绝缘体，绝缘物nonconductive adj非导体的，绝缘的antenna n天线；触角modeling n建模，造型simulation n 仿真；模拟prototype n 原型array n 排队，编队vector n 向量，矢量wavelet n 微波，小浪sine 正弦cosine 余弦inverse adj倒转的，反转的n反面；相反v倒转high-performance 高精确性，高性能two-dimensional 二维的；缺乏深度的three-dimensional 三维的；立体的；真实的object-oriented programming面向对象的程序设计spectral adj 光谱的attenuation n衰减；变薄；稀释distortion n 失真，扭曲，变形wavelength n 波长refractive adj 折射的ATM 异步传输模式Asynchronous TransferModeADSL非对称用户数字线Asymmetric digitalsubscriber lineVDSL甚高速数字用户线very high data ratedigital subscriber lineHDSL高速数据用户线high rate digitalsubscriber lineFDMA频分多址(Frequency Division MultipleAccess)TDMA时分多址(Time Division Multiple Access)CDMA同步码分多址方式(Code Division MultipleAccess)WCDMA宽带码分多址移动通信系统(WidebandCode Division Multiple Access)TD-SCDMA(Time Division Synchronous CodeDivision Multiple Access)时分同步码分多址SDLC(synchronous data link control)同步数据链路控制HDLC(high-level data link control)高级数据链路控制IP/TCP(internet protocol /transfer ControlProtocol)网络传输控制协议ITU (International Telecommunication Union)国际电信联盟ISO国际标准化组织（InternationalStandardization Organization）；OSI开放式系统互联参考模型（Open SystemInterconnect）GSM全球移动通信系统（Global System forMobile Communications）FDD(frequency division duplex)频分双工TDD(time division duplex)时分双工VPI虚路径标识符（Virtual Path Identifier）；ISDN（Integrated Services Digital Network）综合业务数字网IDN综合数字网（integrated digital network）HDTV (high definition television)高清晰度电视DCT(Discrete Cosine Transform)离散余弦变换VCI(virtual circuit address)虚通路标识MAN城域网Metropolitan area networksLAN局域网local area networkWAN广域网wide area network同步时分复用STDM Synchronous Time DivisionMultiplexing统计时分复用STDM Statistical Time DivisionMultiplexing单工传输simplex transmission半双工传输half-duplex transmission全双工传输full-duplex transmission交换矩阵Switching Matrix电路交换circuit switching分组交换packet switching报文交换message switching奇偶校验parity checking循环冗余校验CRC Cyclic Redundancy Check虚过滤Virtual filter数字滤波digital filtering伪随机比特Quasi Random Bit带宽分配Bandwidth allocation信源information source信宿destination数字化digitalize数字传输技术Digital transmission technology灰度图像Grey scale images灰度级Grey scale level幅度谱Magnitude spectrum相位谱Phase spectrum频谱frequency spectrum智能设备Smart Device软切换Soft handover硬切换Hard Handover相干检测Coherent detection边缘检测Edge detection冲突检测collision detection业务集合service integration业务分离/综合service separation/ integration网络集合network integration环形网Ring networks令牌环网Token Ring network网络终端Network Terminal用户终端user terminal用户电路line circuit电路利用率channel utilization（通道利用率）相关性coherence相干解调coherent demodulation数字图像压缩digital image compression图像编码image encoding有损/无损压缩lossy/lossless compression解压decompression呼叫控制Call Control误差控制error control存储程序控制stored program control存储转发方式store-and-forward manner语音\视频传输voice\video transmission视频点播video-on-demand(VOD)会议电视Video Conference有线电视cable television量化quantization吞吐量throughput话务量traffic多径分集Multipath diversity多媒体通信MDM Multimedia Communication多址干扰Multiple Access Interference-路由算法Routing Algorithm目标识别Object recognition话音变换Voice transform中继线trunk line传输时延transmission delay远程监控remote monitoring光链路optical link拓扑结构Topology均方根root mean squarewhatsoever=whatever 0switchboard (电话)交换台bipolar （电子）双极的premise （复）房屋，前提cursor (计算机尺的)游标，指导的elapse （时间）经过，消失vaporize （使）蒸发subsystem （系统的）分部，子系统，辅助系统metallic （像）金属的，含金属的，（声音）刺耳的dispatch （迅速）派遣，急件consensus （意见）一致，同意deadline （最后）期限，截止时间tomographic X线体层摄像的alas 唉，哎呀cluster 把…集成一束，一组，一簇，一串，一群encyclopedia 百科全书millionfold 百万倍的semiconductor 半导体radius 半径范围，半径，径向射线half-duplex transmission 半双工传输accompaniment 伴随物，附属物reservation 保留，预定quotation 报价单，行情报告，引语memorandum 备忘录redundancy 备用be viewed as 被看作…be regards as 被认为是as such 本身；照此；以这种资格textual 本文的，正文的verge 边界variation 变化，变量conversion 变化，转化identity 标识；标志criterion 标准，准则in parallel on 并联到，合并到juxtapose 并置，并列dialing pulse 拨号脉冲wave-guide 波导wavelength division multiplexed 波分复用baud rate 波特率playback 播放（录音带，唱片）no greater than 不大于update 不断改进，使…适合新的要求，更新asymmetric 不对称的irrespective 不考虑的，不顾的inevitably 不可避免的inevitable 不可避免的，不可逃避的，必定的segment 部分abrasion 擦伤，磨损deploy 采用，利用，推广应用take the form of 采用…的形式parameter 参数，参量layer 层dope 掺杂FET(field effect transistors) 场效应管audio recording 唱片ultra-high-frequency(UHF) 超高频in excess of 超过in excess of 超过hypertext 超文本ingredient 成分，因素ingredient 成分，组成部分，要素metropolitan-area network(WAN) 城域网metropolitan area network(WAN) 城域网，城市网络congestion 充满，拥挤，阻塞collision 冲突extractive 抽出；释放出extract 抽取，取出，分离lease 出租，租约，租界期限，租界物pass on 传递，切换transmission 传输facsimile 传真innovative=innovatory 创新的，富有革新精神的track 磁道impetus 促进，激励cluster 簇stored-program control(SPC) 存储程序控制a large number of 大量的peal 大声响，发出supersede 代替supplant 代替，取代out-of-band signaling 带外信号simplex transmission 单工传输monochromatic 单色的，单色光的，黑白的ballistic 弹道的，射击的，冲击的conductor 导体hierarchy 等级制度，层次infrastructure 底层结构，基础结构geographic 地理的，地区的geographically 地理上GIS(ground instrumentation system) 地面测量系统ground station 地面站earth orbit 地球轨道extraterrestrial 地球外的，地球大气圈外的Land-sat 地球资源卫星rug 地毯，毯子ignite 点火，点燃，使兴奋electromagnetic 电磁的inductive 电感arc 电弧telephony 电话（学），通话dielectric 电介质，绝缘材料；电解质的，绝缘的capacitor 电容telecommunication 电信，无线电通讯scenario 电影剧本，方案modem pool 调制解调器（存储）池superimposing 叠加，重叠pin 钉住，扣住，抓住customize 定做，定制monolithic 独立的，完全统一的aluminize 镀铝strategic 对全局有重要意义的，战略的substantial 多的，大的，实际上的multi-path fading 多径衰落multi-path 多路，多途径；多路的，多途径的multi-access 多路存取，多路进入multiplex 多路复用multiplex 多路复用的degradation 恶化，降级dioxide 二氧化碳LED(light-emitting-diode) 发光二极管evolution 发展，展开，渐进feedback 反馈，回授dimension 范围，方向，维，元scenario 方案scenario 方案，电影剧本amplifer 放大器noninvasive 非侵略的，非侵害的tariff 费率，关税率；对…征税distributed functional plane(DFP) 分布功能平面DQDB(distributed queue dual bus) 分布式队列双总线hierarchy 分层，层次partition 分成segmentation 分割interface 分界面，接口asunder 分开地，分离地detached 分离的，分开的，孤立的dispense 分配allocate 分配，配给；配给物centigrade 分为百度的，百分度的，摄氏温度的fractal 分形molecule 分子，微小，些微cellular 蜂窝状的cellular 蜂窝状的，格形的，多孔的auxiliary storage(also called secondary storage)辅助存储器decay 腐烂，衰减，衰退negative 负电vicinity 附近，邻近vicinity 附近地区，近处sophisticated 复杂的，高级的，现代化的high-frequency(HF) 高频high definition television 高清晰度电视chromium 铬annotate 给…作注解in terms of 根据，按照disclosure 公布，企业决算公开public network 公用网functionality 功能，功能度mercury 汞resonator 共鸣器resonance 共振whimsical 古怪的，反复无常的administration 管理，经营cursor 光标（显示器），游标，指针optical computer 光计算机photoconductor 光敏电阻optical disks 光盘optically 光学地，光地wide-area networks 广域网specification 规范，说明书silicon 硅the international telecommunication union(ITU)国际电信联盟excess 过剩obsolete 过时的，废弃的maritime 海事的synthetic 合成的，人造的，综合的synthetic 合成的，综合性的rational 合乎理性的rationalization 合理化streamline 合理化，理顺infrared 红外线的，红外线skepticism 怀疑论ring network 环形网hybrid 混合物counterpart 伙伴，副本，对应物electromechanical 机电的，电动机械的Robot 机器人Robotics 机器人技术，机器人学accumulation 积累infrastructure 基础，基础结构substrate 基质，底质upheaval 激变，剧变compact disc 激光磁盘（CD）-concentrator 集中器，集线器centrex system 集中式用户交换功能系统converge on 集中于，聚集在…上lumped element 集总元件CAI(computer-aided instruction) 计算机辅助教学computer-integrated manufacturing(CIM) 计算机集成制造computer mediated communication(CMC) 计算机中介通信record 记录register 记录器，寄存器expedite 加快，促进weight 加权accelerate 加速，加快，促进categorize 加以类别，分类in addition 加之，又，另外hypothetical 假设的rigidly 坚硬的，僵硬的compatibility 兼容性，相容性surveillance 监视surveillance 监视retrieval 检索，（可）补救verification 检验simplicity 简单，简明film 胶片，薄膜take over 接管，接任ruggedness 结实threshold 界限，临界值with the aid of 借助于，用，通过wire line 金属线路，有线线路coherent 紧凑的，表达清楚的，粘附的，相干的compact 紧密的approximation 近似undertake 进行，从事transistor 晶体管elaborate 精心制作的，细心完成的，周密安排的vigilant 警戒的，警惕的alcohol 酒精，酒local area networks(LANs) 局域网local-area networks(LANs) 局域网drama 剧本，戏剧，戏剧的演出focus on 聚集在，集中于，注视insulator 绝缘root mean square 均方根uniform 均匀的open-system-interconnection(OSI) 开放系统互连expire 开始无效，满期，终止immunity 抗扰，免除，免疫性take…into account 考虑，重视…programmable industrial automation 可编程工业自动化demountable 可拆卸的tunable 可调的reliable 可靠be likely to 可能，大约，像要videotex video 可视图文电视negligible 可以忽略的aerial 空气的，空中的，无形的，虚幻的；天线broadband 宽（频）带pervasive 扩大的，渗透的tensile 拉力的，张力的romanticism 浪漫精神，浪漫主义discrete 离散，不连续ion 离子force 力量；力stereophonic 立体声的continuum 连续统一体，连续统，闭联集smart 灵巧的；精明的；洒脱的token 令牌on the other hand 另一方面hexagonal 六边形的，六角形的hexagon 六角形，六边形monopoly 垄断，专利video-clip 录像剪辑aluminum 铝pebble 卵石，水晶透镜forum 论坛，讨论会logical relationships 逻辑关系code book 码本pulse code modulation(PCM) 脉冲编码调制roam 漫步，漫游bps(bits per second) 每秒钟传输的比特ZIP codes 美国邮区划分的五位编码susceptible(to) 敏感的，易受…的analog 模拟，模拟量pattern recognition模式识别bibliographic 目录的，文献的neodymium 钕the european telecommunicationstandardization institute(ETSI) 欧洲电信标准局coordinate 配合的，协调的；使配合，调整ratify 批准，认可bias 偏差；偏置deviate 偏离，与…不同spectrum 频谱come into play 其作用entrepreneurial 企业的heuristic methods 启发式方法play a …role(part) 起…作用stem from 起源于；由…发生organic 器官的，有机的，组织的hypothesis 前提front-end 前置，前级potential 潜势的，潜力的intensity 强度coincidence 巧合，吻合，一致scalpel 轻便小刀，解剖刀inventory 清单，报表spherical 球的，球形的distinguish 区别，辨别succumb 屈服，屈从，死global functional plane(GFP) 全局功能平面full-duplex transmission 全双工传输hologram 全息照相，全息图deficiency 缺乏thermonuclear 热核的artifact 人工制品AI(artificial intelligence) 人工智能fusion 熔解，熔化diskettes(also called floppy disk) 软盘sector 扇区entropy 熵uplink 上行链路arsenic 砷neural network 神经网络very-high-frequency(VHF) 甚高频upgrade 升级distortion 失真，畸变identification 识别，鉴定，验明pragmatic 实际的implementation 实施，实现，执行，敷设entity 实体，存在vector quantification 矢量量化mislead 使…误解，给…错误印象，引错vex 使烦恼，使恼火defy 使落空facilitate 使容易，促进retina 视网膜compatible 适合的，兼容的transceiver 收发两用机authorize 授权，委托，允许data security 数据安全性data independence 数据独立data management 数据管理database 数据库database management system(DBMS) 数据库管理信息系统database transaction 数据库事务data integrity 数据完整性，数据一致性attenuation 衰减fading 衰落，衰减，消失dual 双的，二重的transient 瞬时的deterministic 宿命的，确定的algorithm 算法dissipation 损耗carbon 碳diabetes 糖尿病cumbersome 讨厌的，麻烦的，笨重的razor 剃刀，剃go by the name of 通称，普通叫做commucation session 通信会话traffic 通信业务（量）synchronous transmission 同步传输concurrent 同时发生的，共存的simultaneous 同时发生的，同时做的simultaneous 同时发生的，一齐的coaxial 同轴的copper 铜statistical 统计的，统计学的dominate 统治，支配invest in 投资perspective 透视，角度，远景graphics 图示，图解pictorial 图像的coating 涂层，层deduce 推理reasoning strategies 推理策略inference engine 推理机topology 拓扑结构heterodyne 外差法的peripheral 外界的，外部的，周围的gateway 网关hazardous 危险的microwave 微波（的）microprocessor 微处理机，微处理器microelectronic 微电子nuance 微小的差别（色彩等）encompass 围绕，包围，造成，设法做到maintenance 维护；保持；维修satellite communication 卫星通信satellite network 卫星网络transceiver 无线电收发信机radio-relay transmission 无线电中继传输without any doubt 无疑passive satellite 无源卫星sparse 稀少的，稀疏的downlink 下行链路precursor 先驱，前任visualization 显像feasibility 现实性，可行性linearity 线性度constrain 限制，约束，制约considerable 相当的，重要的geo-stationary 相对地面静止by contrast 相反，而，对比起来coorelation 相关性mutual 相互的mutually 相互的，共同的interconnect 相互连接，互连one after the other 相继，依次-minicomputer 小型计算机protocol 协议，草案protocol 协议，规约，规程psycho-acoustic 心理（精神）听觉的；传音的channelization 信道化，通信信道选择run length encoding 行程编码groom 修饰，准备virtual ISDN 虚拟ISDNmultitude 许多，大批，大量whirl 旋转preference 选择，喜欢avalanche 雪崩pursue 寻求，从事interrogation 询问dumb 哑的，不说话的，无声的subcategory 亚类，子种类，子范畴orbital 眼眶；轨道oxygen 氧气，氧元素service switching and control points(SSCPs) 业务交换控制点service control points(SCPs) 业务控制点service control function(SCF) 业务控制功能in concert 一致，一齐handover 移交，越区切换at a rate of 以……的速率in the form of 以…的形式base on…以…为基础yttrium 钇（稀有金属，符号Y）asynchronous transmission 异步传输asynchronous 异步的exceptional 异常的，特殊的voice-grade 音频级indium 铟give rise to 引起，使产生cryptic 隐义的，秘密的hard disk 硬盘hard automation 硬自动化by means of 用，依靠equip with 用…装备subscriber 用户telex 用户电报PBX(private branch exchange) 用户小交换机或专用交换机be called upon to 用来…，（被）要求…superiority 优势predominance 优势，显著active satellite 有源卫星in comparison with 与…比较comparable to 与…可比preliminary 预备的，初步的premonition 预感，预兆nucleus 原子核valence 原子价circumference 圆周，周围teleprocessing 远程信息处理，遥控处理perspective 远景，前途constrain 约束，强迫mobile 运动的，流动的，机动的，装在车上的convey 运输，传递，转换impurity 杂质impurity 杂质，混杂物，不洁，不纯regenerative 再生的improve over 在……基础上改善play important role in 在…中起重要作用in close proximity 在附近，在很近underlying 在下的，基础的in this respect 在这方面entail 遭遇，导致presentation 赠与，图像，呈现，演示narrowband 窄（频）带deploy 展开，使用，推广应用megabit 兆比特germanium 锗positive 正电quadrature 正交orthogonal 正交的quadrature amplitude modulation(QAM) 正交幅度调制on the right track 正在轨道上sustain 支撑，撑住，维持，持续outgrowh 支派；长出；副产品dominate 支配，统治knowledge representation 知识表示knowledge engineering 知识工程knowledge base 知识库in diameter 直径helicopter 直升飞机acronym 只取首字母的缩写词as long as 只要，如果tutorial 指导教师的，指导的coin 制造（新字符），杜撰fabrication 制造，装配；捏造事实proton 质子intelligence 智能，智力，信息intelligent network 智能网intermediate 中间的nucleus(pl.nuclei) 中心，核心neutrons 中子terminal 终端，终端设备overlay 重叠，覆盖，涂覆highlight 重要的部分，焦点charge 主管，看管；承载dominant 主要的，控制的，最有力的cylinder 柱面expert system 专家系统private network 专用网络transition 转变，转换，跃迁relay 转播relay 转播，中继repeater 转发器，中继器pursue 追赶，追踪，追求，继续desktop publish 桌面出版ultraviolet 紫外线的，紫外的；紫外线辐射field 字段vendor 自动售货机，厂商naturally 自然的；天生具备的synthesize 综合，合成integrate 综合，使完全ISDN(intergrated services digital network) 综合业务数字网as a whole 总体上bus network 总线形网crossbar 纵横，交叉impedance 阻抗initial 最初的，开始的optimum 最佳条件appear as 作为…出现A Analog 模拟A/D Analog to Digital 模-数转换AAC Advanced Audio Coding 高级音频编码ABB Automatic Black Balance 自动黑平衡ABC American Broadcasting Company 美国广播公司Automatic Bass Compensation 自动低音补偿Automatic Brightness Control 自动亮度控制ABL Automatic Black Level 自动黑电平ABLC Automatic Brightness LimiterCircuit 自动亮度限制电路ABU Asian Broadcasting Union 亚洲广播联盟(亚广联ABS American Bureau of Standard 美国标准局AC Access Conditions 接入条件Audio Center 音频中心ACA Adjacent Channel Attenuation 邻频道衰减ACC Automatic Centering Control 自动中心控制Automatic Chroma Control 自动色度(增益ACK Automatic Chroma Killer 自动消色器ACP Additive Colour Process 加色法ACS Access Control System 接入控制系统Advanced Communication Service 高级通信业务Area Communication System 区域通信系统ADC Analog to Digital Converter 模-数转换器Automatic Degaussirng Circuit 自动消磁电路ADL Acoustic Delay Line 声延迟线ADS Audio Distribution System 音频分配系统AE Audio Erasing 音频（声音AEF Automatic Editing Function 自动编辑功能AES Audio Engineering Society 音频工程协会AF Audio Frequency 音频AFA Audio Frequency Amplifier 音频放大器AFC Automatic Frequency Coder 音频编码器Automatic Frequency Control 自动频率控制AFT Automatic Fine Tuning 自动微调Automatic Frequency Track 自动频率跟踪Automatic Frequency Trim 自动额率微调AGC Automatic Gain Control 自动增益控制AI Artificial Intelligence 人工智能ALM Audio-Level Meter 音频电平表AM Amplitude Modulation 调幅AMS Automatic Music Sensor 自动音乐传感装置ANC Automatic Noise Canceller 自动噪声消除器ANT ANTenna 天线AO Analog Output 模拟输出APS Automatic Program Search 自动节目搜索APPS Automatic Program Pause System自动节目暂停系统APSS Automatic Program Search System自动节目搜索系统AR Audio Response 音频响应ARC Automatic Remote Control 自动遥控ASCII American Standard Code forInformation Interchange 美国信息交换标准AST Automatic Scanning Tracking 自动扫描跟踪ATC Automatic Timing Control 自动定时控制Automatic Tone Correction 自动音频校-正ATM Asynchronous Transfer Mode 异步传输模式ATF Automatic Track Finding 自动寻迹ATS Automatic Test System 自动测试系统ATSC Advanced Television Systems Committee （美国高级电视制式委员会）***C Automatic Volume Control 自动音量控制***R Automatic Voltage Regulator 自动稳压器AWB Automatic White Balance 自动白平衡AZC Automatic Zooming Control 自动变焦控制AZS Automatic Zero Setting 自动调零BA Branch Amplifier 分支放大器Buffer Amplifier 缓冲放大器BAC Binary-Analog Conversion 二进制模拟转换BB Black Burst 黑场信号BBC British Broadcasting Corporation 英国广播公司BBI Beijing Broadcasting Institute 北京广播学院BC Binary Code 二进制码Balanced Current 平衡电流Broadcast Control 广播控制BCT Bandwidth Compression Technique 带宽压缩技术BDB Bi-directional Data Bus 双向数据总线BER Basic Encoding Rules 基本编码规则Bit Error Rate 比特误码率BF Burst Flag 色同步旗脉冲BFA Bare Fiber Adapter 裸光纤适配器Brillouin Fiber Amplifier 布里渊光纤放大器BGM Background Music 背景音乐BIOS Basic Input／Output System 基本输入输出系统B-ISDN Broadband-ISDN 宽带综合业务数据网BIU Basic Information Unit 基本信息单元Bus Interface Unit 总线接口单元BM Bi-phase Modulation 双相调制BML Business Management Layer 商务管理层BN Backbone Network 主干网BNT Broadband Network Termination 宽带网络终端设备BO Bus Out 总线输出BPG Basic Pulse Generator 基准脉冲发生器BPS Band Pitch Shift 分频段变调节器BSI British Standard Institute 英国标准学会BSS Broadcast Satellite Service 广播卫星业务BT Block Terminal 分线盒、分组终端British Telecom 英国电信BTA Broadband Terminal Adapter 宽带终端适配器Broadcasting Technology Association (日本BTL Balanced Transformer-Less 桥式推挽放大电路BTS Broadcast Technical Standard 广播技术标准BTU Basic Transmission Unit 基本传输单元BVU Broadcasting Video Unit 广播视频型(一种3/4英寸带录像机记录格式BW BandWidth 带宽BWTV Black and White Television 黑白电视CA Conditional Access 条件接收CAC Conditional Access Control 条件接收控制CAL Continuity Accept Limit 连续性接受极限CAS Conditional Access System 条件接收系统Conditional Access Sub-system 条件接收子系统CATV Cable Television 有线电视，电缆电视Community Antenna Television 共用天线电视C*** Constant Angular Velocity 恒角速度CBC Canadian Broadcasting Corporation加拿大广播公司CBS Columbia Broadcasting System （美国哥伦比亚广播公司CC Concentric Cable 同轴电缆CCG Chinese Character Generator 中文字幕发生器CCIR International Radio ConsultativeCommittee 国际无线电咨询委员会CCITT International Telegraph andTelephone ConsultativeCommittee 国际电话电报咨询委员会CCR Central Control Room 中心控制室CCTV China Central Television 中国中央电视台Close-Circuit Television 闭路电视CCS Center Central System 中心控制系统CCU Camera Control Unit 摄像机控制器CCW Counter Clock-Wise 反时针方向CD Compact Disc 激光唱片CDA Current Dumping Amplifier 电流放大器CD-E Compact Disc Erasable 可抹式激光唱片CDFM Compact Disc File Manager 光盘文件管理(程序CDPG Compact-Disc Plus Graphic 带有静止图像的CD唱盘CD-ROM Compact Disc-Read OnlyMemory 只读式紧凑光盘CETV China Educational Television 中国教育电视台CF Color Framing 彩色成帧CGA Color Graphics Adapter 彩色图形(显示卡CI Common Interface 通用接口CGA Color Graphics Adapter 彩色图形(显示卡CI Common Interface 通用接口CIE Chinese Institute of Electronics 中国电子学会CII China Information Infrastructure 中国信息基础设施CIF Common Intermediate Format 通用中间格式CIS Chinese Industrial Standard 中国工业标准CLV Constant Linear Velocity 恒定线速度CM Colour Monitor 彩色监视器CMTS Cable Modem Termination System线缆调制解调器终端系统CNR Carrier-to-Noise Ratio 载噪比CON Console 操纵台Controller 控制器CPB Corporation of Public Broadcasting（美国公共广播公司CPU Central Processing Unit 中央处理单元CRC Cyclic Redundancy Check 循环冗余校验CRCC CRI Cyclic Redundancy Check Code循环冗余校验码CROM China Radio International 中国国际广播电台CRT Control Read Only Memory 控制只读存储器CS Cathode-Ray Tube 阴极射线管CSC Communication Satellite 通信卫星CSS Color Sub-carrier 彩色副载波Center Storage Server 中央存储服务器Content Scrambling System 内容加扰系统CSU Channel Service Unit 信道业务单元CT Color Temperature 色温CTC Cassette Tape Controller 盒式磁带控制器Channel Traffic Control 通道通信量控制Counter Timer Circuit 计数器定时器电路Counter Timer Control 计数器定时器控制CTE Cable Termination Equipment 线缆终端设备Customer Terminal Equipment 用户终端设备CTV Color Television 彩色电视CVD China Video Disc 中国数字视盘CW Carrie Wave 载波DAB Digital Audio Broadcasting 数字音频广播DASH Digital Audio Stationary Head 数字音频静止磁头DAT Digital Audio Tape 数字音频磁带DBMS Data Base Management System 数据库管理系统DBS Direct Broadcast Satellite 直播卫星DCC Digital Compact Cassette 数字小型盒带Dynamic Contrast Control 动态对比度控制DCT Digital Component Technology 数字分量技术Discrete Cosine Transform 离散余弦变换DCTV Digital Color Television 数字彩色电视DD Direct Drive 直接驱动DDC Direct Digital Control 直接数字控制DDE Dynamic Data Exchange 动态数据交换DDM Data Display Monitor 数据显示监视器DES Data Elementary Stream 数据基本码流Data Encryption Standard 美国数据加密标准DF Dispersion Flattened 色散平坦光纤DG Differential Gain 微分增益DI Digital Interface 数字接口DITEC Digital Television Camera 数字电视摄像机DL Delay Line 延时线DLD Dynamic Linear Drive 动态线性驱动DM Delta Modulation 增量调制Digital Modulation 数字调制DMB Digital Multimedia Broadcasting 数字多媒体广播DMC Dynamic Motion Control 动态控制-DME Digital Multiple Effect 数字多功能特技DMS Digital Mastering System 数字主系统DN Data Network 数据网络DNG Digital News Gathering 数字新闻采集DNR Digital Noise Reducer 数字式降噪器DOB Data Output Bus 数据输出总线DOCSIS Data Over Cable Service Interface Specifications 有线数据传输业务接口规范DOC Drop Out Compensation 失落补偿DOS Disc Operating System 磁盘操作系统DP Differential Phase 微分相位Data Pulse 数据脉冲DPCM Differential Pulse Code Modulation 差值脉冲编码调制DPL Dolby Pro Logic 杜比定向逻辑DSB Digital Satellite Broadcasting 数字卫星广播DSC Digital Studio Control 数字演播室控制DSD Dolby Surround Digital 杜比数字环绕声DSE Digital Special Effect 数字特技DSK Down-Stream Key 下游键DSP Digital Signal Processing 数字信号处理Digital Sound Processor 数字声音处理器DSS Digital Satellite System 数字卫星系统DT Digital Technique 数字技术Digital Television 数字电视Data Terminal 数据终端Data Transmission 数据传输DTB Digital Terrestrial Broadcasting 数字地面广播DTBC Digital Time-Base Corrector 数字时基校正器DTC Digital Television Camera 数字电视摄像机DTS Digital Theater System 数字影院系统Digital Tuning System 数字调谐系统Digital Television Standard 数字电视标准DVB Digital Video Broadcasting 数字视频广播DVC Digital Video Compression 数字视频压缩DVE Digital Video Effect 数字视频特技DVS Desktop Video Studio 桌上视频演播DVTR Digital Video Tape Recorder 数字磁带录像机EA Extension Amplifier 延长放大器EB Electron Beam 电子束EBS Emergency Broadcasting System 紧急广播系统EBU European Broadcasting Union 欧洲广播联盟EC Error Correction 误差校正ECN Emergency Communications Network 应急通信网络ECS European Communication Satellite 欧洲通信卫星EDC Error Detection Code 错误检测码EDE Electronic Data Exchange 电子数据交换EDF Erbium-Doped Fiber 掺饵光纤EDFA Erbium-Doped Fiber Amplifier 掺饵光纤放大器EDL Edit Decision List 编辑点清单EDTV Extended Definition Television 扩展清晰度电视EE Error Excepted 允许误差EFM Eight to Fourteen Modulation 8-14调制EFP Electronic Field Production 电子现场节目制作EH Ethernet Hosts 以太网主机EIN Equivalent Input Noise 等效输入噪声EIS Electronic Information System 电子信息系统EISA Extended Industrial StandardArchitecture 扩展工业标准总线EL Electro-Luminescent 场致发光EM Error Monitoring 误码监测EN End Node 末端节点ENG Electronic News Gathering 电子新闻采集EOT End of Tape 带尾EP Edit Point 编辑点Error Protocol 错误协议EPG Electronic Program Guides 电子节目指南EPS Emergency Power Supply 应急电源ERP Effective Radiated Power 有效辐射功率ES Elementary Stream 基本码流End System 终端系统ESA European Space Agency 欧洲空间局ETV Education Television 教育电视FA Enhanced Television 增强电视FABM FAS Facial Animation 面部动画FC Fiber Amplifier Booster Module 光纤放大器增强模块Fiber Access System 光纤接入系统Frequency Changer 变频器FCC Fiber Channel 光纤通道FD Film Composer 电影编辑系统Federal Communications Commission 美国联邦通信委员会FDCT Frequency Divider 分频器FDDI FDM Fiber Duct 光纤管道FDP Forward Discrete Cosine Transform离散余弦正变换FE Fiber Distributed Data Interface 分布式光纤数据接口Frequency-Division Multiplexing 频分复用FF Fiber Distribution Point 光纤分配点FG Front End 前端FH Framing Error 成帧误差FIT Fast Forward 快进FN Frequency Generator 频率发生器FOA Frequency Hopping 跳频FOC Frame-Interline Transfer 帧一行间转移Fiber Node 光纤节点Fiber Optic Amplifier 光纤放大器FOM Fiber Optic Cable 光缆FON Fiber Optic Communications 光纤通信FOS Fiber Optic Coupler 光纤耦合器FOTC Fiber Optic Modem 光纤调制解调器FS Fiber Optic Net 光纤网Factor of Safety 安全系数Fiber Optic Trunk Cable 光缆干线FT Frame Scan 帧扫描FTP Frame Store 帧存储器FTTB Frame Synchro 帧同步机FTTC France Telecom 法国电信Absorber Circuit 吸收电路AC/AC Frequency Converter 交交变频电路AC power control交流电力控制AC Power Controller交流调功电路AC Power Electronic Switch交流电力电子开关Ac Voltage Controller交流调压电路Asynchronous Modulation异步调制Baker Clamping Circuit贝克箝位电路Bi-directional Triode Thyristor双向晶闸管Bipolar Junction Transistor-- BJT双极结型晶体管Boost-Buck Chopper升降压斩波电路Boost Chopper升压斩波电路Boost Converter升压变换器Bridge Reversible Chopper桥式可逆斩波电路Buck Chopper降压斩波电路Buck Converter降压变换器Commutation换流Conduction Angle导通角Constant Voltage Constant Frequency --CVCF恒压恒频Continuous Conduction--CCM（电流）连续模式Control Circuit 控制电路Cuk Circuit CUK 斩波电路Current Reversible Chopper电流可逆斩波电路Current Source Type Inverter--CSTI 电流（源）型逆变电路Cyclo convertor周波变流器DC-AC-DC Converter直交直电路DC Chopping直流斩波DC Chopping Circuit直流斩波电路DC-DC Converter直流－直流变换器Device Commutation器件换流Direct Current Control直接电流控制Discontinuous Conduction mode （电流）断续模式displacement factor 位移因数distortion power 畸变功率double end converter 双端电路driving circuit 驱动电路electrical isolation 电气隔离fast acting fuse 快速熔断器fast recovery diode快恢复二极管fast revcovery epitaxial diodes 快恢复外延二极管fast switching thyristor快速晶闸管field controlled thyristor场控晶闸管flyback converter 反激电流forced commutation 强迫换流forward converter 正激电路frequency converter 变频器full bridge converter全桥电路full bridge rectifier 全桥整流电路full wave rectifier 全波整流电路fundamental factor基波因数gate turn-off thyristor——GTO 可关断晶闸管general purpose diode 普通二极管giant transistor——GTR 电力晶体管half bridge converter 半桥电路hard switching 硬开关high voltage IC 高压集成电路hysteresis comparison 带环比较方式indirect current control间接电流控制indirect DC-DC converter直接电流变换电路insulated-gate bipolar transistor---IGBT绝缘栅双极晶体管intelligent power module---IPM智能功率模块integrated gate-commutated thyristor---IGCT集成门极换流晶闸管inversion 逆变latching effect 擎住效应leakage inductance 漏感light triggered thyristor---LTT光控晶闸管line commutation 电网换流load commutation 负载换流loop current 环流1 backplane 背板2 Band gap voltage reference 带隙电压参考。

地球物理专业英语常用单词rａypath:射线路径ｒａy trａcｉｎg:射线追踪real time:实时recｏrｄseｃtioｎ记录剖面refleｃtiｏn coefficiｅnt:反射系数ｒefｌectioｎsurvey:反射法勘探refractｉoｎ:折射refrａction ｓurveｙ:折射法勘探refracｔｉoｎwave：折射波：reｓｉｄｕaｌｎormal moｖeout:剩余正常时差reverbｅraｔｉon：交混回响rｅｖeｒse migratiｏn:逆偏移Rｉcker waveｌet:雷克子波ｒms vｅｌoｃity均方根速度R-ｗａｖe:瑞雷波。

sｃatteriｎg：散射sｅｃoｎdary wave次波SEG A,SＥG B, or SＥG C标准磁带格式seismic:地震的ｓeiｓmｉc discontinuitｙ:地震不连续面sｅismic-ｅlectriｃeffect:震电效应ｓeismic survｅy:地震勘探seｉsmogram:震相图seisｍoｇｒaph: 地震仪，地震检波器seismolｏgｉsｔ：地震学家，地震工作者seiｓmology地震学shｅar modulｕs:剪切模量sheａr wave:剪切波sｈotpoｉnt:炮点ｓhｏtpoint gaｐ:炮点间隙S／N:信噪比。

Sｎell'ｓlaw: 斯奈尔定律spａrｋeｒ: 电火花震源spherｉcal diｖergencｅ球面扩散ｓtacｋ叠加Ｇround mixiｎｇ地面混波Instruｍent miｘing仪器混波Verｔicalｓｔacking垂直叠加Uphoｌe staｃkｉｎg井口时间叠加Ｃommｏn－dｅpth-ｐoｉnｔ（CDP）s ｔacking共深度点叠加Ｃoｍmoｎ-ofｆｓｅｔstackｉng同炮检距叠加Ｖelocity fｉlｔerinｇ速度滤波Cｏhｅrency filteｒinｇ／Ａｕtｏ-p ｉｃkinｇ相干滤波／自动拾取Ｄiversity stａckｉｎg相异叠加Autｏmigratiｎg自动偏移sｔackｉnｇvｅloｃｉty:叠加速度Stonelｅy wavｅ:斯通利波streａmer:海上拖缆S-waｖｅ：S-波ｓyｎtｈetｉc seismogram:合成地震记录tanｇｅntialｗａve:切向波ｔracｅequalｉzatｉon:道均衡trace gatｈer:道选排，道集ｔｒace ｉnｔegｒａtiｏn:道积分，道综合ｔransfｏrmeｄwave：变换波tｒough:波谷ｖｅlocitｙanａlｙsis:速度分析velｏcｉｔy ｆilｔeｒ：速度滤波vｅloｃｉｔy inversion: 速度反转ｖelocitｙspectｒｕm：速度谱ｖｅloｃity ｓurｖｅy速度测量ｗave equａtiｏn：波动方程wave form：波形wａｖeｆroｎt:波阵面ｗａｖe impedａnｃe:波阻抗wide－angle reflectioｎ:广角反射Yｏung'ｓmoｄuluｓ：杨氏模量ｚero-phasｅ:零相位Zoｅpｐritｚ'ｓｅqｕａtions:佐普里兹方程acoustｉc log声波测井amplｉtude log:声幅测井borehole ｇraviｍeteｒ:井下重力仪borehｏle ｌog测井曲线cａｌibｒaｔe校正densilｏg密度测井ｄensity loｇ:密度测井ｄip ｌog地层倾角测井ｄipmeter地层倾角测井ｅleｃｔriｃalｌog：电测井ｇamma－ｇaｍma log:伽马-伽马测井gａｍｍa-ｒaｙｌog:γ射线测井induction log：感应测井microlog微电阻率测井ｎeutron log: 中子测井radｉoactｉｖity log:放射性测井ｓｏｎic ｌog:声波测井ｓpｅｃtraｌｌoｇ能谱测井veloｃiｔy lｏg：声速测井ｗell ｌｏg:钻井记录，测井Ampeｒe’ｓlaw：安培定律ａngulaｒfrequｅnｃy:角频率Anomaｌy: 异常ａntｉcline:背斜ａrraｙ:排列autocorreｌatiｏn：自相关baｃkgroｕnd:背景值banｄ-limited functｉｏn:频截函数bａnd-pass:带通band-rｅjｅct filter:带阻滤波器banｄwｉdtｈ:带宽basｅof weatheriｎg:低速带底面bouｎｄary ｃonditioｎ:边界条件bouｎｄary－valuｅpｒoｂｌｅｍ:边值问题ｂｙte:字节characterｉstic vａluｅ:Eigenvaｌｕｅ特性值/特征值Cｏｍpleｘnumber复数cｏntour:等值线contouｒinｔervaｌ:等值线间隔convoluｔｉon：褶积ｃrust:地壳cｕrｌ:旋度db:Ｄｅcibel.分贝。

a level物理激光特点English Answer:Characteristics of Lasers in A-Level Physics.Lasers (Light Amplification by Stimulated Emission of Radiation) are devices that emit highly focused, coherent, and monochromatic light. They are used in a wide range of applications, including telecommunications, medicine, and manufacturing.Key Characteristics of Lasers:Coherence: Laser light waves are in phase with each other, resulting in a high degree of coherence. This allows lasers to produce sharp, well-defined beams.Monochromaticity: Lasers typically emit light of a single wavelength, making them monochromatic. This allows for precise control over the color of the emitted light.High Intensity: Lasers can produce light with extremely high intensity, concentrated in a narrow beam. This makes them ideal for applications such as cutting and welding.Directionality: Laser beams are highly directional, allowing them to travel over long distances with minimal divergence. This makes them suitable for applications such as laser pointers and optical communications.Polarization: Lasers can produce light that is linearly or circularly polarized, giving them specific orientations. This is useful for applications such as optics and spectroscopy.Other Characteristics:Population Inversion: Lasers require a population inversion in the lasing medium, where more atoms are in the excited state than in the ground state.Optical Resonator: Lasers use optical resonators toprovide feedback and amplify the stimulated emission.Gain Medium: The lasing medium is the material that undergoes stimulated emission and generates the laser light.Pumping Source: Lasers require a pumping source to excite the lasing medium and create the population inversion.Advantages of Lasers:High power density.High efficiency.Long coherence length.Narrow bandwidth.High directionality.Applications of Lasers:Medical: Surgery, laser therapy, microscopy.Industrial: Cutting, welding, marking, laser engraving.Telecommunications: Fiber optics, optical communication systems.Research: Spectroscopy, atomic physics, laser cooling.Military: Laser weapons, rangefinders, target designators.Chinese Answer:A-Level物理学中的激光特点。

phys. stat. sol. (a) 203, No. 13, 3207–3225 (2006) / DOI 10.1002/pssa.200671403© 2006 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim Review ArticleSingle defect centres in diamond: A reviewF. Jelezko and J. Wrachtrup *3. Physikalisches Institut, Universität Stuttgart, 70550 Stuttgart, GermanyReceived 9 February 2006, revised 28 July 2006, accepted 9 August 2006Published online 11 October 2006PACS 03.67.Pp, 71.55.–r, 76.30.Mi, 76.70.–rThe nitrogen vacancy and some nickel related defects in diamond can be observed as single quantum sys-tems in diamond by their fluorescence. The fabrication of single colour centres occurs via generation of vacancies or via controlled nitrogen implantation in the case of the nitrogen vacancy (NV) centre. The NV centre shows an electron paramagnetic ground and optically excited state. As a result electron and nuclear magnetic resonance can be carried out on single defects. Due to the localized nature of the electron spin wavefunction hyperfine coupling to nuclei more than one lattice constant away from the defect as domi-nated by dipolar interaction. As a consequence the coupling to close nuclei leads to a splitting in the spec-trum which allows for optically detected electron nuclear double resonance. The contribution discusses the physics of the NV and other defect centre from the perspective of single defect centre spectroscopy.© 2006 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim1 IntroductionThe ever increasing demand in computational power and data transmission rates has inspired researchers to investigate fundamentally new ways to process and communicate information.Among others, physicists explored the usefulness of “non-classical”, i.e. quantum mechanical systems in the world of information processing. Spectacular achievements like Shors discovery of the quantum factoring algorithm [1] or the development of quantum secure data communication gave birth to the field of quantum information processing (QIP) [2]. After an initial period where the physical nature of infor-mation was explored [3] and how information processing can be carried out by unitary transformation in quantum mechanics, researchers looked out for systems which might be of use as hardware in QIP. From the very beginning it became clear that the restrictions on the hardware of choice are severe, in particular for solid state systems. Hence in the recent past scientists working in the development of nanostructured materials and quantum physics have cooperated on different solid-state systems to define quantum me-chanical two-level system, make them robust against decoherence and addressable as individual units. While the feasibility of QIP remains to be shown, this endeavour will deepen our understanding of quan-tum mechanics and also marks a new area in material science which now also has reached diamonds as a potential host material. The usefulness of diamond is based on two properties. First defects in diamond are often characterized by low electron phonon coupling, mostly due to the low density of phonon states i.e. high Debye temperature of the material [4]. Secondly, colour centres in diamond are usually found to be very stable, even under ambient conditions. This makes them unique among all optically active solid-state systems.* Corresponding author: e-mail: wrachtrup@physik.uni-stuttgart.de3208 F. Jelezko and J. Wrachtrup: Single defect centres in diamond: A review© 2006 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim The main goal of QIP is the flexible generation of quantum states from individual two-level systems (qubits). The state of the individual qubits should be changed coherently and the interaction strength among them should be controllable. At the same time, those systems which are discussed for data com-munication must be optically active which means, that they should show a high oscillator strength for an electric dipole transition between their ground and some optically excited state. Individual ions or ion strings have been applied with great success. Here, currently up to eight ions in a string have been cooled to their ground state, addressed and manipulated individually [5]. Owing to careful construction of the ion trap, decoherence is reduced to a minimum [6]. Landmark experiments, like teleportation of quantum states among ions [7, 8] and first quantum algorithms have been shown in these systems [9, 10].In solid state physics different types of hardware are discussed for QIP. Because dephasing is fast in most situations in solids only specific systems allow for controlled generation of a quantum state with preservation of phase coherence for a sufficient time. Currently three systems are under discussion. Su-perconducting systems are either realized as flux or charge quantized individual units [11]. Their strength lies in the long coherence times and meanwhile well established control of quantum states. Main pro-gresses have been achieved with quantum dots as individual quantum systems. Initially the electronic ground as well as excited states (exciton ground state) have been used as definition of qubits [12]. Mean-while the spin of individual electrons either in a single quantum dot or coupled GaAs quantum dots has been subject to control experiments [13–15]. Because of the presence of paramagnetic nuclear spins, the electron spin is subject to decoherence or a static inhomogeneous frequency distribution. Hence, a further direction of research are Si or SiGe quantum dots where practically no paramagnetic nuclear spins play a significant role. The third system under investigation are phosphorus impurities in silicon [16]. Phospho-rus implanted in Si is an electron paramagnetic impurity with a nuclear spin I = 1/2. The coherence times are known to be long at low temperature. The electron or nuclear spins form a well controllable two-level system. Addressing of individual spins is planned via magnetic field gradients. Major obstacles with respect to nanostructuring of the system have been overcome, while the readout of single spins based on spin-to-charge conversion with consecutive detection of charge state has not been successful yet. 2 Colour centres in diamondThere are more then 100 luminescent defects in diamond. A significant fraction has been analysed in detail such that their charge and spin state is known under equilibrium conditions [17]. For this review nitrogen related defects are of particular importance. They are most abundant in diamond since nitrogen is a prominent impurity in the material. Nitrogen is a defect which either exists as a single substitutional impurity or in aggregated form. The single substitutional nitrogen has an infrared local mode of vibration Fig. 1 (online colour at: ) Schematic represen-tation of the nitrogen vacancy (NV) centre structure.phys. stat. sol. (a) 203, No. 13 (2006) 3209 © 2006 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim65070075080050010001500T =300KT =1.8K F l u o r e s c e n c e I n t e n s i t y ,C t s Wavelength,nm ZPL 637.2nmat 1344 cm –1. The centre is at a C 3v symmetry site. It is a deep electron donor, probably 1.7 eV below the conduction band edge. There is an EPR signal associated with this defect, called P1, which identifies it to be an electron paramagnetic system with S = 1/2 ground state [17]. Nitrogen aggregates are, most com-monly, pairs of neighbouring substitutional atoms, the A aggregates, and groups of four around a va-cancy, the B aggregate. All three forms of nitrogen impurities have distinct infrared spectra.Another defect often found in nitrogen rich type Ib diamond samples after irradiation damage is the nitrogen vacancy defect centre, see Fig. 1. This defect gives rise to a strong absorption at 1.945 eV (637 nm) [18]. At low temperature the absorption is marked by a narrow optical resonance line (zero phonon line) followed by prominent vibronic side bands, see Fig. 2. Electron spin resonance measure-ment have indicated that the defect has an electron paramagnetic ground state with electron spin angular momentum S = 1 [19]. The zero field splitting parameters were found to be D = 2.88 GHz and E = 0 indicating a C 3v symmetry of the electron spin wavefunction. From measurements of the hyperfine cou-pling constant to the nitrogen nuclear spin and carbon spins in the first coordination shell it was con-cluded that roughly 70% of the unpaired electron spin density is found at the three nearest neighbour carbon atoms, whereas the spin density at the nitrogen is only 2%. Obviously the electrons spend most of their time at the three carbons next to the vacancy. To explain the triplet ground state mostly a six elec-tron model is invoked which requires the defect to be negatively charged i.e. to be NV – [20]. Hole burn-ing experiments and the high radiative recombination rate (lifetime roughly 11 ns [21], quantum yield 0.7) indicate that the optically excited state is also a spin triplet. The width of the spectral holes burned into the inhomogeneous absorption profile were found to be on the order of 50 MHz [22, 23]. Detailed investigation of the excited state dephasing and hole burning have caused speculations to as whether the excited state is subject to a J an–Teller splitting [24, 25]. From group theoretical arguments it is con-cluded that the ground state is 3A and the excited state is of 3E symmetry. In the C 3v group this state thus comprises two degenerate substrates 3E x,y with an orthogonal polarization of the optical transition. Photon echo experiments have been interpreted in terms of a Jan Teller splitting of 40 cm –1 among these two states with fast relaxation among them [24]. However, no further experimental evidence is found to sup-port this conclusion. Hole burning experiments showed two mechanisms for spectral hole burning: a permanent one and a transient mechanism with a time scale on the order of ms [23]. This is either inter-preted as a spin relaxation mechanism in the ground state or a metastable state in the optical excitation-emission cycle. Indeed it proved difficult to find evidence for this metastable state and also number and energetic position relative to the triplet ground and excited state are still subject of debate. Meanwhile it seems to be clear that at least one singlet state is placed between the two triplet states. As a working hypothesis it should be assumed throughout this article that the optical excitation emission cycle is de-scribed by three electronic levels.Fig. 2 Fluorescence emission spectra of single NVcentres at room temperature and LHe temperatures.Excitation wavelength was 514 nm.3210 F. Jelezko and J. Wrachtrup: Single defect centres in diamond: A review© 2006 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim 3 Optical excitation and spin polarizationGiven the fact that the NV centre has an electron spin triplet ground state with an optically allowed tran-sition to a 3E spin triplet state one might wonder about the influence of optical excitation on the electron spin properties of the defect. Indeed in initial experiments no electron spin resonance (EPR) signal of the defect was detected except when subject to irradiation in a wavelength range between 450 and 637 nm[19]. Later on it became clear that in fact there is an EPR signal even in the absence of light, yet the signal strength is considerably enhanced upon illumination [26]. EPR lines showed either absorptive or emissive line shapes depending on the spectral position. This indicates that only specific spin sub-levels are affected by optical excitation [27]. In general a S = 1 electron spin system is described by a spin Hamiltonian of the following form: e ˆˆˆH g S SDS β=+B . Here g e is the electronic g -factor (g = 2.0028 ± 0.0003); B 0 is the external magnetic field and D is the zero field splitting tensor. This ten-sor comprises the anisotropic dipolar interaction of the two electron spins forming the triplet state aver-aged over their wave function. The tensor is traceless and thus characterized by two parameters, D and E as already mentioned above. The zero field splitting causes a lifting of the degeneracy of the spin sub-levels m s = ±1,0 even in the absence of an external magnetic field. Those zero field spin wave functions T x,y,z do not diagonalize the full high-field Hamiltonian H but are related to these functions by121212=x T T T ββαα-+-=-〉〉,121211y T T T ββαα-++=+〉〉,12120|.z T T αββα+=〉〉 The expectation value of S z for all three wave functions ,,,,||x y z z x y z T S T 〈〉 is zero. Hence there is no magnetization in zero external field. There are different ways to account for the spin polarization process in an excitation scheme involving spin triplets. To first order optical excitation is a spin state conserving process. However spin–orbit (LS) coupling might allow for a spin state change in the course of optical excitation. Cross relaxation processes on the other hand might cause a strong spin polarization as it is observed in the optical excitation of various systems, like e.g. GaAs. However, optical spectroscopy and in particular hole burning data gave little evidence for non spin conserving excitation processes in the NV centre. In two laser hole burning experiments data have been interpreted by assuming different zero field splitting parameters in ground and excited state exc exc (2GHz,0,8GHz)D E ªª by an otherwise spin state preserving optical excitation process [28]. Indeed this is confirmed by later attempts to gener-ate ground state spin coherence via Raman process [29], which only proves to be possible when ground state spin sublevels are brought close to anticrossing by an external magnetic field. Another spin polaris-ing mechanism involves a further electronic state in the optical excitation and emission cycle [30, 31]. Though being weak, LS coupling might be strong enough to induce intersystem crossing to states with different spin symmetry, e.g. a singlet state. Indeed the relative position of the 1A singlet state with re-spect to the two triplet states has been subject of intense debate. Intersystem crossing is driven by LS induced mixing of singlet character into triplet states. Due to the lack of any emission from the 1A state or noticeable absorption to other states, no direct evidence for this state is at hand up to now. However, the kinetics of photo emission from single NV centres strongly suggests the presence of a metastable state in the excitation emission cycle of the state. As described below the intersystem crossing rates from the ex-cited triplet state to the singlet state are found to be drastically different, whereas the relaxation to the 3A state might not depend on the spin substate. This provides the required optical excitation dependent relaxa-tion mechanism. Bulk as well as single centre experiments show that predominantly the m s = 0 (T z ) sublevel in the spin ground state is populated. The polarization in this state is on the order of 80% or higher [27].phys. stat. sol. (a) 203, No. 13 (2006) 3211 © 2006 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim4 Spin properties of the NV centreBecause of its paramagnetic spin ground and excited state the NV centre has been the target of numerous investigations regarding its magnetooptical properties. Pioneering work has been carried out in the groups of Manson [32–36], Glasbeek [37–39] and Rand [26, 40, 41].The hyperfine and fine structure splitting of the NV ground state has been used to measure the Aut-ler–Townes splitting induced by a strong pump field in a three level system. Level anticrossing among the m s = 0 and m s = –1 allows for an accurate measurement of the hyperfine coupling constant for the nitrogen nucleus, yielding an axially symmetric hyperfine coupling tensor with A || = 2.3 MHz and A ^ = 2.1 MHz [42, 43]. The quadrupole coupling constant P = 5.04 MHz. Because of its convenient access to various transitions in the optical, microwave and radiofrequency domain the NV centre has been used as a model system to study the interaction between matter and radiation in the linear and non-linear regime. An interesting set of experiments concerns electromagnetically induced transparency in a Λ-type level scheme. The action of a strong pump pulse on one transition in this energy level scheme renders the system transparent for radiation resonant with another transitions. Experiments have been carried out in the microwave frequency domain [44] as well as for optical transitions among the 3A ground state and the 3E excited state [29]. Here two electron spin sublevels are brought into near level anticrossing such that an effective three level system is generated with one excited state spin sublevel and two allowed optical transitions. A 17% increase in transmission is detected for a suitably tuned probe beam.While relatively much work has been done on vacancy and nitrogen related impurities comparatively little is known about defects comprising heavy elements. For many years it was difficult to incorporate heavy elements as impurities into the diamond lattice. Only six elements have been identified as bonding to the diamond lattice, namely nitrogen, boron, nickel, silicon, hydrogen and cobalt. Attempts to use ion implantation techniques for incorporation of transition metal ions were unsuccessful. This might be due to the large size of the ions and the small lattice parameters of diamond together with the metastability of the diamond lattice at ambient pressure. Recent developments in crystal growth and thin film technology have made it possible to incorporate various dopants into the diamond lattice during growth. This has enabled studies of nickel defects [45, 46]. Depending on the annealing conditions Ni can form clusters with various vacancies and nitrogen atoms in nearest neighbour sites. Different Ni related centres are listed with NE as a prefix and numbers to identify individual entities. The structure and chemical compo-k 23k 12k 31k 213A 3E 1AOptical excitation 3A 3E 1A z x,yz´x´y´k 23k 31a bFig. 3 a) Three level scheme describing the optical excitation and emission cycle of single NV centres. 3A and 3E are the triplet ground and excited state. 1A is a metastable singlet state. No information is at hand presently about the number and relative position of singlet levels. The arrows and k ij denote the rates of transition among the various states. b) More detailed energy level scheme differentiating between trip-let sublevels in the 3A and 3E state.3212 F. Jelezko and J. Wrachtrup: Single defect centres in diamond: A review© 2006 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim sition of defects have mostly been identified by EPR on the basis of the hyperfine coupling to nitrogen nuclei [46]. A particularly rich hyperfine structure has been identified for the NE8 centre.Analysis of the angular dependence of the EPR spectrum for the NE8 centre showed that this centre has electronic spin S = 1/2 and a g -value typical of a d -ion with more than half filled d -shell. The NE8 centre has been found not only in HPHT synthetic diamonds but also in natural diamonds which contain the nickel-nitrogen centres NE1 to NE3 [46]. The structure of the centre is shown in Fig. 4. It comprises 4 substitutional nitrogen atoms and an interstitial Ni impurity. The EPR signature of the system has been correlated to an optical zero phonon transition at around 794 nm. The relative integral intensity of the zero phonon line and the vibronic side band at room temperature is 0.7 (Debey–Waller factor) [47]. The fluorescence emission statistics of single NE8 emitters shows a decay to a yet unidentified metastable state with a rate of 6 MHz.5 Single defect centre experimentsExperiments on single quantum systems in solids have brought about a considerable improvement in the understanding of the dynamics and energetic structure of the respective materials. In addition a number of quantum optical phenomena, especially when light–matter coupling is concerned, have been investi-gated. As opposed to atomic systems on which first experiments on single quantum systems are well established, similar experiments with impurity atoms in solids remain challenging. Single quantum sys-tems in solids usually strongly interact with their environment. This has technical as well as physical consequences. First of all single solid state quantum systems are embedded in an environment which, for example, scatters excitation light. Given a diffraction limited focal volume usually the number of matrix atoms exceed those of the quantum systems by 106–108. This puts an upper limit on the impurity content of the matrix or on the efficiency of inelastic scattering processes like e.g. Raman scattering from the matrix. Various systems like single hydrocarbon molecules, proteins, quantum dots and defect centres have been analysed [48]. Except for some experiments on surface enhanced Raman scattering the tech-nique usually relies on fluorescence emission. In this technique an excitation laser in resonance with a strongly allowed optical transition of the system is used to populate the optically excited state (e.g. the 3E state for the NV centre), see Fig. 3a. Depending on the fluorescence emission quantum yield the system either decays via fluorescence emission or non-radiatively, e.g. via inter-system-crossing to a metastable Fig. 4 (online colour at: ) Structure of the NE8 cen-tre.phys. stat. sol. (a) 203, No. 13 (2006) 3213© 2006 WILEY-VCH Verlag GmbH & Co. KGaA, WeinheimF l u o r .I n t e n s i t y ,k C t s /s Excitation power,mW.state (1A in the case of the NV). The maximum numbers of photons emitted are given when the optical transition is saturated. In this case the maximum fluorescence intensity is given as312123F max 3123()=.2k k k I k k Φ++ Here k 31 is the relaxation rate from the metastable to the ground state and k 21 is the decay rate of the opti-cally excited state, k 23 is the decay rate to the metastable state and φF marks the fluorescence quantum yield. For the NV centre I max is about 107 photon/s. I max critically depends on a number of parameters. First of all the fluorescence quantum yield limits the maximum emission. A good example to illustrate this is the GR1 centre, the neutral vacancy defect in diamond. The overall lifetime of the excited state for this defect is 1 ns at room temperature. However, the radiative lifetime is on the order of 100 ns. Hence φF is on the order of 0.01. Given the usual values for k 21 and k 31 this yields an I max which is too low to allow for detecting single GR1 centres with current technology. Figure 5 shows the saturation curve of a single NV defect. Indeed the maximum observable emission rate from the NV centre is around 105 pho-tons/s which corresponds well to the value estimated above, if we assume a detection efficiency of 0.01. Single NV centres can be observed by standard confocal fluorescence microscopy in type Ib diamond. In confocal microscopy a laser beam is focussed onto a diffraction limited spot in the diamond sample and the fluorescence is collected from that spot. Hence the focal probe volume is diffraction limited with a volume of roughly 1 µm 3. In order to be able to detect single centres it is thus important to control the density of defects. For the NV centre this is done by varying the number of vacancies created in the sam-ple by e.g. choosing an appropriate dose of electron irradiation. Hence the number of NV centres de-pends on the number of vacancies created and the number of nitrogen atoms in the sample. Figure 7 shows an image of a diamond sample where the number of defects in the sample is low enough to detect the fluorescence from single colour centres [49]. As expected the image shows diffraction limited spots. From the image alone it cannot be concluded whether the fluorescence stems from a single quantum system or from aggregates of defects. To determine the number of independent emitters in the focal vol-ume the emission statistics of the NV centre fluorescence can be used [50–52]. The fluorescence photon number statistics of a single quantum mechanical two-level system deviates from a classical Poissoniandistribution. If one records the fluorescence intensity autocorrelation function 2()()=()t I t g t ΙττΙ+2〈()〉〈〉 for short time τ one finds g 2(0) = 0 if the emission stems from a single defect centre (see Fig. 6). This is due to the fact that the defect has to be excited first before it can emit a single photon. Hence a single defect never emits two fluorescence photons simultaneously, in contrast to the case when a number of independent emitters are excited at random. If one adopts the three level scheme from Fig. 3a, rate equa-tions for temporal changes of populations in the three levels can be set up. The equations are solved by 12(2)()=1(1)e e ,k k g K K τττ-++Fig. 5 Saturation curve of the fluorescence inten-sity of a single NV centre at T = 300 K. Excitationwavelength is 514 nm. The power is measured atthe objective entrance.3214F. Jelezko and J. Wrachtrup: Single defect centres in diamond: A review © 2006 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheimg (2)(τ)τ,nswith rates 1,2=k -P = k 21 + k 12 + k 23 + k 31 and Q = k 31(k 21 + k 12) + k 23(k 31 + k 12) with23231123112= .k k k k k K k k+-- This function reproduces the dip in the correlation function g 2(τ) for τ → 0 shown in Fig. 6, which indicates that the light detected originates from a single NV. The slope of the curve around 0τ= is de-terminded by the pumping power of the laser k 12 and the decay rate k 21. For larger times τ a decay of the correlation function becomes visible. This decay marks the ISC process from the excited triplet 3E to the metastable singlet state 1A. Besides the spin quantum jumps detected at low temperature the photon sta-tistics measurements are the best indication for detection of single centres. It should be noted that the radiative decay time depends on the refractive index of the surrounding medium as 1/n medium . Because n medium of diamond is 2.4 the decay time should increase significantly if the refractive index of the sur-rounding is reduced. This is indeed observed for NV centres in diamond nanocrystals [51]. It should beFig. 7 (onl ine col our at: ) Confocal fl uorescence image of various diamond sampl es with different electron irradiation dosages.Fig. 6 Fluorescence intensity autocorrelation function of a single NV defect at room temperature.phys. stat. sol. (a) 203, No. 13 (2006) 3215 © 2006 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheimnoted, that owing to their stability single defect centres in diamond are prime candidates for single pho-ton sources under ambient conditions. Such sources are important for linear optics quantum computing and quantum cryptography. Indeed quantum key distribution has been successful with fluorescence emis-sion from single defect centres [53].A major figure of merit for single photon sources is the signal to background ratio, given (e.g.) by the amplitude of the correlation function at 0τ=. This ratio should be as high as possible to ensure that a single bit of information is encoded in a single photon only. The NV centre has a broad emission range which does not allow efficient filtering of background signals. This is in sharp contrast to the NE8 defect which shows a very narrow, only 1.2 nm wide spectrum. As a consequence the NE8 emission can be filtered out efficiently [47]. The correlation function resembles the one from the NV centre. Indeed the photophysical parameters of the NV and NE8 are similar, yet under comparable experimental conditions the NE8 shows an order of magnitude improvement in signal-to-background ratio because of the nar-rower emission range.Besides application in single photon generation, photon statistical measurements also allow to derive conclusions on photoionization and photochromism of single defects. Most notably the NV centre is speculated to exist in two charge forms, the negatively charged NV with zero phonon absorption at 637 nm and the neutral from NV 0 with absorption around 575 nm [20, 54]. Although evidence existed that both absorption lines stem from the same defect no direct charge interconversion has been shown in bulk experiments. The best example for a spectroscopically resolved charge transfer in diamond is the vacancy, which exists in two stable charge states. In order to observe the charge transfer from NV to NV 0 photon statistical measurements similar to the ones described have been carried out, except for a splitting of photons depending on the emission wavelength [55]. This two channel set up allows to detect the emission of NV 0 in one and NV in another detector arm. Figure 8 shows the experimental result. For delay time 20,()g ττ= shows a dip, indicating the sub-Poissonian statistics of the light emitted. It should -300-200-10001002000,00,40,8g (2)(τ)τ,nsPhotonsDichroicBSStartNV 0Stop NV - Fig. 8 (online colour at: ) Fluorescence cross correlation function between the NV 0 and NV emission of a single defect.。

The relative importance of intensity and phase
Photographs of my wife Linda and me:
Composite photograph made using the
spectral intensity of Linda’s photo and the spectral phase of mine (and inverse-Fourier-
A Gaussian with a complex width!
Fourier-Transforming yields:
neglecting the negative-frequency term due to the c.c.
E()
E0
exp
1/
4
i
0
2
A chirped Gaussian pulse Fourier-Transforms to itself!!!
Sout () Sin () exp[ ()L]
out ()
in
()
n()
c
L
The pulse length
t
There are many definitions of the
width or length of a wave or pulse.
ห้องสมุดไป่ตู้
t
The effective width is the width of a rectangle whose height and area are the same as those of the pulse.
Negative 3rd-order spectral phase