
二面角复习
【基础训练】
(1)正方形ABCD-A 1B 1C 1D 1中,二面角B-A 1C-A 的大小为___ _;(2)将∠A 为60°的棱形ABCD 沿对角线BD 折叠,使A 、C 的距离等于BD , 则二面角A-BD-C 的余弦值是____ __;
(3)正四棱柱ABCD —A 1B 1C 1D 1中对角线BD 1=8,BD 1与侧面B 1BCC 所成的为30°,则二面角C 1—BD 1—B 1的大小为____ __;
(4)从点P 出发引三条射线PA 、PB 、PC ,每两条的夹角都是60°,则二面角B-PA-C 的余弦值是___ ___;
(5)二面角α-l -β的平面角为120°,A 、B ∈l ,AC ?α,BD ?β,AC ⊥l ,BD ⊥l ,若AB=AC=BD=1,则CD 的长___ ___; (6)ABCD 为菱形,∠DAB =60°,PD ⊥面ABCD ,且PD =AD ,则面PAB 与面PCD 所成的锐二面角的大小为___ ___。
【例题选讲】:
例1.空间三条射线CA 、CP 、CB ,∠PCA=∠PCB=600,∠ACB=900,求二
面角B-PC-A 的大小。
例2.如图:Rt ∠ABC 中,斜边AB 在平面α内,C ?α,AC 、BC 与α所成角分别为450和300,求平面ABC 与α所成角。
例3.如图ABCD 为菱形,∠DAB =60°,PD ⊥面ABCD ,且PD =AD ,求面PAB 与面PCD 所成的锐二面角的大小。
D
α
C B
A
H
P
B
α
C A E F
D
P F
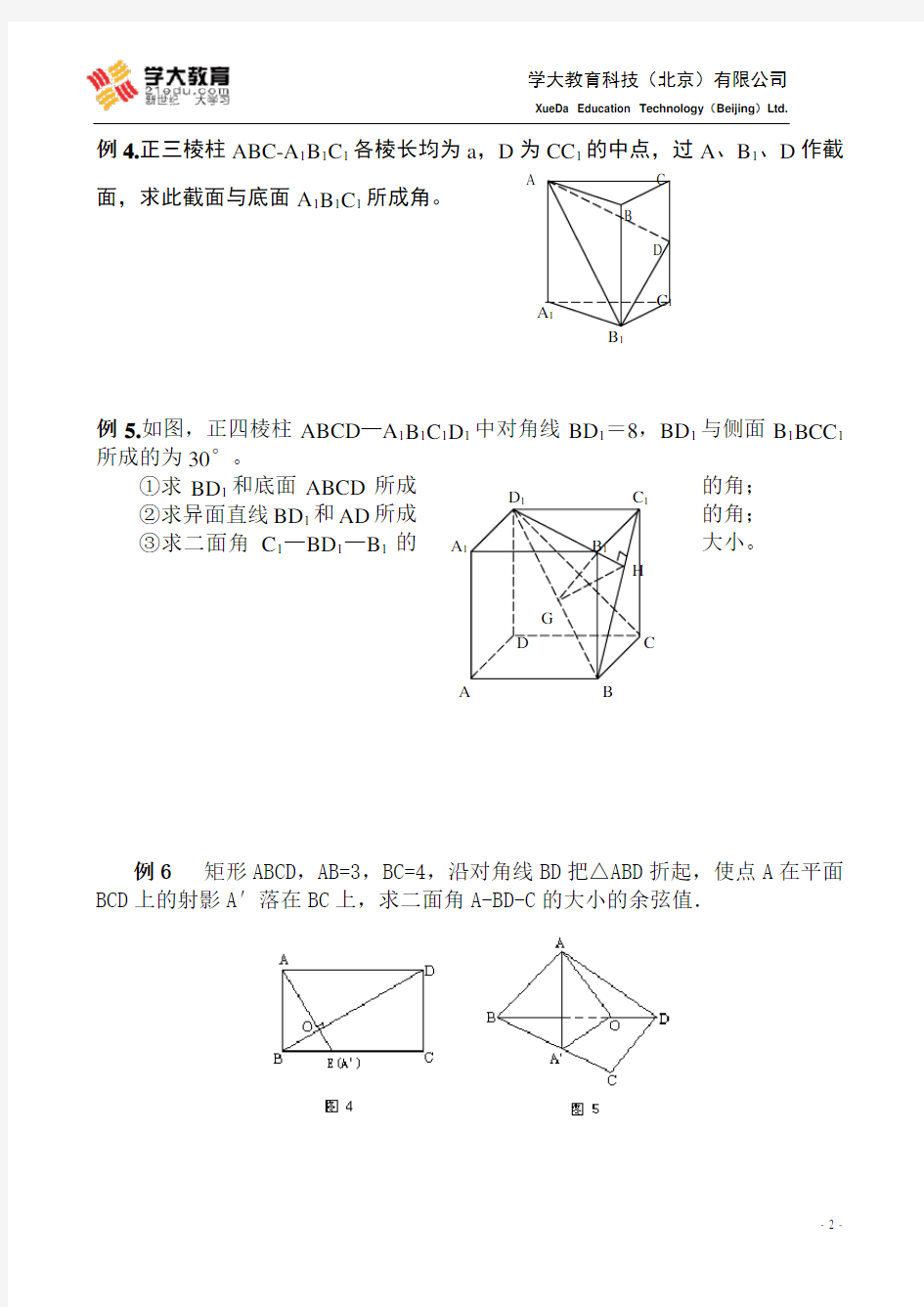
例4.正三棱柱ABC-A 1B 1C 1各棱长均为a ,D 为CC 1的中点,过A 、B 1、D 作截
面,求此截面与底面A 1B 1C 1所成角。
例5.如图,正四棱柱ABCD —A 1B 1C 1D 1中对角线BD 1=8,BD 1与侧面B 1BCC 1所成的为30°。
①求BD 1和底面ABCD 所成的角; ②求异面直线BD 1和AD 所成的角; ③求二面角C 1—BD 1—B 1的大小。
例6 矩形ABCD ,AB=3,BC=4,沿对角线BD 把△ABD 折起,使点A 在平面BCD 上的射影A ′落在BC 上,求二面角A-BD-C 的大小的余弦值.
B
A
C A 1
B 1
C 1
D D
C A
【巩固练习】
1.如图1—122,山坡的倾斜度(坡面与水平面所成二面角的度数)是60°,山坡上有一条直道CD ,它和坡脚的水平线AB 的夹角是30°,沿这条路上山,行走100米后升高多少米?
2.已知:如图1—126,二面角α—AB —β为30°,P ∈α,P 到平面β的距离为10cm .求P 到AB 的距离.
3.在正方体ABCD-A 1B 1C 1D 1中,棱长为2,E 为BC 的中点,求面B 1D 1E 与面BB 1C 1C 所成的二面角的大小的正切值.
4.如图10,在正方体ABCD-A 1B 1C 1D 1中,E 是BC 的中点,F 在AA 1上,且A 1F ∶FA=1∶2,求平面B 1EF 与底面A 1C 1所成的二面角大小的正切值.
5.已知:如图12,P是正方形ABCD所在平面外一点,PA=PB=PC=PD=a,AB=a.
求:平面APB与平面CPD相交所成较大的二面角的余弦值.
6.如图,正方体AC1中,已知O为AC与BD的交点,M为DD1的中点。
(1)求异面直线B1O与AM所成角的大小。(2)求二面角B1—MA—C的正切值。(14分)
7.在正方体AC1中,E为BC中点(1)求证:BD1∥平面C1DE;
(2)在棱CC1上求一点P,使平面A1B1P⊥平面C1DE;
(3)求二面角B—C1D—E的余弦值。(14分)
B
A C
A1
B1C1
D
【参考答案】
(答:60)(答:13
)(答:)(答:13)(答:2
)(答:arctan )
解:过PC 上的点D 分别作DE ⊥AC 于E ,DF ⊥BC 于F ,连EF ,∴∠EDF 为二面角B-PC-A 的平面角,设CD=a ,∵∠PCA=∠PCB=600
,
∴CE=CF=2a ,DE=DF=a 3,
又∵∠ACB=900,∴EF=,
∴∠EDF=31
328332
222=?-+a
a a a ,
解:过点C 作CD ⊥α于D ,连AD 、BD ,∴∠DAC 和∠CBD 分别为AC 、BC 与α所成角,即∠DAC=450,
∠CBD=300,过点D 作DH ⊥AB 于H ,连CH ,∴CH ⊥AB ,即∠CHD 为 平面ABC 与
α所成角,设CD =a ,∴AC=a 2,BC=2a ,AB=a 6,CH=a 3
3
2,∠CHD=600,即为平面ABC 与α所成的角。(∵AB ∥DC ,P 为面PAB 与面PCD 的公共点,作PF
∥AB ,则PF 为面PCD 与面PAB 的交线……)(①;②;③)
arcsin arcsin 34606
3o
这是一道由平面图形折叠成立体图形的问题,解决问题的关键在于搞清折叠
前后的“变”与“不变”.
如果在平面图形中过A 作AE ⊥BD 交BD 于O 、交BC 于E ,则折叠后OA ,OE 与BD 的垂直关系不变.但OA 与OE 此时变成相交两线并确定一平面,此平面必与棱垂直.
由特征(2)可知,面AOE 与面ABD 、面CBD 的交线OA 与OE 所成的角,即为所求二面角的平面角.
另外,A 在面BCD 上的射影必在OE 所在的直线上,又题设射影落在BC 上,所以E 点就是A ′,这样的定位给下面的定量提供了可能.
在Rt △AA ′O 中,∠AA ′O=90°,
P
B
α
C
A
E F
D
解:已知CD=100米,设DH垂直于过BC的水平平面,垂足为H,线段DH的长度就是所求的高度.在平面DBC内,过点D作DG⊥BC,垂足是G,连结GH.∵DH⊥平面BCH,DG⊥BC,
∴GH⊥BC.
因此,∠DGH就是坡面DGC和水平平面BCH所成的二面角的平面角,∠DGH =60°,由此得:
≈43.3(米).
答:沿直道前进100米,升高约43.3米.
注:在解题中要特别注意书写规范.如:
∵DG⊥BC,GH⊥BC,
∴∠DGH是坡面DGC和水平面BCH所成二面角的平面角.解:在β内作点P 的射影O,过点P作PQ⊥AB于Q,连结OQ,根据三垂线定理,可得OQ⊥AB.∴∠PQO为二面角α—AB—β的平面角,即∠PQO=3O°.
∵PO=10cm,
∴PQ=20cm.
即P到AB的距离为20cm.
分析:在给定的平面B1EF与底面A1C1所成的二面角中,没有出现二面角的棱,我们可以设法在二面角的两个面内找出两个面的共点,则这两个公共点的连线即为二面角的棱,最后借助这条棱作出二面角的平面角.
略解:如图10.
在面BB1CC1内,作EH⊥B1C1于H,连结HA1,显然直线EF在底面A1C1的射影为HA1.
延长EF,HA1交于G,过G,B1的直线为所求二面角的棱.
在平面A1B1C1D1内,作HK⊥GB1于K,连EK,
则∠HKE为所求二面角的平面角.
在平面A1B1C1D1内,作B1L⊥GH于L,利用Rt△GLB1∽Rt△GKH,可求得KH.又在Rt△EKH中,设EH=a,容易得到:所求二面角大小的正切值
分析:为了找到二面角及其平面角,必须依据题目的条件,找出两个平面的交线.
解:因为 AB ∥CD ,CD 平面CPD ,AB 平面CPD . 所以 AB ∥平面CPD .
又 P ∈平面APB ,且P ∈平面CPD , 因此 平面APB ∩平面CPD=l ,且P ∈l .
所以 二面角B-l-C 就是平面APB 和平面CPD 相交所得到的一个二面角. 因为 AB ∥平面CPD ,AB 平面APB ,平面CPD ∩平面APB=l , 所以 AB ∥l .
过P 作PE ⊥AB ,PE ⊥CD . 因为 l ∥
AB ∥CD , 因此 PE ⊥l ,PF ⊥l ,
所以 ∠EPF
是二面角B-l-C 的平面角.
因为 PE 是正三角形APB 的一条高线,且AB=a ,
因为 E ,F 分别是AB ,CD 的中点, 所以 EF=BC=a . 在△EFP 中,
19.(1)AM
O B MAO O B O
B MO MO D B MB a
MB a MO a O B a AC O B AC BO ⊥∴⊥∴⊥∴+====
⊥∴⊥11122
121111,2
3
,23,26,,,:面则
设正方体的棱长为方法一
方法二:取AD 中点N ,连结A 1N ,则A 1N 是B 1O 在侧面ADD 1A 1上的射影. 易证AM ⊥A 1N
∴AM ⊥B 1O (三垂线定理)
(2)连结MB 1,AB 1,MC ,过O 作OH ⊥AM 于H 点,连结B 1H , ∵B 1O 平面MAC ,∴∠B 1HO 就是所求二面角B 1—MA —C 的平面角.
5
tan ,1030,211==∠∴?=∴?=?HO
O
B HO B BHO Rt HO MO A
C AM HO 中在 20.证E
C P B CC P CC P P C C E C P B B E
C B A B BCC E C B BCC B A DE C B
D D
E C E
F DE C BD BD EF F CD D C 11111111111111111111111111,,.
,
,)2(.
//,,,//,)1(⊥⊥⊥∴?⊥∴??的中点时为当事实上的中点为此时点即可于交作故保要过平面面面面面则于交连
即为所求由余弦定理中在的平面角即为二面角则连结则连结平面平面平面从而3
2
2cos :2
1
2
6,23,.,,,,,,)3(.
,222211
1111111111=
∠=
=+==+=?--∠∴⊥⊥==⊥∴⊥EFB BE BC CF BF CF CE EF BEF E D C B EFB DC EF DC BF BF EC ED BC BD BC BD DE C P B A P B A E C
立体几何二面角求法 一:知识准备 1、二面角的概念:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面. 2、二面角的平面角的概念:平面角是指以二面角的棱上一点为端点,在两个半平面内分别做垂直于棱的两条射线,这两条射线所成的角就叫做该二面角的平面角。 3、二面角的大小范围:[0°,180°] 4、三垂线定理:平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它就和这条斜线垂直 5、平面的法向量:直线L垂直平面α,取直线L的方向向量,则这个方向向量叫做平面α的法向量。(显然,一个平面的法向量有无数个,它们是共线向量) 6、二面角做法:做二面角的平面角主要有3种方法:(1)、定义法:在棱上取一点,在两个半平面内作垂直于棱的2 条射线,这2条所夹的角; (2)、垂面法:做垂直于棱的一个平面,这个平面与2个半平面分别有一条交线,这2条交线所成的角;(3)、三垂线法:过一个半平面内一点(记为A)
α βa O A B 做另一个半平面的一条垂线,过这个垂足(记为B)再做棱的垂线,记垂足为C,连接AC,则∠ACB即为该二面角的平面角。 7、两个平面的法向量的夹角与这两个平面所成的二面角的平面角有怎样的关系? 二:二面角的基本求法及练习 1、定义法: 从一条直线出发的两个半平面所组成的图 形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取 点,分别在两面内引两条射线与棱垂直, 这两条垂线所成的角的大小就是二面角的平面角。 本定义为解题提供了添辅助线的一种规律。如例1中从二面角S—AM—B中半平面ABM上的一已知点(B)向棱AM作垂线,得垂足(F);在另一半平面ASM内过该垂足(F)作棱AM的垂线(如GF),这两条垂线(BF、GF)便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。 例1.在正方体ABCD—A1B1C1D1中,求(1)二面
立体几何 G5 空间中的垂直关系 18.、[2014·广东卷] 如图1-4,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E. (1)证明:CF⊥平面ADF; (2)求二面角D- AF- E的余弦值. 图1-4 19.、[2014·湖南卷] 如图1-6所示,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD =O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形. (1)证明:O1O⊥底面ABCD; (2)若∠CBA=60°,求二面角C1-OB1-D的余弦值. 19.解:(1)如图(a),因为四边形ACC1A1为矩形,所以CC1⊥AC.同理DD1⊥BD. 因为CC1∥DD1,所以CC1⊥BD.而AC∩BD=O,因此CC1⊥底面ABCD. 由题设知,O1O∥C1C.故O1O⊥底面ABCD. (2)方法一:如图(a),过O1作O1H⊥OB1于H,连接HC1. 由(1)知,O1O⊥底面ABCD O1O⊥A1C1. 又因为四棱柱ABCD-A1B1C1D1的所有棱长都相等,所以四边形A1B1C1D1是菱形, 因此A1C1⊥B1D1,从而A1C1⊥平面BDD1B1,所以A1C1⊥OB1,于是OB1⊥平面O1HC1. 进而OB1⊥C1H.故∠C1HO1是二面角C1-OB1-D的平面角.
不妨设AB =2.因为∠CBA =60°,所以OB =3,OC =1,OB 1=7. 在Rt △OO 1B 1中,易知O 1H =OO 1·O 1B 1OB 1=237.而O 1C 1=1,于是C 1H =O 1C 21+O 1H 2 = 1+12 7 = 197 . 故cos ∠C 1HO 1=O 1H C 1H = 23 7197 =25719. 即二面角C 1-OB 1-D 的余弦值为257 19 . 方法二:因为四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等,所以四边形ABCD 是菱形,因此AC ⊥BD .又O 1O ⊥底面ABCD ,从而OB ,OC ,OO 1两两垂直. 如图(b),以O 为坐标原点,OB ,OC ,OO 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系O -xyz ,不妨设AB =2.因为∠CBA =60°,所以OB =3,OC =1,于是相关各点的坐标为O (0,0,0), B 1(3,0,2), C 1(0,1,2). 易知,n 1=(0,1,0)是平面BDD 1B 1的一个法向量. 设n 2=(x ,y ,z )是平面OB 1C 1的一个法向量,则?????n 2·OB →1=0,n 2·OC →1=0,即???3x +2z =0, y +2z =0. 取z =-3,则x =2,y =23,所以n 2=(2,23,-3). 设二面角C 1-OB 1-D 的大小为θ,易知θ是锐角,于是 cos θ=|cos 〈,〉|=??????n 1·n 2|n 1|·|n 2|=2319=25719. 故二面角C 1-OB 1-D 的余弦值为25719 . 19. 、、[2014·江西卷] 如图1-6,四棱锥P - ABCD 中,ABCD 为矩形,平面PAD ⊥平面ABCD . 图1-6 (1)求证:AB ⊥PD .
αβa O A B 立体几何二面角求法 一:知识准备 1、二面角的概念:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面. 2、二面角的平面角的概念:平面角是指以二面角的棱上一点为端点,在两个半平面内分别做垂直于棱的两条射线,这两条射线所成的角就叫做该二面角的平面角。 3、二面角的大小范围:[0°,180°] 4、三垂线定理:平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它就和这条斜线垂直 5、平面的法向量:直线L 垂直平面α,取直线L 的方向向量,则这个方向向量叫做平面α的法向量。(显然,一个平面的法向量有无数个,它们是共线向量) 6、二面角做法:做二面角的平面角主要有3种方法: (1)、定义法:在棱上取一点,在两个半平面内作垂直于棱的2 条射线,这2条所夹 的角; (2)、垂面法:做垂直于棱的一个平面,这个平面与2个半平面分别有一条交线,这2条交线所成的角; (3)、三垂线法:过一个半平面内一点(记为A )做另一个半平面的一条垂线,过这个垂足(记为B )再做棱的垂线,记垂足为C ,连接AC ,则∠ACB 即为该二面角的平面角。 7、两个平面的法向量的夹角与这两个平面所成的二面角的平面角有怎样的关系? 二:二面角的基本求法及练习 1、定义法: 从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这 两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直, 这两条垂线所成的角的大小就是二面角的平面角。 本定义为解题提供了添辅助线的一种规律。如例1中从二面角S —AM —B 中半平面ABM 上的一已知点(B )向棱AM 作垂线,得垂足(F ); 在另一半平面ASM 内过该垂足(F )作棱AM 的垂线(如GF ),这两条垂线(BF 、GF )便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。 例1.在正方体ABCD —A 1B 1C 1D 1中,求 (1)二面角11A B C A --的大小; (2)平面11A DC 与平面11ADD A 所成角的正切值。 C1
αβa O A B 立体几何二面角求法 一:知识准备 1、二面角的概念:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面. 2、二面角的平面角的概念:平面角是指以二面角的棱上一点为端点,在两个半平面内分别做垂直于棱的两条射线,这两条射线所成的角就叫做该二面角的平面角。 3、二面角的大小范围:[0°,180°] 4、三垂线定理:平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它就和这条斜线垂直 5、平面的法向量:直线L 垂直平面α,取直线L 的方向向量,则这个方向向量叫做平面α的法向量。(显然,一个平面的法向量有无数个,它们是共线向量) 6、二面角做法:做二面角的平面角主要有3种方法: (1)、定义法:在棱上取一点,在两个半平面内作垂直于棱的2 条射线,这2条所夹 的角; (2)、垂面法:做垂直于棱的一个平面,这个平面与2个半平面分别有一条交线,这2条交线所成的角; (3)、三垂线法:过一个半平面内一点(记为A )做另一个半平面的一条垂线,过这个垂足(记为B )再做棱的垂线,记垂足为C ,连接AC ,则∠ACB 即为该二面角的平面角。 7、两个平面的法向量的夹角与这两个平面所成的二面角的平面角有怎样的关系? 二:二面角的基本求法及练习 1、定义法: 从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这 两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直, 这两条垂线所成的角的大小就是二面角的平面角。 本定义为解题提供了添辅助线的一种规律。如例1中从二面角S —AM —B 中半平面ABM 上的一已知点(B )向棱AM 作垂线,得垂足(F ); 在另一半平面ASM 内过该垂足(F )作棱AM 的垂线(如GF ),这两条垂线(BF 、GF )便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。 例1.在正方体ABCD —A 1B 1C 1D 1中,求 (1)二面角11A B C A --的大小; (2)平面11A DC 与平面11ADD A 所成角的正切值。 C1
二轮大题专练16—立体几何(二面角) 1.如图,在四棱柱1111ABCD A B C D -中,底面ABCD 是以AB ,CD 为底边的等腰梯形,且 24AB AD ==,60DAB ∠=?,1AD D D ⊥. (1)证明:1AD BD ⊥. (2)若112D D D B ==,求二面角1A BC B --的正弦值. (1)证明:在ABD ?中,4AB =,2AD =,60DAB ∠=?, 由余弦定理得222cos6023BD AB AD AB AD =+-??= 则222AD BD AB +=,即AD BD ⊥, 又1AD D D ⊥,1BD D D D =,故AD ⊥平面1D DB . 而1BD ?平面1D DB ,1AD BD ∴⊥. (2)解:取BD 的中点O ,11D D D B =,1D O BD ∴⊥. 由(1)可知平面1D DB ⊥平面ABCD ,故1D O ⊥平面ABCD . 由ABCD 是等腰梯形,且24AB AD ==,60DAB ∠=?,得DC CB =, 则CO BD ⊥,2211431D O DD DO --=. 以O 为原点,分别以OB ,OC ,1OD 的方向为x ,y ,z 的正方向建立空间直角坐标系O xyz -,
则(3,2,0)A --,(3,0,0)B ,(0C ,1,0),(3,0,0)D -,1(0D ,0,1), (23,2,0)AB =,11(3,0,1)BB DD ==,(3,1,0)BC =-. 设平面1B BC 的法向量为(,,)n x y z =, 则13030n BB x z n BC x y ??=+=???=-+=?? , 令1x =,则3y =,3z =-,有(1,3,3)n =-. 又(0,0,1)m =是平面ABC 的一个法向量. ∴||321|cos ,|||||771 m n m n m n ???===?, ∴二面角1BC B Λ--的正弦值为32717- =. 2.如图,已知三棱锥S ABC -中,ABC ?是边长为2的等边三角形,4SB SC ==,点D 为SC 的中点,2DA =. (1)求证:平面SAB ⊥平面ABC ; (2)求二面角S AB D --的正弦值.
高二数学二面角专项练习题及参考答案 班级_____________姓名_____________ 一、定义法:直接在二面角的棱上取一点,分别在两个半平面内作棱的垂线,得出平面角. 例1 在四棱锥P-ABCD 中,ABCD 是正方形,PA ⊥平面ABCD ,PA=AB=a ,求二面角B-PC-D 的大小。二、垂线法:已知二面角其中一个面内一点到一个面的垂线, 或逆定理作出二面角的平面角; 例2 在四棱锥P-ABCD 中,ABCD 是平行四边形,PA ⊥平面PA=AB=a ,∠ABC=30°,求二面角P-BC-A 的正切。夹的角就是二面角的平面角 例3 在四棱锥P-ABCD 中,ABCD 是正方形,PA ⊥平面ABCD PA=AB=a ,求B-PC-D 的大小。四、投影面积法:一个平面a 上的图形面积为S ,它在另一个平面b 上的投影面积为S',这两个平面的夹角为q ,则S'=Scosq 或cosq= / S S 例4在四棱锥P-ABCD 中,ABCD 为正方形,PA ⊥平面ABCD ,PA =AB =a ,求平面PBA 与平面PDC 所成二面角的大小。再选用上述方法(尤其要考虑射影法)。例5、在四棱锥P-ABCD 中,ABCD 为正方形,PA ⊥平面ABCD 与平面PDC 所成二面角的大小。 方法归纳:二面角的类型和求法可用框图展习] 二面角是指() A 两个平面相交所组成的图形 B 一个平面绕这个平面内一条直线旋转所组成的图形 C 从一个平面内的一条直线出发的一个半平面与这个平面所组成的图形 D 从一条直线出发的两个半平面所组成的图形 2.平面α与平面β、γ都相交,则这三个平面可能有() A 1条或2条交线 B 2条或3条交线 C 仅2条交线 D 1条或2条或3条交线 3.在300的二面角的一个面内有一个点,若它到另一个面的距离是10,则它到棱的距离是 ( )
F E D C B A ; 立体几何专题复习 热点一:直线与平面所成的角 例1.(2014,广二模理 18) 如图,在五面体ABCDEF 中,四边形ABCD 是边长为2的正方形,EF ∥ 平面ABCD , 1EF =,,90FB FC BFC ? =∠=,3AE = . (1)求证:AB ⊥平面BCF ; (2)求直线AE 与平面BDE 所成角的正切值. · ! 变式1:(2013湖北8校联考)如左图,四边形ABCD 中,E 是BC 的中点,2,1,5,DB DC BC === 2.AB AD ==将左图沿直线BD 折起,使得二面角A BD C --为60,?如右图. (1)求证:AE ⊥平面;BDC (2)求直线AC 与平面ABD 所成角的余弦值.
] 变式2:[2014·福建卷] 在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图1-5所示. (1)求证:AB⊥CD; (2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
热点二:二面角 例2.[2014·广东卷] 如图1-4,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E. ? (1)证明:CF⊥平面ADF; (2)求二面角D-AF-E的余弦值. 变式3:[2014·浙江卷] 如图1-5,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED =90°,AB=CD=2,DE=BE=1,AC= 2. — (1)证明:DE⊥平面ACD;(2)求二面角B-AD-E的大小. 变式4:[2014·全国19] 如图1-1所示,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2. (1)证明:AC1⊥A1B; (2)设直线AA1与平面BCC1B1的距离为3,求二面角A1 -AB -C的大小. 【
专题一:空间角 一、基础梳理 1.两条异面直线所成的角 (1)异面直线所成的角的范围:(0, ]2 π 。 (2)异面直线垂直:如果两条异面直线所成的角是直角,则叫两条异面直线垂直。两条异面直线,a b 垂直,记作a b ⊥。 (3)求异面直线所成的角的方法: (1)通过平移,在一条直线上(或空间)找一点,过该点作另一(或两条)直线的平行线; (2)找出与一条直线平行且与另一条相交的直线,那么这两条相交直线所成的角即为所求。 平移技巧有:平行四边形对边平移、三角形中位线平移、补形平移技巧等。 2.直线和平面所成的角(简称“线面角”) (1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角。 一直线垂直于平面,所成的角是直角;一直线平行于平面或在平面内,所成角为0?角。 直线和平面所成角范围:[0, 2 π]。 (2)最小角定理:斜线和平面所成角是这条斜线和平面内 经过斜足的直线所成的一切角中最小的角。 (3)公式:已知平面α的斜线a 与α内一直线b 相交成θ角, 且a 上的射影c 与b 相交成?2角, 则有θ??cos cos cos 21= 。 内的射影所成角,是这条斜线和这个平面内的任一条直 线所成角中最小的角。 3.二面角 (1)二面角的概念:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面。若棱为l ,两个面分别为,αβ的二面角记为l αβ--。 (2)二面角的平面角: 过二面角的棱上的一点O 分别在两个半平面内...... 作棱的两条垂线,OA OB ,则AOB ∠叫做二面角 l αβ--的平面角。 说明:①二面角的平面角范围是[]0,π,因此二面 角有锐二面角、直二面角与钝二面角之分。 ②二面角的平面角为直角时,则称为直二面角, 组成直二面角的两个平面互相垂直。 (3)二面角的求法:(一)直接法:作二面角的平面角的作法:①定义法;②棱的垂面法;③三垂线定理或逆定理法;(注意一些常见模型的二面角的平面角的作法) (二)间接法:面积射影定理的方法。 (4)面积射影定理: 面积射影定理:已知ABC ?的边BC 在平面α内,顶点A α?。设ABC ?的面积为S ,它在平 ?2?1c b a θP αO A B l B' O' A' B O A βα
二面角的求法 (1)定义法——在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。注:o 点在棱上,用定义法。 (2)垂线法(三垂线定理法)——利用三垂线定理作出平面角,通过解直角三角形求角的大小。注:o 点在一个半平面上,用三垂线定理法。 (3)垂面法——通过做二面角的棱的垂面,两条交线所成的角即为平面角。注:点O 在二面角内,用垂面法。 (4)射影面积法——若多边形的面积是S ,它在一个平面上的射影图形面积是S`,则二面角θ的大小为COS θ= S`÷ S A 图3 α β O B l O 图5 β α C B A
例题讲解 1、(本小题满分14分)如图所示,在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱 PD ⊥底面,,ABCD PD CD E =是PC 的中点,作EF PB ⊥交PB 于点F 。 (I )求证://PA 平面EDB ; (II )求证:PB ⊥平面EFD ; (III )求二面角P BC D --的大小。 2、 如图1-125, PC ⊥平面ABC ,AB =BC=CA =PC ,求二面角B -PA -C 的平面角的正切值。(三垂线定理法) 3.在棱长为1的正方体1AC 中, (1)求二面角11A B D C --的大小的余弦值; (2)求平面1C BD 与底面ABCD 所成二面角1C BD C --的平面角大小 的正切值。 18、(本题满分14分) 如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AB AD AC CD ⊥⊥,, 60ABC ∠=°,PA AB BC ==,E 是PC 的中点. (Ⅰ)求PB 和平面PAD 所成的角的大小; (Ⅱ)证明⊥AE 平面PCD ; (Ⅲ)求二面角A PD C --的正弦值. O 1 A 1 C 1 D 1 B 1 D C B A A C D P E
二面角的平面角专题学案 一、二面角定义 从一条直线出发的两个半平面所组成的图形就叫做二面角。二面角的大小是用二面角的平面角来衡量的。而二面角的平面角是指在二面角βα--l 的棱上任取一点O ,分别在两个半平面内作射线l BO l AO ⊥⊥,,则AOB ∠为二面角βα--l 的平面角。 二、二面角的求法: 1.几何法:二面角转化为其平面角,要掌握以下三种基本做法: ①直接利用定义,图4(1)。 ②利用三垂线定理及其逆定理,图4(2)最常用。 ③作棱的垂面,图4(3)。 α β A O P A B O P α β 4(1) 4(2) 4(3)
典型例题: 例1.在正四面体ABCD 中,求相邻两个平面所成的二面角的平面角的大小. 例2.在棱长为1的正方体1AC 中,(1)求二面角11A B D C --的大小; (2)求平面1C BD 与底面ABCD 所成二面角1C BD C --的平面角大小. 例3.已知:二面角l αβ--且,A A α∈到平面β 的距离为A 到l 的距离为4,求二面角l αβ--的大小. l B O A β α
例4.如图,AB ⊥平面BCD ,BD CD ⊥,若2AB BC BD ==,求二面角B AC D --的正弦值. 课堂练习: 1.正方体AC 1中M 是BC 中点,求二面角D 1—AB 1—M 的平面角的正切值. 2.ABC 为等腰直角三角形,∠C=900 . PA ⊥面ABC ,AC=a. PA=2a. 求A —PB —C 大小. 3.直三棱柱棱长均相等. ∠ADC 1=900 . 求D —AC 1—C 大小. A B C D E F
二面角的求法 一、 定义法: 从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。 本定义为解题提供了添辅助线的一种规律。如例1中从二面角S —AM —B 中半平面ABM 上的一已知点(B )向棱AM 作垂线,得垂足(F );在另一半平面ASM 内过该垂足(F )作棱AM 的垂线(如GF ),这两条垂线(BF 、GF )便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。 例1 如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD ,AD = 2DC SD ==,点M 在侧棱SC 上,ABM ∠=60° (I )证明:M 在侧棱SC 的中点 (II )求二面角S AM B --的大小。 证(I )略 解(II ):利用二面角的定义。在等边三角形ABM 中过点B 作BF AM ⊥交AM 于点F ,则点F 为AM 的中点,过F 点在平面ASM 内作GF AM ⊥,GF 交AS 于G , 连结AC ,∵△ADC ≌△ADS ,∴AS-AC ,且M 是SC 的中点, ∴AM ⊥SC , GF ⊥AM ,∴GF ∥AS ,又∵F 为AM 的中点, ∴GF 是△AMS 的中位线,点G 是AS 的中点。 则GFB ∠即为所求二面角. ∵2= SM ,则2 2 = GF , 又∵6= =AC SA ,∴2=AM ,∵2==AB AM ,060=∠ABM ∴△ABM 是等边三角形,∴ 3=BF 。在△GAB 中,26= AG ,2=AB ,0 90=∠GAB ,∴2 11423=+=BG 366 23 2 22211 32 12cos 2 2 2 -=-=??- +=?-+=∠FB GF BG FB GF BFG ∴二面角S AM B --的大小为)3 6arccos(- F G F G
线面垂直专题练习 一、定理填空: 1.直线和平面垂直 如果一条直线和 ,就说这条直线和这个平面垂直. 2.线面垂直判定定理和性质定理 线面垂直判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直 于这个平面. 判定定理1:如果两条平行线中的一条 于一个平面,那么 判定定理2:一条直线垂直于两个平行平面中的一个平面,那么 . 性质定理3:如果两条直线同垂直于一个平面,那么这两条直线 . 二、精选习题: 1.设M 表示平面,a 、b 表示直线,给出下列四个命题: ① M b M a b a ⊥????⊥// ②b a M b M a //????⊥⊥ ③????⊥⊥b a M a b ∥M ④?? ?? ⊥b a M a //b ⊥M . 其中正确的命题是 ( ) A.①② B.①②③ C.②③④ D.①②④ 2.如图所示,在正方形ABCD 中,E 、F 分别是AB 、BC 的中点.现在沿DE 、DF 及EF 把△ADE 、△CDF 和△BEF 折起,使A 、B 、C 三点重合,重合后的点记为P .那么,在四面体P —DEF 中,必有 ( ) A.DP ⊥平面PEF B.DM ⊥平面PEF C.PM ⊥平面DEF D.PF ⊥平面DEF 3.设a 、b 是异面直线,下列命题正确的是 ( ) A.过不在a 、b 上的一点P 一定可以作一条直线和a 、b 都相交 B.过不在a 、b 上的一点P 一定可以作一个平面和a 、b 都垂直 C.过a 一定可以作一个平面与b 垂直 D.过a 一定可以作一个平面与b 平行 4.如果直线l ,m 与平面α,β,γ满足:l =β∩γ,l ∥α,m ?α和m ⊥γ,那么必有 ( ) A.α⊥γ且l ⊥m B.α⊥γ且m ∥β C.m ∥β且l ⊥m D.α∥β且α⊥γ 5.有三个命题: ①垂直于同一个平面的两条直线平行; ②过平面α的一条斜线l 有且仅有一个平面与α垂直; ③异面直线a 、b 不垂直,那么过a 的任一个平面与b 都不垂直 其中正确命题的个数为 ( )A.0 B.1 C.2 D.3 第3题图
1. 如图,四棱锥中,底面为矩形,底面, ,点M 在侧棱上,=60° (I )证明:M 在侧棱的中点 (II )求二面角的大小。 2. 如图,已知四棱锥P -ABCD ,底面ABCD 为菱形,PA ⊥平面ABCD , 60ABC ∠=?,E ,F 分别是BC , PC 的中点. (Ⅰ)证明:AE ⊥PD ; (Ⅱ)若H 为PD 上的动点,EH 与平面PAD 所成最大角的正切值为6 2 ,求二面角E —AF —C 的余弦值. 3.如图,在直四棱柱ABCD-A B C D 中,底面ABCD 为等腰梯形,AB//CD ,AB=4, BC=CD=2, AA =2, E 、E 、F 分别是棱AD 、AA 、AB 的中点。 (1) 证明:直线EE //平面FCC ;求二面角B-FC -C 的余弦 值。 4.如图,在四棱锥ABCD P -中,底面ABCD 是矩形. 已知 60,22,2,2,3=∠====PAB PD PA AD AB . (Ⅰ)证明⊥AD 平面PAB ; (Ⅱ)求异面直线PC 与AD 所成的角的大小; (Ⅲ)求二面角A BD P --的大小. S ABCD -ABCD SD ⊥ABCD 2AD =2DC SD ==SC ABM ∠SC S AM B --11111 11111E A B C F E 1 A 1 B 1 C 1 D 1 D
5.如图所示,四棱锥P -ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60°, E 是CD 的中点,PA ⊥底面ABCD ,PA =2. (Ⅰ)证明:平面PBE ⊥平面PAB ; (Ⅱ)求平面PAD 和平面PBE 所成二面角(锐角)的大小. 6.如图,在三棱锥P ABC -中,2AC BC ==,90ACB ∠=, AP BP AB ==,PC AC ⊥. (Ⅰ)求证:PC AB ⊥; (Ⅱ)求二面角B AP C --的大小; 6. 已知斜三棱柱ABC —A 1B 1C 1的棱长都是a ,侧棱与底面成600的角,侧面BCC 1B 1⊥底面ABC 。 (1)求证:AC 1⊥BC ; (2)求平面AB 1C 1与平面 ABC 所成的二面角(锐角)的大小。 7. 如图,E 为正方体ABCD -A 1B 1C 1D 1的棱CC 1的中点,求平面AB 1E 和底面A 1B 1C 1D 1所成锐角的余弦值. 8.如图,在五面体ABCDEF 中,FA 平面ABCD, AD//BC//FE ,AB AD ,M 为EC 的中点,AF=AB=BC=FE= AD (I) 求异面直线BF 与DE 所成的角的大小; ⊥⊥1 2 A B C E D P A B B 1 C 1 A 1 L A C B P A D B C E D B A 图5
二面角的求法 一、 定义法: 从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。 本定义为解题提供了添辅助线的一种规律。如例1中从二面角S —AM —B 中半平面ABM 上的一已知点(B )向棱AM 作垂线,得垂足(F );在另一半平面ASM 内过该垂足(F )作棱AM 的垂线(如GF ),这两条垂线(BF 、GF )便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。 例1 如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD ,2AD = 2DC SD ==,点M 在侧棱SC 上,ABM ∠=60° (I )证明:M 在侧棱SC 的中点 (II )求二面角S AM B --的大小。 ? 证(I )略 解(II ):利用二面角的定义。在等边三角形ABM 中过点B 作BF AM ⊥交AM 于点F ,则点F 为AM 的中点,过F 点在平面ASM 内作GF AM ⊥,GF 交AS 于G , 连结AC ,∵△ADC ≌△ADS ,∴AS-AC ,且M 是SC 的中点, · ∴AM ⊥SC , GF ⊥AM ,∴GF ∥AS ,又∵F 为AM 的中点, ∴GF 是△AMS 的中位线,点G 是AS 的中点。 则GFB ∠即为所求二面角. ∵2= SM ,则2 2 = GF , 又∵6= =AC SA ,∴2=AM ,∵2==AB AM ,060=∠ABM ∴△ABM 是等边三角形,∴ 3=BF 。在△GAB 中,26= AG ,2=AB ,0 90=∠GAB ,∴2 11423=+=BG 366 23 2 22211 32 12cos 2 2 2 -=-=??- +=?-+=∠FB GF BG FB GF BFG F G F G
线线角、线面角、面面角专题 一、异面直线所成的角 1.已知两条异面直线,a b ,经过空间任意一点O 作直线//,//a a b b '',我们把a '与b '所成的锐角(或直角)叫异面直线,a b 所成的角。 2.角的取值范围:090θ<≤?; 垂直时,异面直线当b a ,900=θ。 例1.如图, 在直三棱柱111ABC A B C -中,13,4,5,4AC BC AB AA ==== ,点D 为AB 的中点求 异面直线1AC 与1B C 所成角的余弦值 二、直线与平面所成的角 1. 定义:平面的一条斜线和它在平面上的射影所成的锐角, 叫这条斜线和这个平面所成的角 2.角的取值范围:? ? ≤≤900θ。 例2. 如图、四面体ABCS 中,SA,SB,SC 两两垂直,∠SBA=45°, ∠SBC=60°, M 为 AB 的中点, 求(1)BC 与平面SAB 所成的角。 (2)SC 与平面ABC 所成的角的正切值。 B M H S C A _ C _1 _1 _ A _1 A _ C
一、 二面角: 1. 从一条直线出发的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱,这两个半 平面叫做二面角的面。 2. 二面角的取值范围:? ? ≤≤1800θ 两个平面垂直:直二面角。 3.作二面角的平面角的常用方法有六种: 1.定义法 :在棱上取一点O ,然后在两个平面内分别作过棱上O 点的垂线。 2.三垂线定理法:先找到一个平面的垂线,再过垂足作棱的垂线,连结两个垂足即得二面角的平面角。 3.向量法:分别作出两个半平面的法向量,由向量夹角公式求得。二面角就是该夹角或其补角。 二面角一般都是在两个平面的相交线上,取恰当的点,经常是端点和中点。 例3.如图,E 为正方体ABCD -A 1B 1C 1D 1的棱CC 1的中点,求 (1)二面角111D C A D --所成的角的余弦值 (2)平面AB 1E 和底面C C BB 11所成锐角的正切值. 巩固练习 A 1 D 1 B 1 C 1 E D B C A
二面角专题训练 一.解答题(共110小题) 1.如图,在四棱锥S﹣ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2; E为BS的中点,, 求:(Ⅰ)点A到平面BCS的距离; (Ⅱ)二面角E﹣CD﹣A的大小. 中 点作GH⊥CD,交AB于H, ,故 中, , 可得 1111 (1)证明:AB⊥A1C; (2)求二面角A﹣A1C﹣B的余弦值.
= ADB=,ADB= 的余弦值为 3.如,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC, BE (Ⅰ)证明:C,D,F,E四点共面; (Ⅱ)设AB=BC=BE,求二面角A﹣ED﹣B的大小. BC得 同理可得
的平面角. 的大小 4.如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,.沿它的对角线BD把△BDC0折起,使点C0到达平面ABC0D外点C的位置. (Ⅰ)证明:平面ABC0D⊥平面CBC0; (Ⅱ)如果△ABC为等腰三角形,求二面角A﹣BD﹣C的大小. 与二面角有关的立体几何综合题;平面与平面垂直的判定。 所以与 的大小.由夹角公式求与 ,所以∠ AE,CE. ,所以AEBD为正方形,AE=1. AC>1. 因此只有 中,
,的坐标为 ,所以与夹角的大小等于二面角 , .即二面角 5.如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1ABB1. (Ⅰ)求证:AB⊥BC; (Ⅱ)若AA1=AC=a,直线AC与平面A1BC所成的角为θ,二面角A1﹣BC﹣A的大小为φ,求证:θ+φ=. ,即可得到结论. 所成的角, ABA1=β. =D=, D. =.
二面角 1.二面角的计算: 1)定义法; 2)三垂线定理法; 3)垂面法; 4)面积射影法; 例1、已知P 是二面角AB αβ--棱上一点,过P 分别在αβ、内引射线PM ,PN ,且45,60BPM BPN MPN ∠=∠=?∠=?,求此二面角的度数。 例2、已知P 为锐二面角l αβ--棱上的点,,4530PQ PQ l αβ???与成,与成,则二面角l αβ--的度数是多少。 例3、已知二面角l αβ--的度数为θ,在面α内有一条射线AB 与棱l 成锐角δ,与面βγ成角,则必有( ) (A )sin sin sin θδγ= (B )sin sin cos θδγ= (C )cos cos sin θδγ= (D )cos cos cos θδγ=
例4、在120?的二面角l αβ--的面α、β内分别有A 、B 两点,且A 、B 到棱l 的距离AC 、BD 分别长2、4,AB=10,求: (1)直线AB 与棱l 所成角的正弦值。 (2)直线AB 与平面β所成角的正弦值。 例5、已知二面角MN αβ--为60?,,,A B BC AB αββ∈∈为在上的射影,且C 在棱MN 上,AB 与β所成角为60?,且5,45AC MCB = ∠=?,求线段AB 的长。 例6、已知二面角DC αβ--的度数为θ,,,A B ADC αβ∈∈?的面积为S ,且DC=m ,AB DC ⊥,AB 与平面β成30?角,当θ变化时,求DBC ?面积最大值。
例7、已知C 是以AB 为直径的圆周上的一点,30ABC ∠=?, 45PA ABC PBA ⊥∠=?面,,求二面角A-PB-C 的正弦值。 例8、在正方体1111ABCD A B C D -中,利用cos S S θ=射影 解下列各题 1)P 、Q 分别为1,A A AB 的中点,求平面1C PQ 与底面ABCD 所成角的余弦值 2)求二面角11C BD C --的大小; 3)M 是棱BC 的中点,求二面角111D B M C --的余弦值。
线线角、线面角、二面角知 识点及练习 -标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII
线线角、线面角、面面角专题 一、异面直线所成的角 1.已知两条异面直线,a b ,经过空间任意一点O 作直线 //,//a a b b '',我们把a '与b '所成的锐角(或直角)叫异面直 线,a b 所成的角。 2.角的取值范围:090θ<≤?; 垂直时,异面直线当b a ,900=θ。 例1.如图, 在直三棱柱111ABC A B C -中,13,4,5,4AC BC AB AA ==== ,点D 为AB 的中点求异面直线1AC 与1B C 所成角的余弦值 二、直线与平面所成的角 1. 定义:平面的一条斜线和它在平面上的射影所成的锐角, 叫这条斜线和这个平面所成的角 2.角的取值范围:??≤≤900θ。 例2. 如图、四面体ABCS 中,SA,SB,SC 两两垂直,∠SBA=45°, ∠SBC=60°, M 为 AB 的中点,求(1)BC 与平面SAB 所成的角。 (2)SC 与平面ABC 所成的角的正切值。 _ C _1 _ 1 _A _ 1 A _ C
一、二面角: 1. 从一条直线出发的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱,这两个半平面叫做二面角的面。 2. 二面角的取值范围:??≤≤1800θ 两个平面垂直:直二面角。 3.作二面角的平面角的常用方法有六种: 1.定义法 :在棱上取一点O ,然后在两个平面内分别作过棱上O 点的垂线。 2.三垂线定理法:先找到一个平面的垂线,再过垂足作棱的垂线,连结两个垂足即得二面角的平面角。 3.向量法:分别作出两个半平面的法向量,由向量夹角公式求得。二面角就是该夹角或其补角。 二面角一般都是在两个平面的相交线上,取恰当的点,经常是端点和中点。 例3.如图,E 为正方体ABCD -A 1B 1C 1D 1的棱CC 1的中点,求 (1)二面角111D C A D --所成的角的余弦值 B M H S C A
二面角的求法 一、定义法: 从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱 , 这两个半平面叫 做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角 的平面角。 本定义为解题提供了添辅助线的一种规律。如例1中从二面角 S —AM —B 中半平面ABM 上的一已知 点(B )向棱AM 作垂线,得垂足( F );在另一半平面 ASM 内过该垂足(F )作棱AM 的垂线(如GF ), 这两条垂线(BF 、GF )便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。例1如图,四棱锥 S ABCD 中,底面ABCD 为矩形,SD 底面ABCD , 2 AD 2DC SD ,点M 在侧棱SC 上, ABM =60° (I )证明:M 在侧棱SC 的中点(II )求二面角S AM B 的大小。 证(I )略 解(II ):利用二面角的定义。在等边三角形ABM 中过点B 作BF AM 交AM 于点F ,则点F 为 AM 的中点,过F 点在平面ASM 内作GF AM ,GF 交AS 于G , 连结AC ,∵△ADC ≌△ADS ,∴AS-AC ,且M 是SC 的中点,∴AM ⊥SC , GF ⊥AM ,∴GF ∥AS ,又∵F 为AM 的中点,∴GF 是△AMS 的中位线,点 G 是AS 的中点。 则 GFB 即为所求二面角.∵2SM ,则2 2GF , 又∵ 6AC SA ,∴2AM ,∵2AB AM , 60ABM ∴△ABM 是等边三角形,∴ 3BF 。在△GAB 中,2 6AG ,2AB , 90GAB ,∴2 114 2 3BG 3 66 23 2 22 211321 2cos 2 22 FB GF BG FB GF BFG ∴二面角S AM B 的大小为) 36arccos( F G F G
二面角的求法 一、 定义法: 从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。 本定义为解题提供了添辅助线的一种规律。如例1中从二面角S —AM —B 中半平面ABM 上的一已知点(B )向棱AM 作垂线,得垂足(F );在另一半平面ASM 内过该垂足(F )作棱AM 的垂线(如GF ),这两条垂线(BF 、GF )便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。 例1 如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD ,2AD = 2DC SD ==,点M 在侧棱SC 上,ABM ∠=60° (I )证明:M 在侧棱SC 的中点 (II )求二面角S AM B --的大小。 证(I )略 解(II ):利用二面角的定义。在等边三角形ABM 中过点B 作BF AM ⊥交AM 于点F ,则点F 为AM 的中点,过F 点在平面ASM 内作GF AM ⊥,GF 交AS 于G , 连结AC ,∵△ADC ≌△ADS ,∴AS-AC ,且M 是SC 的中点, ∴AM ⊥SC , GF ⊥AM ,∴GF ∥AS ,又∵F 为AM 的中点, ∴GF 是△AMS 的中位线,点G 是AS 的中点。 则GFB ∠即为所求二面角. ∵2= SM ,则2 2 = GF , 又∵6= =AC SA ,∴2=AM ,∵2==AB AM ,060=∠ABM ∴△ABM 是等边三角形,∴ F G