六、关于共线点与共点线
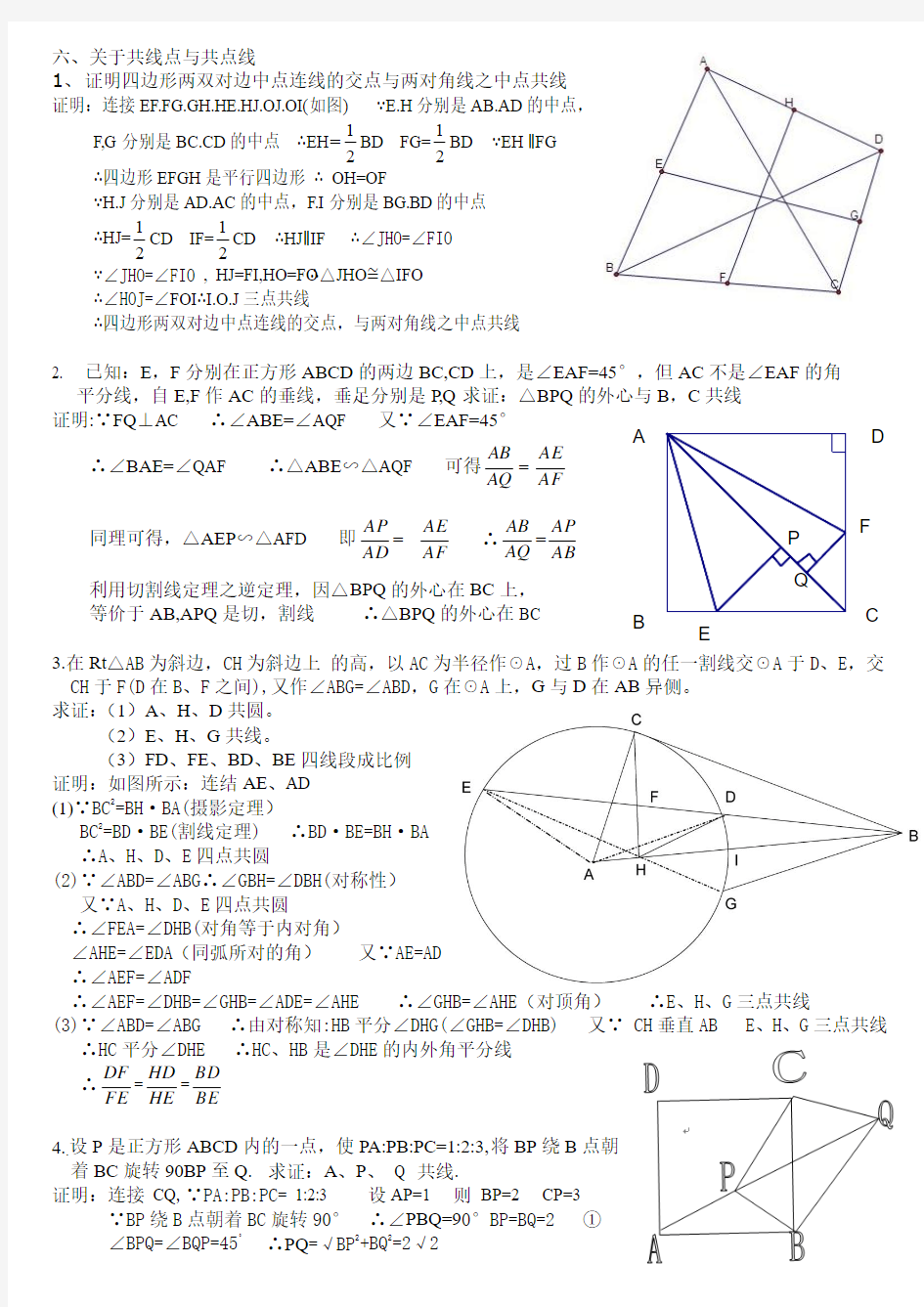
1、 证明四边形两双对边中点连线的交点与两对角线之中点共线 证明:连接EF.FG.GH.HE.HJ.OJ.OI(如图) ∵E.H 分别是AB.AD 的中点,
F,G 分别是BC.CD 的中点 ∴EH =12BD FG=1
2
BD ∵EH ∥FG
∴四边形EFGH 是平行四边形 ∴ OH=OF
∵H.J 分别是AD.AC 的中点,F.I 分别是BG.BD 的中点
∴HJ=12CD IF=1
2
CD ∴HJ ∥IF ∴∠JHO=∠FIO
∵∠JHO=∠FIO , HJ=FI,HO=FO ∴△JHO ?△IFO ∴∠HOJ=∠FOI ∴I.O.J 三点共线
∴四边形两双对边中点连线的交点,与两对角线之中点共线
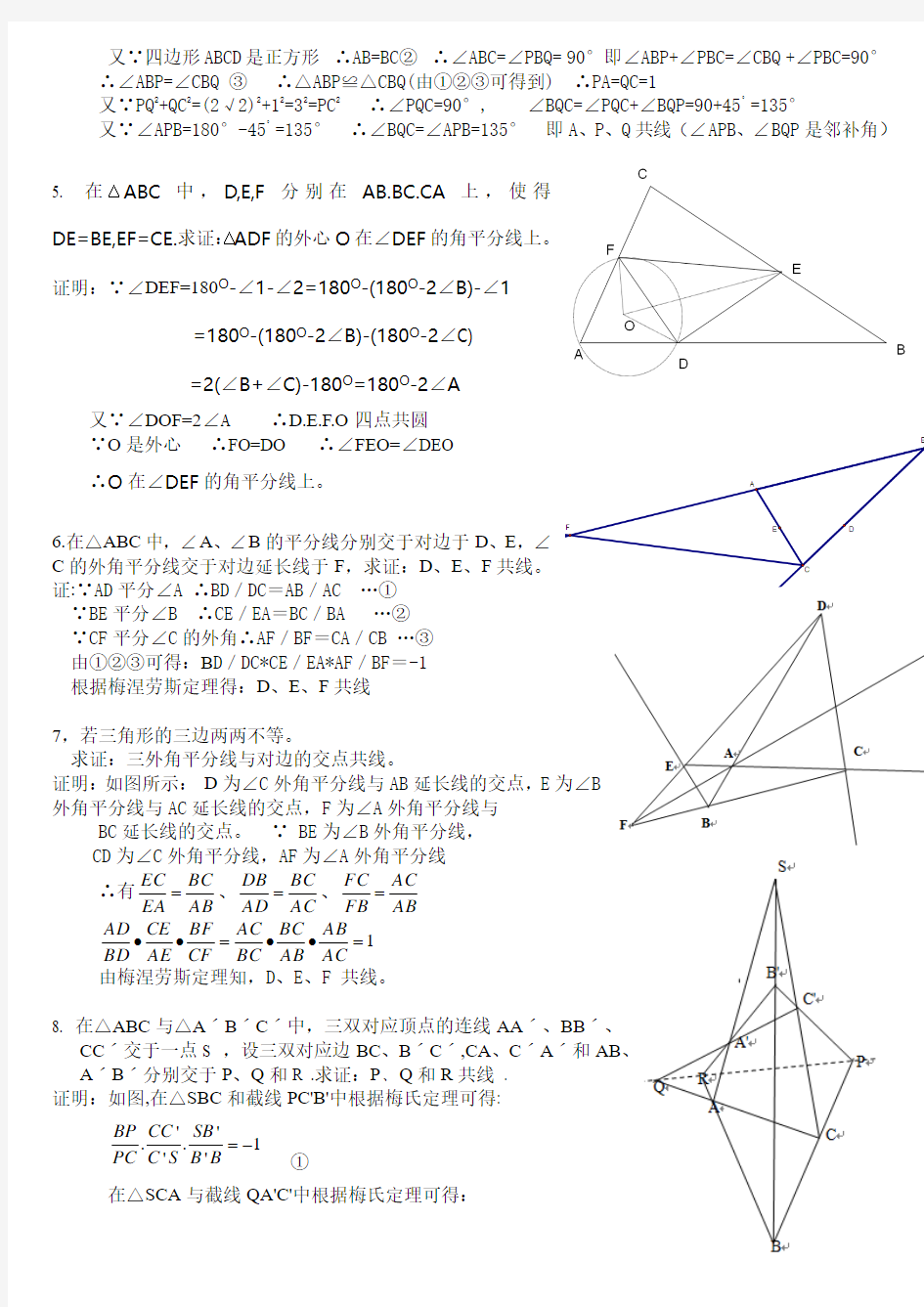
2. 已知:E ,F 分别在正方形ABCD 的两边BC,CD 上,是∠EAF=45°,但AC 不是∠EAF 的角 平分线,自E,F 作AC 的垂线,垂足分别是P,Q 求证:△BPQ 的外心与B ,C 共线 证明:∵FQ ⊥AC ∴∠ABE=∠AQF 又∵∠EAF=45°
∴∠BAE=∠QAF ∴△ABE ∽△AQF 可得 AQ AB AF
AE
同理可得,△AEP ∽△AFD 即
AD
AP
=AF
AE
∴AQ AB =AB AP
利用切割线定理之逆定理,因△BPQ 的外心在BC 上, 等价于AB,APQ 是切,割线 ∴△BPQ 的外心在BC
3.在Rt △AB 为斜边,CH 为斜边上 的高,以AC 为半径作☉A ,过B 作☉A 的任一割线交☉A 于D 、E ,交 CH 于F(D 在B 、F 之间),又作∠ABG=∠ABD ,G 在☉A 上,G 与D 在AB 异侧。 求证:(1)A 、H 、D 共圆。 (2)E 、H 、G 共线。 (3)FD 、FE 、BD 、BE 四线段成比例 证明:如图所示:连结AE 、AD (1)∵BC 2=BH ·BA(摄影定理)
BC 2=BD ·BE(割线定理) ∴BD ·BE=BH ·BA ∴A 、H 、D 、E 四点共圆
(2)∵∠ABD=∠ABG ∴∠GBH=∠DBH(对称性) 又∵A 、H 、D 、E 四点共圆
∴∠FEA=∠DHB(对角等于内对角)
∠AHE=∠EDA (同弧所对的角) 又∵AE=AD ∴∠AEF=∠ADF
∴∠AEF=∠DHB=∠GHB=∠ADE=∠AHE ∴∠GHB=∠AHE (对顶角) ∴E 、H 、G 三点共线
(3)∵∠ABD=∠ABG ∴由对称知:HB 平分∠DHG(∠GHB=∠DHB) 又∵ CH 垂直AB E 、H 、G 三点共线 ∴HC 平分∠DHE ∴HC 、HB 是∠DHE 的内外角平分线
∴FE DF =HE HD =BE BD
4..设P 是正方形ABCD 内的一点,使PA:PB:PC=1:2:3,将BP 绕B 点朝 着BC 旋转90BP 至Q. 求证:A 、P 、 Q 共线.
证明:连接 CQ ,∵PA:PB:PC= 1:2:3 设AP=1 则 BP=2 CP=3
∵BP 绕B 点朝着BC 旋转90° ∴∠PBQ=90°BP=BQ=2 ①
∠BPQ=∠BQP=45° ∴PQ =√BP 2+BQ 2=2√2
A
D
C F
B
E P
Q
又∵四边形ABCD 是正方形 ∴AB=BC ② ∴∠ABC=∠PBQ= 90°即∠ABP+∠PBC=∠CBQ +∠PBC=90° ∴∠ABP=∠CBQ ③ ∴△ABP ≌△CBQ(由①②③可得到) ∴PA=QC=1
又∵PQ 2+QC 2=(2√2)2+12=32=PC 2 ∴∠PQC=90°, ∠BQC=∠PQC+∠BQP=90+45°=135°
又∵∠APB=180°-45°=135° ∴∠BQC=∠APB=135° 即A 、P 、Q 共线(∠APB 、∠BQP 是邻补角)
5. 在?ABC 中,D,E,F 分别在AB.BC.CA 上,使得DE=BE,EF=CE.求证:?ADF 的外心O 在∠DEF 的角平分线上。 证明:∵∠DEF=180O -∠1-∠2=180O -(180O -2∠B)-∠1
=180O -(180O -2∠B)-(180O -2∠C) =2(∠B+∠C)-180O =180O -2∠A
又∵∠DOF=2∠A ∴D.E.F.O 四点共圆 ∵O 是外心 ∴FO=DO ∴∠FEO=∠DEO ∴O 在∠DEF 的角平分线上。
6.在△ABC 中,∠A 、∠B 的平分线分别交于对边于D 、E ,∠C 的外角平分线交于对边延长线于F ,求证:D 、E 、F 共线。 证:∵AD 平分∠A ∴BD /DC =AB /AC …①
∵BE 平分∠B ∴CE /EA =BC /BA …② ∵CF 平分∠C 的外角∴AF /BF =CA /CB …③ 由①②③可得:B D /DC*CE /EA*AF /BF =-1 根据梅涅劳斯定理得:D 、E 、F 共线
7,若三角形的三边两两不等。
求证:三外角平分线与对边的交点共线。
证明:如图所示: D 为∠C 外角平分线与AB 延长线的交点,E 为∠B 外角平分线与AC 延长线的交点,F 为∠A 外角平分线与
BC 延长线的交点。 ∵ BE 为∠B 外角平分线, CD 为∠C 外角平分线,AF 为∠A 外角平分线
∴有AB BC EA EC =、AC BC AD DB =、AB AC FB FC =
1=??=??AC
AB
AB BC BC AC CF BF AE CE BD AD 由梅涅劳斯定理知,D 、E 、F 共线。
8. 在△ABC 与△A ˊB ˊC ˊ中,三双对应顶点的连线AA ˊ、BB ˊ、 CC ˊ交于一点S ,设三双对应边BC 、B ˊC ˊ,CA 、C ˊA ˊ和AB 、 A ˊB ˊ分别交于P 、Q 和R .求证:P ﹑Q 和R 共线 . 证明:如图,在△SBC 和截线PC'B'中根据梅氏定理可得:
''..1''BP CC SB PC C S B B =- ①
在△SCA 与截线QA'C'中根据梅氏定理可得:
''
..1''CQ AA SC QA A S C C =- ② 在△SAB 与截线RA'B'中根据梅氏定理可得:
''..1''AR BB SA RB B S S A =- ③ 将上式①②③相乘可得:
..1
B P
C Q A R
P C Q A R B =- 根据梅氏定理可得P 、Q 、R 三点共线。
9. □EFGH 的顶点在□ABCD 各边,求证: 对角线AC,BD,EG , FH 共点
证:连接BE,DG 在□ABCD 中,∠B=∠D ,A D ∥BC ∴∠BGE=∠DEG 在□EFGH 中,EH=FG , EH ∥FG , ∴∠FGE=∠HEG ∴∠FGB=∠HED ∴△FBG ≌△HDE ∴BG=DE ∴四边形BGDE 为平行四边形,BD,EG 为对角线
同理四边形AFCH 为平行四边形,AC,FH 为其对角线 ∴AC,BD,EG , FH 共点
10. 有两个正方形ABCD 与AB 1C 1D 1,B 与B 1不重合。求证:直线BB 1、CC 1和DD 1共点。 证明:设BB 1、CC 1交于P ,在连结AC 、AC 1,
则有22'∠=∠?A、B、C、P共圆
11'∠=∠ 22'∠=∠
∴?ABB'∞?ACC'
∴33'∠=∠ ∴A 、B'、C'、P 共圆
又
A 、
B 、
C 、P ∴P 是两正方形外接圆的交点
∴P 在DD'上 ∴直线BB 1、CC 1和DD 1共点。
11. I 为△ABC 的内心,X 、Y 分别为内切圆与AB 、BC 的切点,D 、E 分别为BC 、CA 的中点. 求证:AI 、XY 与ED 共点.
思路:利用内切特性,证两线交点在第三线上。
证:设AB=c ,AC=b ,BC=a ,DE 与XY 交于P ,如图所示。 现应证P 在∠A 的角平分线上,为此,只需计算出
()
2b
PE AE = =
即可。而计算PE ,又分步如下:由切线等长性可知
1
()2AX a a b c s
+ =++ =
∴ AX s a = -
同理
BX s b = BY = -
O
H
D
B
C
A E F G I A
B
C
D
Y
X
E
P
2BD BY DY s b DY
a
==-=--
∴2
a
D Y s b
=--
,
DE AB BX BY
// =
∴2
a
DP DY s b
==--
∴()
222
s b AE
c a b
PE DE DP---==
=-=
∴AE
∠APE=∠P再由DE AB
//即知AP平分∠A
12. 四边形ABCD外切于圆O,AC⊥BD并交于E,P、Q、R、S顺
次为边AB、BC、CD、DA上的切点,连结PR、QS,
求证:(1)四边形ABCD以其一条对角线为对称轴
(2)PR与QS都过E.
证明:设lAB、lBC、lCD 、lDA分别表示四边形ABCD
各边之长,则由四边形ABCD外切于圆。可知
lAB+ LCD= lBC+ lAB (1) 再由四边形垂直又有
LAB*+lCD*=lBC*+lAB* (2) (1)*-(2)再除以2,得
lAB?lCD=lBC?lAB (3)
(1).(3)两式表明:lAB lCD lBC lDA都是X*+px+q=0的一对根,故
只有如下两种情况LAB=lBC, lCD=lAB或lAB=lAD,lCD=lBC
前者表明BD为对称轴,如右图所示,后者断定AC是对称轴,由
此得证
证(2)∵∠1=∠2=∠3=∠4 QS过点E 同理:PR也过点E
13. △ABC的内切圆⊙I分别切三边BC,CA和AB于A1,B1和C1,
线段AI,BI,和CI分别与⊙I交于A2,B2,C2.求证:直线A1A2,B1B2,
C1C2共点。
证明:连接A1,B1和C1 ∵圆I内切于△ABC,
∴AI,BI,CI分别平分∠A,∠B,∠C,
即AI,BI,CI分别平分弧B1C1,C1A1,B1A1
∴A1A2,B1B2,C1C2是△A1B1C1的内角平分线
∴A1A2,B1B2,C1C2共点。
14、等圆⊙O1与⊙O2交于AB,O为AB的中点,过O引⊙O1的弦CD
交⊙O2于P,过O引⊙O2的弦EF交⊙O1于Q,求证:AB、CQ、
EP三线交于一点。
证明:设CQ,EP分别交于AB于M、N
为证M≡N,应做CD关于AB对
称线段C’D’,则C’、D’在⊙O2上,
∵C’、D’、P、E共圆
∴∠C’EG=∠C’D’P=∠C’OA
∵OD’=OD=OP ∴∠PD’D=90°
又∵D,D’对称∴AB⊥DD’
∴PD’∥AB ∴C’,O,N,E共圆
由等角转化可得△OC’N≌△OCM
∴N≡M
即CQ,EP与AB共点。
D'
C'
M Q
P
E
C
B
A
O1O2
D
F
错位相减法求和专项.}{a分别是等差数列和等比数列,在应用过{ab}型数列,其中错位相减法求和适用于nn`nn 程中要注意: 项的对应需正确; 相减后应用等比数列求和部分的项数为(n-1)项; 若等比数列部分的公比为常数,要讨论是否为1 数列的前项已知二次函数的图象经过坐标原点,其导函数,1. 均在函数,点的图象上.和为 )求数列Ⅰ(的通项公式; 是数列的前项和,求.(Ⅱ)设, [解析]考察专题:,,,;难度:一般 [答案] (Ⅰ)由于二次函数的图象经过坐标原点,
,,则设 ∴,∴, 又点均在函数的图象上, ∴. 时,,当∴ 又,适合上式,∴............(7分) ,)知,Ⅰ)由(Ⅱ (. ∴, ∴, 上面两式相减得:
. 整理得..............(14分) 是数列的前n2.项和,且已知数列的各项均为正数, . )求数列的通项公式;1 ( )的值.(2][答案查看解析 时,解出an = 1 = 3,] [解析(1)当12-①34S又= a + 2a nnn = + 2a-4s3 ②当时n-1n1- 即,, -①② , ∴. (),
是以3为首项,2为公差的等差数列,6分 . )2③ ( 又④ ③④- = 12分 设函数,19,12分)(2013年四川成都市高新区高三4月月考,3. ,数列前数列.项和,满足, )求数列的通项公式;(Ⅰ
,证明:的前,数列.项和为(Ⅱ)设数列的前项和为 ,得由Ⅰ[答案] () 为公比的等比数列,故.是以 )由(Ⅱ得, …, …+,记
用错位相减法可求得: (注:此题用到了不等式:进行放大. . ) 与的等比中项.4.已知等差数列是中,; )求数列的通项公式:(Ⅰ 项和Ⅱ)若的前.求数列 ( 的等比中项.所以,是([解析]Ⅰ)因为数列与是等差数列,
— 1. 设等差数列{}n a 的前n 项和为n S ,且244S S =,122+=n n a a (Ⅰ)求数列{}n a 的通项公式 (Ⅱ)设数列{}n b 满足 *12 12 1 1,2 n n n b b b n N a a a +++ =-∈ ,求{}n b 的前n 项和n T 2. (2012年天津市文13分) 已知{n a }是等差数列,其前n 项和为n S ,{n b }是等比数列,且1a =1=2b ,44+=27a b ,44=10S b -. (Ⅰ)求数列{n a }与{n b }的通项公式; (Ⅱ)记1122=++ +n n n T a b a b a b ,+n N ∈,证明1+18=n n n T a b --+(2)n N n >∈,。 … 【答案】解:(1)设等差数列的公差为d ,等比数列的公比为q , 由1a =1=2b ,得3 44423286a d b q s d =+==+,,。
由条件44+=27a b ,44=10S b -得方程组 3 3 23227 86210 d q d q ?++=??+-=??,解得 3 2d q =??=?。 ∴+ 312n n n a n b n N =-=∈,,。 (Ⅱ)证明:由(1)得,()23225282132n n T n =?+?+?+-?+ ①; ∴()234+12225282132n n T n =?+?+?+?+- ②; 由②-①得, : ()()234+1122232323+2332n n n T n =-?-?+?+?-+??+ ()()()()()()+12341+1+1+1+11=4+323222+2412111=4+323=4+32+1232142 =8+3=+8 n n n n n n n n n n n n a b ----?+++??---? --?----- ∴1+18=n n n T a b --+ (2)n N n >∈,。 3.(2012年天津市理13分)已知{n a }是等差数列,其前n 项和为n S ,{n b }是等比数列,且1a =1=2b ,44+=27a b ,44=10S b -. (Ⅰ)求数列{n a }与{n b }的通项公式; (Ⅱ)记1121=++ +n n n n T a b a b a b -,+n N ∈,证明:+12=2+10n n n T a b -+()n N ∈. 【答案】解:(1)设等差数列的公差为d ,等比数列的公比为q , 由1a =1=2b ,得3 44423286a d b q s d =+==+,,。 & 由条件44+=27a b ,44=10S b -得方程组 3 3 23227 86210 d q d q ?++=??+-=??,解得 3 2d q =??=?。 ∴+ 312n n n a n b n N =-=∈,,。 (Ⅱ)证明:由(1)得,231212222n n n n n T a a a a --=+++?+ ①;[
初等几何研究试题答案(II ) 二、关于和、差、倍、分线段(角) 1、 等腰ABC 中,0100,A B ∠=∠的平分线交AC 于D ,证明: BD+AD=BC 。 D ' B C A 43 2 1 证:在BC 上取点D , ,使BD , =BD,连结DD , 0100A ∠=且 BD 平分∠ABC 00120,40C ∴∠=∠= 又BD=BD ,,0380∴∠=,23C ∠+∠=∠ 0240∴∠= 即2C ∠=∠ ,,CD DD ∴= 又03180A ∠+∠= ∴点A 、D 、D , 、B 四点共圆且14∠=∠ ∴DD , =AD
BC=BD , +CD , =BD+AD 已知,ABCD 是矩形,BC=3AB,P 、Q 位于BC 上,且BP=PQ=QC, 求证:∠DBC +∠DPC=∠DQC 解:作矩形BCEF 与矩形ABCD 相等,在EF 上选取点O 使得 FO=2EO.连结BO 、DO 。 由图可知,由BO=DO ,且有△BF O ≌△OED, ∵∠FBO+∠BOF=90o ∠BOF=∠DOE ∴∠BOF+∠DOE=90o ∴∠BOD=90o △BOD 为等腰直角三角形 有∠DBO=45o ∴∠DBP+∠QBO=45o ∵∠DPC=∠QBO ∴∠DBP+∠DPC=45o ∵△DQC 为等腰直角三角形 ∴有∠DQC=45o 因此,有∠DBP+∠DPC=∠DQC P Q A B C F E O P D
3、圆内接四边形ABCD 的对角线AC 、BD 交于X ,由X 向AB 、BC 、CD 和DA 作垂线,垂足分别为A ′、B ′、C ′和D ′. 求证:A ′B ′+C ′D ′=B ′C ′+D ′A ′ 证明:(方法一) ∵X 、A ′、A 、D ′四点共圆(对角和180°) ∴∠XA ′D ′=∠XAD ′ 又∵∠XAD ′=∠XBC(圆周角) 同理∠XA ′B ′=∠XBC,即∠XA ′D ′=∠XA ′B ′ 同理可得∠XB ′A ′=∠XB ′C ′,∠XC ′B ′=∠XC ′D ′, ∠XD ′C ′=∠XD ′A ′ ∴X 是四边形A ′B ′C ′D ′的内心。 ∴A ′B ′+C ′D ′=B ′C ′+A ′D ′ (方法二)利用正弦定理. 设r 是四边形ABCD 的外接圆 C A B A ′ C ′ D B ′ D ′ X
错位相减法求和专项 错位相减法求和适用于{a n'b n}型数列,其中{a n},{b n}分别是等差数列和等比数列,在应用过程中要注意: 项的对应需正确; 相减后应用等比数列求和部分的项数为(n-1)项; 若等比数列部分的公比为常数,要讨论是否为1 1.已知二次函数的图象经过坐标原点,其导函数/■]■:I “亠],数列?的前 项和为,点均在函数:=y:/.::的图象上? (I)求数列的通项公式; (n)设,,■是数列的前」项和,求?’? [解析]考察专题:2.1 , 2.2 , 3.1 , 6.1 ;难度:一般 [答案](I)由于二次函数-的图象经过坐标原点, 则设, 又点「均在函数的图象上, 二当心时,?、、= J ;:? ;?■■■ L] 5 T
又忙:=.:「=乜,适合上式,
I ............................................... (7 分) (n)由(i)知 - 2 - :' 2 - :......................................... |;■:■: 2 ? ? :' - 'I+(2?+ l)^"kl,上面两式相减得 =3 21 +2 (21 +23十…4『r)-(2打+ 】 卜2* 4屮一才丨, , : ■ . 1=2 整理得:,?................. 2.已知数列’的各项均为正数,是数列’ (14 分)的前n项和,且 (1)求数列’的通项公式; (2)二知二一- [答案]查看解析 解出a i = 3, [解 析] 又4S n = a n? + 2a n —3 ①
初等几何研究试题答案(I) 、线段与角的相等 1. O O、O Q相交于A B, O O的弦BC交O Q于E, O 02的弦BD交O 0于F, 求证:(1)若2 DBA2 CBA贝卩 若DF二CE则 / DBA M CBA. 证明:⑴连接AC AE AF、AD 在O 0 中,由/ CBA W DBA得AC=AF 在O O 中,由/ CBA W DBA得AE=AD 由A C、B、E四点共圆得/仁/2 由A D B、E四点共圆得/ 3二/4 所以△ ACE^A AFD ??? DF=CE (2) 由(1)得/ 仁/ 2, / 3=2 4 v DF=CE ? △ACE^A AFD
??? AD=AE 在O Q 中,由AD=AE^得/ DBA M CBA 2. 在厶ABC中,AC=BC,Z ACB=90,D是AC上的一点,AE丄BD的延长线于E,又AE=1BD, 2 求证:BD平分/ ABC. 证明:延长AE,BC交于点F 7 AED "BCA =90 ADE "BDC ?CBD =/CAF 又7 ACF BCA = 90 AC 二BC ?ACF 三BCD . AF = BD 1 1 又、:AE BD . AE AF 2 2 又ABEE _ BE ■ BE平分ABF 即BD平分.ABC 3. 已知在凸五边形ABCDE中, / BAE=3 ,BC=CD=DE M/ BCD玄CDE=180-
求证:/ BAC 2 CAD h DAE. 证明:过点B 作BDL BC,交圆周于点D,连结CD ?D ???/ DBC=90, ? CD 是直径,则/ CAD=90 证明:连接BD,得△ CBD 是等腰三角形 且底角是/ CDB=[18(0-(180o — 2 - )] -2=. :丄 BDE=(180° — 2G )-O (=180O — 3? ??? A B 、D E 共圆 同理A C D E 共圆 ? h BAC h CAD h DAE 4. 设H 为锐角△ ABC 的垂心,若AH 等于外接圆的半 径
《初等几何研究》作业 一、填空题 1、对直线a 上任意两点A 、B ,把B 以及a 上与B 在A 同侧的点的集合称作 射线(或半直线),; ,并记作 AB 。 2、在绝对几何中,外角定理的内容是: 三角形的外角大于任一不相邻的内角 。 3、第四组公理由 两 条公理组成,它们的名称分别是 度量公理(或阿基米德公理)和康托儿公理 。 4、欧氏平行公理是:对任意直线a 及其外一点A ,在a 和A 决定的平面上,至多有一条过A 与a 不相交的直线 。 5、罗氏几何公理系统与欧氏几何公理系统的共同之处是 前4组公理(或绝对几何) ,不同之处是 平行公理 。 6、几何证明的基本方法,从推理形式上分为 演绎 法与归纳法;从思维方向上分为 综合 法与分析法;从命题结构上分为 直接 证法与间接证法,其中间接证法包括 反证 法与 同一 法。 7、过反演中心的圆,其反演图形是 不过 (过或不过)反演中心的 直线 。 8、锐角三角形的所有内接三角形中,周长最短的是 垂足三角形。 9、锡瓦定理:设⊿ABC 的三边(所在直线)BC 、CA 、AB 上分别有点X 、Y 、Z ,则AX 、BY 、CZ 三线共点(包括平行)的充要条件是 1=??ZB AZ YA CY XC BX 。 10、解作图问题的常用方法有: 交轨法 、三角奠基法、 代数法 、 变换法 等。 11、数学公理系统的三个基本问题是 相容性、 独立性和 完备 性. 33.①答案不惟一. 34.①(0,+∞),②,(0,π/2),③连续,④单调递减. 35.①平移,②旋转,③轴对称. 36. ①1 =??ZB AZ YA CY XC BX (或-1) 37.①写出已知与求作,②分析,③作法,④证明,⑤讨论.
数列练习题 一、单选题 1.设数列{}n a 的前n 项和2n S n =,则8a 的值为( ) A .15 B .16 C .49 D .64 二、填空题 2.已知公差不为0的等差数列{}n a ,其前n 项和为n S ,首项12a =,且1a ,2a ,4a 成等比数列,则7S 的值为___________. 三、解答题 3.正项等比数列{}n a 的前n 项和为n S ,且12461,4a S S S =+=. (1)求{}n a 的通项公式; (2)求数列{}n a n +的前n 项和n T . 4.已知公差不为零的等差数列{}n a 满足132a a =,是1a 与7a 的等比中项. (1)求{}n a 的通项公式; (2)是否存在n 值,使得{}n a 的前n 项和27n S =?
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。 5.已知在递增等差数列{a n }中,a 1=1,a 3是a 1和a 9的等比中项. (1)求数列{a n }的通项公式; (2)若112 n a n n n b a a +=+?,求数列{b n }的前n 项和S n . 6.已知n S 为{}n a 的前n 项和,{}n b 是等比数列且各项均为正数,且23122n S n n =+,12b =,2332 b b +=. (1)求{}n a 和{}n b 的通项公式; (2)记()41n n n a c b += ,求数列{}n c 的前n 项和n T .
7.已知数列{}n a 的前n 项和243n S n n =-+,求: (1)数列{}n a 的通项公式; (2)求数列{}n a 的前n 项和n S 的最小值. 8.已知等差数列{}n a 满足23a =,4822a a +=. (1)求数列{}n a 的通项公式; (2)设1 1n n n b a a += ,求数列{}n b 的前n 项和n T . 9.已知数列{}n a 的前n 项的和235n S n n =+. (1)求{}n a 的通项公式; (2)设1 3n n n b a a +=,求数列{}n b 的前n 项和.
《初等几何研究》作业参考答案 一.填空题 1.①射线(或半直线),②。 2、 ①两,②度量公理(或阿基米德公理)与康托儿公理。 3.①前4组公理(或绝对几何),②平行公理。 4.①平移,②旋转,③轴对称、 5. 1=??ZB AZ YA CY XC BX 。 6.①交轨法,②三角奠基法,③代数法,④变换法。 7.①反身性、②对称性、③传递性、④可加性、 8.外角、 9.答案不惟一、 10.①演绎,②综合,③直接,④反证,⑤同一; 11. 1=??ZB AZ YA CY XC BX 、(答-1也对) 12. ①过两点可作一条直线(或其部分),②已知圆心与半径可作一圆(或其部分)、 13.①不共线的三点A 、B 、C 及(AB)、(BC)、(CA)构成的点的集合。 14.连续、 15.答案不惟一、 16.①不过,②圆、 17.1 =??ZB AZ YA CY XC BX (或-1)、 18.①写出已知与求作,②分析,③作法,④证明,⑤讨论、 19.①相容,②独立,③完备、 20.合同变换、相似变换、射影变换、反演变换等 21.对任意直线a 及其外一点A,在a 与A 决定的平面上,至少有两条过A 与a 不相交的直线、 22.①代数,②解析,③三角,④面积,⑤复数,⑥向量、 23.相等。 24.所求的量可用已知量的有理式或只含平方根的无理式表出. 二.问答题 1.对于公理系统∑,若有一组具体事物M,其性质就是已知的,在规定∑中每一个基本概念指M 中某一具体事物后,可验证∑中每个公理在M 中都成立,则称M 为公理系统∑的一个模型; 2.①若AB ≡B A '',则d(AB)=d(B A ''); ②当C B A ?时,有d(AB)+d(BC)=d(AC)、
初等几何研究试题答案()(李长明版)
————————————————————————————————作者:————————————————————————————————日期:
初等几何研究试题答案(I) 一、线段与角的相等 1. ⊙O1、⊙O2相交于A、B,⊙O1的弦BC交⊙O2于E,⊙O2的弦BD交⊙O1于F, 求证: (1)若∠DBA=∠CBA,则DF=CE; (2) 若DF=CE,则∠DBA=∠CBA. 证明:(1)连接AC、AE、AF、AD 在⊙O1中,由∠CBA=∠DBA得AC=AF 在⊙O2中,由∠CBA=∠DBA得AE=AD 由A、C、B、E四点共圆得∠1=∠2 由A、D、B、E四点共圆得∠3=∠4 所以△ACE≌△AFD ∴DF=CE (2)由(1)得∠1=∠2,∠3=∠4 ∵DF=CE ∴△ACE≌△AFD
∴AD=AE 在⊙O 2中,由AD=AE 可得∠DBA=∠CBA 2. 在△ABC 中,AC=BC,∠ACB=90O ,D 是AC 上的一点,AE ⊥BD 的延长线于E,又AE=1 2 BD, 求证:BD 平分∠ABC. 证明:延长AE,BC 交于点F AED BCA 90 ADE BDC CBD CAF ACF BCA 90 AC BC ACF BCD AF BD 11 AE BD AE AF 22 ABEE BE BE ABF BD ABC ∠=∠=?∠=∠∴∠=∠∠=∠=?=∴???∴==∴=⊥∴∠∠Q Q Q Q 又又又平分即平分 3. 已知在凸五边形ABCDE 中,∠BAE=3α,BC=CD=DE,且∠BCD=∠CDE=180o-2α,
特定数列求和法—错位相减法 在高中所学的数列求合的方法有很多,比如倒序相加法、公式法、数学归纳法、裂项相消法、错位相减法等等,在此处我们就只着重讲解一种特定数列求和的方法——错位相减法。那到底什么是错位相减法呢?现在咱们来回忆当初学习等比数列时老师是怎么一步步推导出等比数列的求和公式的,下面是推导过程: 数列{}n a 是由第一项为1a ,且公比为q 的等比数列,它的前n 项和是 111121...n n a a q a q a q s -=++++ ,求 n s 的通项公式。 解 由已知有 111121...n n a a q a q a q s -=++++, ○ 1 两端同乘以q ,有 ○ 1-○2得 当1q =时,由○ 1可得 当1q ≠时,由○ 3可得 于是 1(1)n s na q == 或者 11(1)1n n a a q s q q -=≠- 通过上述推导过程老师运用了一种特殊的推导方法将本来很复杂的运算简化了,从而得到等比数列的求和公式,这种方法叫错位相减法,那我们是不是遇到复杂的运算就都可以用这种方法呢?答案当然不是,我们仔细观察这推导过程,就会发现其实错位相减法是用来计算一个等比数列乘以一个等差数列而成的复杂数列的。可以归纳数学模型如下: 已知数列{}n a 是以1a 为首项,d 为公差的等差数列,数列{}n b 是以1b 为首项,(1)q q ≠为公比的等比数列,数列n n n c a b =,求数列{}n c 的前n 项和. 解 由已知可知 两端同乘以q 可得 = 11223311...n n n n n qc a b q a b q a b q a b q a b q --=+++++
专项训练:错位相减法 目录 1.(2003北京理16) (2) 2.(2005全国卷Ⅰ) (2) 4.(2005湖北卷) (2) 5.(2006安徽卷) (2) 6.(2007山东理17) (2) 7.2007全国1文21) (2) 8.(2007江西文21) (2) 9.(2007福建文21) (2) 10.(2007安徽理21) (3) 11.(2008全国Ⅰ19) (3) 12.(2008陕西20) (3) 13.(2009全国卷Ⅰ理) (3) 14.(2009山东卷文) (3) 15.(2009江西卷文) (3) 16.(2010年全国宁夏卷17) (3) 17.(2011辽宁理17) (4) 18.(2012天津理) (4) 19.2012年江西省理 (4) 20.2012年江西省文 (4) 21.2012年浙江省文 (4) 22.(2013山东数学理) (4) 23.(2014四川) (4) 24.(2014江西理17) (5) 25.(2014安徽卷文18) (5) 26.(2014全国1文17) (5) 27.(2014四川文19) (5) 28.(2015山东理18) (5) 29.(2015天津理18) (5) 30.(2015湖北,理18) (5) 31.(2015山东文19) (5) 32.(2015天津文18) (6) 33.(2015浙江文17) (6) 专项训练错位相减法答案 (7)
已知数列{}n a 是等差数列且12a =,12312a a a ++= (1)求数列{}n a 的通项公式; (2)令()n b a x x R =?∈ 数列{}b 的前n 项和的公式 在等差数列{}n a 中,11a =,前n 项和n S 满足条件 242 ,1,2,1 n n S n n S n +==+L , (1)求数列{}n a 的通项公式; (2)记(0)n a n n b a p p =>,求数列 b 的前n 项和n T ? 设{}n a 为等比数列,11a =,23a =. (1)求最小的自然数n ,使2007n a ≥; (2)求和:212321232n n n T a a a a = -+--L . 9.(2007福建文21) 数列{}n a 的前n 项和为n S ,11a =,* 12()n n a S n +=∈N . (1)求数列{}n a 的通项n a ; (2)求数列{}n na 的前n 项和n T .
数列专练(裂项相消法) 1. 已知数列{}n a 的前项和2 2n S n n =+; (1)求数列的通项公式n a ;(2)设1234 1 23111 1 n n n T a a a a a a a a +=++++ ,求n T . 2. 已知数列{}n a 的前项和为n S ,且满足213 (1,) 22n S n n n n N *=+≥∈ (1)求数列{}n a 的通项公式; (2)设n T 为数列? ?? ??? +11n n a a 的前n 项和,求使不等式20121005>n T 成立的n 的最小值. 2. 已知数列{}n a 的前n 项和为n S ,且11a =,()11 1,2,3, 2 n n a S n +==. (1)求数列{}n a 的通项公式; (2)当()312 log 3n n b a +=时,求证:数列11n n b b +??? ??? 的前n 项和1n n T n = +. 3. 已知数列{}n a 的前n 项和为n S ,点), (n s n n 在直线2 1121+=x y 上,数列{}n b 满足0212=+-++n n n b b b ,() *N n ∈,113=b ,且其前9项和为153. (1)求数列{}n a ,{}n b 的通项公式; (2)设) 12)(112(3 --=n n n b a c ,求数列{}n c 前n 项的和n T . 4. 已知数列{}n a 的前n 项和为n S ,且22n n S a =-,(1,2,3)n =???;数列{}n b 中,11,b = 点 1(,)n n P b b +在直线20x y -+=上.
《初等几何研究》综合测试题(二十) 适用专业:数学教育专业考试时间:120分钟 一、选择题(本题共8小题,每小题3分,共24分) 1.两个三角形有两边和一角对应相等,则两个三角形__________。 A.一定全等; B.一定不全等; C.可能全等,可能不全等; D.以上都不是。 2.在在正三角形、等腰梯形、矩形和圆这四种图形中是轴对称图形,又是中心对称图形的有__________。 A.1种; B.2种; C.3种; D.4种。 3.如图,在等腰梯形ABCD中,AD//BC,AC与BD相交于点O, 则图中面积相等的三角形共有___________。 A.1对; B.2对; C.3对; D.4对。 4. 在正三角形、等腰梯形、矩形和圆这四种图形中是轴对称图形,又是中心对称图形的有__________。 A.1种; B.2种; C.3种; D.4种。 5.如图,在 ABC中,DE//BC,如果AE:EC=3:2, 那么DE:BC等于________。 A.3:5;B.3:2; C.2:3;D.2:5。 6.⊙O中,AB、CD是两条平行弦,位于圆心的两侧,AB=40cm,CD=48cm,AB、CD的距离为22cm,则⊙O的半径是__________。 A.15cm; B.20cm; C.25cm; D.30cm。 7.在平移过程中,对应线段 A.互相平行且相等; B.互相垂直且相等; C.互相平行(或在同一条直线上)且相等; D.以上都不对。 8.下列关于平移的说法中正确的是___________。 A.原图形中两个顶点连成的线段长是平移的距离; B.平移后的两个图形中两个顶点连成的线段长是平移的距离; C.以对应点中的一点为端点的射线是平移的方向。 D.以原图形中的一点为端点,且经过它的对应点的射线的方向是平移的方向; 二、判断题(本题共5小题,每小题2分,共10分) 1.正方形形既是中心对称图形又是轴对称图形。(√) 2.位似中心一定在两个图形之间。(×) 3.位似中心在连接两个对应点的线段之外的位似图形叫做外位似。(√) 4.两个位似图形对应点连线的交点个数为1或2。(×) 5.设点A与B关于x轴对称,点A与点C关于y轴对称,则点B与点C关于x对称。(×) 三、填空题(本题共4小题,每小题4分,共16分) 1.一个角的补角和它的余角的3倍的和等于它的周角的11 12 ,则这个角的度数是________. 2. 如图,铁路上A、B两站(视为直线上两点)相距25km,C、D为两村庄(视为两个点),
错位相减法求和专题训练 1.已知数列{}n a 满足22,{ 2,n n n a n a a n ++=为奇数为偶数 ,且*12,1,2n N a a ∈==. (1)求 {}n a 的通项公式; (2)设* 1,n n n b a a n N +=?∈,求数列{}n b 的前2n 项和2n S ; (3)设()2121n n n n c a a -=?+-,证明: 123 111154 n c c c c ++++ < 2.设正项数列{}n a 的前n 项和为n S ,且满足37a =, 2 1691n n a S n +=++, *n N ∈. (1)求数列{}n a 的通项公式; (2)若正项等比数列{}n b 满足1132,b a b a ==,且n n n c a b =?,数列{}n c 的前n 项和为n T . ①求n T ; ②若对任意2n ≥, *n N ∈,均有()2 563135n T m n n -≥-+恒成立,求实数m 的取值范 围. 3.已知*n N ∈,设n S 是单调递减的等比数列{}n a 的前n 项和, 112 a = 且224433,,S a S a S a +++成等差数列. (1)求数列{}n a 的通项公式; (2)记数列{}n na 的前n 项和为n T ,求证:对于任意正整数n , 1 22 n T ≤<. 4.递增的等比数列{}n a 的前n 项和为n S ,且26S =, 430S =. (1)求数列{}n a 的通项公式; (2)若12 log n n n b a a =,数列{}n b 的前n 项和为n T ,求1 250n n T n ++?>成立的正整数n 的 最小值. 5.已知数列{}n a 及()2 12n n n f x a x a x a x =++ +,且()()11?n n f n -=-, 1,2,3, n =. (1)求123a a a ,,的值; (2)求数列{}n a 的通项公式;
五、关于平行与垂直 1、I 是△ABC 的内心,AI 、BI 和CI 的延长线分别交△ABC 的外接圆于 D 、 E 和F. 求证:E F ⊥AD. 证明:已知I 是△ABC 的内心, ∴AD 、BE 和CF 是∠BAC 、∠ABC 和∠ACB 的角平分线 ∴⌒BD =⌒CD ,⌒BF =⌒AF ,⌒AE =⌒CE ∴⌒BD +⌒BF +⌒AE =⌒CD +⌒AF +⌒CE ∴⌒DF +⌒AE =⌒DE +⌒AF ∴∠AIF=∠AIE=∠DIF=∠DIE ∴EF ⊥AD 2. A 、B 、C 、D 是圆周上“相继的”四点,P 、Q 、R 、S 分别是弧AB 、BC 、CD 、DA 的中点,求证:PR ⊥QS.
Q 证明:∵P 、Q 、R 、S 分别是AB 、BC 、CD 、DA 的中点 ∴⌒ AP =⌒ PB ,⌒BQ =⌒ QC ,⌒CR =⌒ RD ,⌒ DS =⌒ SA ∴⌒ AP +⌒QC +⌒CR +⌒SA =⌒PB +⌒BQ +⌒ RD +⌒ DS 又∵⌒ PQ +⌒RS =⌒PB +⌒BQ +⌒RD +⌒ DS , ⌒SP +⌒ RQ =⌒AP +⌒QC +⌒ CR +⌒ SA ∴⌒ PQ +⌒RS =⌒SP +⌒RQ ∴SQ ⊥PR 3、凸四边形ABCD 的每条对角线皆平分它的面积,求证:ABCD 是平行四边形。 证明:设AC 和BD 相交于点O , 作AE ⊥ BD 于E ,CF ⊥BD 于F ,
连接AF,CE ∵对角线BD平分四边形ABCD的面积 ∴S△ABD=S△CBD ∴AE=CF 又∵AE⊥BD,CF⊥BD ∴AE∥CF ∴四边形AECF为平行四边形 ∴AO=CO 同理可得 BO=DO ∴四边形ABCD是平行四边形 4、已知△BCX和△DAY是□ABCD外的等边三角形,E、F、G和H是YA、AB、XC和CD的中点。求证:EFGH是平行四边形。 G C H D Y E A F B X 证:∵ABCD是平行四边形,且F、H是AB、CD的中点∴CH=AF,∠BCD=∠BAD,且AD=BC ∵△BCX、△DAY是分别以BC、AD为边的等边三角形且E、G分别是AY、XC的中点 ∴∠XCB=∠DAY,CG=AE ∴∠GCH=∠EAF ∴△GCH≌△AEF ∴EF=GH 且∠GHC=∠AFE ∵AB∥CD ∴∠AFH=∠AEF,∠GHF=∠EFH ∴EF∥HG,∴四边形EFGH是平行四边形
错位相减法的运用 错位相减法是一种常用的数列求和方法, 形如{}n n b a 的数列,其中{n a }为等差数列,{}n b 为等比数列;分别列出n S ,再把所有式子同时乘以等比数列的公比q ,即n qS ;然后错一位,两式相减即可。适用于一个等差数列和一个等比数列对应项相乘构成的数列求和。 典型例题: 例 1. (2012年四川省文12分)已知数列{}n a 的前n 项和为n S ,常数0λ>,且 11n n a a S S λ=+对一切正整数n 都成立。 (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设10a >,100λ=,当n 为何值时,数列1 {lg }n a 的前n 项和最大? 【解析】(I )由题意,n=1时,由已知可知11(2)0a a λ-=,分类讨论:由1a =0及1a 0≠,结合数列的和与项的递推公式可求。 (II )由10a >且100λ=时,令1 lg n n b a =,则2lg 2n b n =-,结合数列的单调性可 求和的最大项 。 【答案】解:(Ⅰ)取n=1,得2 1112=2a S a λ=,∴11(2)0a a λ-=。 若1a =0,则1S =0, 当n 2≥时,1=0n n n a S S --=。 若1a 0≠,则12 a λ = , 当n 2≥时,22n n a S λ=+,112 2n n a S λ --=+, 两个相减得:12n n a a -=,∴n 2n a λ = 。∴数列{}n a 公比是2的等比数列。 综上所述,若1a =0, 则 n 0a =;若1a 0≠,则n 2n a λ =。 (Ⅱ)当10a >且100λ=时,令1 lg n n b a =,则2lg 2n b n =-。 ∴{}n b 是单调递减的等差数列(公差为-lg2) 则 b 1>b 2>b 3>…>b 6=01lg 64100 lg 2 100lg 6 =>=; 当n≥7时,b n ≤b 7=01lg 128100 lg 2 100lg 7=<=。 ∴数列{lg n a 1}的前6项的和最大,即当n =6时,数列1 {lg }n a 的前n 项和最大。 【考点】等差数列、等比数列、对数等基础知识,分类与整合、化归与转化等数学思想的应 用。 例2. (2012年天津市理13分)已知{n a }是等差数列,其前n 项和为n S ,{n b }是等比数列,且1a =1=2b ,44+=27a b ,44=10S b -. (Ⅰ)求数列{n a }与{n b }的通项公式; (Ⅱ)记1121=+++n n n n T a b a b a b -L ,+ n N ∈,证明+12=2+10n n n T a b -+()n N ∈.
初等几何研究试题答案(I) 一、线段与角的相等 1. ⊙O1、⊙O2相交于A、B,⊙O1的弦BC交⊙O2于E,⊙O2的弦BD交⊙O1于F, 求证: (1)若∠DBA=∠CBA,则DF=CE; (2) 若DF=CE,则∠DBA=∠CBA. 证明:(1)连接AC、AE、AF、AD 在⊙O1中,由∠CBA=∠DBA得AC=AF 在⊙O2中,由∠CBA=∠DBA得AE=AD 由A、C、B、E四点共圆得∠1=∠2 由A、D、B、E四点共圆得∠3=∠4 所以△ACE≌△AFD ∴DF=CE (2)由(1)得∠1=∠2,∠3=∠4 ∵DF=CE ∴△ACE≌△AFD
∴AD=AE 在⊙O 2中,由AD=AE 可得∠DBA=∠CBA 2. 在△ABC 中,AC=BC,∠ACB=90O ,D 是AC 上的一点,AE ⊥BD 的延长线于E,又AE=1 2 BD, 求证:BD 平分∠ ABC. 证明:延长AE,BC 交于点F AED BCA 90 ADE BDC CBD CAF ACF BCA 90 AC BC ACF BCD AF BD 11AE BD AE AF 22 ABEE BE BE ABF BD ABC ∠=∠=?∠=∠∴∠=∠∠=∠=?=∴???∴==∴=⊥∴∠∠Q Q Q Q 又又又平分即平分 3. 已知在凸五边形ABCDE 中,∠BAE=3α,BC=CD=DE,且∠BCD=∠CDE=180o-2α,
求证:∠BAC=∠CAD=∠DAE. 证明:连接BD,得ΔCBD是等腰三角形 且底角是∠CDB=[180o-(180o-2α)]÷2=α. ∴∠BDE=(180°-2α)-α=180o-3α ∴A、B、D、E共圆 同理A、C、D、E共圆 ∴∠BAC=∠CAD=∠DAE 4. 设H为锐角△ABC的垂心,若AH等于外接圆的半径. 求证:∠BAC=60o 证明:过点B作BD⊥BC,交圆周于点D,连结CD、AD C ∵∠DBC=90o, ∴CD是直径,则∠CAD=90o
初等几何研究作业参考答案
《初等几何研究》作业参考答案 一.填空题 1.①射线(或半直线),②。 2. ①两,②度量公理(或阿基米德公理)和康托儿公理。 3.①前4组公理(或绝对几何),②平行公理。 4.①平移,②旋转,③轴对称. 5. 1=??ZB AZ YA CY XC BX 。 6.①交轨法,②三角奠基法,③代数法,④变换法。 7.①反身性、②对称性、③传递性、④可加性. 8.外角. 9.答案不惟一. 10.①演绎,②综合,③直接,④反证,⑤同一; 11. 1=??ZB AZ YA CY XC BX .(答-1也对) 12. ①过两点可作一条直线(或其部分),②已知圆心 和半径可作一圆(或其部分). 13.①不共线的三点A 、B 、C 及(AB)、(BC)、(CA)构成 的点的集合。 14.连续.
15.答案不惟一. 16.①不过,②圆. 17.1=??ZB AZ YA CY XC BX (或-1). 18.①写出已知与求作,②分析,③作法,④证明,⑤ 讨论. 19.①相容,②独立,③完备. 20.合同变换、相似变换、射影变换、反演变换等 21.对任意直线a 及其外一点A ,在a 和A 决定的平面上,至少有两条过A 与a 不相交的直线. 22.①代数,②解析,③三角,④面积,⑤复数,⑥向 量. 23.相等。 24.所求的量可用已知量的有理式或只含平方根的无理 式表出. 二.问答题 1.对于公理系统∑,若有一组具体事物M ,其性质是已知的,在规定∑中每一个基本概念指M 中某一具体事物后,可验证∑中每个公理在M 中都成立,则称M 为公理系统∑的一个模型;
数列综合练习(一) 1.等比数列前n 项和公式: (1)公式:S n =???? a 1(1-q n )1-q =a 1-a n q 1-q (q ≠1) na 1 (q =1) . (2)注意:应用该公式时,一定不要忽略q =1的情况. 2.若{a n }是等比数列,且公比q ≠1,则前n 项和S n =a 1 1-q (1-q n )=A (q n -1).其中 A =a 1 q -1 . 3.推导等比数列前n 项和的方法叫错位相减法.一般适用于求一个等差数列与一个等比数列对应项积的前n 项和. 4.拆项成差求和经常用到下列拆项公式: (1)1n (n +1)=1n -1n +1 ; 一、选择题 1.设S n 为等比数列{a n }的前n 项和,8a 2+a 5=0,则S 5 S 2 等于( ) A .11 B .5 C .-8 D .-11 答案 D 解析 由8a 2+a 5=0得8a 1q +a 1q 4=0, ∴q =-2,则S 5S 2=a 1(1+25 ) a 1(1-22) =-11. 2.记等比数列{a n }的前n 项和为S n ,若S 3=2,S 6=18,则S 10 S 5 等于( ) A .-3 B .5 C .-31 D .33 答案 D 解析 由题意知公比q ≠1,S 6 S 3=a 1(1-q 6)1-q a 1(1-q 3) 1-q =1+q 3=9, ∴q =2,S 10S 5=a 1(1-q 10)1-q a 1(1-q 5) 1-q =1+q 5 =1+25=33. 3.设等比数列{a n }的公比q =2,前n 项和为S n ,则S 4 a 2 等于( ) A .2 B .4 C.152 D.172
三、关于比例相似形 1.从.KBCD 的各顶向不过该顶的对角线引垂 线,垂足为 E 、 F 、 G H,求证: (j )EFG H 是 Q (ii) ZEFGH S Z ^ABCD. 证明:(1) V AEIBD DH 丄 AC ??? A 、D E 、H 四点共圆(视 角相等) ???∠ OEH ∠ OAD 同理 ∠ OGF ∠OCB 又 V AD// BC ?∠ OAD ∠ OCB ?∠ OEH ∠ OGF ? EH// GF 同理EF // GH ?四边形EFGH 为平行四边形 EFGH 与」BCD 对角线夹角相等且对角线又 成比例 ? ^EFGH S^BCD 3.已知:AD 是厶ABC 的中线,过C 的一直线分别交 AD 、AB 与E 、F 。求证:AE ?BF=2A F ED 证明:延长CF 至点H,使得CE=El 连结BH V 点D 是BC 上的中点 ? DE >△ CBH 的中位线 即 DE // BH a DE= - BH V DE// BH 2 ?∠ CED ∠ CHB ∠ AEF ∠ AFE=∠ BFH ? △ AFE sA BFH OE OH (H)V △ OE SA OAD OA OD EG 二 £H ? AC BD
AE AF ?竺=AF ,且BH=2ED ?AE ?BF=2A?ED BH BF 4.直线I与□ ABCD勺边AB AD和对角线AC依次相交于E、F和G求证:型?如=M AE AF AG 证明:连结BF、BE、CF 禾口CE, V AB AE F F C E A A S S -F F B E A A S S AD= S ADE= S ACE AF S AEF S AEF
初等几何研究试题答案 一、线段与角的相等 P491 1. ⊙O 1、⊙O 2相交于A 、B,⊙O 1的弦BC 交⊙O 2于E,⊙O2的弦BD 交⊙O 1于F, 求证: (1)若∠DBA=∠CBA,则DF=CE; (2) 若DF=CE,则∠DBA=∠CBA. 证明:(1)连接AC 、AE 、AF 、AD 在⊙O 1中,由∠CBA=∠DBA 得AC=AF 在⊙O 2中,由∠CBA=∠DBA 得AE=AD 由A 、C 、B 、E 四点共圆得∠1=∠2 由A 、D 、B 、E 四点共圆得∠3=∠4 所以△ACE ≌△AF ∴DF=CE (2)由(1)得∠1=∠2,∠3=∠4 ∵DF=CE ∴△ACE ≌△AFD ∴AD=AE 在⊙O 2中,由AD=AE 可得∠DBA=∠CBA 2.在△ABC 中,AC=BC,∠ACB=90O ,D 是AC 上的一点,AE ⊥BD 的延长线于E,又AE=1 2 BD,求证:BD 平分∠ABC. 证明:延长AE,BC 交于点F AED BCA 90 ADE BDC CBD CAF ACF BCA 90 AC BC ACF BCD AF BD 11 AE BD AE AF 22 ABEE BE BE ABF BD ABC ∠=∠=?∠=∠∴∠=∠∠=∠=?=∴???∴==∴=⊥∴∠∠Q Q Q Q 又又又平分即平分 3.已知在凸五边形ABCDE 中,∠BAE=3α,BC=CD=DE,且∠BCD=∠CDE=180o-2α, 求证:∠BAC=∠CAD=∠DAE. 证明:连接BD,得ΔCBD 是等腰三角形 且底角是∠CDB=[180o-(180o-2α)]÷2=α. ∴∠BDE=(180°-2α)-α=180o-3α ∴A 、B 、D 、E 共圆 同理A 、C 、D 、E 共圆 ∴∠BAC=∠CAD=∠DAE 4.设H 为锐角△ABC 的垂心,若AH 等于外接圆的半径.求证:∠BAC=60o 证明:过点B 作BD ⊥BC,交圆周于点D,连结CD 、AD ∵∠DBC=90o, ∴CD 是直径,则∠CAD=90o 由题,可得AH ⊥BC, BH ⊥ AC