
一、相似真题与模拟题分类汇编(难题易错题)
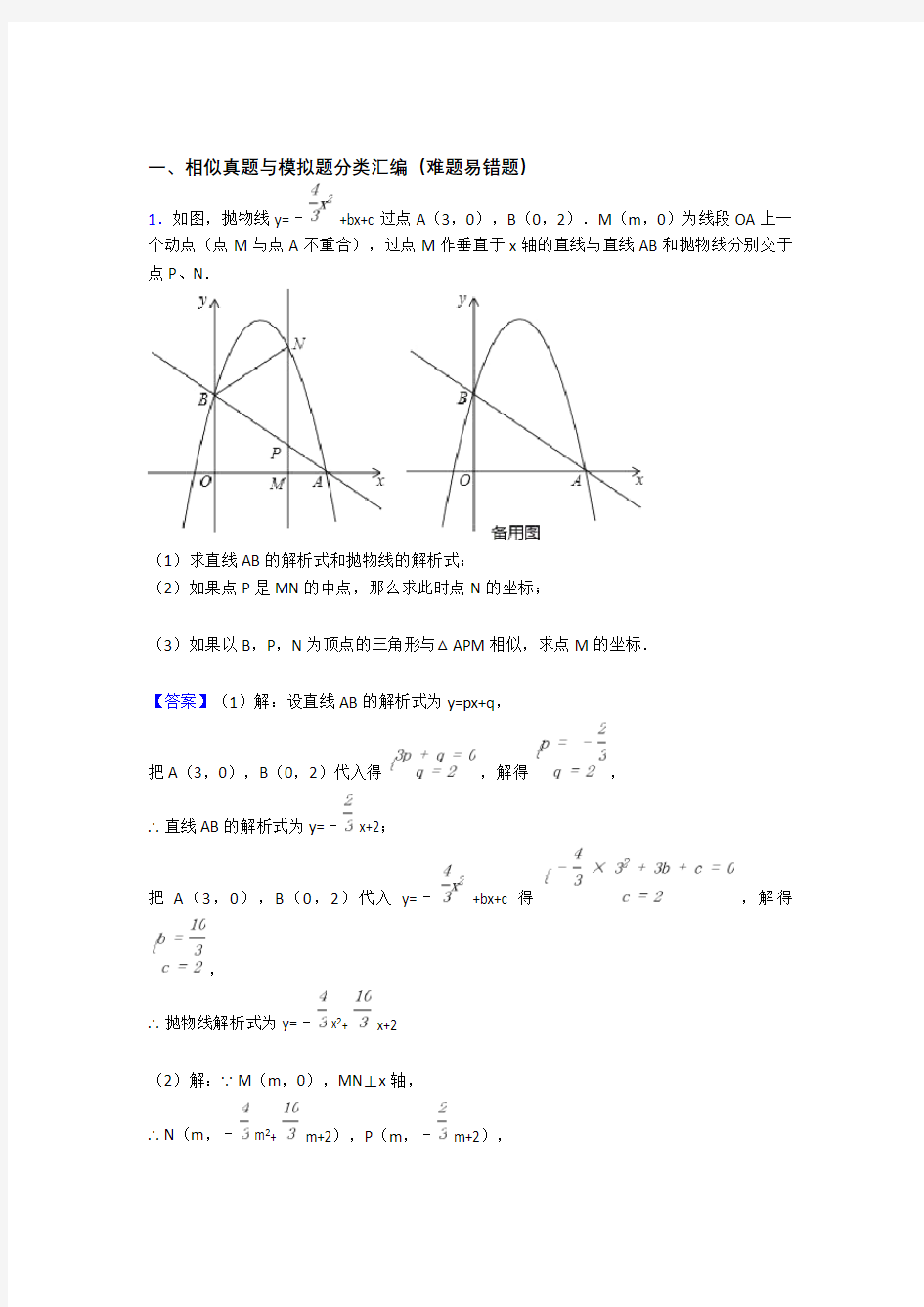
1.如图,抛物线y=﹣ +bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)如果以B,P,N为顶点的三角形与△APM相似,求点M的坐标.
【答案】(1)解:设直线AB的解析式为y=px+q,
把A(3,0),B(0,2)代入得,解得,
∴直线AB的解析式为y=﹣ x+2;
把A(3,0),B(0,2)代入y=﹣ +bx+c得,解得,
∴抛物线解析式为y=﹣ x2+ x+2
(2)解:∵M(m,0),MN⊥x轴,
∴N(m,﹣ m2+ m+2),P(m,﹣ m+2),
∴NP=﹣ m2+4m,PM=﹣ m+2,
而NP=PM,
∴﹣ m2+4m=﹣ m+2,解得m1=3(舍去),m2= ,
∴N点坐标为(,)
(3)解:∵A(3,0),B(0,2),P(m,﹣ m+2),
∴AB= = ,BP= = m,
而NP=﹣ m2+4m,
∵MN∥OB,
∴∠BPN=∠ABO,
当 = 时,△BPN∽△OBA,则△BPN∽△MPA,即 m:2=(﹣ m2+4m):,
整理得8m2﹣11m=0,解得m1=0(舍去),m2= ,
此时M点的坐标为(,0);
当 = 时,△BPN∽△ABO,则△BPN∽△APM,即 m: =(﹣ m2+4m):2,
整理得2m2﹣5m=0,解得m1=0(舍去),m2= ,
此时M点的坐标为(,0);
综上所述,点M的坐标为(,0)或(,0)
【解析】【分析】(1)因为抛物线和直线AB都过点A(3,0)、B(0,2),所以用待定系数法求两个解析式即可;
(2)由题意知点P是MN的中点,所以PM=PN;而MN OA交抛物线与点N,交直线AB于点P,所以M、P、N的横坐标相同且都是m,纵坐标分别可用(1)中相应的解析式表
示,即P(m,),N(m,),PM与PN的长分别为相应两点的纵坐标的绝对值,代入PM=PN即可的关于m的方程,解方程即可求解;
(3)因为以B,P,N为顶点的三角形与△APM相似,而△APM是直角三角形,所以分两种情况:当∠PBN=时,则可得△PBN∽△PMA,即得相应的比例式,可求得m的值;当∠PNB=时,则可得△PNB∽△PMA,即得相应的比例式,可求得m的值。
2.如图,在四边形ABCD中,AD//BC,,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设的面积为,直接写出与之间的函数关系式是________(不写取值范围).
(2)当B,P,Q三点为顶点的三角形是等腰三角形时,求出此时的值.
(3)当线段PQ与线段AB相交于点O,且2OA=OB时,直接写出 =________. (4)是否存在时刻,使得若存在,求出的值;若不存在,请说明理由.
【答案】(1)
(2)解:如图1,过点P作PH⊥BC于点H,
∴∠PHB=∠PHQ=90°,
∵∠C=90°,AD∥BC,
∴∠CDP=90°,
∴四边形PHCD是矩形,
∴PH=CD=3,HC=PD=2t,
∵CQ=t,BC=4,
∴HQ=CH-CQ=t,BH=BC-CH=4-2t,BQ=4-t,
∴BQ2= ,BP2= ,PQ2= ,
由BQ2=BP2可得:,解得:无解;
由BQ2=PQ2可得:,解得:;
由BP2= PQ2可得:,解得:或,
∵当时,BQ=4-4=0,不符合题意,
∴综上所述,或;
(3)
(4)解:如图3,过点D作DM∥PQ交BC的延长线于点M,
则当∠BDM=90°时,PQ⊥BD,即当BM2=DM2+BD2时,PQ⊥BD,
∵AD∥BC,DM∥PQ,
∴四边形PQMD是平行四边形,
∴QM=PD=2t,
∵QC=t,
∴CM=QM-QC=t,
∵∠BCD=∠MCD=90°,
∴BD2=BC2+DC2=25,DM2=DC2+CM2=9+t2,
∵BM2=(BC+CM)2=(4+t)2,
∴由BM2=BD2+DM2可得:,解得:,
∴当时,∠BDM=90°,
即当时,PQ⊥BD.
【解析】【解答】解:(1)由题意可得BQ=BC-CQ=4-t,点P到BC的距离=CD=3,
∴S△PBQ= BQ×3= ;
( 3 )解:如图2,过点P作PM⊥BC交CB的延长线于点M,
∴∠PMC=∠C=90°,
∵AD∥BC,
∴∠D=90°,△OAP∽△OBQ,
∴四边形PMCD是矩形,,
∴PM=CD=3,CM=PD=2t,
∵AD=6,BC=4,CQ=t,
∴PA=2t-6,BQ=4-t,MQ=CM-CQ=2t-t=t,
∴,解得:,
∴MQ= ,
又∵PM=3,∠PMQ=90°,
∴tan∠BPQ= ;
【分析】(1)点P作PM⊥BC,垂足为M,则四边形PDCM为矩形,根据梯形的面积公式就可以利用t表示,就得到s与t之间的函数关系式。
(2)以B、P、Q三点为顶点的三角形是等腰三角形,可以分PQ=BQ、BP=BQ、PB=PQ三种情况,在Rt△PMQ中根据勾股定理,就得到一个关于t的方程,就可以求出t。
(3)根据相似三角形对应边比例可列式求出t,从而根据正切的定义求出值;
(4)首先假设存在,然后根据相似三角形对应边成比例求证。
3.在平面直角坐标系中,二次函数的图象与轴交于A(-3,0),B (1,0)两点,与y轴交于点C.
(1)求这个二次函数的解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
【答案】(1)解:由抛物线过点A(-3,0),B(1,0),
则
解得
∴二次函数的关系解析式
(2)解:连接PO,作PM⊥x轴于M,PN⊥y轴于N.
设点P坐标为(m,n),则.
PM = ,,AO=3.
当时,=2.
∴OC=2.
=
==.∵=-1<0,∴当时,函数有最大值.
此时=.
∴存在点,使△ACP的面积最大.
(3)解:存在点Q,坐标为:,.
分△BQE∽△AOC,△EBQ∽△AOC,△QEB∽△AOC三种情况讨论可得出
【解析】【分析】(1)由题意知抛物线过点A(-3,0),B(1,0),所以用待定系数法即可求解;
(2)因为三角形ACP是任意三角形,所以可做辅助线,连接PO,作PM⊥x轴于M,
PN⊥y轴于N.则三角形ACP的面积=三角形APM的面积+矩形PMON的面积-三角形AOC 的面积-三角形PCN的面积。于是可设点P的横坐标为m,则纵坐标可用含m的代数式表
示出来,即M(m,??m + 2),
则三角形ACP的面积可用含m的代数式表示,整理可得是一个二次函数,利用二次函数的性质即可求解;
(3)根据对应顶点的不同分三种情况(△BQE∽△AOC,△EBQ∽△AOC,△QEB∽△AOC)讨论即可求解。
4.在平面直角坐标系中,O为坐标原点,抛物线y=ax2+(a+3)x+3(a<0)从左到右依次交x轴于A、B两点,交y轴于点C.
(1)求点A、C的坐标;
(2)如图1,点D在第一象限抛物线上,AD交y轴于点E,当DE=3AE,OB=4CE时,求a 的值;
(3)如图2,在(2)的条件下,点P在C、D之间的抛物线上,连接PC、PD,点Q在点B、D之间的抛物线上,QF∥PC,交x轴于点F,连接CF、CB,当PC=PD,∠CFQ=2∠ABC,求BQ的长.
【答案】(1)解:当x=0时,y=3,∴C(0,3).
当y=0时,ax2+(a+3)x+3=0,
(ax+3)(x+1)=0,解得x1=- ,x2=-1.
∵a<0,
∴- >0,
∴A(-1,0)
(2)解:如图1,过点D作DM⊥AB于M.
∵OE∥DM,
∴,
∴OM=3,
∴D点纵坐标为12a+12.
∵tan∠EAO= =3a+3,
∴OE=3a+3,
∴CE=OC-OE=3-(3a+3)=-3a.
∵OB=4CE,
∴- =-12a,
∵a<0,
∴a=-
(3)解:如图2,过点D作DT⊥y轴于点T,过点P作PG⊥y轴于点G,连接TP.
∵a=- ,
∴抛物线的解析式为y=- x2+ x+3,D(3,6),DT=3,OT=6,CT=3=DT,
又∵PC=PD,PT=PT,
∴△TCP≌△TDP,
∴∠CTP=∠DTP=45°,TG=PG.
设P(t,- t2+ t+3),
∴OG=- t2+ t+3,PG=t,
∴TG=OT-OG=6-(- t2+ t+3)= t2- t+3,
∴ t2- t+3=t,解得t=1或6,
∵点P在C、D之间,
∴t=1.
过点F作FK∥y轴交BC于点K,过点Q作QN⊥x轴于点N,则∠KFC=∠OCF,∠KFB=∠CON=90°.
∵FQ∥PC,
∴∠PCF+∠CFQ=180°,∠PCF+∠PCG+∠OCF=180°,
∴∠CFQ=∠PCG+∠OCF,
∴∠CFK+∠KFQ=∠PCG+∠OCF,
∴∠KFQ=∠PCG.
∵P(1,5),∴PG=1,CG=OG-OC=5-3=2,
∴tan∠PCG= ,
∵tan∠ABC= ,
∴∠PCG=∠ABC,
∴∠KFQ=∠ABC.
∵∠CFQ=2∠ABC,
∴∠CFQ=2∠KFQ,
∴∠KFQ=∠KFC=∠OCF=∠ABC,
∴tan∠OCF= ,
∴OF= .
设FN=m,则QN=2m,Q(m+ ,2m),
∵Q在抛物线上,
∴- (m+ )2+ ×(m+ )+3=2m,
解得m= 或m=- (舍去),
∴Q(4,5),
∵B(6,0),
∴BQ= .
【解析】【分析】(1)令x=0,求出y的值,得到C点坐标;令y=0,求出x的值,根据a<0得出A点坐标;(2)如图1,过点D作DM⊥AB于M.根据平行线分线段成比例定理求出OM=3,得到D点纵坐标为12a+12.再求出OE=3a+3,那么CE=OC-OE=-3a.根据
OB=4CE,得出- =-12a,解方程求出a=- ;(3)如图2,过点D作DT⊥y轴于点T,过点P作PG⊥y轴于点G,连接TP.利用SSS证明△TCP≌△TDP,得出∠CTP=∠DTP=45°,那么
TG=PG.设P(t,- t2+ t+3),列出方程 t2- t+3=t,解方程求得t=1或6,根据点P在C、D之间,得到t=1.过点F作FK∥y轴交BC于点K,过点Q作QN⊥x轴于点N,根据平行线的性质以及已知条件得出∠KFQ=∠PCG,进而证明∠KFQ=∠KFC=∠OCF=∠ABC,由
tan∠OCF= =tan∠ABC= ,求出OF= .设FN=m,则QN=2m,Q(m+ ,2m),根据
Q在抛物线上列出方程- (m+ )2+ ×(m+ )+3=2m,解方程求出满足条件的m的值,得到Q点坐标,然后根据两点间的距离公式求出BQ.
5.如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连结AB.点P从点B出发,以每秒4个单位长度的速度沿BC方向运动,到点C停止.当点P与B、C两点不重合时,作
PD⊥BC交AB于D,作DE⊥AC于E.F为射线CB上一点,且∠CEF=∠ABC.设点P的运动时间为x(秒).
(1)用含有x的代数式表示CE的长;
(2)求点F与点B重合时x的值;
(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式;
(4)当x为某个值时,沿PD将以D、E、F、B为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x值. 【答案】(1)解:∵∠C=90°,PD⊥BC,
∴DP∥AC,
∴△DBP∽△ABC,四边形PDEC为矩形,
CE=PD..
∴ .
∴CE=6x;
(2)解:∵∠CEF=∠ABC,∠C为公共角,
∴△CEF∽△CBA,
∴ .
∴ .
当点F与点B重合时,
CF=CB,9x=20.
解得 .
(3)解:当点F与点P重合时,BP+CF=CB,4x+9x=20,
解得 .
当时,
=-51x2+120x.当<x≤ 时,
= (20-4x)2.
(或)
(4)解:①如图③,当PD=PF时,6x=20-13x,解得:x= ;△B′DE为拼成的三角形;
②如图④当点F与点P重合时,4x+9x=20,解得:x= ;△BDC为拼成的三角形;
③如图⑤,当DE=PB,20-4x=4x,解得:x= ,△DPF为拼成的三角形.
【解析】【分析】(1)首先证明△ABC∽△DBP∽△FEC,即可得出比例式进而得出表示CE的长;(2)根据当点F与点B重合时,FC=BC,即可得出答案;(3)首先证明
Rt△DOE∽Rt△CEF,得出,即可得出y与x之间的函数关系式;(4)根据三角形边长相等得出答案.
6.在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA ,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F , G.
(1)如图,点D在线段CB上,四边形ACDE是正方形.
①若点G为DE中点,求FG的长.
②若DG=GF,求BC的长.
(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
【答案】(1)①在正方形ACDE中,有DG=GE=6
在Rt△AEG中,AG=
∵EG∥AC
∴△ACF∽△GEF
∴,
∴
∴
②如图1,在正方形ACDE中,AE=ED
∠AEF=∠DEF=45°,
又EF=EF,∴△AEF≌△DEF
∴∠1=∠2(设为x)
∵AE∥BC
∴∠b=∠1=x
∵GF=GD
∴∠3=∠2=x
在△dbf中,∠3+∠FDb+∠b=180°
∴x+(x+90°)+x=180°,解得x=30°
∴∠B=30°
∴在Rt△ABC中,BC=
(2)在Rt△ABC中,AB=
如图2,当点D在线段BC上时,此时只有GF=GD
∵DG∥AC
∴△BDG∽△BCA
设BD=3x,则DG=4x,BG=5x
∴GF=GD=4x,则AF=15-9x
∵AE∥CB,
∴△AEF∽△BCF
∴
∴,即
解得x1=1,x2=5(舍去)
∴腰长G D=4x=4
如图3,当点D在线段BC的延长线上,且直线AB,CE的交点在AE上方时,此时只有GF=Dg,
设AE=3x,则E G=4x,A G=5x,
∴F G=DG=12+4x,
∵AE∥BC
∴△AEF∽△BCF
∴
∴,即x2=4
解得x1=2,x2=-2(舍去)
∴腰长GD=4x+12=20
如图4,当点D在线段BC的延长线上,且直线AB,EC的交点在BD下方时,此时只有DF=DG,过点D作D H⊥FG。
设AE=3x,则EG=4x,AG=5x,DG=4x+12
∴FH=GH=DG·cos∠DGB=
∴GF=2G H= ,
∴AF=GF-AG=
∵AC∥DG
∴△ACF∽△GEF
∴
∴,即7x2=288cos
解得x1= ,x2= (舍去)
∴腰长GD=4x+12=
如图5,当点D在线段Cb的延长线上时,此时只有DF=D g,过点D作D h⊥AG,
设AE=3x,则EG=4x,AG=5x,DG=4x-12
∴FH=GH=DG·cos∠DGB=
∴AF=AG?FG=
∵AC∥EG
∴△ACF∽△GEF
∴
∴,即7x2=288
解得x1= ,x2= (舍去)
∴腰长GD=4x-12=
综上所述,等腰△DFG的腰长为4,20,,
【解析】【分析】(1)①此小题考查相似三角形的判定与性质;由正方形的性质可得AG//EG,则△ACF∽△GEF,即可得FG:AF=EG:AC=1:2,则只要由勾股定理求出AG即可;
②由正方形性的对称性,不难得出∠1=∠2,而由GF=GD可知∠3=∠2,在△BDF中,由三角形内角和为180度,不难求出∠b的度数,可知是一个特殊角的度数,从而求出BC即可;(2)因为BC=9,所以B是定点,动点是D,因为点D是直线BC上一点,随着点D 的位置的变化,E和F点的位置也跟着变化;需要分类计论点D在线段BC上,点D在BC 的延长线和点D在CB的延长线上,再逐个分析等腰三角形的存在性,根据相似三角形的
性及三角函数分析解答即可.
7.已知一次函数y=? x?12的图象分别交x轴,y轴于A,C两点。
(1)求出A,C两点的坐标;
(2)在x轴上找出点B,使△ACB∽△AOC,若抛物线过A,B,C三点,求出此抛物线的解析式;
(3)在(2)的条件下,设动点P、Q分别从A,B两点同时出发,以相同速度沿AC、BA向C,A运动,连接PQ,设AP=m,是否存在m值,使以A,P,Q为顶点的三角形与△ABC 相似?若存在,求出所有m值;若不存在,请说明理由。
【答案】(1)解:
在一次函数y=? x?12中,当x=0时,y=?12;
当y=0时,x=?16,即A(?16,0),C(0,?12)
(2)解:过C作CB⊥AC,交x轴于点B,显然,点B为所求。
则OC2=OA?OB,此时OB=9,可求得B(9,0);
此时经过A. B. C三点的抛物线的解析式为y= x2+ x?12
(3)解:当PQ∥BC时,如图(1),△APQ∽△ACB;则有:
= ,即 = ,
解得m= .
当PQ⊥AB时,△APQ∽△ACB;有:
= ,即 = ,
解得m= .
【解析】【分析】(1)令直线的解析式y=0,可得A的坐标,令x=0,可得C的坐标(2)要使△ACB∽△AOC,则B点必为过C点且垂直于AC的直线与x轴的交点.那么根据射影定理不难得出B点的坐标,然后用待定系数法即可求得抛物线的解析式.(3)本题可分两种情况进行求解:①当PQ∥BC时,△APQ∽△ACB;②当PQ⊥AB时,△APQ∽△ACB.可根据各自得出的不同的对应成比例线段求出m的值.
8.如图,在矩形ABCD中,AB=4,BC=3,点P是边AB上的一动点,连结DP.
(1)若将△DAP沿DP折叠,点A落在矩形的对角线上点A′处,试求AP的长;
(2)点P运动到某一时刻,过点P作直线PE交BC于点E,将△DAP与△PBE分别沿DP 与PE折叠,点A与点B分别落在点A′,B′处,若P,A′,B′三点恰好在同一直线上,且A′B′=2,试求此时AP的长;
(3)当点P运动到边AB的中点处时,过点P作直线PG交BC于点G,将△DAP与△PBG 分别沿DP与PG折叠,点A与点B重合于点F处,连结CF,请求出CF的长.
【答案】(1)解:①当点A落在对角线BD上时,设AP=PA′=x,
在Rt△ADB中,∵AB=4,AD=3,∴BD==5,
∵AB=DA′=3,∴BA′=2,
在Rt△BPA′中,(4﹣x)2=x2+22,解得x=,
∴AP= .
②当点A落在对角线AC上时,
由翻折性质可知:PD⊥AC,则有△DAP∽△ABC,
∴=,∴AP=== .
∴AP的长为或
(2)解:①如图3中,设AP=x,则PB=4﹣x,
根据折叠的性质可知:PA=PA′=x,PB=PB′=4﹣x,