增量式PID控制算法

增量式pid参数整定方法增量式PID参数整定方法PID控制是一种常用的自动控制方法，它在工业控制中被广泛应用。

PID控制器的参数整定是保证控制系统性能的关键。

本文将介绍一种常用的增量式PID参数整定方法，帮助工程师们更好地掌握和应用PID控制。

一、什么是增量式PID控制增量式PID控制是一种基于增量调节量的PID控制方法。

传统的PID控制通过计算当前控制量与期望值之间的误差，然后根据误差大小调整控制器的输出。

而增量式PID控制则是根据当前控制量与上一时刻的控制量之差，来调整控制器的输出。

增量式PID控制的优点是可以减小输出信号的突变，提高系统的稳定性。

二、增量式PID参数整定方法增量式PID参数整定方法主要包括以下步骤：1. 设定比例系数Kp需要根据被控对象的特性和应用需求，设定适当的比例系数Kp。

比例系数Kp的大小决定了控制器输出的变化速度，过大或过小都会导致系统不稳定。

一般来说，可以先根据经验选择一个初始值，然后再进行调整。

2. 设定积分时间Ti积分时间Ti是控制器对偏差的积分作用时间，用来消除系统存在的稳态误差。

设定积分时间的方法有很多，可以通过试探法、经验法或者系统辨识等方式进行。

一般来说，积分时间越大，系统的稳定性越好，但过大的积分时间会导致系统的响应速度变慢。

3. 设定微分时间Td微分时间Td决定了控制器对偏差变化率的敏感程度。

在增量式PID 控制中，微分时间的设定比较重要，可以通过试探法或者经验法来选择合适的值。

一般来说，微分时间越大，系统的响应速度越快，但过大的微分时间会导致系统产生震荡。

4. 计算增量调节量在增量式PID控制中，需要计算出当前控制量与上一时刻的控制量之差，作为增量调节量。

增量调节量可以通过以下公式计算：Delta_u(k) = Kp * (e(k) - e(k-1)) + Ki * e(k) + Kd * (e(k) - 2 * e(k-1) + e(k-2))其中，Delta_u(k)为增量调节量，e(k)为当前时刻的偏差，e(k-1)为上一时刻的偏差，e(k-2)为上上一时刻的偏差，Kp、Ki和Kd分别为比例、积分和微分系数。

位置式PID控制算法和增量式PID控制算法1.位置式PID控制算法：u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt其中，u(t)为控制量，Kp为比例增益，Ki为积分增益，Kd为微分增益，e(t)为偏差即系统输出值与期望值的差值，∫e(t)dt为偏差的积分，de(t)/dt为偏差的微分。

-简单易懂：位置式PID控制算法的计算公式直接描述了控制量与偏差之间的关系，容易理解和实现。

-稳定性好：位置式PID控制算法通过不断修正控制量的大小，能够使系统快速、准确地达到期望值，具有较好的稳定性和控制精度。

-适用范围广：位置式PID控制算法适用于各种控制系统，包括线性系统和非线性系统。

2.增量式PID控制算法：增量式PID控制算法是相对于位置式PID控制算法而言的，它的基本原理是通过计算当前偏差和上一次偏差之间的差异来决定修正控制量的大小，从而达到系统稳定的状态。

增量式PID控制算法的计算公式如下：u(t)=u(t-1)+Kp*[e(t)-e(t-1)]+Ki*e(t)+Kd*[e(t)-2*e(t-1)+e(t-2)]其中，u(t)为控制量，Kp为比例增益，Ki为积分增益，Kd为微分增益，e(t)为当前的偏差，e(t-1)为上一次的偏差，e(t-2)为上两次的偏差。

增量式PID控制算法的特点：-相对稳定性好：增量式PID控制算法通过计算偏差的变化速率，能够更快地修正控制量的大小，对系统的稳定性有着较大的改善。

-抗积分饱和：增量式PID控制算法在积分项的计算中，使用了当前的偏差，而非历史的偏差，减小了积分饱和的影响。

-操作舒适性好：增量式PID控制算法的输出量是控制量的增量，对控制对象的操作更加平稳，减少了骤变和震荡。

综上所述，位置式PID控制算法和增量式PID控制算法各有其优势，应根据具体的系统需求和控制目标选择使用。

一般来说，位置式PID控制算法适用于对控制精度要求较高的系统，而增量式PID控制算法则适用于要求操作平稳度较高的系统。

增量式PID的整型算法对于PID控制的程序算法，很多书上都讲了。

但是，最近真正要用PID算法的时候，发现书上的代码在我们51单片机上来实现还不是那么容易的事情。

简单的说来，就是不能直接调用。

仔细分析你可以发现，教材上的、网上现行的PID实现的C语言代码几乎都是用浮点型的数据来做的，可以想象，如果我们的计算使用浮点数据，那我们的51单片机来运行的话会有多痛苦。

所以，本人自己琢磨着弄了一个整型变量来实现了PID算法，由于是用整型数来做的，所以也不是很精确，但是对于很多的使用场合，这个精度也够了。

关于系数和采样电压全部是放大10倍处理的。

所以精度不是很高，但是也不是那么低，大部分的场合都够用了。

实在觉得精度不够，可以再放大10倍或者100倍处理，但是要注意不超出整个数据类型的范围就可以了。

以下是具体的程序代码：typedef struct PIDValue{uint32 Ek_Uint32[3]; //差值保存，给定和反馈的差值uint8 EkFlag_Uint8[3]; //符号，1则对应的Ek[i]为负数，0为对应的Ek[i]为正数uint8 KP_Uint8;uint8 KI_Uint8;uint8 KD_Uint8;uint8 B_Uint8; //死区电压uint8 KP; //显示修改的时候用uint8 KI;uint8 KD;uint8 B;uint16 Uk_Uint16; //上一时刻的控制电压}PIDValueStr;PIDValueStr xdata PID;//PID = Uk + (KP*E(k) - KI*E(k-1) + KD*E(k-2));void PIDProcess(void){uint32 idata Temp[3]; //uint32 idata PostSum; //正数和uint32 idata NegSum; //负数和Temp[0] = 0;Temp[1] = 0;Temp[2] = 0;PostSum = 0;NegSum = 0;if( ADPool.Value_Uint16[UINADCH] > ADPool.Value_Uint16[UFADCH] )//给定大于反{Temp[0] = ADPool.Value_Uint16[UINADCH] - ADPool.Value_Uint16[UFADCH];//计算Ek[0]if( Temp[0] > PID.B_Uint8 ){//数值移位PID.Ek_Uint32[2] = PID.Ek_Uint32[1];PID.Ek_Uint32[1] = PID.Ek_Uint32[0];PID.Ek_Uint32[0] = Temp[0];//符号移位PID.EkFlag_Uint8[2] = PID.EkFlag_Uint8[1];PID.EkFlag_Uint8[1] = PID.EkFlag_Uint8[0];PID.EkFlag_Uint8[0] = 0; //当前EK为正数Temp[0] = (uint32)PID.KP_Uint8 * PID.Ek_Uint32[0]; // KP*EK0Temp[1] = (uint32)PID.KI_Uint8 * PID.Ek_Uint32[1]; // KI*EK1Temp[2] = (uint32)PID.KD_Uint8 * PID.Ek_Uint32[2]; // KD*EK2}}else //反馈大于给定{Temp[0] = ADPool.Value_Uint16[UFADCH] - ADPool.Value_Uint16[UINADCH]; //计算Ek[0]if( Temp[0] > PID.B_Uint8 ){//数值移位PID.Ek_Uint32[2] = PID.Ek_Uint32[1];PID.Ek_Uint32[1] = PID.Ek_Uint32[0];PID.Ek_Uint32[0] = Temp[0];//符号移位PID.EkFlag_Uint8[2] = PID.EkFlag_Uint8[1];PID.EkFlag_Uint8[1] = PID.EkFlag_Uint8[0];PID.EkFlag_Uint8[0] = 1; //当前EK为负数Temp[0] = (uint32)PID.KP_Uint8 * PID.Ek_Uint32[0]; // KP*EK0Temp[1] = (uint32)PID.KI_Uint8 * PID.Ek_Uint32[1]; // KI*EK1Temp[2] = (uint32)PID.KD_Uint8 * PID.Ek_Uint32[2]; // KD*EK2}}/*以下部分代码是讲所有的正数项叠加，负数项叠加*/if(PID.EkFlag_Uint8[0]==0){PostSum += Temp[0]; //正数和}else{NegSum += Temp[0]; //负数和} // KP*EK0if(PID.EkFlag_Uint8[1]!=0){PostSum += Temp[1]; //正数和}else{NegSum += Temp[1]; //负数和} // - kI * EK1if(PID.EkFlag_Uint8[2]==0){PostSum += Temp[2]; //正数和}else{NegSum += Temp[2]; //负数和} // KD * EK2PostSum += (uint32)_Uint16; //if( PostSum > NegSum ) // 是否控制量为正数{Temp[0] = PostSum - NegSum;if( Temp[0] < (uint32)ADPool.Value_Uint16[UMAXADCH] )//小于限幅值则为计算值输出 {_Uint16 = (uint16)Temp[0];}else{_Uint16 = ADPool.Value_Uint16[UMAXADCH]; //否则为限幅值输出}}else //控制量输出为负数，则输出0{_Uint16 = 0;}}=============================================================================== //总体调节=比例系数×压力误差＋积分系数×积分误差+微分系数×（本次误差-前次误差）//P就是比例，就是输入偏差乘以一个系数；//I就是积分，就是对输入偏差进行积分运算；//D就是微分，对输入偏差进行微分运算；PIDValueStr xdata PID;void PIDCalc(unsigned int idata data1,unsigned int idata data2,unsigned int idata minfreq){unsigned int idata svdata;unsigned int idata pvdata;unsigned long idata dError,Error;unsigned long idata ResultP,ResultI,ResultD,PIDout,Result;svdata=data1;pvdata=data2;if(svdata>pvdata){Error=svdata-pvdata;// 压力偏差PID.SumError+=Error;// 积分dError=PID.LError-PID.PError;// 当前微分PID.PError=PID.LError;PID.LError=Error;ResultP=PID.KP*Error*100;// 比例项ResultI=PID.KI*(PID.SumError);// 积分项ResultD=PID.KD*dError;// 微分项PIDout=ResultP+ResultI+ResultD;Result+=PIDout;if(PIDout>=5000){PIDout=5000;PID.SumError-=Error;}else{ PIDout=ResultP+ResultI+ResultD;}}if(svdata<pvdata){Error=svdata-pvdata;// 压力偏差PID.SumError+=Error;// 积分dError=PID.LError-PID.PError;// 当前微分PID.PError=PID.LError;PID.LError=Error;ResultP=PID.KP*Error*100;//比例项ResultI=PID.KI*(PID.SumError);// 积分项ResultD=PID.KD*dError;// 微分项PIDout=ResultP+ResultI+ResultD;Result+=PIDout;if (PIDout>=5000){PIDout=0;PID.SumError-=Error;}else{ PIDout=ResultP+ResultI+ResultD;}}if (PIDout<minfreq){PIDout=0;}=PIDout; }。

PID控制应该算是非常古老而且应用非常广泛的控制算法了，小到热水壶温度控制，大到控制无人机的飞行姿态和飞行速度等等。

在电机控制中，PID算法用得尤为常见。

一、位置式PID1.计算公式在电机控制中，我们给电机输出的是一个PWM占空比的数值。

话不多说，直接上位置式PID基本公式：控制流程图如下：上图中的目标位置一般我们可以通过按键或者开关等方式编程实现改变目标值，测量位置就是通过stm32 去采集编码器的数据。

目标位置和测量位置之间作差就是目前系统的偏差。

送入PID 控制器进行计算输出，然后再经过电机驱动的功率放大控制电机的转动去减小偏差，最终达到目标位置的过程。

2.C语言实现如何把我们以上的理论分析和控制原理图使用C 语言写出来呢，这是一个有趣且实用的过程。

位置式PID 具体通过C 语言实现的代码如下：int Position_PID (int Encoder,int Target){static float Bias,Pwm,Integral_bias,Last_Bias;Bias=Target- Encoder; //计算偏差Integral_bias+=Bias; //求出偏差的积分//PID基本公式Pwm=Position_KP*Bias+Position_KI*Integral_bias+Position_KD*(Bias-Last_Bias);Last_Bias=Bias; //保存上一次偏差return Pwm; //输出}入口参数为编码器的位置测量值和位置控制的目标值，返回值为电机控制PWM(现在再看一下上面的控制框图是不是更加容易明白了)。

第一行是相关内部变量的定义。

第二行是求出位置偏差，由测量值减去目标值。

第三行通过累加求出偏差的积分。

第四行使用位置式PID 控制器求出电机PWM。

第五行保存上一次偏差，便于下次调用。

最后一行是返回。

二、增量式PID1.计算公式速度闭环控制就是根据单位时间获取的脉冲数（这里使用了M 法测速）测量电机的速度信息，并与目标值进行比较，得到控制偏差，然后通过对偏差的比例、积分、微分进行控制，使偏差趋向于零的过程。

LASERH=laser.Num[0];
LASERL=laser.Num[1];
}
}
///////////////////////////////////////////////////////////////////////
//rtion="0"
vPID. SetPoint = //根据实际情况设定
while(1)
{
Verror=Measure(); //得到AD的输出值
Error =vPID. SetPoint- Verror; //与设定值比较，得到误差值
tempi=PIDCal(&vPID, Error;
laser.Value+=tempi; // Value与Num[2]为共同体，共同体名laser
//增量式PID算法（需要控制的不是控制量的绝对值，而是控制量的增量）
int pError,dError,iError;
long templ;
pError = ThisError-pp->LastError;
iError = ThisError;
dError = ThisError-2*(pp->LastError)+pp->PreError;
int Integral; // Integral积分系数
int Derivative; // Derivative微分系数
int LastError; // Error[-1]前一拍误差
int PreError; // Error[-2]前两拍误差
} PID;
main()
{
PID vPID; //定义结构变量名
//Input: PID的P、I控制常数和之前的误差量（PID *pp）&当前误差量（ThisError）

在过程控制中，由偏差的比例（P），积分（I）和微分（D）控制的PID控制器（也称为PID调节器）是使用最广泛的自动控制器。

具有原理简单，易于实现，应用范围广，控制参数独立，参数选择简单等优点。

从理论上可以证明，对于过程控制的典型对象“一阶滞后+纯滞后”，对于“二阶滞后+纯滞后”的控制对象，PID控制器是一种最优控制。

控制点目前包含三种比较简单的ＰＩＤ控制算法，分别是：增量式算法，位置式算法，微分先行。

这三种ＰＩＤ算法虽然简单，但各有特点，基本上能满足一般控制的大多数要求。

算法种类：1) PID增量式算法离散化公式：注：各符号含义如下u(t);;;;; 控制器的输出值。

e(t);;;;; 控制器输入与设定值之间的误差。

Kp;;;;;;; 比例系数。

Ti;;;;;;; 积分时间常数。

Td;;;;;;; 微分时间常数。

T;;;;;;;; 调节周期。

对于增量式算法，可以选择的功能有：(1) 滤波的选择可以对输入加一个前置滤波器，使得进入控制算法的给定值不突变，而是有一定惯性延迟的缓变量。

(2) 系统的动态过程加速在增量式算法中，比例项与积分项的符号有以下关系：如果被控量继续偏离给定值，则这两项符号相同，而当被控量向给定值方向变化时，则这两项的符号相反。

由于这一性质，当被控量接近给定值的时候，反号的比例作用阻碍了积分作用，因而避免了积分超调以及随之带来的振荡，这显然是有利于控制的。

但如果被控量远未接近给定值，仅刚开始向给定值变化时，由于比例和积分反向，将会减慢控制过程。

为了加快开始的动态过程，我们可以设定一个偏差范围v，当偏差|e(t)|< β时，即被控量接近给定值时，就按正常规律调节，而当|e(t)|>= β时，则不管比例作用为正或为负，都使它向有利于接近给定值的方向调整，即取其值为|e(t)-e(t-1)|，其符号与积分项一致。

利用这样的算法，可以加快控制的动态过程。

(3) PID增量算法的饱和作用及其抑制在PID增量算法中，由于执行元件本身是机械或物理的积分储存单元，如果给定值发生突变时，由算法的比例部分和微分部分计算出的控制增量可能比较大，如果该值超过了执行元件所允许的最大限度，那么实际上执行的控制增量将时受到限制时的值，多余的部分将丢失，将使系统的动态过程变长，因此，需要采取一定的措施改善这种情况。

共三十六页
积分(jīfēn)调节器
e(t) t
0 y
t 0
图2积分作用(zuòyòng)响应曲线
共三十六页
比例(bǐlì)积分调节器
❖若将比例和积分两种作用结合起来(qǐ lái)，就构成 PI调节器，调节规律为：
❖
(3)
❖ PI调节器的输出特性曲线如图3所示
共三十六页
比例(bǐlì)积分调节器
❖ e（t）作为PID 控制器的输入，u（t）作为PID 控制器的 输出和被控对象的输入。
共三十六页
❖所以模拟PID控制器的控制规律为：
u(t)
K
p
e(t)
1 TI
t
e(t)dt
0
TD
de(t)
dt
uo
❖其中 ： (qízhōng) u(t)——调节器的输出信号；
❖ e(t)——调节器的偏差信号，它等于给定值与测量值之差
微分时间选择合适情况下，可以减少超调，减少调节时间。微分作用对噪声干扰有
放大作用，因此过强的加微分调节，对系统抗干扰不利。
共三十六页
❖ 三个参数要综合考虑，一般先将I,D设为0，调好 P,达到基本的响应速度和误差，再加上I,使误差 为0，这时再加入D,三个参数要反复调试，最终 达到较好的结果。不同(bù tónɡ)的控制对象，调试的 难度相差很大！
?uk第k次采样时刻的计算机输出值?ek第k次采样时刻输入的偏差值?ek?1第k1次采样时刻输入的偏差值?ki积分系数积分时间ti即为累积多少次个t?kd微分系数?u0开始进行pid控制时的原始初值应为前一次的给定值?如果采样周期取得足够小则以上近似计算可获得足够精确的结果离散控制过程与连续控制过程十分接近

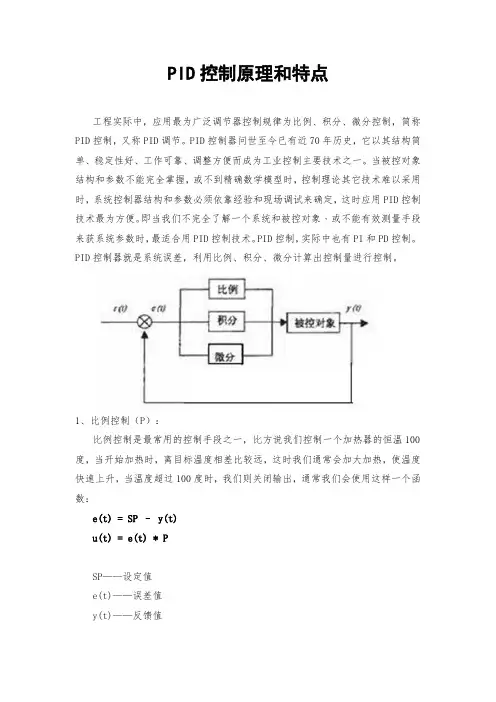
PID控制原理和特点工程实际中，应用最为广泛调节器控制规律为比例、积分、微分控制，简称PID控制，又称PID调节。

PID控制器问世至今已有近70年历史，它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制主要技术之一。

当被控对象结构和参数不能完全掌握，或不到精确数学模型时，控制理论其它技术难以采用时，系统控制器结构和参数必须依靠经验和现场调试来确定，这时应用PID控制技术最为方便。

即当我们不完全了解一个系统和被控对象﹐或不能有效测量手段来获系统参数时，最适合用PID控制技术。

PID控制，实际中也有PI和PD控制。

PID控制器就是系统误差，利用比例、积分、微分计算出控制量进行控制。

1、比例控制（P）：比例控制是最常用的控制手段之一，比方说我们控制一个加热器的恒温100度，当开始加热时，离目标温度相差比较远，这时我们通常会加大加热，使温度快速上升，当温度超过100度时，我们则关闭输出，通常我们会使用这样一个函数：e(t) = SP – y(t)u(t) = e(t) * PSP——设定值e(t)——误差值y(t)——反馈值u(t)——输出值P——比例系数滞后性不是很大的控制对象使用比例控制方式就可以满足控制要求，但很多被控对象中因为有滞后性。

也就是如果设定温度是200度，当采用比例方式控制时，如果P选择比较大，则会出现当温度达到200度输出为0后，温度仍然会止不住的向上爬升，比方说升至230度，当温度超过200度太多后又开始回落，尽管这时输出开始出力加热，但温度仍然会向下跌落一定的温度才会止跌回升，比方说降至170度，最后整个系统会稳定在一定的范围内进行振荡。

如果这个振荡的幅度是允许的比方说家用电器的控制，那则可以选用比例控制。

2、比例积分控制（PI）：积分的存在是针对比例控制要不就是有差值要不就是振荡的这种特点提出的改进，它常与比例一块进行控制，也就是PI控制。

其公式有很多种，但大多差别不大，标准公式如下：u(t) = Kp*e(t) + Ki*∑e(t) + u0u(t)——输出Kp——比例放大系数Ki——积分放大系数e(t)——误差u0——控制量基准值（基础偏差）大家可以看到积分项是一个历史误差的累积值，如果光用比例控制时，我们知道要不就是达不到设定值要不就是振荡，在使用了积分项后就可以解决达不到设定值的静态误差问题，比方说一个控制中使用了PI控制后，如果存在静态误差，输出始终达不到设定值，这时积分项的误差累积值会越来越大，这个累积值乘上Ki后会在输出的比重中越占越多，使输出u(t)越来越大，最终达到消除静态误差的目的。

51单片机PID算法程序(一)PID算法(原创文章，转载请注明出处/tengjingshu) 比例，积分，微分的线性组合，构成控制量u(t)，称为：比例(Proportional)、积分(Integrating)、微分(Differentiation)控制，简称PID控制图1控制器公式在实际应用中，可以根据受控对象的特性和控制的性能要求，灵活地采用不同的控制组合，构成比例(P)控制器比例+积分(PI)控制器比例+积分+微分(PID)控制器式中或式中控制系统中的应用在单回路控制系统中，由于扰动作用使被控参数偏离给定值，从而产生偏差。

自动控制系统的调节单元将来自变送器的测量值与给定值相比较后产生的偏差进行比例、积分、微分(PID)运算，并输出统一标准信号，去控制执行机构的动作，以实现对温度、压力、流量、也为及其他工艺参数的自动控制。

比例作用P只与偏差成正比；积分作用I是偏差对时间的积累；微分作用D 是偏差的变化率；比例(P)控制比例控制能迅速反应误差，从而减少稳态误差。

除了系统控制输入为0和系统过程值等于期望值这两种情况，比例控制都能给出稳态误差。

当期望值有一个变化时，系统过程值将产生一个稳态误差。

但是，比例控制不能消除稳态误差。

比例放大系数的加大，会引起系统的不稳定。

图2比例(P)控制阶跃响应积分(I)控制在积分控制中，控制器的输出与输入误差信号的积分成正比关系。

为了减小稳态误差，在控制器中加入积分项，积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。

这样，即使误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大使稳态误差进一步减少，直到等于零。

积分(I)和比例(P)通常一起使用，称为比例+积分(PI)控制器，可以使系统在进入稳态后无稳态误差。

如果单独用积分(I)的话，由于积分输出随时间积累而逐渐增大，故调节动作缓慢，这样会造成调节不及时，使系统稳定裕度下降。

图3积分(I)控制和比例积分(PI)控制阶跃相应微分(D)控制在微分控制中，控制器的输出与输入误差信号的微分（即误差的变化率）成正比关系。

2、PID 算法的两种表达形式及各自的特点。

答：①位置型算式：u(n)=Kp{e(n)+T/Ti ∑(n,i=0)e(j)+Td/T[e(n)-e(n-1)]}特点：计算机实现位置式算式不够方便，其D/A 转换器具有零阶保持器的作用。

②增量型算式： △u (n)=Kp{[e(n)-e(n-1)]+T/Tie(n)+Td/T[e(n)-2e (n-1)+e(n-2)]} u(n)=u(n-1)+△u(n)特点：釆用增量型算式计算u(n)的优点是编程简单，历史数据可以递推使用，占用存储单元少，运算速度快，但它仅仅是计算方法上的改进，并没有改变位置算式的本质。

3、PID 参数的自整定方法有哪些？答：①模型参数法：即在线辩识被控对象的模型参数，再利用这些模型参数来自整定PID 控制器的参数；②特征参数法：即抽取被控对象的某些技术参数，以其为依据自动整定PID 控制参数；③专家整定：即模仿人工自整定参数的推理决策过程，自动整定PID 控制参数。

3-1、简述用特征参数法进行PID 参数自整定的思路。

答：所谓特征参数法就是抽取控制对象的某些特征参数，以其为依据自动整定PID 控制参数，下面以釆用具有滞环的继电器非线性反馈控制系统为例说明，系统框图如下：首先通过人工控制使系统进入稳定工况，然后将整定开关S 接通T ，获得极限环，使被按量y 出现临界等幅振带。

其振带幅值勤a ，振荡周期即为临界周期Tu ，临界增益为Ku=4d /∏a ，一旦获得Tu 和Ku ，再查表即可得到PID 控制器的整定参数，最后整定开关S 接通A ，使PID 控制器投入正常运行。

3-2、简述用专家整定法进行PID 参数自整定的思路。

答：所谓专家整定法就是模仿人工整定参数的推理，决策过程，自整定PID 控制参数，其系系列整定规则，再对实时釆集的被控系统信息进行分析判断，然后自动选择某个整定规则，并将被控对象的响应曲线与控制目标曲线比较，反复调整比较直到满足控制目标为止。

增量式pid算法
增量式 PID 控制算法是一种改进的 PID 控制算法，它避免了
每次更新 PID 控制器输出时重新计算所有的控制参数。

该算
法将 PID 控制器的输出信号视为增量（差量）信号，即在前
一次控制信号基础上作出新的调整。

实现增量式 PID 算法的关键是保存前一次控制器的输出信号
以及相应的误差。

在每次控制周期内，首先根据当前的误差计算出 PID 控制器的增量部分，然后用前一次的控制信号加上
增量部分得到新的控制信号。

增量式 PID 算法的公式为：
Output(n) = Output(n-1) + Kp * (Error(n) - Error(n-1)) + Ki *
Error(n) + Kd * (Error(n) - 2 * Error(n-1) + Error(n-2))
其中，Output(n) 表示第 n 次控制的输出信号，Output(n-1) 表
示第n-1 次控制的输出信号，Error(n) 表示第n 次控制的误差，Error(n-1) 表示第 n-1 次控制的误差，Error(n-2) 表示第 n-2 次
控制的误差，Kp、Ki 和Kd 分别表示比例、积分和微分增益。

增量式 PID 算法的优点是可以减少计算量，提高控制器的响
应速度。

然而，由于增量式 PID 算法使用误差的差值计算增
量部分，因此对于系统初始状态的响应较慢。

此外，如果系统具有较大的噪声干扰或非线性特性，增量式 PID 算法可能出
现较大的误差累积。

因此，在实际应用中需要根据具体情况选择适当的 PID 控制算法。

图1
控制器公式
在实际应用中，可以根据受控对象的特性和控制的性能要求，灵活地采用不同的控制组合，构成
比例(P)控制器
比例+积分(PI)控制器
比例+积分+微分(PID)控制器
式中
或ቤተ መጻሕፍቲ ባይዱ
式中
控制系统中的应用
在单回路控制系统中，由于扰动作用使被控参数偏离给定值，从而产生偏差。自动控制系统的调节单元将来自变送器的测量值与给定值相比较后产生的偏差进行比例、积分、微分(PID)运算，并输出统一标准信号，去控制执行机构的动作，以实现对温度、压力、流量、也为及其他工艺参数的自动控制。
T ——采样周期。
如果采样周期足够小，则（2-4）的近似计算可以获得足够精确的结果，离散控制过程与连续过程十分接近。
51单片机PID算法程序(一)PID算法
(原创文章，转载请注明出处/tengjingshu)
比例，积分，微分的线性组合，构成控制量u(t)，称为：比例(Proportional)、积分(Integrating)、微分(Differentiation)控制，简称PID控制
（图1，表1）
2）Atmel8-bit AVR Microcontrollers Application Note:AVR221: Discrete PID controller
（图2，图3，图4，图5，表2）
3）使用Ziegler-Nichols方法的自整定控制
/2007-03/200733042815.htm
最好的寻找PID参数的办法是从系统的数学模型出发，从想要的反应来计算参数。很多时候一个详细的数学描述是不存在的，这时候就需要实际地调节PID的参数.
Ziegler-Nichols方法

增量式PID控制算法程序;T、TD、TI、KP依次从30H，33H，36H，39H开始。

;A，B，C的值依次存在BLOCK1，BLOCK2，BLOCK3的地址里; 这里R(k)给的是定值;ORG 0000HBLOCK1 EQU 43H ;A,B ,CBLOCK2 EQU 46HBLOCK3 EQU 49HUK EQU 4CH ;存结果UKRK EQU 50HEK EQU 53H ;存放偏差值E(k)的始址EK1 EQU 56H ;存放E(k-1)的始址EK2 EQU 59H ;存放E(k-2)的始址CK EQU 5CH ;采样数据始址BUFF EQU 60H ;暂存区BUFF1 EQU 63HBUFF2 EQU 66HREC EQU 69HTEST:MOV RK,#01H ;常数Rk的BCD码浮点数MOV RK+1,#12H ;1.25MOV RK+2,#50HMOV 3CH,#01H ;常数1的BCD码浮点数MOV 3DH,#10HMOV 3EH,#00HMOV 40H,#01H ;常数2的BCD码浮点数MOV 41H,#20HMOV 42H,#00HMOV 30H,#01H ;T的BCD 码浮点数MOV 31H,#23H ;2.34MOV 32H,#40HMOV 33H,#01H ;Td的BCD码浮点数MOV 34H,#35H ;3.54MOV 35H,#40HMOV 36H,#01H ;Ti的BCD码浮点数MOV 37H,#11H ;1.12MOV 38H,#20HMOV 39H,#01H ;Kp的BCD码浮点数MOV 3AH,#12H ;1.25MOV 3BH,#50HMOV R0,#RK ;指向ＢＣＤ码浮点操作数LCALL BTOF ;将其转换成二进制浮点操作数MOV R0,#3CHLCALL BTOFMOV R0,#40HLCALL BTOFMOV R0,#39HLCALL BTOFMOV R0,#36H ;指向ＢＣＤ码浮点操作数Ti LCALL BTOF ;将其转换成二进制浮点操作数MOV R0,#33H ;指向ＢＣＤ码浮点操作数Td LCALL BTOF ;将其转换成二进制浮点操作数MOV R0,#30H ;指向ＢＣＤ码浮点操作数T LCALL BTOF ;将其转换成二进制浮点操作数MOV R1, #BUFF1 ;保存30H中的值即T值LCALL FMOVR0MOV R1, #36H ;计算A值(1+T/Ti+Td/T).Kp LCALL FDIVMOV R1,#3CH ;常数1LCALL FADDMOV R0,#33H ;保存33H中的值MOV R1,#BUFFLCALL FMOVR0MOV R1,#BUFF1LCALL FDIVMOV R1,#30H ;30H里存的是T/Ti+1LCALL FADDMOV R1,#39HLCALL FMULMOV R1 ,#BLOCK1 ;将结果保存在BLOCK1中LCALL FMOVR0MOV R1,#BUFF1 ;30H恢复原值MOV R0,#30HLCALL FMOVMOV R1,#BUFF ;33H恢复原值MOV R0,#33HLCALL FMOVMOV R0,#40H ;计算B的值Kp.(1+2.Td/T) MOV R1,#33HLCALL FMULMOV R1,#30HLCALL FDIVLCALL FADDMOV R1,#39HLCALL FMULMOV R1,#BLOCK2 ;保存B值到BLOCK2中LCALL FMOVR0MOV R0,#39H ;计算C的值Kp.Td/TMOV R1,#33HLCALL FMULMOV R1,#30HLCALL FDIVMOV R1,#BLOCK3 ;保存C值到BLOCK3中LCALL FMOVR0MOV R0,#EK1 ;将EK1，EK2设初值0LCALL FCLRMOV R0,#EK2LCALL FCLRMOV REC,#03H ;设置采样次数LOOP: MOV CK,#7eH ;采样数据暂时给了一个定值MOV CK+1,#21H ;0.002112MOV CK+2,#12HMOV R0,#CKLCALL BTOFMOV R0,#RK ;保存R（k）中的值MOV R1,#BUFFLCALL FMOVR0MOV R1,#CKLCALL FSUB ;计算R(k)-C(k)的值送给E（k）MOV R1,#EKLCALL FMOVR0MOV R1,#BUFF ;恢复RK的值释放BUFFMOV R0,#RKLCALL FMOVMOV R0,#BLOCK2 ;将B.e(k-1)的值暂存在BUFF1中MOV R1,#BUFF ;保存BLCALL FMOVR0MOV R1,#EK1LCALL FMULMOV R1,#BUFF1LCALL FMOVR0MOV R1,#BUFF ;恢复B释放BUFFLCALL FMOVMOV R0,#BLOCK3 ;将C.e(K-2)的值暂存在BUFF2中MOV R1,#BUFF ;保存CMOV R1,#EK2LCALL FMULMOV R1,#BUFF2LCALL FMOVR0MOV R1,#BUFF ;恢复C释放BUFFLCALL FMOVMOV R0,#BLOCK1 ;A.E(k)MOV R1,#BUFFLCALL FMOVR0MOV R1,#EKLCALL FMULMOV R1,#BUFF1 ;计算Uk值A.E(k)-B.E(k-1)+C.E(k-2) LCALL FSUBMOV R1,#BUFF2LCALL FADDMOV R1,#UK ;保存结果到UK中LCALL FMOVR0MOV R1,#BUFF ;恢复A 释放BUFFLCALL FMOVMOV R0,#UK ;UK转换成BCD码浮点数输出LCALL FTOBMOV R1,#EK1 ;将E(k-1)-->E(k-2),E(k)-->E(k-1)MOV R0,#EK2LCALL FMOVMOV R1,#EKMOV R0,#EK1LCALL FMOVLCALL DELAY ;等待采样时刻DJNZ REC,NEXT1SJMP $NEXT1: LJMP LOOPDELAY: MOV R7,#02HDELAY1: MOV R6,#0FFHDELAY2: DJNZ R6,DELAY2DJNZ R7,DELAY1RET; （１）标号：ＦＳＤＴ功能：浮点数格式化;入口条件：待格式化浮点操作数在[R0]中。

一开始见到PID计算公式时总会问“为什么是这样子的一道公式”，为了理解那几道公式，当时将其未简化前的公式活生生地算了一遍，现在想来，这样的演算过程固然有助于理解，但假如一开始就带着对疑问的答案已有一定抽象了解后再进行演算则会理解的更快！PID就是对输入偏差进行比例积分微分运算，然后将运算的叠加结果去控制执行机构。

实践练习中，如何把这一原理转化为程序？为什么是用那几个error进行计算?以下是一段PID程序，我曾用其对智能车的速度进行闭环控制：P：Proportional 比例I：Integrating 积分D：Differentiation 微分Pwm_value：输出Pwm暂空比的值Current_error：当前偏差last_error：上次偏差prev_error：上上次偏差增量式PID计算公式：P=Kp*(current_error﹣last_error)；D=Kd*(current_error﹣2*last_error﹢prev_error)；I=Ki*current_error；PID_add=Pwm_value+P﹢I﹢D；一、为什么是PID_add=Pwm_value+（P﹢I﹢D）而不是PID_add=P+I+D？如上图，有一个人前往目的地A，他用眼睛视觉传感器目测到距离目的地还有100m，即当前与目的地的偏差为100，他向双脚输出Δ=100J的能量，跑呀跑，10s之后，他又目测了一次，此时距离为40m，即current_error=40，他与10s前的偏差last_error=10对比，即current_error - last_error=-60，这是个负数，他意识到自己已经比较接近目的地，可以不用跑那么快，于是输出Δ=100+(-60)=40J的能量，40J的能量他刚好以4m/s的速度跑呀跑，10s之后，他发现已经到达目的点，此时current_error=0，大脑经过思考得出current_error—last_error=0 -40=-40，两脚获得的能量Δ=40+(-40)=0，即他已经达到目的地，无需再跑。

增量式PID控制算法当执行机构需要的不是控制量的绝对值，而是控制量的增量（例如去驱动步进电动机）时，需要用PID的“增量算法”。

增量式PID控制算法可以通过（2-4）式推导出。

由(2-4)可以得到控制器的第k-1个采样时刻的输出值为：(2-5)将（2-4）与（2-5）相减并整理，就可以得到增量式PID控制算法公式为：（2-6）其中由（2-6）可以看出，如果计算机控制系统采用恒定的采样周期T，一旦确定A、B、C，只要使用前后三次测量的偏差值，就可以由（2-6）求出控制量。

增量式PID控制算法与位置式PID算法（2-4）相比，计算量小得多，因此在实际中得到广泛的应用。

位置式PID控制算法也可以通过增量式控制算法推出递推计算公式：（2-7）（2-7）就是目前在计算机控制中广泛应用的数字递推PID控制算法。

增量式PID控制算法C51程序位置式PID控制算法当采样时间很短时，可用一阶差分代替一阶微分，用累加代替积分。

连续时间的离散化，即t=KT (K=0,1,2,…,n)1.离散的PID表达式积分用累加求和近似得（1）微分用一阶差分近似得（2）T ——为采样周期；k——为采样序号，k＝0，1，2，…；e（k）——系统在第次采样时刻的偏差值；e（k-1）——为系统在第k-1次采样时刻的偏差值。

（3）将式（1）和式（2）代入式（3），则可得到离散的PID表达式（4）2.物理模型式（4）表示的控制算法提供了执行机构的位置u（k）（如阀门开度），即输出值与阀门开度一一对应，所以称为位置式PID控制算法。

3.离散化的PID位置式控制算法的编程表达式对于式（4），令称为积分系数,称为微分系数则离散化的PID位置式控制算法的编程表达式为由式可以看出，每次输出与过去的状态有关，要想计算u（k），不仅涉及到e （k-1）和e（k-2），且须将历次相加。

上式计算复杂，浪费内存。

考虑到第次采样时有两式相减，得其中上式是PID的递推形式，是编程时常用的形式之一。

基于增量式PID算法的循迹小车的设计与实现一、引言在现代科技的快速发展下，无人驾驶技术已经成为了一个非常热门的领域。

循迹小车作为其中的一种代表，其设计与实现一直备受关注。

其中PID算法作为控制系统中常用的一种算法，因其稳定性及高效性而备受青睐。

本文将围绕基于增量式PID算法的循迹小车设计与实现进行探讨。

二、基于增量式PID算法的设计思路在设计循迹小车时，首先需要明确其目标：即按照规定的轨迹行驶。

而基于增量式PID算法的设计思路，核心就在于PID控制器。

PID控制器是由比例项、积分项和微分项组成的，通过调节这三个部分的参数，我们可以实现对小车的精准控制。

而增量式PID算法则是对传统PID算法的优化，其核心思想是通过对比当前的输出值和上一次的输出值，来调整PID参数，使得系统的动态响应更加灵活、迅速。

这就意味着循迹小车在行驶轨迹时能够更加精准地调整方向，从而更好地适应各种场景。

基于增量式PID算法的设计思路还需要考虑在循迹小车上实现传感器的选择及安装、电机的控制与调整、实时数据的采集与处理等问题。

三、循迹小车的硬件设计与实现在循迹小车的硬件设计中，我们通常需要考虑以下几个方面：轮子的布置与材料选择、电机的种类与功率、传感器的种类与数量。

首先是轮子的布置与材料选择，对于循迹小车而言，轮子的布置直接关系到其行驶稳定性及灵活性。

一般来说，我们可以选择四个轮子的布置方式，这样可以提高小车的稳定性。

轮子的材料选择也非常重要，一般我们可以选择橡胶或者塑料材料，这样可以提高轮子的耐磨性及抓地力。

其次是电机的选择与功率，对于循迹小车来说，我们通常选择直流电机。

电机的功率也需要根据循迹小车的重量及行驶速度来进行选择，一般来说，我们可以选择功率在1-5W 之间的直流电机。

最后是传感器的选择与数量，对于循迹小车来说，我们通常需要选择红外线传感器、超声波传感器等，以便实现对环境的感知与调整。

首先是PID控制算法的编写与优化，基于增量式PID算法的设计思路，我们需要对PID 控制算法进行编写与优化。

(2) 系统的动态过程加速
在增量式算法中，比例项与积分项的符号有以下关系：如果被控量继续偏离给定值，则这两项符号相同，而当被控量向给定值方向变化时，则这两项的符号相反。
由于这一性质，当被控量接近给定值的时候，反号的比例作用阻碍了积分作用，因而避免了积分超调以及随之带来的振荡，这显然是有利于控制的。但如果被控量远未接近给定值，仅刚开始向给定值变化时，由于比例和积分反向，将会减慢控制过程。
(2) 积分控制Ｔｉ对系统性能的影响：
积分作用使系统的稳定性下降，Ｔｉ小（积分作用强）会使系统不稳定，但能消除稳态误差，提高系统的控制精度。
(3) 微分控制Ｔｄ对系统性能的影响：
微分作用可以改善动态特性，Ｔｄ偏大时，超调量较大，调节时间较短。Ｔｄ偏小时，超调量也较大，调节时间也较长。只有Ｔｄ合适，才能使超调量较小，减短调节时间。
e(t);;;;; 控制器输入与设定值之间的误差。
Kp;;;;;;; 比例系数。
Ti;;;;;;; 积分时间常数。
Td;;;;;;; 微分时间常数。
T;;;;;;;; 调节周期。
对于增量式算法，可以选择的功能有：
(1) 滤波的选择
可以对输入加一个前置滤波器，使得进入控制算法的给定值不突变，而是有一定惯性延迟的缓变量。
如果实际实现的控制量为U=U（上限值或下限值），则有效偏差可以逆推出，即：
=
然后，由该值计算积分项
3) 微分先行PID算法
当控制系统的给定值发生阶跃时，微分作用将导致输出值大幅度变化，这样不利于生产的稳定操作。因此在微分项中不考虑给定值，只对被控量（控制器输入值）进行微分。微分先行PID算法又叫测量值微分PID算法。公式如下：
一旦控制变量进入饱和区，将只执行削弱积分项的运算而停止进行增大积分项的运算。具体地说，在计算Ui时，将判断上一个时刻的控制量Ui-1是否已经超出限制范围，如果已经超出，那么将根据偏差的符号，判断系统是否在超调区域，由此决定是否将相应偏差计入积分项。