高中数学中常见的函数符号

高中数学14种函数图像和性质知识解析新人教A版必修1高中数学 14种函数图像和性质知识解析新人教A版必修1高中不得不掌握的函数图像与常用性质高中常用函数有14种，它们是:1.正比例函数；2.反比例函数；3.根式函数；4一次函数；5.二次函数；6双勾函数.；7..双抛函数；8.指数函数；9对数函数；10.三角函数；11分段函数.；12.绝对值函数；13.超越函数；14.抽象函数。

而函数的性质常见的有：1.定义域；2.值域；3.单调性；4.奇偶性；5.周期性；6.对称性；7.有界性；8.反函数；9.连续性.高中都是从函数解析式入手画出函数图像，再利用函数图像研究其性质，下面我们就函数的图像和性质做归纳总结。

1.正比例函数解析式图像定义域：值域：单调性：奇偶性：反函数：2.反比例函数解析式图像性质定义域：值域：单调性：奇偶性：反函数：对称性：定义域：值域：单调性：对称性：3根式函数解析式图像定义域：值域：单调性：奇偶性：反函数：4一次函数解析式图像定义域：值域：1 性质性质性质用心爱心专心单调性：反函数：5二次函数解析式图像定义域：值域：单调性：对称性：定义域：值域：单调性：对称性：6.双勾函数解析式图像定义域：值域：单调性：奇偶性：对称性：定义域：值域：单调性：奇偶性：对称性：7.双抛函数解析式图像定义域：值域：单调性：奇偶性：对称性：定义域：性质性质性质用心爱心专心值域：单调性：奇偶性：对称性：8.指数函数解析式图像定义域：值域：单调性：9.对数函数解析式图像定义域：值域：单调性：10.三角函数解析式图像单调性：周期性：奇偶性：有界性：对称性：定义域：值域：单调性：周期性：奇偶性：有界性：对称性：定义域：值域：单调性：周期性：奇偶性：有界性：对称性：定义域：值域：单调性：周期性：奇偶性：有界性：对称性：11.分段函数分段函数是在其定义域的不同子集上，分别用几个不同的式子来表示对应关系的函数，它是一类较特殊的函数。

f(x)函数知识点f(x)函数是高中数学中的一个基本概念，也是日常生活和各个领域中常用的一种数学工具。

它可以帮助我们描述和分析各种现象和问题，例如，经济学中的需求函数、物理学中的运动规律、生物学中的生长模型等等。

本文将介绍f(x)函数的定义、符号表示、性质、图像、应用等方面的知识。

一、定义f(x)函数是数学中的一种映射关系，它将一个自变量x映射到唯一的因变量y上。

可以用下式表示：y=f(x)，其中y是函数的值，x是自变量，f(x)是函数名。

例如，y=x²就是一个f(x)函数，它定义了一个平面上的曲线，并将每个x值映射到该曲线上对应的y值。

在这个函数中，如果我们已知一个x值，就可以计算出对应的y值；反之，如果我们已知一个y值，也可以通过求解方程x²=y来计算对应的x值。

二、符号表示f(x)函数可以用多种符号进行表示，主要有以下三种：1.函数符号：y=f(x)，其中y是函数的值，x是自变量，f(x)是函数名称。

2.匿名符号：y=f(x)=x²，这种表示方式将函数名称省略，只保留y和x的关系式。

3.小括号符：f(x)=x³-2x，这种表示方式将自变量x放置于小括号内，使得表达式更加简洁和易读。

三、性质f(x)函数具有以下基本性质：1.定义域和值域：函数的定义域是所有自变量可以取值的范围，值域是所有因变量可以取值的范围。

例如，y=x²的定义域为实数集R，值域为非负实数集[0,+∞)。

2.单调性：如果x₁<x₂，则f(x₁)<f(x₂)或f(x₁)>f(x₂)，即函数在定义域内可以单调递增或单调递减。

3.奇偶性：如果f(-x)=f(x)，则函数是偶函数；如果f(-x)=-f(x)，则函数是奇函数；如果不满足上述条件，则函数是一个一般函数。

4.周期性：如果存在正数T，使得f(x+T)=f(x)，则函数是周期函数，周期为T。

5.反函数：如果一个函数满足一一映射的条件，则可以定义它的反函数f⁻¹(x)，满足y=f(x)和x=f⁻¹(y)互为反函数。

数学高中符号知识点总结数学是一门严谨的学科，符号是数学语言中非常重要的部分。

掌握数学符号是学习数学的基础，也是提高数学思维能力的关键。

本文将对高中数学中常见的符号进行总结，希望对广大学生有所帮助。

一、基本符号：1. 加法符号：“＋”，表示两个数相加2. 减法符号：“－”，表示两个数相减3. 乘法符号：“×”或“·”，表示两个数相乘4. 除法符号：“÷”或“/”，表示一个数被另一个数除5. 等于符号：“＝”，表示两个数或表达式相等6. 大于符号：“＞”，表示一个数大于另一个数7. 小于符号：“＜”，表示一个数小于另一个数8. 不等于符号：“≠”，表示两个数或表达式不相等9. 大于等于符号：“≥”，表示一个数大于或等于另一个数10. 小于等于符号：“≤”，表示一个数小于或等于另一个数二、四则运算符号：1. 加法：用“＋”表示，如：2＋3＝52. 减法：用“－”表示，如：5－3＝23. 乘法：用“×”或“·”表示，如：2×3＝6或2·3＝64. 除法：用“÷”或“/”表示，如：6÷2＝3或6/2＝3三、代数符号：1. 变量：通常用字母表示，如：x,y,z2. 常数：通常用数字表示，如：2,3,43. 系数：表示未知数前的数，如：3x中的3就是x的系数4. 指数：表示幂运算，如：3⁴=815. 根号：表示开方运算，如：√9=36. 平方：表示数字的平方，如：3²=97. 立方：表示数字的立方，如：3³=27四、集合符号：1. 集合：用大括号“{}”表示，如：{1,2,3,4,5}2. 元素：表示集合中的个体，用小写字母表示，如：x∈{1,2,3,4,5}3. 不含的元素：用小括号“()”表示，如：x∉{1,2,3,4,5}4. 空集合：用符号“∅”表示，表示没有元素的集合，如：∅={}五、函数符号：1. 函数：用字母表示，如：f(x)2. 自变量：表示函数自变的量，如：f(x)中的x3. 因变量：表示函数依赖的量，如：f(x)中的f4. 定义域：表示函数的取值范围，如：f(x)的定义域是x∈R六、几何符号：1. 点：用大写字母表示，如：A,B,C2. 线段：用小写字母表示，如：ab,cd,ef3. 角：用大写字母表示，如：∠ABC4. 弧：用小写字母表示，如：arcAB七、逻辑符号：1. 与的符号：用“∧”表示2. 或的符号：用“∨”表示3. 非的符号：用“¬”表示4. 蕴含的符号：用“→”表示5. 等价的符号：用“⇔”表示八、统计符号：1. 平均值：用符号“x¯”表示2. 方差：用符号“σ²”表示3. 标准差：用符号“σ”表示4. 期望值：用符号“E(X)”表示九、微积分符号：1. 极限：用符号“lim”表示2. 微分：用符号“d”表示3. 积分：用符号“∫”表示4. 导数：用符号“f’(x)”表示5. 不定积分：用符号“∫f(x)dx”表示总之，数学符号是数学语言中非常重要的部分。

符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax 同 a^xlogba 以b为底a的对数； blogba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值，其值等于 1/cos xcsc x 余割函数的值，其值等于 1/sin xasin x y，正弦函数反函数在x处的值，即 x = sin y acos x y，余弦函数反函数在x处的值，即 x = cos y atan x y，正切函数反函数在x处的值，即 x = tan y acot x y，余切函数反函数在x处的值，即 x = cot y asec x y，正割函数反函数在x处的值，即 x = sec y acsc x y，余割函数反函数在x处的值，即 x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

下边界值写在其下部，上边界值写在其上部。

如j从1到100。

这表示 1 + 2 + … + nM 表示一个矩阵或数列或其它符号表符号含义|v> 列向量，即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化，dy, dz, dr等类似ds 长度的微小变化ρ变量 (x2 + y2 + z2)1/2 或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2 或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值，为一个面积、体积或超体积det M M的行列式M-1 矩阵M的逆矩阵v×w向量v和w的向量积或叉积θvw向量v和w之间的夹角A?B×C标量三重积，以A、B、C为列的矩阵的行列式uw 在向量w方向上的单位向量，即 w/|w|df 函数f的微小变化，足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数，同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数，自变量通常为x?f/?x y、z固定时f关于x的偏导数。

函数图像高考知识点总结一、函数的概念函数是数学中的一个重要概念，函数的概念在高中数学中有着很重要的地位。

函数的概念是传递和扩展我们数学知识，从而推广了我们对数学问题的认识，为我们更好地探求数学规律打下了坚实的基础。

函数的概念最早来源于19世纪的数学家勒贝格的研究成果，函数的概念对于我们学习数学中的其他知识将会起到很大的帮助。

下面来详细介绍一下函数的概念。

1、函数的定义函数是一种特殊的关系，他只有一个自变量，并且每个自变量都对应唯一一个因变量。

函数符号y=f(x)，其中x为自变量，y为因变量，f(x)为函数。

函数的符号表示是：y=f(x)或y=y(x)，这里y表示因变量，x表示自变量，f表示函数名称，称为函数符号。

在函数y=f(x)中，x的取值范围称为定义域，y的所有可能取值构成的s称为值域，定义域与值域构成一个对应关系称为函数的定义域和值域。

定义域和值域的关系对函数的研究非常重要，这是我们学习函数的一个关键点。

只有知道了函数的定义域和值域，我们才能更好的对函数进行研究。

2、函数的图像函数的图像是指函数的自变量和因变量之间的关系所表现出来的几何图形。

函数的图像是我们理解函数的重要手段之一，通过函数的图像我们可以直观地了解函数的性质和特点。

函数的图像在我们学习函数的时候起重要的作用，通过函数图像我们可以更好的理解函数的性质。

二、函数图像的性质函数图像有很多重要的性质，这些性质对于我们理解函数图像具有非常重要的作用。

下面我们来详细介绍一下函数图像的性质。

1、函数的奇偶性函数的奇偶性是指函数的图像关于y轴对称还是关于原点对称。

如果函数的图像关于y轴对称，那么函数是偶函数；如果函数的图像关于原点对称，那么函数是奇函数。

通过函数的奇偶性，我们可以更好的理解函数的性质。

2、函数的周期性函数的周期性是指函数的图像在一定范围内具有重复的规律性。

如果函数的图像在一个固定的范围内有重复的特点，那么这个函数就具有周期性。

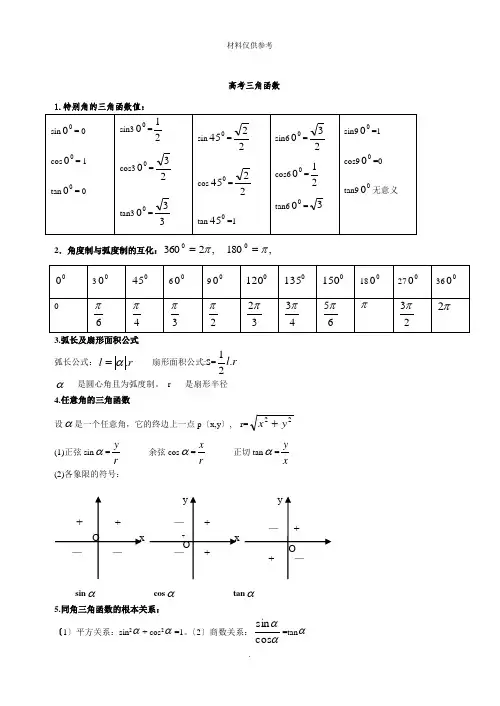
高考三角函数1.特别角的三角函数值：2．角度制与弧度制的互化：,2360π= ,1800π=3.弧长及扇形面积公式 弧长公式：r l.α= 扇形面积公式:S=r l .21α----是圆心角且为弧度制。

r-----是扇形半径4.任意角的三角函数设α是一个任意角，它的终边上一点p 〔x,y 〕, r=22y x +(1)正弦sin α=ry 余弦cos α=r x 正切tan α=xy(2)各象限的符号：sin α cos α tan α 5.同角三角函数的根本关系：〔1〕平方关系：sin 2α+ cos 2α=1。

〔2〕商数关系：ααcos sin =tan αxy+O— —+xyO — ++ — +yO— + + —〔z k k ∈+≠,2ππα〕6.诱导公式：()()1sin 2sin k παα+=，()cos 2cos k παα+=，()()tan 2tan k k παα+=∈Z ． ()()2sin sin παα+=-，()cos cos παα+=-，()tan tan παα+=． ()()3sin sin αα-=-，()cos cos αα-=，()tan tan αα-=-．()()4sin sin παα-=，()cos cos παα-=-，()tan tan παα-=-．口诀：函数名称不变，符号看象限．()5sin cos 2παα⎛⎫-=⎪⎝⎭，cos sin 2παα⎛⎫-= ⎪⎝⎭． ()6sin cos 2παα⎛⎫+=⎪⎝⎭，cos sin 2παα⎛⎫+=-⎪⎝⎭． 口诀：正弦与余弦互换，符号看象限． 7正弦函数、余弦函数和正切函数的图象与性质三角形面积定理.111sin sin sin 222S ab C bc A ca B ===.1．直角三角形中各元素间的关系：如图，在△ABC 中，C ＝90°，AB ＝c ，AC ＝b ，BC ＝a 。

2.1。

1 函数-2.1。

2 函数的表示方法自主整理1。

函数的概念设集合A是一个非空的数集，对A内任意数x,按照确定的法则f,都有唯一确定的数值y与它对应,则这种对应关系叫做集合A上的一个函数，记作y=f（x)，x∈A.其中，x叫做自变量，自变量的取值范围A叫做函数的定义域；如果自变量取值a,则由法则f确定的值y称作函数在a处的函数值，记作y=f（a)或y｜x=a.所有函数值构成的集合｛y｜y=f（x）,x∈A}叫做函数的值域。

2。

两个函数的相等函数的定义含有三个要素,即定义域A、值域C和对应法则f.当且仅当两个函数的定义域和对应法则都分别相同时,这两个函数才是同一个函数。

3.区间(1)在数轴上,区间可以用一条以a,b为端点的线段来表示（如下表）。

用实心点表示端点包括在区间内，用空心点表示端点不包括在区间内.定义名称符号数轴表示{x｜a≤x≤b｝闭区间[a,b］｛x|a〈x<b｝开区间(a，b）｛x|a≤x〈b} 半开半闭区间［a，b){x｜a<x≤b}半开半闭区间(a，b］(2）无穷区间的概念：关于-∞,+∞作为区间的一端或两端的区间称为无穷区间，它的定义和符号如下表：{x｜x≥a｝[a，+∞）｛x|x>a｝(a,+∞)｛x|x≤a}(-∞，a］{x｜x〈a} （-∞，a)R (—∞，+∞)取遍数轴上所有值4.映射的概念设A、B是两个非空的集合，如果按某种对应法则f，对A内任意一个元素x，在B中有一个且仅有一个元素y与x 对应，则称f是集合A到集合B的映射。

这时，称y是x在映射f的作用下的象，记作f(x).于是y=f（x）,x称作y的原象,映射f也可记为f:A→B，x→f （x）。

其中A叫做映射f的定义域（函数定义域的推广），由所有象f（x）构成的集合叫做映射f的值域，通常记作f(A). 5。

常用的函数表示法（1)列表法:通过列出自变量与对应函数值的表来表达函数关系的方法；（2）图象法:就是用函数图象来表达函数关系；(3）解析法:如果在函数y=f（x)（x∈A)中,f（x）是用代数式（或解析式）来表达的，则这种表达函数的方法叫做解析法(也称公式法）.6。

高中数学符号读法大全引言在高中数学学习中，学生们不可避免地会接触到各种各样的数学符号。

正确理解这些符号的含义和读法，对于学习和理解数学概念和定理都至关重要。

本文将为大家提供一个高中数学符号读法大全，帮助大家更好地掌握这些符号的含义和读法。

数字和运算符号•数字：0、1、2、3、4、5、6、7、8、9•负号：-•加号：+•减号：-•乘号：×、\*、或直接省略•除号：÷、/•等号：=•不等号：≠•大于号：>•小于号：<•大于等于号：≥•小于等于号：≤基本数学符号•加法：a + b•减法：a - b•乘法：a × b、a \* b、ab、a · b （中点表示）•除法：a ÷ b、a / b、a⁄b•求和：∑（大写希腊字母Sigma）•平方：a²•立方：a³•平方根：√•立方根：∛•其他次方根：∜•百分号：%•小数点：.希腊字母•α（Alpha）•β（Beta）•γ（Gamma）•δ（Delta）•ε（Epsilon）•ζ（Zeta）•η（Eta）•θ（Theta）•ι（Iota）•κ（Kappa）•λ（Lambda）•μ（Mu）•ν（Nu）•ξ（Xi）•ο（Omicron）•π（Pi）•ρ（Rho）•σ（Sigma）•τ（Tau）•υ（Upsilon）•φ（Phi）•χ（Chi）•ψ（Psi）•ω（Omega）关系运算符•等于：=•不等于：≠•大于：>•小于：<•大于等于：≥•小于等于：≤•约等于：≈•相似于：∼数学函数和常用符号•绝对值：|x|•平均值：μ•最大值：max•最小值：min•阶乘：n!•自然对数：ln•对数：log•指数函数：exp•三角函数：sin、cos、tan、cot、sec、csc•反三角函数：arcsin、arccos、arctan、arccot、arcsec、arccsc•积分：∫•微分：d•极限：lim•无穷大：∞•空集：∅其他特殊符号•分数线：/•并集：∪•交集：∩•包含于：⊂•包含等于：⊆•元素属于：∈•空集：∅•直角符号：∠•向量符号：→•无理数：π（圆周率）、e（自然对数底数）结论本文列举了高中数学中常用的符号及其读法，希望能够帮助学生们更好地理解和掌握这些符号。

高中数学中常见的函数符号1 数学函数1.1 取整函数int(x) 取不大于x的最大整数。

fix(x) 舍去x的小数部分。

1.2 绝对值函数abs(x) 求x的绝对值。

1.3 符号函数sgn(x) 求x的符号代码，x为负数时函数值为-1 。

1.4 平方根函数sqr(x) 求x的算术平方根，x必须大于0 。

1.5 指数函数exp(x) 求以e为底x为指数的值。

1.6 对数函数log(x) 求以e为底的对数函数值。

1.7 三角函数sin(x) 求x的正弦值。

con(x) 求x的余弦值。

tan(x) 求x的正切值。

Atn(x) 求x的反正切值。

1.8 数制转换函数hex(x) 十进制转换为对应的十六进制数。

oct(x) 十进制转换为对应的八进制数。

2 日期时间函数2.1 系统日期时间函数now() 读取系统当前日期时间。

date() 读取系统当前日期。

time() 读取系统当前时间。

2.2 日期时间分解函数year(日期字符串) 返回日期字符串中的年份。

month(日期字符串) 返回日期字符串中的月份。

day(日期字符串) 返回日期字符串中的日子。

weekday(日期字符串) 返回日期字符串中的星期。

hour(时间字符串) 返回时间字符串中的小时。

minute(时间字符串) 返回时间字符串中的分钟。

secont(时间字符串) 返回时间字符串中的秒数。

2.3 日期时间数值化函数dateValue(日期字符串) 把日期字符串转换为当日至1889-12-30的天数。

timeValue(时间字符串) 把时间字符串转换为0,1之间变体型时间值。

2.4 日期时间运算函数dateSerial(年,月,日) 把年月日连接成日期字符串。

timeSerial(时,分,秒) 把时分秒连接成时间字符串。

timer() 计算午夜起至当前系统时间所历经的秒数。

3 字符串处理函数3.1 删除空格函数Trim(字符串) 删除字符串两端空格字符。

高中数学公式符号大全sA= N+N+╮＋－×÷±＜＞•∶∴∵∷≰∫∮∝∞∧∨º¹²³ ´ ¶ µ≠≤≥≈≡‖＝≌∸≮≯∑∏∪∩ⅰ⊿≲√∟㎗㎖￠∠≱％‰℅°℃℉′〒¤▚µ㎎㎏㎐㎑㎒㎓㎔㎕㎗＄￡￥㎘□■ X¹ X² X³ 1°1′1〃↑ ↓ ← → ↖↗↙↘㊣◉⊕≰▚ ▬ △▖☆★◇◆□▔▽▘§￥￡※■□∵∴θω ░ ▒▞▝▟▢◈♤▥‛♨▣♧▤♡▦▩▣▧▨▤▥▪ ▫ ▛ ▜ ☏☎☜☞◑◐▭ ° ☑₪╮，、～％＃＊‧；∶… ¨ ，• ˙ ‘ ’〃′ εїз ™ ✿｡◕‿◕｡◉▝▞▗▙▧▨◐◑↔ ↕ ㊊㊋㊌㊍㊎㊏㊐▀▄ █ ▌▕ (ε.メ)▣▤▥▦▩♭☀ஐ☈➽〠〄㍿㊚㊛㊙℗♯♩♫♬¤큐≡:,⊆⊂⊇⊃试比较cos1°与tan44°的大小。

1、几何符号≱‖∠≲≰≡≌△° |a| ≱∸∠↛‖|2、代数符号? ∝∧∨～∫ ≤ ≥ ≈ ∞ :〔〕〈〉《》「」『』】【〖3、运算符号{× ‚ √ ± ≠ ≡≮≯4、集合符号∪∩ⅰΦ ? ￠sA= N+N+{ } [ ] （）5、特殊符号∑ π（圆周率）＠＃☆★◈●◉◇◆□▔▓⊿※￥Γ Δ Θ ∧Ξ Ο ∏ ∑ Φ Χ Ψ Ω ∏6、推理符号ⅬⅭⅮⅯ↖↗↘↙∴∵∶∷T ? ü7、标点符号` ˉ ˇ ¨ 、· ‘’8、其他& ; § ℃№ ＄￡￥‰ ℉☈☇≳≴≵≶≷≸≹≺≻≼Γ Δ Θ ∧Ξ Ο ∏ ∑ Φ Χ Ψ Ωα β γ δ ε δ ε ζ η θ ι κ λ μ ν π ξ ζ η υ θ χ ψ ωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹⅰ∏ ∑ ↚√ ∝∞ ↛∠↜‖∧∨∩∪∫ ∮∴∵∶∷∸≈ ≌≈ ≠ ≡≤ ≥ ≤ ≥ ≮≯⊕≰≱⊿≲指数0123：o123 〃? ? ?符号意义∞ 无穷大PI 圆周率|x| 函数的绝对值∪集合并∩集合交≥ 大于等于≤ 小于等于≡恒等于或同余ln(x) 以e为底的对数lg(x) 以10为底的对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数{x} 小数部分x - floor(x)∫f(x)δx 不定积分∫[a:b]f(x)δx a到b的定积分∑[1≤k≤n]f(k) 对n进行求和,可以拓广至很多情况，如：∑[n is prime][n < 10]f(n)∑∑[1≤i≤j≤n]n^2lim f(x) (x->?) 求极限C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除n(m,n)=1 m与n互质a ⅰA a属于集合ACard(A) 集合A中的元素个数|a| ≱∸△∠∩∪≠ ∵∴≡± ≥ ≤ ⅰⅬⅭⅮⅯ↖↗↘↙‖∧∨¼ ½ ¾§≳≴≵≶≷≸≹≺≻≼α β γ δ ε δ ε ζ η θ ι κ λ μ ν π ξ ζ η υ θ χ ψ ωⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹⅰ∏∑↚√∝∞↛∠↜‖∧∨∩∪∫∮∴∵∶∷∸≈≌≈≠≡≤≥≤≥≮≯⊕≰≱⊿≲为了方便，也做些约定！x的平方，可以打成x^2 （其它的以此类推）x+1的开方，可以打成√(x+1)，记住加括号；x分之一，可以输入1/x;如果是x+1分之一，请输入1/(x+1)，分子、分母请加括号<> 或>< 表示不等于例：a<>b 即a不等于b；<= 表示小于等于（不大于）例：a<=b 即a不大于b；>= 表示大于等于（不小于）例：a>=b 即a不小于b；^ 表示乘方例：a^b 即a的b次方, 也可用于开根号，例：a^(1/2) 表示a的平方根* 表示乘……/ 表示浮点除例：3/2=1.5\ 表示整除例：3\2=1……1（）广义括号，允许多重嵌套，无大、中、小之分，优先级最高1 几何符号≱‖∠≲≰≡ ≌△2 代数符号∝∧∨～∫ ≠ ≤ ≥ ≈ ∞ ∶3运算符号× ‚ √ ±4集合符号∪∩ ⅰ5特殊符号∑ π（圆周率）6推理符号|a| ≱∸△∠∩ ∪≠ ≡ ± ≥ ≤ ⅰ←↑ → ↓ ↖↗↘↙‖∧∨&; §≳≴≵≶≷≸≹≺≻≼Γ Δ Θ ∧Ξ Ο ∏ ∑ Φ Χ Ψ Ωα β γ δ ε δ ε ζ η θ ι κ λμ ν π ξ ζ η υ θ χ ψ ωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹⅰ∏ ∑ ∕ √ ∝∞ ∟ ∠↜‖∧∨∩ ∪∫ ∮∴∵∶∷∸≈ ≌≈ ≠ ≡ ≤ ≥ ≤ ≥ ≮≯⊕≰≱⊿≲℃指数0123：º¹²³符号意义∞ 无穷大PI 圆周率|x| 函数的绝对值∪集合并∩ 集合交≥ 大于等于≤ 小于等于≡ 恒等于或同余ln(x) 自然对数lg(x) 以2为底的对数log(x) 常用对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数{x} 小数部分x - floor(x)∫f(x)δx 不定积分∫[a:b]f(x)δx a到b的定积分[P] P为真等于1否则等于0∑[1≤k≤n]f(k) 对n进行求和,可以拓广至很多情况如：∑[n is prime][n < 10]f(n)∑∑[1≤i≤j≤n]n^2lim f(x) (x->?) 求极限f(z) f关于z的m阶导函数C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除nm≱n m与n互质a ⅰA a属于集合A#A 集合A中的元素个数∑(n=p,q)f(n) 表示f(n)的n从p到q逐步变化对f(n)的连加和，如果f(n)是有结构式，f(n)应外引括号；∑(n=p,q ; r=s,t)f(n,r) 表示∑(r=s,t)[∑(n=p,q)f(n,r)],如果f(n，r)是有结构式，f(n，r)应外引括号；∏(n=p,q)f(n) 表示f(n)的n从p到q逐步变化对f(n)的连乘积, 如果f(n)是有结构式，f(n)应外引括号；∏(n=p,q ; r=s,t)f(n,r) 表示∏(r=s,t)[∏(n=p,q)f(n,r)],如果f(n，r)是有结构式，f(n，r)应外引括号；lim(x→u)f(x) 表示f(x) 的x 趋向u 时的极限,如果f(x)是有结构式，f(x)应外引括号；l im(y→v ; x→u)f(x,y) 表示lim(y→v)[lim(x→u)f(x,y)],如果f(x，y)是有结构式，f(x，y)应外引括号；∫(a,b)f(x)dx 表示对f(x) 从x=a 至x=b 的积分,如果f(x)是有结构式，f(x)应外引括号；∫(c,d ; a,b)f(x,y)dxdy 表示∫(c,d)[∫(a,b)f(x,y)dx]dy,如果f(x，y)是有结构式，f(x，y)应外引括号；∫(L)f(x,y)ds 表示f(x,y) 在曲线L 上的积分,如果f(x，y)是有结构式，f(x，y)应外引括号；∫∫(D)f(x,y,z)dζ 表示f(x,y,z) 在曲面D 上的积分,如果f(x，y，z)是有结构式，f(x，y，z)应外引括号；∮(L)f(x,y)ds 表示f(x,y) 在闭曲线L 上的积分,如果f(x，y)是有结构式，f(x，y)应外引括号；∮∮(D)f(x,y,z)dζ 表示f(x,y,z) 在闭曲面 D 上的积分,如果f(x，y)是有结构式，f(x，y)应外引括号；∪(n=p,q)A(n) 表示n从p到q之A(n)的并集，如果A(n)是有结构式，A(n)应外引括号；∪(n=p,q ; r=s,t)A(n,r) 表示∪(r=s,t)[∪(n=p,q)A(n,r)],如果A(n，r)是有结构式，A(n，r)应外引括号；∩(n=p,q)A(n) 表示n从p到q逐步变化对A(n)的交集,如果A(n)是有结构式，A(n)应外引括号；∩(n=p,q ; r=s,t)A(n,r) 表示∩(r=s,t)[∩(n=p,q)A(n,r)], 如果A(n，r)是有结构式，A(n，r)应外引括号；。