第三章习题解答

第三章习题解答一、判断下列说法是否正确，凡对的在括号内打“√”，否则打“×”。

（1）现测得两个共射放大电路空载时的电压放大倍数均为－100，将它们连成两级放大电路，其电压放大倍数应为10000。

( )（2）阻容耦合多级放大电路各级的Q点相互独立，( )它只能放大交流信号。

( )（3）直接耦合多级放大电路各级的Q点相互影响，( )它只能放大直流信号。

( )（4）只有直接耦合放大电路中晶休管的参数才随温度而变化。

( )（5）互补输出级应采用共集或共漏接法。

( )二、现有基本放大电路：A.共射电路B.共集电路C.共基电路D.共源电路E.共漏电路根据要求选择合适电路组成两级放大电路。

（1）要求输入电阻为1kΩ至2kΩ，电压放大倍数大于3000，第一级应采用，第二级应采用。

（2）要求输入电阻大于10MΩ，电压放大倍数大于300，第一级应采用，第二级应采用。

（3）要求输入电阻为100kΩ～200kΩ，电压放大倍数数值大于100，第一级应采用，第二级应采用。

（4）要求电压放大倍数的数值大于10，输入电阻大于10MΩ，输出电阻小于100Ω，第一级应采用，第二级应采用。

（5）设信号源为内阻很大的电压源，要求将输入电流转换成输出电压，且，输出电阻R o＜100，第一级应采用，第二级应采用。

三、选择合适答案填入空内。

（1）直接耦合放大电路存在零点漂移的原因是。

A.电阻阻值有误差B.晶体管参数的分散性C.晶体管参数受温度影响D.电源电压不稳定（2）集成放大电路采用直接耦合方式的原因是。

A.便于设计B.放大交流信号C.不易制作大容量电容（3）选用差分放大电路的原因是。

A.克服温漂B. 提高输入电阻C.稳定放入倍数（4）差分放大电路的差模信号是两个输入端信号的，共模信号是两个输入端信号的。

A.差B.和C.平均值（5）用恒流源取代长尾式差分放大电路中的发射极电阻R e，将使电路的。

A.差模放大倍数数值增大B.抑制共模信号能力增强C.差模输入电阻增大（6）互补输出级采用共集形式是为了使。

第三章存储系统(习题解答)————————————————————————————————作者：————————————————————————————————日期：第三章存储系统（习题参考答案）1．有一个具有20位地址和32位字长的存储器，问：（1）该存储器能存储多少个字节的信息？（2）如果存储器由512K×8位SRAM芯片组成，需要多少芯片？（3）需要多少位地址作芯片选择？解：（1）∵ 220= 1M，∴ 该存储器能存储的信息为：1M×32/8=4MB （2）（1024K/512K）×（32/8）= 8（片）（3）需要1位地址作为芯片选择。

（选择两个512K×32位的存储体）2. 已知某64位机主存采用半导体存储器，其地址码为26位，若使用256K×16位的DRAM芯片组成该机所允许的最大主存空间，并选用模块板结构形式，问：（1）每个模块板为1024K×64位，共需几个模块板？（2）每个模块板内共有多少DRAM芯片?（3）主存共需多少DRAM芯片? CPU如何选择各模块板？解：(1)最大主存空间为：226×64位，每个模块板容量为：1024K×64位=220×64位设：共需模块板数为m：则：m=（226×64位）/（220×64位）= 64 (块)(2). 设每个模块板内有DRAM芯片数为n:n=(/) ×(64/16)=16 (片)(3) 主存共需DRAM芯片为：m×n = 64×16=1024 (片)每个模块板有16片DRAM芯片，容量为1024K×64位，需20根地址线(A19~A0)完成模块板内存储单元寻址。

一共有64块模块板，采用6根高位地址线(A25~A20)，通过6:64译码器译码,产生片选信号对各模块板进行选择。

3．用16K×8位的DRAM芯片组成64K×32位存储器，要求：(1) 画出该存储器的组成逻辑框图。

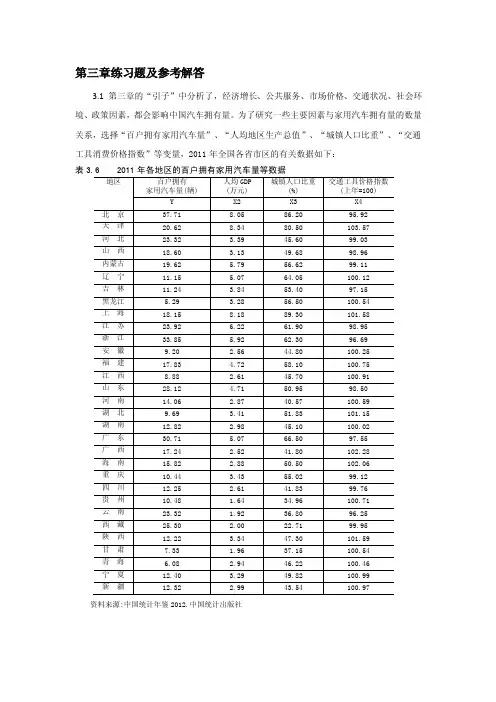
第三章练习题及参考解答3.1 第三章的“引子”中分析了，经济增长、公共服务、市场价格、交通状况、社会环境、政策因素，都会影响中国汽车拥有量。

为了研究一些主要因素与家用汽车拥有量的数量关系，选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“交通工具消费价格指数”等变量，2011年全国各省市区的有关数据如下：表3.6 2011年各地区的百户拥有家用汽车量等数据资料来源:中国统计年鉴2012.中国统计出版社1）建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验，检验结论的依据是什么?。

2)分析模型参数估计结果的经济意义,你如何解读模型估计检验的结果?3) 你认为模型还可以如何改进?【练习题3.1参考解答】:1)建立线性回归模型: 1223344t t t t t Y X X X u ββββ=++++ 回归结果如下:由F 统计量为17.87881, P 值为0.000001,可判断模型整体上显著,“人均地区生产总值”、“城镇人口比重”、“交通工具消费价格指数”等变量联合起来对百户拥有家用汽车量有显著影响。

解释变量参数的t 统计量的绝对值均大于临界值0.025(27) 2.052t =,或P 值均明显小于0.05α=，表明在其他变量不变的情况下,“人均地区生产总值”、“城镇人口比重”、“交通工具消费价格指数”分别对百户拥有家用汽车量都有显著影响。

2）X2的参数估计值为5.9911,表明随着经济的增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近6辆。

由于城镇公共交通的大力发展,有减少家用汽车的必要性,X3的参数估计值为-0.5231,表明随着城镇化的推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0.5231辆。

汽车价格和使用费用的提高将抑制家用汽车的使用, X4的参数估计值为-2.2677,表明随着家用汽车使用成本的提高,“交通工具消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少2.2677辆。

第3章 力学基本定律与守恒律 习题及答案1．作用在质量为10 kg 的物体上的力为i t F)210(+=N ，式中t 的单位是s ，(1)求4s 后，这物体的动量和速度的变化．(2)为了使这力的冲量为200 N ·s ，该力应在这物体上作用多久，试就一原来静止的物体和一个具有初速度j 6-m ·s -1的物体,回答这两个问题．解: (1)若物体原来静止，则i t i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向，ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速，则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理， 12v v ∆=∆,12I I=这说明，只要力函数不变，作用时间相同，则不管物体有无初动量，也不管初动量有多大，那么物体获得的动量的增量(亦即冲量)就一定相同，这就是动量定理． (2)同上理，两种情况中的作用时间相同，即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ，(s 20='t 舍去)2．一颗子弹由枪口射出时速率为10s m -⋅v ，当子弹在枪筒内被加速时，它所受的合力为 F =(bt a -)N(b a ,为常数)，其中t 以秒为单位：(1)假设子弹运行到枪口处合力刚好为零，试计算子弹走完枪筒全长所需时间；(2)求子弹所受的冲量．(3)求子弹的质量． 解: (1)由题意，子弹到枪口时，有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入，得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 3．如图所示，一质量为m 的球，在质量为M 半径为R 的1/4圆弧形滑槽中从静止滑下。

第三章热力学本章提要1．准静态过程系统连续经过的每个中间态都无限接近平衡态的一种理想过程。

准静态过程可以用状态图上的曲线表示。

2．内能系统内所有分子热运动动能和分子之间相互作用势能的和，其数学关系式为(,)E E V T=内能是态函数。

3．功功是过程量。

微分形式：VpA dd=积分形式：⎰=21dV VV pA4．热量两个物体之间或物体内各局部之间由于温度不同而交换的热运动能量。

热量也是过程量。

5．热力学第一定律热力学第一定律的数学表达式：Q E A=∆+热力学第一定律的微分表达式：d d dQ E A=+由热力学第一定律可知，第一类永动机是不可能造成的。

6．理想气体的热功转换〔1〕等体过程：d 0A = 热量增量为m m (d )d d V V MQ E C T μ,,==或m 21m 21V ,V ,MQ E E C (T T )μ=-=-〔2〕等压过程: 热量增量为(d )d d d d p Q E A E p V =+=+因m 21()V ME C T T μ∆,-=212121()()V V MA p V p V V R T T μd ==-=-⎰那么)()(21212T T R MT T R i M Q P -+-=μμ 〔3〕等温过程：d 0E =热量增量为(d )d d V Q A p V ==因2121d ln V T V V MV MA RT RT V V μμ==⎰那么2112lnln T T V pMM Q A RT RT V p μμ=== 〔4〕绝热过程：d 0Q = 根据热力学第一定路可得d d 0E A +=那么m d d d d V ,MA p V E C Tμ==-=-或221121m ()d d V V V ,V V MA E E p V C T μ=--==-⎰⎰)(112211V p V p A --=γ 在绝热过程中理想气体的p 、V 、T 三个状态参量之间满足如下关系：常量=γpV常量=-1γTV 常量=--γγT p 17．热容量等体摩尔热容量：m (d )d d d V V Q EC T T,== 等压摩尔热容量：m (d )d d d d d p p Q E VC p TT T,==+ 对于理想气体，假设分子自由度为i ，那么m 2V ,i C R = m 22P,i C R +=迈耶公式：m m p,V ,C C R =+比热容比：m m22p,V ,C i C γ+==8．焓在等压过程中，由热力学第一定律可得2121()()P Q E p V E E V V =∆+∆=-+-由于12P P P ==，上式可写为222111()()P Q E p V E pV =+-+ 如果令H E pV =+21P Q H H H =-=∆焓是一个态函数。

第三章微分中值定理与导数的应用答案§3.1 微分中值定理1． 填空题（１）函数x x f arctan )(=在]1 ,0[上使拉格朗日中值定理结论成立的ξ是ππ-4．（２）设)5)(3)(2)(1()(----=x x x x x f ，则0)(='x f 有 3 个实根，分别位于区间)5,3(),3,2(),2,1(中．2． 选择题 （１）罗尔定理中的三个条件:)(x f 在],[b a 上连续，在),(b a 内可导，且)()(b f a f =，是)(x f 在),(b a 内至少存在一点ξ，使0)(='ξf 成立的（ B ）．A ． 必要条件B ．充分条件C ． 充要条件D ． 既非充分也非必要条件 （２）下列函数在]1 ,1[-上满足罗尔定理条件的是（ C ）．A . xe xf =)( B. ||)(x x f = C. 21)(x x f -= D. ⎪⎩⎪⎨⎧=≠=0,00,1sin )(x x xx x f （３）若)(x f 在),(b a 内可导，且21x x 、是),(b a 内任意两点，则至少存在一点ξ，使下式成立（ B ）．A ． ),()()()()(2112b a f x x x f x f ∈'-=-ξξB ． ξξ)()()()(2121f x x x f x f '-=-在12,x x 之间C ． 211221)()()()(x x f x x x f x f <<'-=-ξξD ． 211212)()()()(x x f x x x f x f <<'-=-ξξ3．证明恒等式：)(2cot arctan ∞<<-∞=+x x arc x π．证明： 令x arc x x f cot arctan )(+=，则01111)(22=+-+='x x x f ，所以)(x f 为一常数．设c x f =)(，又因为(1)2f π=，故 )(2c o t a r c t a n ∞<<-∞=+x x arc x π．4．若函数)(x f 在),(b a 内具有二阶导数，且)()()(321x f x f x f ==，其中12a x x <<3x b <<，证明:在),(31x x 内至少有一点ξ，使得0)(=''ξf ．证明：由于)(x f 在],[21x x 上连续,在),(21x x 可导,且)()(21x f x f =，根据罗尔定理知，存在),(211x x ∈ξ， 使0)(1='ξf ． 同理存在),(322x x ∈ξ，使0)(2='ξf ． 又)(x f '在],[21ξξ上 符合罗尔定理的条件，故有),(31x x ∈ξ，使得0)(=''ξf ．5． 证明方程062132=+++x x x 有且仅有一个实根． 证明：设621)(32x x x x f +++=， 则031)2(,01)0(<-=->=f f ，根据零点存在定理至少存在一个)0,2(-∈ξ， 使得0)(=ξf ．另一方面，假设有),(,21+∞-∞∈x x ，且21x x <，使0)()(21==x f x f ，根据罗尔定理，存在),(21x x ∈η使0)(='ηf ，即02112=++ηη，这与02112>++ηη矛盾．故方程062132=+++x x x 只有一个实根． 6． 设函数)(x f 的导函数)(x f '在],[b a 上连续，且0)(,0)(,0)(<><b f c f a f ，其中c 是介于b a ,之间的一个实数． 证明： 存在),(b a ∈ξ, 使0)(='ξf 成立.证明： 由于)(x f 在],[b a 内可导，从而)(x f 在闭区间],[b a 内连续，在开区间(,)a b 内可导．又因为()0,()0f a f c <>，根据零点存在定理，必存在点1(,)a c ξ∈，使得0)(1=ξf ． 同理，存在点2(,)c b ξ∈，使得0)(2=ξf ．因此()f x 在[]21,ξξ上满足罗尔定理的条件，故存在),(b a ∈ξ， 使0)(='ξf 成立．7. 设函数)(x f 在]1,0[上连续, 在)1,0(内可导. 试证:至少存在一点(0,1)ξ∈, 使证明： 只需令2)(x x g =，利用柯西中值定理即可证明. 8．证明下列不等式（１）当π<<x 0时，x xxcos sin >． 证明： 设t t t t f cos sin )(-=，函数)(t f 在区间],0[x 上满足拉格朗日中值定理的条件，且t t t f sin )(=', 故'()(0)()(0), 0f x f f x x ξξ-=-<<, 即0sin cos sin >=-ξξx x x x (π<<x 0)因此， 当π<<x 0时，x xxcos sin >．（２）当 0>>b a 时，bba b a a b a -<<-ln ． 证明：设x x f ln )(=，则函数在区间[,]b a 上满足拉格朗日中值定理得条件，有因为'1()f x x=，所以1ln ()a a b b ξ=-，又因为b a ξ<<，所以111a b ξ<<，从而bb a b a a b a -<<-ln ． §3.1 洛毕达法则1． 填空题 （１） =→xxx 3cos 5cos lim2π35-（２）=++∞→xx x arctan )11ln(lim0 （３）)tan 11(lim 20x x x x -→=31（４）0lim(sin )xx x +→=1 ２．选择题（１）下列各式运用洛必达法则正确的是（ B ） A ． ==∞→∞→nn n n n en ln limlim11lim=∞→nn eB ． =-+→x x x x x sin sin lim0 ∞=-+→xxx cos 1cos 1lim 0C ． xx x x x x x x x cos 1cos1sin 2lim sin 1sin lim020-=→→不存在 D ． x x e x 0lim →=11lim 0=→x x e（２） 在以下各式中，极限存在，但不能用洛必达法则计算的是（ C ）A ． x x x sin lim 20→B ． x x x tan 0)1(lim +→C ． x x x x sin lim +∞→D ． x nx e x +∞→lim3． 求下列极限（１）nn mm a x a x a x --→lim ．解： n n m m a x a x a x --→lim =nm n m a x a nm nx mx ---→=11lim． （２）20222lim x x x x -+-→．解： 20222lim xx x x -+-→=x x x x 22ln 22ln 2lim 0-→-=2)2(ln 2)2(ln 2lim 220x x x -→+=2)2(ln ． （３）30tan sin lim x xx x -→ ．解：30tan sin lim x x x x -→＝32030)21(lim )1(cos tan lim x x x x x x x x -⋅=-→→＝21-． （４） 20)(arcsin 1sin lim x x e x x --→．解：20)(arcsin 1sin lim x x e x x --→＝201sin lim x x e x x --→＝212sin lim 2cos lim00=+=-→→x e x x e x x x x ． （５）x x x x xx ln 1lim 1+--→．解： )ln 1()(x x x xx +='， x x x x xx ln 1lim1+--→＝xx x xx 11)ln 1(1lim 1+-+-→＝22111)ln 1(limx x x x x xx x --+-→2])ln 1([lim 1221=++=++→x x x x x x ．（６） )111(lim 0--→x x e x ．解：2121lim )1(1lim )111(lim 22000==---=--→→→xxe x x e e x x x xx x x （７） xx xtan 0)1(lim +→ ．解：1)1(lim 202000sin limcsc 1lim cot ln limln tan lim tan 0=====+→+→+→+→+----→x xxx x x xx x x x x x x eeeex．（８）)31ln()21ln(lim xxx +++∞→．解： )31ln()21ln(lim x x x +++∞→=2ln 23ln(12)12lim ln(12)3lim 3lim1x x x x x x x x x →+∞→+∞→+∞+++== =xxx 212lim 2ln 3++∞→=2ln 3．（９） n n n ∞→l i m ．解： 因为1lim1limln 1lim===∞→∞→∞→xxxxx x x eex ，所以nn n ∞→lim=1．§3.3 泰勒公式 １．按1-x 的幂展开多项式43)(24++=x x x f ．解： 10)1(,64)(3='+='f x x x f ，同理得24)1(,24)1(,18)1()4(=='''=''f f f ，且0)()5(=x f ．由泰勒公式得：43)(24++=x x x f =432)1()1(4)1(9)1(108-+-+-+-+x x x x ．2． 求函数xe x xf 2)(=的带有佩亚诺型余项的n 阶麦克劳林公式．解：因为)(!!2!112n nxx o n x x x e +++++= ， 所以xe x xf 2)(==2222[1()]1!2!(2)!n n x x x x o x n --+++++-=)()!2(!2!1432n n x o n x x x x +-++++ ． 3． 求一个二次多项式)(x p ，使得)()(22x x p x ο+=． 解：设xx f 2)(=，则2ln 2)(x x f ='，2)2(ln 2)(x x f =''． 2)2(ln )0(,2ln )0(,1)0(=''='=f f f ，故 )(!2)2(ln !12ln 12222x x x xο+++=， 则 222)2(ln 2ln 1)(x x x p ++=为所求． 4．利用泰勒公式求极限)]11ln([lim 2xx x x +-∞→．解：因为 ))1((3)1(2)1(1)11ln(332xo x x x x ++-=+，所以 )11ln(2x x x +-=)])1((3)1(2)1(1[3322x o x x x x x ++--=)1(3121x o x +-，故 21)]1(3121[lim )]11ln([lim 2=+-=+-∞→∞→x o x x x x x x ．5． 设)(x f 有三阶导数,且0)1(,0)(lim 20==→f x x f x ,证明在)1,0(内存在一点ξ,使0)(='''ξf ．证明： 因为 0)(lim 20=→x x f x ，所以0)0(,0)0(,0)0(=''='=f f f ．由麦克劳林公式得：332!3)(!3)(!2)0()0()0()(x f x f x f x f f x f ξξ'''='''+''+'+= （ξ介于0与x 之间），因此 !3)()1(ξf f '''=，由于0)1(=f ，故0)(='''ξf ．§3.4函数的单调性与曲线的凹凸性1． 填空题（１） 函数)ln(422x x y -=的单调增加区间是),21()0,21(+∞-，单调减少区间)21,0()21,( --∞．（２）若函数)(x f 二阶导数存在，且0)0(,0)(=>''f x f ，则xx f x F )()(=在+∞<<x 0上是单调 增加 ．（３）函数12+=ax y 在),0(∞+内单调增加，则a 0>．（４）若点（1，3)为曲线23bx ax y +=的拐点，则=a 23-，=b 29，曲线的凹区间为)1,(-∞，凸区间为),1(∞．2． 单项选择题（１）下列函数中，（ A ）在指定区间内是单调减少的函数. A . xy -=2),(∞+-∞ B . xy e = )0,(-∞C . x y ln = ),0(∞+D . x y sin = ),0(π（２）设)12)(1()(+-='x x x f ，则在区间)1,21(内（ B ）． A . )(x f y =单调增加，曲线)(x f y =为凹的 B. )(x f y = 单调减少，曲线)(x f y =为凹的 C. )(x f y =单调减少，曲线)(x f y =为凸的 Ｄ．)(x f y =单调增加，曲线)(x f y =为凸的（３）)(x f 在),(+∞-∞内可导, 且21,x x ∀,当 21x x >时, )()(21x f x f >,则( D ) A. 任意0)(,>'x f x B. 任意0)(,≤-'x f xC. )(x f -单调增D. )(x f --单调增（４）设函数)(x f 在]1,0[上二阶导数大于0, 则下列关系式成立的是（ B ） A. )0()1()0()1(f f f f ->'>' B. )0()0()1()1(f f f f '>->' C. )0()1()0()1(f f f f '>'>- D. )0()1()0()1(f f f f '>->' 2． 求下列函数的单调区间 （１）1--=x e y x．解：1-='x e y ，当0>x 时，0>'y ,所以函数在区间),0[+∞为单调增加； 当0<x 时，0<'y ，所以函数在区间]0,(-∞为单调减少．（２）(2y x =-解：)1(31031-='-x x y ， 当1>x ，或0<x 时，0>'y ,所以函数在区间),1[]0,(+∞-∞ 为单调增加； 当01x <<时，0<'y ，所以函数在区间]1,0[为单调减少．（３）)1ln(2x x y ++=解： 011111222>+=++++='xxx x x y ，故函数在),(+∞-∞单调增加．3． 证明下列不等式（１）证明： 对任意实数a 和b , 成立不等式||1||||1||||1||b b a a b a b a +++≤+++．证明：令xxx f +=1)(，则0)1(1)(2>+='x x f ， )(x f 在) , 0 [∞+内单调增加. 于是, 由 |||| ||b a b a +≤+, 就有 ) |||| () || (b a f b a f +≤+, 即（２）当1>x 时, 1)1(2ln +->x x x ．证明：设)1(2ln )1()(--+=x x x x f ， 11ln )('-+=xx x f ，由于当1x >时，211()0f x x x''=->, 因此)(x f '在),1[+∞单调递增, 当 1x >时, 0)1()(='>'f x f , 故)(x f 在),1[+∞单调递增, 当 1>x 时, 有0)1()(=>f x f .故当1>x 时,0)1(2ln )1()(>--+=x x x x f ,因此1)1(2ln +->x x x ．（３）当 0>x 时，6sin 3x x x ->．证明：设6sin )(3x x x x f +-=, 021cos )(2=+-='x x x f ，当0>x ，()sin 0f x x x ''=->，所以)(x f '在),0[+∞单调递增, 当 0>x 时, 0)0()(='>'f x f , 故)(x f 在),0[+∞单调递增, 从而当 0>x 时, 有0)0()(=>f x f . 因此当 0>x 时，6sin 3x x x ->．4． 讨论方程k x x =-sin 2π(其中k 为常数)在)2,0(π内有几个实根． 解：设()sin ,2x x x k πϕ=-- 则()x ϕ在]2,0[π连续, 且k k -=-=)2(,)0(πϕϕ， 由()1cos 02x x πϕ'=-=，得2arccos x π=为)2,0(π内的唯一驻点．()x ϕ在2[0,arccos ]π上单调减少，在2[arccos ,]2ππ上单调增加．故k ---=242arccos )2(arccos 2πππϕ为极小值，因此)(x ϕ在]2,0[π的最大值是k -,最小值是k ---242arccos 2ππ．（１） 当,0≥k 或242arccos 2--<ππk 时,方程在)2,0(π内无实根；（２） 当0242arccos 2<<--k ππ时,有两个实根；（３） 当242arccos2--=ππk 时，有唯一实根．5． 试确定曲线d cx bx ax y +++=23中的a 、b 、c 、d ，使得2-=x 处曲线有水平切线，)10,1(-为拐点，且点)44,2(-在曲线上．解： c bx ax y ++='232,b ax y 26+=''，所以 解得： 16,24,3,1=-=-==d c b a ．6．求下列函数图形的拐点及凹或凸的区间（１）12-+=x xx y 解： 222)1(11-+-='x x y , 323)1(62-+=''x xx y , 令0=''y ,得0=x ，当1x =±时y ''不存在．当01<<-x 或1>x 时, 0>''y ,当1-<x 或10<<x 时, 0<''y ．故曲线12-+=x xx y 在)1,0()1,( --∞上是凸的, 在区间和),1()0,1(+∞- 上是凹的，曲线的拐点为)0,0(．（２）32)52(x x y -=拐点及凹或凸的区间解：y '=，y ''=． 当0=x 时，y y ''',不存在；当21-=x 时，0=''y ．故曲线在)21,(--∞上是凸的, 在),21(+∞-上是凹的，)23,21(3--是曲线的拐点,7．利用凹凸性证明: 当π<<x 0时, πx x >2sin 证明：令πx x x f -=2sin )(, 则π12cos 21)(-='x x f , 2sin 41)(xx f -=''．当π<<x 0时, 0)(<''x f , 故函数πxx x f -=2sin )(的图形在),0(π上是凸的, 从而曲线)(x f y =在线段AB （其中)(,()),0(,0(ππf B f A ）的上方，又0)()0(==πf f , 因此0)(>x f ,即πx x >2sin ．§3.5 函数的极值与最大值最小值1． 填空题（１）函数xx y 2=取极小值的点是1ln 2x =-． （２） 函数31232)1()(--=x x x f 在区间]2,0[上的最大值为322)21(=f ，最小值为(0)1f =- ．2．选择题（１） 设)(x f 在),(+∞-∞内有二阶导数，0)(0='x f ，问)(x f 还要满足以下哪个条件，则)(0x f 必是)(x f 的最大值？（ C ）A ． 0x x =是)(x f 的唯一驻点B ． 0x x =是)(x f 的极大值点C ． )(x f ''在),(+∞-∞内恒为负D ． )(x f ''不为零 （２） 已知)(x f 对任意)(x f y =满足xex f x x f x --='+''1)]([3)(2，若00()0 (0)f x x '=≠，则（ B ）A. )(0x f 为)(x f 的极大值B. )(0x f 为)(x f 的极小值C.))(,00x f x （为拐点 D. )(0x f 不是极值点, ))(,00x f x （不是拐点 （３）若)(x f 在0x 至少二阶可导, 且1)()()(lim2000-=--→x x x f x f x x ,则函数)(x f 在0x 处( Ａ ) A ． 取得极大值 B ． 取得极小值 C ． 无极值 D ． 不一定有极值 3． 求下列函数的极值 （１） ()3/223x x x f -=． 解：由13()10f x x-'=-=，得1=x ．4''31(),(1)03f x x f -''=>，所以函数在1=x 点取得极小值．（２）xx x f 1)(=．解：定义域为),0(+∞，11ln 21, (1ln )x xxy ey xx x'==-， 令0y '=得驻点x e =，当(0,)x e ∈时，0y '>，当(,)x e ∈+∞时，0y '<．因此ee e y 1)(=为极大值．4． 求14123223+-+=x x x y 的在]4,3[-上的最大值与最小值． 解：(3)23, (4)132y y -==．由266120y x x '=+-=，得1=x , 2-=x ．而34)2(,7)1(=-=y y , 所以最大值为132，最小值为7．5． 在半径为R 的球内作一个内接圆锥体，问此圆锥体的高、底半径为何值时，其体积V 最大． 解：设圆锥体的高为h , 底半径为r ,故圆锥体的体积为h r V 2 31π=， 由于222)(R r R h =+-，因此)2( 31)(2h Rh h h V -=π )20(R h <<， 由0)34( 31)(2=-='h Rh h V π，得34R h =，此时R r 322=． 由于内接锥体体积的最大值一定存在,且在)2,0(R 的内部取得. 现在0)(='h V 在)2,0(R 内只有一个根,故当34Rh =, R r 322=时, 内接锥体体积的最大． 6. 工厂C 与铁路线的垂直距离AC 为20km , A 点到火车站B 的距离为100km . 欲修一条从工厂到铁路的公路CD , 已知铁路与公路每公里运费之比为3:5，为了使火车站B 与工厂C 间的运费最省, 问D 点应选在何处？ 解: 设AD x =, B 与C 间的运费为y , 则)100(340052x k x k y -++= （1000≤≤x ）， 其中k 是某一正数． 由 0)34005(2=-+='xx k y , 得15=x .由于k y x 400|0==, k y x 380|15==, 2100511500|+==x y , 其中以k y x 380|15==为最小, 因此当AD =15=x km 时, 总运费为最省．7． 宽为b 的运河垂直地流向宽为a 的运河. 设河岸是直的,问木料从一条运河流到另一条运河去,其长度最长为多少?解： 问题转化为求过点C 的线段AB 的最大值. 设木料的长度为l , y CB x AC ==,，木料与河岸的夹角为t ，则l y x =+，且t by t a x sin ,cos ==, t b t a l sin cos += )2,0(π∈t ．则ttb t t a l 22sin cos cos sin -='， 由0='l 得3tan abt =, 此时233232)(b a l +=， 故木料最长为233232)(b a l +=．§3.6 函数图形的描绘１．求23)1(+=x x y 的渐近线. 解：由 -∞=+-→231)1(limx x x ，所以1x =为曲线)(x f y =的铅直渐近线． 因为 2)1(lim )(lim ,1)1(limlim 2322-=-+=-=+=∞→∞→∞→∞→x x x x y x x x y x x x x 所以2-=x y 为曲线)(x f y =的斜渐近线．2．作函数23)1(22--=x x y 的图形。

第三章 消费者行为理论2. 假设某消费者的均衡如图3—1(即教材中第96页的图3—22)所示。

其中，横轴OX 1和纵轴OX 2分别表示商品1和商品2的数量，线段AB 为消费者的预算线，曲线图3—1 某消费者的均衡U 为消费者的无差异曲线，E 点为效用最大化的均衡点。

已知商品1的价格P 1＝2元。

(1)求消费者的收入；(2)求商品2的价格P 2；(3)写出预算线方程；(4)求预算线的斜率；(5)求E 点的MRS 12的值。

解答：(1)图中的横截距表示消费者的收入全部购买商品1的数量为30单位，且已知P 1＝2元，所以，消费者的收入M ＝2元×30＝60元。

(2)图中的纵截距表示消费者的收入全部购买商品2的数量为20单位，且由(1)已知收入M ＝60元，所以，商品2的价格P 2＝M 20＝6020＝3元。

(3)由于预算线方程的一般形式为 P 1X 1＋P 2X 2＝M 所以，由(1)、(2)可将预算线方程具体写为：2X 1＋3X 2＝60。

(4)将(3)中的预算线方程进一步整理为X 2＝－23X 1＋20。

很清楚，预算线的斜率为－23。

(5)在消费者效用最大化的均衡点E 上，有MRS 12＝P 1P 2，即无差异曲线斜率的绝对值即MRS 等于预算线斜率的绝对值P 1P 2。

因此，MRS 12＝P 1P 2＝23。

5. 已知某消费者每年用于商品1和商品2的收入为540元，两商品的价格分别为P 1＝20元和P 2＝30元，该消费者的效用函数为U ＝3X 1X 22，该消费者每年购买这两种商品的数量应各是多少？每年从中获得的总效用是多少？解答：根据消费者的效用最大化的均衡条件MU 1MU 2＝P 1P 2其中，由U ＝3X 1X 22可得 MU 1＝d TU d X 1＝3X 22； MU 2＝d TU d X 2＝6X 1X 2 于是，有 3X 226X 1X 2＝2030 整理得 X 2＝43X 1 (1) 将式(1)代入预算约束条件20X 1＋30X 2＝540，得20X 1＋30·43X 1＝540 解得 X 1＝9 将X 1＝9代入式(1)得 X 2＝12因此，该消费者每年购买这两种商品的数量应该为X 1＝9 ；X 2＝12。

第三章习题集答案本章习题一、名词解释均衡产出或收入消费函数边际消费倾向平均消费倾向储蓄函数边际储蓄倾向平均储蓄倾向乘数投资乘数政府支出乘数税收乘数政府转移支出乘数平衡预算乘数对外贸易乘数相对收入消费理论生命周期消费理论永久收入消费理论二、判断题1．投资乘数起作用的关键因素是有确定的边际消费倾向值。

2．在一个没有政府的封闭经济中，经济均衡时一定是投资等于储蓄；在一个有政府的开放经济中情况仍是这样。

3．在均衡产出的情况下，企业的非意愿存货投资必然为零。

4．在045线上，消费支出和收入并不总是相等。

5．在经济学上，家庭储蓄是指可支配收入中未用于消费而放在银行的存款。

6．一般来说，高收入家庭消费倾向越高，低收入家庭消费倾向越低。

三、选择题1．收入超过支出，公司将减少生产，因为非计划存货量为( )A. 正；B. 负；C. 零；D.不确定。

2．消费函数为C=100+0.8（Y-T），政府支出乘数是( )A. 0.8B. 1.2C. 4D. 5。

3．消费函数的斜率取决于( )A. 边际消费倾向；B. 与可支配收入无关的消费总量；C. 平均消费倾向；D. 由于收入变化引起的投资量。

4．下列四种情况中，投资乘数最大的是( )A. 边际消费倾向为0.4 ； B . 边际储蓄倾向为0.1 ；C. 边际消费倾向为0.6 ；D. 边际储蓄倾向为0.35．在四部门经济中，其他条件不变，投资、储蓄、政府购买、税收、进口同时增加，则均衡收入( )A. 保持不变； B . 趋于增加； C. 趋于减少； D. 变化趋势不能确定。

6．在凯恩斯45°线图中，消费函数与45°线相交点的产出水平表示( )A. 净投资支出I大于零时的GNP水平；B. 均衡的GNP水平；C. 消费C和投资I相等；D. 没有任何意义，除非投资I恰好为零。

7．如果由于计划投资支出的减少而导致原来国民收入Y的均衡水平改变，可以预期( )A. Y将下降，但储蓄S不变；B. Y将下降，但储蓄S将上升；C. Y和储蓄S都将下降；D. Y不变，但储蓄S下降8．如果边际消费倾向为常数，那么消费函数将是( )A. 一条不通过原点的直线；B. 一条相对于横轴向上凸的曲线；C. 一条相对于横轴向下凹的曲线；D. 一条通过原点与横轴成45°的直线；E. 以上说法均不准确。