有向无环图及其应用

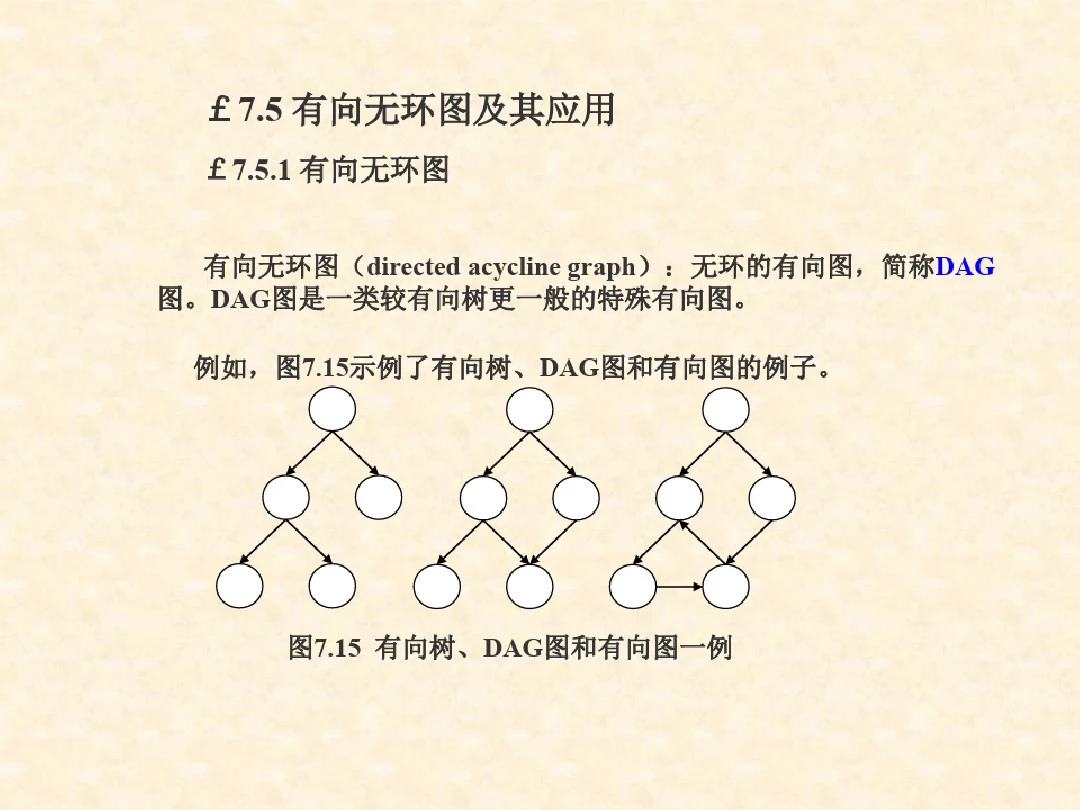
有向无环图及其应用

第七章图 7.1图的基本概念 7.2图的存储 7.3图的遍历 7.4图的连通性问题 7.5有向无环图及其应用7.6最短路径

7.1图的基本概念 ?图(graph)： –一个顶点（vertex）的有穷集V(G)和一个弧(arc)的集合E(G)组成。记做：G＝(V，E)。V是数据结构中的数据元素，E是集合上的关系 ?弧(arc)、弧头（终点）、弧尾（起点）：–表从v到w的弧 ?有向图(digraph)、无向图(undigraph)、边:–(v,w)代表和https://www.doczj.com/doc/77651755.html,/ ?有向网、无向网： –带权的有向图和无向图 ?完全图（complete graph）：边e为n(n-1)/2 ?有向完全图：弧e为n(n-1)

?稀疏图（sparse graph）：有向图enlogn ?子图（subgraph）: –G=(V,E),G’=(V’,E’),如V’≦V且E≦E’,则称G’是G的子图 ?度(degree)、出度(OutDegree)、入度(Indegree): –称u邻接到v，或v邻接自u。邻接到某顶点的弧的数目称该顶点的入度ID(v)；邻接自某顶点的弧的数目称该顶点的出度OD(u)；某顶点的入度、出度之和为该顶点的度TD(v) ?路径和回路： –有向路径/无向路径，路径长度、回路或环 ?连通图和连通分量： –连通图(无向)，强连通图（有向），连通分量 ?生成树、生成森林： –连通图的生成树是极小连通子图。 –有向图的生成森林由若干有向树组成，含有图中全部顶点和部分足以构成若干颗不相交有向树的狐。

判断一个图是否有环 无向图 有向图

一、无向图： 方法1： ?如果存在回路，则必存在一个子图，是一个环路。环路中所有顶点的 度>=2。 ? n算法： 第一步：删除所有度<=1的顶点及相关的边，并将另外与这些边相关的其它顶点的度减一。 第二步：将度数变为1的顶点排入队列，并从该队列中取出一个顶点重复步骤一。 如果最后还有未删除顶点，则存在环，否则没有环。 ? n算法分析： 由于有m条边，n个顶点。 i)如果m>=n，则根据图论知识可直接判断存在环路。（证明：如果没有环路，则该图必然是k棵树k>=1。根据树的性质，边的数目m = n-k。k>=1，所以：m=V，这样算法的复杂度也只能为O(V + E)。其次，在每次循环时，删除度为1的顶点，那么就必须将与这个顶点相连的点的度减一，并且执行delete node from list[list[node]]，这里查找的复杂度为list[list[node]]的长度，只有这样才能保证当degree[i]=1时，list[i]里面只有一个点。这样最差的复杂度就为O(EV)了。 方法2： DFS搜索图，图中的边只可能是树边或反向边，一旦发现反向边，则表明存在环。该算法的复杂度为O(V)。 方法3： 摘自： https://www.doczj.com/doc/77651755.html,/lzrzhao/archive/2008/03/13/2175787.aspx PS：此方法于2011-6-12补充 假定：图顶点个数为M，边条数为E