
上机操作8:曲线估计的spss分析
习题:落叶松林单位面积的蓄积量(V)和胸高断面积(D)的测定数据如下表,试建立V与D的经验回归方程,并且检验回归的显著性。
解: 1.定义变量,输入数据:在变量视图中写入变量名称“蓄积量V”和“胸高断面积D”,宽度均为8,小数均为0。并在数据视图依次输入变量。
2.分析过程:
(1)正态分布检验:
工具栏“图形”——“P-P图”,在“变量”中放入“蓄积量”,“检验分布”为“正态”,“确定”。
(2)相关性检验:
a.工具栏“分析”——“相关”——“双变量”。
b.在“变量”中放入“灌水”、“施肥”“生物量”。
c.点击“双侧检验”,在“相关系数”中点击“Pearson”,点击“标记显著性相关”。
d.“确定”。
(3)回归方程:
a.工具栏“分析”——“回归”——“曲线估计”。
b.在“因变量”中放入“蓄积量V”。
c.在“自变量”中放入“胸高断面积D”。点击“在等式中包含常量”和“根据模型绘图”。
d.在“模型”中点击除“线性”之外的10个模型,“上线”设定为122。
e.单击“确定”。
3.生成图表,输出结果分析:
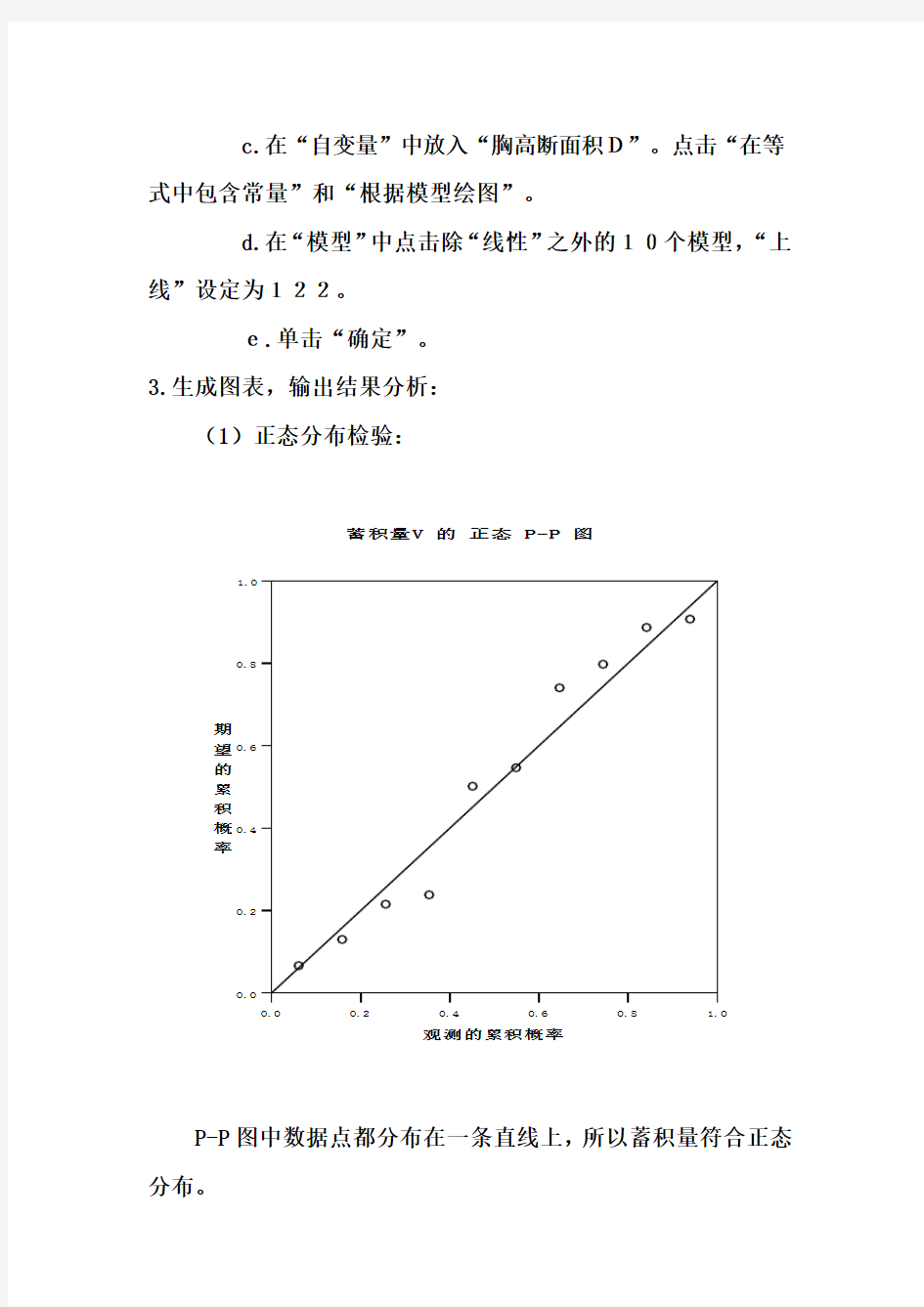
(1)正态分布检验:
P-P图中数据点都分布在一条直线上,所以蓄积量符合正态分布。
(2)相关性检验:
表1-1
由表1-1可知,pVD<0.01,所以“蓄积量V”和“胸高断面积D”之间有极显著的相关性。
(3)回归方程:
MODEL: MOD_3.
_
Independent: 胸高断面积D
Upper
Dependent Mth Rsq d.f. F Sigf bound b0 b1 b2 b3
蓄积量V LOG .945 8 137.41 .000 -77.683 78.1523
蓄积量V INV .909 8 80.37 .000 159.789 -569.98
蓄积量V QUA .951 7 67.53 .000 -15.578 14.5084 -.2782
9 蓄积量V CUB .951 7 67.82 .000 -10.586 12.4064 -.0116
蓄积量V COM .929 8 105.26 .000 29.1749 1.1292
蓄积量V POW .956 8 171.97 .000 10.4228 .9851
蓄积量V S .950 8 153.32 .000 5.3528 -7.3037
蓄积量V GRO .929 8 105.26 .000 3.3733 .1215
蓄积量V EXP .929 8 105.26 .000 29.1749 .1215
蓄积量V LGS .782 8 28.77 .001 122.00 .2589 .5688
Notes:
9 Tolerance limits reached; some dependent variables were not entered.
表1-2
表1-3
由表1-2和表1-3可知:
蓄积量和胸高断面积的对数函数方程为V=-77.683+78.1523lnD,R2=0.945,Sigf<0.01。
蓄积量和胸高断面积的逆函数方程为V=159.789-569.98/D,R2=0.909,Sigf<0.01。
蓄积量和胸高断面积的二次函数方程为V=-15.578+14.5084D-0.2782D2,R2=0.951,Sigf<0.01。
蓄积量和胸高断面积的三次函数方程为
V=-10.586+12.4064D-0.0116D3,R2=0.951,Sigf<0.01。
蓄积量和胸高断面积的幂函数方程为V=10.4228D0.9851,R2=0.956,Sigf<0.01。
蓄积量和胸高断面积的复合函数方程为V=29.1749*1.1292D,R2=0.929,Sigf<0.01。
蓄积量和胸高断面积的S曲线函数方程为V=e5.3528-7.3037/D,R2=0.950,Sigf<0.01。
蓄积量和胸高断面积的Logistic函数方程为V=1/(1/122+0.2589*0.5688D),R2=0.782,Sigf<0.01。
蓄积量和胸高断面积的增长函数方程为V=e3.3733+0.1215D,R2=0.929,Sigf<0.01。
蓄积量和胸高断面积的指数函数方程为V=29.1749e0.1215D,R2=0.929,Sigf<0.01。
回归方程的显著性都比较高,相关系数最大的是幂函数方程。
《统计分析软件》试(题)卷 班级xxx班xxx 学号xxx 说明:1.本试卷分析结果写在每个题目下面(即所留空白处); 2.考试时间为100分钟; 3.每个试题20分。 一、(20分)已经给出某个班的学生基本情况及其学习成绩的两个SPSS数据文件,学生成绩一.sav;学生成绩二.sav。要求: (1)将所给的两个SPSS数据文件“学生成绩一.sav”与“学生成绩二.sav”合并,并保存为“成绩.sav.” (2)对所建立的数据文件“成绩.sav”进行以下处理: 1)按照性别求出男、女数学成绩的各种统计量(包括平均成绩、标准差等)。 2)计算每个学生的总成绩、并按照总成绩的大小进行排序 3)把数学成绩分成优、良、中三个等级,规则为优(X≥85),良(75≤X≤84),中(X≤74),并对优良中的人数进行统计。
分析: (2) 描述统计量 性别N 极小值极大值均值标准差 男数学 4 77.00 85.00 82.2500 3.77492 有效的N (列表状态) 4 女数学16 67.00 90.00 78.5000 7.09930 有效的N (列表状态)16
注:成绩优良表示栏位sxcj 优为1 良为2 中为3 由表统计得,成绩为优的同学有4人,占总人数的20%;良的同学有12人,占总人数的60%;中的同学有4人,占总人数的40%。 二、(20分)为了解笔记本电脑的市场情况,针对笔记本电脑的3种品牌,进行了满意度调查,随机访问了30位消费者,让他们选出自己满意的品牌,调查结果见下表,其中变量“职业”的取值中,1表示文秘人员,2表示管理人员,3表示工程师,4表示其他人;3个品牌变量的取值中,1表示选择,0表示未选数据见Excel 数据文件“调查.exe”。根据所给数据完成以下问题 (1)将所给数据的Excel文件导入到SPSS中,要求SPSS数据文件写出数据结构(包括变量名,变量类型,变量值标签等)命,并保存为:“调查. Sav”。 (2)试利用多选项分析,利用频数分析来分析消费者对不同品牌电脑的满意度状况;分析不同职业消费者对笔记本品牌满意度状况。
曲线拟合与回归分析 1、有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下: (1)说明两变量之间的相关方向; (2)建立直线回归方程; (3)计算估计标准误差; (4)估计生产性固定资产(自变量)为1100万元时的总资产(因变量)的可能值。 解:由表格易知:工业总产值是随着生产性固定资产价值的增长而增长的,而知之间存在正向相关性。 用spss回归有: (2)、可知:若用y表示工业总产值(万元),用x表示生产性固定资产,二者可用如下的表达式近似表示: =x .0+ y . 567 395 896
(3)、用spss回归知标准误差为80.216(万元)。 (4)、当固定资产为1100时,总产值可能是(0.896*1100+395.567-80.216~0.896*1100+395.567+80.216)即(1301.0~146.4)这个范围内的某个值。 另外,用MATLAP也可以得到相同的结果: 程序如下所示: function [b,bint,r,rint,stats] = regression1 x = [318 910 200 409 415 502 314 1210 1022 1225]; y = [524 1019 638 815 913 928 605 1516 1219 1624]; X = [ones(size(x))', x']; [b,bint,r,rint,stats] = regress(y',X,0.05); display(b); display(stats); x1 = [300:10:1250]; y1 = b(1) + b(2)*x1; figure;plot(x,y,'ro',x1,y1,'g-'); industry = ones(6,1); construction = ones(6,1); industry(1) =1022; construction(1) = 1219; for i = 1:5 industry(i+1) =industry(i) * 1.045; construction(i+1) = b(1) + b(2)* construction(i+1); end display(industry); display( construction); end 运行结果如下所示:b = 395.5670 0.8958 stats = 1.0e+004 * 0.0001 0.0071 0.0000 1.6035 industry = 1.0e+003 * 1.0220 1.0680 1.1160 1.1663 1.2188 1.2736
《统计分析软件》试(题)卷 班级 xxx班姓名 xxx 学号 xxx 说明:1.本试卷分析结果写在每个题目下面(即所留空白处); 2.考试时间为100分钟; 3.每个试题20分。 一、(20分)已经给出某个班的学生基本情况及其学习成绩的两个SPSS数据文件,学生成绩一.sav;学生成绩二.sav。要求: (1)将所给的两个SPSS数据文件“学生成绩一.sav”与“学生成绩二.sav”合并,并保存为“成绩.sav.” (2)对所建立的数据文件“成绩.sav”进行以下处理: 1)按照性别求出男、女数学成绩的各种统计量(包括平均成绩、标准差等)。 2)计算每个学生的总成绩、并按照总成绩的大小进行排序 3)把数学成绩分成优、良、中三个等级,规则为优(X≥85),良(75≤X ≤84),中(X≤74),并对优良中的人数进行统计。
分析: 描述统计量 性别N极小值极大值均值标准差 男数学477.0085.0082.2500 3.77492有效的 N (列表状态)4 女数学1667.0090.0078.50007.09930有效的 N (列表状态)16
注:成绩优良表示栏位sxcj 优为1 良为2 中为3 由表统计得,成绩为优的同学有4人,占总人数的20%;良的同学有12人,占总人数的60%;中的同学有4人,占总人数的40%。 二、(20分)为了解笔记本电脑的市场情况,针对笔记本电脑的3种品牌,进行了满意度调查,随机访问了30位消费者,让他们选出自己满意的品牌,调查结果见下表,其中变量“职业”的取值中,1表示文秘人员,2表示管理人员,3表示工程师,4表示其他人;3个品牌变量的取值中,1表示选择,0表示未选数据见Excel数据文件“调查.exe”。根据所给数据完成以下问题 (1)将所给数据的Excel文件导入到SPSS中,要求SPSS数据文件写出数据结构(包括变量名,变量类型,变量值标签等)命,并保存为:“调查. Sav”。 (2)试利用多选项分析,利用频数分析来分析消费者对不同品牌电脑的满意度状况;分析不同职业消费者对笔记本品牌满意度状况。 分析:
SPSS 10.0高级教程十二:多元线性回归与曲线拟合 2009年,国内生物医药的突破之年。不仅有干细胞发现的新突破,还有转基因作物政策的新举措。 回归分析是处理两个及两个以上变量间线性依存关系的统计方法。在医学领域中,此类问题很普遍,如人头发中某种金属元素的含量与血液中该元素的含量有关系,人的体表面积与身高、体重有关系;等等。回归分析就是用于说明这种依存变化的数学关系。 §10.1Linear过程 10.1.1 简单操作入门 调用此过程可完成二元或多元的线性回归分析。在多元线性回归分析中,用户还可根据需要,选用不同筛选自变量的方法(如:逐步法、向前法、向后法,等)。 例10.1:请分析在数据集Fat surfactant.sav中变量fat对变量spovl的大小有无影响? 显然,在这里spovl是连续性变量,而fat是分类变量,我们可用用单因素方差分析来解决这个问题。但此处我们要采用和方差分析等价的分析方法--回归分析来解决它。 回归分析和方差分析都可以被归入广义线性模型中,因此他们在模型的定义、计算方法等许多方面都非常近似,下面大家很快就会看到。 这里spovl是模型中的因变量,根据回归模型的要求,它必须是正态分布的变量才可以,我们可以用直方图来大致看一下,可以看到基本服从正态,因此不再检验其正态性,继续往下做。 10.1.1.1 界面详解 在菜单中选择Regression==>liner,系统弹出线性回归对话框如下:
除了大家熟悉的内容以外,里面还出现了一些特色菜,让我们来一一品尝。 【Dependent框】 用于选入回归分析的应变量。 【Block按钮组】 由Previous和Next两个按钮组成,用于将下面Independent框中选入的自变量分组。由于多元回归分析中自变量的选入方式有前进、后退、逐步等方法,如果对不同的自变量选入的方法不同,则用该按钮组将自变量分组选入即可。下面的例子会讲解其用法。 【Independent框】 用于选入回归分析的自变量。 【Method下拉列表】 用于选择对自变量的选入方法,有Enter(强行进入法)、Stepwise(逐步法)、Remove(强制剔除法)、Backward(向后法)、Forward(向前法)五种。该选项对当前Independent框中的所有变量均有效。
课程名称:《SPSS分析方法与应用》 课程号: 2007422 一、单项选择题(共112小题) 1、试题编号:1000110,答案:RetEncryption(D)。 SPSS的安装类型有() A. 典型安装 B.压缩安装 C.用户自定义安装 D.以上都是 2、试题编号:1000310,答案:RetEncryption(D)。 数据编辑窗口的主要功能有() A.定义SPSS数据的结构 B.录入编辑和管理待分析的数据 C.结果输出 和B 3、试题编号:1000410,答案:RetEncryption(A)。 ()文件格式是SPSS独有的,一般无法通过Word,Excel等其他软件打开。 4、试题编号:1000510,答案:RetEncryption(D)。 ()是SPSS为用户提供的基本运行方式。 A.完全窗口菜单方式 B.程序运行方式 C.混合运行方式 D.以上都是 5、试题编号:1000810,答案:RetEncryption(D)。 ()是SPSS中有可用的基本数据类型 A.数值型 B.字符型 C.日期型 D.以上都是 6、试题编号:1000910,答案:RetEncryption(D)。 spss数据文件的扩展名是( ) A..htm B..xls C..dat D..sav 7、试题编号:1001010,答案:RetEncryption(B)。 数据编辑窗口中的一行称为一个() A.变量 B.个案 C.属性 D.元组 8、试题编号:1001110,答案:RetEncryption(C)。
变量的起名规则一般:变量名的字符个数不多于() A. 6 B. 7 C. 8 D. 9 9、试题编号:1001210,答案:RetEncryption(A)。 统计学依据数据的计量尺度将数据划分为三大类,它不包括() A. 定值型数据 B.定距型数据 C.定序型数据 D.定类型数据 10、试题编号:1001310,答案:RetEncryption(A)。 在横向合并数据文件时,两个数据文件都必须事先按关键变量值() A.升序排序 B.降序排序 C.不排序 D.可升可降 11、试题编号:1001810,答案:RetEncryption(A)。 SPSS算术表达式中,字符型()应该用引号引起来。 A 常量 B变量 C算术运算符 D函数 12、试题编号:1001910,答案:RetEncryption(A)。 复合条件表达式又称逻辑表达式,在逻辑运算中,下列()运算最优先。 B AND C OR D都不是 13、试题编号:1002010,答案:RetEncryption(A)。 数据选取的方法中,()是按符合条件的数据进行选取。 A 按指定条件选取 B 随即选取 C选取某一区域内样本 D过滤变量选取 14、试题编号:1002110,答案:RetEncryption(B)。 通过()可以达到将数据编辑窗口中的技术数据还原为原始数据的目的。 A 数据转置 B 加权处理 C 数据才分 D以上都是 15、试题编号:1002210,答案:RetEncryption(A)。 SPSS的()就是将数据编辑窗口中数据的行列互换 A 数据转置 B 加权处理 C 数据才分 D以上不都是 16、试题编号:1002310,答案:RetEncryption(B)。 SPSS软件是20世纪60年代末,由()大学的三位研究生最早研制开发的。 A、哈佛大学 B、斯坦福大学 C、波士顿大学 D、剑桥大学 17、试题编号:1002710,答案:RetEncryption(D)。 SPSS中进行参数检验应选择()主窗口菜单。 A、视图 B、编辑 C、文件 D、分析 18、试题编号:1002810,答案:RetEncryption(A)。 SPSS中进行输出结果的保存应选择()主窗口菜单。 A、视图 B、编辑 C、文件 D、分析 19、试题编号:1002910,答案:RetEncryption(C)。 SPSS中进行数据的排序应选择()主窗口菜单。 A、视图 B、编辑 C、数据 D、分析
利用S P S S拟合非线性回归模型
利用SPSS拟合非线性回归模型 ——以S型曲线为例 1.原始数据 下表给出了某地区1971—2000年的人口数据(表1)。试用SPSS软件对该地区的人口变化进行曲线拟合,并对今后10年的人口发展情况进行预测。 表1 某地区人口变化数据 年份时间变量t=年份-1970 人口y/人 1971133 815 1972233 981 1973334 004 1974434 165 1975534 212 1976634 327 1977734 344 1978834 458 1979934 498 19801034 476 19811134 483 19821234 488 19831334 513 19841434 497 19851534 511 19861634 520 19871734 507 19881834 509 19891934 521 19902034 513 19912134 515 19922234 517 19932334 519 19942434 519 19952534 521 19962634 521 19972734 523
1998 28 34 525 1999 29 34 525 2000 30 34 527 根据上表中的数据,做出散点图,见图1。 , 33700 33800 3390034000341003420034300 3440034500346001970197219741976197819801982198419861988199019921994199619982000 年份 人口 图1 某地区人口随时间变化的散点图 从图1可以看出,人口随时间的变化呈非线性过程,而且存在一个与横坐标轴平行的渐近线,近似S 曲线。 下面,我们用SPSS 软件进行非线性回归分析拟合计算。 2.用SPSS 进行回归分析拟合计算 在SPSS 中可以直接进行非线性拟合,步骤如下(假定已经进行了数据输入,关于数据输入方法见SPSS 相关基础 教程):
SPSS在教育研究中的应用某大学学生对本校的满意度调查 学院:教育学院 专业:课程与教学论 学号:201411000156 姓名:李平 2014年12月13日
目录 一、研究问题的提出 (3) 二、研究内容与方法 (3) (一) 研究内容 (3) (二) 研究方法 (3) 三、调查对象及人数 (4) 四、问卷分析 (5) (一)回收情况 (5) (二)信度分析 (5) 五、数据统计与分析 (6) (一)数据输入 (6) (二)数据分析 (7) 1.描述统计 (7) (1)多选题描述统计 (7) (2)单选题描述统计 (9) 2.推断统计 (12) (1)独立样本T检验 (12) (2)单一样本T检验 (15) (3)单因素方差分析 (17) (4) X2检验 (21) 3.相关分析 (22) (1)变量间相关分析 (22) (2)维度间相关分析 (23) 六、结论 (27) 七、附录 (28)
一、研究问题的提出 学生的学校生活和成长密切相关。我们通过对他们的大学生活满意度的调查结果向有关部门提出建议,并希望能引起学校对这一系列问题的关注,最终希望大学生对其大学的满意度有所提升,大学生是一个庞大的群体,特别是近几年,随着高校的扩招,我国越来越多人能够上大学。上大学是很多人的梦想,他们都憧憬着大学校园的生活,然而当他们进了大学后才发现大学生活并非所想的美好,取而代之的却是对校园生活的不满,大学生是十分宝贵的人才资源,他们对校园生活的体验和感受,与他们的更好的学习。 二、研究内容与方法 (一)研究内容 了解学生对于学校的师资水平、环境、日常管理等各方面的满意度。 (二)研究方法 1.问卷编制 本研究采用自编问卷,问卷共由两部分组成:基本情况部分包括被调查者的性别、年级等,问卷主体部分包括师资水平、学校环境、日常管理三大维度,细分为12个三级指标(见表2-1),问卷采用五点制计分法,即“非常满意”、“满意”、“一般”、“不满意”、“非常不满意”,分别赋值5分、4分、3分、2分、1分。 表2-1 某大学学生对本校的满意度测评指标体系 一 级指标 二级指标(潜在变量)三级指标(观测变量) 对自己师资水平对教师教学方法、对教师工作态 度、对教师人品修养、对师资配备 学校的意学校环境对学习环境、对就餐环境、对居住 环境、对校园绿化环境 满度指数日常管理对专业课时安排、对收费标准、对 奖、助学金制度、对学校治安
●一。变量的赋值 1.乘方(**),例如二的三次方:2**3 2.不同规则的赋值:转换→计算变量(如果),每一个规则的赋值都要重新进行此步骤(但注意每一遍的变量名都不变,并且他都会问你要不要替换成新的变量,你选是就行了) 3.不同规则的赋值:(1)转换→重新编码为不同变量:输入变量,输出变量,要点击“变化量”才可保存输出变量→新值和旧值:值(直接选取取值)、范围(最大到最小的范围,包含端点值),点击“添加”成功保存新值和旧值→所有不同取值规则都完成后点击继续、确定,则在变量视图多出一个新变量(2)若不想包含端点值,可以采取小数的方式变换,eg. 899.9(小数位比该变量属性的小数位多一位就行了) (3)这种要先把BMI按照男女分开,然后再分组的,可以在对话框中点击“如果”选项进行设置,并且要分别对男女进行上述操作(一共做两遍)。 二。离散化 1可视离散化:转换→可视分箱,分割点:所以想生成几组,就定义几个分割点;填写第一个分割点的时候就必须填写最小值;一定要选中上端点排除。 三。排序 1.转换→自动重新编码:不分组,从头到尾排序 2.转换→个案排秩(1)多层次数据:基于A变量对B变量进行排序。(例如,基于职称对收入进行排序,就是不同职称各自组内排工资的高低)(2)设置秩1;绑定值 四。时间序列:转换→变动值 五。查找与计数:转换→对个案内的值计数(查找“基本工资800-900女职工”,生成新变量,满足这个条件的标为1,不符合这个标准的标为0,男职工标为缺失。范围:包含上限下限) ●六。数据→个案排序:把变量顺序完全按照你想要的标准排序,所有的变量顺序都会改变 七。拆分文件:要分男女进行数据统计:数据→拆分文件→比较组/按组输出,分组依据。不分男女进行数据统计:数据→拆分文件→分析所有个案 八。选择个案(例如只选择三年级的变量进行分析):数据→选择个案→如果条件满足:如果;随机个案样本;基于时间或个案范围;使用过滤变量(例如要把身高为缺失值和值为0的剔除)→输出:过滤(不符合条件的数据会画上“/”,原始数据并未删除);将选定个案复制到新数据集(形成一个新的SPSS数据文件,原始数据并未删除);删除未选定的个案(删除原始数据,不建议使用)→之后在分析的时候就只会分析三年级的变量。不想只分析三年及,记得重新做这一步。 九。加权个案:数据→加权个案(例。100分的有5人)。不想加权了,记得重新做这一步。 十。分类汇总(1)例如算不同年级的人的身高的均值、方差…(只能计算函数)(2)数据→汇总,分界变量(分类标准变量),变量摘要(计算变量),函数:选择计算变量函数,变量名称与标签:定义新生成变量的名称与标签 ●十一。长宽数据的转换 1.长数据变宽数据:索引变量消失变成score的尾缀 (1)数据→重组(重构)→个案重组为变量,标识变量,索引变量,电脑会自动帮你选出是xx xx要重构(不同疗程值不同的变量)。选完上述这些之后就一直点下一步&完成&立即重构&确定即可 (2)注意:当有多个变量需要重构时要自己决定“新变量组的顺序”。(A1A2B1B2;A1B1A2B2) 2.宽数据变长数据:score的尾缀消失变成索引变量 (1)数据→重组(重构)→变量重组为个案,个案组标识:使用选定变量,固定变量(手动选择,电脑不会自动帮你选出了),要转置的变量即值不固定的要重构的变量(手动选择,电脑不会自动帮你选出了)。选完上述这些之后就一直点击下一步&完成&立即重构数据&确定就行了 (2)当有多个变量需要重构时,这块的操作要特别注意:○1首先在“变量组数目”中选择“多个”○2然后在“选择变量”里要对于不同的“目标变量”分别定义“要转置的变量”(在本题中,即对于kidid目标变量定义一遍要转置的变量;对于age目标变量在定义一遍要转置的变量。其中,这两个要转置的变量必须是完全不同的)。但只需要定义一次“个案组标识”&“固定变量”(固定变量是相对于kidid & age都固定的那些变量;而不是说在对kidid进行转置的时候,age就是固定变量了;因此,固定变量只用定义一次且固定变量可以为空)。并且,你要特别注意,“个案组标识”里选择的变量& n个“要转置的变量”里选择的变量&“固定变量”里选择的变量都必须是完全不相同的。
《统计分析软件》试(题)卷 班级xxx班姓名xxx 学号xxx 题号一二三四五六总成绩成绩 说明:1.本试卷分析结果写在每个题目下面(即所留空白处); 2.考试时间为100分钟; 3.每个试题20分。 一、(20分)已经给出某个班的学生基本情况及其学习成绩的两个SPSS数据文件,学生成绩一.sav;学生成绩二.sav。要求: (1)将所给的两个SPSS数据文件“学生成绩一.sav”与“学生成绩二.sav”合并,并保存为“成绩.sav.” (2)对所建立的数据文件“成绩.sav”进行以下处理: 1)按照性别求出男、女数学成绩的各种统计量(包括平均成绩、标准差等)。 2)计算每个学生的总成绩、并按照总成绩的大小进行排序 3)把数学成绩分成优、良、中三个等级,规则为优(X≥85),良(75≤X ≤84),中(X≤74),并对优良中的人数进行统计。
分析: (2) 描述统计量 性别N 极小值极大值均值标准差 男数学 4 77.00 85.00 82.2500 3.77492 有效的N (列表状态) 4 女数学16 67.00 90.00 78.5000 7.09930 有效的N (列表状态)16
注:成绩优良表示栏位sxcj 优为1 良为2 中为3 由表统计得,成绩为优的同学有4人,占总人数的20%;良的同学有12人,占总人数的60%;中的同学有4人,占总人数的40%。 二、(20分)为了解笔记本电脑的市场情况,针对笔记本电脑的3种品牌,进行了满意度调查,随机访问了30位消费者,让他们选出自己满意的品牌,调查结果见下表,其中变量“职业”的取值中,1表示文秘人员,2表示管理人员,3表示工程师,4表示其他人;3个品牌变量的取值中,1表示选择,0表示未选数据见Excel数据文件“调查.exe”。根据所给数据完成以下问题 (1)将所给数据的Excel文件导入到SPSS中,要求SPSS数据文件写出数据结构(包括变量名,变量类型,变量值标签等)命,并保存为:“调查. Sav”。 (2)试利用多选项分析,利用频数分析来分析消费者对不同品牌电脑的满意度状况;分析不同职业消费者对笔记本品牌满意度状况。 分析:
上机操作8 曲线回归估计的SPSS分析 习题:落叶松林单位面积的蓄积量(V)和胸高断面积(D)的测定数据如下表, (1)定义变量:打开SPSS数据编辑器,点击“变量视图”,在名称列下输入“V”、“D”,改“类型”栏均为“数字”,“小数”栏分别保留0位和1位。 (2)输入数据:在“数据视图”模式 下,在各名称列输入相应的数据,如图所 示: 二、分析过程 分析→回归→曲线估计,将“V”添加 到“因变量”中,将“D”添加到“变量” 中,勾选模型中的“二次模型”、“复合”、 “对数”、“立方模型”、“指数”、“幂”、“”、 “Logistic”,→确定。 三、输出结果分析 曲线拟合 MODEL: MOD_1. Dependent variable.. V Method.. LOGARITH(对数曲线模型) Listwise Deletion of Missing Data Multiple R (负相关系数) .97210 R Square(决定系数) .94498 Adjusted R Square .93811 Standard Error 6.59944 Analysis of Variance(方差分析): DF(自由度) Sum of Squares Mean Square(均方) Regression(回归) 1 5984.4787 5984.4787 Residuals(残差) 8 348.4213 43.5527 F = 137.40787 Signif F = .0000 (小于0.05,具有极显著性) -------------------- Variables in the Equation (方程中的变量)-------------------- Variable B(系数) SE B Beta T Sig T(T的显著性水平) D 78.152283 6.667083 .972102 11.722 .0000(小于0.05) (Constant) -77.682919 14.110257 -5.505 .0006(小于0.05)分析可知:蓄积量(V)与胸高段面积(D)的相关性为0.97210,它们的F 检验Sig.<0.01,说明蓄积量(V)与胸高段面积(D)达到极显著水平,即蓄积量(V)与胸高段面积(D)的方程具有统计学意义。胸高段面积(D)的T检验Sig.<0.01,说明胸高段面积(D)前的系数具有统计学意义。其方程如下: V=78.152283*ln(D)-77.682919
---------------------------------------------装--------------------------------- --------- 订 -----------------------------------------线---------------------------------------- 班级 姓名 学号 - 广 东 财 经 大 学 答 题 纸(格式二) 课程 数据处理技术与SPSS 20 15 -20 16 学年第 1 学期 成绩 评阅人 评语: ========================================== (题目)关于本部学生对收费代课现象支持度的调查报告 (正文) 一、调查背景 如今,大学生逃课现象屡见不鲜,随之衍生了“收费代课”的现象。据了解,在全国近百所高校中,存在“收费代课”现象的高校居然有一半之多。当“收费代课”现象衍变成了一种行业,成为有领导、有组织、有规模、有纪律的机构,不仅仅应当引起社会的关注,更应引起校方对教育方式的深刻反思。“有偿代课”作为一种不正常的校园现象,有其存在的社会土壤,其原因有多方面,值得让人对当前大学教育深思。在“收费代课”现象蔚然成风之时,我们学校的学生们也加入了这支大队伍。对于这样的一种收费代课的行为,同学们褒贬不一,每个人都有自己的看法。然而,这种行为经常在我们的身边发生着,无疑应该引起我们的关注,并引发我们的深思,形成一定的判别能力与认知能力。
二、调查目的 我们希望通过本次调查了解广东财经大学本部学生选择收费代课的原因,以及对本专业学习、实习实践的认知程度,是否支持放弃学习去实习或者做自己的事情,是否支持收费代课。同时,我们也希望通过这份调查报告揭露出的一些情况,一方面,帮助学生更好地权衡学习与实习的利弊,更加理性地对待收费代课的行为,做出对自己正确合适的选择;另一方面,引起学校对这种收费代课现象的重视,给学校提一些建议,希望学校采取一些措施改善这种不良校风。 三、调查方法 从可行性角度出发,本次调查采用非概率随机抽样的街头拦截法,集中对象为本部大三大四的同学,以自愿形式对本部同学分发调查问卷,总共发出80份问卷,回收80份,有效问卷80份。收集问卷之后,利用spss软件进行数据整理与分析,最后把结论整理成调查报告。调查报告中采用的数据分析方法主要有:频数分析、多选项分析、交叉列联表行列变量间关系的分析、单因素方差分析等。 四、描述统计 1、对样本性别作频数分析 从上表可以看出,这次填写问卷的女生较多,占了样本的66.3%,这与我们学校男女比例不均衡有很大的关系,样本的男女比例不相等,也可以较好地接近学校的实际情况,有利于我们得到更为准确的结论。 2、对样本年级作频数分析 从上表可知,参加问卷调查的大三大四学生比例明显比较高,这与一开始我们预期相符,样本中大三大四学生所占比例较多,有利于我们得到更为有针对性的结论。
【摘要】logistic阻滞增长模型在人口预测中有着广泛应用,应用spss软件能较为简便地进行logistic曲线的拟合。文章介绍了spss拟合logistic人口预测方程的两种方法及其步骤,并通过其结果分析比较二者的优缺点。 【关键词】logistic;spss软件;拟合方法 logistic模型为荷兰数学家及生物学家verhulst.pearl在修正非密度方程时提出,其目的为研究受到生存资源制约的情况下生物种群的增长规律。在logistic模型中,有限空间内种群不能无限增长,而是存在着数量上限。由于自然资源、环境条件等因素对种群的增长起着阻滞作用,并且随着种群数量的增大,阻滞作用逐步增大,即实测增长率是一个减函数,且随着种群数量的增大而减小,当种群数量趋于上限时,种群增长亦趋于稳定。由于logistic 阻滞增长模型所需的数据少,计算简单,对中短期时间内的种群数量预测较为准确,亦常应用于人口预测方面。 一、logistic阻滞增长模型 如上文述,人口增长率为以人口数量x为自变量的函数r(x),这里r(x)为减函数。假设r(x)= r ?sx,s>0,这里r为初始值r(),即当人口无生存环境和资源限制时的固有增长率。当人口数量达到人口最大容量,将有r()=0,此时人口达到稳定状态。由线性关系r()=r-s,可得s=r/。假设x是时间t的函数x(t),从而有解变量可分离方程。 二、spss软件拟合logistic人口阻滞增长模型 通过模型方程(ⅰ)可知,logistic模型拟合的重点为参数和的确定。下采用两种spss 软件的回归拟合方法,利用1990-2010年人口调查数据(如表1)进行人口数量的预测。 (一)非线性回归(nonlinear regression)拟合 在spss(spss19.0)的变量视图中定义两变量人口数量x及年份t,在数据视图中由上而下录入人口数据(如图1所示)。 在菜单栏依次选择分析(analyze)―回归(regression)―非线性估计(nonlinear),打开非线性回归窗口。将年末总人口[x]送入因变量一栏,在模型表达式输入框中输入模型公式 a/(1 +(a / 114333 - 1)* exp(- r *(t - 1990)))(如图2)。此处以a代替人口最大容量,由于时间以1990年为初始年份,原方程中的t转为t-1990。选择“参数”项进行参数a和r初始值的设定(如图3),这里a初始值选择人数中的最大值134091(万人),r 的初始值选择1991年的人口增长率0.013,“使用上一分析的起始值”一栏选中,单击“继续”。单击“保存”项,打开对话框如图4,选中预测值和残差项,便于检验模型方程的拟合效果,选择“继续”返回非线性回归窗口,选择“确定”运行。在输出(output)窗口中,可以得到参数a的迭代计算过程、参数估计等内容。由参数估计得参数估计值,=0.0675。r2=1.000。 (二)曲线估计法 采用spss的曲线估计进行模型拟合,须先求参数。对估计的方法很多,这里采用三点法进行求取。 选择分析(analyze)―回归(regression)―曲线估计(curve estimation),打开曲线估计窗口,将年末总人口[x]和年份[t]分别送入因变量和自变量输入框,在“模型”区选中logistic,在上限一栏填入142515.5576,在“保存”对话框中选中预测值和残差,其他依照默认选择。选择“确定”。 三、对两种方法所得拟合方程的讨论 从可决系数r2来看,两种方法所得拟合方程的r2均得1,则两种方法对logistic人口预测模型的拟合性都很好。分别用两种方法所得方程对2011年和2012年的年末人口数进行
第1题:基本统计分析1 分析:本题要求随机选取80%的样本,因而需要选用随机抽样的方法,在此选择随机抽样中的近似抽样方法进行抽样。其基本操作步骤如下:数据→选择个案→随机个案样本→大约(A)80 所有个案的%。 1、基本思路: (1)由于存款金额为定距型变量,直接采用频数分析不利于对其分布形态的把握,因而采用数据分组,先对数据进行分组再编制频数分布表。此处分为少于500元,500~2000元,2000~3500元,3500~5000元,5000元以上五组。分组后进行频数分析并绘制带正态曲线的直方图。 (2)进行数据拆分,并分别计算不同年龄段储户的一次存取款金额的四分位数,并通过四分位数比较其分布上的差异。 操作步骤: (1)数据分组:【转换→重新编码为不同变量】,然后选择存取款金额到【数字变量→输出变量(V)】框中。在【名称(N)】中输入“存取款金额1”,单击【更改(H)】按钮;单击【旧值和新值】按钮进行分组区间定义。 存取款金额1 频率百分比有效百分比累积百分比 有效1.00 82 34.6 34.6 34.6 2.00 76 32.1 32.1 66.7 3.00 10 4.2 4.2 70.9 4.00 22 9.3 9.3 80.2 5.00 47 19.8 19.8 100.0 合计237 100.0 100.0 (2)【分析→描述统计→频率】;选择“存款金额分组”变量到【变量(V)】框中;单击【图标(C)】按钮,选择【直方图】和【在直方图上显示正态曲线】;选中【显示频率表格】,确定。
(3)【数据→拆分文件】,选择“年龄”变量到【分组方式】框中,选中【比较组】和【按分组变量排序文件】,确定;【分析→描述统计→频率】,选择“存款金额”到【变量】框中,单击【统计量】按钮,选择【四分位数】→继续→确定。 统计量 存(取)款金额 20岁以下 N 有效 1 缺失 0 百分位数 25 50.00 50 50.00 75 50.00 20~35岁 N 有效 131 缺失 0 百分位数 25 500.00 50 1000.00 75 5000.00 35~50岁 N 有效 73 缺失 0 百分位数 25 500.00 50 1000.00 75 4500.00 50岁以上 N 有效 32 缺失 0 百分位数 25 525.00 50 1000.00 75 2000.00 结果及结果描述: 频数分布表表明,有一半以上的人的一次存取款金额少于2000元,且有34.6%的人的存取款金额少于500元,19.8%的人的存取款金额多于5000元,下图为相应的带正态曲线的直方图。
《SPSS统计软件》课程作业 要求:数据计算题要求注明选用的统计分析模块和输出结果;并解释结果的意义。完成后将作业电子稿发送至 1. 某单位对100名女生测定血清总蛋白含量,数据如下: 计算样本均值、中位数、方差、标准差、最大值、最小值、极差、偏度和峰度,并给出均值的置信水平为95%的置信区间。 解: 描述 统计量标准误 血清总蛋白含量均值.39389 均值的 95% 置信区间下限 上限
5% 修整均值 中值 方差 标准差 极小值 极大值 范围 四分位距 偏度.054.241 峰度.037.478 样本均值为:;中位数为:;方差为:;标准差为:;最大值为:;最小值为:;极差为:;偏度为:;峰度为:;均值的置信水平为95%的置信区间为:【,】。 2. 绘出习题1所给数据的直方图、盒形图和QQ图,并判断该数据是否服从正态分布。解:
正态性检验 Kolmogorov-Smirnov a Shapiro-Wilk 统计量 df Sig. 统计量 df Sig. 血清总蛋白含量 .073 100 .200* .990 100 .671 a. Lilliefors 显著水平修正 *. 这是真实显著水平的下限。 表中显示了正态性检验结果,包括统计量、自由度及显著性水平,以K-S 方法的自由度sig.=,明显大于,故应接受原假设,认为数据服从正态分布。 3. 正常男子血小板计数均值为9 22510/L , 今测得20名男性油漆工作者的血小板计数值(单位:9 10/L )如下: 220 188 162 230 145 160 238 188 247 113
SPSS期末报告 关于员工受教育程度对其工资水平的影响 统计分析报告 课程名称:SPSS统计分析方法 姓名:汤重阳 学号:1402030108 所在专业:人力资源管理 所在班级:三班
目录 一、数据样本描述 (1) 二、要解决的问题描述 (1) 1 数据管理与软件入门部分 (1) 1.1 分类汇总 (1) 1.2 个案排秩 (1) 1.3 连续变量变分组变量 (1) 2 统计描述与统计图表部分 (1) 2.1 频数分析 (1) 2.2 描述统计分析 (1) 3 假设检验方法部分 (1) 3.1 分布类型检验 (2) 3.1.1 正态分布 (2) 3.1.2 二项分布 (2) 3.1.3 游程检验 (2) 3.2 单因素方差分析 (2) 3.3 卡方检验 (2) 3.4 相关与线性回归的分析方法 (2) 3.4.1 相关分析(双变量相关分析&偏相关分析) (2) 3.4.2 线性回归模型 (2) 4 高级阶段方法部分 (2) 三、具体步骤描述 (3) 1 数据管理与软件入门部分 (3) 1.1 分类汇总 (3) 1.2 个案排秩 (4) 1.3 连续变量变分组变量 (4) 2 统计描述与统计图表部分 (5) 2.1 频数分析 (5) 2.2 描述统计分析 (7) 3 假设检验方法部分 (8) 3.1 分布类型检验 (8) 3.1.1 正态分布 (8) 3.1.2 二项分布 (10) 3.1.3 游程检验 (10) 3.2 单因素方差分析 (12) 3.3 卡方检验 (13) 3.4 相关与线性回归的分析方法 (14) 3.4.1 相关分析 (14) 3.4.2 线性回归模型 (15) 4 高级阶段方法部分 (17) 4.1 信度 (18) 4.2 效度 (18)
利用SPSS拟合非线性回归模型 ——以S型曲线为例 1.原始数据 下表给出了某地区1971—2000年的人口数据(表1)。试用SPSS软件对该地区的人口变化进行曲线拟合,并对今后10年的人口发展情况进行预测。 表1 某地区人口变化数据 年份时间变量t=年份-1970人口y/人 1971133 815 1972233 981 1973334 004 1974434 165 1975534 212 1976634 327 1977734 344 1978834 458 1979934 498 19801034 476 19811134 483 19821234 488 19831334 513 19841434 497 19851534 511 19861634 520 19871734 507 19881834 509 19891934 521 19902034 513 19912134 515 19922234 517 19932334 519 19942434 519 19952534 521 19962634 521
1997 27 34 523 1998 28 34 525 1999 29 34 525 2000 30 34 527 根据上表中的数据,做出散点图,见图1。, 33700 3380033900340003410034200343003440034500346001970197219741976197819801982198419861988199019921994199619982000 年份 人口 图1 某地区人口随时间变化的散点图 从图1可以看出,人口随时间的变化呈非线性过程,而且存在一个与横坐标轴平行的渐近线,近似S 曲线。 下面,我们用SPSS 软件进行非线性回归分析拟合计算。 2.用SPSS 进行回归分析拟合计算 在SPSS 中可以直接进行非线性拟合,步骤如下(假定已经进行了数据输入,关于数据输入方法见SPSS 相关基础 教程): Analysis->Regression->Cubic,在弹出的对话框(见图一)中选择拟合的变量和自变量,本例分别选择y (人口),t (时间变量)为变量(Dependent )和自变
1.为研究某合作游戏对幼儿合作意愿的影响,将18名幼儿随机分到甲、乙、丙3个组,每组6人,分别参加不同的合作游戏,12周后测量他们的合作意愿,数据见表,问不同合作游戏是否对幼儿的合作意愿产生显著影响? 单因素分析单因素方差分析:因变量—合作意愿得分;自变量—不同合作游戏(3种不同的水平) 显著性水平为0.541,大于0.05,说明这三组数据总体方差相等,适合方差齐性检验 从上表可以看出组间离差平方和为2.528,组内离差平方和为4.035,组间方差检验F=4.698,对应的显著性水平0.026,小于显著性水平0.05,说明3组中至少有一组与另外一组存在显著性差异。
由上表可以看出甲组与乙组的显著性为0.184 大于0.05,说明这两组的合作意愿得分没有显著差异,,但是甲组和乙组的相伴概率为0.008,说明这两组的合作意愿得分有显著性差异。
2.现有10名男生进行观察能力的训练,训练前后各进行一次测验,结果如下表所示。 解答:两配对样本T检验 从上表可以看出样本有10个,训练前10个男生的观察能力的样本均值是71,标准差是10.477,训练后观察能力的均值是79.50,标准差是9.823 由上表可以得出训练前后的相伴概率为0.028小于显著性水平0.05,说明训练前后能力的相关性较高 由上表可以得出t统计量为-3.341,相伴概率为0.009,小于0.05,说明训练能够是10个男生的观察能力有显著性的变化 3.某教师为考察复习方法对学生记忆单词效果的影响,将20名学生随机分成4组,每组5人采用一种复习方法,学生学完一定数量单词之后,在规定时间内进行复习,然后进行测试。结果见表。问各种方法的效果是否有差异?并将各种复习方法按效果好坏排序