
第三讲
一、三角函数的化简、计算、证明的恒等变形的应用技巧
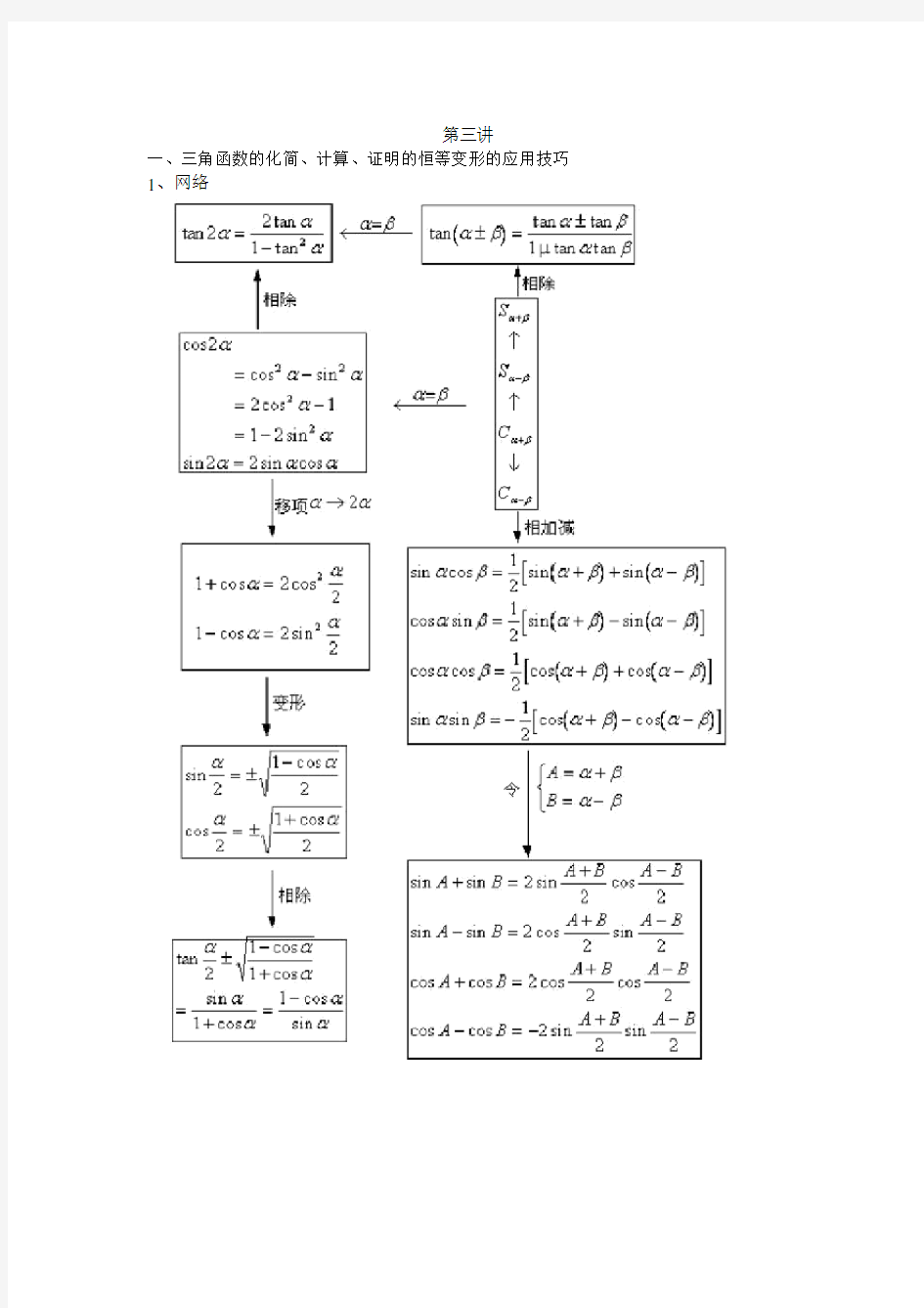
1、网络
2、三角函数变换的方法总结
(1)变换函数名
对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需
变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通
过同一和化归以有利于问题的解决或发现解题途径。
【例 1】已知θ同时满足和,且 a、b 均不为 0,求 a、b 的关系。
练习:已知sin(α+β )=,cos(α-β)=,求的值。
2)变换角的形式
对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相
表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/ 2 可看作α/ 4 的倍角;(45°+α)可看成( 90°+ 2α)的半角等等。
【例 2】求 sin(θ+ 75°)+ cos(θ+ 45°)-cos(θ+ 15°)的值。练习已知,求的值
【例 3】已知 sinα=A sin(α+β)(其中cosβ≠ A),试证明:tan(α
+β)=
提示: sin[(α+β)-β ]=A sin (α+β)
(3)以式代值
利用特殊角的三角函数值以及含有 1 的三角公式,将原式中的 1 或其他特殊值用式子代换,往往有助于问题得到简便地解决。这其中以“1”的变换为最常
见且最灵活。“ 1”可以看作是
222222 sin x+cos x,sec x -tan x,csc x -cot x,
tanxcotx, secxcosx, tan45 °等,根据解题的需要,适时地将“ 1”作某种变形,常能获得较理想的解题方法。
【例 4】化简:
(4)和积互化
积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化
的特殊情形。这往往用到倍、半角公式。
【例 5】解三角方程: sin 2 x+ sin 22x= sin 23x
(5)添补法
与代数恒等变换一样,在三角变换中有时应用添补法对原式作一定的添项裂项会使某些问题很便利地得以解决。将原式“配”上一个因子,同时除以这个式子也是添补法的一种特殊情形。
【例 6】求证:=
(6)代数方法
三角问题有时稍作置换,用各种代数方法对三角函数式作因式分解、等量置
换等的变形,从而将三角问题转换成代数问题来解,而且更加简捷。这其中有设元转化、利用不等式等方法。
【例 7】锐角α、β满足条件,则下列结论中正确的是()
A. α+β≠
B.α+β<
C. α+β>
D.α+β=
(7)数形结合
有的三角变换问题蕴含着丰富的几何直观,此时若能以数思形,数形渗透,
两者交融,则可开辟解题捷径。利用单位圆,构造三角形,利用直线、曲线的方
程等方法都是数形结合的思想。
【例 9】已知:,,求的值。
5.非特殊角的化简、求值问题的解题方法探究
非特殊角的化简求值是给角求值中一类常见的三角求值类型,对于此类求值问题,由于涉及到的三角公式及其变形灵活多样,因而如何利用三角公式迅速准确的求值应是解决这类问题的重点,现在我们通过一个题目的解法探寻,体会非特殊角三角函数的求法。
【题目】求的值。
练习
1 若,则的值为()
A. B.
C. D.
2 函数的值域是()
A. B. C. D.
3. 已知等腰三角形顶角的余弦值等于,则这个三角形底角的正弦值为()
A. B. C. D.
4.等于()
A. - 1
B. 1
C. 2
D. -2
二、辅助角公式及其应用
辅助角公式
对于形如y=asinx+bcosx的三角式,可变形如下:
y=asinx=bcosx
22a b。
a b (sin x·a2b2cos x·a2b2
)
1求周期
例 1 求函数y 2cos(x x)3 sin2x 的最小正周期。
) cos(
44
2.求最值
例 2.已知函数f(x)=cos4x-2sinxcosx-sin4x。若x[ 0, ] ,求f(x)的最大值和最小值。
2
3求值域
例 4.求函数f x6k16k1
( ) cos(
3
2x) cos( 2 x) 2 3 sin(2x)
33
( x R, k Z) 的值域。
4图象对称问题
例 6.如果函数y=sin2x+acos2x的图象关于直线x=对称,那么a=( )
8
( A) 2 (B)2(C)1(D)-1
5.图象变换
例 7 已知函数y 1 cos23
sin x cos x1, x R。该函数的图象可由y sin x( x R)的22
图象经过怎样的平移和伸缩变换得到?
6.求值
例 8.已知函数 f(x)= 3 sin2 x +sinxcosx。设α∈(0,π),f()= 1
3,求 sin α
242的值。
7.求系数
例 9.若函数 f(x)= 1 cos2x a sin x
cos(
x
) 的最大值为2,试确定常数 a 的值。
4 sin(x )22
2
8.解三角不等式
例 10.已知函数f(x)=sin2x+sin2x,x[0,2 ] ,求使f(x)为正值的x 的集合。
g3.1049 三角函数的化简、求值与证明 一、知识回顾 1、三角函数式的化简:(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③ 三角公式的逆用等。(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数 2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如2(),()()ααββααβαβ=+-=++-等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。 3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明。 二、基本训练 1、已知θ是第三象限角,且445 9 sin cos θθ+=,那么2sin θ等于 ( ) A 、223 B 、223- C 、23 D 、23 - 2、函数23 232 y sin x cos x =--+的最小正周期 ( ) A 、2π B 、π C 、3π D 、4π 3、tan 70cos10(3tan 201)- 等于 ( ) A 、1 B 、2 C 、-1 D 、-2 4、已知46 sin 3cos (4)4m m m αα--=≠-,则实数m 的取值范围是______。 5、设1 0,sin cos 2 απαα<<+=,则cos2α=_____。 三、例题分析 例1、化简: 4221 2cos 2cos 2.2tan()sin () 44 x x x x ππ -+ -+ 例2、设3177cos(),45124 x x π ππ +=<< ,求2sin 22sin 1tan x x x +-的值。 例3、求证:sin(2)sin 2cos().sin sin αββ αβαα +-+=
课题:二倍角的三角函数 本节考试要求为B 级 一、知识梳理 1、二倍角公式 =α2sin ;=α2cos ;=α2tan . 2、公式变形 =α2sin ;=α2cos ;=-αcos 1 ; =+αcos 1 ;=-α2sin 1 ;=+α2sin 1 . 3、技巧:(1)巧变角;(2)切化弦;(3)变逆用;(4)幂升降;(5)变结构;(6)1代换;(7)三兄妹. 二、三基能力强化 1、已知5 3 )4sin( = -x π ,则=x 2sin . 2、已知θ是第三象限角,且9 5cos sin 4 4=+θθ,那么θ2sin = . 3、在ABC ?中,6cos 4sin 3=+B A ,1cos 3sin 4=+A B ,则C sin 的值为 . 4、教材习题改编)已知1tan 2tan 1=+-θθ,则=++)4 tan(42tan π θθ . 5、已知βα,均为锐角,且α αα αβsin cos sin cos tan +-=,则=+)tan(βα . 三、典例互动 三角函数式的化简:化简的要求 例1:(1)化简)4 cos(6)4sin( 2x x -+-π π ; (2)α αααα2sin ) 1cos )(sin 1sin (cos +--+ 规律总结: 三角函数式的求值:求值的方法 例2:求值:0 01000 1cos 20sin10(tan 5tan 5)2sin 20-+-- 又如:ο ο ο ο 78sin 66sin 42sin 6sin =
例3:已知),43(ππα∈,3 10 tan 1tan =+αα,求 ) 2 sin(28 2 cos 112 cos 2 sin 82 sin 52 2 π αα α α α --++的 值。 变题:本题条件不变,求 ) 3 sin(cos 22sin 2π ααα- -的值。 例4:已知ββαsin 3)2sin(=+,设x =αtan ,y =βtan ,记)(x f y = (1)求)(x f 的解析式;(2)若角α是一个三角形的最小内角,试求函数)(x f 的值域 四、课堂反馈 1.已知cos2α=1 4 ,则sin 2α=________. 2.2sin2α1+cos2α·cos 2αcos2α 等于________. 3.已知α,β,γ∈(0,π 2),且sin α+sin γ=sin β,cos β+cos γ=cos α,则α-β的值等于________. 4.定义运算a b =ab 2+a 2b ,则sin15°cos15°的值是________. 5.(原创题)已知sin θ=4 5 ,且cos θ-sin θ+1<0,则sin2θ=________. 6.化简:2cos 4x -2cos 2x + 1 2 2tan(π4-x )·sin 2(π 4+x ) .
第三讲 一、三角函数的化简、计算、证明的恒等变形的应用技巧 1、网络
2、三角函数变换的方法总结 (1)变换函数名 对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。 【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。 练习:已知sin(α+β)=,cos(α-β)=,求的值。 2)变换角的形式 对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。 【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。练习已知,求的值
【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α +β)= 提示:sin[(α+β)-β]=Asin (α+β) (3)以式代值 利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。这其中以“1”的变换为最常见且最灵活。“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。 【例4】化简: (4)和积互化 积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。这往往用到倍、半角公式。 【例5】解三角方程:sin2x+sin22x=sin23x
4三角函数得化简、求值与证明日期:2009年月日星期 ,能正确地运用三角公式进行三角函数式得化简与恒等式得证明、 用、 (1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③三角公式得逆用等。(2)化简要求:①能求出值得应求出值; ②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数 2、三角函数得求值类型有三类:(1)给角求值:一般所给出得角都就就是非特殊角,要观察所给角与特殊角间得关系,利用三角变换消去非特殊角,转化为求特殊角得三角函数值问题;(2)给值求值:给出某些角得三角函数式得值,求另外一些角得三角函数值,解题得关键在于“变角”,如等,把所求角用含已知角得式子表示,求解时要注意角得范围得讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得得所求角得函数值结合所求角得范围及函数得单调性求得角。 3、三角等式得证明:(1)三角恒等式得证题思路就就是根据等式两端得特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端得化“异”为“同”;(2)三角条件等式得证题思路就就是通过观察,发现已知条件与待证等式间得关系,采用代入法、消参法或 、三角函数得求值: ,化非特殊角为特殊角; ?2、正确灵活地运用公式,通过三角变换消去或约去一些非特殊角得三角函数值; ?3、一些常规技巧:“1”得代换、切割化弦、与积互化、异角化同角等、 1、三角函数式得化简: 三角函数式得化简常用方法就就是:异名函数化为同名三角函数,异角化为同角,异次化为同次,切割化弦,特殊值与特殊角得三角函数互化、 ?2、三角恒等式得证明: 三角恒等式包括有条件得恒等式与无条件得恒等式、①无条件得等式证明得基本方法就就是化繁为简、左右归一、变更命题等,使等式两端得“异”化为“同”;②有条件得:代入法、消去法、综合法、分析法等、 ( A) A、B、C、D、 2、函数得最小正周期( B) A、B、C、D、 3、等于( D) A、1 B、2 C、-1 D、-2 4、已知,则实数得取值范围就就是__[-1,]___。 ____。 ,(),则?( ) ???或 略解:由得或(舍),∴,∴、 例2、已知,就就是第三象限角,求得值、 解:∵就就是第三象限角,∴(), ∵,∴就就是第四象限角,∴, ?∴原式 221 cos(15)sin(15)sin(75)cos(75) 3αααα + =---=+-+=-、 例3、已知,求得值、
简单的三角恒等变换——化简与证明 学习目标:能正确地运用三角函数的有关公式进行三角函数式的求值,化简与恒等式的证明. 学习重点:三角函数的有关公式的灵活应用和一些简单的变性技巧. 学习过程 一、知识清单 1.证明了cos()a b -= ?cos()a b += ?cos()2p a -= ,cos()2 p a += ?sin()a b += sin()a b -= ?tan()a b += ,tan()a b -= 2. cos (+)a b = ?cos 2a = = = sin()a b += ?sin 2a = tan()a b += ?tan 2a = 3.倍角的相对性 sin a = ,cos a = ,tan a = 4.要掌握这些公式的推导和联系,用时注意公式的“正用”,“逆用”和“变用”. 如:降幂扩角公式 2sin a = ;2 cos a = ; 1cos a += ;1cos a -= ; 1sin a += ;1sin a -= . 5. 划一公式:sin cos a x b x += (其中tan f = ,f 所在象限由 确定). 二、范例解析 题型一 三角函数式的化简和证明 1.三角函数式的化简要求:
通过对三角函数式的恒等变形使最后所得到的结果中: ①所含函数和角的名称或种类最少;②各项的次数尽可能地低;③出现的项数最少; ④一般应使分母和根号不含三角函数式;⑤对能求出具体数值的,要求出值. 2.三角变换的三项基本原则: (1)角的变换:划同角(角的拆分,配角和凑角,1的变换); (2)函数名称的变换:划同名(正切划弦); (3)幂指数的变换:划同次(升幂、降幂公式,同角公式). 例1化简下列各式 ; ②1sin 2cos 21sin 2cos 2a a a a +-=++ ; ③2sin 2cos 1cos 2a a a -=+ ; ④222cos 12tan()sin ()44 a p p a a -=-+ ; 例2 证明下列各式(从左到右或从右到左或左右开攻中间会师,一般化繁为简) ①22tan 2sin 1tan 2a a a =+ ②2 2 1tan 2cos 1tan 2a a a -=+ ③sin 1cos tan 21cos sin a a a a a -==+ ④[]1sin cos sin()sin()2a b a b a b =++- ⑤sin sin 2sin cos 22 q f q f q f +-+=. 三、课下练习: 课本142P 2 ; 143P A 组 1, 2, 3, 4;B 组 1; 146P 8;147P 5.
三角函数的求值、化简与证明 教学目标 1、 掌握两角和与差的正弦、余弦、正切公式。掌握二倍角的正弦、余弦、正切公式,能正 确运用三角公式进行三角函数的化简证明求值; 2、 培养学生分析问题解决问题的能力,培养热爱数学。 教学重点 掌握两角和与差的正弦、余弦、正切公式。掌握二倍角的正弦、余弦、正切公式。 教学难点 能正确运用三角公式进行三角函数的化简证明求值 教学过程 一、知识归纳 1、两角和与差公式: ()sin sin cos cos sin αβαβαβ±=± ()cos cos cos sin sin αβαβαβ±= , ()t a n t a n t a n 1t a n t a n αβαβαβ±±= 2、二倍角公式:sin 22sin cos ααα=, 22t a n t a n 21t a n αα α=- 22cos 2cos sin ααα=-22cos 1α=-212sin α=- 公式变形:1sin cos sin 22 ααα= 21cos 2sin 2αα-=,21cos 2cos 2αα+= 3、三角函数式化简的一般要求: ①函数名称尽可能少, ②项数尽可能少,③次数尽可能低,尽可能求出值 ④尽量使分母不含三角函数,⑤尽量使被开方数不含三角函数 4、求值问题的基本类型及方法: (1)“给角求值”一般所给的角都是非特殊角,解题时应注意观察非特殊角与特殊角之间的 关系。 (2)“给值求值”即给出某些角的的三角函数式的值,求另一些角的三角函数值,解题关键 在于变角,使其角相同。 (3)“给值求角”关键是变角,把所求的角用含已知角的式子表示。 5、证明三角恒等式的思路和方法: ①思路:利用三角公式进行化名,化角,使等式两端化“异”为“同”。 ②证明三角不等式的方法: 比较法、配方法、反证法、分析法,利用函数单调性,利用正余弦函数的有界性,利用 单位圆三角函数线及判别法等。 二、典例分析: 题型一:三角函数式的化简 例1:化简 : 22221sin sin cos cos cos 2cos 22 αβαβαβ?+?-? 分析:化简时使角尽量少,幂次尽量低,不含切割函数,时时要注意角之间的内在联系。
三角函数化简求值专题复习 高考要求 1、理解任意角的概念、弧度的意义、正确进行弧度与角度的换算;掌握任意角三角函数的定义、会利用单位圆中的三角函数线表示正弦、余弦、正切。 2、 掌握三角函数公式的运用(即同角三角函数基本关系、诱导公式、和差及倍角公式) 3、 能正确运用三角公式进行简单三角函数式的化简、求值和恒等式证明。 热点分析 1.近几年高考对三角变换的考查要求有所降低,而对本章的内容的考查有逐步加强的趋势,主要表现在对三角函数的图象与性质的考查上有所加强. 2.对本章内容一般以选择、填空题形式进行考查,且难度不大,从1993年至2002年考查的内容看,大致可分为四类问题(1)与三角函数单调性有关的问题;(2)与三角函数图象有关的问题;(3)应用同角变换和诱导公式,求三角函数值及化简和等式证明的问题;(4)与周期有关的问题 3.基本的解题规律为:观察差异(或角,或函数,或运算),寻找联系(借助于熟知的公式、方法或技巧),分析综合(由因导果或执果索因),实现转化.解题规律:在三角函数求值问题中的解题思路,一般是运用基本公式,将未知角变换为已知角求解;在最值问题和周期问题中,解题思路是合理运用基本公式将表达式转化为由一个三角函数表达的形式求解. 【例1】求值: ? +?? ??+?+?80cot 40csc 10sin 20tan 10cos 20sin 2. 解:原式的分子? ? ?+??+?=20cos 10sin 20sin 20cos 10cos 20sin 2 ??+?=20cos 10cos 20sin 2? ? +?= 20cos 10cos 40sin 320cos 20cos 60sin 220cos 80sin 40sin =? ? ?=??+?= , 原式的分母= ? ? +?= ??+?80sin 80cos 40cos 280sin 80cos 40sin 1 ()??+?+?=80sin 80cos 40cos 40cos ?? ?+?= 80sin 20cos 60cos 240cos 310cos 10cos 30cos 280sin 20cos 40cos =? ? ?=??+?= , 所以,原式=1. 【变式】1、求值 () ? +??+?+?10cos 110tan 60tan 110cos 40cos 2 解:()()2 5cos 25cos 45cos 225cos 250cos 40cos 25cos 21060cos 240cos 25cos 210sin 23 10cos 21240cos 25cos 210sin 310cos 40cos 2=? ??=??+?=??-?+?=? ?? ? ? ???+?+?=??+?+?=·原式 【变式】2、求0 020 210 sin 21 )140cos 1 140sin 3( ?- 。 分析:原式= 202020210sin 21140cos 140sin 140sin 140cos 3? -
三角函数的化简与证明 一、知识点 1、化简 (1)化简目标:项数习量少,次数尽量低,尽量不含分母和根号 (2)化简三种基本类型: 1) 根式形式的三角函数式化简 2) 多项式形式的三角函数式化简 3) 分式形式的三角函数式化简 (3)化简基本方法:用公式;异角化同角;异名化同名;化切割为弦;特殊值与特殊角的三角函数值互化。 2、证明及其基本方法 (1)化繁为简法 (2)左右归一法 (3)变更命题法 (4)条件等式的证明关键在于分析已知条件与求证结论之间的区别与联系。 3、无论是化简还是证明都要注意: (1)角度的特点 (2)函数名的特点 (3)化切为弦是常用手段 (4)升降幂公式的灵活应用 二、范例解析 例1:(1)已知α为第四象限角,化简:α αααααcos 1cos 1sin sin 1sin 1cos +-++- (2)已知 360270<<α,化简 α2cos 2 1212121++ 解:(1)因为α为第四象限角 所以原式=α ααααα22 22cos 1)cos 1(sin sin 1)sin 1(cos --+-- ()ααααα ααααα sin cos cos 1sin 1sin cos 1sin cos sin 1cos -=---=--+-= (2) 360270<<α,02cos ,0cos <>∴α α
所以原式=2cos 2cos 2cos 1cos 212122cos 1212122ααααα-==+=+=++ 思路点拨:根式形式的三角函数式化简常采用有理化如(1)或升幂公式如(2) 例2、P(55 例1) 试求函数Y=sinx+cosx+2sinx cosx +2 的最大值,最小值. 若[0,]2 x π∈呢? 解: 练习:a,b 为何值时,函数()x b a x b a y 22cos 2 sin ++-=的值为2?(a=3,b=1) 思路点拨:注意角度α22-x 与α-x 关系,先化简整理。 例3 _sin(2)sin :2cos()sin sin αββαβαα +-+=求证 练习、求证:()x x x x 4cos 14cos 32cot tan 22-+=+ 思路点拨:要据角度x 与4x 的特点和函数名的特点,可采用化切为弦,并用倍角公式证明。 证:左边= ()x x x x x x x x x x x x x x x 2sin 2sin 242sin 41cos sin 2cos sin cos sin cos sin sin cos cos sin 222222 2222442222-=-+=+=+ 右边=()()() x x x x x x 2sin 22sin 242sin 22sin 2422sin 2112sin 2132222222-=-=---+ 所以左边=右边,即等式成立。 本题采用了左、右归法,从左到右或从右到左见书本。 例4、P 是以F 1, F 2 为焦点的椭圆上一点,且1221,2PF F PF F αα∠=∠= 求证:椭圆的离心率e=2cosa-1 预备:例5 在ΔABC 中,设tanA+tanC=2tanB,求证cos(B+C-A)= C C 2cos 452cos 54++. 证明:C C B A tan )tan()tan(-=-=+π C B A B A tan tan tan 1tan tan -=-+∴C B A C B A tan tan tan tan tan tan ??=++? 由条件得B C B A tan 3tan tan tan =++ ∴C B A B tan tan tan tan 3??=
2008高考数学专题训练 三角函数的化简与求值 学校 学号 班级 姓名 知能目标 1. 掌握同角的三角函数的基本关系式: 掌握正弦,余弦的诱导公式;掌握两角和与两角 差的正弦,余弦,正切公式;掌握二倍角的在正弦,余弦,正切公式. 2. 能正确运用三角公式,进行简单三角函数式的化简,求值和恒等式证明. 综合脉络 三角变换是运算化简过程中运用较多的变换, 也是历年高考命题的热点. 提高三 角变换能力, 要学会设置条件, 灵活运用三角公式, 掌握运算、化简的方法和技能. 常 用的数学思想方法技巧如下: 1. 角的变换: 在三角化简、求值、证明中, 表达式往往出现较多的相异角, 可根据角与角之 间的和差、倍半、互补、互余的关系, 运用角的变换, 沟通条件与结论中的差异, 使问题 获解.对角的变形如下: )2()2()(,2304560304515α -β-β+α=β-β+α=α=-=-= , )4()4()()(2α-π-α+π=β-α+β+α=α,)4 (24α-π -π=α+π 特别地, α+π4与α-π 4 为互余角, 它们之间可以互相转化, 在三角变形中使用频率高. 2. 函数名称变换: 三角变形中, 常常需要变函数名称为同名函数. 如在三角函数中正余弦是 基础, 通常化切、割为弦, 变异名为同名. 3. 常数代换: 在三角函数运算、求值、证明中, 有时需要将常数转化为三角函数值, 例如常 数“1”的代换变形有: α-α=α-α=α+α=2 2 2 2 2 2 cot csc tan sec cos sin 1. 4. 幂的变换: 降幂是三角变换时常用方法, 对次数较高的三角函数式, 一般采用降幂处理的 方法. 常用降幂公式有: 1cos sin ,2 2cos 1cos ,22cos 1sin 2222 =α+αα +=αα-= α 等, 三角变换时, 有时需要升幂, 如对无理式α+cos 1常用升幂化为有理式, 升幂公式与 降幂公式是相对而言的. 5. 公式变形式: 三角公式是变换的依据, 应熟练掌握三角公式的直接应用, 逆用以及变形式 的应用. 如: )tan tan 1)(tan(tan tan ,sin 22sin cos β?αβ±α=β±αα α =α 等. (一) 典型例题讲解: 例1. (1)当2x 0π <<时,函数x 2sin x sin 8x 2cos 1)x (f 2++=的最小值为 ( ) A. 2 B. 32 C. 4 D. 34
第1页,总5页 绝密★启用前 xxx 学校_____学年度数学(理)试卷 注意事项: 1.答题前填写好自己的姓名、班级、考号等信息\r\n2.请将答案正确填写在答题卡上 第I 卷(选择题) 一、选择题(本题共12道小题,每小题0 分,共0分) 1. 已知1tan()42π α+=,且02 π α-<<,则22sin sin 2cos()4 ααπα +-等于 A . B . C . D 2. 已知函数()3sin 4cos 1f x x x =++,实常数,,p q r 使得()()2018pf x qf x r ++=对任意的实数x R ∈恒成立,则cos p r q +的值为( ) A .-1009 B .0 C.1009 D .2018 3. 已知向量a =(k ,cos 3π),向量b =(sin 6π,tan 4π ),若a ∥b ,则实数k 的值为( ) A .4 1 - B .﹣1 C .41 D .1 4. 已知,,,66t R ππαβ?? ∈-∈????,且5sin 30t αα+-=,5181sin3 03t ββ++=,则()ln 3cos 3αβ-+=????( ) A .ln2 B .ln3 C .5 ln 2 D .ln 3? ?? 5. 若1 tan()43π α-=-,则cos2α=( ) A .35 B .35- C . 45- D .45 6. 设f (n )=cos( 2n π+4 π ),则f (1)+ f (2)+ f (3)+…+ f (2006)=( ) A .-2 B .- 2 C .0 D . 2 7. 2cos553sin 5 -的值为( ) A .2 B .3 C . 2 3 D .1 8. 设函数()cos sin f x x x =-,把)(x f 的图象按向量)0,(m 平移后,图象恰为函数 ()y f x '=的图象,则m 的值可以是 A. 2π B.4 π C.4π- D.2π- 9. 已知2sin 23 α=,则2 cos (4 πα+=( ) A .16 B .16 C .12 D .23 10. 将函数()2cos f x x x =-的图象向左平移?(0?>)个单位长度,所得图象对应的函数为偶函数,则?的最小值为 ( ) A . 6π B . 3π C .23π D .56 π 11. 若 )4 2sin(21 )22cos( cos 22π+α-α+π +α=4,则tan (2α+4π)=( ) A .21 B .31 C .41 D .5 1 12. 若sin(2cos )4 π ααα+=+,则sin 2α=( ) A .45- B .45 C. 35- D .3 5
课题:三角函数式的化简、求值与证明 教学目标:能正确地运用三角函数的有关公式进行三角函数式的求值,化简与恒等式的证明. 教学重点:有关公式的灵活应用及一些常规技巧的运用. (一)主要知识: 1三角函数求值问题一般有三种基本类型: 1. 给角求值,即在不查表的前提下,求三角函数式的值; 2. 给值求值,即给出一些三角函数,而求与这些三角函数式有某种联系的三角式的值; 3. 给值求角,即给出三角函数值,求符合条件的角. 2. 三角函数式的化简要求: 通过对三角函数式的恒等变形使最后所得到的结果中: ①所含函数和角的名类或种类最少;②各项的次数尽可能地低;③出现的项数最少; ④一般应使分母和根号不含三角函数式;⑤对能求出具体数值的,要求出值. 3. 三角恒等式的证明要求:利用已知三角公式通过恒等变形,论证所给等式左、右相等?(二)主要方法: 1.寻求角与角之间的关系,化非特殊角为特殊角; 2?正确灵活地运用公式,通过三角变换消去或约去一些非特殊角的三角函数值; 3. 一些常规技巧:“ 1”的代换、切割化弦、和积互化、异角化同角等. 4. 三角函数式的化简常用方法是:异名函数化为同名三角函数,异角化为同角,异次化为同次,切割化弦,特殊值与特殊角的三角函数互化. 5. 三角恒等式的证明: 三角恒等式包括有条件的恒等式和无条件的恒等式. ①无条件的等式证明的基本方法是化繁为简、左右归一、变更命题等,使等式两端的“异”化为“同”:②有条件的等式常用方法有:代入法、消去法、综合法、分析法等. (三)典例分析: 问题1 1已知tan— 2 ,求------- 1 2的值; 42si n cos cos 2已知sin?2 sin2 1,求3cos 4 cos2sin 1的值.
必修4—三角函数的化简、求值与证明 一、知识要点 1、三角函数式的化简:(1)常用方法:①直接应用公式进行降次、消项;②切化弦,异名化同名,异角化同角;③ 三角公式的逆用等。(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数 2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如2(),()()ααββααβαβ=+-=++-等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。 3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明。 二、巩固练习 A 组 1、已知θ是第三象限角,且4 4 5 9 sin cos θθ+= ,那么2sin θ等于---------------( ) A 、3 B 、3 - C 、23 D 、23- 2 、函数2 2y sin x x =-的最小正周期 -------------------------------( ) A 、2π B 、π C 、3π D 、4π 3 、tan70cos10201)- 等于 -------------------------------------------------( ) A 、1 B 、2 C 、-1 D 、-2 4 、已知46 sin (4)4m m m αα-= ≠-,则实数m 的取值范围是______。 5、设1 0,sin cos 2απαα<<+=,则cos 2α=_____。 6、化简: 4221 2cos 2cos 2.2tan()sin () 44x x x x ππ -+ -+ 7、设3177cos(),45124x x πππ+=<<,求2sin 22sin 1tan x x x +-的值。 8、求证: sin(2)sin 2cos().sin sin αββ αβαα +-+= 9、已知1 1 sin()cos [sin(2)cos ],02 2 αβααβββπ+-+-= <<,求β的值。
1049 三角函数的化简、求值与证明 一、知识回顾 1、三角函数式的化简:(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③ 三角公式的逆用等。(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数 2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题; (2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如2(),()()ααββααβαβ=+-=++-等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。 3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明。 二、基本训练 1、已知θ是第三象限角,且4459 sin cos θθ+=,那么2sin θ等于 ( ) A 、3 B 、3 - C 、23 D 、23- 2 、函数222 y sin x x =-+的最小正周期 ( ) A 、2π B 、π C 、3π D 、4π 3、tan70cos10(3tan 201)-等于 ( ) A 、1 B 、2 C 、-1 D 、-2 4、已知46sin (4)4m m m αα--=≠-,则实数m 的取值范围是______。 5、设10,sin cos 2 απαα<<+=,则cos 2α=_____。 三、例题分析 例1、化简: 42212cos 2cos 2.2tan()sin ()44 x x x x ππ-+-+ 例2、设3177cos(),45124x x π ππ+=<<,求2sin 22sin 1tan x x x +-的值。 例3、求证:sin(2)sin 2cos().sin sin αββαβαα +-+=
课题:三角函数的求值、化简、证明 考纲要求: ①掌握以两角和与差的正余弦公式为核心的公式组. ②理解这一些公式之间的关系;③以公式应用为基础解决三角函数的性质问题. 教材复习 ①两角和与差的正余弦公式:()cos αβ±= ; ()sin αβ±= ②倍角公式及其推论:二倍角公式:cos 2α= = ? = ? sin 2α= , tan 2α= 1sin α+= ;1sin α-= ; 1cos α+= ;1cos α-= tan tan αβ±= sin cos a b αα+= 基本知识方法 1.寻求角与角之间的关系,化非特殊角为特殊角; 2.正确灵活地运用公式,通过三角变换消去或约去一些非特殊角的三角函数值; 3.一些常规技巧:“1”的代换、切割化弦、和积互化、异角化同角等. 4.三角函数式的化简常用方法是:异名函数化为同名三角函数,异角化为同角,异次 化为同次,切割化弦,特殊值与特殊角的三角函数互化. 5.三角恒等式的证明: 三角恒等式包括有条件的恒等式和无条件的恒等式. ①无条件的等式证明的基本方法是化繁为简、左右归一、变更命题等,使等式两端的“异”化为“同”;②有条件的等式常用方法有:代入法、消去法、综合法、分析法等. (三)典型分析: 问题1.()1(2012重庆) cos 47sin17cos30cos17?-??=? .A -.B 12-.C 12.D
()2(09届高三上海市育才中学期中)若0, 2πα?? ∈ ?? ? ,且cos()6 4 π α+ =- , 则cos α= ()3(08 山东文)已知cos sin 6παα? ?-+= ?? ?7sin 6πα??+= ??? . A 5 - . B 5 .C 45 - . D 45 () 4= .A sin 4-.B sin 4.C sin 42cos 4-.D 2cos 4sin 4- 问题2.(06安徽)已知 34παπ<<,10 tan cot 3 αα+=- (Ⅰ)求tan α的值; (Ⅱ)求 2 2 5sin 8sin cos 11cos 8 2 2 2 2 2α α α α πα++-? ? - ? ? ?的值
1. 已知21tan(),tan()544 παββ+=-=,则tan()4πα+的值是 。 2. 函数sin 3cos (0)2y x x x π=+≤≤ 的值域是 。 3. 若170,cos ,sin()239παβαβ<< =-+=且,则sin α等于 。 4. sin10sin30sin50sin 70的值是 。 5. 若450cos(),sin()2513 πβααβαβ<<<+=-=且,那么c o s 2α的值是____________。 6. 化简221 3cos 80cos 10-=______________________。 7. 求值tan 20tan 40tan120tan 20tan 40 ++=______________________。 8. 若270360α<< 则1111cos22222 α++=_________________。 9. 计算:cos103sin10 1cos80+-=____________________.。 10. (1)已知tan 3α=,求 2221sin cos 34αα+的值. (2)已知11tan 1α=-,求 1 1sin cos αα+的值. 11. 已知2sin()cos()3 παπα--+= ()2παπ<<,求下列各式的值: (1)sin cos αα- (2)33sin ()cos ()22ππαα-++ 12. 已知函数 2()sin 2(,)()4f x x acox x a R a y f x π =+∈=为常数,且是函数的零点 (I)求a 的值,并求函数()f x 的最小正周期; (Ⅱ)当[0,]2 x π ∈ 时,求函数()f x 的值域,并写出()f x 取得最大值时值.
A B C B 【例4] 在中,若sin2_2 +sin2y +sin2y =cos2_2 , tan—? tan —=-. 2 2 3 B 满足关系式:V3 (tan a ? t^n B +a) +tan a =0,则tan B 二 c- f(1+a)D- T(1~a) A. V3 (1+a) B. V3 (1 — 爲)
三角函数的化简 1、三角函数式的化简:(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③三角公式的逆用等。(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少; ③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数 2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如& =(? + "丿—0,2Q =(Q +"丿+ (?-0丿等,把所求角用含己知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。 3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化 繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察, 发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明。 一、化简 [例求值.2sin2(P + cosl0o + tan20。sin 10° esc 40° + cot 80°
课时作业22 三角函数式的求值、化简与证明 时间:45分钟 分值:100分 一、选择题(每小题5分,共30分) 1.下列各式中,值为3 2的是 ( ) A .2sin15°cos15° B .cos 2 15°-sin 2 15° C .2sin 215°-1 D .sin 215°+cos 215° 解析:cos 215°-sin 215°=cos30°=3 2 . 答案:B 2.已知角α在第一象限且cos α=3 5,1+2cos(2α-π 4) sin(α+π 2 ) = ( ) A.2 5 B.75 C.14 5 D .-25 解析:∵角α是第一象限角且cos α=35,∴sin α=4 5 , ∴1+2cos(2α-π 4) sin(α+π2 ) =1+cos2α+sin2α cos α =2cos 2 α+2sin αcos αcos α =2cos α+2sin α=145, 故正确答案是C. 答案:C 3.设a =12 (sin56°-cos56°),b =cos50°·cos128°+cos40°·cos38°,c =1 2(cos80°-2cos 250° +1),则a ,b ,c 的大小关系是 ( ) A .a >b >c B .b >a >c C .c >a >b D .a >c >b 解析:∵a =sin56°·22-cos56°·2 2 =sin(56°-45°)=sin11°, b =cos50°·(-cos52°)+cos40°·cos38° =-sin40°·cos52°+cos40°·sin52°, =sin(52°-40°)=sin12°. c =1 2(cos80°+1-2cos 250°) =1 2 (2cos 240°-2sin 240°)=cos80°=sin10°. ∴b >a >c . 答案:B 4.已知sin αsin β=1,则cos(α-β)的值为
三角函数式的化简和求值练习 一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有 且只有一项符合题目要求. 1.sin 2·cos 3·tan 4的值( ) A .小于0 B .大于0 C .等于0 D .不存在 2.已知角α的终边过点(4,3)P a a - 则ααcos sin 2+的值为 A.52- B.5 2 C.0 D. 52-或52 3.设a=2cos 2280-1, b= 22(cos180-sin180), c=log 2 122 , 则 ( ) A. a