
图论的发展及其在生活中的应用
数学与应用数学张佳丽
指导教师刘秀丽
摘要主要介绍了图论的起源与发展及其生活中的若干应用,如:渡河问题、旅游推销员问题、最小生成树问题、四色问题、安排问题、中国邮递员问题。同时也涉及到了几种在图论中应用比较广泛的方法,如:最邻近法、求最小生成树的方法、求最优路线的方法等。
关键词图论生活问题应用
Graph Theory Development and the Application in Life
Mathematics and applied mathematics Zhang Jiali
Tutor Liu Xiuli
Abstract This paper mainly introduces the origin and development of graph theory and its several applications in our life, such as: crossing river problem, traveling salesman problem, minimum spanning tree problem, four color problem,arrangement problem,Chinese postman problem.It also researches several methods that are more widely applied in graph theory, for example: the method of most neighboring, the method of solving the minimum spanning tree,the method of the best route,and so on.
Key words graph theory life problem application
引言
图论是一门古老的学科,是数学中有广泛应用的一个分支,与其他的数学分支,如群论、矩阵论、概率论、拓扑学、数分析等有着密切的联系.图论中以图为研究对象,图形中我们用点表示对象,两点之间的连线表示对象之间的某种特定的关系.事实上,任何一个包含了二元关系的系统都可以用图论来模拟.而且,图论能把纷杂的信息变的有序、直观、清晰.由于我们感兴趣的是两对象之间是否有某种特定关系,所以图形中两点间连接与否尤为重要,而图形的位置、大小、形状及连接线的曲直长短则无关紧要.图论在自然科学、社会科学等各个领域都有广泛的应用.随着科学的发展,以及生产管理、军事、交通运输等方面提出了大量实际的需要,图论的理论及其应用研究得到飞速发展。从20世纪50年代以后,由于计算机的迅速发展,有力地推动了图论的发展,加速了图论向各个学科的渗透,尤其是网络理论的建立,图论与线性规划、动态规划等优化理论和方法互相渗透。同时,计算机的发展使图论成为数学领域中发展最快的分支
之一.
1 图论的起源与发展
1.1 图论的起源[1]
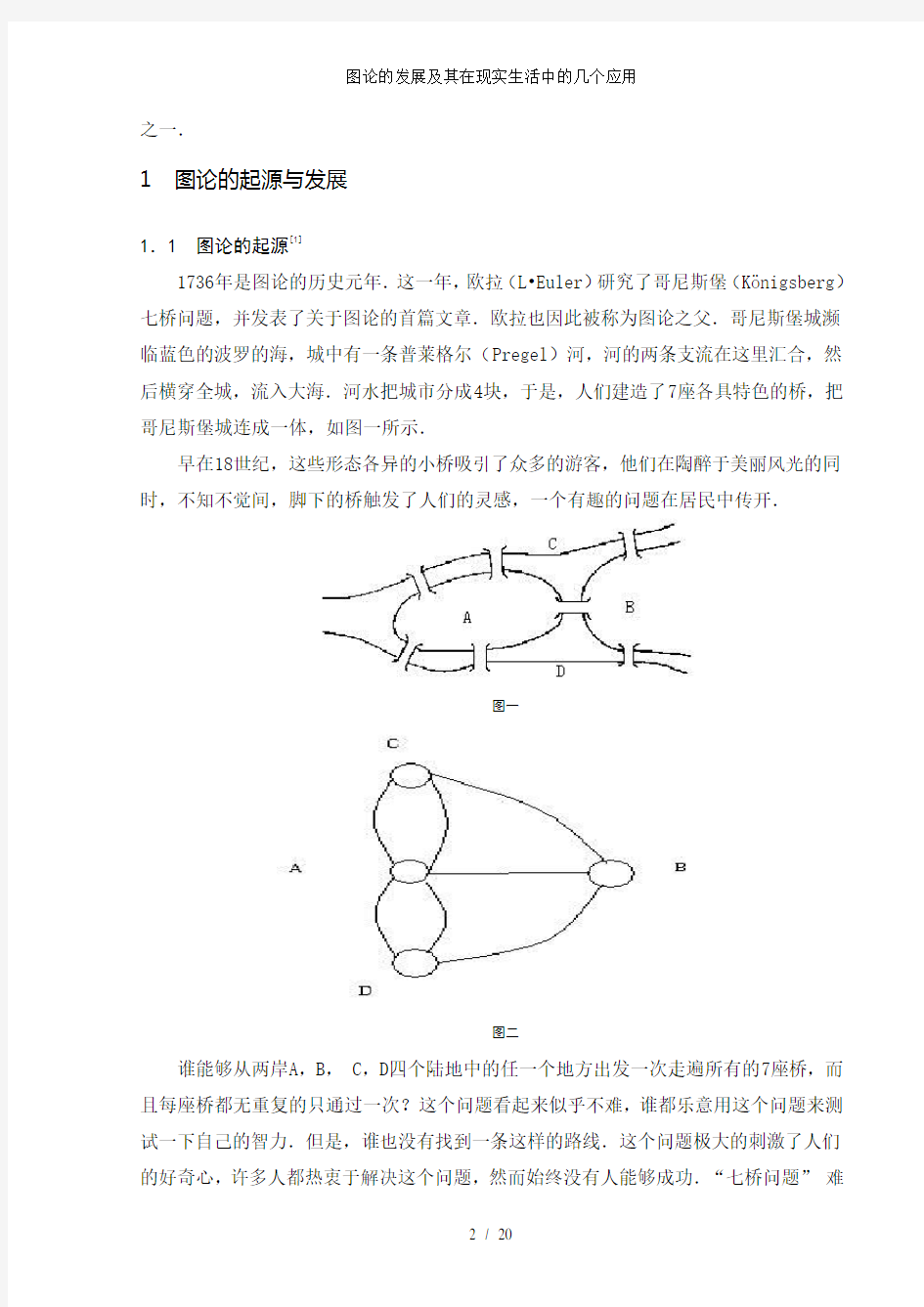
1736年是图论的历史元年.这一年,欧拉(L?Euler)研究了哥尼斯堡(K?nigsberg)七桥问题,并发表了关于图论的首篇文章.欧拉也因此被称为图论之父.哥尼斯堡城濒临蓝色的波罗的海,城中有一条普莱格尔(Pregel)河,河的两条支流在这里汇合,然后横穿全城,流入大海.河水把城市分成4块,于是,人们建造了7座各具特色的桥,把哥尼斯堡城连成一体,如图一所示.
早在18世纪,这些形态各异的小桥吸引了众多的游客,他们在陶醉于美丽风光的同时,不知不觉间,脚下的桥触发了人们的灵感,一个有趣的问题在居民中传开.
图一
图二
谁能够从两岸A,B, C,D四个陆地中的任一个地方出发一次走遍所有的7座桥,而且每座桥都无重复的只通过一次?这个问题看起来似乎不难,谁都乐意用这个问题来测试一下自己的智力.但是,谁也没有找到一条这样的路线.这个问题极大的刺激了人们的好奇心,许多人都热衷于解决这个问题,然而始终没有人能够成功.“七桥问题”难
住了哥尼斯堡城的所有居民.哥尼斯堡城也因“七桥问题”而出了名.这就是数学史上著名的七桥问题.
问题看来并不复杂,但就是谁也解决不了,也说不出所以然来.1736年,当时著名的数学家欧拉仔细研究了这个问题,他将上述四块陆地与七座桥间的关系用一个抽象图形来描述(见图二),其中A、B、C、D四个陆地分别用四个点来表示,而陆地之间有桥相连者则用连接两个点的连线来表示,这样,上述的哥尼斯堡七桥问题就变成了由点和边所组成的如下问题:
试求从图中的任一点出发,不重复的通过每条边一次,最后返回到该点,这样的路线是否存在?这样问题就变得简洁明了了,同时问题也变得更一般、更深刻了.这样,七桥问题就转变为图论中的一笔画问题.即能不能不重复的一笔画出图二中的这个图形.
原先人们是要求找出一条不重复的路线,欧拉想,既然成千上万的人都失败了,那么这样的路线也许根本就不存在.于是,欧拉就想:这样不重复的路线究竟存不存在?由于改变了一下提问的角度,欧拉抓住了问题的实质.最后,欧拉认真考虑了一笔画图形的结构特征.
欧拉发现,凡是能用一笔画成的图形,都有这样一个特点:每当画一条线进入中间的一个点时,还必须画一条线离开这个点.否则,这个图形就不可能用一笔画出.也就是说,单独考察图中的任何一点(起点和终点除外),这个点都应该与偶数条线相连;如果起点与终点重合,那么,连这个点也应该与偶数条线相连.
在七桥问题的几何图中,A、B、D三点分别与3条线相连,C点与5条线相连.连线数都是奇数条.因此,欧拉断定:一笔画出这个图形是不可能的.也就是说,不重复地通过7座桥的路线是根本不存在的!天才的欧拉只用了一步就证明了这个难题,从这里我们也可以看到图论的强大威力.
欧拉对七桥问题的研究,是拓扑学研究的先声.
1750年,欧拉又发现了一个有趣的的现象.欧拉因此得到了后人以他的名字命名的“多面体欧拉公式”.正4面体有4个顶点、6条棱,它的面数加顶点数减去棱数等于2;正6面体有8个顶点、12条棱,它的面数加顶点数减去棱数也等于2.接着,欧拉又考察了正12面体、正24面体,发现都有相同的结论.于是继续深入研究这个问题,终于发现了一个著名的定理:
F(面数) +V(顶点数) -E(棱数) =2
这个公式证明了多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体五种.这个定理成为拓扑学的第一个定理,这个公式被认为开启了数学史上新的一页,促成了拓扑学的发展.
1.2 图论的发展
图论的产生和发展经历了二百多年的历史,大体上可以分为三个阶段:
第一阶段是从1736年到19世纪中叶.当时的图论问题是盛行的迷宫问题和游戏问题.最具代表性的工作是著名数学家欧拉于1736年解决的哥尼斯堡七桥问题(见1.1).第二阶段是从19世纪中叶到1936年.图论主要研究一些游戏问题:迷宫问题、博弈问题、棋盘上马的行走路线问题等,[2]随着对这些问题的深入研究,图论又产生了新的一系列问题,例如:连通性、嵌入问题、染色问题、矩阵表示以及网络流等.连通性是图论研究的基本问题之一,欧拉路、中国邮路问题、哈密顿问题、树与图的支撑树、匹配问题都是连通性的典型问题;地图着色问题即是对无论多么复杂的地图,只需用四种颜色就足够将相邻的区域分开.平面图的染色问题是与四色问题紧密相联的.于是产生了着色问题即给定一个图,如果要求把所有顶点涂上颜色,使得相邻顶点具有不同的颜色,问最少需要几种不同的颜色?这个问题叫做图的点着色问题.如果对给定图的全部边都涂上颜色,使相邻的边有不同的颜色,问至少需要几种颜色?这个问题叫做边的着色问题,边的着色问题可以转化为点着色问题.由这些问题人们逐渐丰富并发展了图论学科知识.同时出现了以图为工具去解决其他领域中一些问题的成果.1847年德国的克希霍夫将树的概念和理论应用于工程技术的电网路方程组的研究.1936年匈牙利的数学家哥尼格写出了第一本图论专著《有限图与无限图的理论》.标志着图论成为了一门独立学科.
第三阶段是1936年以后.由于生产管理、军事、交通运输、计算机和通讯网路等方面大量实际问题的出现,大大促进了图论的发展.特别是电子计算机的大量应用,使大规模问题的求解成为可能.实际问题如电网络、交通网络、电路设计、数据结构以及社会科学中的问题所涉及到的图形都很复杂的,需要计算机的帮助才有可能进行分析和解决.目前,图论在物理、化学、运筹学、计算机科学、电子学、信息论、控制论、网络理论、社会科学及经济管理等几乎所有学科领域中都有应用.
2 图论在生活中几种应用
2.1 渡河问题
2.1.1 基本理论
定义2.1[3]有向图:一个有向图是一个有序的二元组,V E,记作D,其中
(1)V≠?称为顶点集,其元素称为顶点或结点.
(2)E为边集,它是笛卡尔积V V
?的多重子集,其元素称为有向边,简称边.2.1.2 应用举例
例[4] (渡河问题)一个摆渡人要把一只狼,一只羊和一捆菜运过河去,由于船很小,每次摆渡人至多只能带一样东西.另外,如果人不在旁时,狼就要吃羊,羊就要吃菜.问这个人怎样才能安全的将它们运过河去?
解用F表示摆渡人,W表示狼,S表示羊,C表示菜
若用F W S C表示人和其他三样东西在河的原岸的状态,这样原岸全部可能出现的状态为以下16种:
FWSC FWS FWC FSC
WSC FW FS FC
WS WC SC F
W S CΦ
Φ表示原岸什么也没有,即人、狼、羊、菜都运到河对岸了
根据题意,我们知道这16种情况中有6种是不允许的,它们是WSC、FW、FC、WS、SC、F,如FC表示人和菜在原岸而狼和羊在对岸,这当然是不允许的.因此,允许出现的情况只有10种.以这10种状态为结点,以摆渡前原岸的一种状态与摆渡一次后出现在原岸的状态所对应的结点之间的连线为边,作有向图2.1:
Φ
FSW
图2.1
上图给出了两种方案,方案为上图中从FWSC到Φ的不同的基本通路:
⑴FWSC→WC→FWC→C→FSC→S→FS→Φ
⑵FWSC→WC→FWC→W→FWS→S→FS→Φ.
它们的长度均为7故摆渡人只需摆渡7次就能将它们全部运到对岸,并且羊和菜完好无损.
2.2 旅行推销员问题
该问题是说:“给定n 个城市和它们之间的距离,问如何设计一条路线,使得一个推销员从他所在的城市出发途经其余1n -个城市刚好一次,最后回到原驻地并使得行程最短[5]?”
2.2.1 基本理论
定义2.2[6] 给定图,G V E =(G 为无向图或有向图),设W :E R →(R 为实数集),对G 中任意的边(),i j e v v = (G
为有向图时,,i j e v v =),设()W e =ij w ,称实数ij w 为边e 上的权,并将ij w 标注在边e 上,称G 为带权图,此时常将带权图G 记作,,V E W .设G G '?,称
()()e E G W e '∈∑为G '的权,记作()W G ',即()W G '=()()e E G W e '∈∑.
最邻近法[7] (1)由任意选择的结点开始,找与该点最近(即权最小)的点,形成有一条边的初始路径.
(2)设X 表示最新加到这条路上的结点,从不在路上的所有结点中选一个与X 最靠近的结点,把连接X 与这一结点的边加到这条路上,重复这一步,直到G 中所有结点包含在路上.
(3)将连接起始点与最后加入的结点之间的边加到这条路上,就得到一个圈,即为问题的近似解.
2.2.2 应用举例
例[8] 某流动售票员居住在A 城,为推销货物他要访问B 、C 、D 城后返回A 城,若该四城间的距离如下图2.2所示,找出完成该访问的最短路线.
图2.2
解步骤如下图①—④
D
①
D
②
③
④
最短距离为:8+6+7+11=32.
2.3 最小生成树
习题一: ● 。 证明:作映射f : v i ? u i (i=1,2….10) 容易证明,对?v i v j ∈E ((a)),有f (v i v j,),=,u i,u j,∈,E,((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知,图(a)与(b)是同构的。 ● 5.证明:四个顶点的非同构简单图有11个。 证明:设四个顶点中边的个数为m ,则有: m=0: m=1 : m=2: m=3: m=4: (a) v 23 4 (b)
m=5: m=6: 因为四个顶点的简单图最多就是具有6条边,上面所列出的情形是在不同边的条件下的不同构的情形,则从上面穷举出的情况可以看出四个顶点的非同构简单图有11个。 ● 11.证明:序列(7,6,5,4,3,3,2)和(6,6,5,4,3,3,1) 不是图序列。 证明:由于7个顶点的简单图的最大度不会超过6,因此序列(7,6,5,4,3,3,2)不是图序列; (6,6,5,4,3,3,1)是图序列 1 1 12312(1,1,,1,,,)d d n d d d d d π++=---是图序列 (5,4,3,2,2,0)是图序列,然而(5,4,3,2,2,0)不是图序列,所以(6,6,5,4,3,3,1)不是图序列。 ● 12.证明:若 ,则包含圈。 证明:下面仅对连通图的下的条件下进行证明,不连通的情形可以通过分成若干 个连通的情形来证明。设 , 对于中的路 若与邻接,则构成一个闭路。若是一条路,由于,因 此,对于,存在与之邻接,则构成一个圈。 ● 17.证明:若G 不连通,则连通。 证明:对于任意的 ,若与属于G 的连通分支,显然与在中连通;
电子科技大学研究生试题 《图论及其应用》(参考答案) 考试时间:120分钟 一.填空题(每题3分,共18分) 1.4个顶点的不同构的简单图共有__11___个; 2.设无向图G 中有12条边,已知G 中3度顶点有6个,其余顶点的度数均小于3。则G 中顶点数至少有__9___个; 3.设n 阶无向图是由k(k ?2)棵树构成的森林,则图G 的边数m= _n-k____; 4.下图G 是否是平面图?答__是___; 是否可1-因子分解?答__是_. 5.下图G 的点色数=)(G χ______, 边色数=')(G χ__5____。 图G 二.单项选择(每题3分,共21分) 1.下面给出的序列中,是某简单图的度序列的是( A ) (A) (11123); (B) (233445); (C) (23445); (D) (1333). 2.已知图G 如图所示,则它的同构图是( D ) 3. 下列图中,是欧拉图的是( D ) 4. 下列图中,不是哈密尔顿图的是(B ) 5. 下列图中,是可平面图的图的是(B ) A C D A B C D
6.下列图中,不是偶图的是( B ) 7.下列图中,存在完美匹配的图是(B ) 三.作图(6分) 1.画出一个有欧拉闭迹和哈密尔顿圈的图; 2.画出一个有欧拉闭迹但没有哈密尔顿圈的图; 3.画出一个没有欧拉闭迹但有哈密尔顿圈的图; 解: 四.(10分)求下图的最小生成树,并求其最小生成树的权值之和。 解:由克鲁斯克尔算法的其一最小生成树如下图: 权和为:20. 五.(8分)求下图G 的色多项式P k (G). 解:用公式 (G P k -G 的色多项式: )3)(3)()(45-++=k k k G P k 。 六.(10分) 22,n 3个顶点的度数为3,…,n k 个顶点的度数为k ,而其余顶点的度数为1,求1度顶点的个数。 解:设该树有n 1个1度顶点,树的边数为m. 一方面:2m=n 1+2n 2+…+kn k 另一方面:m= n 1+n 2+…+n k -1 v v 1 3 图G
图论及其应用答案电子科 大 Newly compiled on November 23, 2020
习题三: ● 证明:e 是连通图G 的割边当且仅当V(G)可划分为两 个子集V1和V2,使对任意u ∈V 1及v ∈V 2, G 中的路(u ,v )必含e . 证明:充分性: e 是G 的割边,故G ?e 至少含有两个连通分支,设V 1是其中一个连通分支的顶点集,V 2是其余分支的顶点集,对12,u V v V ?∈?∈,因为G 中的u,v 不连通, 而在G 中u 与v 连通,所以e 在每一条(u,v)路上,G 中的(u,v)必含e 。 必要性:取12,u V v V ∈∈,由假设G 中所有(u,v)路均含有边e ,从而在G ?e 中不存在从 u 与到v 的路,这表明G 不连通,所以e 是割边。 ● 3.设G 是阶大于2的连通图,证明下列命题等价: (1) G 是块 (2) G 无环且任意一个点和任意一条边都位于同一个圈上; (3) G 无环且任意三个不同点都位于同一条路上。 (1)→(2): G 是块,任取G 的一点u ,一边e ,在e 边插入一点v ,使得e 成为两条边,由此得到新图G 1,显然G 1的是阶数大于3的块,由定理,G 中的u,v 位于同一个圈上,于是G 1中u 与边e 都位于同一个圈上。 (2)→(3): G 无环,且任意一点和任意一条边都位于同一个圈上,任取G 的点u ,边e ,若u 在e 上,则三个不同点位于同一个闭路,即位于同一条路,如u 不在e 上,由定理,e 的两点在同一个闭路上,在e 边插入一个点v ,由此得到新图G 1,显然G 1的是阶数大于3的块,则两条边的三个不同点在同一条路上。
图论及其应用答案电子科 大 This model paper was revised by the Standardization Office on December 10, 2020
习题三: 证明:e是连通图G 的割边当且仅当V(G)可划分为两个子集V1和V2,使对任意u ∈V 1及v ∈V 2, G 中的路(u,v)必含e . 证明:充分性: e是G的割边,故G ?e至少含有两个连通分支,设V 1是其中一个连通分支的顶点集,V 2是其余分支的顶点集,对12,u V v V ?∈?∈,因为G中的u ,v不连通, 而在G中u与v连通,所以e在每一条(u ,v )路上,G中的(u ,v )必含e。 必要性:取12,u V v V ∈∈,由假设G中所有(u ,v )路均含有边e,从而在G ?e中不存在从 u与到v的路,这表明G不连通,所以e 是割边。 3.设G 是阶大于2的连通图,证明下列命题等价: (1) G 是块 (2) G 无环且任意一个点和任意一条边都位于同一个圈上; (3) G 无环且任意三个不同点都位于同一条路上。 (1)→(2): G是块,任取G的一点u,一边e,在e边插入一点v,使得e成为两条边,由此得到新图G 1,显然G 1的是阶数大于3的块,由定理,G中的u,v 位于同一个圈上,于是G 1中u 与边e都位于同一个圈上。 (2)→(3): G无环,且任意一点和任意一条边都位于同一个圈上,任取G的点u ,边e ,若u在e 上,则三个不同点位于同一个闭路,即位于同一条路,如u不在e上,由定理,e的两点在同一个闭路上,在e边插入一个点v ,由此得到新图G 1,显然G 1的是阶数大于3的块,则两条边的三个不同点在同一条路上。 (3)→(1): G连通,若G不是块,则G中存在着割点u,划分为不同的子集块V 1, V 2, V 1, V 2无环,12,x v y v ∈∈,点u在每一条(x ,y )的路上,则与已知矛盾,G是块。 7.证明:若v 是简单图G 的一个割点,则v 不是补图G ?的割点。 证明:v是单图G的割点,则G ?v有两个连通分支。现任取x ,y ∈V (G ?v ), 如果x ,y 不在G ?v的同一分支中,令u是与x ,y处于不同分支的点,那么,x ,与y在G ?v的补图中连通。若x ,y在G ?v的同一分支中,则它们在G ?v的补图中邻接。所以,若v是G 的割点,则v不是补图的割点。 12.对图3——20给出的图G1和G2,求其连通度和边连通度,给出相应的最小点割和最小边割。 解:()12G κ= 最小点割 {6,8} 1()2G λ= 最小边割{(6,5),(8,5)}
习题三: ● 证明:e 是连通图G 的割边当且仅当V(G)可划分为两个子集V1和V2,使对任意u ∈V 1及v ∈V 2, G 中的路(u ,v )必含e . 证明:充分性: e 是G 的割边,故G ?e 至少含有两个连通分支,设V 1是其中一个连通分支的顶点集,V 2是其余分支的顶点集,对12,u V v V ?∈?∈,因为G 中的u,v 不连通,而在G 中u 与v 连 通,所以e 在每一条(u,v)路上,G 中的(u,v)必含e 。 必要性:取12,u V v V ∈∈,由假设G 中所有(u,v)路均含有边e ,从而在G ?e 中不存在从u 与到v 的 路,这表明G 不连通,所以e 是割边。 ● 3.设G 是阶大于2的连通图,证明下列命题等价: (1) G 是块 (2) G 无环且任意一个点和任意一条边都位于同一个圈上; (3) G 无环且任意三个不同点都位于同一条路上。 (1)→(2): G 是块,任取G 的一点u ,一边e ,在e 边插入一点v ,使得e 成为两条边,由此得到新图G 1,显然G 1的是阶数大于3的块,由定理,G 中的u,v 位于同一个圈上,于是G 1中u 与边e 都位于同一个圈上。 (2)→(3): G 无环,且任意一点和任意一条边都位于同一个圈上,任取G 的点u ,边e ,若u 在e 上,则三个不同点位于同一个闭路,即位于同一条路,如u 不在e 上,由定理,e 的两点在同一个闭路上,在e 边插入一个点v ,由此得到新图G 1,显然G 1的是阶数大于3的块,则两条边的三个不同点在同一条路上。 (3)→(1): G 连通,若G 不是块,则G 中存在着割点u ,划分为不同的子集块V 1, V 2, V 1, V 2无环, 12,x v y v ∈∈,点u 在每一条(x,y)的路上,则与已知矛盾,G 是块。 ● 7.证明:若v 是简单图G 的一个割点,则v 不是补图G ?的割点。 证明:v 是单图G 的割点,则G ?v 有两个连通分支。现任取x,y ∈V(G ?v), 如果x,y 不在G ?v 的同一分支中,令u 是与x,y 处于不同分支的点,那么,x,与y 在G ?v 的补图中连通。若x,y 在G ?v 的同一分支中,则它们在G ?v 的补图中邻接。所以,若v 是G 的割点,则v 不是补图的割点。 ● 12.对图3——20给出的图G1和G2,求其连通度和边连通度,给出相应的最小点割和最小边割。 解:()12G κ= 最小点割 {6,8} 1()2G λ= 最小边割{(6,5),(8,5)} ()25G κ= 最小点割{6,7,8,9,10} 2()5G λ= 最小边割{(2,7)…(1,6)} ● 13.设H 是连通图G 的子图,举例说明:有可能k(H)> k(G). 解: 通常k (H ) 图和子图 图 图 G = (V, E), 其中 V = {νv v v ,......,,21} V ---顶点集, ν---顶点数 E = {e e e 12,,......,ε} E ---边集, ε---边数 例。 左图中, V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意, 左图仅仅是图G 的几何实现(代表), 它们有无穷多个。真正的 图G 是上面所给出式子,它与顶点的位置、边的形状等无关。不过今后对两者将经常不加以区别。 称 边 ad 与顶点 a (及d) 相关联。也称 顶点 b(及 f) 与边 bf 相关联。 称顶点a 与e 相邻。称有公共端点的一些边彼此相邻,例如p 与af 。 环(loop ,selfloop ):如边 l 。 棱(link ):如边ae 。 重边:如边p 及边q 。 简单图:(simple graph )无环,无重边 平凡图:仅有一个顶点的图(可有多条环)。 一条边的端点:它的两个顶点。 记号:νε()(),()().G V G G E G ==。 习题 1.1.1 若G 为简单图,则 εν≤?? ?? ?2 。 1.1.2 n ( ≥ 4 )个人中,若每4人中一定有一人认识其他3人,则一定有一 人认识其他n-1人。 同构 在下图中, 图G 恒等于图H , 记为 G = H ? V (G)=V(H), E(G)=E(H)。 图G 同构于图F ? V(G)与V(F), E(G)与E(F)之间各存在一一对应关系,且这二对应关系保持关联关系。 记为 G ?F 。 注 往往将同构慨念引伸到非标号图中,以表达两个图在结构上是否相同。 d e f G = (V, E) y z w c G =(V , E ) w c y z H =(V ?, E ?) ?a ? c ? y ? e ?z ? F=(V ??, E ??) 图论及其应用 学时:40 学分:2 课程属性:专业选修课开课单位:理学院 先修课程:高等代数后续课程:无 一、课程的性质 《图论及其应用》是数学与应用数学专业的专业选修课程。 二、教学目的 通过教学,使学生掌握图论及其算法的基本理论和基本技巧,初步掌握图论及其算法的基本应用手段、基本算法设计及编程,并能用所学理论解决一些应用问题。 三、教学内容 1.图的基本概念 2.图的连通性 3.树的基本性质及其应用 4.Euler Graphs and Hamilton Graphs with Applications 5.平面图性质 6.匹配,求最大匹配算法及应用 7.图的染色及应用 8.极图理论 四、学时分配 章课程内容学时 1 图的基本概念 4 2 图的连通性 6 3 树的基本性质及其应用 6 4 Euler Graphs and Hamilton Graphs with Applications 4 5 平面图性质 6 6 匹配,求最大匹配算法及应用 6 7 图的染色及应用 4 8 极图理论 4 合计40 五、教学方式 本课程采用多媒体课堂讲授,结合实际范例深入浅出讲解讨论。 六、考核方式 本课程考核采用平时与期末考核相结合的办法,特别注重平时的考核,作业采用简单练习、论文等形式,期末考试采用简单考题或论文形式。 七、教材及教学参考书 参考教材: [1] J.A.Bondy and U.S.R.Murty. Graph Theory with Applications, The Macmillan Press LTD,1976. [2] 蒋长浩.图论与网络流.北京:中国林业出版社,2000. 参考书目: [1] Bela Bollobas.Modern Graph Theory(现代图论,影印版).北京:科学出版社,2001. [2] 殷剑宏、吴开亚.图论及其算法.合肥:中国科学技术大学出版社,2003. [3] 谢金星、邢文训.网络优化.北京:清华大学出版社.2000. [4] 程理民、吴江、张玉林.运筹学模型与方法教程.北京:清华大学出版社,2000. [5] 三味工作室.SPSS V10.0 for Windows 实用基础教程.北京:北京希望电子出版社2001. [6] 孙魁明、张海彤.Mathematica工具软件大全.北京:中国铁道出版社,1994. [7] 楼顺天、于卫、闫华梁.MATLAB程序设计语言.西安:西安电子科技大学出版社,1997.八、教学基本内容及要求 第一章图的基本概念 1.教学基本要求 掌握的图的基本概念、特殊图概念,了解最短路问题。 2.教学具体内容 图的基本概念,路和圈,最短路问题。 习题三: ● 证明:是连通图G 的割边当且仅当V(G)可划分为两个子集V1和V2,使对任意及, G 中的路必含. 证明:充分性: 是的割边,故至少含有两个连通分支,设是其中一个连通分支的顶点集,是其余分支的顶点集,对12,u V v V ?∈?∈,因为中的不连通,而在中与连通,所以在每一条路上,中的必含。 必要性:取12,u V v V ∈∈,由假设中所有路均含有边,从而在中不存在从与到的路,这表明不连通,所以e 是割边。 ● 3.设G 是阶大于2的连通图,证明下列命题等价: (1) G 是块 (2) G 无环且任意一个点和任意一条边都位于同一个圈上; (3) G 无环且任意三个不同点都位于同一条路上。 : 是块,任取的一点,一边,在边插入一点,使得成为两条边,由此得到新图,显然的是阶数大于3的块,由定理,中的u,v 位于同一个圈上,于是 中u 与边都位于同一个 圈上。 : 无环,且任意一点和任意一条边都位于同一个圈上,任取的点u ,边e ,若在上,则三个不同点位于同一个闭路,即位于同一条路,如不在上,由定理,的两点在同一个闭路上,在边插入一个点v ,由此得到新图,显然的是阶数大于3的块,则两条边的三个不同点在同一条路上。 : 连通,若不是块,则中存在着割点,划分为不同的子集块,,,无环,12,x v y v ∈∈,点在每一条的路上,则与已知矛盾,是块。 ● 7.证明:若v 是简单图G 的一个割点,则v 不是补图的割点。 证明:是单图的割点,则有两个连通分支。现任取, 如果不在的 同一分支中,令是与 处于不同分支的点,那么,与在的补图中连通。若在的同一分支中,则它们在的补图中邻接。所以,若是的割点,则不是补图的割点。 ● 12.对图3——20给出的图G1和G2,求其连通度和边连通度,给 出相应的最小点割和最小边割。 解:()12G κ= 最小点割 {6,8} 1()2G λ= 最小边割{(6,5),(8,5)} ()25G κ= 最小点割{6,7,8,9,10} 2()5G λ= 最小边割{(2,7)…(1,6)} ● 13.设H 是连通图G 的子图,举例说明:有可能k(H)> k(G). 解: 通常. 整个图为,割点左边的图为的的子图, ,则. e H 电子科技大学研究生试题图论及其应用参考答 案 HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】 电子科技大学研究生试题 《图论及其应用》(参考答案) 考试时间:120分钟 一.填空题(每题3分,共18分) 1.4个顶点的不同构的简单图共有__11___个; 2.设无向图G 中有12条边,已知G 中3度顶点有6个,其余顶点的度数均小于3。则G 中顶点数至少有__9___个; 3.设n 阶无向图是由k(k2)棵树构成的森林,则图G 的边数m= _n-k____; 4.下图G 是否是平面图?答__是___; 是否可1-因子分解?答__是_. 5.下图G 的点色数=)(G χ______, 边色数=')(G χ__5____。 图G 二.单项选择(每题3分,共21分) 1.下面给出的序列中,是某简单图的度序列的是( A ) (A) (11123); (B) (233445); (C) (23445); (D) (1333). 2.已知图G 如图所示,则它的同构图是( D ) 3. 下列图中,是欧拉图的是( D ) 4. 下列图中,不是哈密尔顿图的是(B ) 5. 下列图中,是可平面图的图的是(B ) 6.下列图中,不是偶图的是( B ) 7.下列图中,存在完美匹配的图是(B ) 三.作图(6分) 1.画出一个有欧拉闭迹和哈密尔顿圈的图; 2.画出一个有欧拉闭迹但没有哈密尔顿圈的图; 3.画出一个没有欧拉闭迹但有哈密尔顿圈的图; 解: 四. A C D 1 2 3 A B C D 解:由克鲁斯克尔算法的其一最小生成树如下图: 权和为:20. 五.(8分) 求下图G 的色多项式P k (G). 解:用公式 )(e G P k -G 的色多项式: )3)(3)()(345-++=k k k G P k 。 六.(10分) 一棵树有n 2个顶点的度数为2,n 3个顶点的度数为3,…,n k 个顶点的度数 为k ,而其余顶点的度数为1,求1度顶点的个数。 解:设该树有n 1个1度顶点,树的边数为m. 一方面:2m=n 1+2n 2+…+kn k 另一方面:m= n 1+n 2+…+n k -1 由上面两式可得:n 1=n 2+2n 3+…+(k -1)n k 七.证明:(8分) 设G 是具有二分类(X,Y)的偶图,证明(1)G 不含奇圈;(2)若|X |≠|Y |,则G 是非哈密尔顿图。 证明:(1) 若不然,设C=v 1v 2…v m v 1为G 的一个奇圈,不妨设v 1X, v 5 v v v 6 图G 习题一(yangchun): 4.证明下面两图同构。 证明:作映射f : v i ? u i (i=1,2….10) 容易证明,对?v i v j ∈ E ((a)),有f (v i v j,),=,u i,u j,∈,E,((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知,图(a)与(b)是同构的。 5.证明:四个顶点的非同构简单图有11个。 证明:设四个顶点中边的个数为m ,则有: m=0: m=1 : m=2: m=3: m=4: (a) v 23 4 (b) m=5: m=6: 因为四个顶点的简单图最多就是具有6条边,上面所列出的情形是在不同边的条件下的不同构的情形,则从上面穷举出的情况可以看出四个顶点的非同构简单图有11个。 11.证明:序列(7,6,5,4,3,3,2)和(6,6,5,4,3,3,1)不是图序列。 证明:由于7个顶点的简单图的最大度不会超过6,因此序列(7,6,5,4,3,3,2)不是图序列; (6,6,5,4,3,3,1)是图序列 1 1 12312(1,1,,1,,,)d d n d d d d d π++=--- 是图序列 (5,4,3,2,2,0)是图序列,然而(5,4,3,2,2,0)不是图序列,所以(6,6,5,4,3,3,1)不是图序列。 ● 12.证明:若 ,则包含圈。 证明:下面仅对连通图的下的条件下进行证明,不连通的情形可以通过分成若干 个连通的情形来证明。设 , 对于中的路 若与邻接,则构成一个闭路。若是一条路,由于,因 此,对于,存在与之邻接,则构成一个圈。 ● 17.证明:若G 不连通,则连通。 证明:对于任意的 ,若与属于G 的连通分支,显然与在中连通; 图论的发展及其在生活中的应用 数学与应用数学张佳丽 指导教师刘秀丽 摘要主要介绍了图论的起源与发展及其生活中的若干应用,如:渡河问题、旅游推销员问题、最小生成树问题、四色问题、安排问题、中国邮递员问题。同时也涉及到了几种在图论中应用比较广泛的方法,如:最邻近法、求最小生成树的方法、求最优路线的方法等。 关键词图论生活问题应用 Graph Theory Development and the Application in Life Mathematics and applied mathematics Zhang Jiali Tutor Liu Xiuli Abstract This paper mainly introduces the origin and development of graph theory and its several applications in our life, such as: crossing river problem, traveling salesman problem, minimum spanning tree problem, four color problem,arrangement problem,Chinese postman problem.It also researches several methods that are more widely applied in graph theory, for example: the method of most neighboring, the method of solving the minimum spanning tree,the method of the best route,and so on. Key words graph theory life problem application 引言 图论是一门古老的学科,是数学中有广泛应用的一个分支,与其他的数学分支,如群论、矩阵论、概率论、拓扑学、数分析等有着密切的联系.图论中以图为研究对象,图形中我们用点表示对象,两点之间的连线表示对象之间的某种特定的关系.事实上,任何一个包含了二元关系的系统都可以用图论来模拟.而且,图论能把纷杂的信息变的有序、直观、清晰.由于我们感兴趣的是两对象之间是否有某种特定关系,所以图形中两点间连接与否尤为重要,而图形的位置、大小、形状及连接线的曲直长短则无关紧要.图论在自然科学、社会科学等各个领域都有广泛的应用.随着科学的发展,以及生产管理、军事、交通运输等方面提出了大量实际的需要,图论的理论及其应用研究得到飞速发展。从20世纪50年代以后,由于计算机的迅速发展,有力地推动了图论的发展,加速了图论向各个学科的渗透,尤其是网络理论的建立,图论与线性规划、动态规划等优化理论和方法互相渗透。同时,计算机的发展使图论成为数学领域中发展最快的分支 在通信领域中,传输信息的方法有两种,其一是等长码制方法,其二是非等长码制方式;字符出现的频率不同,在传输中采用非等长二进制编码传输会提高传输效率,在字符的出现频率已知前提下,采用最优二叉正则树算法,可以得到最佳前缀码。 关键字正则二叉树 前缀码 最优二叉树 哈夫曼编码 频率 java 程序 引言 在通信中,通常采用二进制编码表示符号,如果每个要传输的符号使用频率相同,则采用等长码表示即可,但事实上不同符号在传输过程中出现的频率并不相同,有些符号出现频率相差很大,此时采用非等长编码可节省二进制数位,可达到提高效率的目的。 相关基础知识 下面介绍有关二叉树以及哈夫曼编码的相关知识: 定义1:一个有向图,若不考虑他的方向,他是一棵树,则称这个有向图为有向树。一颗有向树,如果恰有一个结点的入度为0,其余所有结点的入度都为1,则称为根树,其中入度为0的结点称为树根,出度为0的结点称为树叶,出度不为0的结点称为分支点或内点。 在根树中,称从树根到结点v 的距离称为该点的层次。 定义2:在根树中,若从i v 到 j v 可达,则称i v 是j v 的祖先,j v 是i v 的后代,又若),(j i v v 是树根中的有向边,则称i v 是j v 的父亲,j v 是i v 的儿子;如果两个结点是同一结点的儿子,则称这两个结点是兄弟。 定义3:在根树中,任一结点v 及其v 的后代和从v 出发的所有有向路中的边构成的子图称为以v 为根的子路,根树中的结点u 的子树是以u 的儿子为根的子树。 定义4:如果在根树中规定了每一层次上结点的次序,这样的根树称为有序树。在有序树中规定了同一层次结点的次序是从左至右。 定义5:一个有向图,如果他的每个连通分支是有向树,则称该有向图为森林;在森林中,如果所有树都是有序树且给树指定了次序,则称此森林为有序森林。 学号:201321010808 姓名:马涛 习题1 4.证明图1-28中的两图是同构的 证明 将图1-28的两图顶点标号为如下的(a)与(b)图 作映射f : f(v i )→u i (1≤ i ≤ 10) 容易证明,对?v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知,图1-27的两个图是同构的。 6.设G 是具有m 条边的n 阶简单图。证明:m =???? ??2n 当且仅当G 是完全图。 证明 必要性 若G 为非完全图,则? v ∈V(G),有d(v)< n-1 ? ∑ d(v) < n(n-1) ? 2m 证明 由于G 为k 正则偶图,所以,k | V 1 | =m = k | V 2 | ? ∣V 1∣= ∣V 2 ∣。 12.证明:若δ≥2,则G 包含圈。 证明 只就连通图证明即可。设V(G)={v 1,v 2,…,v n },对于G 中的路v 1v 2…v k ,若v k 与v 1邻接,则构成一个圈。若v i1v i2…v in 是一条路,由于δ≥ 2,因此,对v in ,存在点v ik 与之邻接,则v ik ?v in v ik 构成一个圈 。 17.证明:若G 不连通,则G 连通。 证明 对)(,_G V v u ∈?,若u 与v 属于G 的不同连通分支,显然u 与v 在_ G 中连通;若u 与v 属于g 的同一连通分支,设w 为G 的另一个连通分支中的一个顶点,则u 与w ,v 与w 分别在_ G 中连通,因此,u 与v 在_ G 中连通。 习题2 证明:每棵恰有两个1度顶点的树均是路。 证明:设树T 为任意一个恰有两个1度顶点的树,则T 是连通的,且无圈,令V 1 、V 2 为度为1的顶点,由于其他的顶点度数均为0或者2,且T 中无圈,则从V 1到V 2 有且只有一条连通路。所以,每棵恰有两个1度顶点的树均是路。得证。 证明:正整数序列),...,,(21n d d d 是一棵树的度序列当且仅当)1(21-=∑=n d n i i 。 证明:设正整数序列),...,,(21n d d d 是一棵树T 的度序列,则满足E d n i i 21 =∑=,E 为T 的边数,又有边数和顶点的关系1+=E n ,所以)1(21 -=?∑=n d n i i 证明:若e 是n K 的边,则3)2()(--=-n n n n e K τ。 若e 为Kn 的一条边,由Kn 中的边的对称性以及每棵生成树的边数为n-1,Kn 的所有生成树的总边数为:2)1(--n n n ,所以,每条边所对应的生成树的棵数 为: 32 2)1(2 1 )1(--=--n n n n n n n ,所以,K n - e 对应的生成树的棵数为: 332)2(2)(----=-=-n n n n n n n n e K τ Kruskal 算法能否用来求: 习题一 1. (题14):证明图1-28中的两图是同构的 证明 将图1-28的两图顶点标号为如下的(a)与(b)图 作映射f : f(v i )→u i (1≤ i ≤ 10) 容易证明,对?v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知,图1-27的两个图是同构的。 2. (题6)设G 是具有m 条边的n 阶简单图。证明:m =???? ??2n 当且仅当G 是 完全图。 证明 必要性 若G 为非完全图,则? v ∈V(G),有d(v)< n-1 ? ∑ d(v) < n(n-1) ? 2m 证明 由于G 为k 正则偶图,所以,k | V 1 | =m = k | V 2 | ? ∣V 1∣= ∣V 2 ∣。 4. (题12)证明:若δ≥2,则G 包含圈。 证明 只就连通图证明即可。设V(G)={v 1,v 2,…,v n },对于G 中的路v 1v 2…v k ,若v k 与v 1邻接,则构成一个圈。若v i1v i2…v in 是一条路,由于δ≥ 2,因此,对v in ,存在点v ik 与之邻接,则v ik ?v in v ik 构成一个圈 。 5. (题17)证明:若G 不连通,则G 连通。 证明 对)(,_ G V v u ∈?,若u 与v 属于G 的不同连通分支,显然u 与v 在_ G 中连通;若u 与v 属于g 的同一连通分支,设w 为G 的另一个连通分支中的一个顶点,则u 与w ,v 与w 分别在_ G 中连通,因此,u 与v 在_ G 中连通。 习题二 2、证明:每棵恰有两个1度顶点的树均是路。 证明:设树T 为任意一个恰有两个1度顶点的树,则T 是连通的,且无圈,令V 1 、V 2 为度为1的顶点,由于其他的顶点度数均为0或者2,且T 中无圈,则从V 1到V 2 有且只有一条连通路。所以,每棵恰有两个1度顶点的树均是路。得证。 5、证明:正整数序列),...,,(21n d d d 是一棵树的度序列当且仅当 )1(21 -=∑=n d n i i 。 证明:设正整数序列),...,,(21n d d d 是一棵树T 的度序列,则满足 E d n i i 21 =∑=,E 为T 的边数,又有边数和顶点的关系1+=E n ,所以)1(21 -=? ∑=n d n i i 14、证明:若e 是n K 的边,则3 )2()(--=-n n n n e K τ。 若e 为Kn 的一条边,由Kn 中的边的对称性以及每棵生成树的边数为n-1,Kn 的所有生成树的总边数为:2 )1(--n n n ,所以,每条边所对应的生成树的棵数为: 32 2)1(2 1 )1(--=--n n n n n n n ,所以,K n - e 对应的生成树的棵数为: 332)2(2)(----=-=-n n n n n n n n e K τ 16、Kruskal 算法能否用来求: (1)赋权连通图中的最大权值的树? (2)赋权图中的最小权的最大森林?如果可以,怎样实现? 1. (题14):证明图1-28中的两图是同构的 证明 将图1-28的两图顶点标号为如下的(a)与(b)图 作映射f : f(v i )u i (1 i 10) 容易证明,对v i v j E((a)),有f(v i v j )u i u j E((b)) (1 i 10, 1j 10 ) 由图的同构定义知,图1-27的两个图是同构的。 2. (题6)设G 是具有m 条边的n 阶简单图。证明:m =???? ??2n 当且仅当G 是 完全图。 证明 必要性 若G 为非完全图,则 v V(G),有d(v) n-1 d(v) n(n-1) 2m n(n-1) m n(n-1)/2=??? ? ??2n , 与已知矛盾! 充分性 若G 为完全图,则 2m= d(v) =n(n-1) m= ??? ? ??2n 。 3. (题9)证明:若k 正则偶图具有二分类V = V 1∪V 2,则 | V 1| = |V 2|。 证明 由于G 为k 正则偶图,所以,k V 1 =m = k V 2 V 1 = V 2 。 4. (题12)证明:若δ≥2,则G 包含圈。 图1-28 (a) v 1 v 2 v 3 v 4 v 5 v 6 v 7 v 8 v 9 v 10 u 1 u 2 u 3 u 4 u 5 u 6 u u 8 u u 10 (b) 证明 只就连通图证明即可。设V(G)={v 1,v 2,…,v n },对于G 中的路v 1v 2…v k ,若v k 与v 1邻接,则构成一个圈。若v i1v i2…v in 是一条路,由于 2,因此,对v in ,存在点v ik 与之邻接,则v ik v in v ik 构成一个圈 。 5. (题17)证明:若G 不连通,则G 连通。 证明 对)(,_ G V v u ∈?,若u 与v 属于G 的不同连通分支,显然u 与v 在_ G 中连通;若u 与v 属于g 的同一连通分支,设w 为G 的另一个连通分支中的一个顶点,则u 与w ,v 与w 分别在_ G 中连通,因此,u 与v 在_ G 中连通。 习题二 2、证明:每棵恰有两个1度顶点的树均是路。 证明:设树T 为任意一个恰有两个1度顶点的树,则T 是连通的,且无圈,令V 1 、V 2 为度为1的顶点,由于其他的顶点度数均为0或者2,且T 中无圈,则从V 1到V 2 有且只有一条连通路。所以,每棵恰有两个1度顶点的树均是路。得证。 5、证明:正整数序列),...,,(21n d d d 是一棵树的度序列当且仅当 )1(21 -=∑=n d n i i 。 证明:设正整数序列),...,,(21n d d d 是一棵树T 的度序列,则满足 E d n i i 21 =∑=,E 为T 的 边数,又有边数和顶点的关系1+=E n ,所以)1(21 -=? ∑=n d n i i 14、证明:若e 是n K 的边,则3 )2()(--=-n n n n e K τ。 若e 为Kn 的一条边,由Kn 中的边的对称性以及每棵生成树的边数为n-1,Kn 的所有生 成树的总边数为: 2 )1(--n n n ,所以,每条边所对应的生成树的棵数为: 32 2)1(2 1 )1(--=--n n n n n n n ,所以,K n - e 对应的生成树的棵数为: 332)2(2)(----=-=-n n n n n n n n e K τ 16、Kruskal 算法能否用来求: (1)赋权连通图中的最大权值的树? (2)赋权图中的最小权的最大森林?如果可以,怎样实现? 解:(1)不能,Kruskal 算法得到的任何生成树一定是最小生成树。 (2)可以,步骤如下: 习题一 证明将图1-28的两图顶点标号为如下的(a)与(b)图 n(n-1)/2= 2,与已知矛盾! 充分性若G为完全图,则2m= d(v) =n(n-1) 3. (题9)证明:若k正则偶图具有二分类V= V1U V2,则| V1I = | 10) U i (1 i E((a)),有f(v i V j) UU j E((b)) (1 i 10, 1 j 1-27的两个图是同构的。 2.(题6)设G是具有m条边的n阶简单图。证明: ;当且仅当G是 完全图。 证明必要性若G为非完全图,则v V(G),有d(v) n(n-1) 2m n(n-1) n-1 d(v) m= 1.(题14):证明图1-28中的两图是同构的 图1-28 i) V i V 作映射f: f(v 容易 证明,对 10 ) 由图的同构定义知,图 2 证明 由于G 为k 正则偶图,所以,k V i =m= k V 2 V 1 = V 2 。 4. (题12)证明:若3》2,则G 包含圈。 证明 只就连通图证明即可。设 V(G)= {V l ,V 2,…,v n },对于G 中的路V l V 2… V k ,若V k 与V i 邻接,则构成一个圈。若V ii V i2…V in 是一条路,由于 2,因此, 对V in ,存在点V ik 与之邻接,则V ik V in V ik 构成一个圈。 5. (题17)证明:若G 不连通,则G 连通。 证明 对u,V V(G),若u 与V 属于G 的不同连通分支,显然u 与V 在G 中 连通;若u 与V 属于g 的同一连通分支,设w 为G 的另一个连通分支中的一个顶 点,则u 与w, V 与w 分别在G 中连通,因此,u 与V 在G 中连通。 习题二 2、证明:每棵恰有两个 1度顶点的树均是路。 证明:设树T 为任意一个恰有两个1度顶点的树,则 T 是连通的,且无圈,令 V i 、V 2为度为1的顶点,由于其他的顶点度数均为 0或者2,且T 中无圈,则从 M 到V 2有且 只有一条连通路。所以,每棵恰有两个 1度顶点的树均是路。得证。 n 5、证明:正整数序列(d 「d 2,…,d n )是一棵树的度序列当且仅当 d i 2(n 1)。 i 1 n 证明:设正整数序列(d^d ?,…,d n )是一棵树T 的度序列,则满足 d j i 1 n 边数,又有边数和顶点的关系 n E 1,所以 d i 2(n 1) i 1 14、证明:若e 是K n 的边,则(K n e) (n 2)n n 3。 若e 为Kn 的一条边,由Kn 中的边的对称性以及每棵生成树的边数为 n-1,Kn 的所有生 所以,K n - e 对应的生成树的棵数为: n 2 n 3 n 3 (K n e) n 2n (n 2)n 16、Kruskal 算法能否用来求: (1 )赋权连通图中的最大权值的树 2E ,E 为T 的 成树的总边数为:(n 1)n n 2 ,所以,每条边所对应的生成树的棵数为: n 2 (n 1)n 」 n(n 1) 2 小 n 3 2n 习题1 1. 证明在n阶连通图中 (1)至少有n-1条边。 (2)如果边数大于n-1,则至少有一条闭通道。 (3)如恰有n-1条边,则至少有一个奇度点。 证明(1) 若对v∈V(G),有d(v)≥2,则:2m=∑d(v)≥2n ? m≥n>n-1,矛盾! 若G中有1度顶点,对顶点数n作数学归纳。 当n=2时,G显然至少有一条边,结论成立。 设当n=k时,结论成立, 当n=k+1时,设d(v)=1,则G-v是k阶连通图,因此至少有k-1条边,所以G 至少有k条边。 (2) 考虑v1→v2→?→v n的途径,若该途径是一条路,则长为n-1,但图G的边数大于n-1,因此存在v i,v j,使得v i adgv j,这样,v i→v i+1→?→v j并上v i v j构成一条闭通道;若该途径是一条非路,易知,图G有闭通道。 (3) 若不然,对v∈V(G),有d(v)≥2,则:2m=∑d(v)≥2n ? m≥n>n-1,与已知矛盾! 2.设G是n阶完全图,试问 (1)有多少条闭通道? (2)包含G中某边e的闭通道有多少? (3)任意两点间有多少条路? 答(1) (n-2)! (2) (n-1)!/2 (3) 1+(n-2)+(n-2)(n-3)+(n-2)(n-3)(n-4)+…+(n-2)…1. 3.证明图1-27中的两图不同构: 图1-27 证明容易观察出两图中的点与边的邻接关系各不相同,因此,两图不同构。 4.证明图1-28中的两图是同构的 图1-28 证明将图1-28的两图顶点标号为如下的(a)与(b)图 作映射f : f(v i )→u i (1≤ i ≤ 10) 容易证明,对v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知,图1-27的两个图是同构的。 5. 证明:四个顶点的非同构简单图有11个。 证明 m=0 1 2 3 4 5 6 由于四个顶点的简单图至多6条边,因此上表已经穷举了所有情形,由上表知:四个顶点的非同构简单图有11个。 6. 设G 是具有m 条边的n 阶简单图。证明:m =??? ? ??2n 当且仅当G 是完全图。 证明 必要性 若G 为非完全图,则 v ∈V(G),有d(v)< n-1 ? ∑ d(v) < n(n-1) ? 2m 图论及其应用
图论及其应用(精)
图论及其应用 答案电子科大
电子科技大学研究生试题图论及其应用参考答案完整版
图论及其应用第一章答案(电子科大版)
图论的发展及其在现实生活中的几个应用
图论及其应用期末论文
图论及其应用1-3章习题答案(电子科大) (1)
图论及其应用13章习题答案电子科大
图论及其应用1-3章习题答案
图论及其应用1-3章习题答案
图论与应用第一章完整作业