(整理)实验六函数的极值.
- 格式:doc
- 大小:333.50 KB
- 文档页数:9

函数求极值的方法总结函数求极值的方法总结数学主要以函数为研究对象,而函数极值无论在初等数学还是在高等数学里都是函数部分的一个重要问题,下文是函数求极值的方法,希望对同学们有帮助!一、利用二次方程的判别式求极值在求某一类分式函数的极值时,若其分子或分母是关于x的二次式,可将其变为关于x的一元二次方程,根据x在实数范围内有解,由判别式求的。
例1、求函数y=求函数极值的若干方法的极值。
解:将原函变形为关于x的二次方程(y-1)x 求函数极值的若干方法 -2yx-3y=0∵x∈R,且x≠3,x≠-1,∴上方程在实数范围内一定有解。
△= (-2y) 求函数极值的若干方法 -4 (-3y)(y-1)= 4y(4y-3)≥0解之得y≤0 或y≥ 求函数极值的若干方法这里虽然y无最大(小)值,但对应于y=0和y= 求函数极值的若干方法的x分别为x=0和x=-3,所以当x=0时,y有极大值0,当x=-3时,y有极小值求函数极值的若干方法。
例2、求函数y= 求函数极值的若干方法的值域。
解:将原函数变形得:y+yx 求函数极值的若干方法 =2x∵x∈R,∴△= 4-4y 求函数极值的若干方法≥0,解之得:-1≤y≤1∴函数y= 求函数极值的若干方法值域为[-1,1]由上面两例可以看出,用二次方程的判别式求函数的极值时,实际上就是将y看作x的系数,利用函数的定义域非空,即方程有解,将问题转化为解一元二次不等式。
但要注意的是:在变型过程中,可能会将x的取值范围扩大,但所求函数的极值一定在不等式的解集内,此时,要注意检验,即招2出y取极值时的x是否有意义,若无意义必须舍去,再重新考虑其极值。
二、利用倒数关系求极值对于有些分式函数,当其分子不含变量时,可由分母的极值来求整个函数的极值。
例3、求函数y=2- 求函数极值的若干方法的最小值。
解:∵x 求函数极值的若干方法 -2x+6 = (x-1) 求函数极值的若干方法 +5>0∴函数的定义域为一切实数,又由x 求函数极值的若干方法-2x+6=(x-1) 求函数极值的若干方法 +5 知当x=1时,求函数极值的若干方法取最小值求函数极值的若干方法 ,∴ 求函数极值的若干方法取最大值求函数极值的若干方法 ,此时 y=2- 求函数极值的若干方法取最小值 2- 求函数极值的若干方法 ,即当x=1时,有y的最小值是 2- 求函数极值的若干方法。


研究函数的极值与最值问题在数学中,研究函数的极值和最值问题是非常重要的。
通过研究函数的极值和最值,我们可以了解函数的性质,并解决许多实际问题。
一、极值问题函数的极值是指在一定范围内的最大值或最小值。
为了求得函数的极值,我们需要先求出函数的导数,然后令导数为零并解方程,得到极值对应的自变量值。
接下来,可以通过代入自变量值进入原函数来求得极值。
举个例子,考虑函数 f(x) = 2x^3 - 3x^2 - 12x + 4 在区间 [-2, 3] 上的极值问题。
首先,我们求得导数 f'(x) = 6x^2 - 6x - 12。
令 f'(x) = 0,解方程可以得到x = -1 和 x = 2。
接着,我们将这两个值代入原函数 f(x) 中,可以得到 f(-1) = -7 和 f(2) = 6。
所以,在区间 [-2, 3] 上,函数 f(x) 的最小值为 -7,对应的自变量 x = -1,函数 f(x) 的最大值为 6,对应的自变量 x = 2。
二、最值问题函数的最值是指函数在整个定义域内的最大值或最小值。
为了求得函数的最值,我们需要先求得函数的导数,并研究其在定义域内的增减性以及边界情况。
根据导数和边界的关系,可以找到函数在定义域内的最值。
以函数 g(x) = x^2 + 4x - 3 为例,我们可以求得导数 g'(x) = 2x + 4。
通过观察导数的符号,我们可以发现在 x < -2 时,导数为负数,表示函数 g(x) 单调递减;在 x > -2 时,导数为正数,表示函数 g(x) 单调递增。
由于函数 g(x) 是一个二次函数,我们可以知道当 x 趋近无穷大或无穷小时,函数的值无限增大,因此函数g(x) 在无穷大时没有最大值。
另外,函数 g(x) 在定义域内都是连续的,所以可以确定函数 g(x) 存在最小值。
为了找到函数 g(x) 的最小值,我们可以考虑其导数为零的情况。


实验六 函数极值及零点的求解一、实验目的熟悉函数极值及零点的求解方法及相关指令二、实验原理1. 函数的极值的求解全局极小值:绘制函数曲线,粗略观察全局极小值范围,然后在此范围内利用下面的局部极小值求解函数求极小值。
局部极小值:fminbnd 函数:只能用于一元函数极小值求解,调用格式为[x,fval,exitflag,output]=fminbnd(fun,x1,x2,options)fun 为待求解的函数,可以用字符串、内联对象、匿名函数或函数文件句柄表达,x1,x2为求解时自变量的取值区间。
x 为搜索到的最小值对应的自变量值,fval 为函数最小值,exitflag 返回是否搜索到最小值标志,output 给出优化算法及迭代次数等信息。
fminsearch :一元或多元函数极小值求解,调用格式为[x,fval,exitflag,output]=fminsearch(fun,x0,options)x0是由各变量构成的搜索起点,也可以是多个搜索起点构成的矩阵,每一列代表一个搜索起点,此时找到多个极值。
fval 为搜索到的单个极小值或多个极值中最小的那个函数值。
其他参量与fminbnd 函数参量含义相同。
2.函数零点的求解fzero 函数:只能用于求解一元函数零点,调用格式为[x,fval]=fzero(fun,x0)fun 是字符串、内联对象、匿名函数或函数文件句柄表达的函数式,求解函数式等于零时的解,x0为搜索范围或在其附近搜索解。
fsolve 函数:可用于求解一元或多元函数零点,调用格式为[x,fval]=fsolve(fun,x0)求解多元函数零点时,各变量需写成一个列向量作为一个变量。
参数与fzero 含义及使用方法一致。
三、实验内容及步骤1.求函数5.08.1)2cos(5.1))5(sin()(206.02++-=t t t e t t f t 在区间[-5,5]中的最小值点。
2. 求0))sin(sin(105.02.0=-+--t e t t 的实数解。

函数的极值与最值的求解(导数法)函数的极值与最值是数学中重要的概念,它们在数学建模、优化问题等方面具有广泛的应用。
在本文中,我们将介绍如何使用导数法求解函数的极值与最值问题。
一、函数的极值与最值在介绍如何求解函数的极值与最值之前,我们首先需要明确这两个概念的定义。
对于函数f(x),如果存在一个区间I,对于区间内的任意x,都有f(x)≤f(x0)(或f(x)≥f(x0)),那么f(x0)就是函数在区间I内的极小值(或极大值)。
而函数f(x)在整个定义域内的最小值和最大值则被称为函数的最小值和最大值。
二、导数法求解极值与最值导数法是求解函数极值与最值常用的方法之一。
通过求解函数的导数和判断导数的正负,可以找到函数的极值点及其对应的极值。
1. 求解函数的极值点首先,我们需要求解函数f(x)的导数,并令导数等于零,即f'(x)=0。
解这个方程可以得到函数的临界点(即导函数为零的点),也就是可能的极值点。
2. 判断极值类型在求得了函数的临界点之后,我们需要判断每个临界点对应的极值类型,即是极小值还是极大值。
我们可以通过求解导数的二阶导数来判断,即求解f''(x),其中f''(x)表示函数f(x)的二阶导数。
若f''(x) > 0,则说明该临界点对应的极小值;若f''(x) < 0,则说明该临界点对应的极大值;若f''(x) = 0,则需要进行其他方法进一步判断。
3. 比较端点值除了求解临界点之外,我们还需要比较函数在区间的端点值,并找出其中的最大值和最小值。
三、实例分析为了更好地理解导数法求解极值与最值的过程,我们举一个实例来进行说明。
假设我们要求解函数f(x)=x^3-3x^2+2x在区间[-1, 3]的极值和最值。
1. 求解导数和临界点首先,求解函数f(x)的导数,得到f'(x)=3x^2-6x+2。


函数的极值知识点总结
函数的极值是数学中一个重要的知识点,它在微积分和数学建
模中起着关键作用。
极值包括最大值和最小值,下面我将从定义、
求解方法以及应用等多个角度对函数的极值进行总结。
首先,函数的极值是指在定义域内取得的最大值和最小值。
具
体来说,对于函数f(x),如果存在使得f(x)≥f(x0)(或
f(x)≤f(x0))成立的x0,那么f(x0)就是函数f(x)的最大值(或
最小值)。
这里需要注意的是,极值点可以是函数的端点,也可以
是函数的驻点(即导数为0的点)。
其次,求解函数的极值可以通过导数的方法来进行。
首先,找
出函数的驻点,即求解f'(x)=0的点,然后通过一阶导数的符号变
化来判断极值的情况。
具体来说,如果f'(x)在x0的左侧由正变负,那么x0是函数的极大值点;如果f'(x)在x0的左侧由负变正,那
么x0是函数的极小值点。
需要注意的是,这只是判断极值的充分条件,还需要验证端点的情况。
此外,函数的极值在实际问题中有着广泛的应用。
比如在经济
学中,利润函数的极大值可以帮助企业确定最优产量;在物理学中,
某些物理量的最大值可以对问题进行优化等等。
综上所述,函数的极值是数学中一个重要的知识点,通过对其定义、求解方法以及应用的全面了解,可以更好地理解和应用函数的极值。
希望以上总结对你有所帮助。

函数的极值与最值求解的方法和步骤在数学中,函数的极值与最值是研究函数性质的重要内容之一。
通过求解函数的极值与最值,我们可以找到函数的最高点和最低点,从而更好地理解函数的特性。
本文将介绍一些常见的方法和步骤,帮助读者更好地理解和应用这一概念。
一、函数的极值与最值的定义在开始讨论求解方法之前,我们首先需要明确函数的极值与最值的概念。
对于定义在某个区间上的函数f(x),如果存在一个点c,使得在c的邻域内,对于任意的x都有f(x)≤f(c) 或f(x)≥f(c),那么我们称c为函数f(x)的极值点。
如果函数在整个定义域上的极值点中有一个最大值或最小值,那么我们称之为函数的最值。
二、求解函数极值与最值的方法1. 导数法导数法是求解函数极值与最值的常用方法之一。
通过求解函数的导数,我们可以找到函数的极值点。
具体步骤如下:(1)求出函数f(x)的导函数f'(x);(2)解方程f'(x)=0,求得函数的驻点;(3)通过二阶导数判别法,判断驻点是极大值点还是极小值点;(4)将驻点代入原函数f(x),求得函数的极值。
2. 区间法区间法是一种直观且易于理解的方法。
通过将函数在给定区间内的所有值进行比较,我们可以找到函数的最大值和最小值。
具体步骤如下:(1)确定函数f(x)的定义域;(2)将定义域分成若干个子区间;(3)在每个子区间内求出函数的值,并进行比较;(4)找出子区间中的最大值和最小值,即为函数的最值。
3. Lagrange乘数法Lagrange乘数法是一种用于求解约束条件下的极值问题的方法。
当我们需要求解函数在一定条件下的最值时,Lagrange乘数法可以帮助我们进行求解。
具体步骤如下:(1)建立拉格朗日函数L(x,y,...,λ)=f(x,y,...)-λg(x,y,...),其中f(x,y,...)为目标函数,g(x,y,...)为约束条件;(2)对拉格朗日函数求偏导数,得到一组方程;(3)求解方程组,得到函数的驻点;(4)通过二阶导数判别法,判断驻点是极大值点还是极小值点;(5)将驻点代入原函数f(x,y,...),求得函数的极值。

专题06 利用导数研究函数的极值和最值及最值的应用目录类型一:求函数的极值或极值点 (1)类型二:利用极值或极值点求参数的值 (3)类型三:利用导数求最值的应用 (4)类型一:求函数的极值或极值点....【答案】B【分析】令y=0,可排除AC,求导,再根据函数的单调性和极值点可排除D,即可得解【详解】y=(x―2))=x(x―2)e x,令0得x=0或x=2,故函数y=x(x―2)e有两个零点0,2,故错误;A.f(x)在(―2,1)上单调递增C.f(x)在x=―2处取得极小值类型二:利用极值或极值点求参数的值【详解】(1)f′(x)=3ax2+2bx,由题意可得f(1)=a+b=3f′(1)=3a+2b=0,解得a=―6b=9,检验:f′(x)=―18x2+18x,令f′(x)=0,解得x=0或x=1,当x∈(―∞,0)∪(1,+∞)时,f′(x)<0,f(x)单调递减;当x∈(0,1)时,f′(x)>0,f(x)单调递增,满足题意;(2)由(1)得f(x)=―6x3+9x2,所以f′(x)=―18x2+18x.所以f(―1)=15,f′(―1)=―36.所以所求切线方程为y―15=―36(x+1),即36x+y+21=0.类型三:利用导数求最值的应用题型专练:设正四棱柱底面边长为a,高为∵△MO1C∽△MO2E,∴MO1MO2=O1CO2E,即:33―ℎ33∴ℎ=33―62a,又∵a>0ℎ>0⇒a>033―6a故选:D.23.(2023·河南·郑州一中校联考模拟预测)已知菱形ABCD 的边长为2,CD 上,且EF //AC ,将△DEF 沿EF 折到△D ′EF 的位置,则当五棱锥D ′―ABCFE ―DEF 外接球的表面积为( )A .4πB .409πC .143πD .5【答案】B【点睛】求解几何体外接球有关的问题,首先要找到球心的位置,可利用几何体各面的外心来确定球心的A.32103B.64103C.128103【答案】D【分析】先确定原图中哪一条线段是侧棱,哪条线段是底边,再设立变量,求出体积关于变量的函数解析式,求导,根据函数的单调性求解.【详解】根据题意,PG是侧棱,底面EFGH的对角线的一半是GC,,则有PG2=(10―x)2+102,OF=OG=x,四棱锥的高ℎ2=PG2―OG2=200―20x,EFGH的面积S=4×S△OFG=2x2,四棱锥P-EFGH的体积V=23x2200―20x,200―20x,则x=200―t2,0≤t2<200,+5【答案】2π3【分析】连接CD,【详解】连接CD,由对称性,设∠CBE==所以BE=BD=CDtanθ易知∠MCE=∠NCD=又AC=3,故AB=AC 令sinθ0=1且θ0∈0,3由△SAB∼△SDE可得则该三棱柱的体积V时,V′>当0<r<23时,V取得最大值,且最大值为所以r=23.故答案为:3328.(2023·北京海淀上的动点(不与如图所示.给出下列四个结论:①AC//平面PEF;②△PEC不可能为等腰三角形;③存在点E,P,使得PD⊥AE④当四棱锥P―ACFE的体积最大时,④当底面ACFE的面积一定时,平面平面ABC⊥平面PEF 最大,设FC=x,EF=BF=PF=2―x,0<x<2V P―ACFE=13×12×(2―x+2)⋅x⋅(2―x)=16x3―x2+43xV′=1x2―2x+4=1(3x2―12PQ∥A1C1,确定平面ACPQ,则则五边形ACHE1G为平面ACE根据相似可得F1GGF =12,所以GF所以AG=GF2+AF2=49ℎ同理可得CH=21029,E1H=故当削去的雪最少时,平面ACE故答案为:41029+4669+2【点睛】关键点睛:本题考查了利用导数求体积的最值,截面问题,意在考查学生的计算能力,空间想象能力和综合应用能力,其中将体积的最值转化为函数的最值,并确定截面是解题的关键。
楚 雄 师 范 学 院2006—2007学年 第二 学期期末考试试卷 《数学实验》(B )卷 评分标准答题要求:1、写出各实验的MATLAB求解命令或程序2、除绘图题外,写出各实验的实验结果一、完成以下实验(每个实验5分,共20分)。
实验一 曲线绘图1.抛物线223y x x =-+-解:clear;x=-2:0.1:2;y=-x.^2+2*x-2;plot(x,y) 5分2.圆的渐开线2(cos sin ),2(sin cos )x t t t y t t t =+=-解:clear;t=linspace(0,2*pi);x=2*(cos(t)+t.*sin(t));y=2*(sin(t)-t.*cos(t));plot(x,y) 5分实验二 极限与导数3.求极限)lim x x →∞ 解:clear;syms x;s=limit(sqrt(x^2+3*x)-x,x,1)s =1 5分4.求函数()ln ln y x =的一阶导数解:syms x;y=log(log(x));dy=diff(y,x,1)dy =1/x/log(x) 5分二、完成以下实验(每个实验5分,共20分)。
实验三 级数5.求出()arctan f x x =马克劳林展开式的前5项解:clear;syms x;y=atan(x);f=taylor(y,0,5)f =x-1/3*x^3 5分6.求级数1n ∞=∑的和 解:clearsyms ns=sqrt(n+2)-2*sqrt(n+1)+sqrt(n);symsum(s,n,1,inf)ans =sum((n+2)^(1/2)-2*(n+1)^(1/2)+n^(1/2),n = 1 .. Inf) 5分实验四 积分 7.计算积分153cos dx x -⎰解:clear;syms x;s=int(1/(5-3*cos(x)),x)s =1/2*atan(2*tan(1/2*x)) 5分8.选用一种计算数值积分的方法,求数值积分20sin(2)x e x dx π⎰法1 复化梯形求积公式x=0:0.01:2*pi;y=exp(x).*sin(2*x);s1=trapz(x,y)s1 = -213.7824 5分法2 复化抛物线求积公式先编写M-函数文件function y=ex08(x)y=exp(x).*sin(2*x);保存后,在命令 命令运行指令:s2=quad('ex08',0,2*pi)2=quad('ex08',0,2*pi)s2 = -213.7967法3 牛顿-科兹求积公式s3=quadl('ex08',0,1)s3 =-213.7967三、完成以下实验(每个实验5分,共20分)。
实验六 多元函数的极值【实验目的】1. 多元函数偏导数的求法。
2. 多元函数自由极值的求法 3. 多元函数条件极值的求法.4. 学习掌握MATLAB 软件有关的命令。
【实验内容】求函数32824-+-=y xy x z 的极值点和极值【实验准备】1.计算多元函数的自由极值对于多元函数的自由极值问题,根据多元函数极值的必要和充分条件,可分为以下几个步骤:步骤1.定义多元函数),(y x f z =步骤2.求解正规方程0),(,0),(==y x f y x f y x ,得到驻点步骤3.对于每一个驻点),(00y x ,求出二阶偏导数,,,22222yzC y x z B x z A ∂∂=∂∂∂=∂∂=步骤4. 对于每一个驻点),(00y x ,计算判别式2B AC -,如果02>-B AC ,则该驻点是极值点,当0>A 为极小值, 0<A 为极大值;,如果02=-B AC ,判别法失效,需进一步判断;如果02<-B AC ,则该驻点不是极值点.2.计算二元函数在区域D 内的最大值和最小值设函数),(y x f z =在有界区域D 上连续,则),(y x f 在D 上必定有最大值和最小值。
求),(y x f 在D 上的最大值和最小值的一般步骤为:步骤1. 计算),(y x f 在D 内所有驻点处的函数值;步骤2. 计算),(y x f 在D 的各个边界线上的最大值和最小值;步骤3. 将上述各函数值进行比较,最终确定出在D 内的最大值和最小值。
3.函数求偏导数的MATLAB 命令diff (f,x,n )求函数f 关于自变量x 的n 阶导数。
jacobian (f ,x )求向量函数f 关于自变量x (x 也为向量)的jacobian 矩阵。
练习 1 求函数32824-+-=y xy x z 的极值点和极值.(1)首先用diff 命令求z 关于x,y 的偏导数 clear; syms x y; z=x^4-8*x*y+2*y^2-3; diff(z,x) diff(z,y) 结果为ans =4*x^3-8*y ans =-8*x+4*y 即.48,843y x yzy x x z +-=∂∂-=∂∂ (2)再求解正规方程,求得各驻点的坐标。
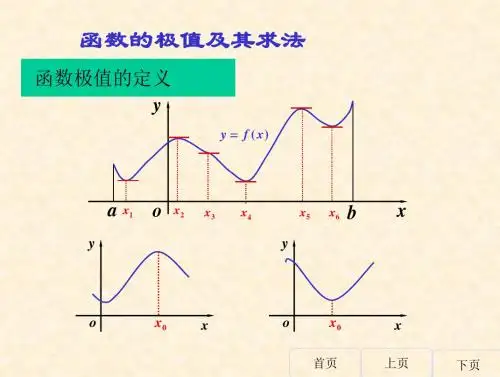
5.3.2导数的极值与最大(小)值一、导数的极值1、极值的概念:极大值与极小值统称为极值(1)函数的极大值:一般地,设函数y =f (x )在点x 0及附近有定义,如果对x 0附近的所有的点,都有f (x )<f (x 0),就说f (x 0)是函数y =f (x )的一个极大值,记作y 极大值=f (x 0),x 0是极大值点.(2)函数的极小值:一般地,设函数y =f (x )在点x 0及附近有定义,如果对x 0附近的所有的点,都有f (x )>f (x 0),就说f (x 0)是函数y =f (x )的一个极小值,记作y 极小值=f (x 0),x 0是极小值点.2、极值与导数的关系如图(1),若x 0是极大值点,则在x 0的左侧附近f (x )只能是增函数,即f ′(x )>0,在x 0的右侧附近f (x )只能是减函数,即f ′(x )<0.如图(2),若x 0是极小值点,则在x 0的左侧附近f (x )只能是减函数,即f ′(x )<0;在x 0的右侧附近f (x )只能是增函数,即f ′(x )>0.综合以上情形,可以得到:若x 0满足f ′(x 0)=0,且在x 0的两侧f (x )的导数异号,则x 0是f (x )的极值点,f (x 0)是极值.若f ′(x )在x 0的两侧满足“左正右负”,则x 0是f (x )的极大值点,f (x 0)是极大值;若f ′(x )在x 0的两侧满足“左负右正”,则x 0是f (x )的极小值点,f (x 0)是极小值.【注意】(1)可导函数的极值点.必须是导数为0的点,但导数为0的点不一定是极值点.即“点x 0是可导函数f (x )的极值点”是“f ′(x 0)=0”的充分不必要条件.不可导的点可能是极值点也可能不是极值点.例如:①导数为0的点是极值点:y =x 2,y ′|x =0=0,x =0是极值点.②导数为0的点不是极值点:y =x 3,y ′|x =0=0,x =0不是极值点.③不可导的点是极值点:y =|sin x |,x =0不可导,但x =0是极值点.(2)函数的极值只是一个局部性的概念,是仅对某一点及左、右两侧区域而言的.在函数的整个定义区间内可能有多个极大值或极小值,且极大值不一定比极小值大,如图,点x 1、x 3是极大值点,x 2、x 4是极小值点,且在点x 1处的极大值小于在点上x 4处的极小值.(3)极值点是自变量的值,极值指的是函数值.(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点.(5)若f (x )在(a ,b )内有极值,那么f (x )在(a ,b )内绝对不会是单调函数,即在区间上的单调函数没有极值.3、利用导数求函数极值的方法步骤(1)求导数f ′(x );(2)求方程f ′(x )=0的所有实数根;(3)观察在每个根x 0附近,从左到右导函数f ′(x )的符号如何变化.①如果f ′(x )的符号由正变负,则f (x 0)是极大值;②如果由负变正,则f (x 0)是极小值.③如果在f ′(x )=0的根x =x 0的左右侧f ′(x )的符号不变,则不是极值点.题型一已知函数求极值或极值点【例1】已知函数()()()2312f x x x =--,则()f x 的极大值点为()A.1B.75C.-1D.2【答案】B【解析】因为()()()()()()()()32222123121275'=-----=---f x x x x x x x x ,所以()f x 在(,1)-∞,7,5⎛⎫+∞ ⎪⎝⎭上单调递减,在71,5⎛⎫ ⎪⎝⎭上单调递增,所以()f x 的极大值点为75.所以B 正确.故选:B.【变式1-1】设函数()1x f x xe =+,则()A.1x =为()f x 的极大值点B.1x =为()f x 的极小值点C.1x =-为()f x 的极大值点D.1x =-为()f x 的极小值点【答案】D【解析】由()1x f x xe =+,可得()(1)x f x x e '=+,令()0f x '>可得1x >-,即函数()f x 在(1,)-+∞上是增函数;令()0f x '<可得1x <-,即函数()f x 在(1)-∞-上是减函数,所以1x =-为()f x 的极小值点.故选:D.【变式1-2】求下列函数的极值:(1)()2221xf x x =-+;(2)()ln xf x x=.【答案】(1)极小值为3-;极大值为1-;(2)极大值为1e,没有极小值【解析】(1)因为()()()()()()22222221421111x x x x f x x x +-+-'==++.令()0f x '=,解得11x =-,21x =.当x 变化时,()f x ',()f x 的变化情况如下表:x(),1-∞--1()1,1-1()1,+∞()f x '-0+0-()f x 单调递减-3单调递增-1单调递减由上表看出,当=1x -时,()f x 取得极小值,为()13f -=-;当1x =时,()f x 取得极大值,为()11f =-.(2)函数()ln x f x x =的定义域为()0,∞+,且()21ln xf x x -'=.令()0f x '=,解得e x =.当x 变化时,()f x '与()f x 的变化情况如下表:x()0,e e()e,+∞()f x '+0-()f x 单调递增1e单调递减因此,e x =是函数的极大值点,极大值为()1e ef =,没有极小值.【变式1-3】知函数ln ()=xxf x e 的极值点为0x x =,则0x 所在的区间为()A.10,2⎛⎫ ⎪⎝⎭B.1,12⎛⎫⎪⎝⎭C.()1,2D.()2,e 【答案】C【解析】由ln ()=x x f x e ,得'1ln ()xxx f x e-=(0x >),令1()ln g x x x =-(0x >),则'211()0g x x x=+>,所以()g x 在(0,)+∞上单调递增,因为1(1)10,(2)ln 2ln 202g g =-<=-=->,所以存在0(1,2)x ∈,使0()0g x =,即'0()0f x =,当01x x <<时,'()0,()0g x f x <>,当02x x <<时,'()0,()0g x f x ><,所以0x 为ln ()=xxf x e 的极大值点,所以0x 所在的区间为()1,2,故选:C 【变式1-4】已知函数()1ex af x x =++,求函数()f x 的极值.【答案】见解析.【解析】()1e x a f x x =++,定义域为R ,()e 1e ex x x a af x -=-='.①当0a ≤时,()0f x '>,()f x 在R 上为增函数,()f x 无极值.②当0a >时,令()0f x '=,得e x a =,ln x a =.当(),ln x a ∈-∞,()0f x '<;当()ln ,x a ∈+∞,()0f x '>;∴()f x 在(),ln a -∞上单调递减,在()ln ,a +∞上单调递增,()f x 在ln x a =取得极小值,极小值为()ln ln 2f a a =+,无极大值.综上所述,当0a ≤时,()f x 无极值;当0a >时,()f x 有极小值()ln ln 2f a a =+,无极大值.题型二函数(导函数)图象与极值的关系【例2】函数()f x 的定义域为(),a b ,导函数()f x '在(),a b 内的图像如图所示,则下列命题不正确的是()A.函数()f x 在(),a b 内一定不存在最小值B.函数()f x 在(),a b 内只有一个极小值点C.函数()f x 在(),a b 内有两个极大值点D.函数()f x 在(),a b 内可能没有零点【答案】A【解析】设()0f x '=的根为1x ,2x ,3x ,且123a x x x b <<<<,则由图可知,函数()f x 在()1,a x 内单调递增,在()12,x x 内单调递减,在()23,x x 内单调递增,在()3,x b 内单调递减;所以函数()f x 在区间(),a b 内有极小值()2f x ,当()()2f x f a ≤,()()2f x f b ≤时,()2f x 是函数()f x 在区间(),a b 内的最小值,所以A 错误,B 正确;函数()f x 在区间(),a b 内有极大值()1f x 、()3f x ,所以C 正确;当()0f a ≥,()20f x >,()0f b ≥时,函数()f x 在(),a b 内没有零点,所以D 正确.故选:A.【变式2-1】设函数()f x 在R 上可导,其导函数为()f x ',且函数()()g x x f x =⋅'的图象如图所示,则下列结论中一定成立的是()A.()f x 有两个极值点B.(2)f -为函数的极大值C.()f x 有两个极小值D.(1)f -为()f x 的极小值【答案】C【解析】()()g x x f x '=⋅,并结合其图像,可得到如下情况,当<2x -时,()0,()0g x f x '><,()f x 在(,2)-∞-单调递减;当20x -<<时,()0,()0g x f x '<>,()f x 在(2,0)-单调递增;当01x <<时,()0,()0g x f x '<<,()f x 在(0,1)单调递减;当1x >时,()0,()0g x f x '>>,()f x 在()1,∞+单调递增∴()f x 在2x =-和1x =处取得极小值,故B,D 错,C 正确;在0x =处取得极大值.所以()f x 有3个极值点,故A 错.故选:C.【变式2-2】函数()f x 的导函数是()f x ',下图所示的是函数()()()1R y x f x x '=+⋅∈的图像,下列说法正确的是()A.=1x -是()f x 的零点B.2x =是()f x 的极大值点C.()f x 在区间()2,1--上单调递增D.()f x 在区间[]2,2-上不存在极小值【答案】B【解析】当2<<1x --时,10x +<,而0y >,故()0f x '<;当12x -<<时,10x +>,而0y >,故()0f x '>;当2x >时,10x +>,而0y <,故()0f x '<;所以(2,1),(2,)--+∞上()f x 递减;(1,2)-上()f x 递增,则=1x -、2x =分别是()f x 的极小值点、极大值点.故A、C、D 错误,B 正确.故选:B【变式2-3】如图,可导函数()f x 在点()()00,P x f x 处的切线方程为()y g x =,设()()()h x g x f x =-,()h x '为()h x 的导函数,则下列结论中正确的是()A.()00h x '=,0x 是()h x 的极大值点B.()00h x '=,0x 是()h x 的极小值点C.()00h x '≠,0x 不是()h x 的极大值点D.()00h x '≠,0x 是()h x 的极值点【答案】B【解析】由题得,()h x 的几何意义为当x 取同值时,()g x 到()f x 的距离.根据题意,当()0,x x ∞∈-+时,()h x 单调递减,当()0,x x ∈+∞时,()h x 单调递增,又()()()0000h x g x f x =-''=',则有0x 是()h x 的极小值点,故选:B.题型三根据函数的极值或极值点求参数【例3】函数32()422f x x ax bx =--+在1x =处有极值3-,则a b -的值等于()A.0B.6C.3D.2【答案】A【解析】2()1222f x x ax b'=--因为()f x 在1x =处有极值3-,所以(1)12220(1)4223f a b f a b =--=⎧⎨=--+=-'⎩,解得3a b ==所以0a b -=故选:A【变式3-1】设函数()()330f x x mx n m =-+>的极大值为6,极小值为2,则m n +=__________.【答案】5【解析】()(2333f x x m x x '=-=,∴当(),x ∈-∞+∞时,()0f x '>;当(x ∈时,()0f x '<;∴()f x 在(,-∞,)+∞上单调递增,在(上单调递减,∴的极大值(26f m n ==;极小值22f n =-=,4n ∴=,1m =,5m n ∴+=.【变式3-2】已知函数()f x 321132x x cx d =+--有极值,则c 的取值范围为()A.14c <-B.14c ≤-C.14c ≥-D.14c >-【答案】D【解析】由题意知,定义域为R ,()2f x x x c '=+-,要使函数()f x 有极值,则()f x '必有两个不等的实根,则140c ∆=+>,解得14c >-.故选:D.【变式3-3】已知函数32()3(1)3(1)3f x x m x m x =+-+++既有极大值,又有极小值,则m 的取值范围是()A.3m ≥或0m ≤B.3m >或0m <C.3m >D.0m <【答案】B【解析】由2()3[2(1)(1)]f x x m x m '=+-++,又()f x 有极大值、极小值,所以()f x '有两个变号零点,则24(1)4(1)0m m ∆=--+>,整理得230m m ->,可得3m >或0m <.故选:B【变式3-4】若函数()()22e xx a f x x =++⋅在R 上无极值,则实数a 的取值范围()A.()2,2-B.(-C.⎡-⎣D.[]22-,【答案】D【解析】由()()22e xx a f x x =++⋅可得()()()()222e 2e 22e x x xx a x ax x a x f a x ⎡⎤=+⋅+++⋅=++++⋅⎣⎦',e 0x >恒成立,()222y x a x a =++++为开口向上的抛物线,若函数()()22e xx a f x x =++⋅在R 上无极值,则()2220y x a x a =++++≥恒成立,所以()()22420a a ∆=+-+≤,解得:22a -≤≤,所以实数a 的取值范围为[]22-,,故选:D.题型四利用导数求函数的最值【例4】函数e x y x =在[]2,4x ∈上的最小值为()A.22e B.1eC.44e D.22e 【答案】A【解析】∵e x y x =,∴()e e 1e x x xy x x '=+=+,当[]2,4x ∈时,()1e 0xy x '=+>∴函数e x y x =在区间[]2,4上单调递增,∴当2x =时,函数e x y x =取得最小值,2min 2e y =,∴函数e x y x =在[]2,4x ∈上的最小值为22e .故选:A.【变式4-1】函数()e cos x f x x =在区间3π0,4⎡⎤⎢⎥⎣⎦上取得最大值时x 的值为()A.0B.π4C.π2D.3π4【答案】B【解析】由()e cos x f x x =得()πe cos e sin cos 4x x xf x x x x ⎛⎫=-+ ⎝'⎪⎭,令()0f x '=,即πcos()04x +=在区间3π0,4⎡⎤⎢⎥⎣⎦上解得π4x =,当π04x ≤<时,()0f x '>,()f x 为增函数,当π3π44x ≤≤时,()0f x '<,()f x 为减函数,所以当π4x =时,()f x 取得最大值.故选:B.【变式4-2】已知函数()ln 2f x x =+,设函数()()12h x f x x =+--,则()h x 的最大值是______.【答案】0【解析】因为()()ln 1h x x x =+-定义域为()1,-+∞,所以()1111xh x x x '=-=-++.当()1,0x ∈-时,()0h x '>;当()0,x ∈+∞时,()0h x '<.所以()h x 在()1,0-上为增函数,在()0,∞+上为减函数,从而()()max 00h x h ==.【变式4-3】设函数()()2ln 23f x x x =++(1)讨论()f x 的单调性;(2)求()f x 在区间31,44⎡⎤-⎢⎥⎣⎦的最大值和最小值.【答案】(1)函数()f x 单调递增区间为31,1,22⎛⎫⎛⎫---+∞ ⎪ ⎪⎝⎭⎝⎭;单调递减区间为11,2⎛⎫-- ⎪⎝⎭;(2)()f x 在区间31,44⎡⎤-⎢⎥⎣⎦上的最大值为17ln 162+,最小值为1ln 24+.【解析】(1)函数()()2ln 23f x x x =++的定义域为32⎛⎫-+∞ ⎪⎝⎭,,又()()141232223232x x f x x x x x ⎛⎫++ ⎪⎛⎫⎝⎭'=+=>- ⎪++⎝⎭.令()0f x '>,解得12x >-或312x -<<-;令()0f x '<,解得112x -<<-.所以函数()f x 单调递增区间为31,1,22⎛⎫⎛⎫---+∞ ⎪ ⎪⎝⎭⎝⎭;单调递减区间为11,2⎛⎫-- ⎪⎝⎭;(2)由(1)可得:函数()f x 在区间31,42⎡⎤--⎢⎥⎣⎦内单调递减,在11,24⎡⎤-⎢⎣⎦内单调递增.所以当12x =-时,函数()f x 取得最小值11ln 224f ⎛⎫-=+ ⎪⎝⎭,又393ln 4162f ⎛⎫-=+ ⎪⎝⎭,117ln 4162f ⎛⎫=+ ⎪⎝⎭,而319317131ln ln ln ln044162162272f f ⎛⎫⎛⎫--=-=+<+ ⎪ ⎝⎭⎝⎭,所以当14x =时,函数()f x 取得最大值为:17ln 162+.即()f x 在区间31,44⎡⎤-⎢⎥⎣⎦上的最大值为17ln 162+,最小值为1ln 24+.题型五已知函数的最值求参数【例5】若函数323()42a f x x x =-+在区间[1,2]上的最小值为0,则实数a 的值为()A.-2B.-1C.2D.103【答案】C【解析】由323()42a f x x x =-+,得2()333()f x x ax x x a '=-=-,当0a ≤时,()0f x '>在[1,2]上恒成立,所以()f x 在[1,2]上递增,所以min 3()(1)1402a f x f ==-+=,解得103a =(舍去),当0a >时,由()0f x '=,得0x =或x a =,当01a <≤时,()0f x '>在[1,2]上恒成立,所以()f x 在[1,2]上递增,所以min 3()(1)1402a f x f ==-+=,解得103a =(舍去),当12a <<时,当1x a <<时,()0f x '<,当2a x <<时,()0f x '>,所以()f x 在(1,)a 上递减,在(,2)a 上递增,所以当x a =时,()f x 取得最小值,所以323()402a f a a a =-+=,解得2a =(舍去),当2a ≥时,当12x ≤≤时,()0f x '<,所以()f x 在[1,2]上递减,所以3min 3()(2)24402af x f ==-⨯+=,解得2a =,综上,2a =,故选:C 【变式5-1】若函数()ln 12,0()1,0x ax x f x x a x x ⎧+-->⎪=⎨++<⎪⎩的最大值为2a -,则实数a 的取值范围为()A.(,e]-∞B.10,e ⎛⎤⎥⎝⎦C.1,e∞⎡⎫+⎪⎢⎣⎭D.[e,)+∞【答案】C【解析】当x <0时,()11()2f x x a x a a a xx =++=--++≤-=--,当且仅当x =−1时,()f x 取得最大值f (−1)=a −2,由题意可得x >0时,()()ln 12f x x ax =+--的值域包含于(−∞,a −2],即ln(1)22x ax a +--≤-在x >0时恒成立即ln(1)1x a x +≥+在x >0时恒成立,即maxln(1)1x a x +⎡⎤≥⎢⎥+⎣⎦设ln(1)()1x g x x +=+,21ln(1)()(1)x g x x -+'∴=+当0e 1x <<-时,()0,()g x g x >'在(0,e 1)-上单调递增,当e 1x >-时,()0,()g x g x <'在(e 1,)-+∞上单调递减,()()max ln e 1e 1e e g x g ∴=-==1ea ∴≥,故选:C.【变式5-2】若函数()33f x x x =-在区间()2,3a a +上有最小值,则实数a 的取值范围是()A.12,2⎛⎫- ⎪⎝⎭B.()2,1-C.11,2⎡⎫-⎪⎢⎣⎭D.(]2,1--【答案】C【解析】因为函数()33f x x x =-,所以()233f x x ¢=-,当1x <-或1x >时,()0f x '>,当11x -<<时,()0f x '<,所以当1x =时,()f x 取得最小值,因为()f x 在区间()2,3a a +上有最小值,且(1)(2)2f f =-=-所以2213a a -≤<<+,解得112a -≤<,所以实数a 的取值范围是1[1,)2-.故选:C【变式5-3】若函数()()()()2=ln +21,+f x x ax a x x ∞--∈有最小值,则实数a 的取值范围为()A.()1,0-B.(),1-∞-C.()0,1D.()1,1-【答案】A【解析】由题意可得:()()()()112122ax x f x ax a xx+-'=-+-=∵1x >,则120x -<当0a ≥,则10ax +>当1x >时恒成立,即()0f x '<∴()f x 在()1,+∞上单调递减,则()f x 在()1,+∞上无最值,即0a ≥不成立当1a ≤-,则10ax +<当1x >时恒成立,即()0f x '>,∴()f x 在()1,+∞上单调递增,则()f x 在()1,+∞上无最值,即1a ≤-不成立当10a -<<,令10ax +<,则11x a>->∴()f x 在1,a⎛⎫-+∞ ⎪⎝⎭上单调递增,在11,a ⎛⎫- ⎪⎝⎭单调递减,则()f x 在()1,+∞上有最小值1f a ⎛⎫- ⎪⎝⎭,即10a -<<成立故选:A.【变式5-4】设函数()()3230f x ax ax b a =-+>在区间[]1,4上有最大值23,最小值3,求a ,b 的值.【答案】1a =,7b =【解析】因为()323f x ax ax b =-+,所以()236f x ax ax'=-令()()236320f x ax ax ax x '=-=-=,则0x =或2x =由于0a >,[]14x ∈,当()12x ∈,时,()0f x '<;当()24x ∈,时,()0f x '>故在2x =,()323f x ax ax b =-+取得最小值3所以()()28124313223f a a b a b f a a b a b =-+=-+=⎧⎪⎨=-+=-+=⎪⎩或者()()281243464481623f a a b a b f a a b a b =-+=-+=⎧⎪⎨=-+=+=⎪⎩所以10a =,43b =或者1a =,7b =若10a =,43b =,则()32103043f x x x =-+而()3241043044320323f =⨯-⨯+=>,不合题意,舍去;若1a =,7b =,则()3237f x x x =-+,而()3211317523f =-⨯+=<故1a =,7b =题型六函数的极值与最值综合应用【例6】已知函数()ln 2f x x x =--.(1)求曲线()=y f x 在=1x 处的切线方程;(2)记函数21()2()2g x x bx f x =---,设1x ,212()x x x <是函数()g x 的两个极值点,若32b ≥,且()()12g x g x k -≥恒成立,求实数k 的最大值.【答案】(1)1y =-;(2)152ln2.8-【解析】(1)()11f x x'=-,所以切线斜率为()10f '=,又()11f =-,切点为()11-,,所以切线方程为:1y =-.(2)21()ln (1)2g x x x b x =+-+,21(1)1()(1),x b x g x x b x x -++'∴=+-+=若32b ≥,则()()()214310b b b +-=+->恒成立,121x x b ∴+=+,121x x =,22112121221()()ln ()(1)()2-=+--+-x g x g x x x b x x x 11221ln (1)()2=-+-x b x x x 11212212()()1ln2+-=-x x x x x x x x 1122211ln ()2=--x x x x x x ,120x x <<,设12x t x =,则01t <<,令11()ln ()2G t t t t =--,01t <<,则222111(1)()(1)022t G t t t t -'=-+=-<,()G t ∴在()01,上单调递减;32b ≥,225(1)4b ∴+≥,2222112212122(1)()x x x x b x x x x +++=+=1221122x x t x x t =++=++,12524t t ∴++≥,241740t t ∴-+≥,104t ∴<≤,∴当14t =时,min 115()()2ln 248==-G t G ,152ln 28∴≤-k ,即实数k 的最大值为152ln 2.8-【变式6-1】己知函数21()2ln (21)(0)2f x x ax a x a =-+->.(1)若曲线(=)y f x 在点(1,(1))f 处的切线经过原点,求a 的值;(2)设2()2g x x x =-,若对任意(0,2]s ∈,均存在(0,2]t ∈,使得()()f s g t <,求a 的取值范围.【答案】(1)=4a ;(2)(0,1ln 2)-.【解析】(1)由21()2ln (21)(0)2f x x ax a x a =-+->,可得2()21f x ax a x'=-+-.因为(1)2211f a a a '=-+-=+,13(1)21122f a a a =-+-=-,所以切点坐标为3(1,1)2a -,切线方程为:()311(1)2a y a x ⎛⎫--=+- ⎪⎝⎭,因为切线经过(0,0),所以3112aa -=+,解得=4a .(2)由题知()f x 的定义域为(0,)+∞,21()[(21)2]f x ax a x x '=----,令()f x '=2(21)20ax a x ---=,解得1x a=-或=2x ,因为0,a >所以10a -<,所以12a-<,令()0f x '>,即2(21)20ax a x ---<,解得:12x a -<<,令()0f x '<,即2(21)20ax a x --->,解得:1x a<-或2x >,所以()f x 增区间为(0,2),减区间为(2,)+∞.因为()22()211g t t t t =-=--,所以函数()g t 在区间(0,2]的最大值为0,函数()f s 在(0,2)上单调递增,故在区间(0,2]上max ()(2)2ln 222f s f a ==+-,所以2ln 2220a +-<,即ln 210a +-<,故1ln 2a <-,所以a 的取值范围是(0,1ln 2)-.【变式6-2】已知实数a 满足12a <≤,设函数()321132a f x x x ax +=-+.(1)当=2a 时,求()f x 的极小值;(2)若函数()()()324362g x x bx b x b =+-+∈R 与()f x 的极小值点相等,证明:()g x 的极大值不大于10.【答案】(1)23;(2)证明见解析【解析】(1)当=2a 时()3213232f x x x x =-+,所以()()()23212f x x x x x =-+=--'.列表如下:x (),1-∞1()1,22()2,+∞()f x '+0-0+()f x 单调递增极大值单调递减极小值单调递增所以()f x 的极小值为()223f =.(2)证明:()()()()211f x x a x a x x a '=-++=--.由于1a >,所以当x a >或1x <时()0f x '>,当1x a <<时()0f x '<,即()f x 在(),1-∞和(),a +∞上单调递增,在()1,a 上单调递减,所以当=x a 时,()f x 取极小值,所以()g a 为()g x 的极小值,而()()()()2=12+66+2=612++2g x x bx b x x b --',所以22b a +=-,即()21b a =-+.所以当x a >或1x <时()0g x '>,当1x a <<时()0g x '<,即()g x 在(),1-∞和(),a +∞上单调递增,在()1,a 上单调递减,又因为12a <≤,所以()()()14362386210g x g b b b a ==+-+=--=-≤极大值.故()g x 的极大值不大于10.【变式6-3】已知函数()2e xf x x -=.(1)求()f x 的单调区间和极值.(2)若关于x 的方程()f x k =有唯一的实数根,求实数k 的取值范围.【答案】(1)递增区间为()0,2,递减区间为(),0∞-,()2,+∞,极小值为0,极大值为24e -;(2){}()204e,-+∞【解析】(1)()()()222e e 2e 2e x x x xf x x x x x x x ----'=-=-+=--,由()0f x '<得0x <或2x >,由()0f x '>得02x <<,所以()f x 的递增区间为()0,2,递减区间为(),0∞-,()2,+∞.极小值为()00f =,极大值为()224e f -=.(2)方程()f x k =有唯一的实数根等价于函数()y f x =与直线y k =有唯一的交点,画出()f x 的大致图像如图所示,所以实数k 的取值范围为{}()204e,-+∞.。
函数的极值与最值的求解在数学中,我们经常需要求解函数的极值和最值。
函数的极值指的是函数在某个定义域内取得的最大值或最小值,最值则是函数在整个定义域内的最大值或最小值。
本文将介绍如何求解函数的极值和最值的方法。
一、函数的极值求解方法1. 导数法导数法是求解函数极值的一种常用方法。
根据函数的极值定义,极值点处函数的导数为零或不存在。
因此,我们可以通过以下步骤求解函数的极值:1)求函数的导数;2)令导数等于零,解方程得到极值点的横坐标;3)将极值点的横坐标代入原函数,求得纵坐标。
例如,对于函数f(x) = x^2 - 2x + 1,我们可以进行如下计算:1)求导:f'(x) = 2x - 2;2)令导数等于零:2x - 2 = 0,解得x = 1;3)将x = 1代入原函数:f(1) = 1^2 - 2(1) + 1 = 0,得到极小值0。
2. 二阶导数法在某些情况下,使用二阶导数可以更方便地求解函数的极值。
根据函数的极值定义,当函数的一阶导数为零且二阶导数大于零时,函数取得极小值;当一阶导数为零且二阶导数小于零时,函数取得极大值。
例如,对于函数f(x) = x^3 - 6x^2 + 9x + 2,我们可以进行如下计算:1)求导:f'(x) = 3x^2 - 12x + 9;2)求二阶导数:f''(x) = 6x - 12;3)令一阶导数等于零,解方程得到极值点的横坐标:3x^2 - 12x +9 = 0,解得x = 1;4)将x = 1代入二阶导数:f''(1) = 6 - 12 = -6,表明函数在x = 1处取得极大值。
二、函数的最值求解方法函数的最值即为整个定义域内的最大值或最小值。
求解函数最值的方法有以下几种:1. 导数法和求解极值类似,我们可以通过求解函数在定义域内的导数来找到函数的最值。
例如,对于函数f(x) = -x^2 + 4x - 3,我们可以进行如下计算:1)求导:f'(x) = -2x + 4;2)令导数等于零,解方程得到最值点的横坐标:-2x + 4 = 0,解得x = 2;3)将x = 2代入原函数:f(2) = -(2^2) + 4(2) - 3 = 1,得到函数的最大值1。
实验报告课程名称:MATLAB语言与应用技术实验名称:函数的极值院(系):机电学院专业班级:工程机械1101姓名:甘超学号:110730123指导教师:郑建校2013 年11 月12日实验六:函数的极值实验地点:大楼五楼八号机房 试验时间:2013年11月12日 实验目的:1. 多元函数偏导数的求法。
2. 多元函数自由极值的求法 3. 多元函数条件极值的求法.4. 学习掌握MATLAB 软件有关的命令。
实验内容练习1 求函数32824-+-=y xy x z 的极值点和极值.首先用diff 命令求z 关于x,y 的偏导数>>clear; syms x y; >>z=x^4-8*x*y+2*y^2-3; >>diff(z,x) >>diff(z,y)结果为ans =4*x^3-8*y ans =-8*x+4*y 即.48,843y x yz y x x z +-=∂∂-=∂∂再求解正规方程,求得各驻点的坐标。
一般方程组的符号解用solve 命令,当方程组不存在符号解时,solve 将给出数值解。
求解正规方程的MATLAB 代码为:>>clear;>>[x,y]=solve('4*x^3-8*y=0','-8*x+4*y=0','x','y')结果有三个驻点,分别是P(-2,-4),Q(0,0),R(2,4).下面再求判别式中的二阶偏导数:>>clear; syms x y;>>z=x^4-8*x*y+2*y^2-3; >>A=diff(z,x,2) >>B=diff(diff(z,x),y) >>C=diff(z,y,2)结果为A=2*x^2 B =-8 C =4由判别法可知)2,4(--P 和)2,4(Q 都是函数的极小值点,而点Q(0,0)不是极值点,实际上,)2,4(--P 和)2,4(Q 是函数的最小值点。
当然,我们可以通过画函数图形来观测极值点与鞍点。
>>clear;>>x=-5:0.2:5; y=-5:0.2:5; >>[X,Y]=meshgrid(x,y); >>Z=X.^4-8*X.*Y+2*Y.^2-3; >>mesh(X,Y,Z)>>xlabel('x'),ylabel('y'),zlabel('z') 结果如图6.1图6.1 函数曲面图可在图6.2种不容易观测极值点与鞍点,这是因为z 的取值范围为[-500,100],是一幅远景图,局部信息丢失较多,观测不到图像细节.可以通过画等值线来观测极值.>>contour(X,Y,Z, 600) >>xlabel('x'),ylabel('y') 结果如图6.2图6.2 等值线图由图6.2可见,随着图形灰度的逐渐变浅,函数值逐渐减小,图形中有两个明显的极小值点)2,4(--P 和)2,4(Q .根据提梯度与等高线之间的关系,梯度的方向是等高线的法方向,且指向函数增加的方向.由此可知,极值点应该有等高线环绕,而点)0,0(Q 周围没有等高线环绕,不是极值点,是鞍点.练习2 求函数xy z =在条件1=+y x 下的极值..构造Lagrange 函数)1(),(-++=y x xy y x L λ求Lagrange 函数的自由极值.先求L 关于λ,,y x 的一阶偏导数>>clear; syms x y k >>l=x*y+k*(x+y-1); >>diff(l,x) >>diff(l,y) >>diff(l,k)得,1,,-+=∂∂+=∂∂+=∂∂y x L x y L y x L λλλ再解正规方程 >>clear; syms x y k>>[x,y,k]=solve('y+k=0','x+k=0','x+y-1=0','x','y','k')得,21,21,21-===λy x 进过判断,此点为函数的极大值点,此时函数达到最大值.练习3 抛物面22y x z +=被平面1=++z y x 截成一个椭圆,求这个椭圆到原点的最长与最短距离.这个问题实际上就是求函数222),,(z y x z y x f ++=在条件22y x z +=及1=++z y x 下的最大值和最小值问题.构造Lagrange 函数)1()(),,(22222-+++-++++=z y x z y x z y x z y x L μλ求Lagrange 函数的自由极值.先求L 关于μλ,,,,z y x 的一阶偏导数>>clear; syms x y z u v>>l=x^2+y^2+z^2+u*(x^2+y^2-z)+v*(x+y+z-1); >>diff(l,x) >>diff(l,y) >>diff(l,z) >>diff(l,u) >>diff(l,v)得μλμλμλ+-=∂∂++=∂∂++=∂∂z z L y y y L x x x L 2,22,22 1,22-++=∂∂-+=∂∂z y x L z y x L μλ 再解正规方程>>clear;>>[x,y,z,u,v]=solve('2*x+2*x*u+v=0','2*y+2*y*u+v=0','2*z-u+v=0', 'x^2+y^2-z=0','x+y+z-1=0','x','y','z','u','v')得.32,231,33117,3353 =±-==±-=±-=z y x μλ 上面就是Lagrange 函数的稳定点,求所求的条件极值点必在其中取到。
由于所求问题存在最大值与最小值(因为函数f 在有界闭集}1,:),,{(22=++=+z y x z y x z y x ,上连续,从而存在最大值与最小值),故由359.)32,231,231(=±-±-f 求得的两个函数值,可得椭圆到原点的最长距离为359+,最短距离为359-。
练习4 求函数72422+--+=y x y x z 在上半圆0,1622≥≤+y y x 上的最大值和最小值。
首先画出等高线进行观测,相应的MATLAB 程序代码为:>>clear;>>x=-4:0.1:4; y=-4:0.1:4; >>[X,Y]=meshgrid(x,y); >>Z=X.^2+Y.^2-4*X-2*Y+7; >>contour(X,Y,Z,100) >>xlabel('x'),ylabel('y')结果如图6.3观测图6.3可看出,在区域D 内部有唯一的驻点,大约位于)1,2(在该点处汉书趣的最小值。
在圆弧与直线的交点处取得最大值,大约位于)2,4(-。
下面通过计算加以验证。
求函数在区域D 内的驻点,计算相应的函数值。
求z 关于x,y 的偏导数>>clear; syms x y; >>z=x^2+y^2-4*x-2*y+7; >>diff(z,x) >>diff(z,y)结果得,22,42-=∂∂-=∂∂y yzx x z 解正规方程 >>clear; [x,y]=solve('2*x-4=0','2*y-2=0','x','y')得驻点为(2,1),相应的函数值为2。
求函数在直线边界44,0≤≤-=x y 上的最大值和最小值。
将0=y 代入原函数,则二元函数变为一元函数.44,742≤≤-+-=x x x z首先观测此函数图形,相应的MATLAB 程序代码为:>>x=-4:0.01:4; y=x.^2-4*x+7; >>plot(x,y);>>xlabel('x'),ylabel('z')结果如图6.4所示由图6.4可看出,当4-=x 时函数取得最大值,2=x 时函数取得最小值。
下面用计算验证。
对函数求导>>clear; syms x ; >>z=x^2-4*x+7; diff(z,x) 得42-=x dxdz,可知驻点为2=x ,而边界点为4±=x ,计算着三个点上的函数值可得当4-=x 时函数取得最大值39,2=x 时函数取得最小值3。
求函数在圆弧边界线上0,1622≥≤+y y x 的最大值和最小值。
此边界线可用参数方程π≤≤==t t y t x 0,sin 4,cos 4表示。
则二元函数变为一元函数23sin 8cos 16+--=t t z首先观测此函数图形,相应的MATLAB 程序代码为:>>t=0:0.01*pi:pi; z=-16*cos(t)-8*sin(t)+23;>>plot(t,z);>>xlabel('t'),ylabel('z')结果如图6.5所示图6.5 函数图由图6.5可看出,当5.0≈t 时函数取得最小值,π=x 时函数取得最大值。
下面用计算验证。
对函数求导>>clear; syms t ;>>z=-16*cos(t)-8*sin(t)+23; diff(z,t) 得t t dtdzcos 8sin 18-=,解正规方程>>clear;>>t=solve('16*sin(t)-8*cos(t)=0','t') >>numeric(t) %求出t 的数值得4636,021arctan ≈=t,边界点为π,0=t ,计算着三个点上的函数值可得当4636.0=t 时函数取得最小值0.5111,)0,4(,=-==y x t π时函数取得最小值39。