三角形堰实用流量计算公式
- 格式:doc
- 大小:82.50 KB
- 文档页数:3
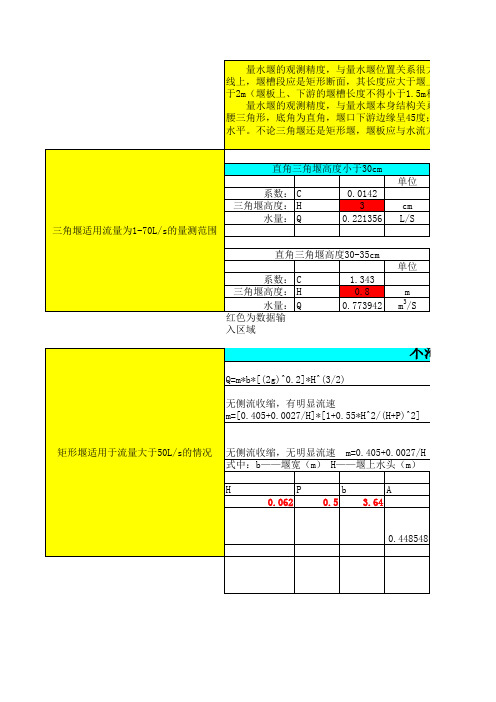

直角三角形量水堰流量计算公式一、引言水是生命之源,对于农田灌溉、城市供水等各个领域都起着重要的作用。
为了科学合理地利用水资源,我们需要对水的流量进行准确测量。
而直角三角形量水堰流量计算公式就是一种常用的方法,可以帮助我们快速计算出水的流量。
本文将详细介绍直角三角形量水堰流量计算公式的原理和应用。
直角三角形量水堰流量计算公式是基于三角形相似原理和流体力学公式推导而来的。
根据三角形相似原理,我们可以得到两个相似直角三角形的对应边长之比相等的关系。
而流体力学公式中,流量与流速和横截面积之间有着密切的关系。
综合这两个原理,我们可以推导出直角三角形量水堰流量计算公式。
三、直角三角形量水堰流量计算公式的推导假设直角三角形的直角边长为a,斜边长度为b。
在水流入堰口的地方,我们可以测量到水的高度为h,水的流速为v。
根据流体力学公式,流量Q等于流速v乘以横截面积A。
而横截面积A可以根据直角三角形的形状得到,即A等于直角边长a乘以水的高度h的一半。
综上所述,我们可以得到直角三角形量水堰流量计算公式为:Q = avh/2。
四、直角三角形量水堰流量计算公式的应用直角三角形量水堰流量计算公式可以广泛应用于各个领域的水流量测量中。
以农田灌溉为例,农民通过测量堰口水的高度和水流速度,可以利用该公式计算出灌溉水的流量。
这样一来,农民可以根据实际需求合理安排水的使用,提高水资源的利用效率。
同样,在城市供水领域,通过对供水管道的流量进行测量,可以确保城市居民得到足够的饮用水和生活用水。
五、注意事项在使用直角三角形量水堰流量计算公式时,需要注意以下几点:1. 确保测量数据的准确性,避免因误差导致计算结果的不准确。
2. 了解水流的特性和环境条件,比如水的温度、压力等因素,以便更准确地计算流量。
3. 注意单位的统一,确保计算结果的单位与实际需求一致。
4. 在实际应用中,可以结合其他的测量方法和设备,以提高测量的准确性和可靠性。
六、总结直角三角形量水堰流量计算公式是一种简单、快速且准确的水流量测量方法。

问题:三角形堰实用流量计算公式
说明:三角形堰是堰口形状为等腰三角形的薄壁堰,如图12-6所示。
当明渠流量较小时,如果使用矩形堰或全宽堰测量流量,则上下游的液位差很小,这会使得测量误差增大,为了使测量结果更加准确可以使用三角形堰。
对于三角形堰,当上游液位h变化时,堰口液流的宽度b也同时随着变化。
因此,三角形堰的流量计算公式应和三角形的顶角θ有关。
三角形堰堰口的曲线方程是
将上式代入式(12-4),沿高度方向对整个液流进行流量的积分,可以得到流经三角形堰的流体流量qv公式为
当堰口顶角时,三角形堰的流量实际计算公式(也称为Kindsvater-Shen公式)为
式中,C e是三角形堰的流量系数,还是三个变量的函数:
式中,p是三角形堰的顶角到堰底的距离;B是堰的宽度,he是有效水头,he=h+K h;h是实测水头;Kh是水头的修正值。
当时,C e的值可查图12-7,K h等于O.85mm
对于的兰角形堰,目前还缺乏经验数据以确定C e、h/p和p/B的函数关系。
但是,在堰口面积与明渠的通流面积相比很小时,h/p、p/B对C e值影响可以忽略不计,C e只是θ的函数,如图12-8所示,相应K h可以从图12-9查到。
式(12-27)的适用条件为
当时,要把h/p和p/B限制在图12-7所列的范围内;
当时,h/p≤0.35,1.5>p/B>O.1,h≥0.06m,p≥0.09mo
为了准确地测量比直角三角形堰的流量测量范围更小的流量,可以使用锐角三角形堰。
在IS0
1438-75中还给出了的三角形堰以及三角形堰在不同的水头下流量系数和流量的表。
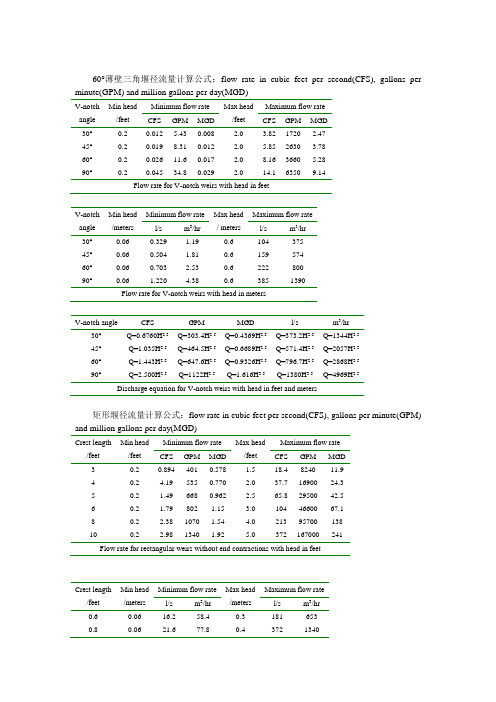
60°薄壁三角堰径流量计算公式:flow rate in cubic feet per second(CFS), gallons per minute(GPM) and million gallons per day(MGD)V-notch angle Min head/feetMinimum flow rate Max head/feetMaximum flow rate CFS GPM MGD CFS GPM MGD30°0.2 0.012 5.43 0.008 2.0 3.82 1720 2.47 45°0.2 0.019 8.31 0.012 2.0 5.85 2630 3.78 60°0.2 0.026 11.6 0.017 2.0 8.16 3660 5.28 90°0.2 0.045 34.8 0.029 2.0 14.1 6350 9.14 Flow rate for V-notch weirs with head in feetV-notch angle Min head/metersMinimum flow rate Max head/ metersMaximum flow rate l/s m3/hr l/s m3/hr30°0.06 0.329 1.19 0.6 104 37545°0.06 0.504 1.81 0.6 159 57460°0.06 0.703 2.53 0.6 222 80090°0.06 1.220 4.38 0.6 385 1390Flow rate for V-notch weirs with head in metersV-notch angle CFS GPM MGD l/s m3/hr30°Q=0.6760H2.5Q=303.4H2.5Q=0.4369H2.5Q=373.2H2.5Q=1344H2.545°Q=1.035H2.5Q=464.5H2.5Q=0.6689H2.5Q=571.4H2.5Q=2057H2.560°Q=1.443H2.5Q=647.6H2.5Q=0.9326H2.5Q=796.7H2.5Q=2868H2.590°Q=2.500H2.5Q=1122H2.5Q=1.616H2.5Q=1380H2.5Q=4969H2.5Discharge equation for V-notch weirs with head in feet and meters矩形堰径流量计算公式:flow rate in cubic feet per second(CFS), gallons per minute(GPM) and million gallons per day(MGD)Crest length/feet Min head/feetMinimum flow rate Max head/feetMaximum flow rate CFS GPM MGD CFS GPM MGD3 0.2 0.894 401 0.578 1.5 18.4 8240 11.94 0.2 4.19 535 0.770 2.0 37.7 16900 24.35 0.2 1.49 668 0.962 2.5 65.8 29500 42.56 0.2 1.79 802 1.15 3.0 104 46600 67.1 8 0.2 2.38 1070 1.54 4.0 213 95700 138 10 0.2 2.98 1340 1.92 5.0 372 167000 241Flow rate for rectangular weirs without end contractions with head in feetCrest length/feet Min head/metersMinimum flow rate Max head/metersMaximum flow rate l/s m3/hr l/s m3/hr0.6 0.06 16.2 58.4 0.3 181 653 0.8 0.06 21.6 77.8 0.4 372 13401.0 0.06 27.0 97.3 0.5 650 23401.5 0.06 40.5 146 0.75 1790 64502.0 0.06 54.0 195 1.0 3680 132003.0 0.06 81.1 292 1.5 10100 36500Flow rate for rectangular weirs without end contractions with head in metersDischarge equation for rectangular weirs without end contractions with head in feet and metersDischarge equationCFS GPM MGD l/s m3/hrQ=3.330LH1.5Q=1495LH1.5Q=2.152LH1.5Q=1838LH1.5Q=6618LH1.5Where Q= flow rate, L= crest length of weir in feet or meters, H= head on the weir。

问题:三角形堰实用流量计算说明:三角形堰是堰口形状为等腰三角形的薄壁堰,如图12-6所示。
当明渠流量较小时,如果使用矩形堰或全宽堰测量流量,则上下游的液位差很小,这会使得测量误差增大,为了使测量结果更加准确可以使用三角形堰。
对于三角形堰,当上游液位h变化时,堰口液流的宽度b也同时随着变化。
因此,三角形堰的流量计算公式应和三角形的顶角θ有关。
三角形堰堰口的曲线方程是将上式代入式(12-4),沿高度方向对整个液流进行流量的积分,可以得到流经三角形堰的流体流量qv公式为当堰口顶角时,三角形堰的流量实际计算公式(也称为Ki ndsvater-Shen公式)为式中,C是三角形堰的流量系数,还是三个变量的函数:e式中,p是三角形堰的顶角到堰底的距离;B是堰的宽度,he是有效水头,he=h+Kh;h是实测水头;Kh是水头的修正值。
当时,Ce 的值可查图12-7,Kh等于O.85mm对于的兰角形堰,目前还缺乏经验数据以确定Ce、h/p和p/B的函数关系。
但是,在堰口面积与明渠的通流面积相比很小时,h/p、p/B对Ce 值影响可以忽略不计,Ce只是θ的函数,如图12-8所示,相应Kh可以从图12-9查到。
式(12-27)的适用条件为当时,要把h/p和p/B限制在图12-7所列的范围内;当时,h/p≤0.35,1.5>p/B>O.1,h≥0.06m,p≥0.09mo为了准确地测量比直角三角形堰的流量测量范围更小的流量,可以使用锐角三角形堰。
在IS01438-75中还给出了的三角形堰以及三角形堰在不同的水头下流量系数和流量的表。

实用堰水力计算公式1、游水位较低,水流在流出堰顶时将产生第二次跌落。
10hH2、4、时,用明渠流理论解决不能用堰流理论。
f不可忽略。
同一堰,当堰上水头H较大时,视为实用堰;当堰上水头较小时,视为宽顶堰。
0§8-2堰流的基本方程以宽顶堰为例来推求堰流的基本方程取渐变流断面1-1C-C(近似假设渐变流)以堰顶为基准面,列两断面能量方程:H0v02ghc0vc22gvc22ghc0H0v02gH0作用水头hc与H有关,引入一修正系数k。
则kH0机hcokH0。
修正系数k取决于堰口的形状和过流断面的变化。
vc1代入上式,整理得:1k2gH01k32gH02QvchcbvcRH0bk1kb2gH032mb2gH0式中:b——堰宽1——流速系数m——流量系数,mk1k适用:堰流无侧向收缩注:堰流存在侧向收缩或堰下游水位对堰流的出水能力产生影响时,可对此公式进行修正。
§8-3薄壁堰一、一、分类:矩形薄壁堰→较大流量按堰口形状:三角形薄壁堰→较小流量梯形薄壁堰→较大流量1、1、矩形薄壁堰①①矩形薄壁堰的自由出流;在无侧向收缩的影响时,其流量公式为:3Qmb2gH0上式为关于流速的隐式方程,了;两边均含有流速,一般计算法进行计算,较复杂,于是,为计算简便,将上式改写成:32Qm0b2gH2m0——已考虑流速影响的薄壁堰的流量系数m0的确定:矩形薄壁8的流量系数由1898年法国工程师Bain提出经验公式为:H式中:H——堰上水头(m)m0(0.4050.0027)[10.55(HHp)]2p——上游堰高(m)适用条件:H0.25~1.24mp0.24~0.75mb0.2~2.0m2、2、三角形薄壁堰:当流量较小时,堰上水头较小时,采用三角形薄壁堰⑴公式:3取微元,则流量表达式为:dQm0设h为db处水头,则由几何关系:dQm0tg2gh2db(某)b(Hh)tg2dbtg2dh23代入某式,得2gh2dh03积分得:Q2m0tg45m0tg22gH5h2dh22gH252当90,H0.05~0.25m时,实验得m00.395。
三角堰流量计算公式
三角堰的流量计算公式,是由威廉•萨特曼在1936年提出的,公式为:Q= 2.6274 × h^2.5 (1-0.2h) \sqrt{2g tan\alpha},其中。
Q:三角堰流量(m³/s);
h:三角堰消能器坝顶处水位高度(m);
g:重力加速度(m/s²);
α:三角堰消能器坝面坡度(rad)。
代入上式得到的流量,是指在充足的源水条件下,三角堰能够把水流
进行放缓沉淀、排放的最大量,同时它也是给定三角堰的消能器坝高和坡
度情况下,计算出可以被放缓沉淀、排放的最大量,该公式经过不断的理
论分析、数据测试以及实际应用,其精度可以达到±2%,被广泛应用在水
利工程中。
60°薄壁三角堰径流量计算公式:flow rate in cubic feet per second(CFS), gallons per minute(GPM) and million gallons per day(MGD)V-notch angle Min head/feetMinimum flow rate Max head/feetMaximum flow rate CFS GPM MGD CFS GPM MGD30°0.2 0.012 5.43 0.008 2.0 3.82 1720 2.47 45°0.2 0.019 8.31 0.012 2.0 5.85 2630 3.78 60°0.2 0.026 11.6 0.017 2.0 8.16 3660 5.28 90°0.2 0.045 34.8 0.029 2.0 14.1 6350 9.14 Flow rate for V-notch weirs with head in feetV-notch angle Min head/metersMinimum flow rate Max head/ metersMaximum flow rate l/s m3/hr l/s m3/hr30°0.06 0.329 1.19 0.6 104 37545°0.06 0.504 1.81 0.6 159 57460°0.06 0.703 2.53 0.6 222 80090°0.06 1.220 4.38 0.6 385 1390Flow rate for V-notch weirs with head in metersV-notch angle CFS GPM MGD l/s m3/hr30°Q=0.6760H2.5Q=303.4H2.5Q=0.4369H2.5Q=373.2H2.5Q=1344H2.545°Q=1.035H2.5Q=464.5H2.5Q=0.6689H2.5Q=571.4H2.5Q=2057H2.560°Q=1.443H2.5Q=647.6H2.5Q=0.9326H2.5Q=796.7H2.5Q=2868H2.52.5 2.5 2.5 2.5 2.5Discharge equation for V-notch weirs with head in feet and meters矩形堰径流量计算公式:flow rate in cubic feet per second(CFS), gallons per minute(GPM) and million gallons per day(MGD)Crest length/feet Min head/feetMinimum flow rate Max head/feetMaximum flow rate CFS GPM MGD CFS GPM MGD3 0.2 0.894 401 0.578 1.5 18.4 8240 11.94 0.2 4.19 535 0.770 2.0 37.7 16900 24.35 0.2 1.49 668 0.962 2.5 65.8 29500 42.56 0.2 1.79 802 1.15 3.0 104 46600 67.1 8 0.2 2.38 1070 1.54 4.0 213 95700 138 10 0.2 2.98 1340 1.92 5.0 372 167000 241Flow rate for rectangular weirs without end contractions with head in feetCrest length/feet Min head/metersMinimum flow rate Max head/metersMaximum flow rate l/s m3/hr l/s m3/hr0.6 0.06 16.2 58.4 0.3 181 653 0.8 0.06 21.6 77.8 0.4 372 13401.0 0.06 27.0 97.3 0.5 650 23401.5 0.06 40.5 146 0.75 1790 64502.0 0.06 54.0 195 1.0 3680 132003.0 0.06 81.1 292 1.5 10100 36500Flow rate for rectangular weirs without end contractions with head in metersDischarge equation for rectangular weirs without end contractions with head in feet and metersDischarge equationCFS GPM MGD l/s m3/hrQ=3.330LH1.5Q=1495LH1.5Q=2.152LH1.5Q=1838LH1.5Q=6618LH1.5Where Q= flow rate, L= crest length of weir in feet or meters, H= head on the weir。
直角三角堰流量计算公式
直角三角堰是一种常用的水流量测量设备,用于计算水流的体积或流量。
直角
三角堰流量计算公式基于伯努利方程和托勒密定理,通过测量水流面积和水位差来确定流量。
直角三角堰流量计算公式如下:
Q = Cd × W × H^(3/2)
其中,Q表示流量,Cd表示流量系数,W表示顶宽,H表示水位差。
流量系数Cd是一个实验确定的常数,取决于直角三角堰的形状和尺寸。
它反
映了流量计算中的各种损失和摩擦因素。
顶宽W是直角三角堰的宽度,通常以米为单位。
水位差H是水位高度的差异,通常以米为单位。
它是从水流顶部到直角三角堰底部的垂直距离。
通过测量顶宽和水位差,然后将它们代入上述公式,就可以计算出直角三角堰
的流量。
需要注意的是,直角三角堰流量计算公式假设水流为理想流体,且在计算过程
中忽略了一些实际情况中的细微变化。
因此,在实际应用中,应根据具体情况对公式进行修正和调整。
总之,直角三角堰流量计算公式是通过测量顶宽和水位差来确定水流量的公式。
这个公式在水力学和水资源管理领域中有着广泛的应用,并可以帮助解决涉及水流量测量的问题。
三角形堰实用流量计算公式
点击次数:683 发布时间:2010-12-1
三角形堰是堰口形状为等腰三角形的薄壁堰,如图12-6所示。
当明渠流量较小时,如果使用矩形堰或全宽堰测量流量,则上下游的液位差很小,这会使得测量误差增大,为了使测量结果更加准确可以使用三角形堰。
对于三角形堰,当上游液位h变化时,堰口液流的宽度b也同时随着变化。
因此,三角形堰的流量计算公式应和三角形的顶角θ有关。
三角形堰堰口的曲线方程是
将上式代入式(12-4),沿高度方向对整个液流进行流量的积分,可以得到流经三角形堰的流体流量qv公式为
当堰口顶角时,三角形堰的流量实际计算公式(也称为Kindsvater-Shen公式)为
式中,C e是三角形堰的流量系数,还是三个变量的函数:
式中,p是三角形堰的顶角到堰底的距离;B是堰的宽度,he是有效水头,he=h+K h;h是实测水头;Kh是水头的修正值。
当时,C e的值可查图12-7,K h等于O.85mm
对于的兰角形堰,目前还缺乏经验数据以确定C e、h/p和p/B的函数关系。
但是,在堰口面积与明渠的通流面积相比很小时,h/p、p/B对C e值影响可以忽略不计,C e只是θ的函数,如图12-8所示,相应K h可以从图12-9查到。
式(12-27)的适用条件为
当时,要把h/p和p/B限制在图12-7所列的范围内;
当时,h/p≤0.35,1.5>p/B>O.1,h≥0.06m,p≥0.09mo
为了准确地测量比直角三角形堰的流量测量范围更小的流量,可以使用锐角三角形堰。
在IS01438-75中还给出了的三角形堰以及三角形堰在不同的水头下流量系数和流量的表。