
第五章回归分析
§5.1 一元线性回归
在自然界的现象中,同一过程中的各种变量之间往往存在着一定的关系,这种关系大致可以分为两类:
确定性关系
例如电路中的电压V、电阻R和电流I三者之间服从欧姆定律V=IR只要知道其中两个变量的值,另一个变量的值就唯一确定了.
相关关系
例如人的年龄、身高、体重和血压之间也存在一定的关系,一般来说年龄大的、体重重的人血压也要相应的高一些,但这种关系并不是确定的,因为即使年龄和体重都相同的人,其血压也不一定相同.
又如在土地和耕作条件相同的条件,每亩的施肥量、播种量与农作物的产量之间也存在一定的关系,一般来说施肥量、播种量适当时产量较高,同样这种关系也不是确定的,具有某种随机性,
变量之间这种不确定性关系在社会现象和自然现象中普遍存在,其原因主要是由于一些随机因素的干扰和测量上的误差,我们称变量之间的这种不确定关系为相关关系.
回归分析就是分析和处理这些具有相关关系的变量之间关系的一种有效方法.
在研究具有相关关系的变量之间的关系时,往往要考虑一些变量的变化对另一些变量的影响,这其中的一些变量就相当于通常函数中的自变量,对它们能赋予一个需要的值(如施肥量、播种量)或能取到一个可观测但不能人为控制的值(如年龄、身高),这类变量称为自变量(预报变量),而因自变量变化而变化的这类变量称为因变量(响应变量).
“回归”一词是英国统计学家高尔顿(P.Galton 1882-1911)在1889年发表的关于遗传的论文中首先应用的.他在研究前辈与后代身高之间的关系时,发现儿子的身高介于父亲身高与种族(父辈)平均身高之间,有回归于种族平均身高的趋势.后来他的朋友,英国著名统计学家K.Pearson等人搜集了上千个家庭成员的身高数据,分析出儿子的身高y与父亲的身高x大致可归结为以下关系:
y = 0.516 x +33.73 (英寸)
从而进一步证明了Galton的回归定律.这就是“回归”一词最早在遗传学上的含义.发展到今天,回归的现代意义要比原始的意义广泛的多.
在回归分析中要研究的主要问题是:
(1)确定因变量(响应变量)和自变量(预报变量)之间的定量关系表达式即建立回归模型.
(2)对回归模型进行检验.
(3)从众多的自变量中选择出对因变量影响显著的自变量.
(4)利用所建立的回归模型进行预测和控制.
§5.1 一元线性回归
我们先从最简单的情况开始讨论,只考虑一个因变量y和一个自变量x之间的关系.
一.一元线性回归模型
我们先看一个例子.
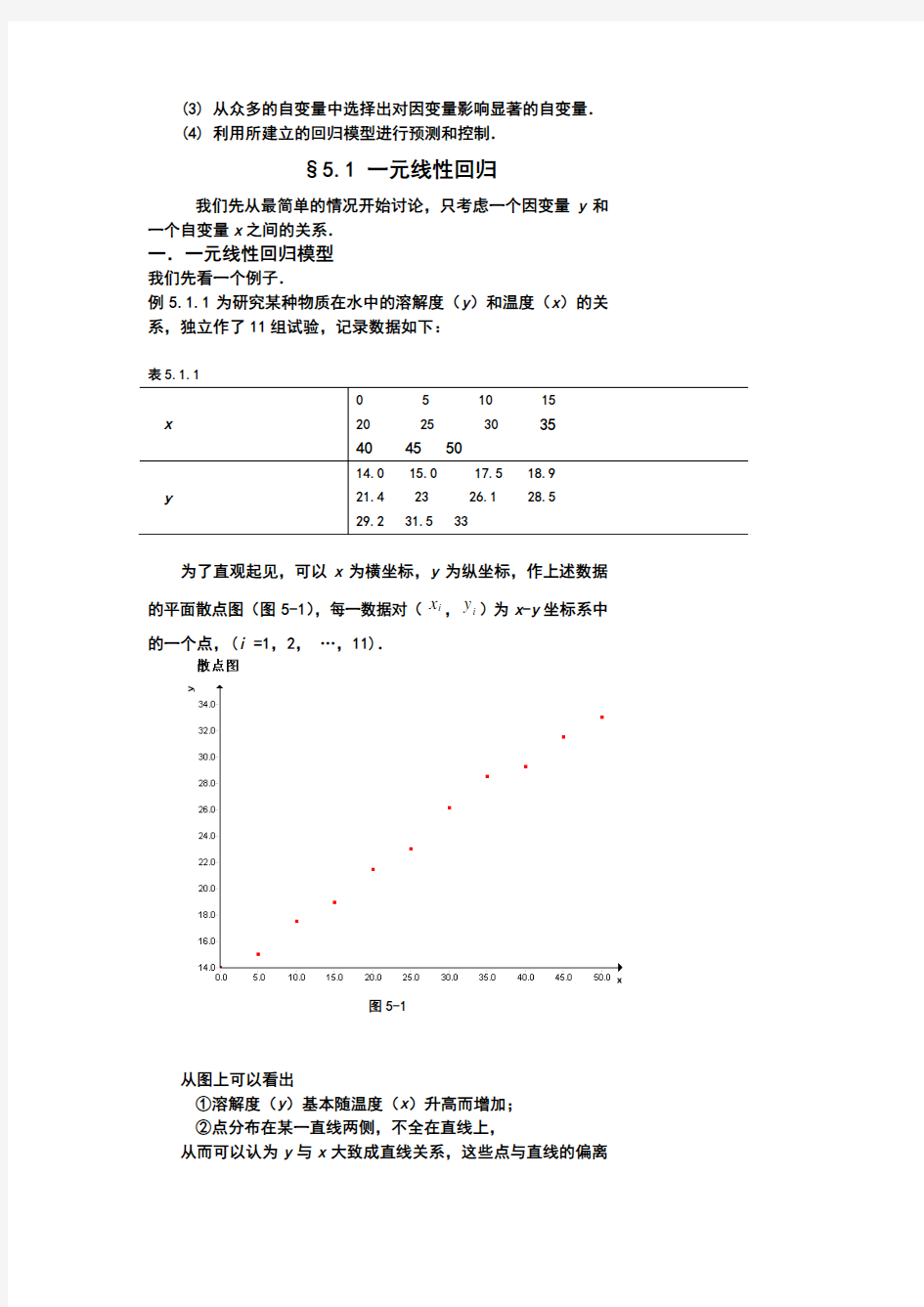
例5.1.1为研究某种物质在水中的溶解度(y)和温度(x)的关系,独立作了11组试验,记录数据如下:
表5.1.1
为了直观起见,可以x为横坐标,y为纵坐标,作上述数据的平面散点图(图5-1),每一数据对(x i,y i)为x-y坐标系中的一个点,(i =1,2,…,11).
图5-1
从图上可以看出
①溶解度(y)基本随温度(x)升高而增加;
②点分布在某一直线两侧,不全在直线上,
从而可以认为y与x大致成直线关系,这些点与直线的偏离
是由其他一些不确定的因素的影响所造成的.
因此可以假设y 与 x 满足以下关系:
y = β0 +β1x +ε (5.1.1) 其中β0+x β1为y 随x 线性变化的部分,β0 和β1是未知待估计的参数;ε是许多不可控或不了解的随机因素的总和,所以是不可观测的随机变量,但为了估计上的方便,通常假定
E ε= 0 D ε= σ2<∞ 未知 (5.1.2) y 是可观测的随机变量.
一般,称由(5.1.1)和(5.1.2)所确定的模型为一元线性回归模型.记为
???==++=σ
εεε
ββ2
10,0D E x y (5.1.3) 未知参数β0为常数项,β1称为回归系数,自变量x 称为回归变量.显然有
E y = β0 +β1x (5.1.4)
(5.1.4)称为回归函数.
注意:这里我们说一个模型是线性的,是指它关于参数(β0和β1)是线性的,模型中自变量的最高次幂为该模型的阶,如 y = β0 +β1x +β2x 2+ε
是一个二阶(x 的)线性(对β0,β1,β2)回归模型. 若利用试验数据求出β0和β1的估计值β∧0
和β∧
1,于是有
y ∧
=β∧0
+β∧
1x (5.1.5)
y ∧
为由估计值β∧
和β∧
1确定后对给定的x 值相应y 的回归值(预报值).
(5.1.5)称为 回归方程(预报方程).其对应的直线称为回归直线(预报直线).
图5-2
二.β0和β1的最小二乘估计及其性质
设有n 组独立的样本观测值(x i ,y i )(i = 1,2,…, n ),由(5.1.3)有
???==++=σ
εεεββ2
10,0i i i
i i D E x y i = 1,2,…, n ,εεεn ,,,21 相互独立.(5.1.6)
称为样本回归模型. 1.β0和β1的最小二乘估计
如何利用样本数据求出β0和β1的估计值β∧0和β∧
1呢?一个
最直观的想法就是在散点图上确定一条直线l :β0+β1x ,使得所有的点总的看来最接近这条直线.这时将直线l 的截距β0的取值与斜率β1的取值,作为β0和β1的估计值β∧
0和β∧
1是比较合适的.所谓所有的点总的看来最接近这条直线的含义即可以认为是
使得
Q (β0,β1) =∑=n i i 1
2ε=()∑-=n
i i i y E y 1
2
=()∑--=n
1
102
i i i x y ββ
达到最小.求出使函数Q (β0,β1)达到最小的β0,β1 的值,作为β0和β1的估计值β∧
0和β∧
1.即β∧0
和β∧
1应满足
Q (β∧0,β∧
1)=),(min 101
0ββββQ R
∈
则称β∧0
和β∧
1为β0和β1的最小二乘估计(L.S 估计).
由Q (β0,β1)是β0,β1的二元函数,要使Q 达到最小值,必要条件是β0,β1满足
???????=--∑-=??=--∑-=??==0)(20)(21011
1010
x i x i i y i Q x i y i Q
n n i ββββββ 即
??
???∑=??? ??∑+=+==n i i i n i i y x x x n y n x n n 1112010ββββ (5.1.9) 其中x =
∑=n i i x n 11,y =∑=n
i i y n 1
1,
(5.1.9)称为正规方程组. 由正规方程组解得
??
?-==x y l l xx
xy βββ10
1/ (5.1.10) 其中 =l xx ∑-=n
i x x i 12
)(,=l xy )()(1
y y x x i n
i i -∑-=,因为
??
? ????ββ1
22
Q - β022??Q β1
2
2
??Q =()
x n 22-2n ×2∑=n i x i 12
= --4 n l xx <0及
β0
2
2
??Q
=2n >0
所以(5.1.9)的解β∧0,β∧
1使Q 取到最小值.于是β0和β1的
最小二乘估计为
?????∧
-=∧=∧x
y l l xx
xy βββ10
1/
(5.1.11)
由(5.1.11)式可得 x y ββ∧+∧=
1
0,说明由最小二乘估计得到
的回归直线过样本均值),(y x .
下面我们利用(5.1.11)式来计算例5.1.1中的回归直线.
由表5.1.1的数据算得
∑=111i i x =275,x =25,∑=11
1
2
i x i =9625,∑=11
1
i i y = 258.1,y =23.4636,
y x i i i ∑=11
1
=7552.5
=l xx ∑-=11
12
)(i x x i =∑=11
1
2
i x i -11x 2= 9625-6875=2750
=l xy )()(1
y y x x i n i i -∑-==y x i i i ∑=11
1
-11x y =7552.5-6452.49=1100
???
??
=?-=∧
-=∧===∧46
.13254.04636.234.02750/1100/10
1x y l l xx xy βββ 回归方程为
x y 4.046.13+=∧
2.最小二乘估计的统计性质
性质1.β∧0
和β∧
1分别是y y y n ,,,21 的线性组合.
证:β∧
1
=
l l xx
xy =
∑--∑-==n
i i n
i i x x y y x x i 1
2
1
)
()
()(=
y x x x x i n
i n
i i i .)
()
(1
2
1∑-∑-===y b i n
i i ∑=1
(5.1.12) 其中b i =
∑--=n
i i x x x
x i 1
2
)
(=
l x
x xx
i - β∧
0= y -x β∧
1=n 1∑=n
i i y 1-x y b i n i i ∑=1=)1(1b x n i n i ∑-=y i =y c i
n i i ∑=1
(5.1.13) 其中c i =)1
(1b x n
i n i ∑-=
性质
2.E (β∧0
) = β0, E (β∧
1) = β1
(5.1.14)
D (β∧
0) = )1(2
2
l x n xx +σ,D (β∧1) = l xx σ2 ,Cov (β∧
0,β∧1)=-x l xx
σ2
证:由模型(5.1.3)知 E ε= 0 D ε= σ2
则有E (y i )= β0 +β1x i D (y i )=σ2 再由性质(1)有
E β∧
1
= E (y b i n
i i ∑=1
)= E (l y x x xx
n
i i
i ∑-=1
)()= l x x x xx
n
i i i ∑+-=1
10)
)((ββ
=l x x xx
n i i ∑-=1
0)(β+
l x x x xx
n
i i i ∑-=11)(β=
l x x xx
n
i i ∑-=1
2
1)
(β=β1
(注意到:∑--=∑-==n
i i i n
i i i x x x x x x x 1
1
))(()()
E β∧0
= E (y -x β∧1
)= E y -x E β∧
1
=
n 1∑+=n
i i x 1
10)(ββ-x β1 = β0+x β1-x β1=β0
D (β∧1) = D ????
??????∑-=l y x x xx n i i i 1)(=σ2212)(l x x xx i n
i ∑-==l xx σ2 D (β∧
) = D (y -x β∧1
)= D y +x 2D (β∧1
)-2x Cov (y ,β∧
1
)
=σσ2221
1l x n xx
+=)1(2
2l x n xx +σ
由此性质可得:
(1)E y ∧= E y 即预报值y ∧
的均值等于相应的观测值y 的均值.
(2)β0与β1的估计值波动的大小不仅与y 的方差σ2有关,而且还与预报变量x 取值的离散程度有关,x 取值分散,则β∧0与β
∧
1作为β0与β1估计值较精确,反之,若x 在x 的一个较小范围内取值,则β∧0与β∧
1作为β0与β1估计值精确度较差.因此若x 是可控
变量时,则在安排实验时x i (i = 1,2,…, n )应取得尽可能的分散,并且n 不能太小.
3.σ2的无偏估计
由于β∧0
与β∧
1作为β0与β1估计值的精确度与y 的方差σ2有关,而σ2是未知的,所以下面给出σ2的无偏估计
记 e i = y i -y i ∧
= β∧
0-β∧
1x i 称为残差,∑=n
i e i 1
2
为残差平方和或剩
余平方和,记作Q e =∑=n
i e i 12
.
取 σ2∧
=
2-n Q e =2
1
2
-∑=n e n
i i
,则σ2∧为σ2的无偏估计. 因为在模型(5.1.3)下,∑=n
i e i 1
2
有性质
E (Q e )=(n -2)σ2 (5.1.15) 证
Q e =∑=n
i e i 1
2
=∑-=∧
n
i y y i i 12
)(=∑--=∧
∧n
i x y i i 1102
)(ββ=∑-+-=∧
n
i x x y y i i 112
)](([β
=∑-=n
i y y i 12
)(- 2 β∧
1)()(1y y x x i n
i i -∑-=+β∧
21∑-=n
i x x i 12
)( =∑-=n
i y y i 12
)(- 2 β∧1l xy +β∧
21l xx =∑-=n
i y y i 1
2
)(- β∧
21l xx E (Q e )= E ∑-=n
i y y i 1
2
)(- l xx E (β∧
21
)
= E ∑-=n
i y n y i 1
2
2)(-l xx E (β∧
21
)
= ∑-=n
i y nE y E i 1
2
2)()(-l xx E (β∧
21
)
= [
][
]∑+=n
i i y E y D i 12
)
()([][])()(2
y E y D n +--l
xx
?????
???????
+∧∧)()(121ββE D
= []
∑++=n i x i 1102
2
)(ββσ-??
?
?
??++)(1022x n n ββσ-l xx ??
?
???+βσ122l xx =(n -2)σ2
+∑+=n
i x i 1
102
)(ββ-)(102
x n ββ+-l xx β12
=(n -2)σ2+β12
∑-=n
i x n x i 122
)(-l xx β12
=(n -2)σ2
E (Q e )= E (2
12
-∑=n e n
i i
)=σ2
因此 σ2∧
=
2-n Q e
= 2
12
-∑=n e n
i i
为σ2的无偏估计.
三. 回归方程的显著性检验
1.方程的显著性检验
若变量x ,y 之间存在线性关系y = β0 +β1x +ε,则β1≠0 ,因此检验变量x ,y 之间是否真正存在线性关系的问题可化为对假设
H 0:β1= 0; H 1:β1≠0
作显著性检验,若拒绝H 0,则认为变量x ,y 之间存在线性关系,所求出的回归方程有意义;若不拒绝H 0,则认为变量x ,y 之间不存在线性关系,自然也就不能用一元线性回归模型来描述,所得回归方程也就无意义.
为了进行检验,首先对模型(5.1.3)进一步假定 ε~N (0,
σ2),于是模型(5.1.6)改为
???++=)
,0(2
10σεεββN x y i i
i i ~ i = 1,2,…, n ,εεεn ,,,21 相互独立(5.1.16)
在模型(5.1.16)下有如下定理 定理5.1.1
(1)β∧
0~ N (β0 ,)1
(2
2
l x n xx
+σ) (5.1.17)
(2)β∧
1
~ N (β1
,l xx
σ2
) (5.1.18)
(3)
σ2
Q e
=σ2
1
2
∑=n
i e i
~χ2
(n -2) (5.1.19)
(4)y ,β∧
1
,∑=n
i e i 1
2
相互独立.
证:由性质1,β∧0
和β∧
1分别是服从正态分布的随机变量
y y y n ,,21的线性组合,故β∧0
和β∧
1服从正态分布,再由性质2
即得到(1)与(2).
由式(5.1.16)可得
),(210σββx N y i i +~ (i = 1,2,…, n )
将上式写成矩阵形式为
),(210I X I N Y n σββ+~ 其中 I = )1,,1,1('
Y = ),,,(21'
y y y n
X = ),,,(21'
x x x n
I n
为n 阶单位阵. 构造n 阶正交矩阵A ,其中第1,2行分别为 (
n
1,
n
1,…,
n
1)
(
l x x xx
-1,
l x x xx
-2,…,
l x x xx
n -)
作正交变换 Z = A Y Z = (z z z n ,,,21 )’ 则有),(210I AX AI N Z n σββ+~
其中AX AI ββ10+=(0,,0,),(110 l x n xx βββ+)’ 因此z z z n ,,,21 相互独立,且有
),)((2101σββx n N z +~,
),(212σβl N z xx ~
),0(2σN z i ~ (i = 3,4,…, n )
又因 z 1= y n ,z 2=y x x l i n i i xx )(11
∑-==l xx β∧1
所以
∑=n
i e i 12
=∑-=n
i y y i 12
)(-β∧2
1l xx = ∑=n
i y i 1
2-)(2
y n -)(12
β∧
l xx
=∑=n
i z i 12
-z 12-z 22=∑=n
i z i 3
2
故有 σ2
1
2
∑=n
i e i
~χ2
(n -2)
由于z z z n ,,,21 相互独立,且z 1=
y n ,z 2=
l xx β∧
1
,
∑=n
i e i 1
2
=∑=n
i z i 3
2
则有y ,β∧
1
,∑=n
i e i 1
2
相互独立.
为引入合适的检验统计量,介绍如下平方和分解公式:
l yy = U +Q e (5.1.20)
其中
l yy = ∑-=n
i y y i 12
)( 称为 总偏差平方和
U = ∑-=∧
n
i y y i 1
2
)(称为 回归平方和.
Q e = ∑-=∧
n
i y y i
i 1
2
)(称为 残差平方和.
恒等式 y y i -=(y y i
i ∧-)+(y y i
-∧
)的几何意义如图4-2,
由其出发有
∑-=n
i y y i 12
)(=∑-+-=∧
∧n
i y y y y i i i 1
2
)]()([=∑-=∧
n
i y y i i 1
2
)(+∑-=∧
n
i y y i 1
2
)(+2
∑--=∧
∧n
i i i i y y y y 1
))((
=∑-=∧
n
i y y i i 1
2
)(+∑-=∧
n
i y y i 12
)(
其中交叉项
∑--=∧
∧n
i i i i y y y y 1
))((=)()]()[(1y y y y y y i n
i i i -∑---∧
∧=
=)()]()[(11
1x x x x y y i n
i i i -∑---∧
∧=ββ
=β∧
1
l xy -β∧
21l xx = β∧1
l xy -β
∧
1
l l xx
xy l xx
= 0
图5-2
平方和分解公式(5.1.20)说明总的偏差平方和l yy 可以分为两个部分,一部分是Q e ,是由实际观测值y i 与回归值y i
∧
的偏
差即残差所引起的,另一部分U 是由回归直线所引起的.当U 越大时Q e 就越小,则y 与 x 之间的线性关系就越显著,反之y 与 x 之间的线性关系不显著.因此,可考虑当U/Q e 的值较大时,则认为y 与 x 之间的线性关系较显著.
事实上,当H 0成立时,由定理5.1.1知β∧
1
~N (0,l xx
σ2
) ,
由此得
σ
βl xx
∧
1~N (0,1),从而有
σ
2
U
=
σ
β2
2
1l xx ∧
~χ2(1)
由定理5.1.1又知 σ2
1
2
∑=n i e i
=
σ2
Q e
~χ2
(n -2),且U 与Q e 独立,
从而有
σ
2
U
与
σ
2
Q e
独立.因此,由F -分布的定义知,当H 0成立时,
统计量
F =
)
2/(-n Q U
e ~F (1,n -2) (5.1.21)
由前面的分析可知,当F 值较大时,则认为y 与 x 之间的线性关系较显著,即应拒绝H 0,则由(5.1.22)式,可给出如下判别法则:对给定的显著性水平α,当F >)2,1(1--n F α时,拒绝H 0,否则就不能拒绝H 0.
在实际作检验时,通常将此检验过程用表 5.1.2的形式给出,表5.1.2称为方差分析表.
表5.1.2一元正态线性模型的方差分析表
若经过检验拒绝了H 0,也可称回归系数β∧
1
的效果是显著的;
否则,称回归系数β∧
1
的效果不显著.此时y 与 x 的关系可能有如
下几种情况:(1)x 对y 无显著影响,应丢弃x 这个自变量,进而考虑其它自编量;(2)x 对y 有显著影响,但这种影响不是线性的,应考虑非线性回归;(3)除了x 外还有其它自变量对y 有
显著影响,从而减弱了x 对y 的影响程度,这时应考虑采用多元线性回归.
2.样本相关系数和判定系数(拟合优度)
若拒绝了H 0,即y 与 x 之间的线性关系是显著的,我们可用样本相关系数
r =
l l l yy
xx xy (5.1.22)
来刻划y 与 x 之间的线性关系的密切程度.
比较(5.1.23)式与β∧
1
=
l l xx
xy ,得r 与β∧
1
的符号一致。
又有 r 2= l l l yy xy xy 2
= l yy
U
(5.1.23)
称r 2为判定系数(拟合优度)。
由(5.1.21)知| r | ≤1,且r 2值越大,即回归平方和U 越大,残差平方和Q e 越小,y 与 x 之间的线性关系越密切,极端的情况是当| r |=1时,即Q e =0,这时,n 个点(x i ,y i )i =1,2,…,
n 全部落在回归直线y ∧
=β∧0
+β∧
1x 上.故拟合优度可以定量描述回
归方程拟合的好坏。 3.回归系数β1的置信区间
若拒绝了H 0,我们还可以给出回归系数β1的置信区间,由定理5.1.1可推得
l xx
/11σ
ββ∧
-∧
~ t (n -2)
由此β1得置信度为1-α的置信区间为 [β∧
1
- )
2(2/1--n t αl xx
σ
∧
,β∧
1
+ )
2(2/1--n t αl xx
σ
∧
]
(5.1.24)
例5.1.2 (1)对例5.1.1的回归方程进行检验;(2)求出样本相关系数r ,(3)求β1的置信度为1-α的置信区间.(α=0.05)
解 由例5.1.1中计算的结果有
=l xx 2750,=l xy 1100
=l yy ∑-=11
1
2
)(i y y i
=∑=11
1
2
i y i -11y 2
= 6498.77-6055.94
=442.83
U =
l l xy
xy 2
=2750
11002= 440 Q = l yy - U = 442.83 -440=2.83
列出如下方差分析表. 表5.1.3
由α=0.05,查得分位数)9,1(95.0F = 5.12,由于F >)9,1(95.0F = 5.12,故拒绝H 0,
认为已求得的回归方程效果是显著的. (2)由(5.1.24)式得
r 2=
l yy
U
= 0.9936 | r | = 0.9968
由| r |接近于1,又一次说明y 与 x 之间的线性关系是非常显著的.
(3)由α=0.05,1-α/2 = 0.975,查得)9(975.0t = 2.2622,则有
)
9(975.0t l xx
σ∧
= 2.2622×27505583.0=0.0241
由(4.1.25)式得β1的置信度为0.95的置信区间为 [0.3759,0.4241].
四、 回归诊断
对回归模型进行回归诊断的方法有很多,最重要的方法是残
差分析和共线诊断(对多元回归的情况)。 1. 残差分析
残差分析的基本思想是用能够计算出来的残差e i 作为随机误差εi 的估计,利用残差的特征来考察原模型的合理性,主要是对于误差假设的合理性。 残差分析就是检验:
● 误差项正态分布的假设 ● 误差项的独立性假设 ● 误差项的等方差假设
● 观测值中是否有异常值存在
1) 误差项正态分布的假设是否成立的判断:残差的正态性检验,对所得的残差数据作正态性检验。
2) 误差项的独立性假设是否成立的判断:当误差项存在序列相关时,可能导致最小二乘估计的方差变大,回归系数的t 检验失效。 ①可用D-W 检验(J.Durbin 和G .S.Watson 于1951年提出的一种适用于小样本的检验方法)
随机扰动项的一阶自回归的形式为 :u t t t +=-ερε1
H 0:0=ρ
DW=∑∑-==-n
t t n
t t t e e e 22
2
12
)
()
(
0≤DW ≤4
在给定样本容量n 、自变量个数及显著性水平之后,在D-W 检验临界值表中可以查到D-W 检验的下临界值d l 和上临界值d u
②残差的序列图和残差的散点图
残差的序列图:以e t 为纵轴,以时间t 为横轴来绘制的 残差的散点图:分别以e t 和e t 1-为纵轴和横轴来绘制的 序列图呈随机走势,散点图呈随机分布,则认为不存在序列相关
3)误差项的等方差假设是否成立的判断:
残差图:凡是以残差e t 为纵坐标,而以观测值y i ,预测值y i ∧
,自变量Xj (j = 1,2,…,p )或序号、观测时间等为横坐标的散点图,均称为残差图。
如果线性回归模型的等方差假定成立, e i ,(i=1, 2,…,n )应相互独立且近似服从N(0,1),那么残差图中散点应随机地分布在–2到+2的带子里。这样的残差图称为正常的残差图。 4)样本奇异值的诊断:
样本奇异值是样本数据中那些远离均值的样本数据点。它们会对回归方程的拟合产生较大偏差影响。
一般认为,如果某样本点对应的标准化残差的值超出了-3—+3的范围,就可以判定该样本数据为奇异值。
五.预测
若经过检验,拒绝了H 0,说明回归方程是有意义的,即回归方程与实际数据的拟合效果是显著的,则可用已求得的回归方程y ∧
=β∧0
+β∧
1x 来进行预测.
所谓预测是指对自变量x 的某一确定值x 0用已求得的回归方程y ∧=β∧0
+β∧
1x 来估计因变量y 的相应值y 0所在的范围. 设变量y 与x 满足模型(5.1.3),且由数据(x i ,y i )(i =1,2, …,n )求得回归方程y ∧
=β∧0
+β∧
1x ,x 0为x 的某一确定值,
y 0=β∧
+β∧
1x 0+ε0,ε0~N (0,σ2)且ε0,ε1, …,εn 相互
独立.
在以上假设下先给出E y 0的置信区间,然后再给出y 0的预测
区间.
由y
0=β∧
+β∧
1
x0+ε0和定理5.1.1可知
y∧0= y+β∧
1
(x0- x)~N(β
+β
1
x0,[
n
1
+
l
x
x
xx
)
(
2
-
]σ2)
(5.1.25)
且y∧
0与Q
e
独立,再由t-分布的定义有
)2
(
)
(
1
2
2
0/
)
(
-
-
+
-
∧
n
Q
l
x
x
n
y
E
y
e
xx
σ
σ
=
l
x
x
n
y
E
y
xx
)
(
1
)
(
2
-
+
∧
-
∧
σ
~t
(n-2)
于是E y
的置信度为1-α的置信区间为
[y∧
0- )2
(
2/
1
-
-
n
tα
l
x
x
n
xx
)
(
1
2
-
+
∧
σ
,y∧
0+ )2
(
2/
1
-
-
n
tα
l
x
x
n
xx
)
(
1
2
-
+
∧
σ] (5.1.26)
由y∧
0是y i的线性组合(i =1,2,…,n),y
与y i (i =1,
2,…,n)独立,所以y
0与y∧
独立,又y∧
与Q
e
独立,故有y
-y∧
与Q
e
独立.
又y
0~N(β
+β
1
x0,σ2),
y∧0~N(β
+β
1
x0,[
n
1
+
l
x
x
xx
)
(
2
-
]σ2)
故
y 0-y∧
~N(0,[1+
n
1
+
l
x
x
xx
)
(
2
-
]σ2)
再由t-分布的定义有
)
2()
(11)(20
2
00/--++-∧
n Q l x x n y y e
xx
σσ=
l x x n
y y xx
)
(11)
(02
00-++-∧
∧
σ~t
(n -2)
于是y 0的置信度为1-α的预测区间为
[y ∧
0-)2(2/1--n t αl x x n xx
)(1102
-++∧
σ
y ∧
0+)2(2/1--n t αl x x n xx
)
(1102
-+
+∧
σ](5.1.27) 由(5.1.28)式可以看出σ∧
越小y 0的预测区间越窄,则预测精度越高;对给定的样本观测值和置信度,x 0离x 越近,则预测精度越高.
比较(5.1.27)和(5.1.28)式可以看出在同样的置信度下y 0
的预测区间较E y 0的置信区间要宽一些.
由x 0的任意性,及(5.1.28)式可以得到两条曲线: y ∧
1
= y ∧
- )2(2/1--n t αl x x xx
n )(2
11-++∧
σ
y ∧
2= y ∧
+ )2(2/1--n t αl x x xx
n )
(2
11-++∧
σ
夹在这两条曲线之间的部分为y 的置信度为1-α的预测带,如图
5-3
图5-3
特别当n 很大,x 0在x 附近取值时,有
)2(2/1--n t α≈u 2
/1α- ,l x x xx
n )(0112
-++∧
σ≈σ∧ 这时y 0的置信度为1-α的预测区间可近似为:
[y ∧
0-u 2/1α-σ
∧
,y ∧
0+u 2
/1α-σ∧
] (5.1.28)
如图5-4
图5-4
在实际中常用的有:
y 的置信度为0.95的预测区间为[y ∧
-1.96σ∧
,y ∧
+1.96σ∧
]
y 的置信度为0.99的预测区间为[y ∧-2.58σ∧
,y ∧
+2.58σ∧
]
例5.1.3 在例5.1.1中求当温度x 0=23时,E y 0的95%的置信区间,y 0的95%的预测区间.
解 y ∧0=β∧0
+β∧
1x 0= 13.4636+0.4×23=22.6636,
)9(975.0t =2.2622
l x x xx n )(012
-+∧
σ=0.56072750111)2523(2
-+=0.1705 l x x xx
n )
(0
112
-++∧
σ
=0.560727501111)2523(2
-++=0.5860 由(5.1.27)式,E y 0的95%的置信区间为
[22.6636-2.2622×0.1705,22.6636+2.2622×0.1705]=
[22.2779,23.0493]
由(5.1.28)式,y 0的95%的预测区间
[22.6636-2.2622×0.5860,22.6636+2.2622×0.5860]= [21.338,23.9892]
习题五 1 试检验不同日期生产的钢锭的平均重量有无显著差异?(=0.05) 解 根据问题,因素A 表示日期,试验指标为钢锭重量,水平为5. 假设样本观测值(1,2,3,4)ij y j =来源于正态总体2 ~(,),1,2,...,5i i Y N i μσ= . 检验的问题:01251:,:i H H μμμμ===不全相等 . 计算结果: 表5.1 单因素方差分析表 ‘*’ . 查表0.95(4,15) 3.06F =,因为0.953.9496(4,15)F F =>,或p = 0.02199<0.05, 所以拒绝0H ,认为不同日期生产的钢锭的平均重量有显著差异. 2 考察四种不同催化剂对某一化工产品的得率的影响,在四种不同催化剂下分别做试验 试检验在四种不同催化剂下平均得率有无显著差异?(=0.05) 解 根据问题,设因素A 表示催化剂,试验指标为化工产品的得率,水平为4 . 假设样本观测值(1,2,...,)ij i y j n =来源于正态总体2 ~(,),1,2,...,5i i Y N i μσ= .其中
样本容量不等,i n 分别取值为6,5,3,4 . 检验的问题:012341:,:i H H μμμμμ===不全相等 . 计算结果: 表5.2 单因素方差分析表 查表0.95(3,14) 3.34F =,因为0.952.4264(3,14)F F =<,或p = 0.1089 > 0.05, 所以接受0H ,认为在四种不同催化剂下平均得率无显著差异 . 3 试验某种钢的冲击值(kg ×m/cm2),影响该指标的因素有两个,一是含铜量A , 试检验含铜量和试验温度是否会对钢的冲击值产生显著差异?(=0.05) 解 根据问题,这是一个双因素无重复试验的问题,不考虑交互作用. 设因素,A B 分别表示为含铜量和温度,试验指标为钢的冲击力,水平为12. 假设样本观测值(1,2,3,1,2,3,4)ij y i j ==来源于正态总体2 ~(,),1,2,3,ij ij Y N i μσ= 1,2,3,4j = .记i α?为对应于i A 的主效应;记j β?为对应于j B 的主效应; 检验的问题:(1)10:i H α?全部等于零,11 :i H α?不全等于零; (2)20:j H β?全部等于零,21:j H β?不全等于零; 计算结果: 表5.3 双因素无重复试验的方差分析表 查表0.95(2,6) 5.143F =,0.95(3,6) 4.757F =,显然计算值,A B F F 分别大于查表值, 或p = 0.0005,0.0009 均显著小于0.05,所以拒绝1020,H H ,认为含铜量和试验温度都会对钢的冲击值产生显著影响作用. 4 下面记录了三位操作工分别在四台不同的机器上操作三天的日产量:
《应用数理统计》复习题 第一章 概率知识 一、一袋中有5个球,编号1、2、3、4、5. 现从中任取3个,以X 表示所取球的号码的最大值, 求X 的概率分布律. 解:X 的可能取值为3、4、5, 1.010 1 }3{35 33== ==C C X P , 3.0103 }4{352311====C C C X P , 6.010 6 }5{35 2411== = =C C C X P , 故X 的概率分布律为 6 .03.01.05 43k p X . 二、设连续型随机变量X 的密度函数为?? ?<≤=., 0, 10,)(其它x Ax x f (1)求常数A ;(2)求X 的分布函数)(x F . 解:(1)由完备性:? ∞+∞ -=1)(dx x f , 有 11 =?Ax , 解得2=A . (2)t d t f x F x ?∞ -=)()( 当0≤x 时, 0)(}{)(?∞ -==≤=x dt t f x X P x F , 当10≤
2、0cos 21 )(22 ??∞ ∞--===π πxdx x dx x xf EX ; ???∞ ∞---====22202 2 22 2 14cos cos 21)(πππ πxdx x xdx x dx x f x EX ; 14 )(2 2 2-= -=∴πEX EX DX . 四、若随机(X ,Y )在以原点为中心的单位圆上服从均匀分布,证明X ,Y 不相互独立. 解:依题意有(X ,Y )的概率密度为221/, 1; (,)0, x y f x y π?+≤=??其它. . 故 11, 11()(,)0, 0, X x x f x f x y dy +∞ -∞ ?-≤≤-≤≤?===????? ? 其它其它; 同理 11()0, Y y f y -≤≤=??其它 . 于是(,)()()X Y f x y f x f y ≠, X 与Y 不相互独立. 五、设X 的概率密度为? ? ?≤≤+=.,0,10,)(其它x bx a x f ,且已知EX =127求DX . 解:由概率密度的完备性有: 1= ?? += ∞+∞ -1 d )(d )(x bx a x x f =b a 5.0+, 且有12 7 =EX = ? ? += ∞+∞ -10 d )(d )(x bx a x x x xf = 3 2b a +, 联立上述两式解得: 1,5.0== b a 又= )(2X E 12 5 d )5.0(1 02= +? x x x , 于是 =DX =-22)()(EX X E 2)12 7(125-14411=. 六、1.设随机变量)3,2(~2 N X ,)()(C X P C X P >=<,则=C ( A ). A . 2 B . 3 C . 9 D . 0 2. 设随机变量),(~2 σμN X ,则随σ增大,}|{|σμ<-X P ( C ). (A) 单调增大; (B) 单调减小; (C) 保持不变; (D) 增减不定
一 填空题 1 设 6 21,,,X X X 是总体 ) 1,0(~N X 的一个样本, 26542321)()(X X X X X X Y +++++=。当常数C = 1/3 时,CY 服从2χ分布。 2 设统计量)(~n t X ,则~2X F(1,n) , ~1 2 X F(n,1) 。 3 设n X X X ,,,21 是总体),(~2 σu N X 的一个样本,当常数C = 1/2(n-1) 时, ∑-=+-=1 1 212 )(n i i i X X C S 为2σ的无偏估计。 4 设)),0(~(2σεε βαN x y ++=,),,2,1)(,(n i y x i i =为观测数据。对于固定的0x , 则0x βα+~ () 2 0201,x x N x n Lxx αβσ?? ? ?- ???++ ??? ?????? ? 。 5.设总体X 服从参数为λ的泊松分布,,2,2,, 为样本,则λ的矩估计值为?λ = 。 6.设总体2 12~(,),,,...,n X N X X X μσ为样本,μ、σ2 未知,则σ2的置信度为1-α的 置信区间为 ()()()()22 2212211,11n S n S n n ααχχ-??--????--???? 。 7.设X 服从二维正态),(2∑μN 分布,其中??? ? ??=∑??? ? ??=8221, 10μ 令Y =X Y Y ???? ??=???? ??202121,则Y 的分布为 ()12,02T N A A A A μ??= ??? ∑ 。 8.某试验的极差分析结果如下表(设指标越大越好): 表2 极差分析数据表
《应用数理统计》吴翊李永乐第五章方差分析课后作业 参考答案 标准化文件发布号:(9312-EUATWW-MWUB-WUNN-INNUL-DQQTY-
第五章 方差分析 课后习题参考答案 下面给出了小白鼠在接种三种不同菌型伤寒杆菌后的存活日数: 设小白鼠存活日数服从方差相等的正态分布,试问三种菌型的平均存活日数有无显著差异(01.0=α) 解:(1)手工计算解答过程 提出原假设:() 3,2,10:0==i H i μ 记 167.20812 11112 =??? ? ??-=∑∑∑∑====r i n j ij r i n j ij T i i X n X S 467.70112 112 11=???? ??-???? ??=∑∑∑∑====r i n j ij r i n j ij i A i i X n X n S 7 .137=-=A T e S S S 当 H 成立时, ()() ()r n r F r n S r S F e A ----= ,1~/1/ 本题中r=3 查表得 ()()35 .327,2,195.01==---F r n r F α且F=>,在95%的置信度下,拒绝原假 设,认为不同菌型伤寒杆菌对小白鼠的存活日数有显著影响。 (2)软件计算解答过程
组建效应检验 Dependent Variable: 存活日数a 70.429235.215 6.903 .004 137.73727 5.101 208.167 29 方差来源菌型误差总和 平方和自由度 均值F 值P 值R Squared = .338 (Adjusted R Squared = .289) a. 从上表可以看出,菌种不同这个因素的检验统计量F 的观测值为,对应的检验概率p 值为,小于,拒绝原假设,认为菌种之间的差异对小白鼠存活日数有显著影响。 现有某种型号的电池三批,他们分别是甲、乙、丙三个工厂生产的,为评论其质量,各随机抽取6只电池进行寿命试验,数据如下表所示: 工厂 寿命(小时) 甲 40 48 38 42 45 乙 26 34 30 28 32 丙 39 40 43 50 50 试在显著水平0.05α=下,检验电池的平均寿命有无显著性差异并求 121323,μμμμμμ---及的95%置信区间。这里假定第i 种电池的寿命 2i X (,)(1,2,3) i N i μσ=。 解:手工计算过程: 1.计算平方和 其检验假设为:H0:,H1:。 2.假设检验: 所以拒绝原假设,即认为电池寿命和工厂显著相关。 6 .615])394.44()3930()396.42[(*4)()(4 .216)3.28108.15(*4*))(1()(832 429.59*14*))(1()(2221 22 1 21 22 222=-+-+-=-=-==++=-==-===-==-=∑∑∑∑∑∑∑∑∑===r i i i i A r i i i r i i i i ij e ij T X X n X X S S n S n X X S s n ns X X S 0684 .170333 .188 .30712/4.2162/6.615)/()1/(===--= r n S r S F e A 89 .3)12,2(),1(95.01==-->-F r n r F F α
应用数理统计复习题 1.设总体~(20,3)X N ,有容量分别为10,15的两个独立样本,求它们的样本均值之差的绝对值小于0.3的概率. 解:设两样本均值分别为,X Y ,则1~(0,)2 X Y N - (||0.3)(0.424)(0.424)0.328P X Y -<=Φ-Φ-= 其中(01)θθ<<为未知参数,已知取得了样本值1231,2,1x x x ===,求θ的矩估计和最大似然估计. 解:(1)矩估计:2 2 22(1)3(1)23EX θθθθθ=+?-+-=-+ 14 (121)33 X =++= 令EX X =,得5?6 θ=. (2)最大似然估计: 2 2 5 6 ()2(1)22L θθθθθθθ=??-=- 45ln() 10120d d θθθθ=-= 得5?6 θ= 3. 设某厂产品的重量服从正态分布,但它的数学期望μ和方差2 σ均未知,抽查10件,测得重量为i X 斤10,,2,1Λ=i 。算出 10 11 5.410i i X X ===∑ 10 21 () 3.6i i X X =-=∑ 给定检验水平0.05 α=,能否认为该厂产品的平均重量为5.0斤? 附:t 1-0.025(9)=2.2622 t 1-0.025(10)=2.2281 t 1-0.05(9)=1.8331 t 1-0.05(10)=1.8125 解: 检验统计量为0 | |/X T S n m -=
将已知数据代入,得2t = = 1/2 0.975(1)(9) 2.26222t n t a - -==> 所以接受0H 。 4. 在单因素方差分析中,因素A 有3个水平,每个水平各做4次重复实验,完成下列方差分析表,在显著水平0.05α=下对因素A 是否显著做检验。 解: 0.95(2,9) 4.26F =,7.5 4.26F =>,认为因素A 是显著的. 5. 现收集了16组合金钢中的碳含量x 及强度y 的数据,求得 0.125,45.7886,0.3024,25.5218xx xy x y L L ====,2432.4566yy L =. (1)建立y 关于x 的一元线性回归方程01 ???y x ββ=+; (2)对回归系数1β做显著性检验(0.05α=). 解:(1)1 25.5218 ?84.39750.3024 xy xx l l β== = 01 ??35.2389y x ββ=-= 所以,?35.238984.3975y x =+ (2)1?2432.456684.397525.5218278.4805e yy xy Q l l β=-=-?= 2 278.4805 ?19.8915214 e Q n σ ===- ? 4.46σ ==
第二章 参数估计 课后习题参考答案 2.1 设总体X 服从二项分布()n X X X p p N B ,,,,11,,21 <<为其子样,求N 及p 的矩法估计。 解: ()()()p Np X D Np X E -==1, 令() ?????-==p Np S Np X 12 解上述关于N 、p 的方程得: 2.2 对容量为n 的子样,对密度函数22 (),0(;)0,0x x f x x x ααααα ?-?=??≤≥? 其中参数α的矩法估计。 解:12 2 ()()a E x x x dx α αα== -? 22 02 2 ()x x dx α α α=- ? 232 1 22 133 3 αααααα α = - =-= 所以 133a x α∧ == 其中121,21 (),, ,n n x x x x x x x n = +++为n 个样本的观察值。 2.3 使用一测量仪器对同一值进行了12次独立测量,其结果为(单位:mm) 232.50,232.48,232.15,232.52,232.53,232.30 232.48,232.05,232.45,232.60,232.47,232.30 试用矩法估计测量的真值和方差(设仪器无系统差)。 ?? ? ??? ? -=-==X S p S X X p X N 2221???
解: () () () ∑∑====-= ===n i i n i i S X X n X D X X n X E 1 22 1 0255 .01 4025 .2321 2.4 设子样1.3,0.6,1.7,2.2,0.3,1.1是来自具有密度函数()10,1 ,<<=ββ βx f 的总 体,试用矩法估计总体均值、总体方差及参数β。 解: () ()()()4.22?2 ,1 ,407 .012 .110 1 2 2 1==== === =-===? ?∑∑==X X dx x dx x xf X E x f X X n S X n X n i i n i i β β β ββ ββ β参数:总体方差:总体均值: 2.5 设n X X X ,,,21 为()1N , μ的一个字样,求参数μ的MLE ;又若总体为( )2 1N σ,的 MLE 。 解:(1) ()()()()() ()()() () ()X x n x x L x n x L e x L x f e x f n i i n i i i n i i i x n i n i i x i n i i i =∑=∑=-=??∑---=∑= == ===--=-- =∏1 112 2 2 1 2 1?0,ln 212ln 2,ln 21 ,,21,1 2 2 μ μμ μμπμπμμπ μμμ
北航2010《应用数理统计》考试题及参考解答 09B 一、填空题(每小题3分,共15分) 1,设总体X 服从正态分布(0,4)N ,而12 15(,,)X X X 是来自X 的样本,则22 110 22 11152() X X U X X ++=++服从的分布是_______ . 解:(10,5)F . 2,?n θ是总体未知参数θ的相合估计量的一个充分条件是_______ . 解:??lim (), lim Var()0n n n n E θθθ→∞ →∞ ==. 3,分布拟合检验方法有_______ 与____ ___. 解:2 χ检验、柯尔莫哥洛夫检验. 4,方差分析的目的是_______ . 解:推断各因素对试验结果影响是否显著. 5,多元线性回归模型=+Y βX ε中,β的最小二乘估计?β的协方差矩阵?βCov()=_______ . 解:1?σ-'2Cov(β) =()X X . 二、单项选择题(每小题3分,共15分) 1,设总体~(1,9)X N ,129(,, ,)X X X 是X 的样本,则___B___ . (A ) 1~(0,1)3X N -; (B )1 ~(0,1)1X N -; (C ) 1 ~(0,1) 9X N -; (D ~(0,1)N . 2,若总体2(,)X N μσ,其中2σ已知,当样本容量n 保持不变时,如果置信度1α-减小,则μ的 置信区间____B___ . (A )长度变大; (B )长度变小; (C )长度不变; (D )前述都有可能. 3,在假设检验中,就检验结果而言,以下说法正确的是____B___ . (A )拒绝和接受原假设的理由都是充分的; (B )拒绝原假设的理由是充分的,接受原假设的理由是不充分的; (C )拒绝原假设的理由是不充分的,接受原假设的理由是充分的; (D )拒绝和接受原假设的理由都是不充分的. 4,对于单因素试验方差分析的数学模型,设T S 为总离差平方和,e S 为误差平方和,A S 为效应平方和,则总有___A___ .
第二章 参数估计(续) P68 2.13 设总体X 服从几何分布:{}()1 1k P X k p p -==-,12k = ,,,01p <<,证明 样本均值1 1 n i i X X n == ∑是()E X 的相合、无偏和有效估计量。 证明: 总体X 服从几何分布, ∴()1= E X p ,()2 1-= p D X p . 1 () ()1 11 11 11==????===??== ? ????? ∑ ∑ n n i i i i E X E X E X n E X n n n p p . ∴样本均值11n i i X X n == ∑ 是()E X 的无偏估计量。 2 () 2222 1 11 1111==--???? ===??= ? ?????∑ ∑n n i i i i p p D X D X D X n n n n p np . ()()()()11 11 ln ln 1ln 1ln 1-??=-=+--??;X f X p p p p X p . () 111ln 111111f X p X X p p p p p ?--= - =+?--;. () () 2 11 2 2 2 ln 11 1f X p X p p p ?-=- + ?-;. ()()()()21112 2 2 22ln 11 1111f X p X X I p E E E p p p p p ???? ?? ?--=-=--+=+???????--?????? ? ?? ? ; () ()() ()12 2 2 2 2 211 11 111111111??-= + -= + ?-=+? ?---?? p E X p p p p p p p p ()()() () 2 2 2 111 1 111-+= + = = ---p p p p p p p p p .
习题三 1 正常情况下,某炼铁炉的铁水含碳量2(4.55,0.108)X N :.现在测试了5炉铁水,其含碳量分别为4.28,4.40,4.42,4.35,4.37. 如果方差没有改变,问总体的均值有无显著变化?如果总体均值没有改变,问总体方差是否有显著变化(0.05α=)? 解 由题意知 2~(4.55,0.108),5,0.05 X N n α==, 1/20.975 1.96u u α-==,设立统计原假设 0010:,:H H μμμμ=≠ 拒 绝域为 {} 00K x c μ=->,临界值 1/2 1.960.108/0.0947c u α-==?=, 由于 0 4.364 4.550.186x c μ-=-=>,所以拒绝0H ,总体 的均值有显著性变化. 设立统计原假设 22220010:,:H H σσσσ=≠ 由于0μμ=,所以当0.05α=时 22220.0250.9751 1()0.03694,(5)0.83,(5)12.83,n i i S X n μχχ==-===∑% 22 10.025 20.975(5)/50.166,(5)/5 2.567c c χχ==== 拒绝域为 {}2222 00201//K s c s c σσ=><%%或 由于220/ 3.167 2.567S σ=>%,所以拒绝0H ,总体的方差有 显著性变化. 2 一种电子元件,要求其寿命不得低于1000h .现抽测25件,得其均值为x =950h .已知该种元件寿命
2(100,)X N σ:,问这批元件是否合格(0.05α=)? 解 由题意知 2(100,)X N σ:,设立统计原假设 0010:,:,100.0.05.H H μμμμσα≥<== 拒绝域为 {}00K x c μ=-> 临界值为 0.050.0532.9c u u =?=?=- 由于 050x c μ-=-<,所以拒绝0H ,元件不合格. 3 某食品厂用自动装罐机装罐头食品,每罐标准重量为500g ,现从某天生产的罐头中随机抽测9罐,其重量分别为510,505,498,503,492,502,497,506,495(g ),假定罐头重量服从正态分布. 问 (1)机器工作是否正常(0.05α=)? 2)能否认为这批罐头重量的方差为5.52 (0.05α=)? 解 (1)设X 表示罐头的重量(单位:g). 由题意知 2(,)X N μσ:,μ已知 设立统计原假设 0010 :500,:H H μμμμ==≠,拒绝域 {}00K x c μ=-> 当0.05α=时,2500.89,34.5, 5.8737x s s === 临界值 12(1) 4.5149c t n α-=-?=,由于 00.8889x c μ-=<, 所以接受0H ,机器工作正常. (2)设X 表示罐头的重量(单位:g). 由题意知 2(,)X N μσ:,σ 已知
材料学院研究生会 学术部 2011 年12 月 2007-2008学年第一学期期末试卷 一、(6 分,A 班不做)设x1,x2,?,x n是来自正态总体N( , 2) 的样本,令 2(x1 x2) T (x3 x4)2 (x5 x6)2 , 试证明T 服从t-分布t(2) 二、( 6 分, B 班不做 ) 统计量F-F(n,m) 分布,证明 1的 (0< <1)的分位点x 是1。 F F1 (n,m) 。 三、(8分)设总体X 的密度函数为 其中1,是位置参数。x1,x2,?,x n是来自总体X 的简单样本, 试求参数的矩估计和极大似然估计。 四、(12分)设总体X 的密度函数为 1x exp ,x p(x; ) 0 , 其它 其中, 已知,0, 是未知参数。x1,x2,?,x n 是来自总体X 的简单样本。
1)试求参数的一致最小方差无偏估计; 2) 是否为的有效估计?证明你的结论。 五、(6分,A 班不做)设x1,x2,?,x n是来自正态总体N( 1, 12) 的 简单样本,y1,y2,?,y n 是来自正态总体N( 2, 22) 的简单样本,且两样本相互独立,其中1, 12, 2, 22是未知参数,1222。为检验假设H0 : 可令z i x i y i, i 1,2,..., n ,1 2 , 1 2, H1 : 1 2, 则上述假设检验问题等价于H0 : 1 0, H1: 1 0,这样双样本检验问题就变为单检验问题。基于变换后样本z1,z2,?,z n,在显著性水平下,试构造检验上述问题的t-检验统计量及相应的拒绝域。 六、(6 分,B 班不做)设x1,x2,?,x n是来自正态总体N( 0, 2) 的简单样本,0 已知,2未知,试求假设检验问题 H0: 202, H1: 202的水平为的UMPT。 七、(6 分)根据大作业情况,试简述你在应用线性回归分析解决实际问题时应该注意哪些方面? 八、(6 分)设方差分析模型为 总离差平方和 试求E(S A ) ,并根据直观分析给出检验假设H0 : 1 2 ... P 0的拒绝域形式。 九、(8分)某个四因素二水平试验,除考察因子A、B、C、D 外,还需考察 A B ,B C 。今选用表L8(27 ) ,表头设计及试验数据如表所示。试用极差分析指出因子的主次顺序和较优工艺条件。
习题五 1 某钢厂检查一月上旬内的五天中生产的钢锭重量,结果如下:(单位:k g) 日期重旦量 1 5500 5800 5740 5710 2 5440 5680 5240 5600 4 5400 5410 5430 5400 9 5640 5700 5660 5700 10 5610 5700 5610 5400 试检验不同日期生产的钢锭的平均重量有无显著差异? ( =0.05) 解根据问题,因素A表示日期,试验指标为钢锭重量,水平为 5. 2 假设样本观测值y j(j 123,4)来源于正态总体Y~N(i, ),i 1,2,...,5 检验的问题:H。:i 2 L 5, H i : i不全相等. 计算结果: 注释当=0.001表示非常显著,标记为*** '类似地,=0.01,0.05,分别标记为 查表F0.95(4,15) 3.06,因为F 3.9496 F0.95(4,15),或p = 0.02199<0.05 ,所 以拒绝H。,认为不同日期生产的钢锭的平均重量有显著差异 2 考察四种不同催化剂对某一化工产品的得率的影响,在四种不同催化剂下分别做试验 解 根据问题,设因素A表示催化剂,试验指标为化工产品的得率,水平为 4 . 2 假设样本观测值y j(j 1,2,..., nJ来源于正态总体Y~N(i, ), i 1,2,...,5 .其中样本容量不等,n分别取值为6,5,3,4 .
日产量 操作工 查表 F O .95(3,14) 3.34,因为 F 2.4264 F °.95(3,14),或 p = 0.1089 > 0.05, 所以接受H 。,认为在四种不同催化剂下平均得率无显著差异 3 试验某种钢的冲击值(kg Xm/cm2 ),影响该指标的因素有两个,一是含铜量 A ,另 一个是温度 试检验含铜量和试验温度是否会对钢的冲击值产生显著差异? ( =0.05 ) 解 根据问题,这是一个双因素无重复试验的问题,不考虑交互作用 设因素A,B 分别表示为含铜量和温度,试验指标为钢的冲击力,水平为 12. 2 假设样本观测值y j (i 1,2,3, j 1,2,3,4)来源于正态总体 Y j ~N (j , ),i 1,2,3, j 1,2,3,4 .记i 为对应于A 的主效应;记 j 为对应于B j 的主效应; 检验的问题:(1) H i 。: i 全部等于零,H i — i 不全等于零; (2) H 20 : j 全部等于零,H 21: j 不全等于零; 计算结果: 查表F 0.95(2,6) 5.143 ,局.95(3,6) 4.757 ,显然计算值F A , F B 分别大于查表值, 或p = 0.0005 , 0.0009均显著小于0.05,所以拒绝H i°,H 20,认为含铜量和试验温度 都会对钢的冲击值产生显著影响作用 . 4 下面记录了三位操作工分别在四台不同的机器上操作三天的日产量: 检验的问题:H 0: 1 计算结果: H i : i 不全相等
应用数理统计复习题 1.设总体,有容量分别为10,15的两个独立样本,求它们的样本均值之差的绝对值小于0.3的概率. 解:设两样本均值分别为,则 2. 设总体具有分布律 1 2 3 其中为未知参数,已知取得了样本值,求的矩估计和最大似然估计. 解:(1)矩估计: 令,得. (2)最大似然估计: 得 3. 设某厂产品的重量服从正态分布,但它的数学期望和方差均未知,抽查10件,测得重量为斤。算出 给定检验水平,能否认为该厂产品的平均重量为5.0斤? 附:t1-0.025(9)=2.2622 t1-0.025(10)=2.2281 t1- 0.05(9)=1.8331 t1-0.05(10)=1.8125 解: 检验统计量为
将已知数据代入,得 所以接受。 4. 在单因素方差分析中,因素有3个水平,每个水平各做4次重复实验,完成下列方差分析表,在显著水平下对因素是否显著做检验。 来源平方和自由度均方和F比 因素 4.2 误差 2.5 总和 6.7 解: 来源平方和自由度均方和F比 因素 4.2 2 2.1 7.5 误差 2.5 9 0.28 总和 6.7 11 ,,认为因素是显著的. 5. 现收集了16组合金钢中的碳含量及强度的数据,求得 ,. (1)建立关于的一元线性回归方程; (2)对回归系数做显著性检验(). 解:(1) 所以, (2)
拒绝原假设,故回归效果显著. 6.某正交试验结果如下 列号 试验号A B C 1 2 3 结果 1 2 3 4 1 1 1 1 2 2 2 1 2 2 2 1 13.25 16.54 12.11 18.75 (1)找出对结果影响最大的因素; (2)找出“算一算”的较优生产条件;(指标越大越好) (3)写出第4号实验的数据结构模型。 解: 列号 试验号A B C 1 2 3 结果 1 2 3 4 1 1 1 1 2 2 2 1 2 2 2 1 13.25 16.54 12.11 18.75 ⅠⅡR 29.79 25.36 32.0 30.86 35.29 28.65 1.07 9.9 3.35 (1)对结果影响最大的因素是B; (2)“算一算”的较优生产条件为 (3) 4号实验的数据结构模型为 ,
应用数理统计答案 学号: 姓名: 班级:
目录 第一章数理统计的基本概念 (2) 第二章参数估计 (14) 第三章假设检验 (24) 第四章方差分析与正交试验设计 (29) 第五章回归分析 (32) 第六章统计决策与贝叶斯推断 (35) 对应书目:《应用数理统计》施雨著西安交通大学出版社
第一章 数理统计的基本概念 1.1 解:∵ 2 (,)X N μσ ∴ 2 (,)n X N σμ ∴ (0,1)N 分布 ∴(1)0.95P X P μ-<=<= 又∵ 查表可得0.025 1.96u = ∴ 2 2 1.96n σ= 1.2 解:(1) ∵ (0.0015)X Exp ∴ 每个元件至800个小时没有失效的概率为: 800 0.00150 1.2 (800)1(800) 10.0015x P X P X e dx e -->==-<=-=? ∴ 6个元件都没失效的概率为: 1.267.2 ()P e e --== (2) ∵ (0.0015)X Exp ∴ 每个元件至3000个小时失效的概率为: 3000 0.00150 4.5 (3000)0.00151x P X e dx e --<===-? ∴ 6个元件没失效的概率为: 4.56 (1)P e -=- 1.4 解:
i n i n x n x e x x x P n i i 1 2 2 )(ln 2121)2(),.....,(1 22 =-- ∏∑ = =πσμσ 1.5证: 2 1 1 2 2)(na a x n x a x n i n i i i +-=-∑∑== ∑∑∑===-+-=+-+-=n i i n i i n i i a x n x x na a x n x x x x 1 2 2 2 2 11) ()(222 a) 证: ) (1111 1+=+++=∑n n i i n x x n x ) (1 1 )(1 1 11n n n n n x x n x x x n n -++=++=++
4-45. 自动车床加工中轴,从成品中抽取11根,并测得它们的直径(mm )如下: 10.52,10.41,10.32,10.18,10.64,10.77,10.82,10.67,10.59,10.38,10.49 试用W 检验法检验这批零件的直径是否服从正态分布?(显著性水平05.0=α) (参考数据:) 4-45. 解:数据的顺序统计量为: 10.18,10.32,10.38,10.41,10.49,10.52,10.59,10.64,10.67,10.77,10.82 所以 6131 .0][)()1(5 1 ) (=-= -+=∑k k n k k x x a L , 又 5264.10=x , 得 38197 .0)(11 1 2 =-∑=i i x x 故 984.0) (11 1 2 2 =-= ∑=i i x x L W , 又 当n = 11 时,85.005.0=W 即有 105.0< 山东科技大学2016—2017学年第一学期硕士研究生 《应用统计》考试试卷 2017.06 班级 姓名 学号 一、填空题(每空3分,共36分) 1.当样本观测值12345(,,,,)(1,4,6,4,3)x x x x x =--时,对应次序统计量的观测值为 ;秩统计量的观测值为 . 2.设128,,,(0,4)X X X iid N L ,8118i i X X ==∑,则4814i i i i E X X ==?? ????=?? ????????? ∑∑ ; 821()i i E X X =??-=????∑ ;421()i i E X X =??-=???? ∑ . 3.设129,,,(1,1)X X X iid N L ,则() 9 2 11 1i i Y X == -∑服从 分布; () ()4 8 2 2 21 5 11i i i i Y X X ===--∑∑服从 分布;( 311Y X =-服从 分布. 4.设总体2(,)X N μσ:,样本1,n X X L ,2 σ已知, X 样本均值,2 S 为样本方差, 若 )~(0,1)X N μσ-,则μ的一个双侧1α-置信区间为 ;μ的一个单侧 1α-置信上限为 。 5.在样本量41n =、水平数5a =的单因子方差分析模型中,若总离差平方和200SS =,误 差平方和120e SS =,则因素平方和A SS = ;F 检验统计量的值= . 二、计算与证明(1、4小题每题20分,2、3小题每题12分,共64分) 1.设总体的分布密度函数为1 ,02()20,x f x θθ?≤≤? =???其他 ,1,n X X L 是从中抽取的样本, 应用数理统计试题 1.设15,,X X 是独立且服从相同分布的随机变量,且每一个()1,2,,5i X i = 都服从()0,1.N (1)试给出常数c ,使得()22 12c X X +服从2χ公布,并指出它的自由度; (2)试给出常数,d 使得 服从t 分布,并指出它的自由度. 2.设总体X 的密度函数为 ???<<+=其他, 01 0,)1();(x x x f ααα 其中1->α是未知参数, ),,(1n X X 是一样本, 试求: (1) 参数α的矩估计量; (2) 参数α的最大似然估计量. 3.有一种新安眠剂,据说在一定剂量下能比某种旧安眠剂平均增加睡眠时间3小时,为了检验新安眠剂的这种说法是否正确,收集到一组使用新安眠剂的睡眠时间(单位:小时): 26.7, 22.0, 24.1, 21.0, 27.2, 25.0, 23.4. 根据资料用某种旧安眠剂时平均睡眠时间为20.8小时,假设用安眠剂后睡眠时间服从正态分布,试问这组数据能否说明新安眠剂的疗效?()0.05.α= 4.若总体X 服从正态分布() 22.1,1N ,样本n X X X ,,,21 来自总体X ,要使样本均值X 满足不等式{}95.01.19.0≥≤≤X P ,求样本容量n 最少应取多少? 5.在某种产品表明进行腐蚀刻线实验,得到腐蚀深度y 与腐蚀时间x 对应的一 (1)预测腐蚀时间75s 时,腐蚀深度的范围(α-1=95%); (2)若要求腐蚀深度在10~20um 之间,问腐蚀时间应如何控制? 6.简述方差分析,主成分分析的基本思想 附:统计查表数据 0.025(6) 2.447t =,0.025(7) 2.365t =,(1.96)0.975Φ= 参考答案: 1.设15,,X X 是独立且服从相同分布的随机变量,且每一个()1,2,,5i X i = 都服从()0,1.N (1)试给出常数c ,使得() 22 12c X X +服从2χ公布,并指出它的自由度; (2)试给出常数,d 使得服从t 分布,并指出它的自由度. 解 (1)由于()()()22 21212~0,1,~0,1, ~2X N X N X X +χ故 因此1c =,1222 X X +服从自由度为2的2χ分布. (2)由于()()~0,11,2,5i X N i = 且独立,则()12~0,2X X N + ()~0,1N 而 ()22223453X X X ++=χ ()~3,t ()~3t 所以d =自由度为3. 2. 设总体X 的密度函数为 ???<<+=其他, 01 0,)1();(x x x f ααα 其中1->α是未知参数, ),,(1n X X 是一样本, 试求: 习题三 1 正常情况下,某炼铁炉的铁水含碳量2 (4.55,0.108)X N .现在测试了5炉铁水,其含碳量分别为4.28,4.40,4.42,4.35,4.37. 如果方差没有改变,问总体的均值有无显著变化?如果总体均值没有改变,问总体方差是否有显著变化(0.05α=)? 解 由题意知 2 ~(4.55,0.108),5,0.05X N n α==,1/20.975 1.96u u α-==,设立 统计原假设 0010:,:H H μμμμ=≠ 拒 绝 域 为 {} 00K x c μ=->,临界值 1/2 1.960.108/0.0947c u α-==?=, 由于 0 4.364 4.550.186x c μ-=-=>,所以拒绝0H ,总体的均值有显著性 变化. 设立统计原假设 2 2 2 2 0010:,:H H σσσσ=≠ 由于0μμ=,所以当0.05α=时 2 222 0.0250.9751 1()0.03694,(5)0.83,(5)12.83,n i i S X n μχχ==-===∑ 22 10.02520.975(5)/50.166,(5)/5 2.567c c χχ==== 拒绝域为 {} 2222 00201//K s c s c σσ=><或 由于22 0/ 3.167 2.567S σ=>,所以拒绝0H ,总体的方差有显著性变化. 2 一种电子元件,要求其寿命不得低于1000h .现抽测25件,得其均值为 x =950h .已知该种元件寿命2(100,)X N σ,问这批元件是否合格(0.05α=)? 解 由题意知 2 (100,)X N σ,设立统计原假设 0010:,:,100.0.05.H H μμμμσα≥<== 拒绝域为 {} 00K x c μ=-> 临界值为 0.050.0532.9c u u =?=?=- 由于 050x c μ-=-<,所以拒绝0H ,元件不合格. 第一章 数理统计的基本概念 P26 1.2 设总体X 的分布函数为()F x ,密度函数为()f x ,1X ,2X ,…,n X 为X 的子样,求最大顺序统计量()n X 与最小顺序统计量()1X 的分布函数与密度函数。 解:(){}{}()12n n i n F x P X x P X x X x X x F x =≤=≤≤≤=???? ,,,. ()()()()1n n n f x F x n F x f x -'=??=??????. (){}{}1121i n F x P X x P X x X x X x =≤=->>> ,,,. {}{}{}121n P X x P X x P X x =->>> {}{}{}121111n P X x P X x P X x =-?-≤??-≤??-≤??????? ()11n F x =-?-??? ()()()()1111n f x F x n F x f x -'=??=?-???? ?. 1.3 设总体X 服从正态分布()124N , ,今抽取容量为5的子样1X ,2X ,…,5X ,试问: (i )子样的平均值X 大于13的概率为多少? (ii )子样的极小值(最小顺序统计量)小于10的概率为多少? (iii )子样的极大值(最大顺序统计量)大于15的概率为多少? 解:()~124X N , ,5n =,4 ~125 X N ?? ∴ ?? ?,. (i ) {}{ } ()13113111 1.1210.86860.1314P X P X P φφ???? ???>=-≤=-=-=-=-=. (ii )令{}min 12345min X X X X X X =,,,,,{}max 12345max X X X X X X =,,,,. {}{}{}min min 125101*********P X P X P X X X <=->=->>> ,,, {}{}{}55 5 1 1 11011101110i i i i P X P X P X ===->=-?-
应用数理统计试题
概率数理统计试题及答案
清华大学杨虎应用数理统计课后习题参考答案
应用数理统计作业题及参考答案(第一章 )