第三章参数估计第四章假设检验回归

第三章 参数估计

2.区间估计：

一般可用在食品及药品某些主要指标的含量、产品的使用寿命（均值）以及离散程度等数字特征，用抽样的样本去推断总体的特性。设总体为X ,含未知参数θ，12,,......,n X X X 是样本，()12,,....,,1,2i i n X X X i θθ==，都是样本的函数（不含任何未知参数），对0<α<<1,使得()αθθθ-=≤≤121P ，即未知参数θ以大概率100（1α-）%落在区间[]12,θθ内，称（1α-）为置信度（可相信的程度），[]12,θθ为θ的置信区间，12,θθ分别为置信上下限。以上过程称为对θ的区间估计，可分为双侧与单侧区间估计。由中心极限定理，大容量的样本一般都假设总体

X ~()2,σμN ，对单个正态总体的未知参数μ，2σ作区间估计，

其估计量用 μ

及 2σ表示。 例1:某厂生产一批清漆，为考虑该批清漆的平均干燥时间及离散程度，任取n=9个样本。测得干燥时间分别为6.0，5.7，5.8，6.5，7.0，6.3，5.6，6.1，5.0小时；设总体X 的干燥时间服从一般正态分布，即 X ~()2,σμN 。

（1）若2σ=0.36，求总体平均干燥时间μ的95%的置信区间；

解：1、 总体的方差2σ已知， 对μ作区间估计，

取统计量及分布：

)1,0(~N n X U σ

μ

-=

，

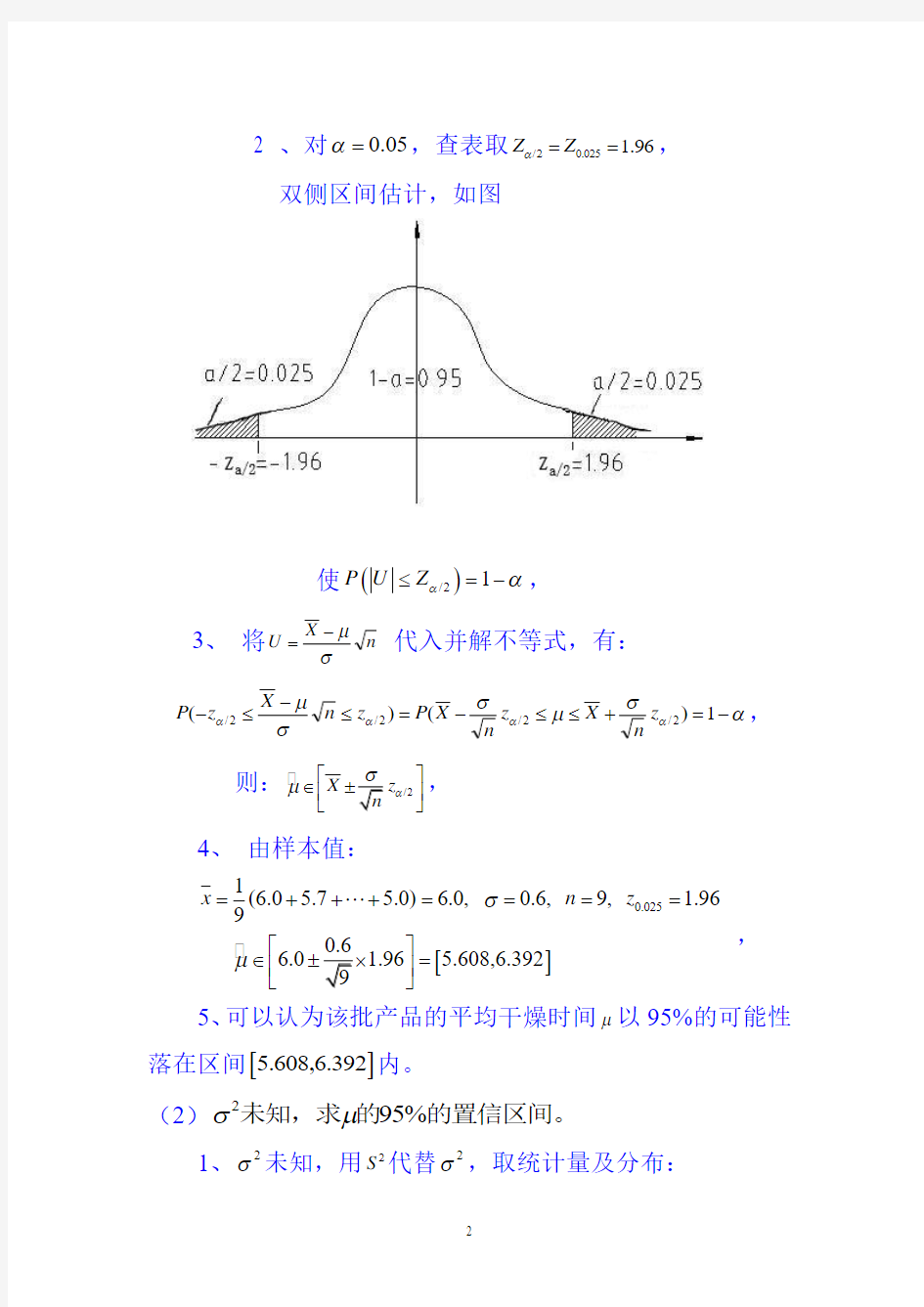
2 、对0.05α=，查表取/20.025 1.96Z Z α==， 双侧区间估计，如图

使()/21P U Z αα≤=-，

3、 将n X U σ

μ

-=

代入并解不等式，有：

ασ

μσ

σ

μ

αααα-=+

≤≤-

=≤-≤

-1)()(2/2/2/2/z n

X z n

X P z n X z P ，

则：

/2X z αμ??∈?

??

?

， 4、 由样本值：

[]0.0251

(6.0 5.7 5.0) 6.0, 0.6, 9, 1.96

9

6.0 1.96 5.608,6.392x n z σμ=+++====??∈±=?

???

， 5、可以认为该批产品的平均干燥时间μ以95%的可能性落在区间[]5.608,6.392内。

（2）2

95%σμ未知，求的的置信区间。

1、2σ未知，用2S 代替2σ，取统计量及分布：

)1(~--=

n t n S

X T μ

2、对 0.05α=，双侧区间估计，取/20.025(1)(8) 2.306a t n t -==， 如图示，使：

((1))1P T t n αα

≤-=-

3、

将统计量代入

/2/2/2/2/2 ((1)(1)) ((1)(1))

1 [(1)]P t n t n P X n u X n X n αααααα

μ

--≤≤-=--≤≤-=-∈-， 4、代样本值， 6.0x =

[]2

2

2122220.025

1()

11(6.0 5.7..... 5.096)0.3391

0.574, (8) 2.306,9,

6.0 2.306 5.558,6.442n

i i S x n x n S t n μ-==--=+++-?=-===??∈±=????

∑

5、可以认为该批产品当方差未知时，平均干燥时间μ以95%

的可能性落在区间[]5.558,6.442内。 （3）求2σ的95%的置信区间。

1、取统计量及其分布，

2

222

1

~(1)n s n χχσ-=

-，

2、对05.0=α，双侧区间估计，

取2222

/20.0251/20.975(1)(8)17.535, (1)(8) 2.18n n ααχχχχ--==-==，

使αχχχαα-=-≤≤--1))1

()1((2

2/222/1n n P ， 如图：

3、代222

1

n s χσ-=

有：

2221/2/22

222

22/21/222

2

22/21/21

((1)(1))=

(1)(1)()1(1)(1)(1)(1), (1)(1)n P n S n n S n S P n n n S n S n n ααααααχχσσαχχσχχ-----≤

≤---≤≤=---??--∈??

--??

4、由样本值：

[]2

2

80.3380.330.339, ,0.1505,1.21117.535 2.18s n σ????==?∈=????

，， 5、可以认为该批产品平均干燥时间的方差2σ以95%的可能性落在区间[]0.1505,1.211内。

例2、单侧区间估计。

科学上重大发现往往是年轻人作出的，美国科学院统计了15世纪到20世纪12名科学伟人。 （1）哥白尼 1543年 日心学说 40岁

（2）伽利略 1600年 天文学，望远镜 34岁 （3）牛顿 1665年 三大定律，微积分 23岁 （4）富兰克林 1746年 电的本质 40岁 （5）拉瓦锡 1774年 氧气及燃烧本质 31岁 （6）莱尔 1830年 地球的演化过程 33岁 （7）达尔文 1858年 生物进化论 49岁 （8）麦克斯维尔 1864年 光 磁 电场 33岁 （9）居里 1896年 放射性 34岁 （10）普朗克 1911年 量子论 43岁

（11）爱因斯坦 1905年 广义狭义相对论 26岁 （12）薛定谔 1926年 量子论数学基础 39岁

求：重大发现伟人年龄的上限。 解： 由2σ未知，取统计量及分布：

)1(~--=

n t n S

X T μ

（求年龄的上限用单侧区间估计）

()0.052

22222

0.05, (1)(11) 1.7959

1

4034....3935.4212

14034...391235.427.23121t n t x s αα=-===

+++=??=+++-?=?

?-

(1))1(1))1(1)35.42 1.795939.15P t n P t n X n ααα

ααμ≥--=-≤-=-=+-=+=或者， 基于该统计，数学最高奖菲尔兹奖（四年颁发一次），只奖励给40岁以下的年轻人。

第四章 假设检验

统计推断一般分为两大类：一类是对未知参数作点估计及区间估计，另一类是对总体的分布和未知参数的某些特性作假设检验。假设检验首先是提出假设，然后根据假设选取适合的统计量及分布，再用随机抽样的样本去推断假设的合理性，是拒绝或是接受假设，假设检验是概率论中的反证法。 1、对参数的假设检验：

其步骤是先对参数提出原假设，如00:μμ=H ，检验总体

的均值。0μ为额定的标准，0H 称其为原假设，及01:μμ≠H ，称1H 为备择或对立假设。由检验均值选择统计量，若方差2σ未知时，选取统计量及其分布：

)1(~--=

n t n S

X T μ

，（称为T -检验法）

对10<<<α， 取)1(2/-n t α，使ααα,))1((2/=-≥n t T P 为显著性水平，取等式时为双侧检验，取不等式时为单侧检验。

统计推断的基本原理是：小概率事件在一次随机试验

中几乎不会发生，若小概率事件发生，则说明假设不真，则有拒绝域ω或接受域。如ω：)1(2/-≥n t T α，在0H 为真的条件下，由样本值去推断是否在拒绝域内，作出对总体的某些特性是拒绝或是接受的推断。

例1 某盐业公司用一台包装机包装精碘盐，额定标准每袋净重g 5000=μ,随机抽取9=n ,其净重分别为497、506、518、524、488、511、510、515、512.对05.0=α，检验包装机工作是否正常。假设每袋的净重)15,(~2μN X ，由经验得标准差15g σ=。 解： （1）g H 500:00==μμ，

01:μμ≠H ，

（2）由总体标准差已知，选取统计量及其分布。

)1,0(~N n X U σ

μ

-=

，（称为U -检验法）

（3）对显著性水平05.0=α，查表取96.1025.02/==z z α， 使αα=≥)(2/z U P ，拒绝域ω为2/ασ

μ

z n X U

≥-=

双侧检验，

（4）由样本值509)512506497(9

1=+++= x

当g H 500:00==μμ 成立时，

96.18.1915

500

509<=-=

U ， （5）小概率事件没有发生，样本值不在拒绝域内，接受0H ，即认为包装机工作正常。

说明：在假设检验中提出假设时有可能发生假设错误，一般可用区间估计作验证。在本例中，

[]

/2509 1.96499.2,518.8

x z αμ?

???

∈±=±=?

???????

， []500499.8,518.8∈。

例2：某厂生产某种固体燃料，其燃烧率),40(~2σN X ,额定标准s cm /400=μ。现给出一种新的生产方法，任取新方法生产的25n =根产品，测得41.25/x cm s =，样本标准差 2.0s =,

对0.025α=，检验新方法较原方法生产的固体燃料其燃烧率是否有显著提高。

解：（1）00:μμ≤H ，（给出反假设，一般否定0H 比肯定0H 更具说服力）

01:μμ>H ，

（2）总体方差

2σ未知，检验总体μ，取~t (1)T n =-

，

（3）对显著性水平0.025α=，取 0639.2)24()1(025.0==-t n t α，

单侧检验（检验不等式时为单侧检验）， 使((1))P T t n αα≥-=,

其拒绝域: (1)T t n αω=

>- ，

当00:μμ≤H 成立时，

0μμ-≥-, n S

X n S X T 0μμ

-≥-=

则拒绝域)1(:0->-=

n t n S

X T αμω

(4)由样本值 41.25

/x c m s =，0μ=40，25n =, 2.0S =，

3.125 2.0639T =

>， (5) 样本值在拒域内的小概率事件发生，拒绝00:μμ≤H ，接受01:μμ>H ，即认为新方法生产的产品燃烧率有显著性提高。

例3：两个正态总体的假设检验：

假设两个公司生产同类型电子产品，其使用寿命分别为

()211~,,X N μσ()2

22~,Y N μσ，为检验两个公司的产品质量是否一

致。任取1n =9个样本，测得2211532, 423x S ==，2n =18个

样本，测得2

22

1412,380y S ==，对显著性水平0.05α=，检验两个公司生产的同类电子产品的质量是否有显著性差异。 解：（1） 首先检验正态总体的均值差，

1、0:210=-μμH ， 或者 210:μμ=H ， 211:μμ≠H ，

2、 在22212σσσ==条件下， 取统计量及其分布：

)2(~11)

()(212

121-++

---=

n n t n n S Y X T p μμ，（称为T -检验法）

其中，2

)1()1(212

222112-+-+-=n n S n S n S p

，

3、 对显著性水平0.05α=，查表()/2120.025t (2)25 2.0595n n t α+-==，

使得 αα=-+≥))2((212/n n t T P ，

在210:μμ=H 成立下， 拒绝域)2(11212/2

1-+≥+-=

n n t n n S Y X T p

α，

4、由样本值，

0.40825

=， ()()222

291423181380 394.279182

p

S -+-=

=+-，

0595.2)25()2(025.0212/==-+t n n t α，

0595.27455.040825

.027.3941412

1532<=?-=

T ，

5、样本值不在拒绝域内，小概率事件没有发生，即

可认为两家公司产品的寿命没有显著性差异。

（2）检验产品使用寿命的方差比 1、 22210:σσ=H ，

22211:σσ≠H ， 2、 选取统计量及其分布，

)1,1(~//2121

222

2

2122222121--==n n F S S S S F σσσσ，（称为F

-检验法）

3、 对显著性水平0.05,α=查表 ，

06.3)17,8()1,1(025.0212/==--F n n F α，

2463.006

.41

)8,17(1)17,8()1,1(025.0975.0212

1===

=---

F F n n F

α，

使：()12/2121/2(0(1,1))((1,1))P F F n n P F n n F ααα-<≤--+--≤<+∞=，

拒绝域ω ：()121/20(1,1))F F n n α-<≤--， 或者 +∞<≤--F n n F )1,1(212/α，双侧检验，

4、 当 22210:σσ=H 成立时，代样本值，

239.1380

4232

2

2221===S S F ， 5、由 06.3239.12463.0<< ，样本值不在拒绝域内，

接受0H ，即可认为产品使用寿命方差没有显著性差异。 综合（1）（2）可以认为两家公司生产同类产品质量没有显著性差异。

例4、 据推测：工作和经历相类似的人群中，矮个子人的寿命较高个子人寿命长，美国科学院统计了31位自然死亡的总统，其中5位个子矮<5’8’’, 5英尺8寸， 1英尺=0.304785米, 5’8’’≈1.77m ; 26位高个子>5’8’’， 5位矮个子总统身高从 1.65~1.76m ，寿命从65~90岁；26位高个子总统从1.77~1.97m ,寿命从53~90。 矮、高个子的寿命分别是随机变

量，记为 Y X ,， 且 ),(~),,(~2

2

2211σμσμN Y N X 。 解答：210:μμ≤H ，反假设否定0H 更有说服力

211:μμ>H ，

在方差相等的条件下，选取：

)2(~11)

()(212

121-++

---=

n n t n n S Y X T p μμ，

2)1()1(212

2

22112-+-+-=

n n S n S n S p

，

不等式检验，为单侧检验，对显著性水平：05.0=α，

6991.1)29()2(05.021==-+t n n t α，

拒绝域ω；当0H 成立时，0)(21≥--μμ

12(2)T t n n α=

≥≥+-，

由样本值

()(

)222

2

1222

112222

1280.2,73.7; 69.2,86.8119.222

0.48880.269.2

2.445 1.6991

9.220.488

p

x s y s n S n S S n n T ====-+-=

=+-==-=

=>?

小概率事件发生，拒绝0H ，接受211:μμ>H 推测成立。

2、两类错误，

假设检验作统计推断是基于小概率事件在一次随机试验几乎不会发生的原理。但并不说明小概率事件不会发生。由此假设检验作统计推断时可能发生两类错误： （1）弃真错误 （第一类）P （拒绝0H |0H 为真时）=α， （2）取伪错误 （第二类）P （接受0H |0H 不真时）=β，

一般控制犯第一类错误的概率为α，

α越小有利于假设0H 的成立，但否定0H ，又更有说服力。犯第二类错误的概率β，β越大，有利于假设1H ，如在对犯罪嫌疑人做无罪推断时。

0H 嫌疑人无罪， 1H

嫌疑人有罪

P （拒绝0H |0H 为真时）=α， P （接受0H |0H 不真时）=β，

那种情况对社会危害大？

经分析：应是第一种。若要使两类错误发生都较小，可增加样本的容量n (寻找新证据以形成证据链)。 在生产实际中由0-C 准则，σδ

β

αz z n +≥

，以作为样本容量n

选取的参考标准。

例5、 工业产品的抽样方案：某公司生产了一大批产品、产品质量的主要指标),(~2σμN X ，要求μ值越小越好。抽验方案中公司对高质量的产品，0μμ<能以高概率1-α被买方接受，

而买方对于低质量产品δμμ+≥0能以高1-β被拒绝。公司与购买方协商一次抽验确定是否接受该批产品。

取α=β=0.05，0μ=120，δ=20，30σ=， 解：

00:μμ

δμμ+≥01:H ， 645.105.0===z z z βα，

35.24)3020

645.1645.1(2=?+≥n ，

取样本容量为25，用区间估计，其上限87.129645.125

30

120=?+

<μ

即若抽样的平均值小于129.87，买方接受该批产品，否则拒收该批产品。

参数估计与假设检验的区别和联系

参数估计与假设检验的区别和联系 统计学方法包括统计描述和统计推断两种方法，其中，推断统计又包括参数估计和假设检验。 1.参数估计就是用样本统计量去估计总体的参数，它的方法有点估计和区间估计两种。 点估计是用估计量的某个取值直接作为总体参数的估计值。点估计的缺陷是没法给出估计的可靠性，也没法说出点估计值与总体参数真实值接近的程度。 区间估计是在点估计的基础上给出总体参数估计的一个估计区间，该区间通常是由样本统计量加减估计误差得到的。在区间估计中，由样本估计量构造出的总体参数在一定置信水平下的估计区间称为置信区间。统计学家在某种程度上确信这个区间会包含真正的总体参数。 在区间统计中置信度越高，置信区间越大。置信水平为1-a, a为小概率事件或者不可能事件，常用的置信水平值为99%，95%，90%，对应的a为0.01, 0.05，0.1 置信区间是一个随机区间，它会因样本的不同而变化,而且不是所有的区间都包含总体参数。 一个总体参数的区间估计需要考虑总体是否为正态分布,总体方差是否已知，用于估计的样本是大样本还是小样本等 （1）来自正态分布的样本均值，不论抽取的是大样本还是小样本，均服从正态分布 （2）总体不是正态分布，大样本的样本均值服从正态分布,小样本的服从t 分布 （3）不论已判断是正态分布还是t 分布，如果总体方差未知,都按t 分布来处理 （4）t 分布要比标准正态分布平坦，那么要比标准正态分布离散，随着自由度的增大越接近 （5）样本均数服从的正态分布为N（u a^2/n）远远小于原变量离散程度N (u a^2) 2. 假设检验是推断统计的另一项重要内容，它与参数估计类似，但角度不同，参数估计是利用样本信息推断未知的总体参数，而假设检验则是先对总体参数提出一个假设值，然后利用样本信息判断这一假设是否成立。 假设检验的基本思想：先提出假设，然后根据资料的特点，计算相应的统计量，来判断假设是否成立，如果成立的可能性是一个小概率的话，就拒绝该假设，因此称小概率的反证法。最重要的是看能否通过得到的概率去推翻原定的假设，而不是去证实它<2>统计学中假设检验的基本步骤：（1）建立假设，确定检验水准α--假设有零假设（H0）和备择假设（H1）两个，零假设又叫作无效假设或检验假设。H0和H1的关系是互相对立的，如果拒绝H0，就要接受H1，根据备择假设不同，假设检验有单、双侧检验两种。检验水准用α表示，通常取0.05或0.10，检验水准说明了该检验犯第一类错误的概率。（2）根据研究目的和设计类型选择适合的检验方法 这里的检验方法，是指参数检验方法，有u检验、t检验和方差分析三种，对应于不同的检验公式。 （3）确定P值并作出统计结论 u检验得到的是u统计量或称u值，t检验得到的是t统计量或称t值。方差分析得到的是F统计量或称F值。将求得的统计量绝对值与界值相比，可以确定P值。当α＝0.05时，u值要和u界值1.96相比较，确定P值。如果u＜1.96，则P＞0.05.反之，如u＞1.96，则P＜0.05.t值要和某自由度的t界值相比较，确定P值。如果t值＜t界值，故P＞0.05.反之，如t＞t 界值，则P＜0.05。相同自由度的情况下，单侧检验的t界值要小于双侧检验的t界值，因此有可能出现算得的t值大于单侧t界值，而小于双侧t界值的情况，即单侧检验显著，双侧检验未必就显著，反之，双侧检验显著，单侧检验必然会显著。即单侧检验更容易出现阳性结论。当P＞0.05时，接受零假设，认为差异无统计学意义，或者说二者不存在质的区别。当P＜0.05时，拒绝零假设，接受备择假设，认为差异有统计学意义，也可以理解为二者存在质的区别。但即使检验结果是P＜0.01甚至P＜0.001，都不说明差异相差很大，只表示更有把握认为二者存在差异。 3.参数估计与假设检验之间的联系与区别： （1）主要联系：a.都是根据样本信息推断总体参数；b.都以抽样分布为理论依据，建立在概率论基础之上的推断；c.二者可相互转换，形成对偶性。 （2）主要区别：a.参数估计是以样本资料估计总体参数的真值，假设检验是以样本资料检验对总体参数的先验假设是否成立;b.区间估计求得的是求以样本估计值为中心的双侧置信区间，假设检验既有双侧检验，也有单侧检验；c.区间估计立足于大概率，假设检验立足于小概率。

参数估计与假设检验

参数估计与假设检验 统计学方法包括统计描述和统计推断两种方法，其中，推断统计又包括参数估计和假设检验。 1.参数估计就是用样本统计量去估计总体的参数，它的方法有点估计和区间估计两种。 点估计是用估计量的某个取值直接作为总体参数的估计值。点估计的缺陷是没法给出估计的可靠性，也没法说出点估计值与总体参数真实值接近的程度。 区间估计是在点估计的基础上给出总体参数估计的一个估计区间，该区间通常是由样本统计量加减估计误差得到的。在区间估计中，由样本估计量构造出的总体参数在一定置信水平下的估计区间称为置信区间。统计学家在某种程度上确信这个区间会包含真正的总体参数。 在区间统计中置信度越高，置信区间越大。置信水平为1-a, a为小概率事件或者不可能事件，常用的置信水平值为99%，95%，90%，对应的a为0.01, 0.05，0.1 置信区间是一个随机区间，它会因样本的不同而变化,而且不是所有的区间都包含总体参数。 一个总体参数的区间估计需要考虑总体是否为正态分布,总体方差是否已知，用于估计的样本是大样本还是小样本等 （1）来自正态分布的样本均值，不论抽取的是大样本还是小样本，均服从正态分布 （2）总体不是正态分布，大样本的样本均值服从正态分布,小样本的服从t 分布 （3）不论已判断是正态分布还是t 分布，如果总体方差未知,都按t 分布来处理 （4）t 分布要比标准正态分布平坦，那么要比标准正态分布离散，随着自由度的增大越接近 （5）样本均数服从的正态分布为N（u a^2/n）远远小于原变量离散程度N (u a^2) 2. 假设检验是推断统计的另一项重要内容，它与参数估计类似，但角度不同，参数估计是利用样本信息推断未知的总体参数，而假设检验则是先对总体参数提出一个假设值，然后利用样本信息判断这一假设是否成立。 假设检验的基本思想：先提出假设，然后根据资料的特点，计算相应的统计量，来判断假设是否成立，如果成立的可能性是一个小概率的话，就拒绝该假设，因此称小概率的反证法。最重要的是看能否通过得到的概率去推翻原定的假设，而不是去证实它<2>统计学中假设检验的基本步骤：（1）建立假设，确定检验水准α--假设有零假设（H0）和备择假设（H1）两个，零假设又叫作无效假设或检验假设。H0和H1的关系是互相对立的，如果拒绝H0，就要接受H1，根据备择假设不同，假设检验有单、双侧检验两种。检验水准用α表示，通常取0.05或0.10，检验水准说明了该检验犯第一类错误的概率。（2）根据研究目的和设计类型选择适合的检验方法 这里的检验方法，是指参数检验方法，有u检验、t检验和方差分析三种，对应于不同的检验公式。 （3）确定P值并作出统计结论 u检验得到的是u统计量或称u值，t检验得到的是t统计量或称t值。方差分析得到的是F统计量或称F值。将求得的统计量绝对值与界值相比，可以确定P值。当α＝0.05时，u值要和u界值1.96相比较，确定P值。如果u＜1.96，则P＞0.05.反之，如u＞1.96，则P＜0.05.t值要和某自由度的t界值相比较，确定P值。如果t值＜t界值，故P＞0.05.反之，如t＞t 界值，则P＜0.05。相同自由度的情况下，单侧检验的t界值要小于双侧检验的t界值，因此有可能出现算得的t值大于单侧t界值，而小于双侧t界值的情况，即单侧检验显著，双侧检验未必就显著，反之，双侧检验显著，单侧检验必然会显著。即单侧检验更容易出现阳性结论。当P＞0.05时，接受零假设，认为差异无统计学意义，或者说二者不存在质的区别。当P＜0.05时，拒绝零假设，接受备择假设，认为差异有统计学意义，也可以理解为二者存在质的区别。但即使检验结果是P＜0.01甚至P＜0.001，都不说明差异相差很大，只表示更有把握认为二者存在差异。 3.参数估计与假设检验之间的联系与区别： （1）主要联系：a.都是根据样本信息推断总体参数；b.都以抽样分布为理论依据，建立在概率论基础之上的推断；c.二者可相互转换，形成对偶性。 （2）主要区别：a.参数估计是以样本资料估计总体参数的真值，假设检验是以样本资料检验对总体参数的先验假设是否成立;b.区间估计求得的是求以样本估计值为中心的双侧置信区间，假设检验既有双侧检验，也有单侧检验；c.区间估计立足于大概率，假设检验立足于小概率。

第四章假设检验

第四章假设检验 参数估计与假设检验的关系：参数估计和假设检验是推断统计方法的两个重要组成部分。共同点：都是利用样本信息对总体数量特征进行推断。不同点：推断的角度不同 4.1 假设检验的基本问题 1、假设检验——是指先对总体的参数或分布形式提出某种假设，然后利用样本信息判断假设是否成立的过程； 包括参数检验和非参数检验；逻辑上运用的是概率反证法；统计依据为小概率原理。 2、小概率事件——若事件A发生的概率P(A)很小很小或接近于0。一般在假设检验中，通常要求P(A)≤0.05。 3、原假设——又称零假设，是指研究者想收集证据予以反对的假设，表示为H0。总是有 符号=、≤或 ≥ 备择假设——也称研究假设，是指研究者想收集证据予以支持的假设，表示为H1。总是有符号≠、<或> 4、原假设和备择假设是一个完备事件组，而且相互对立。在一项假设检验中，原假设和备择假设必有一个成立，而且只有一个成立； 先确定备择假设，再确定原假设。因为备择假设大多是人们关心并想予以支持和证实的，一般比较清楚和容易确定； 等号“=”总是放在原假设上； 因研究目的不同，对同一问题可能提出不同的假设，也可能得出不同的结论。 假设检验主要是搜集证据来推翻和拒绝原假设。 5、双侧检验——是指备择假设没有特定的方向性，并含有符号≠的假设检验，又称为双尾检 验。 单侧检验——是指备择假设具有特定的方向性，并含有符号>或<的假设检验，又称为单尾检验。 6、第Ⅰ类错误(弃真错误) 原假设为真时拒绝原假设。第Ⅰ类错误的概率记为α，又被称为显著性水平。 又称为显著性水平，常被用于检验结论的可靠性度量； 既是一个概率值；又是抽样分布拒绝域面积的大小（表示犯第Ⅰ类错误概率的最大允许值）；常用的α 值有0.01，0.05，0.10；由研究者事先确定。 第Ⅱ类错误(取伪错误) 原假设为假时未拒绝原假设。第Ⅱ类错误的概率记为β。

第七章 非参数检验习题 医学统计学习题

第七章非参数检验习题 一、 选择题 1．配对比较秩和检验的基本思想是：若检验假设成立，则对样本来说（）。 A．正秩和与负秩和的绝对值不会相差很大B．正秩和与负秩和的绝对值相等C．正秩和与负秩和的绝对值相差很大D．不能得出结论 E．以上都不对 2．设配对资料的变量值为1X 和2X ，则配对资料的秩和检验是（）。 A．把1X 和2X 的差数从小到大排序B．分别按1X 和2X 从小到大排序C．把1X 和2X 综合从小到大排序D．把1X 和2X 的和数从小到大排序E．把1X 和2X 的差数的绝对值从小到大排序 3．下列哪项不是非参数统计的优点（）。 A．不受总体分布的限制B．适用于等级资料C．适用于未知分布型资料 D．适用于正态分布资料 E．适用于分布呈明显偏态的资料4．等级资料的比较宜采用（）。A．秩和检验 B．F 检验 C．t 检验 D．2 检验 E．u 检验 5．在进行成组设计两样本秩和检验时，以下检验假设哪种是正确的（）。 A．两样本均数相同 B．两样本的中位数相同C．两样本对应的总体均数相同D．两样本对应的总体分布相同 E．两样本对应的总体均数不同 6．以下检验方法中，不属于非参数检验方法的是（）。 A．Friedman 检验B．符号检验C．Kruskal-Wallis 检验 D．Wilcoxon 检验 E．t 检验 7．成组设计两样本比较的秩和检验中，描述不正确的是（）。 A．将两组数据统一由小到大编秩 B．遇有相同数据，若在同一组，按顺序编秩C．遇有相同数据，若不在同一组，按顺序编秩D．遇有相同数据，若不在同一组，取其平均值 E．遇有相同数据，若在同一组，取平均致词 二、简答题 1．简要回答进行非参数统计检验的适用条件。2．你学过哪些设计的秩和检验，各有什么用途？3．试写出非参数统计方法的主要有缺点。三、计算题 1．对8份血清分别用HITAH7600全自动生化分析仪（仪器一）和OLYMPUS AU640全自动生化分析仪（仪器二）测乳酸脱氢酶（LDH），结果见表7-1。问两种仪器所得结果有无差别？

参数估计和假设检验习题解答

参数估计和假设检验习题 1.设某产品的指标服从正态分布，它的标准差σ已知为150，今抽了一个容量为26的样本，计算得平均值为1637。问在5％的显著水平下，能否认为这批产品的指标的期望值μ为1600? 0.05,α=26,n = 0:1600H μ=, 即,以95%的把握认为这批产品的指标 的期望值μ为1600. 2.某纺织厂在正常的运转条件下，平均每台布机每小时经纱断头数为O.973根，各台布机断头数 的标准差为O.162根，该厂进行工艺改进，减少经纱上浆率，在200台布机上进行试验，结果平均每台每小时经纱断头数为O.994根，标准差为0.16根。问,新工艺上浆率能否推广(α=0.05)? 解: 012112:, :,H H μμμμ≥< 3.某电器零件的平均电阻一直保持在2.64Ω，改变加工工艺后，测得100个零件的平均电阻为2.62Ω，如改变工艺前后电阻的标准差保持在O.06Ω，问新工艺对此零件的电阻有无显著影响(α=0.05)? 解: 01: 2.64, : 2.64,H H μμ=≠已知标准差σ=0.16,拒绝域为2 Z z α>,取0.0252 0.05, 1.96z z αα===, 100,n =由检验统计量 3.33 1.96Z = ==>,接受1: 2.64H μ≠, 即, 以95%的把握认为新工艺对此零件的电阻有显著影响. 4.有一批产品，取50个样品，其中含有4个次品。在这样情况下，判断假设H 0：p ≤0.05是否成立(α=0.05)? 解: 01:0.05, :0.05,H p H p ≤>采用非正态大样本统计检验法,拒绝域为Z z α>,0.950.05, 1.65z α==, 50,n =由检验统计量0.9733 Z = ==<1.65,接受H 0：p ≤0.05. 即, 以95%的把握认为p ≤0.05是成立的.

病理生理学考试-- 病理生理学考试--第七章 非参数检验(答案)

第七章 非参数检验（答案） 一、选择题 1．A 2．E 3．D 4．A 5．D 6．E 7．C 二、简答题 1．答：（1）资料不符合参数统计法的应用条件（总体为正态分布、且方差相等）或总体分布类型未知；（2）等级资料；（3）分布呈明显偏态又无适当的变量转换方法使之满足参数统计条件；（4）在资料满足参数检验的要求时，应首选参数法，以免降低检验效能。 2. 答：（1）配对设计的符号秩和检验（Wilcoxon 配对法）是推断其差值是否来自中位数为零的总体的方法，可用于配对设计差值的比较和单一样本与总体中位数的比较；（2）成组设计两样本比较的秩和检验（Wilcoxon 两样本比较法）用于完全随机设计的两个样本的比较，目的是推断两样本分别代表的总体分布是否吸纳共同。（3）成组设计多样本比较的秩和检验（Kruskal-Wallis 检验），用于完全随机设计的多个样本的比较，目的是推断两样本分别代表的总体的分布有无差别。（4）随机区组设计资料的秩和检验（Friedman 检验），用于配伍组设计资料的比较。 3. 答：优点：（1）适用范围广，不受总体分布的限制；（2）对数据的要求不严；（3）方法简便，易于理解和掌握。 缺点：如果对符合参数检验的资料用了非参数检验，因不能充分利用资料提供的信息，会使检验效能低于非参数检验；若要使检验效能相同，往往需要更大的样本含量。 三、 计算题 1．解： （1）建立检验假设，确定检验水准 0H ：用方法一和方法二测得乳酸脱氢酶含量的差值的总体中位数为零，即0d M = 1H :0d M ≠ 0.05α= （2）计算检验统计量T 值 ①求各对的差值 见表7-4第（4）栏。 ②编秩 见表7-4第（5）栏。 ③求秩和并确定统计量T 。 5.5T += 30.5T -= 取 5.5T =。 （3）确定P 值，做出推断结论 本例中8n =， 5.5T =，查附表T 界值表，得双侧0.05P <；按照0.05α=检验水准，拒绝0H ，接受1H 。认为用方法一和方法二测得乳酸脱氢酶含量差别有统计学意义。 表7-4 8份血清用原法和新法测血清乳酸脱氢酶（U/L ）的比较 编号 原法 新法 差值d 秩次 （1） （2） （3） （4）=（2）—（3） （5） 1 100 120 -20 -8 2 121 130 -9 -5 3 220 225 -5 -3.5 4 186 200 -14 -6

第4章非参数检验作业

第四章非参数检验 1.为研究心脏病人猝死人数与日期的关系，收集了168个观察数据，见数据文件“非参数检验（心脏病猝死）.sav”，其中：用1、2、3、4、5、6、7表示是星期几死的。现利用这批数据，推断心脏病人猝死人数与日期的关系是否是： 2.8:1:1:1:1:1:1.,使用总体分布的卡方检验方法进行检验。 解:取显著性水平为0.05（题设未给出） H0：心脏病人猝死人数与日期的关系是：2.8:1:1:1:1:1:1. H1：心脏病人猝死人数与日期的关系不是：2.8:1:1:1:1:1:1. 操作步骤：

结果：

由SPSS输出结果可知， P=0.256，大于显著性水平0.05，不能拒绝原假设。 2.为验证某批产品的合格品率是否达到90%,现从该批产品中随机抽取23个样品进行检验，得到最后的检测结果数据，见数据文件“非参数检验（产品合格率）.sav”，其中：1表示一级品，0表示非一级品。使用二项分布检验方法检验一级品率为90%. 解: H0：这批产品一级品率的分布符合二项分布(p=90%) H1：这批产品一级品率的分布不符合二项分布(p=90%) 设显著性水平为0.05. 首先读入数据文件“非参数检验（产品合格率）.sav”，选择非参数检验的二 项分布检验，并将检验比例设置为0.90。如下图所示。

得到结果如下： 从图中的分析结果我们可以看到P值为0.193>0.05，因此我们不拒绝原假设，可以认为这批产品合格品率达到90% 3.收集到21个关于周岁儿童身高的样本数据，见数据文件“非参数检验（单样本KS-儿童身高）.sav”，试利用K－S方法检验周岁儿童的身高是否服从正态分

第5章参数估计与假设检验练习题(精)

第5章 参数估计与假设检验练习题 1、设随机变量 X 的数学期望为 μ ，方差为 σ2 ，（X 1 ，X 2 ，···，X n ）为X 的一个样本， 试比较 ))(1(1 2 ∑=-n i i X n E μ 与 ))(1(12∑=-n i i X X n E 的大小。 （ 前者大于后者 ） 2、设随机变量 X 与Y 相互独立，已知 EX = 3，EY = 4，DX = DY = σ2 ，试问：k 取何值时，Z = k ( X 2 - Y 2 ) + Y 2 是 σ2 的无偏估计 。 （ 16 / 7 ） 3、设正态总体 X ~ N ( μ , σ2 ) ，参数 μ ，σ2 均未知，（ X 1 ，X 2 ，… ，X n ）（ n ≥ 2 ） 为简单随机样本，试确定 C ，使得 ∑-=+-=1 1212 )(?n i i i X X C σ 为 σ2 的无偏估计。 （ ) 1(21 -n ） 4、假设总体 X 的数学期望为 μ ，方差为 σ 2 ，),...,,(21n X X X 为来自总体 X 的一个样本， X 、S 2 分别为样本均值和样本方差，试确定常数 c ，使得 22cS X - 为 μ 2 的无偏估计量. （ 1 / n ） 5、设 X 1 ，X 2 是取自总体 N ( μ , σ2 ) （ μ 未知）的一个样本，试说明下列三个统计量 2114341?X X +=μ ，2122121?X X +=μ ，2132 1 31?X X +=μ 中哪个最有效。 （ 2?μ ）

6、设某总体 X 的密度函数为：??? ??><=其它 03),(3 2θθθx x x f ，（ X 1 ，X 2 ，… ，X n ）为该 总体的样本， Y n = max ( X 1 , X 2 , … , X n ) ，试比较未知参数 θ 的估计量 X 3 4 与 n Y n n 31 3+ 哪个更有效？ （ n > 1 时，n Y n n 31 3+ 更有效 ） 7、从某正态总体取出容量为10的样本，计算出 15010 1 =∑=i i x ，272010 1 2=∑=i i x 。求总体期望与 方差的矩估计 μ ? 和 2?σ 。 （ 15 ；47 ） 8、设总体 X 具有密度 ?? ? ??≤>=+-C x C x x C x f 01);()1 1(1???? ，其中参数 0 < ? < 1，C 为已知常数，且C > 0，从中抽得一样本 X 1 ，X 2 ，… ，X n ，求参数 ? 的矩估计量。 （ 1 - C /?X ，其中 ∑==n i i X n X 1 1 ） 9、设总体 X 服从（ 0，? ）上的均匀分布，其中 ? > 0 是未知参数，（ X 1 ，X 2 ，… ， X n ）为简单随机样本，求出 ? 的矩估计量 ? ? ，并判断 ?? 是否为 ? 的无偏估计量。 （ 2?X ，其中 ∑==n i i X n X 1 1 ；是 ） 10、设（ X 1 ，X 2 ，… ，X n ）为总体 X 的一组样本，总体 X 密度函数为：

实验3 参数假设检验

实验编号：1四川师大SPSS实验报告2017 年3月27日 计算机科学学院2015级5班实验名称：参数假设检验 姓名：唐雪梅学号：2015110538 指导老师：__朱桂琼___ 实验成绩:___ 实验三参数假设检验 一．实验目的及要求 1.了解SPSS 特点结构操作 2.利用SPSS进行简单数据统计 二．实验内容 1．对12名来自城市的学生与14名来自农村的学生进行心理素质测验，他们的分数如下： 城市学生得分：4.75 6.40 2.62 3.44 6.50 5.30 5.60 3.80 4.30 5.78 3.76 4.15 农村学生得分：2.38 2.60 2.10 1.80 1.90 3.65 2.30 3.80 4.60 4.85 5.80 4.25 4.22 3.84 试分析农村学生与城市学生心理素质有无显著差别。 2、一汽车厂商声称其发动机排放标准的一个指标平均低于20个单位。在抽查了10台发动机之后，得到下面的排放数据：17.0、21.7、17.9、22.9、20.7、22.4、17. 3、21.8、24.2、25.4。目的是检验该申明是否正确 3. 用SPSS Samples数据文件“Employee data.sav”资料， 问：清洁工（jobcat=1）的受教育年数（Educational Level）与保管员（jobcat=2）和经理（jobcat=3）的受教育年数是否有显著差异？其中，显著性水平ɑ=0.05. ? 4. 用SPSS Samples数据文件“Employee data.sav”资料， 分析：美国企业现在工资（Current Salary）与过去工资（beginning Salary）是否有显著差异？ 三、实验主要流程、基本操作或核心代码、算法片段（该部分如不够填写，请另加附页） 1.数据录入

非参数统计第4章 两独立样本的非参数检验

第四章 两独立样本的非参数检验 在单样本位置问题中，人们想要检验的是总体的中心是否等于一个已知的值．但在实际问题中，更受注意的往往是比较两个总体的位置参数；比如。两种训练方法中哪一种更出成绩，两种汽 油中哪一个污染更少，两种市场营销策略中那种更有效等等． 作为一个例子．我国沿海和非沿海省市区的人均国内生产总值(GDP)的1997年抽样数据如下(单位为元)．沿海省市区为(Y1，Y2，…，Y12): 15044 12270 5345 7730 22275 8447 9455 8136 6834 9513 4081 5500 而非沿海的为对（x1,x2,…，x18）： 5163 4220 4259 6468 3881 3715 4032 5122 4130 3763 2093 3715 2732 3313 2901 3748 3731 5167 人们想要知道沿海和非沿海省市区的人均GDP 的中位数是否一样．这就是检验两个总体的位置参数是否相等的问题． 假定代表两个独立总体的随机样本(Y1，Y2，…，Y12)和（x1,x2,…，x18），则问题归结为检验它们总体的均值(或中位数)的差是否相等，或是否等于某个已知值．换言之，即检验 0H ：021D =-μμ；1H ： 021D ≠-μμ 0H ：021D =-μμ；1H ： 021D <-μμ 0H ：021D =-μμ；1H ： 021D >-μμ 在正态假定下，这些问题化为：)2(~11)(0-++ --= m n t m n s D y x t 2 ) ()(1 2 1 2 -+-+ -= ∑∑==n m y y x x S m i i n i i t 检验并不稳健，在不知总体分布时，应用t 检验时会有风险的。 3.1 Brown-Mood 中位数检验 令沿海地区的人均GDP 的中位数为M X ，而内地的为M Y 。零假设为 0H ：y x M M =；1H ： y x M M > 显然，在零假设下，中位数如果一样的话，它们共同的中位数，即这(12十18)=30个数的样 本中位数(记为此xy M )，应该对于每一列数据来说都处于中间位置．也就是说，(Y1，Y2，…，Y12) 和（x1,x2,…，x18）中大于或小于xy M 的样本点应该大致一样多，计算他们的混合样本中位数为

实验六 参数估计与假设检验

实验六参数估计与假设检验 一、实验目的： 学习利用spss对数据进行参数估计与假设检验（参数估计，单样本、独立样本、配对样本T 检验）。 二、实验内容： 某助眠药物临床实验征集了20位被试，试验后得数据表包含被试的性别、身高、体重、用药前睡眠时长及用药后睡眠时长。试就该数据估计性别对未使用药物时睡眠时长的影响、检验被试总体身高与165差距是否显著、对不同性别的被试的身高和体重变量进行独立样本T 检验、并检验药物是否对被试有用。 三、实验步骤： 参数估计 1、定义变量并输入数据 2、选择菜单“分析→描述统计→探索”弹出“探索”对话框，将对话框左侧的变量框中“用药前睡眠时长”添加到因变量列表，“性别”添加到自变量列表 3、点击“统计量”，弹出“探索：统计量”对话框，勾选描述性并设置均值置信区间为95%，单击“继续” 4、单击“确定”按钮，得到输出结果，对结果进行分析解释。 单样本T检验 1、定义变量并输入数据 2、选择菜单“分析→比较均值→单样本T检验”，弹出“单样本T检验”对话框，将对话框左侧的变量框中的“身高”添加到右侧的“检验变量”框中，将检验值设为165； 3、点击“选项”，弹出“选项”对话框，将置信区间百分比设为95%，点击“继续” 4、单击“确定”按钮，得到输出结果，对结果进行分析解释。 独立样本T检验 1、定义变量并输入数据 2、选择菜单“分析→比较均值→独立样本T检验”，弹出“独立样本T检验”对话框，在对话框左侧的变量列表中选变量“身高”“体重”进入检验变量框，选变量“性别”进入控制列表框 3、点击定义组，在组1（1）中填写1，组2(2)中填写2，点击继续， 4、点击“确定”按钮，得到输出结果。对结果进行分析解释。 配对样本T检验 1.打开一份可用数据。 2.选择分析→比较平均值→配对样本T检验，选择一对配对样本“用药前睡眠时长”和“用 药后睡眠时长”，将“用药前睡眠时长”拖至“variable1”，“用药后睡眠时长”拖至“variable2”，单击“选项”设置置信区间为95%，点击“确定”查看自定义结果。

第四章-非参数检验

第四章非参数检验 非参数检验（non-parametric test） 卡方检验（test）、 Runs 检验（Runs test）、 Kolmogorov-Smirnov 单样本检验（Kolmogorov-Smirnov one-sample test）、 Mann-Whitney 等级和检验（Mann-Whitney rank-sum test）、 符号检验（sign test）、 Wilcoson 配对符号等级检验（Wilcoson matched-pairs signed-ranks test）、 Fridman 单因素方差分析（Fridman one-way analysis of variance） 多样本中数检验（K-sample median test）。 一、卡方检验 检验（也叫做Pearson Chi-Square test）：配合度检验（the test of goodness of fit）和独立性检验（independence test）。 （一）配合度检验 配合度检验: 推断某变量不同取值观测分数的频数和对应的期望频数（expected frequency）是否有显著性差异。 作零假设：f0=f e f0和f e分别为变量的每个水平的观测频数和期望频数。 配合度检验的自由度为：N-1，N为变量水平数。 【配合度检验·例】 配合度检验实际上是检验某变量的不同水平值的观测分数频率的分布是否服从某种期望或者理论分布。 某研究者进行了一次问卷调查。调查对象是300 名高中三年级学生；调查目的是考查学生对英语学习兴趣的自我评价：你对英语的学习兴趣□ 很浓、□ 较浓、□ 一般、□ 有点和□ 没有。获得原始数据如表4-1 所示。似乎较多人认为自己对英语的学习兴趣一般，较少人认为自己英语学习兴趣浓厚或没有兴趣。 该研究者想通过卡方分析证明：①对英语学习有不同兴趣的学生人数不均等和②其英语学习兴趣很浓、较浓、一般、有点和没有各等级的人数比接近1:4:8:4:2。 表4-1 300 名学生对英语学习兴趣调查题目的反馈* 学生编号兴趣 001 2 002 3 003 5 …… 300 3 * 英语学习兴趣很浓、较浓、一般、有点和没有5 个等级分别以数字5、4、3、2 和1 表示。 ①对英语学习有不同兴趣的学生人数不均等。

第七章--spss非参数估计

第七章非参数检验 1、为分析不同年龄段人群对某商品满意程度的异同，进行随机调查收集到以下数据：请选择恰当的非参数检验方法，以恰当形式组织上述数据，分析不同年龄段人群对该商品满意程度的分布状况是否一致。 原假设:不同年龄段人群对该商品满意程度的分布无显著差异。 步骤：建立SPSS数据数据→加权个案→对频次进行加权→分析→非参数检验→旧对话框→两个独立样本→把年龄段导入分组变量、满意程度导入检验变量列表→确定 表7-1 检验统计量a 满意程度 最极端差别绝对值.121 正.121 负.000 Kolmogorov-Smirnov Z 2.217 渐近显著性(双侧).000 a. 分组变量: 年龄段 分析：从上表中可以看出，在显著水平为0.05下得到的sig值均为0.00<0.05，故拒绝原假设，即认为不同年龄段人群对该商品满意程度的分布存在显著差异。 2、利用习题二第6题数据，选择恰当的非参数检验方法，分析本次存款金额的总体分布与正态分布是否存在显著差异。 原假设：本次存款金额的总体分布与正态分布无显著差异 步骤：分析→非参数检验→旧对话框→单个独立样本K-S检验→本次存款金额导入检验变量列表→正太分布检验→确定 表7-2 单样本 Kolmogorov-Smirnov 检验 本次存款金额 N282 正态参数a,b均值4738.09 标准差10945.569 最极端差别绝对值.333 正.292 负-.333 Kolmogorov-Smirnov Z 5.585 渐近显著性(双侧).000 a. 检验分布为正态分布。 b. 根据数据计算得到。 分析：如上表，在显著水平为0.05下得到的sig值均为0.00<0.05，故拒绝原假设，认为本次存款金额的分布与正太分布有显著差异。 3、利用习题二第6题数据，选择恰当的非参数检验方法，分析不同常住地人群本次存款金

参数估计和假设检验

第五章参数估计和假设检验 本章重点 1、抽样误差的概率表述； 2、区间估计的基本原理； 3、小样本下的总体参数估计方法； 4、样本容量的确定方法； 本章难点 1、一般正态分布 标准正态分布； 2、t分布； 3、区间估计的原理； 4、分层抽样、整群抽样中总方差的分解。 统计推断：利用样本统计量对总体某些性质或数量特征进行推断。 两类问题：参数估计和假设检验 基本特点：（1）以随机样本为基础； （2）以分布理论为依据； （3）推断的只是一种可能的结果； （4）是归纳推理和演绎推理的结合。本章主要内容：阐述常用的几种参数估计方法。 第一节参数估计 一、参数估计的基本原理 两种估计方法

点估计 区间估计 1．点估计：以样本指标直接估计总体参数。 点估计优良性评价准则 （1）无偏性。估计量 的数学期望等于总体参数，即 ， 该估计量称为无偏估计。 （2）有效性。当 为 的无偏估计时， 方差 越小， 无偏估计越有效。 （3）一致性。对于无限总体，如果对任意 ，有 ,则称 是 的一致估计。 （4）充分性。一个估计量如能完全地包含未知参数信息，即为 充分估计量。 2．点估计的缺点：不能反映估计的误差和精确程度 区间估计：利用样本统计量和抽样分布估计总体参数的可能区间 【例1】CJW 公司是一家专营体育设备和附件的公司，为了监控公司的服务质量， CJW 公司每月都要随即的抽取一个顾客样本进行调查以了解顾客的满意分数。根据以往的调查，满意分数的标准差稳定在20分左右。最近一次对100名顾客的抽样显示，满意分数的样本均值为82分，试建立总体满意分数的区间。 抽样误差 抽样误差：一个无偏估计与其对应的总体参数之差的绝对值。 抽样误差 = （实际未知） 要进行区间估计，关键是将抽样误差E 求解。若 E 已知，则区间可表示为： 区间估计：估计未知参数所在的可能的区间。 区间估计优良性评价要求 θ θ??θ?θθ=?E θ?0＞ εθ?2)?(θθ-E 0)|?(|=≥-∞ →εθθn n P Lim n θ?θθαθθθ-=1)??(U L P ＜＜[]E x x +-,E

参数估计和假设检验案例(精)

参数估计和假设检验案例 案例一:工艺流程的检测 某公司是一家为客户提供抽样和统计程序方面建议的咨询公司,这些建议可以用来监控客户的制造工艺流程。在一个应用项目中,一名客户向该公司提供了一个样本,该样本由工艺流程正常运行时的 800个观测值组成。这些数据的样本标准差为 0.21;因为有如此多的样本数据,因此,总体标准差被假设为 0.21。然后,该公司建议:持续不断地定期抽取容量为 30的随机样本以对工艺流程进行检测。 通过对这些新样本的分析,客户可以迅速知道,工艺流程的运行状况是否令人满意。当工艺流程的运行状况不能令人满意时,可以采取纠正措施来解决这个问题。设计规格要求工艺流程的均值为 12,该公司建议采用如下形式的假设检验。 H 0 :12 H 1 :12 只要 H 0被拒绝,就应采取纠正措施。 下表为第一天运行新的工艺流程的统计控制程序时,每隔一小时收集的样本数据。

μ=μ≠ 问题: 1、对每个样本在 0.01的显著性水平下进行假设检验,并且确定,如果需要

Z0.005=2.58 2、 4、讨论将显著性水平改变为一个更大的值时的影响?如果增加显著性水平, 哪种错误或误差将增加? 显著性水平增加,置信区间减小,误差减小。 案例二:计算机辅助教学会使完成课程的时间差异缩小吗? 某课程引导性教程采用一种个性化教学系统, 每位学生观看教学录像, 然后给以程式化的教材。每位学生独立学习直至完成训练并通过考试。人们关心的问题是学生完成训练计划的进度不同。有些学生能够相当快地完成程式化教材, 而另一些学生在教材上需要花费较长的时间,甚至需要加班加点才能完成课程。学的较快的学生必须等待学得较慢的学生完成引导性课程才能一起进行其他方面的训练。 建议的替代系统是使用计算机辅助教学。在这种方法中, 所有的学生观看同样的讲座录像,然后每位学生被指派到一个计算机终端来接受进一步的训练。μ= 在整个教程的自我训练过程中,由计算机指导学生独立操作。 为了比较建议的和当前的教学方法, 刚入学的 122名学生被随机地安排到这两种教学系统中。 61名学生使用当前程式化教材, 而另外 61名学生使用建议的计算机辅助方法。记录每位学生的学习时间(小时 ,如表所示。

第4章 两独立样本的非参数检验(非参数统计,西南财大)

第三章 两独立样本的非参数检验 在单样本位置问题中，人们想要检验的是总体的中心是否等于一个已知的值．但在实际问题中，更受注意的往往是比较两个总体的位置参数；比如。两种训练方法中哪一种更出成绩，两种汽 油中哪一个污染更少，两种市场营销策略中那种更有效等等． 作为一个例子．我国沿海和非沿海省市区的人均国内生产总值(GDP)的1997年抽样数据如下(单位为元)．沿海省市区为(Y1，Y2，…，Y12): 15044 12270 5345 7730 22275 8447 9455 8136 6834 9513 4081 5500 而非沿海的为对（x1,x2,…，x18）： 5163 4220 4259 6468 3881 3715 4032 5122 4130 3763 2093 3715 2732 3313 2901 3748 3731 5167 人们想要知道沿海和非沿海省市区的人均GDP 的中位数是否一样．这就是检验两个总体的位置参数是否相等的问题． 假定代表两个独立总体的随机样本(Y1，Y2，…，Y12)和（x1,x2,…，x18），则问题归结为检验它们总体的均值(或中位数)的差是否相等，或是否等于某个已知值．换言之，即检验 0H ：021D =-μμ；1H ： 021D ≠-μμ 0H ：021D =-μμ；1H ： 021D <-μμ 0H ：021D =-μμ；1H ： 021D >-μμ 在正态假定下，这些问题化为：)2(~1 1)(0-++--= m n t m n s D y x t 2 )()(1 2 1 2 -+-+-= ∑∑==n m y y x x S m i i n i i t 检验并不稳健，在不知总体分布时，应用t 检验时会有风险的。 3.1 Brown-Mood 中位数检验 令沿海地区的人均GDP 的中位数为M X ，而内地的为M Y 。零假设为 0H ：y x M M =；1H ： y x M M > 显然，在零假设下，中位数如果一样的话，它们共同的中位数，即这(12十18)=30个数的样本中位数(记为此xy M )，应该对于每一列数据来说都处于中间位置．也就是说，(Y1，Y2，…，Y12)和（x1,x2,…，x18）中大于或小于xy M 的样本点应该大致一样多，计算他们的混合样本中位数为

第五章参数估计和假设检验Stata实现

第五章参数估计和假设检验的Stata实现本章用到的Stata命令有 例5－1 随机抽取某地25名正常成年男子，测得其血红蛋白含量如下： 146 7 125 142 7 128 140 1 7 144 151 117 118 该样本的均数为137.32g/L，标准差为10.63g/L，求该地正常成年男子血红蛋白含量总体均数的95%可信区间。 数据格式为

计算95％可信区间的Stata命令为： 结果为 该地正常成年男子血红蛋白含量总体均数的95%可信区间为（132.93～141.71） 例5－2 某市2005年120名7岁男童的身高X=123.62(cm)，标准差s=4.75(cm)，计算该市7岁男童总体均数90%的可信区间。 在Stata中有即时命令可以直接计算仅给出均数和标准差时的可信区间。 结果为： 该市7岁男童总体均数90%的可信区间（122.90～124.34）。 例5－3 为研究铅暴露对儿童智商(IQ)的影响，某研究调查了78名铅暴露(其血铅水平≥40 g/100ml)的6岁儿童，测得其平均IQ为88.02，标准差为12.21；同时选择了78名铅非暴露的6岁儿童作为对照，测得其平均IQ为92.89，标准

差为13.34。试估计铅暴露的儿童智商IQ的平均水平与铅非暴露儿童相差多少，并估计两个人群IQ的总体均数之差的95%可信区间。 本题也可以应用Stata的即时命令： 结果： 差值为4.86，差值的可信区间为0.81～8.90。 例5-4 为研究肿瘤标志物癌胚抗原(CEA)对肺癌的灵敏度，随机抽取140例确诊为肺癌患者，用CEA进行检测，结果呈阳性反应者共62人，试估计肺癌人群中CEA的阳性率。 Stata即时命令为 结果为 肺癌人群中CEA的阳性率为44.28％，可信区间为35.90％～52.82％。 例5-5 某医生用A药物治疗幽门螺旋杆菌感染者10人，其中9人转阴，试估计该药物治疗幽门螺旋杆菌感染者人群的转阴率。 Stata即时命令为

第六章参数估计和假设检验(精)

第六章参数估计和假设检验 教学目的及要求：了解参数的点估计、区间估计的含义，掌握区间估计的几个概念，包括置信水平、置信区间、小概率事件，熟练掌握参数区间估计的计算方法，了解不同抽样组织形式下的参数估计，掌握参数估计中样本量的确定。了解假设检验的原假设和备择假设的含义，假设检验的两类错误，掌握总体均值的检验方法。 本章重点与难点：区间估计的计算与总体均值的假设检验方法。 计划课时：授课6课时；技能训练2课时。 授课特点：案例教学 第一节点估计和区间估计 一、总体参数估计概述 ?1、总体参数估计定义 ?就是以样本统计量来估计总体参数，总体参数是常数，而统计量是随机变量。 ?2、参数估计应满足的两个条件 二、参数的点估计 ?用样本的估计量直接作为总体参数的估计值 例如：用样本均值直接作为总体均值的估计 例如：根据一个抽出的随机样本计算的平均分数为80分，我们就用80分作为全班考试成绩的平均分数的一个估计值，这就是点估计。 再例如，要估计一批产品的合格率，根据抽样结果合格率为96%，将96%直接作为这批产品合格率的估计值，这也是点估计 三、参数的区间估计 （一）参数的区间估计的含义 ?区间估计：计算抽样平均误差，指出估计的可信程度，进而在点估计的基础上，确定总体参数的所在范围或区间。

（二）有关区间估计的几个概念 置信水平 1. 将构造置信区间的步骤重复很多次，置信区间包含总体参数真值的次数所占的比例称为置信水平 2. 表示为 (1 - α% ) α 为是总体参数未在区间内的比例 3. 常用的置信水平值有 99%, 95%, 90% 相应的显著性水平α 为0.01，0.05，0.10 置信区间 1. 由样本统计量所构造的总体参数的估计区间称为置信区间 2. 统计学家在某种程度上确信这个区间会包含真正的总体参数，所以给它取名为置信区间 3. 用一个具体的样本所构造的区间是一个特定的区间，我们无法知道这个样本所产生的区间是否包含总体参数的真值 我们只能是希望这个区间是大量包含总体参数真值的区间中的一个，但它也可能是少数几个不包含参数真值的区间中的一个 4. 由样本均值的抽样分布可知，在重复抽样或无限总体抽样的情况下，样本均值的数学期望等于总体均值， 5. 样本均值的标准差为 由此可知样本均值落在总体均值μ的两侧各为一个抽样标准差范围内的概率为0。6873 落在总体均值两个抽样标准差范围内的概率为0。9545 落在总体均值三个抽样标准差范围内的概率为0。9973 影响区间宽度的因素 1.总体数据的离散程度，用 σ 来测度 2.样本均值标准差 3.置信水平 (1 - α)，影响 z 的大小 评价估计量的标准 x n x σ σ=