
非线性回归模型的线性化
以上介绍了线性回归模型。但有时候变量之间的关系是非线性的。例如 y t = α 0 + α11βt x + u t y t = α 0 t x e 1α+ u t
上述非线性回归模型是无法用最小二乘法估计参数的,只能采用非线性方法进行估计,但其估计过程非常复杂。计算机的出现大大方便了非线性回归模型的估计,专用软件使这种计算变得非常容易。本章不是介绍这类模型的估计,此方面的系统教材参见Wooldridge J. M.的截面和面板数据计量分析(Econometric Analysis of Cross Section and Panel Data)。
本章主要处理另外一类非线性回归模型。其形式是非线性的,但可以通过适当的变换,转化为线性模型,然后利用线性回归模型的估计与检验方法进行处理。称此类模型为可线性化的非线性模型。下面介绍几种典型的可以做线性化处理的非线性模型。
⑴ 指数函数模型
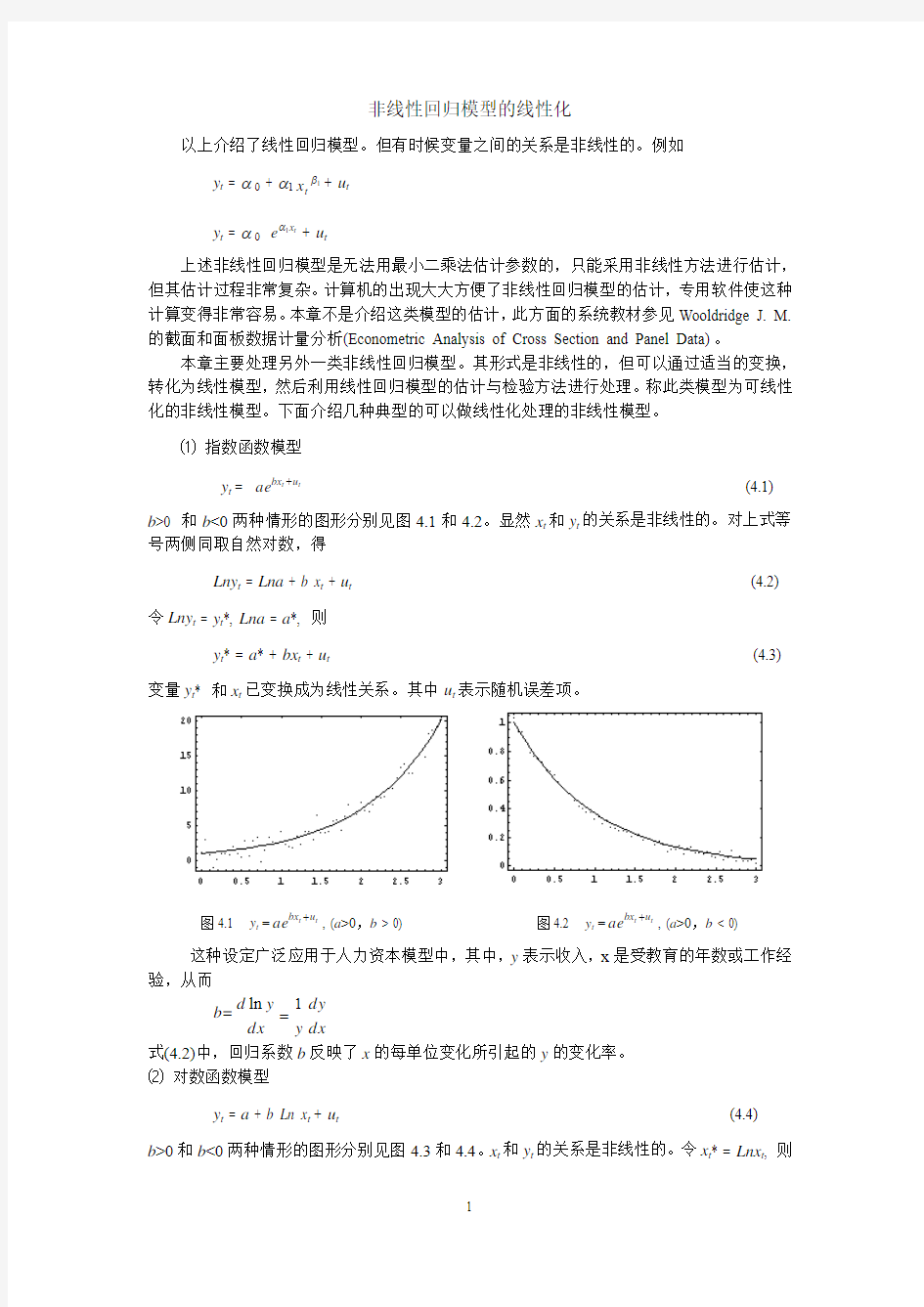
y t = t t u bx ae + (4.1) b >0 和b <0两种情形的图形分别见图4.1和4.2。显然x t 和y t 的关系是非线性的。对上式等号两侧同取自然对数,得
Lny t = Lna + b x t + u t (4.2)
令Lny t = y t *, Lna = a *, 则
y t * = a * + bx t + u t (4.3) 变量y t * 和x t 已变换成为线性关系。其中u t 表示随机误差项。
图4.1 y t =t
t u bx ae
+, (a >0,b > 0) 图4.2 y t =t
t u bx ae +, (a >0,b < 0)
这种设定广泛应用于人力资本模型中,其中,y 表示收入,x 是受教育的年数或工作经验,从而
b=dx dy y dx y d 1ln =
式(4.2)中,回归系数b 反映了x 的每单位变化所引起的y 的变化率。
⑵ 对数函数模型
y t = a + b Ln x t + u t (4.4)
b >0和b <0两种情形的图形分别见图4.3和4.4。x t 和y t 的关系是非线性的。令x t * = Lnx t , 则
y t = a + b x t * + u t (4.5)
变量y t 和x t * 已变换成为线性关系。
图4.3 y t = a + b Lnx t + u t , (b > 0) 图4.4 y t = a + b Lnx t + u t , (b < 0)
图4.3的对数函数常用于家庭预算的截面研究中,这样的一条曲线可以表示一类支出y 和一类收入x 的关系。在预算花费在这种商品之前,收入需要达到某一个确定的临界水平e -a/b (曲线与横轴交点的横坐标)。而且支出随着收入的增加而单调增加,但其增长率递减,该商品消费的边际倾向(b/x )和弹性(b/y )都随着收入增加而递减。
⑶ 幂函数模型
y t = a x t b t u e (4.6) b 取不同值的图形分别见图4.5和4.6。x t 和y t 的关系是非线性的。对上式等号两侧同取对数,得 Lny t = Lna + b Lnx t + u t (4.7) 令y t * = Lny t , a * = Lna , x t * = Lnx t , 则上式表示为
y t * = a * + b x t * + u t (4.8) 变量y t * 和x t * 之间已成线性关系。其中u t 表示随机误差项。(4.7) 式也称作全对数模型。 模型(4.8)中参数b 刚好是y 对x 的弹性:
b=
dx
dy
y x x d y d
ln ln
图4.5 y t = a x t b t u
e 图4.6 y t = a x t b t u
e
⑷ 双曲线函数模型(倒数变换)
1/y t = a + b /x t + u t (4.9)
也可写成,
y t = 1/ (a + b /x t + u t ) (4.10)
b >0情形的图形见图4.7。x t 和y t 的关系是非线性的。令y t * = 1/y t , x t * = 1/x t ,得
y t * = a + b x t * + u t
已变换为线性回归模型。其中u t 表示随机误差项。
图4.7 y t = 1/ (a + b /x t ), (b > 0) 图4.8 y t = a + b /x t , (b > 0)
另一种常见的倒数变换是等轴双曲线函数:
y t = a + b /x t + u t (4.11)
b >0情形的图形见图4.8。x t 和y t 的关系是非线性的。令x t * = 1/x t ,得
y t = a + b x t * + u t 上式已变换成线性回归模型。
该模型经常被用于菲利普斯曲线模型的研究,其中y 表示工资率或价格变动率,x 表示失业率。这种设定有一个不现实的隐含条件,即失业率的渐近线为0。为此,可以考虑另外一种双曲线模型:
1/y t = -a + bx t + u t
该模型允许一个正的最小失业率a/b ,但要以施加工资变动的最小值为零这一约束条件为代
价。两种模型的函数图形如下:
当然,无论是约束最小失业率为零,还是约束最小工资变动为零,似乎都有些主观。严
格的建模过程需要先估计一般的模型,而后对这些约束条件进行检验。一般的双曲线模型通常表示为:
(y t -β1-u t )(x t -β2)=β3
或者
y t =β1+
2
3
ββ-t x +u t
该双曲线的渐近线为y =β1,x =β2。可以利用非线性方法估计这种一般的双曲线模型,而后检验β1=0或β2=0的假设是否与经济理论相一致。
⑸ 多项式方程模型
一种多项式方程的表达形式是
y t = b 0 +b 1 x t + b 2 x t 2 + b 3 x t 3 + u t (4.12)
两种常见情形的图形分别见图4.9和4.10。令x t 1 = x t ,x t 2 = x t 2,x t 3 = x t 3,上式变为 y t = b 0 +b 1 x t 1 + b 2 x t 2 + b 3 x t 3 + u t (4.13) 这是一个三元线性回归模型。如经济学中的总成本曲线与图4.9相似。
图4.9 y t = b 0 +b 1 x t + b 2 x t 2 + b 3 x t 3 + u t 图4.10 y t = b 0 + b 1 x t + b 2 x t 2 + b 3 x t 3 + u t
另一种多项式方程的表达形式是
y t = b 0 + b 1 x t + b 2 x t 2 + u t (4.14)
其中b 1>0, b 2>0和b 1<0, b 2<0情形的图形分别见图4.11和4.12。令x t 1 = x t ,x t 2 = x t 2,上式线性化为,
y t = b 0 + b 1 x t 1 + b 2 x t 2 + u t (4.15) 如经济学中的边际成本曲线、平均成本曲线与图4.11相似。
图4.11 y t = b 0 +b 1x t + b 2x t 2 + u t 图4.12 y t = b 0 + b 1x t + b 2x t 2 + u t
模型(4.15)还有一个重要特点是,x 对y 的边际影响与x 自身水平有关:
x b b dx
dy
212+=
⑹ 生长曲线 (logistic) 模型
y t =
t
u t f e
k
++)(1 (4.16)
一般f (t ) = a 0 + a 1 t + a 2 t 2 + … + a n t n ,常见形式为f (t ) = a 0 - a t
y t =
u
u at a e k +-+)(01=
t
u at be k +-+1 (4.17)
其中b = 0a e 。a > 0情形的图形分别见图4.13和4.14。美国人口统计学家Pearl 和Reed 广泛研究了有机体的生长,得到了上述数学模型。生长模型(或逻辑斯谛曲线,Pearl-Reed 曲线)常用于描述有机体生长发育过程。其中k 和0分别为y t 的生长上限和下限。∞
→t t Limy = k ,
-∞
→t t Limy = 0。a , b 为待估参数。曲线有拐点,坐标为(
a Ln
b ,2
k
),曲线的上下两部分对称于拐点。
图4.13 y t = k / (1 +t
u at be
+-) 图4.14 y t = k / (1 +t
u at be +)
为能运用最小二乘法估计参数a , b ,必须事先估计出生长上极限值k 。线性化过程如下。当k 给出时,作如下变换,
k /y t = 1 + t u at be +- 移项, k /y t - 1 = t u at be +-
取自然对数,Ln ( k /y t - 1) = Lnb - a t + u t (4.18) 令y t * = Ln ( k /y t - 1), b * = Lnb , 则
y t * = b * - a t + u t (4.19) 此时可用最小二乘法估计b *和a 。
⑺ 龚伯斯(Gompertz )曲线
英国统计学家和数学家最初提出把该曲线作为控制人口增长的一种数学模型,此模型可用来描述一项新技术,一种新产品的发展过程。曲线的数学形式是,
y t =at
be
ke --
图4.15 y t =at be ke
--
曲线的上限和下限分别为k 和0,∞
→t t Limy = k , -∞
→t t Limy = 0。a , b 为待估参数。曲线有拐点,坐
标为(
a Ln
b ,e
k
),但曲线不对称于拐点。一般情形,上限值k 可事先估计,有了k 值,龚伯斯曲线才可以用最小二乘法估计参数。线性化过程如下:当k 给定时,
y t / k = at
be e --,
k /y t = at
be e -
Ln (k /y t ) = at be -, Ln [Ln (k /y t )] = Lnb - a t
令y *= Ln [Ln (k /y t )], b * = Lnb ,则
y * = b * - a t
上式可用最小二乘法估计b * 和 a 。 Cobb-Douglas 生产函数
下面介绍柯布-道格拉斯(Cobb-Douglas )生产函数。其形式是
Q = k L α C 1- α (4.24)
其中Q 表示产量;L 表示劳动力投入量;C 表示资本投入量;k 是常数;0 < α < 1。这种生产函数是美国经济学家柯布和道格拉斯根据1899-1922年美国关于生产方面的数据研究得出的。更习惯的表达形式是
y t =t u t t e x x 21210βββ (4.25)
这是一个非线性模型,无法用OLS 法直接估计,但可先作线性化处理。上式两边同取对数,得:
Lny t = Ln β0 + β1 Lnx t 1 + β2 Lnx t 2 + u t (4.26) 取 y t * = Lny t , β0* = Ln β0, x t 1* = Ln x t 1, x t 2* = Ln x t 2,有
y t *= β0* +β1 x t 1* + β2 x t 2* + u t (4.27)
上式为线性模型。用OLS 法估计后,再返回到原模型。若回归参数 β1 + β2 = 1,称模型为规模报酬不变型; β1 + β2 > 1,称模型为规模报酬递增型; β1 + β2 < 1,称模型为规模报酬递减型。
对于对数线性模型,Lny = Ln β0 + β1 Lnx t 1 + β2 Lnx t 2 + u t ,β1和β2称作弹性系数。以β1
为例,
β1 = 1t t Lnx Lny ??= 1111t t t
t x x y y ??--= 11//t t t t x x y y ??= 1
1t t t t x y y x ?? (4.28) 可见弹性系数是两个变量的变化率的比。注意,弹性系数是一个无量纲参数,所以便于在不
同变量之间比较相应弹性系数的大小。
对于线性模型,y t = α0 + α1 x t 1 + α2 x t 2 + u t ,α1和 α2称作边际系数。以α1为例,
α1 =
1
t t
x y ?? (4.29) 通过比较(4.28)和(4.29)式,可知线性模型中的回归系数(边际系数)是对数线性回归模型中弹性系数的一个分量。
例1:此模型用来评价台湾农业生产效率。用台湾1958-1972年农业生产总值(y t ),劳动力(x t 1),资本投入(x t 2)数据(见表4.1)为样本得估计模型, ∧
t Lny = -3.4 + 1.50 Lnx t 1 + 0.49 Lnx t 2 (4.30) (2.78) (4.80) R 2 = 0.89, F = 48.45 还原后得,
t y
?= 0.713 x t 11.50 x t 20.49 (4.31) 1.50 + 0.49 = 1.99,即当劳动力和资本投入都增加1%时,产出增加近2%。
例2:用天津市工业生产总值(Y t ),职工人数(L t ),固定资产净值与流动资产平均余
额(K t )数据 (1949-1997) 为样本得估计模型如下:
Ln Y t = 0.7272 + 0.2587Ln L t + 0.6986 LnK t
(3.12) (3.08) (18.75) R 2 = 0.98, s.e. = 0.17, DW = 0.42, F = 1381.4 因为0.2587 + 0.6986 = 0.9573,所以此生产函数基本上可视为规模报酬不变函数(严格意义上,需要利用假设检验程序)。 例3:硫酸透明度与铁杂质含量的关系(摘自《数理统计与管理》1988.4, p.16)
某硫酸厂生产的硫酸的透明度一直达不到优质指标。经分析透明度低与硫酸中金属杂质的含量太高有关。影响透明度的主要金属杂质是铁、钙、铅、镁等。通过正交试验的方法发现铁是影响硫酸透明度的最主要原因。测量了47个样本,得硫酸透明度(y )与铁杂质含量(x )的散点图如下(file:nonli01):
050100150
200
50
100
150
200
250
X Y
0.00
0.02
0.04
0.06
0.08
0.00
0.01
0.02
0.03
0.04
1/X
1/Y
(1) y = 121.59 - 0.91 x (10.1) (-5.7)
R 2 = 0.42, s.e. = 36.6, F= 32
(2) 1/y = 0.069 - 2.37 (1/x )
(18.6) (-11.9)
R 2 = 0.76, s.e. = 0.009, F= 142
50
100
150
200
0.00
0.01
0.02
0.03
0.04
1/X
Y
2
3
4
5
6
0.00
0.01
0.02
0.03
0.04
1/X
LOG(Y )
(3)y = -54.40 + 6524.83 (1/x )
(-7.2) (16.3)
R 2 = 0.86, s.e. = 18.2, F= 266
(4)Lny = 1.99 + 104.5 (1/x )
(22.0) (21.6)
R 2 = 0.91, s.e. = 0.22, F= 468
还原,Lny = Ln(7.33) + 104.5 (1/x )
y = 7.33
)
1(5.104x e
(5)非线性估计结果是 y = 8.2965
)
1
(1.100x e
R 2 = 0.96,
EViews 命令Y=C(1)*EXP(C(2)*(1/X))
例4 中国铅笔需求预测模型(非线性模型案例,file:nonli6)
中国从上个世纪30年代开始生产铅笔。1985年全国有22个厂家生产铅笔。产量居世界首位(33.9亿支),占世界总产量的1/3。改革开放以后,铅笔生产增长极为迅速。1979-1983年平均年增长率为8.5%。铅笔销售量时间序列见图4.21。1961-1964年的销售量平稳状态是受到了经济收缩的影响。文革期间销售量出现两次下降,是受到了当时政治因素的影响。1969-1972年的增长是由于一度中断了的中小学教育逐步恢复的结果。1977-1978年的增长是由于高考正式恢复的结果。1981年中国开始生产自动铅笔,对传统铅笔市场冲击很大。1979-1985年的缓慢增长是受到了自动铅笔上市的影响。
初始确定的影响铅笔销量的因素有全国人口、各类在校人数、设计人员数、居民消费水平、社会总产值、自动铅笔产量、价格因素、原材料供给量、政策因素等。经过多次筛选、组合和逐步回归分析,最后确定的被解释变量是y t (铅笔年销售量,千万支);解释变量分别是x t 1(自动铅笔年产量,百万支);x t 2(全国人口数,百万人);x t 3(居民年均消费水平,元);x t 4(政策变量)。因政策因素影响铅笔销量出现大幅下降时,政策变量取负值。例如1967、1968年的x t 4值取-2,1966、1969-1971、1974-1977年的x t 4值取-1)。
由图4.22知中国自生产自动铅笔起,自动铅笔产量与铅笔销量存在线性关系。由图4.23知全国人口与铅笔销量存在线性关系。说明人口越多,对铅笔的需求就越大。由图4.24知居民年均消费水平与铅笔销量存在近似对数的关系。散点图说明居民年均消费水平越高,则铅笔销量就越大。但这种增加随着居民消费水平的增加变得越来越缓慢。图4.25显示政策变量与铅笔销量也呈线性关系。
50
10015020025030035062
64
66
68
70
72
74
76
78
80
82
84
Y
铅笔销售量时间序列(1961-1985)(文件名nonli6)
100
200300
400
10
20
30
40
Y
X 1
100
200
300400
600
700
800
900
1000
1100
Y
X 2
Y , X1散点图 Y , X2散点图
100
200300
400
100200
300
400
500
Y
X 3
100
200
300
400
-2.5
-2.0
-1.5
-1.0
-0.5
0.0
0.5
Y
X 4
Y , X3散点图 Y , X4散点图
基于上述分析建立的模型形式是
y t = β0 + β1 x t 1 + β2 x t 2 + β3 Ln (x t 3) + β4 x t 4 + u t (4.40)
y t 与x t 3呈非线性关系。估计结果如下。
t y
?= -907.94 - 2.95 x t 1 + 0.31 x t 2 + 170.19 Ln x t 3 + 45.51 x t 4 (4.41) (-6.4) (-3.7) (4.8) (4.4) (12.6)
R 2 = 0.9885, DW = 2.09, F = 429, s.e. = 10.34
上式说明,在上述期间自动铅笔年产量每增加1百万支,平均使铅笔的年销售量减少2950万支。全国人口数每增加1百万人,平均使铅笔的年销售量增加310万支。对数的居民年均消费水平每增加1个单位,平均使铅笔的年销售量增加17亿支。一般性政策负面变动使铅笔的年销售量减少4.551亿支。当政策出现大的负面变动时,铅笔的年销量会减少9.102亿支。
当y t 对所有变量都进行线性回归时(见下式),显然估计结果不如(4.41)式好。
t y
?= -254.26 - 3.29 x t 1 + 0.42 x t 2 + 0.66 x t 3 + 40.74 x t 4 (4.42) (-12.0) (-3.0) (8.6) (3.5) (11.7)
R 2 = 0.9857, DW = 1.77, F = 346, s.e. = 11.5
例6 中国人口发展曲线(公元前1046~公元2000,file:nolin3)
中国人口数据(中华民国元年以前为推定数据)
中国纪年
公元 人口(亿人, popu )
武王克商(西周建国) -1046 0.0550 周平王元年(东周始)
-771 0.1000 秦始皇称帝
-221 0.2000 汉高祖5年(西汉建国)
-202 0.1310 汉文帝23年 -157 0.2500 汉平帝2年 2 0.6300 汉桓帝11年 157 0.7200 魏文帝(曹丕)元年 220 0.1900 晋武帝(司马炎)元年
265 0.2754 晋惠帝10年 300 0.3479 晋安帝10年 407 0.3228 隋文帝(杨坚)10年 581 0.4530 唐玄宗(李隆基)44年 755 0.9045 宋太祖(赵匡胤)元年
960 0.4598 北宋徽宗10年 1110 1.2066 南宋丁宗28年 1223 1.2480 明嘉靖45年 1566 1.6630 清顺治18年 1661 0.90699616 清道光14年
1834 4.00000000 中华民国元年(内政年鉴) 1911 4.42944529 中华民国8年(申报年鉴) 1919 4.68287473 中华民国18年(内政年鉴)
1928 4.95381199 中华民国26年
1936 4.96723711 中华民国35年(户政导报) 1945 5.16458301 中华人民共和国(统计局) 1949 5.45418598 中华人民共和国(统计局) 1964 7.0499 中华人民共和国(统计局) 1981 10.0072 中华人民共和国(统计局)
2001
12.7627
资料来源:《中国人口通史》,山东人民出版社,2001年1月,第1218-1234页。 注:1.《中国人口通史》为九五期间社科基金重点研究项目成果。 2.数据中-1046年原为-1100。依夏商周断代工程研究成果改动。
5
10
15
-2000
-1000
1000
2000
3000
T
POPU
∧
-)1/30(popu Ln = 4.7831 - 0.0016 t
(30.9) (-13.6) R 2 = 0.88
因为Ln (119.5) = 4.7831,所以popu =
t
e
0016.05.119130
-+
例7.美国的通货膨胀和失业的关系(菲利普斯曲线模型的估计)
使用的数据为1950—1970年美国的年度数据,通货膨胀(INF)为消费者价格指数的年变化率,失业变量(UNE)是指16岁以上民间工人的失业率。通货膨胀变动范围从1959年时的最小值0.69%到1970年时的最高值5.72%。失业率在1957年为4.%,1961年达到顶峰6.7%,并在随后几年稳步下降。通货膨胀对当期失业率、滞后一期失业率,以及滞后一期失业率倒数等散点图如下:
INF=9.13 -1.34UNR(-1)+e t
(9.80) (-7.19)
R 2=0.8117 F=51.74 D.W.=1.47
非线性估计:
C(1) -0.323482 0.548077 -0.590212 0.5670 C(2) 4.889070 1.860566 2.627732 0.0235 C(3)
-2.691611
0.265881
-10.12335
0.0000 R-squared
0.950143 Mean dependent var 2.581752 Adjusted R-squared 0.941078 S.D. dependent var 1.642630 S.E. of regression 0.398729 Akaike info criterion 1.186338 Sum squared resid 1.748830 Schwarz criterion 1.323279 Log likelihood
-5.304368 Durbin-Watson stat
2.873359
2.69
1)UNR(4.89
0.32INF --+
-=
1/INF=-0.99 +0.32UNR(-1)+e t
(-6.03) (9.76) R 2=0.8881 F=95.26 D.W.=3.21
INF=-4.48 +32.98(1/UNR(-1))+e t
(-6.51) (10.50) R 2=0.9018 F=110.19 D.W.=1.72
R 2=0.9018 F=110.19 D.W.=1.72