每周一测2017-2018学年高二数学(理)人教版(课堂同步系列二)+Word版

2017—2018学年度第二学期教学质量检查高二理科数学考生注意：本卷共三大题，22小题，满分150分，考试时间120分钟．不能使用计算器．第Ⅰ卷 选择题一、选择题（本大题共12小题，每小题5分，共60分. 每小题各有四个选择支，仅有一个选择支正确.请用2B 铅笔把答题卡中所选答案的标号涂黑．）1.已知a R ∈,i 是虚数单位，若复数i a a z )1(12++-=为纯虚数，则a =( ) A. 0B. 1C. 1-D. 1±2.曲线x x y +=2在点)2,1(P 处切线的斜率为（ ） A. 1B. 2C. 3D. 43.用反证法证明命题“已知a b N ∈，，如果ab 是7的倍数，那么a ，b 中至少有一个是7的倍数．”则假设的内容是( ) A.a ，b 都是7的倍数B.a ，b 都不是7的倍数C.a ，b 中至多一个是7的倍数D.a ，b 恰有一个不是7的倍数4.设函数()nf x x mx =+的导函数'()21f x x =+，则21()f x dx -⎰的值等于( ) A.56B.12C.23D.165.已知在最小二乘法原理下，具有相关关系的变量x ，y 之间的线性回归方程为0.710.ˆ3yx =-+，且变量x ，y 之间的相关数据如下表所示，则下列说法正确．．的是( )A. 变量x ，y 之间呈现正相关关系B. 可以预测，当20x =时， 3.7y ∧= C.可求得表中 4.7m =D. 由表格数据知，该回归直线必过点()9,46.设实数57,13,35-=-=-=c b a ，则c b a ,,的大小为（ ）A.a b c <<B.c b a <<C.b a c <<D.c a b <<7.)2()1(5+-x x 展开式中含2x 项的系数为( )A ．25B ．5C ．15-D ．20-8.某校将5名插班生甲、乙、丙、丁、戊编入3个班级，每班至少1人，则不同的安排方案共有（ ） A. 150种B. 120种C. 240种D. 540种9.函数33)(x x x f -=在],0[m 上最大值为2，最小值为0，则实数m 取值范围为（ ） A. ]3,1[B. ),1[+∞C. ]3,1(D. ),1(+∞10.我国古代数学名著《九章算术》的论割圆术中有：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周盒体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式+++11111中“ ”即代表无限次重复，但原式却是个定值，它可以通过方程x x =+11求得251+=x ，类似上述）A.2113+C.7D.22 11.一个盒子装有质地、大小、形状都相同的6个球，其中红球3个，黄球2个，蓝球1个.现从中任取两个球，记事件A ：“取出的两个球颜色不同”，事件B ：“取出一个红球，一个黄球”，则()P B A =（ ） A.1511 B.31 C.52 D.116 12.若1(,0(0)()ln ,]kx x f x x e x x --∈-∞⎧=⎨∈⎩图象上恰存在两个点关于y 轴对称，则实数k 的取值范围是（ ）A. 11,1e⎛⎤+ ⎥⎝⎦B. 1{1}(1,)e++∞C. {1}D. ()1,+∞第Ⅱ卷 非选择题二、填空题（本大题共4小题，每小题5分，共20分．请把答案填在答题卡中相应的位置上．） 13.已知i 为虚数单位，N n ∈，计算3424144++++++n n n ni i i i的结果为_______．14.设随机变量()2~1,X N σ，且1(2)5P X >=，则(01)P X <<=__________． 15.已知离散型随机变量X 的取值为2,1,0，且b X P a X P X P ======)2(,)1(,41)0(；若()1E X =，则()D X=__________．16.在1nx ⎛⎫ ⎪⎝⎭的展开式中，各项系数的和为p ，二项式系数之和为q ，且q 是p 与48-的等差中项，则正整数n 的值为_______．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17．（本小题满分10分）已知复数z 满足()1+z i m i =- (其中i 是虚数单位).（Ⅰ）在复平面内，若复数z 的共轭复数对应的点在直线70x y +-=上，求实数m 的值； （Ⅱ）若1z ≤，求实数m 的取值范围.18.（本小题满分12分）《开讲啦》是中国首档青年电视公开课，节目邀请“中国青年心中的榜样”作为演讲嘉宾，分享他们对于生活和生命的感悟，给予中国青年现实的讨论和心灵的滋养.为了了解观众对节目的喜爱程度，电视台分别在A B 、两个地区调查了45和55共100名观众，得到如下的22⨯列联表：已知在被调查的100名观众中随机抽取1名，该观众是 “非常满意”的观众的概率为0.65.（Ⅰ）完成上述表格，并判断能否在犯错误的概率不超过0.1的前提下认为观众的满意程度与所在地区有关系？（Ⅱ）若以抽样调查的频率作为概率，从A 地区所有观众中随机抽取3人，设抽到的观众“非常满意”的人数为X ，求X 的分布列和数学期望. 附表：其中随机变量))()()(()(22d b c a d c b a bc ad n K ++++-=.19. （本小题满分12分）某公司开发了一件新产品，为了研究销售量与单价的关系，进行了市场调查，并获得了销售量y 与单价x 的样本，且进行了数据处理(如下表)，作出散点图.表中102111,10i i i i w w w x ===∑.（Ⅰ）根据散点图判断，a bx y +=与c x dy +=2哪一个更适宜作为y 关于x 的回归方程类型？（不必说明理由）（Ⅱ）根据（Ⅰ）的结论和表中数据，在最小二乘法原理下建立y 关于x 的回归方程；（Ⅲ）利用第（Ⅱ）问求得的回归方程，试估计单价x 范围为多少时，该商品的销售额不小于25?（销售额=销销量⨯单价）附：对于一组数据112233(,),(,),(,),,(,)n n u v u v u v u v ⋅⋅⋅，其回归直线ˆˆˆvu αβ=+的斜率和截距的最小二乘法估计值分别为121()()ˆˆˆ,()niii nii v v uu v u uu βαβ==--==--∑∑.20. （本小题满分12分）已知32()f x ax bx x c =+++，在1=x 与13x =-处都取得极值． （Ⅰ）求实数b a ，的值；（Ⅱ）若对任意[]2 1，-∈x ，都有()2c x f <成立，求实数c 的取值范围．21. （本小题满分12分）已知函数()1ln (0).xf x x a ax-=+> （Ⅰ）若()f x 在点()1,(1)f 处的切线方程为12y x b =+,求()f x 的解析式；（Ⅱ）若对于任意的]1,0(,21∈x x 都有1)()(2121<--x x x f x f 恒成立，求正实数a 的取值范围.22．（本小题满分12分）已知函数()()2221xf x axe x -=--， a R ∈.（Ⅰ）讨论函数()f x 的单调性；（Ⅱ）当01a <<时，求证：函数()f x 有两个不相等的零点1x ，2x ，且121x x ⋅<.第19题图。

1 5月29日 极坐标方程和直角坐标方程的互化
高考频度：★★★★★ 难易程度：★★★☆☆
已知圆1O 和圆2O 的极坐标方程分别为4cos ρθ=，sin ρθ=-．
（1）把圆1O 和圆2O 的极坐标方程化为直角坐标方程；
（2）求经过圆1O 与圆2O 的两个交点的直线的直角坐标方程，并将其化为极坐标方程．
【参考答案】（1）2240x y x +-=，220x y y ++=；（2）40x y +=，tan 4θ=-．
（2）由2240x y x +-=及220x y y ++=，两式相减得40x y +=，
所以经过圆1O 与圆2O 的两个交点的直线的直角坐标方程为40x y +=，
将40x y +=化为极坐标方程为4cos sin 0ρθρθ+=，即tan 4θ=-． 【解题必备】（1）设M 是平面内任意一点，它的直角坐标是(x ，y )，极坐标是(ρ，θ)(ρ≥0)，于是极坐标与直角坐标的互化公式如下表：学科-网
点M
直角坐标(x ，y ) 极坐标(ρ，θ) 互化公式 cos x ρθ=，sin y ρθ= 222x y ρ=+，tan (0)y x x
θ=≠ 在一般情况下，由tan θ确定角时，可根据点M 所在的象限取最小正角．
（2）把直角坐标化为极坐标，求极角θ时，应注意判断点P 所在的象限（即角θ的终边的位置），以便准确地求出角θ．利用两种坐标的互化可以把不熟悉的问题转化为熟悉的问题．。

高级中学2017-2018学年年高二11月周考试题数学（理）班级： 姓名： 得分：必考Ⅰ部分（满分100分）一、选择题：本大题共10小题，每小题5分，满分50分；在每小题给出的四个选项中，只有一项是符合题目要求的．1、已知集合{}0322≤--=x x x A ，{}0≥=x x B ，则=B A ( ) A.{}31≤≤x x B.{}10≤≤x x C.{}30≤≤x x D.{}103≤≤≥x x x 或2、在三角形ABC 中，若0cos sin ≤B A ，则三角形ABC 为( )A.锐角三角形B.钝角三角形C.直角三角形D.钝角三角形或直角三角形 3、已知数列{}n a ，且nn a n +=21，则数列{}n a 前100项的和等于（ ） A.101100 B.10099 C.102101 D.10199 4、不可以作为数列： ,0,2,0,2，的通项公式的是（ )A. ⎪⎩⎪⎨⎧∈=∈-==++),2(0),12(2N k k n N k k n a n B. 2sin 2πn a n = C. 1)1(+-=n n a D.2)1(cos2π-=n a n 5、函数)152lg()(2++-=x x x f 的定义域为（ ） A.)3,5(- B.)5,3(- C.),5()3,(+∞--∞ D.),3()5,(+∞--∞6、在△ABC 中，若cos cos a b B A=，则该三角形一定是 ( ) A ．等腰三角形但不是直角三角形 B ．直角三角形但不是等腰三角形C ．等腰直角三角形D ．等腰三角形或直角三角形7、已知等差数列{}n a 满足02=a ，1086-=+a a ，则=2016a ( )A ．2 014B ．2 015C ．2014-D ．2015-8、已知△ABC 的面积为23，AC ＝2，∠BAC ＝60°，则BC=( )A ．7B ．3C ．325-D ．39、某农户计划种植A 和B 两种蔬菜，种植面积不超过50亩，投入资金不超过54万元，假设种植A 和B 的产量、成本和售价如下表：A 和B 的种植面积(单位：亩)分别为 ( )A ．50,0B ．30,20C ．20,30D ．0,5010、下列说法错误的是（ ）A.等比数列可以是递增、递减、摆动、常数数列B.等差数列不可能是摆动数列C.既是等差数列又是等比数列的数列有且只有一个D.数列通项公式可能不止一个二、填空题：本大题共3小题，每小题5分，共15分.11、在等比数列{}n a 中，16,142==a a ，则公比为 .12、已知,x y 满足约束条件10,230,x y x y --≤⎧⎨--≥⎩当目标函数z ax by =+(0,0)a b >>在该约束条件下取到最小值ab 的最大值为 .13、若△ABC 的内角满足C B A sin 2sin 2sin =+,则C cos 的最小值是 .三、解答题（本题共6个小题，满分75分）14（满分11分）已知点)1,3(),0,0(A O ，点),(y x P 满足220240330x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩，求OP OA ⋅的最大值和最小值..15（满分12分）已知{}n a 是递增的等差数列，32,a a 是方程2560x x -+=的根。

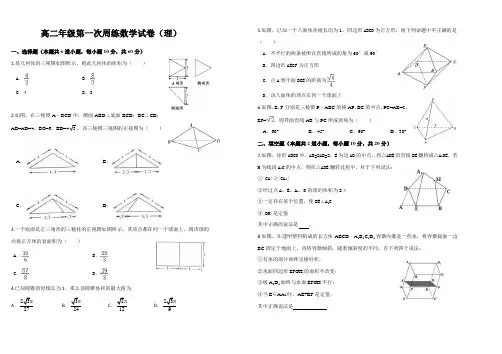
高二年级第一次周练数学试卷（理）一、选择题（本题共6道小题，每小题10分，共60分）1.某几何体的三视图如图所示，则此几何体的体积为（）A ．B ．C．4 D．82.如图，在三棱锥A﹣BCD中，侧面ABD⊥底面BCD，BC⊥CD，AB=AD=4，BC=6，BD=43，该三棱锥三视图的正视图为（）A ．B．C．D．3.一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在同一个球面上，则该球的内接正方体的表面积为（）A．B．C．D．4.已知圆锥的母线长为1，那么该圆锥体积的最大值为A．2327πB．324πC．212πD．239π5.如图，已知一个八面体各棱长均为1，四边形ABCD为正方形，则下列命题中不正确的是（）A．不平行的两条棱所在直线所成的角为60°或90°B．四边形AECF为正方形C．点A到平面BCE的距离为D．该八面体的顶点在同一个球面上6.如图，E，F分别是三棱锥P﹣ABC的棱AP，BC的中点，PC=AB=2，EF=，则异面直线AB与PC所成的角为（）A．60°B．45°C．90°D．30°二、填空题（本题共2道小题，每小题10分，共20分）7.如图，矩形ABCD中，AB=2AD=2，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE，若M为线段A1C的中点，则在△ADE翻转过程中，对于下列说法：①|CA|≥|CA1|②经过点A、E、A1、D的球的体积为2π③一定存在某个位置，使DE⊥A1C④|BM|是定值其中正确的说法是．8.如图，在透明塑料制成的长方体ABCD﹣A1B1C1D1容器内灌进一些水，将容器底面一边BC固定于地面上，再将容器倾斜，随着倾斜度的不同，有下列四个说法：①有水的部分始终呈棱柱状；②水面四边形EFGH的面积不改变；③棱A1D1始终与水面EFGH平行；④当E∈AA1时，AE+BF是定值．其中正确说法是．学号姓名得分一、选择题（本题共6道小题，每小题10分，共60分）题号１２３４５６答案二、填空题（本题共2道小题，每小题10分，共20分）7．8．三、解答题（本题共2道小题,每小题20分,共40分）9.在棱长为1的正方体ABCD﹣A1B1C1D1中，M、N分别是AB1、BC1的中点．（Ⅰ）求证：直线MN∥平面ABCD．（Ⅱ）求B1到平面A1BC1的距离．10.已知直三棱柱ABC﹣A1B1C1中，D，E分别为AA1，CC1的中点，AC⊥BE，点F在线段AB上，且AB=4AF．（1）证明：BC⊥C1D；（2）若M为线段BE上一点，试确定M在线段BE上的位置，使得C1D∥平面B1FM．试卷答案1.B【考点】L!：由三视图求面积、体积．【分析】如图所示，可将此几何体放入一个正方体内，则四棱锥P﹣ABCD即为所求．【解答】解：如图所示，可将此几何体放入一个正方体内，则四棱锥P﹣ABCD即为所求，体积为V==，故选B．2.C【考点】简单空间图形的三视图．【分析】由题意，三棱锥三视图的正视图为等腰三角形，设C在BD上的射影为E，求出CE，即可得出结论．【解答】解：由题意，三棱锥三视图的正视图为等腰三角形，△BCD中，BC⊥CD，BC=6，BD=4，∴CD=2，设C在BD上的射影为E，则12=CE，∴CE=，故选C．【点评】本题考查三视图，考查学生的计算能力，比较基础．3.D【考点】L!：由三视图求面积、体积．【分析】由已知中底面是正三角形的三棱柱的正视图，求出三棱柱的底面边长和高，从而求出它外接球的半径，再求球内接正方体的棱长，即可求出其表面积．【解答】解：由已知中的三棱柱正视图可得：三棱柱的底面边长为2，高为1 则三棱柱的底面外接圆半径为r=，球心到底面的距离为d=；则球的半径为R==；∴该球的内接正方体对角线长是2R=2=a，∴a=2=；∴内接正方体的表面积为：S=6a2=6×=．故选：D．4.B【考点】由三视图求面积、体积．【分析】根据三视图可得四棱锥为正四棱锥，判断底面边长与高的数据，求出四棱锥的斜高，代入棱锥的侧面积公式计算．【解答】解：由三视图知：此四棱锥为正四棱锥，底面边长为4，高为2，则四棱锥的斜高为=2，∴四棱锥的侧面积为S==16．故选B．5.C【考点】MK：点、线、面间的距离计算．【分析】由已知求出图中任意两棱所成角的大小判断A、B正确；再由等积法求出点A到平面BCE的距离说明C错误；由ABCD为正方形，AECF为正方形，且两正方形边长相等，中心都为AC的中点说明D正确．【解答】解：∵八面体的各条棱长均为1，四边形ABCD为正方形，∴在四棱锥E﹣ABCD中，相邻两条侧棱所成的角为60°，∵AE=CE=1，AC=，满足AE2+CE2=AC2，∴AE⊥CE，同理AF⊥CF，则四边形AECF是正方形．再由异面直线所成角概念可知，图中每一条棱与和其异面的棱所成角为60°．故A、B正确；设点A到平面BCE的距离h，由V E﹣ABCD=2V A﹣BCE，得×1×1×=2××，解得h=，∴点A到平面BCE 的距离为，故C错误；由ABCD为正方形，AECF为正方形，且两正方形边长相等，中心都为AC的中点，∴该八面体的顶点在以AC 中点为球心，以为半径的球面上，故D正确．∴不正确的命题是C．故选：C．【点评】本题考查命题的真假判断与应用，考查立体几何中线线关系以及线面关系，利用了等积法求点到平面的距离，是中档题．6.C【考点】异面直线及其所成的角．【分析】先取AC的中点G，连接EG，GF，由三角形的中位线定理可得GE∥PC，GF∥AB 且GE=5，GF=3，根据异面直线所成角的定义，再利用余弦定理求解．【解答】解：取AC的中点G，连接EG，GF，由中位线定理可得：GE∥PC，GF∥AB且GE=1，GF=1，∴∠EGF或补角是异面直线PC，AB所成的角．在△GEF中，有EF2=EG2+FG2，∴∠EGF=90°故选：C7.①④【考点】棱锥的结构特征．【分析】在①中，在△ADE翻转过程中，始终有|CA|≥|CA1|；在②中，A，D，E是定点，A1是动点，经过点A、E、A1、D的球的体积不是定值；在③中，AC与DE不垂直，从而DE 与A1C不垂直；在④中，取DC中点N，连MN，NB，根据余弦定理得到|BM|是定值．【解答】解：在①中，在△ADE翻转过程中，始终有|CA|≥|CA1|，故①正确．在②中，∵AD=AE=A1D=A1E=1，A，D，E是定点，A1是动点，∴经过点A、E、A1、D的球的体积不是定值，故②错误；在③中，∵A1C在平面ABCD中的射影为AC，AC与DE不垂直，∴存在某个位置，使DE⊥A1C不正确，故③不正确．在④中，取DC中点N，连MN，NB，则MN∥A1D，NB∥DE，∴面MNB∥面A1DE，MB⊂面MNB，∴MB∥面A1DE，故④正确；∠A1DE=∠MNB，MN=是定值，NB=DE是定值，根据余弦定理得到：MB2=MN2+NB2﹣2MN•NB•cos∠MNB，∴|BM|是定值，故④正确．故答案为：①④．8.①③④【考点】命题的真假判断与应用．【分析】①由于BC固定，所以在倾斜的过程中，始终有AD∥EH∥FG∥BC，且平面AEFB∥平面DHGC，由此分析可得结论正确；②水面四边形EFGH的面积是改变的；③利用直线平行直线，直线平行平面的判断定理，容易推出结论；④当E∈AA1时，AE+BF是定值．通过水的体积判断即可．【解答】解：根据面面平行性质定理，可得BC固定时，在倾斜的过程中，始终有AD∥EH∥FG∥BC，且平面AEFB∥平面DHGC，故水的形状成棱柱形，故①正确；水面四边形EFGH的面积是改变的，故②错误；因为A1D1∥AD∥CB∥EH，A1D1⊄水面EFGH，EH⊂水面EFGH，所以A1D1∥水面EFGH正确，故③正确；由于水的体积是定值，高不变，所以底面ABFE面积不变，即当E∈AA1时，AE+BF是定值．故④正确．故答案为：①③④．9.【考点】点、线、面间的距离计算；直线与平面平行的判定．【分析】（Ⅰ）连结B1C、AC，则N也是B1C的中点，证明MN∥AC，利用线面平行的判定定理证明MN∥平面ABCD；（Ⅱ）由，求出B1到平面A1BC1的距离．【解答】（Ⅰ）证明：连结B1C、AC，则N也是B1C的中点∴MN是△B1AC的中位线，即有MN∥AC (3)∵MN⊄平面ABCD，AC⊂平面ABCD∴MN∥平面ABCD…（Ⅱ）解：△A1BC1是边长为的等边三角形，∴…设B1到平面A1BC1的距离为h ，由得，∴…10.【分析】（1）先证明AC⊥面BCE，进而AC⊥BC，进而得到BC⊥面ACC1，可得BC⊥C1D；（2）连结AE，在BE上取点M，使BE=4ME，连结FM，B1M，FB1，可得此时C1D∥平面B1FM．【解答】证明：直三棱柱可知CC1⊥平面ABC，AC⊂平面ABC，∴CC1⊥AC，…又∵AC⊥BE，CC1∩BE=E，CC1⊂平面BCE，BE⊂平面BCE，∴AC⊥面BCE，故AC⊥BC，…又在直三棱柱中，CC1⊥BC，AC∩CC1=C，AC⊂平面ACC1，CC1⊂平面ACC1，故BC⊥面ACC1，C1D在平面ACC1内，∴BC⊥C1D…解：（2）连结AE，在BE上取点M，使BE=4ME，…连结FM，B1M，FB1，在△BEA中，由BE=4ME，AB=4AF…∴MF∥AE，…又在面AA1C1C中，∵C1E=AD且C1E∥AD，∴C1D∥AE，又MF∥AE，∴C1D∥MF，C1D⊂/平面B1FM，FM⊂平面B1FM，C1D∥平面B1FM…【点评】本题考查的知识点焊是直线与平面平行的判定，空间中直线与直线之间的位置关系，难度中档．。

2017-2018学年度第二学期期末高二数学（理）试题时间：120分钟 分值：150分一、选择题：本大题共12小题，每小题5分，共60分；在每小题给出的四个选项中，只有一项是符合题目要求的。

1.设集合{}A |43x x x Z =-<<∈，{}|1B x x =≥则A B ⋂= （ ） A ．{}1 B.{}1,2 C. {}01,2， D. {}1,23，2.设集合{}2A |60x x x =+-< {}2|1B x x =≤ ，则 A B ⋂= （ ）A. []1,1-B. (]3,1-C.()1,2-D. [)1,2-3.下列命题中真命题的个数是 （ ） ① 42,x R x x ∀∈>② 若p q ∧ 是假命题，则,p q 都是假命题③ 命题“32,240x R x x ∀∈++≤”的否定为“32000,240x R x x ∃∈++>” A ．0 B ．1 C ．2 D ．34.5x >的一个必要不充分条件是 （ ） A.6x >B.3x >C.6x <D.10x >5.把一枚硬币任意掷两次，事件A=“第一次出现正面”，事件B=“第二次出现正面”，则P （B/A ）= （ ） A.14 B.13 C.12 D.236.方程12x x +=根的个数为 ( ) A.0 B.1 C.2 D.37.在82x ⎛ ⎝的展开式中，常数项是 ( )A.7B.-7C.28D.-288.设 12log 3a = , 0.213b ⎛⎫= ⎪⎝⎭, 12c =,则 ( )A.a b c <<B.c b a <<C.c a b <<D.b a c <<9. 函数与在同一直角坐标系下的图象大致是（ ）图所示的长方形区域内任取一个点(),M x y ，则点M 取自阴影部分的概率为 （ ） A.12 B.14 C.13 D.2311.若函数()y f x =图像与()log 322a y x =-+图像关于直线y x =对称,则函数()y f x =必过定点 （ ）A.（1,2）B.（2,2）C.（2,3）D.（2,1） 12.定义在R 上的偶函数满足，且当时，()12xf x ⎛⎫= ⎪⎝⎭， 则等于 （ ）A.3B.18C.-2D.2 二、填空题：本大题共4小题，每小题5分，共20分13.将3个不同的小球放入4个盒子中，有 ______种不同的放法14.已知随机变量X 服从正态分布N(3,1),且(2X 4)0.6826P ≤≤=，则(X 4)P >= ______ 15.已知()()()220210{xx x x x f x ≤-+>=在[]()1,2a a ->上最大值与最小值之差为4，则a =______16.为方便游客出行，某旅游点有50辆自行车供租赁使用。

2017—2018学年度第一学期期末考试高二理科数学试卷（答题时间：120分钟 满分：150分)一、选择题（本大题共12小题，每小题5分，满分60分）每小题只有一个．．．．正确选项,请将正确选项填到答题卡处1。

设集合{|(1)(2)0}A x x x =+-<， {|13}B x x =<<，则A B = A ．{|13}x x -<< B ．{|11}x x -<<C ．{|12}x x <<D ．{|23}x x <<2.已知抛物线y 2＝2px （p >0）的准线经过点(－1,1),则该抛物线的焦点坐标为A ．(－1，0)B ．（1,0）C ．（0，－1)D ．（0,1）3．设x ，y ∈R ，则“x ≥2且y ≥2”是“x 2＋y 2≥4”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件4．已知等差数列｛a n }的公差为d （d ≠0）,且a 3＋a 6＋a 10＋a 13＝32，若a m ＝8，则m 为A ．12B ．8C ．6D ．45．执行如图所示的程序框图,若输入的n ＝10，则输出的S 等于A .错误!B .错误!C 。

错误!D .错误!6．某学校组织学生参加数学测试，成绩的频率分布直方图如图，数据的分组依次为［20,40),[40,60)，［60,80），［80，100]．若低于60分的人数是15人，则该班的学生人数是A ．45B ．50C ．55D ．607。

若一个正三棱柱的三视图如图所示，则这个正三棱柱的表面积为A .318B 。

315C .3824+D 。

31624+8．已知a ＋b ＋c ＝0,｜a |＝2，|b |＝3，｜c ｜＝4，则向量a 与b 之间的夹角<a ,b 〉为A ．30°B ．45°C ．60°D ．以上都不对9．在长为10厘米的线段AB 上任取一点G ，用AG 为半径作圆,则圆的面积介于36π平方厘米到64π平方厘米的概率是A .错误!B 。

河南省正阳县第二高级中学2017-201学年下期高二数学理科周练（二）一.选择题（只有一个选项是正确的，每小题5分，共60分）1.已知命题p:112x ≤≤,命题q:()(1)0x a x a ---≤,若非p 是非q 的必要不充分条件，则实数a 的取值范围是__________:A.1[0,]2 B.1[,1]2 C.11[,]32 D.1(,1]3 2.若/2()()x f x f x x e =+，则f(1)=（）A.eB.0C.e+1D.e-13.若(6,1,4),(1,2,1),(4,2,3)A B C --，则ABC ∆的形状是（）A.不等边锐角三角形B.直角三角形C.钝角三角形D.等边三角形4.已知椭圆221169x y +=，则以点3(2,)2为中点的弦所在的直线方程为（） A.8x-6y-7=0 B.3x+4y=0 C.3x+4y-12=0 D.6x+8y-25=05.在ABC ∆中，S 为ABC ∆的面积，且2221()2S b c a =+-，则tanB+tanC-2tanBtanC=( ) A.1 B.-1 C.2 D.-26.已知数列{}n a 为等比数列，为其前n 项和，且201720162018,n n S t =⨯-则t=（） A.20152016 B. 20162017 C. 20172018 D. 201820197.在正三棱柱111ABC A B C -中，已知AB=1，12AA =，D 为1BB 的中点，则AD 与平面11AAC C所成角的余弦值为（）A.128.不等式11ax x b+>+的解集为(,1)(3,)-∞-+∞，则不等式220x bx a +-<的解集为（） A.（-2,5） B.（-0.5,0.2） C.（-2,1） D.（-0.5,1） 9.若0<x<1,则121x x x +-的最小值为（）A.10.已知抛物线C ：22(0)y px p =>，过其焦点F 的直线交抛物线C 于点A 、B ，3AF BF =，则AB =（）A.pB.43pC.2pD. 83p 11.从一楼到二楼共有十级台阶，小明从一楼上到二楼，每次可以一部跨一级台阶，也可以跨两级台阶，则小明从一楼上到二楼的方法共有（）种A.87B.88C.89D.9012.已知点P 为椭圆2211612x y +=上的动点，EF 为圆N ：22(1)1x y +-=的任一条直径，则 .PE PF 的最大值和最小值是（）A.16,12-17,13-19,12-20,13-二.填空题（每小题5分，共20分）13.过32()325f x x x x =-++图象上一个动点作此函数图象的切线，则所作切线倾斜角的取值范围是（）14.已知实数x,y 满足不等式组236022010x y x y y -+≥⎧⎪+-≤⎨⎪+≥⎩，则z x y =+的取值范围是（）15.若点P6=所表示的曲线上的点，同时P 又是直线y=4上的点，则点P 的横坐标为（）16.已知：(1)123...2n n n +++++=；(1)(2)1223...(1)3n n n n n ++⨯+⨯+++=； (1)(2)(3)123234...(1)(2)4n n n n n n n +++⨯⨯+⨯⨯++++=， 利用上述结果，计算：3333123..._______n ++++=三.解答题：17.（本题满分10分）已知P:方程22192x y m m+=-表示焦点在x 轴上的椭圆，命题q:双曲线 2215x y m -=的离心率(2e ∈ （1）若椭圆22192x y m m +=-的焦点与双曲线2215x y m-=的顶点重合，求实数m 的值 （2）若“p 且q ”是真命题，求实数m 的取值范围18. （本题满分12分）在ABC ∆中，内角A 、B 、C 的对边分别是a,b,c,且A 、B 、C 成等差数列（1）若2b c =，求ABC ∆的面积（2）若sinA 、sinB 、sinC 成等比数列，试判断ABC ∆的形状19. （本题满分12分）本学期，学校食堂为了更好地服务广大师生员工，对师生员工的主食购买情况做了一个调查（主食只供应米饭和面条，且就餐人数保持稳定），经调查统计发现凡是购买米饭的人下一次会有20℅的人改买面条，而购买面条的人下一次会有30℅的人改买米饭。

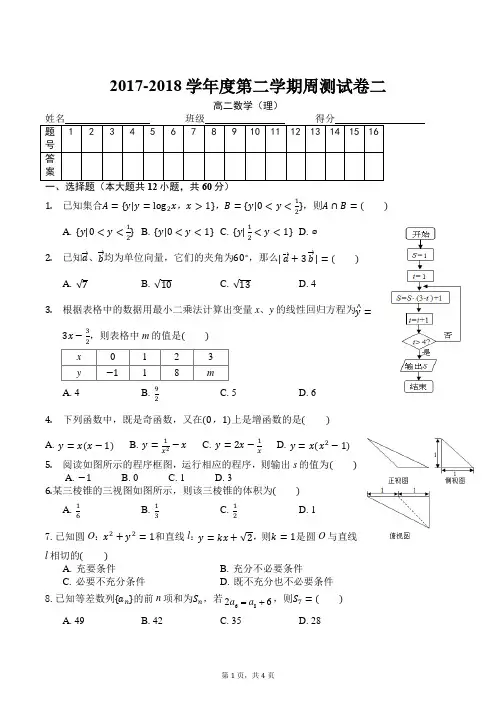
2017-2018学年度第二学期周测试卷二高二数学（理）1. 已知集合A ={y |y =log 2x ，x >1}，B ={y |0<y <12}，则A ∩B =( )A. {y |0<y <12}B. {y |0<y <1}C. {y |12<y <1}D. ⌀2. 已知a 、b 均为单位向量，它们的夹角为60∘，那么|a +3b |=( ) A. 7 B. 10 C. 13 D. 43. 根据表格中的数据用最小二乘法计算出变量x 、y 的线性回归方程为y ∧=3x −32，则表格中m 的值是( )A. 4B. 92C. 5D. 64. 下列函数中，既是奇函数，又在(0，1)上是增函数的是( )A. y =x (x −1)B. y =1x 2−xC. y =2x −1xD. y =x (x 2−1)5. 阅读如图所示的程序框图，运行相应的程序，则输出s 的值为( )A. −1B. 0C. 1D. 36.某三棱锥的三视图如图所示，则该三棱锥的体积为( )A. 16B. 13C. 12D. 17.已知圆O ：x 2+y 2=1和直线l ：y =kx + 2，则k =1是圆O 与直线l 相切的( )A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件8.已知等差数列{a n }的前n 项和为S n ，若6286+=a a ，则S 7=( ) A. 49 B. 42 C. 35 D. 289.已知m ，n 表示两条不同直线，α表示平面，下列说法正确的是( )A. 若m//α，n//α，则m//nB. 若m⊥α，n⊂α，则m⊥nC. 若m⊥α，m⊥n，则n//αD. 若m//α，m⊥n，则n⊥α10.定义行列式运算a1a2a3a4=a1a4−a2a3.将函数f(x)=sin2x3cos2x1的图象向右平移π6个单位后，所得函数图象的一个对称轴是( )A. x=7π12B. x=π2C. x=5π12D. x=π311.在区间[−1，0]上任取两实数x、y，则y<3x的概率是( )A. 16B. 13C. 23D. 5612.已知F1，F2是双曲线E：x2a −y2b=1的左、右焦点，点M在E上，MF1与x轴垂直，sin∠MF2F1=13，则E的离心率为( )A. 2B. 32C. 3D. 2二、填空题（本大题共4小题，共20分）13.如图是某赛季甲乙两名篮球运动员每场比赛得分的茎叶图，则甲乙两人比赛得分的中位数之和是______ ．14.若x，y满足约束条件x−y+1≥0x−2y≤0x+2y−2≤0，则z=x+y的最大值为______．15.已知三个数1m ，1，1n成等差数列；又三个数m2，1，n2成等比数列，则1m+n值为______．16.已知函数f(x)=log12x，x>12x，x≤1若函数g(x)=f(x)+x−3，则y=g(x)的零点个数为___．三、解答题（本大题共6小题，共70分）17.△ABC的内角A，B，C所对的边分别为a，b，c.向量m=(a，3b)与n=(cos A，sin B)平行．(Ⅰ)求A；(Ⅱ)若a=7，b=2，求△ABC的面积．18.共享单车是指企业的校园，地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务，是一种分时租赁模式，某共享单车企业为更好服务社会，随机调查了100人，统计了这100人每日平均骑行共享单车的时间(单位：分钟)，由统计数据得到如下频率分布直方图，已知骑行时间在[60，80)，[20，40)，[40，60)三组对应的人数依次成等差数列(1)求频率分布直方图中a，b的值．(2)若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”，将日平均骑行时间少于40分钟的用户为“潜力用户”，现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人，再从这5人中任取3人，求恰好1人为“忠实用户”的概率．19.如图，ABC−A1B1C1中，侧棱与底面垂直，AB⊥AC，AB=AC=AA1=2，点M，N分别为A1B和B1C1的中点．(1)证明：MN//平面A1ACC1；(2)求二面角N−MC−A的正弦值．20.已知等比数列{a n}中，a2=2，a2，a3+1，a4成等差数列；数列{b n}中的前n项和为S n，S n=n2+n．(1)求数列{a n}，{b n}的通项公式；(2)求数列{a n+4b n b n+1}的前n项和．21.在平面xOy中，已知椭圆C：x2a2+y2b2=1(a>b>0)过点P(2，1)，且离心率e=32．(1)求椭圆C的方程；(2)直线l方程为y=12x+m，直线l与椭圆C交于A，B两点，求△PAB面积的最大值．22.已知二次函数f(x)=ax2+ax−2b，其图象过点(2，−4)，且f′(1)=−3．(Ⅰ)求a，b的值；(Ⅱ)设函数ℎ(x)=x ln x+f(x)，求曲线ℎ(x)在x=1处的切线方程．。

2017-2018学年度第二学期高二年级数学（理科）期中考试试卷（卷面分值：150分，考试时间：120分钟）选择题（共17题，每小题5分，共85分）1．从A 地到B 地，可乘汽车、火车、轮船三种交通工具，如果一天内汽车发3次，火车发4次，轮船发2次，那么一天内乘坐这三种交通工具的不同走法为 ( ) A ．1＋1＋1＝3 B ．3＋4＋2＝9 C ．3×4×2＝24 D ．以上都不对 2．已知C2n ＝10，则n 的值等于 ( ) A ．10 B ．5 C ．3 D ．23．男、女学生共有8人，从男生中选取2人，从女生中选取1人，共有30种不同的选法，其中女生有 ( ) A ．2人或3人 B ．3人或4人 C ．3人 D ．4人4．若100件产品中有6件次品，现从中任取3件产品，至少有1件次品的不同取法的种数是 ( ) A ．C16C294B ．C16C299C ．C3100－C394D ．C3100－C2945已知回归直线方程y ^ ＝b ^x ＋a ^ ，其中a ^＝3且样本点中心为(1,2)，则回归直线方程为 ( )A ．y ＝x ＋3B ．y ＝－2x ＋3C ．y ＝－x ＋3D ．y ＝x －3 6．若随机变量ξ的分布列如下表所示，则p1等于( )ξ －1 2 4P15 23 P1 A.0B.215C.115D ．17．一个口袋装有2个白球和3个黑球，则先摸出1个白球后放回，再摸出1个白球的概率是 ( ) A.23B.14C.25D.158．某同学通过计算机测试的概率为13，他连续测试3次，其中恰有1次通过的概率为( )A.49B.29C.427D.2279．若随机变量ξ的分布列为ξ1P m n，其中m ∈(0,1)，则下列结果中正确的是 ( ) A ．E(ξ)＝m ，D(ξ)＝n3B ．E(ξ)＝n ，D(ξ)＝n2C ．E(ξ)＝1－m ，D(ξ)＝m －m2D ．E(ξ)＝1－m ，D(ξ)＝m210．将一颗骰子连续抛掷三次，它落地时向上的点数依次成等差数列的概率为 ( )A.19B.112C.115D.11811．某大街在甲、乙、丙三处设有红绿灯，汽车在这三处因遇绿灯而通行的概率分别为13，12，23，则汽车在这三处因遇红灯而停车一次的概率为( ) A.19 B.16 C.13D.71812．位于西部地区的A 、B 两地，据多年的资料记载：A 、B 两地一年中下雨天仅占6%和8%，而同时下雨的比例为2%，则A 地为雨天时，B 地也为雨天的概率为 ( ) A.17 B.14 C.13 D.34 13. 一人有n 把钥匙，其中只有一把可把房门打开，逐个试验钥匙，房门恰好在第k 次被打开（1≤k ≤n ）的概率是（ ）A ．1!nB ．1nC ．k nD ．1(1)!k n - 14．将一枚骰子抛掷两次，若先后出现的点数分别为b 、c ，则方程20x bx c ++=有相等实根的概率为（ ）A ．112B ．19C ．136D ．11815．12名同学合影，站成前排4人后排8人，现摄影师要从后排8人中抽2人调整到前排(这样就成为前排6人，后排6人)，若其他人的相对顺序不变，则不同调整方法的总数是( ) A ．C28A23 B ．C28A66 C ．C28A26 D ．C28A2516．设(2－x)6＝a0＋a1x ＋a2x2＋…＋a6x6，则|a1|＋|a2|＋…＋|a6|的值是( )A ．665B ．729C ．728D ．6317．将正方体ABCD —A1B1C1D1的各面涂色，任何相邻两个面不同色，现在有5个不同的颜色，并且涂好了过顶点A 的3个面的颜色，那么其余3个面的涂色方案共有（ ） A ．15种 B ．14种 C ．13种 D ．12种 填空题（共4题，每5分，共20分）18.⎝⎛⎭⎫2x －1x 6的二项展开式中的常数项为______．(用数字作答)19．已知随机变量ξ～B(5，13)，随机变量η＝2ξ－1，则E(η)＝________.20.在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用X 表示这10个村庄中交通不方便的村庄数，则P （X=4）=.（用数字表示）21．某药品研究所研制了5种消炎药a1，a2，a3，a4，a5,4种退烧药b1，b2，b3，b4，现从中取出两种消炎药和一种退烧药同时使用进行疗效实验，但又知a1，a2两种药必须同时使用，且a3，b4两种药不能同时使用，则不同的实验方案有________种． 解答题（共4题，共45分）22（11分）．从4名男同学中选出2人，6名女同学中选出3人，并将选出的5人排成一排． （1）共有多少种不同的排法？（2）若选出的2名男同学不相邻，共有多少种不同的排法？（用数字表示）23（12分）．在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖，某顾客从此10张券中任抽2张，求： （1）该顾客中奖的概率；（2）该顾客获得的奖品总价值ξ（元）的概率分布列和期望ξE .24（12分）同时抛掷两颗均匀的骰子，请回答以下问题： 求两个骰子都出现2点的概率；（2）若同时抛掷两颗骰子180次，其中甲骰子出现20次2点，乙骰子出现30次2点，问两颗骰子出现2点是否相关？（χ2＝n n11n22－n12n212n1＋n2＋n ＋1n ＋2）25．（本小题满分10分） 选修4 - 4：坐标系与参数方程在直角坐标系xOy 中，曲线C1：cos sin x t y t αα=⎧⎨=⎩（t 为参数，t ≠0），其中0≤α<π，在以O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C2：2sin ρθ=，C3：23cos ρθ=。

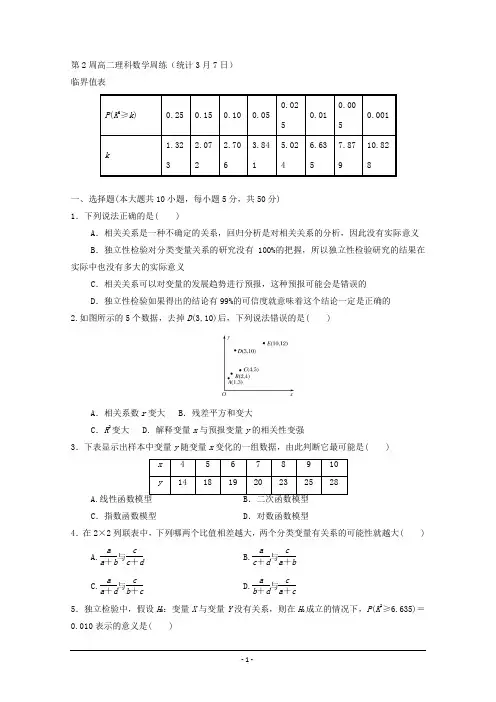
第2周高二理科数学周练（统计3月7日） 临界值表一、选择题(本大题共10小题，每小题5分，共50分) 1．下列说法正确的是( )A．相关关系是一种不确定的关系，回归分析是对相关关系的分析，因此没有实际意义 B ．独立性检验对分类变量关系的研究没有100%的把握，所以独立性检验研究的结果在实际中也没有多大的实际意义C ．相关关系可以对变量的发展趋势进行预报，这种预报可能会是错误的D ．独立性检验如果得出的结论有99%的可信度就意味着这个结论一定是正确的 2.如图所示的5个数据，去掉D (3,10)后，下列说法错误的是( )A ．相关系数r 变大B ．残差平方和变大C ．R 2变大 D ．解释变量x 与预报变量y 的相关性变强3．下表显示出样本中变量y 随变量x 变化的一组数据，由此判断它最可能是( )A.C ．指数函数模型D ．对数函数模型4．在2×2列联表中，下列哪两个比值相差越大，两个分类变量有关系的可能性就越大( )A.a a ＋b 与c c ＋d B.a c ＋d 与c a ＋b C.aa ＋d 与cb ＋cD.ab ＋d 与ca ＋c5．独立检验中，假设H 0：变量X 与变量Y 没有关系，则在H 0成立的情况下，P (K 2≥6.635)＝0.010表示的意义是( )A ．变量X 与变量Y 有关系的概率为1%B ．变量X 与变量Y 没有关系的概率为99.9%C ．变量X 与变量Y 没有关系的概率为99%D ．变量X 与变量Y 有关系的概率为99%6．为了解高中生作文成绩与课外阅读量之间的关系，某研究机构随机抽取了60名高中生，通过问卷调查，得到以下数据：( ) A ．没有充足的理由认为课外阅读量大与作文成绩优秀有关 B ．有0.5%的把握认为课外阅读量大与作文成绩优秀有关 C ．有99.9%的把握认为课外阅读量大与作文成绩优秀有关 D ．有99.5%的把握认为课外阅读量大与作文成绩优秀有关7．若对于变量y 与x 的10组统计数据的回归模型中，相关指数R 2＝0.95，又知残差平方和为120. 53，那么10i ＝1 (y i －y －)2的值为( )A ．241.06B ．2 410.6C ．253.08D ．2 530.88．若回归直线方程为y ^＝2－3.5x ，则变量x 增加一个单位，变量y 平均( )A ．减少3.5个单位B ．增加2个单位C ．增加3.5个单位D ．减少2个单位 9．为了考察两个变量x 和y 之间的线性相关性，甲、乙两个同学各自独立做了10次和15次试验，并且利用线性回归方法，求得回归直线l 1和l 2，已知在两人的试验中发现对变量x 的观测数据的平均值恰好相等，都为s ，对变量y 的观测数据的平均值也恰好相等，都为t ，那么下列说法正确的是( )A ．直线l 1和直线l 2有交点(s ，t )B ．直线l 1和直线l 2相交，但交点未必是点(s ，t )C ．直线l 1和直线l 2由于斜率相等，所以必定平行D ．直线l 1和直线l 2必定重合 10．甲、乙两个班级进行一门考试，按照学生考试成绩优秀和不优秀统计成绩后，得到如下列联表：( )A．0.3～0.4 B．0.4～0.5 C．0.5～0.6 D．0.6～0.7二、填空题(本大题共4小题，每小题5分，共20分)11．已知回归直线的斜率的估计值是 1.23，样本点的中心为(4,5)，则回归直线的方程是___________________________________________________．12．某学校对校选课程“人与自然”的选修情况进行了统计，得到如下数据：13．某数学老师身高176 cm，他爷爷、父亲和儿子的身高分别是173 cm、170 cm和182 cm.因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为__________cm.14．对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究，调查他们是否又发作过心脏病，调查结果如下表所示：____________________________________________．三、解答题(本大题共4小题，第15～17小题各12分，第18小题14分，共50分)15．某学校高三年级有学生1 000名，经调查，其中750名同学经常参加体育锻炼(称为A类同学)，另外250名同学不经常参加体育锻炼(称为B类同学)，现用分层抽样方法(按A类、B类分两层)从该年级的学生中共抽查100名同学，如果以身高达165 cm作为达标的标准，对抽取的100名学生，得到以下列联表：(1)(2)能否在犯错误的概率不超过0.05的前提下认为经常参加体育锻炼与身高达标有关系(K2的观测值精确到0.001)?17．在一段时间内，某种商品的价格x(万元)和需求量y(t)之间的一组数据如下表所示．(1)(2)求出y对x的线性回归方程；(3)如果价格定为1.9万元，预测需求量大约是多少．18．某城市一个交通路口原来只设有红绿灯，平均每年发生交通事件80起，案件的破获率为70%，为了加强该路口的管理，第二年在该路口设置了电子摄像头，该年发生交通事故70起，共破获了56起，第三年白天安排了交警执勤，该年发生交通事故60起，共破获了54起．(1)根据以上材料分析，加强管理后的两年该路口的交通状况发生了怎样的变化？(2)试采用独立性检验进行分析，设置电子摄像头对该路口交通肇事案件的破获产生了什么样的影响？设置电子摄像头和交警白天执勤的共同作用对该路口交通肇事案件的破获产生了什么样的影响？。