
最小二乘法主要用来求解两个具有线性相关关系的变量的回归方程,该方法适用于求
解与线性回归方程相关的问题,如求解回归直线方程,并应用其分析预报变量的取值等.破解此类问题的关键点如下:
①析数据,分析相关数据,求得相关系数r,或利用散点图判断两变量之间是
否存在线性相关关系,若呈非线性相关关系,则需要通过变量的变换转化构造
线性相关关系.
②建模型.根据题意确定两个变量,结合数据分析的结果建立回归模型.
③求参数.利用回归直线y=bx+a的斜率和截距的最小二乘估计公式,求出b,a,的值.从而确定线性回归方程.
④求估值.将已知的解释变量的值代入线性回归方程y=bx+a中,即可求得y
的预测值.
注意:回归直线方程的求解与应用中要注意两个方面:一是求解回归直线方程时,利用样本点的中心(x,y)必在回归直线上求解相关参数的值;二是回归直线
方程的应用,利用回归直线方程求出的数值应是一个估计值,不是真实值.
经典例题:
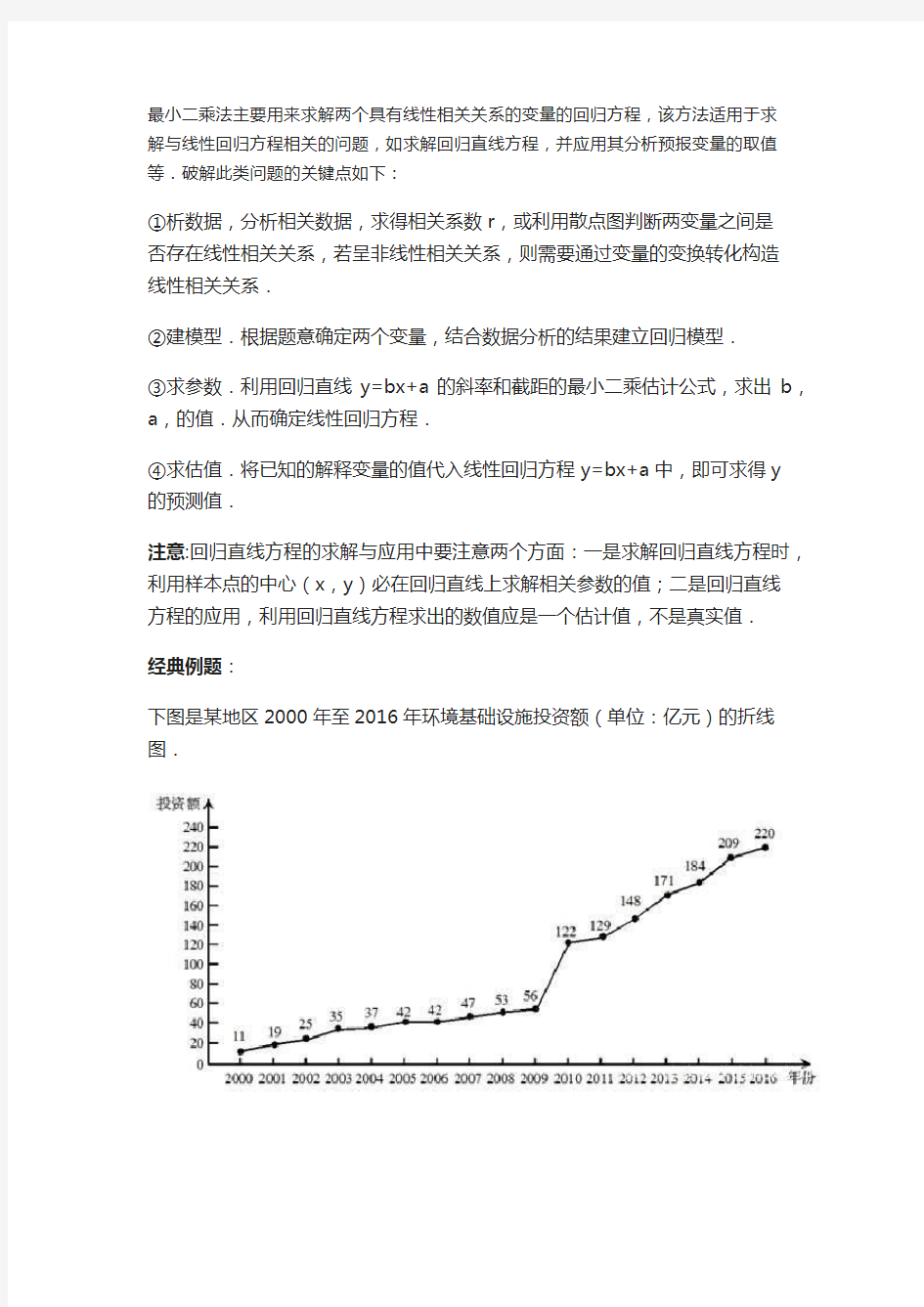
下图是某地区2000年至2016年环境基础设施投资额(单位:亿元)的折线图.
为了预测该地区2018年的环境基础设施投资额,建立了与时间变量的两个线
性回归模型.根据2000年至2016年的数据(时间变量的值依次为1,2.,……,17)建立模型①:y=-30.4+13.5t;根据2010年至2016年的数据(时间变
量的值依次为)建立模型②:y=99+17.5t.
(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
思路分析:(1)两个回归直线方程中无参数,所以分别求自变量为2018时所对应的函数值,就得结果,(2)根据折线图知2000到2009,与2010到2016是两个有明显区别的直线,且2010到2016的增幅明显高于2000到2009,也高于模型1的增幅,因此所以用模型2更能较好得到2018的预测.
解析:(1)利用模型①,该地区2018年的环境基础设施投资额的预测值为
=–30.4+13.5×19=226.1(亿元).
利用模型②,该地区2018年的环境基础设施投资额的预测值为
=99+17.5×9=256.5(亿元).
(2)利用模型②得到的预测值更可靠.理由如下:
(i)从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在
直线y=–30.4+13.5t上下,这说明利用2000年至2016年的数据建立的线性
模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性
增长趋势,利用2010年至2016年的数据建立的线性模型=99+17.5t可以较
好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得
到的预测值更可靠.
(ii)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模
型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的
增幅比较合理,说明利用模型②得到的预测值更可靠.
以上给出了2种理由,考生答出其中任意一种或其他合理理由均可得分.
总结:若已知回归直线方程,则可以直接将数值代入求得特定要求下的预测值;若回归直线方程有待定参数,则根据回归直线方程恒过中心点求参数.
线性回归方程是利用数理统计中的回归分析,来确定两种或两种以上变数间相
互依赖的定量关系的一种统计分析方法之一,线性回归也是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。按自变量个数可分为一元线性回归分析方程和多元线性回归分析方程。线性方程不难,公式会直接给出,有时会出现在选择题,这部分难度同样是在于计算,刚开始学这部分知识的时候很多同学没有耐心计算,其实很简单的列个表格算就行了
某公司要推出一种新产品,分6个相等时长的时段进行试销,并对卖出的产品进行跟踪以及收集顾客的评价情况(包括产品评价和服务评价),在试销阶段共卖出了480件,通过对所卖出产品的评价情况和销量情况进行统计,一方面发现对该产品的好评率为5/6,对服务的好评率为0.75,对产品和服务两项都没有好评有30件,另一方面发现销量和单价有一定的线性相关关系,具体数据如下表:
考点分析:
线性回归方程.
线性回归方程是高考新增内容,主要考查散点图、变量间的相关关系的判断以及线性回归方程的求法。
题干分析:
(1)由题意得到2×2列联表,由公式求出K2的观测值,对比参考表格得结论;
(2)求出样本的中心点坐标,计算回归方程的系数,写出利润函数w的解析式,求出w(x)的最大值以及对应的x的值.
解题反思:
高考对线性回归方程的考查力度逐步增加,以前只有很少题型出现,但在近几年高考试题中就很常见了,逐渐成为高考数学热点问题之一,由此可以看出这部分知识的重要性了。
3.(2017·山东卷)为了研究某班学生的脚长x (单位:厘米)和身高y (单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y 与x 之间
有线性相关关系,设其回归直线方程为y ^=b ^x +a ^.已知∑10i =1x i =225,∑10i =1y i
=1 600,b ^=4.该班某学生的脚长为24,据此估计其身高为( )
A.160
B.163
C.166
D.170
解析 由已知得x =22.5,y =160,
∵回归直线方程过样本点中心(x ,y ),且b
^=4, ∴160=4×22.5+a
^,解得a ^=70. ∴回归直线方程为y ^=4x +70,当x =24时,y ^=166.故选C.
(2)(2016·全国Ⅲ卷)如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
注:年份代码1~7分别对应年份2008~2014.
①由折线图看出,可用线性回归模型拟合y 与t 的关系,请用相关系数加以说明;
②建立y 关于t 的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量. 附注:
参考数据:∑7i =1y i =9.32,∑7i =1t i y i =40.17,∑7
i =1 (y i -y )2=0.55,7≈2.646.
回归方程y ^=a
^+b ^t 中斜率和截距的最小二乘估计公式分别为:
(2)解 ①由折线图中的数据和附注中参考数据得
t =4,∑7i =1
(t i -t )2=28,∑7i =1 (y i -y )2=0.55. ∑7
i =1 (t i -t )(y i -y )=∑7i =1t i y i -t ∑7i =1
y i =40.17-4×9.32=2.89,所以r ≈ 2.890.55×2×2.646
≈0.99. 因为y 与t 的相关系数近似为0.99,说明y 与t 的线性相关程度相当高,从而可以用线性回归模型拟合y 与t 的关系.
②由y =9.327=1.331及(1)得b ^=∑7
i =1 (t i -t )(y i -y )∑7i =1 (t i -t )2=2.8928≈0.103, a
^=y -b ^t ≈1.331-0.103×4≈0.92. 所以,y 关于t 的回归方程为y ^=0.92+0.10t .
将2016年对应的t =9代入回归方程得:y ^=0.92+0.10×9=1.82.
所以预测2016年我国生活垃圾无害化处理量约为1.82亿吨.
探究提高 1.求回归直线方程的关键及实际应用
(1)关键:正确理解计算b
^,a ^的公式和准确地计算. (2)实际应用:在分析实际中两个变量的相关关系时,可根据样本数据作出散点图来确定两个变量之间是否具有相关关系,若具有线性相关关系,则可通过线性回归方程估计和预测变量的值.
(2)(2017·唐山一模)某市春节期间7家超市的广告费支出x i (万元)和销售额y i (万元)数据如下:
②用对数回归模型拟合y 与x 的关系,可得回归方程y ^=12ln x +22,经计算得出线性回归模型和对数模型的R 2分别约为0.75和0.97,请用R 2说明选择哪个回归模型更合适,并用此模型预测A 超市广告费支出为8万元时的销售额.
参数数据及公式:x =8,y =42,∑7i =1x i y i =2 794,∑7
i =1x 2i =708,
(1)解析 ∵k ≈3.918>3.841,且P (K 2≥k 0=3.841)=0.05,根据独立性检验思想“这种血清能起到预防感冒的作用”出错的可能性不超过5%.
答案 B
(2)解 ①∵x =8,y =42,∑7i =1x i y i =2 794,∑7
i =1x 2i =708.
因此a
^=y -b ^x =42-1.7×8=28.4. 所以,y 关于x 的线性回归方程是y ^=1.7x +28.4.
②∵0.75<0.97,
∴对数回归模型更合适.
当x =8时,y ^=12ln 8+22=36ln 2+22=36×0.7+22=47.2万元.
∴广告费支出8万元时,预测A 超市销售额为47.2万元.
最小二乘法及其应用 1. 引言 最小二乘法在19世纪初发明后,很快得到欧洲一些国家的天文学家和测地学家的广泛关注。据不完全统计,自1805年至1864年的60年间,有关最小二乘法的研究论文达256篇,一些百科全书包括1837年出版的大不列颠百科全书第7版,亦收入有关方法的介绍。同时,误差的分布是“正态”的,也立刻得到天文学家的关注及大量经验的支持。如贝塞尔( F. W. Bessel, 1784—1846)对几百颗星球作了三组观测,并比较了按照正态规律在给定范围内的理论误差值和实际值,对比表明它们非常接近一致。拉普拉斯在1810年也给出了正态规律的一个新的理论推导并写入其《分析概论》中。正态分布作为一种统计模型,在19世纪极为流行,一些学者甚至把19世纪的数理统计学称为正态分布的统治时代。在其影响下,最小二乘法也脱出测量数据意义之外而发展成为一个包罗极大,应用及其广泛的统计模型。到20世纪正态小样本理论充分发展后,高斯研究成果的影响更加显著。最小二乘法不仅是19世纪最重要的统计方法,而且还可以称为数理统计学之灵魂。相关回归分析、方差分析和线性模型理论等数理统计学的几大分支都以最小二乘法为理论基础。正如美国统计学家斯蒂格勒( S. M. Stigler)所说,“最小二乘法之于数理统计学犹如微积分之于数学”。最小二乘法是参数回归的最基本得方法所以研究最小二乘法原理及其应用对于统计的学习有很重要的意义。 2. 最小二乘法 所谓最小二乘法就是:选择参数10,b b ,使得全部观测的残差平方和最小. 用数学公式表示为: 21022)()(m in i i i i i x b b Y Y Y e --=-=∑∑∑∧ 为了说明这个方法,先解释一下最小二乘原理,以一元线性回归方程为例. i i i x B B Y μ++=10 (一元线性回归方程)
平均值、标准差、相关系数、回归线及最小二乘法相关性 线性相关 数据在一条直线附近波动,则变量间是线性相关 非线性相关 数据在一条曲线附近波动,则变量间是非线性相关 不相关 数据在图中没有显示任何关系,则不相关 平均值 N个数据的平均值计算公式: 标准差 标准差表示了所有数据与平均值的平均距离,表示了数据的散度,如果标准差小,表示数据集中在平均值附近,如果标准差大则表示数据离标准差比较远,比较分散。标准差计算公式: x、y两个变量组成了笛卡尔坐标系中的一 坐标(x,y),这个坐标标识了一个点的位置。 个 各包含n个常量的X,Y两组数据在笛卡尔坐标系中以n个点来进行表示。 相关系数 相关系数用字母r来表示,表示两组数据线性相关的程度(同时增大或减小的程度),从另一方面度量了点相对于标准差的散布情况,它没有单位。包含n个数值的X、Y两组数据的相关系数r的计算方法: 简单的说,就是r=[(以标准单位表示的x )X(以标准单位表示的y )]的平均数 根据上面点的定义,将X、Y两组数据的关系以点的形式在笛卡尔坐标系中画出,SD线表示了经过中心点(以数据组X、Y平均值为坐标的点),当r>0时,斜率=X的标准
差/Y的标准差;当r<0时,斜率=-X的标准差/Y的标准差;的直线。通常用SD线来直观的表示数据的走向: 1、当r<0时,SD线的斜率小于0时,则说明数据负相关,即当x增大时y减少。 2、当r>0时,SD线的斜率大于0时,则说明数据正相关,此时当x增大时y增大。 3、相关系数r的范围在[-1,1]之间,当r=0时表示数据相关系数为0(不相关)。当r=正负1时,表示数据负相关,此(x,y)点数据都在SD线上。 4、r的值越接近正负1说明(x,y)越靠拢SD线,说明数据相关性越强,r的值越接近0说明(x,y)点到SD线的散度越大(越分散),数据相关性越小。 回归方法主要描述一个变量如何依赖于另一个变量。y对应于x的回归线描述了在不同的x值下y的平均值情况,它是这些平均值的光滑形式,如果这些平均值刚好在一条直线上,则这些平均值刚好和回归线重合。通过回归线,我们可以通过x值来预测y值(已知x值下y值的平均值)。下面是y对应于x的回归线方程: 简单的说,就是当x每增加1个SD,平均而言,相应的y增加r个SD。 从方程可以看出: 1、回归线是一条经过点,斜率为的直线。 2、回归线的斜率比SD线小,当r=1或-1时,回归线和SD线重合。 当用回归线从x预测y时,实际值与预测值之间的差异叫预测误差。而均方根误差就是预测误差的均方根。它度量回归预测的精确程度。y关于x的回归线的均方根误差用下面的公式进行计算: 由公式可以看出,当r越接近1或-1时,点越聚集在回归线附近,均方根误差越小; 反之r越接近0时,点越分散,均方根误差越大。 最小二乘法寻找一条直线来拟合所有的点,使得这条直线到所有的点之间的均方根误差最小。可以看到,当求两个变量之间的关系时,最小二乘法求出的直线实际上就是回归线。只不过表述的侧重点不同:
数学必修3测试题 说明:全卷满分100分,考试时间120分钟,交卷时只需交答题卷,考试时不能使用计算器. 参考:用最小二乘法求线性回归方程系数公式x b y a x n x y x n y x b n i i n i i i -=-?-= ∑∑==, 1 2 21 一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四处备选项中,只有一项是符合 题目要求的. 1 ”可用于( ) A 、输出a=10 a=10 C 、判断a=10 D 、输入a=10 2、已知甲、乙两名同学在五次数学测验中的得分如下:甲:85,91,90,89,95; 乙:95,80,98,82,95。则甲、乙两名同学数学学习成绩( ) A 、甲比乙稳定 B 、甲、乙稳定程度相同 C 、乙比甲稳定 D 、无法确定 3、下列程序语句不正确... 的是( ) A 、INPUT “MA TH=”;a+b+c B 、PRINT “MA TH=”;a+b+c C 、c b a += D 、1a =c b - 4、 在调查分析某班级数学成绩与 物理成绩的相关关系时,对数据进行 统计分析得到散点图(如右图所示), 用回归直线?y bx a =+近似刻画 其关系,根据图形,b 的数值最有 可能是( ) A 、 0 B 、 1.55 C 、 0.85 D 、 —0.24 5、用秦九韶算法求n 次多项式011 1)(a x a x a x a x f n n n n ++++=-- ,当0x x =时,求)(0x f 需要算 乘方、乘法、加法的次数分别为( ) A 、 n n n n ,,2 ) 1(+ B 、n,2n,n C 、 0,2n,n D 、 0,n,n 6、为了在运行下面的程序之后得到输出16,键盘输入x 应该是( ) INPUT x IF x<0 THEN y=(x+1)*(x+1) ELSE y=(x-1)*(x-1) END IF 第4题
最小二乘法主要用来求解两个具有线性相关关系的变量的回归方程,该方法适用于求解与线性回归方程相关的问题,如求解回归直线方程,并应用其分析预报变量的取值等.破解此类问题的关键点如下: ①析数据,分析相关数据,求得相关系数r,或利用散点图判断两变量之间是否存在线性相关关系,若呈非线性相关关系,则需要通过变量的变换转化构造线性相关关系. ②建模型.根据题意确定两个变量,结合数据分析的结果建立回归模型. ③求参数.利用回归直线y=bx+a的斜率和截距的最小二乘估计公式,求出b,a,的值.从而确定线性回归方程. ④求估值.将已知的解释变量的值代入线性回归方程y=bx+a中,即可求得y的预测值. 注意:回归直线方程的求解与应用中要注意两个方面:一是求解回归直线方程时,利用样本点的中心(x,y)必在回归直线上求解相关参数的值;二是回归直线方程的应用,利用回归直线方程求出的数值应是一个估计值,不是真实值. 经典例题: 下图是某地区2000年至2016年环境基础设施投资额(单位:亿元)的折线图.
为了预测该地区2018年的环境基础设施投资额,建立了与时间变量的两个线性回归模型.根据2000年至2016年的数据(时间变量的值依次为1,2.,……,17)建立模型①:y=+;根据2010年至2016年的数据(时间变量的值依次为)建立模型②:y=99+. (1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值; (2)你认为用哪个模型得到的预测值更可靠并说明理由. 思路分析:(1)两个回归直线方程中无参数,所以分别求自变量为2018时所对应的函数值,就得结果,(2)根据折线图知2000到2009,与2010到2016是两个有明显区别的直线,且2010到2016的增幅明显高于2000到2009,也高于模型1的增幅,因此所以用模型2更能较好得到2018的预测. 解析:(1)利用模型①,该地区2018年的环境基础设施投资额的预测值为 =–+×19=(亿元). 利用模型②,该地区2018年的环境基础设施投资额的预测值为 =99+×9=(亿元). (2)利用模型②得到的预测值更可靠.理由如下: (i)从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y=–+上下,这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利
多元线性回归与最小二乘估计 1.假定条件、最小二乘估计量和高斯—马尔可夫定理 多元线性回归模型: y t = β0 +β1x t 1 +β2x t 2 +…+βk - 1x t k -1 + u t (1.1) 其中y t 是被解释变量(因变量),x t j 是解释变量(自变量),u t 是随机误差项,βi , i = 0, 1, … , k - 1是回归参数(通常未知)。 对经济问题的实际意义:y t 与x t j 存在线性关系,x t j , j = 0, 1, … , k - 1, 是y t 的重要 解释变量。u t 代表众多影响y t 变化的微小因素。使y t 的变化偏离了E( y t ) =多元线性回归与最小二乘估计 1.假定条件、最小二乘估计量和高斯—马尔可夫定理 多元线性回归模型: y t = β0 +β1x t 1 +β2x t 2 +…+βk - 1x t k -1 + u t (1.1) 其中y t 是被解释变量(因变量),x t j 是解释变量(自变量),u t 是随机误差项,βi , i = 0, 1, … , k - 1是回归参数(通常未知)。 对经济问题的实际意义:y t 与x t j 存在线性关系,x t j , j = 0, 1, … , k - 1, 是y t 的重要解释变量。u t 代表众多影响y t 变化的微小因素。使y t 的变化偏离了E( y t ) =β0 +β1x t 1 +β2x t 2 +…+βk - 1x t k -1决定的k 维空间平面。 当给定一个样本(y t , x t 1, x t 2 ,…, x t k -1), t = 1, 2, …, T 时, 上述模型表示为 y 1 =β0 +β1x 11 +β2x 12 +…+βk - 1x 1 k -1 + u 1, 经济意义:x t j 是y t 的重要解释变量。 y 2 =β0 +β1x 21 +β2x 22 +…+βk - 1x 2 k -1 + u 2, 代数意义:y t 与x t j 存在线性关系。 ……….. 几何意义:y t 表示一个多维平面。 y T =β0 +β1x T 1 +β2x T 2 +…+βk - 1x T k -1 + u T , (1.2) 此时y t 与x t i 已知,βj 与 u t 未知。 j k j k T Tj T k T k T (T ) (k )(T (T k ) x x x y u x x x y u x x x y u b b b ----创?′骣骣骣骣÷ 鼢??珑?÷鼢??珑?÷鼢??珑?÷鼢??珑?÷鼢??珑?÷鼢?=+?÷珑?鼢??÷珑?鼢?÷?鼢?珑?÷鼢??珑?÷ 鼢??珑?÷鼢?珑??桫桫桫桫 11 11110 1212212121 1111111L L L L L L L L L L M M M L L ) 1 (1.3) Y = X β+ u , (1.4) 为保证得到最优估计量,回归模型(1.4)应满足如下假定条件。 假定 ⑴ 随机误差项u t 是非自相关的,每一误差项都满足均值为零,方差 2 相同且为有限值,即 E(u ) = 0 = 骣÷?÷?÷?÷?÷?÷?÷÷?桫 00M , Var (u ) = E(u ?u ?' ) =σ2I = σ2骣÷ ?÷?÷?÷?÷?÷?÷÷ ?桫10000001O .
曲线拟合(curve-fitting ):工程实践中,用测量到的一些离散的数据},...2,1,0),,{(m i y x i i =求一个近似的函数)(x ?来拟合这组数据,要求所得的拟合曲线能最好的反映数据的基本趋势(即使)(x ?最好地逼近()x f ,而不必满足插值原则。因此没必要取)(i x ?=i y ,只要使i i i y x -=)(?δ尽可能地小)。 原理: 给定数据点},...2,1,0),,{(m i y x i i =。求近似曲线)(x ?。并且使得近似曲线与()x f 的偏差最小。近似曲线在该点处的偏差i i i y x -=)(?δ,i=1,2,...,m 。 常见的曲线拟合方法: 1.使偏差绝对值之和最小 2.使偏差绝对值最大的最小 3.使偏差平方和最小 最小二乘法: 按偏差平方和最小的原则选取拟合曲线,并且采取二项式方程为拟合曲线的方法,称为最小二乘法。 推导过程: 1. 设拟合多项式为: 2. 各点到这条曲线的距离之和,即偏差平方和如下: 3. 问题转化为求待定系数0a ...k a 对等式右边求i a 偏导数,因而我们得到 了: ....... 4、 把这些等式化简并表示成矩阵的形式,就可以得到下面的矩阵: 5. 将这个范德蒙得矩阵化简后可得到:
6. 也就是说X*A=Y,那么A = (X'*X)-1*X'*Y,便得到了系数矩阵A,同时,我们也就得到了拟合曲线。 MATLAB实现: MATLAB提供了polyfit()函数命令进行最小二乘曲线拟合。 调用格式:p=polyfit(x,y,n) [p,s]= polyfit(x,y,n) [p,s,mu]=polyfit(x,y,n) x,y为数据点,n为多项式阶数,返回p为幂次从高到低的多项式系数向量p。x必须是单调的。矩阵s包括R(对x进行QR分解的三角元素)、df(自由度)、normr(残差)用于生成预测值的误差估计。 [p,s,mu]=polyfit(x,y,n)在拟合过程中,首先对x进行数据标准化处理,以在拟合中消除量纲等影响,mu包含标准化处理过程中使用的x的均值和标准差。 polyval( )为多项式曲线求值函数,调用格式: y=polyval(p,x) [y,DELTA]=polyval(p,x,s) y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值。 [y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计Y DELTA。它假设polyfit函数数据输入的误差是独立正态的,并且方差为常数。则Y DELTA将至少包含50%的预测值。 如下给定数据的拟合曲线: x=[,,,,,], y=[,,,,,]。 解:MATLAB程序如下: x=[,,,,,]; y=[,,,,,]; p=polyfit(x,y,2) x1=::; y1=polyval(p,x1); plot(x,y,'*r',x1,y1,'-b') 运行结果如图1 计算结果为: p = 即所得多项式为y=^2++ 图1 最小二乘法曲线拟合示例 对比检验拟合的有效性: 例:在[0,π]区间上对正弦函数进行拟合,然后在[0,2π]区间画出图形,比较拟合区间和非拟合区间的图形,考察拟合的有效性。 在MATLAB中输入如下代码: clear x=0::pi; y=sin(x); [p,mu]=polyfit(x,y,9)
偏最小二乘回归方法 1 偏最小二乘回归方法(PLS)背景介绍 在经济管理、教育学、农业、社会科学、工程技术、医学和生物学中,多元线性回归分析是一种普遍应用的统计分析与预测技术。多元线性回归中,一般采用最小二乘方法(Ordinary Least Squares :OLS)估计回归系数,以使残差平方和达到最小,但当自变量之间存在多重相关性时,最小二乘估计方法往往失效。而这种变量之间多重相关性问题在多元线性回归分析中危害非常严重,但又普遍存在。为消除这种影响,常采用主成分分析(principal Components Analysis :PCA)的方法,但采用主成分分析提取的主成分,虽然能较好地概括自变量系统中的信息,却带进了许多无用的噪声,从而对因变量缺乏解释能力。 最小偏二乘回归方法(Partial Least Squares Regression :PLS)就是应这种实际需要而产生和发展的一种有广泛适用性的多元统计分析方法。它于1983年由S.Wold 和 C.Albano 等人首次提出并成功地应用在化学领域。近十年来,偏最小二乘回归方法在理论、方法和应用方面都得到了迅速的发展,己经广泛地应用在许多领域,如生物信息学、机器学习和文本分类等领域。 偏最小二乘回归方法主要的研究焦点是多因变量对多自变量的回归建模,它与普通多元回归方法在思路上的主要区别是它在回归建模过程中采用了信息综合与筛选技术。它不再是直接考虑因变量集合与自变量集合的回归建模,而是在变量系统中提取若干对系统具有最佳解释能力的新综合变量(又称成分),然后对它们进行回归建模。偏最小二乘回归可以将建模类型的预测分析方法与非模型式的数据内涵分析方法有机地结合起来,可以同时实现回归建模、数据结构简化(主成分分析)以及两组变量间的相关性分析(典型性关分析),即集多元线 性回归分析、典型相关分析和主成分分析的基本功能为一体。下面将简单地叙述偏最小二乘 回归的基本原理。 2 偏最小二乘法的工作目标 2.1 偏最小二乘法的工作目标 在一般的多元线性回归模型中,如果有一组因变量Y={y 1, ?,y q} 和一组自变量 X={x 1, ?,x p} ,当数据总体能够满足高斯—马尔科夫假设条件时,根据最小二乘法,有 Y =X(X T X)-1X T Y Y 将是Y 的一个很好的估计量。从这个公式容易看出,由于(X T X)必须是可逆矩阵,所以
回归系数的最小二乘法 现在我们用最小二乘法来估计模型中的未知参数0β和1β.假设有n 组独立观测值:)()()( 1122,,,,...,,n n x y x y x y (例1中的n=16),则由(2)有 01,1,2,...,i i i y x i n ββε=++= ()21,2,n,n 2 2 0101=1 =1 0,...==(--)i i n i i i i i E D Q Q y x εεσεεεββεββ===∑∑且,,,相互独立记 , 称()01,Q ββ为偏离真实直线的偏差平方和。最小二乘法就是10ββ和的估计 ^ ^ ,01ββ,使得()01 ^^ 0,1,,=min 01Q Q ββββββ?? ??? 为此,将上式分别对01ββ、求偏导数,得n 01=10 n 01=11-2(--)=-2(--) i i i i i i Q y x Q y x ββββββ??=?????????∑∑令上式^^ 0101,,ββββ取代,得 n ^^0=1 ^^ 01=1 (y --)=0(y --)=0i i i i n i i i i x x x ββββ???????∑∑于是有 ^^0111 ^^2011 11n n i i i i n n n i i i i i i i n x y x x x y βββ β=====?+=????+=??∑∑∑∑∑此方程组称为正规方程。 由正规方程解得^ ^0 1^122y x xy x y x x βββ-- ?=-???-=??-? 或^ 1 12 1 ()() () n i i i n i i x x y y x x β==--= -∑∑ 其中2 21111 1111,,,n n n n i i i i i i i i i x x y y x x xy x y n n n n ========∑∑∑∑