山东省华侨中学高一数学寒假作业11 Word版 含答案

2023年高一数学寒假作业答案新的学期即将来临，在剩下的美好的寒假时光，我们要认真完成自己的寒假作业，那么高一数学寒假作业答案有哪些呢下面是小编给大家整理的2023年高一数学寒假作业答案，欢迎大家来阅读。

高一数学寒假作业答案一、1~5 CABCB6~10 CBBCC11~12 BB二、13 ,14 (1) ;(2){1，2，3} N; (3){1} ;(4)0 ;15 -116.略。

三、17 .{0.-1,1};18.略;19. (1) a2-4b=0 (2) a=-4, b=320.略.p2一.1~5 C D B B D6~10 C C C C A11~12 B B二. 13. (1，+∞) 14.13 15 16,三.17.略18、略。

19.解：⑴ 略。

⑵略。

20.略。

p3一、选择题：1.B2.C3.C4.A5.C6.A7.A8.D9.A 10.B 11.B 12.C二、填空题：13. 14. 12 15. ; 16.4-a，三、解答题：17.略18.略19.解：(1)开口向下;对称轴为 ;顶点坐标为 ;(2)函数的值为1;无最小值;(3)函数在上是增加的，在上是减少的。

20.Ⅰ、Ⅱ、p4一、1～8 C B C D A A C C 9-12 B B C D二、13、[—，1] 14、 15、 16、x 2或0三、17、(1)如图所示：(2)单调区间为， .(3)由图象可知：当时，函数取到最小值18.(1)函数的定义域为(—1，1)(2)当a 1时，x (0,1) 当019. 略。

p5一、1～8 C D B D A D B B9～12 B B C D13. 19/6 14. 15. 16.17.略。

20. 解：p7一、选择题：1.D2. C3.D4.C5.A6.C7.D8. A9.C 10.A 11.D 1.B二、填空题13.(-2，8)，(4，1) 14.[-1,1] 15.(0，2/3)∪(1，+∞) 16.[0.5,1)17.略 18.略19.略。

寒假作业（十二）一、选择题：1.甲，乙两人随意入住两间空房，则甲乙两人各住一间房的概率是（ ）A.31B. 41C. 21 D.无法确定 2.掷一枚骰子，则掷得奇数点的概率是（ ）A.61 B. 21 C. `31 D. 41 3. 抛掷一枚质地均匀的硬币，如果连续抛掷1000次，那么第999次出现正面朝上的概率是（ ）A.9991 B. 10001 C. 1000999D. 214. 【选做】从一批产品中取出三件产品，设A=“三件产品全不是次品”，B=“三件产品全是次品”，C=“三件产品不全是次品”，则下列结论正确的是（ ）A. A 与C 互斥B. B 与C 互斥C. 任何两个均互斥D. 任何两个均不互斥二、填空题5. 某班委会由4名男生与3名女生组成，现从中选出2人担任正副班长，其中至少有1名女生当选的概率是______________6.【选做】我国西部一个地区的年降水量在下列区间内的概率如下表所示：则年降水量在 [ 200，300 ] （m,m ）范围内的概率是___________三、解答题7.10本不同的语文书，2本不同的数学书，从中任意取出2本，能取出数学书的概率有多大？寒假作业(十二)答案:1.C2.B3.D4.C5.756. 0.257. 解：基本事件的总数为：12×11÷2＝66“能取出数学书”这个事件所包含的基本事件个数分两种情况： （1） “恰好取出1本数学书”所包含的基本事件个数为： 10×2＝20（2）“取出2本都是数学书”所包含的基本事件个数为：1 所以 “能取出数学书”这个事件所包含的基本事件个数为：20＋1＝21因此, P （“能取出数学书”）＝227。

高一数学寒假作业（1）一、 选择题，每小题只有一项是正确的。

1.下列关系中正确的个数为（ ）； ①R ∈21 ②Q ∉2 ③*|3|N ∉- ④Q ∈-|3|A ．1 个B ．2 个C ．3 个D ．4 个2.设集合A={x |-1≤x ≤2}，B={x |0≤x ≤4}，则A ∩B=( )A ．[0,2]B ．[1,2]C ．[0,4]D ．[1,4]3.已知312.01.0)2(,)22(,2.1-===c b a ，则c b a ,,的大小关系是（ ） A.c b a >> B ．c a b >> C.a c b >> D ．b a c >>4.对于任意实数a ，下列等式一定成立的是（ ）A ．a a =33B ． a a -=33C ．a a =44D ．a a -=445.下列各组函数中，表示同一函数的是 （ ）A ．xxy y ==,1 B ．y y ==C ．21,11x y y x x -==+- D ． ||,y x y == 6.已知()f x 是R 上的奇函数，且当(],0x ∈-∞时，()lg(3)f x x x =--，那么(1)f 的值为（ ）A ．0B ．lg 3C ．lg 3-D ．lg 4-7.若函数()y f x =是函数()1x y a a a =>≠0，且的反函数，且()42f =-，则()f x =（ ）A ．x 21B ．x 21logC ．x 2logD ．2x8.下列函数中既是偶函数，又在区间（0，1）上是减函数的是A ．||y x =B ．2y x =-C ．x x y e e -=+D ．cos y x =9.若定义运算错误!未找到引用源。

，则函数错误!未找到引用源。

的值域是（ ）A ．[1，+∞）B ．（0，+∞）C ．（－∞，+∞）D ．（0，1]二、填空题10.A ＝{1，2}，B ＝{2，3}，则A ∪B ＝ ______________．11.集合{}{}1,062-==<--=x y x B x x x A ，则A B ⋂=_____________12.已知上有两个不同的零点，则m 的取值范围是________．13.给出下列四个命题：①函数1y x=-在R 上单调递增；②若函数221y x ax =++在(,1]-∞-上单调递减，则1a ≤;③若0.70.7log (2)log (1)m m <-，则1m >-；④若()f x 是定义在R 上的奇函数，则(1)(1)0f x f x -+-=. 其中正确的序号是 .三、计算题14.（12分） 集合A ＝｛x ｜x 2－ax ＋a 2－19＝0｝，B ＝｛x ｜x 2－5x ＋6＝0｝，C ＝｛x ｜x 2＋2x －8＝0｝．（Ⅰ）若A ∩B ＝A ∪B ，求a 的值；（Ⅱ）若∅A ∩B ，A ∩C ＝∅，求a 的值．15. 已知函数22()log (1)log (1)f x x x =--+（1）求函数()f x 的定义域；（2）求1111()()()()2014201520142015f f f f ++-+-的值. 16.已知函数()f x 是定义在()0,+∞上的函数，且对于任意的实数,x y 有()()()f xy f x f y =+，当1x >时，()0f x >.（1）求证：()f x 在()0,+∞上是增函数（2）若(2)1f =，对任意的实数t ，不等式22(1)(1)2f t f t kt +--+≤恒成立，求实数k 的取值范围。

寒假是同学们所期待的，在寒假不能光顾着玩，因为要按时完成布置的寒假作业，遇到不会做的题目可以借鉴答案，那么寒假作业答案你知道吗下面为大家收集整理了“2021高一数学寒假作业答案最新”，欢迎阅读与借鉴!高一数学寒假作业答案1参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12答案 D D D A D D B C A C B C1 ; 1 4 ; 1 0.4; 1 ②③1(1)∵A中有两个元素，∴关于的方程有两个不等的实数根，∴，且，即所求的范围是，且;……6分(2)当时，方程为，∴集合A=;当时，若关于的方程有两个相等的实数根，则A也只有一个元素，此时 ;若关于的方程没有实数根，则A没有元素，此时，综合知此时所求的范围是，或.………13分18 解(1) ，得(2) ，得此时，所以方向相反1解:⑴由题义整理得 ,解方程得即的不动点为-1和…………6分⑵由=得如此方程有两解,则有△=把看作是关于的二次函数,则有解得即为所求. …………12分20.解(1)常数m=1…………………4分(2)当k<0时，直线y=k与函数的图象无交点,即方程无解; 当k=0或k 1时, 直线y=k与函数的图象有唯一的交点，所以方程有一解;当0所以方程有两解.…………………12分2解(1)设，有， 2取，则有是奇函数 4(2)设，则，由条件得在R上是减函数，在[-3，3]上也是减函数。

6当x=-3时有最大值 ;当x=3时有最小值，由，，当x=-3时有最大值6;当x=3时有最小值- 8(3)由，是奇函数原不等式就是 10由(2)知在[-2，2]上是减函数原不等式的解集是 122解(1)由数据表知，(3)由于船的吃水深度为7米，船底与海底的距离不少于5米，故在船航行时水深米，令，得 .解得 .取，则 ;取，则 .故该船在1点到5点，或13点到17点能安全进出港口，而船舶要在一天之内在港口停留时间最长，就应从凌晨1点进港，下午17点离港，在港内停留的时间最长为16小时.高一数学寒假作业答案2对数函数及其性质一(设a=log54，b=(log53)2，c=log45，则()A.aC.a解析选D.a=log54<1，log531，故b已知f(x)=loga|x-1|在(0,1)上递减，那么f(x)在(1，+∞)上()A.递增无值B.递减无最小值C.递增有值D.递减有最小值解析选A.设y=logau，u=|x-1|.x∈(0,1)时，u=|x-1|为减函数，∴a>∴x∈(1，+∞)时，u=x-1为增函数，无值.∴f(x)=loga(x-1)为增函数，无值.已知函数f(x)=ax+logax(a>0且a≠1)在[1,2]上的值与最小值之和为loga2+6，则a的值为()A.12B.14C.2D.4解析选C.由题可知函数f(x)=ax+logax在[1,2]上是单调函数，所以其值与最小值之和为f(1)+f(2)=a+loga1+a2+loga2=loga2+6，整理可得a2+a-6=0，解得a=2或a=-3(舍去)，故a=函数y=log13(-x2+4x+12)的单调递减区间是________.解析y=log13u，u=-x2+4x+1令u=-x2+4x+12>0，得-2∴x∈(-2,2]时，u=-x2+4x+12为增函数，∴y=log13(-x2+4x+12)为减函数.答案(-2,2]对数函数及其性质二若loga2<1，则实数a的取值范围是()A.(1,2)B.(0,1)∪(2，+∞)C.(0,1)∪(1,2)D.(0，12)解析选B.当a>1时，loga22;当0若loga2A.0C.a>b>1D.b>a>1解析选B.∵loga2∴0已知函数f(x)=2log12x的值域为[-1,1]，则函数f(x)的定义域是()A.[22，2]B.[-1,1]C.[12，2]D.(-∞，22]∪[2，+∞)解析选A.函数f(x)=2log12x在(0，+∞)上为减函数，则-1≤2log12x≤1，可得-12≤log12x≤12，X k b 1 . co m解得22≤x≤若函数f(x)=ax+loga(x+1)在[0,1]上的值和最小值之和为a，则a的值为()A.14B.12C.2D.4解析选B.当a>1时，a+loga2+1=a，loga2=-1，a=12，与a>1矛盾;当0loga2=-1，a=1函数f(x)=loga[(a-1)x+1]在定义域上()A.是增函数B.是减函数C.先增后减D.先减后增解析选A.当a>1时，y=logat为增函数，t=(a-1)x+1为增函数，∴f(x)=loga[(a-1)x+1]为增函数;当0∴f(x)=loga[(a-1)x+1]为增函数.对数函数及其性质三(2009年高考全国卷Ⅱ)设a=lge，b=(lg e)2，c=lg e，则()A.a>b>cB.a>c>bC.c>a>bD.c>b>a解析选B.∵ 1∴0∵0又c-b=12lg e-(lg e)2=12lg e(1-2lg e)=12lg elg10e2>0，∴c>b，故选B.已知0解析∵00.又∵0答案3f(x)=log21+xa-x的图象关于原点对称，则实数a的值为________.解析由图象关于原点对称可知函数为奇函数，所以f(-x)+f(x)=0，即log21-xa+x+log21+xa-x=0log21-x2a2-x2=0=log21，所以1-x2a2-x2=1a=1(负根舍去).答案1函数y=logax在[2，+∞)上恒有|y|>1，则a取值范围是________.解析若a>1，x∈[2，+∞)，|y|=logax≥loga2，即loga2>1，∴11，∴a>12，∴12答案12已知f(x)=(6-a)x-4a(x<1)logax (x≥1)是R上的增函数，求a的取值范围.解f(x)是R上的增函数，则当x≥1时，y=logax是增函数，∴a>又当x<1时，函数y=(6-a)x-4a是增函数.∴6-a>0，∴a<又(6-a)×1-4a≤loga1，得a≥6∴65≤a<综上所述，65≤a<解下列不等式.(1)log2(2x+3)>log2(5x-6);(2)logx12>解(1)原不等式等价于2x+3>05x-6>02x+3>5x-6，解得65所以原不等式的解集为(65，3).(2)∵logx12>1log212log2x>11+1log2x<0log2x+1log2x<0-12-1012∴原不等式的解集为(12，1).高一数学寒假作业答案3指数与指数幂的运算一将532写为根式，则正确的是()A.352B.35C.532D.53解析选D.532=5根式 1a1a(式中a>0)的分数指数幂形式为() A.a-43 B.a43C.a-34D.a34解析选C.1a1a=a-1(a-1)12=a-32=(a-32)12=a-3 (a-b)2+5(a-b)5的值是()A.0B.2(a-b)C.0或2(a-b)D.a-b解析选C.当a-b≥0时，原式=a-b+a-b=2(a-b);当a-b<0时，原式=b-a+a-b=0.计算(π)0+2-2×(214)12=________.解析(π)0+2-2×(214)12=1+122×(94)12=1+14×32=11 答案118对数与对数运算训练二logab=1成立的条件是()A.a=bB.a=b，且b>0C.a>0，且a≠1D.a>0，a=b≠1解析选D.a>0且a≠1，b>0，a1=b.若loga7b=c，则a、b、c之间满足()A.b7=acB.b=a7cC.b=7acD.b=c7a解析选B.loga7b=cac=7b，∴b=a7c.如果f(ex)=x，则f(e)=()A.1B.eeC.2eD.0解析选A.令ex=t(t>0)，则x=lnt，∴f(t)=lnt.∴f(e)=lne=方程2log3x=14的解是()A.x=19B.x=x3C.x=3D.x=9解析选A.2log3x=2-2，∴log3x=-2，∴x=3-2=1对数与对数运算训练三q.若log2(log3x)=log3(log4y)=log4(log2z)=0，则x+y+z的值为()A.9B.8C.7D.6解析选A.∵log2(log3x)=0，∴log3x=1，∴x=同理y=4，z=∴x+y+z=已知logax=2，logbx=1，logcx=4(a，b，c，x>0且≠1)，则logx(abc)=() A.47 B.27C.72D.74解析选D.x=a2=b=c4，所以(abc)4=x7，所以abc=x7即logx(abc)=7若a>0，a2=49，则log23a=________.解析由a>0，a2=(23)2，可知a=23，∴log23a=log2323=答案1若lg(lnx)=0，则x=________.解析lnx=1，x=e.答案e高一数学寒假作业答案4一、选择题已知f(x)=x-1x+1，则f(2)=()A.1B.12C.13D.14【解析】f(2)=2-12+1=1X【答案】C下列各组函数中，表示同一个函数的是()A.y=x-1和y=x2-1x+1B.y=x0和y=1C.y=x2和y=(x+1)2D.f(x)=(x)2x和g(x)=x(x)2【解析】A中y=x-1定义域为R，而y=x2-1x+1定义域为{x|x≠1};B中函数y=x0定义域{x|x≠0}，而y=1定义域为R;C中两函数的解析式不同;D中f(x)与g(x)定义域都为(0，+∞)，化简后f(x)=1，g(x)=1，所以是同一个函数.【答案】D用固定的速度向如图2-2-1所示形状的瓶子中注水，则水面的高度h和时间t之间的关系是()图2-2-1【解析】水面的高度h随时间t的增加而增加，而且增加的速度越来越快.【答案】B函数f(x)=x-1x-2的定义域为()A.[1,2)∪(2，+∞)B.(1，+∞)C.[1,2]D.[1，+∞)【解析】要使函数有意义，需x-1≥0，x-2≠0，解得x≥1且x≠2，所以函数的定义域是{x|x≥1且x≠2}.【答案】A函数f(x)=1x2+1(x∈R)的值域是()A.(0,1)B.(0,1]C.[0,1)D.[0,1]【解析】由于x∈R，所以x2+1≥1,0<1x2+1≤1，即0【答案】B二、填空题集合{x|-1≤x<0或1【解析】结合区间的定义知，用区间表示为[-1,0)∪(1,2].【答案】[-1,0)∪(1,2]函数y=31-x-1的定义域为________.【解析】要使函数有意义，自变量x须满足x-1≥01-x-1≠0解得x≥1且x≠∴函数的定义域为[1,2)∪(2，+∞).【答案】[1,2)∪(2，+∞)设函数f(x)=41-x，若f(a)=2，则实数a=________. 【解析】由f(a)=2，得41-a=2，解得a=-【答案】-1三、解答题已知函数f(x)=x+1x，求(1)函数f(x)的定义域;(2)f(4)的值.【解】(1)由x≥0，x≠0，得x>0，所以函数f(x)的定义域为(0，+∞).(2)f(4)=4+14=2+14=910.求下列函数的定义域(1)y=-x2x2-3x-2;(2)y=34x+83x-【解】(1)要使y=-x2x2-3x-2有意义，则必须-x≥0，2x2-3x-2≠0，解得x≤0且x≠-12，故所求函数的定义域为{x|x≤0，且x≠-12}.(2)要使y=34x+83x-2有意义，则必须3x-2>0，即x>23，故所求函数的定义域为{x|x>23}.1已知f(x)=x21+x2，x∈R，(1)计算f(a)+f(1a)的值;(2)计算f(1)+f(2)+f(12)+f(3)+f(13)+f(4)+f(14)的值.【解】(1)由于f(a)=a21+a2，f(1a)=11+a2，所以f(a)+f(1a)=(2)法一因为f(1)=121+12=12，f(2)=221+22=45，f(12)=(12)21+(12)2=15，f(3)=321+32=910，f(13)=(13)21+(13)2=110，f(4)=421+42=1617，f(14)=(14)21+(14)2=117，所以f(1)+f(2)+f(12)+f(3)+f(13)+f(4)+f(14)=12+45+15+910+110+1617+117=7法二由(1)知，f(a)+f(1a)=1，则f(2)+f(12)=f(3)+f(13)=f(4)+f(14)=1，即[f(2)+f(12)]+[f(3)+f(13)]+[f(4)+f(14)]=3，而f(1)=12，所以f(1)+f(2)+f(12)+f(3)+f(13)+f(4)+f(14)=7高一数学寒假作业答案5函数f(x)=x2在[0,1]上的最小值是()A.1B.0C.14D.不存在解析选B.由函数f(x)=x2在[0,1]上的图象(图略)知，f(x)=x2在[0,1]上单调递增，故最小值为f(0)=0.函数f(x)=2x+6，x∈[1，2]x+7，x∈[-1，1]，则f(x)的值、最小值分别为()A.10,6B.10,8C.8,6D.以上都不对解析选A.f(x)在x∈[-1,2]上为增函数，f(x)max=f(2)=10，f(x)min=f(-1)= 函数y=-x2+2x在[1,2]上的值为()A.1B.2C.-1D.不存在解析选A.因为函数y=-x2+2x=-(x-1)2+对称轴为x=1，开口向下，故在[1,2]上为单调递减函数，所以ymax=-1+2=函数y=1x-1在[2,3]上的最小值为()A.2B.12C.13D.-12解析选B.函数y=1x-1在[2,3]上为减函数，∴ymin=13-1=1某公司在甲乙两地同时销售一种品牌车，利润(单位万元)分别为L1=-x2+21x和L2=2x，其中销售量(单位辆).若该公司在两地共销售15辆，则能获得的利润为()A.90万元B.60万元C.120万元D.120.25万元解析选C.设公司在甲地销售x辆(0≤x≤15，x为正整数)，则在乙地销售(15-x)辆，∴公司获得利润L=-x2+21x+2(15-x)=-x2+19x+30.∴当x=9或10时，L为120万元，故选C.已知函数f(x)=-x2+4x+a，x∈[0,1]，若f(x)有最小值-2，则f(x)的值为()A.-1B.0C.1D.2解析选C.f(x)=-(x2-4x+4)+a+4=-(x-2)2+4+a.∴函数f(x)图象的对称轴为x=2，∴f(x)在[0,1]上单调递增.又∵f(x)min=-2，∴f(0)=-2，即a=-f(x)max=f(1)=-1+4-2=2021高一数学寒假作业答案最新。

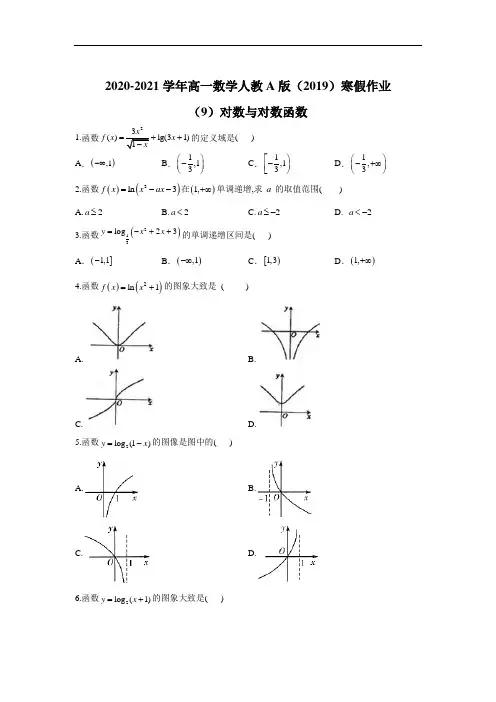
2020-2021学年高一数学人教A 版（2019）寒假作业（9）对数与对数函数1.函数23()lg(31)1x f x x x=++-的定义域是( ) A ．(),1-∞B ．1,13⎛⎫- ⎪⎝⎭C ．1,13⎡⎫-⎪⎢⎣⎭D ．1,3⎛⎫-+∞ ⎪⎝⎭2.函数()()2ln 3f x x ax =--在()1,+∞单调递增,求a 的取值范围( ) A.2a ≤B.2a <C.2a ≤-D. 2a <-3.函数()213log 23y x x =-++的单调递增区间是( ) A ．(]1,1- B ．(),1-∞ C ．[)1,3 D ．()1,+∞4.函数()()2ln 1f x x =+的图象大致是 ( )A. B.C. D.5.函数2log (1)y x =-的图像是图中的( )A. B.C. D.6.函数2log (1)y x =+的图象大致是( )A. B.C. D.7.（多选）已知函数()ln(2)ln(6)f x x x =-+-，则A. ()f x 在(2,6)上的最大值为2ln 2B. ()f x 在(2,6)上单调递增C. ()f x 在(2,6)上无最小值D. ()f x 的图象关于直线4x =对称8.求值：331log 15log 252-=_________.9.函数()2log 1f x x =-___________.10.1ln 238lg5lg 20e ++-=__________.11.函数()2lg 2y x x =+-的单调递增区间是_____________. 12.已知函数()()()log 1log 1a a f x x x =+--，0a >，且1a ≠. (1)求()f x 的定义域.(2)判断()f x 的奇偶性，并予以证明. (3)当1a >时，求使()0f x >的x 的取值范围.答案以及解析1.答案：B解析：函数2()lg(31)f x x ++的定义域是10310x x ->⎧⎨+>⎩，解得113x x <⎧⎪⎨>-⎪⎩，所以函数()f x 的定义域是113x x ⎧⎫-<<⎨⎬⎩⎭．2.答案：C解析：令()23t x x ax =--,由复合函数的单调性可知,11220a a ⎧≤⎪⎨⎪--≥⎩ 解可得,2a ≤-. 故选：C . 3.答案：C解析：令223t x x =-++， 由2230x x -++>，得13x -<<.函数223t x x =-++的对称轴方程为1x =， 二次函数223t x x =-++在[)1,3上为减函数， 而函数13log y t=为定义域内的减函数，∴函数()213log 23y x x =-++的单调增区间是[)1,3 故选：C. 4.答案：A解析：由于函数为偶函数又过(0,0)所以直接选A. 5.答案：C解析：由函数2log (1)y x =-的定义域为{}|1x x <,排除A,B;由复合函数的单调性可知函数为减函数,排除D.故选C. 6.答案：C解析：函数2log (1)y x =+的图象是把函数2log y x =的图象向左平移了一个单位得到的，定义域为(1,)-+∞，过定点(0,0)，在(1,)-+∞上是增函数， 故选：C ． 7.答案：ACD解析：()ln(2)ln(6)ln[(2)(6)]f x x x x x =-+-=--，定义域为(2,6)． 令(2)(6)t x x =--，则ln y t =．因为二次函数(2)(6)t x x =--的图象的对称轴为直线4x =，且在(2,4)上单调递增，在(4,6)上单调递减，所以当4x =时，t 有最大值，所以max ()(4)2ln 2,()f x f f x ==在(2,6)上无最小值． 故选ACD ． 8.答案：1解析：由对数运算,化简可得 331log 15log 252-1233=log 15log 25-33=log 15log 5- 3=log 3=1故答案为:1 9.答案：[)2,+∞解析： 由题意得：2log 1x≥， 解得：2x ≥，∴函数()f x 的定义域是[)2,+∞ 故答案为：[)2,+∞ 10.答案：2解析：1ln 238lg5lg 20e 2lg10022222++-=+-=+-= 11.答案：()1,+∞解析： 由()2lg 2y x x =+-可得2x <-或1x >∵22u x x =+-在()1,+∞单调递增，而lg y u =是增函数，由复合函数的同增异减的法则可得，函数()2lg 2y x x =+-的单调递增区间是()1,+∞ 12.答案：(1)因为()()()log 1log 1a a f x x x =-+-，所以1010x x +>->⎧⎨⎩，解得11x -<<.故所求函数的定义域为{}|11x x -<<. (2)()f x 为奇函数证明如下:由(1)知()f x 的定义域为{}|11x x -<<，且()()()log 1log 1a a f x x x -=-++-()()()log 1log 1a a x x f x =+--=-⎡⎤⎣⎦.故()f x 为奇函数 (3)因为当1a >时，()f x 在定义域{}|11x x -<<上是增函数， 由()0f x >，得111x x+>-，解得01x <<.所以x 的取值范围是(0)1,.。

高一寒假作业数学注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题1．已知集合{}1,2,3A =， ()(){}|120, B x x x x =+−<∈Z ，则A B 等于( )A ． {}1B ． {}1,2C ． {}0,1,2,3D ． {}1,0,1,2,3−2．点）在直线:10l ax y −+=上，则直线l 的倾斜角为( )A ． 120°B ． 60°C ．45°D ． 30°3．函数()f x =的定义域是( )A . {|23}x x <<B ．{|23}x x x <>或C ．{|23}x x x ≤≥或D ．{|23}x x x <≥或4．一个球被两个平行平面截后所得几何体形如我国的一种民族打击乐器“鼓”，该“鼓”的三视图如图所示，则球的表面积为( ) A ． 5π B ． 10π C ． 20πD ．5．设,x y 为正数，且34x y =，当3x py =时，p 的值为( ) A ． 3log 4 B ． 4log 3 C ． 36log 2 D ． 3log 26.定义域为D 的奇函数()f x ，当0x >时，()()12f x f ≤=.给出下列命题：①[1,1]D −；②对任意, |()|2x D f x ∈≤；③存在0x D ∈，使得0()0f x =；④存在1x D ∈，使得1()1f x =.其中所有正确的命题的个数为( )A ．0B ．1C ． 2D ．37．如图，1111ABCD A B C D −为正方体，下列结论错误．．的是( )A ． 11BD CB D ∥平面 B ． 1AC BD ⊥C ． 111AC CBD ⊥平面 D ． 异面直线AD 与1CB 所成角为60°8．定义在R 上的偶函数()f x 的图象关于直线1x =对称，当[0,1]x ∈时，()21f x x =−+，设函数|1|1()(13)2x g x x − =−<<，则函数()f x 与()g x 的图象交点个数为( )A ． 3B ． 4C ． 5D ． 69．如图1，直线EEEE 将矩形纸AAAAAAAA 分为两个直角梯形AAAAEEEE 和AAAAEEEE ，将梯形AAAAEEEE 沿边EEEE 翻折，如图2，在翻折的过程中（平面AAAAEEEE 和平面AAAAEEEE 不重合），下面说法正确的是( )图1 图2A ． 存在某一位置，使得AAAA ∥平面AAAAEEEEB ． 在翻折的过程中，AAEE ∥平面AAAAEE 恒成立C ． 存在某一位置，使得AAEE ⊥平面AAAAEEEE D.在翻折的过程中，AAEE ⊥平面AAAAEEEE 恒成立10．我国魏晋时期的数学家刘徽创立了割圆术，也就是用内接正多边形去逐步逼近圆，即圆内接正多边形边数无限增加时，其周长就越逼近圆周长，这种用极限思想解决数学问题的方法是数学史上的一项重大成就.现作出圆222x y +=的一个内接正八边形，使该正八边形的其中4个顶点在坐标轴上，则下列4条直线中不是该正八边形的一条边所在直线的为( )A ．1)0x y +−−= B ．1)0x y += C ．1)0x y −+= D ．1)0x y −−+=11．设集合{|48}x A x =>，集合2{|210,0}B x x ax a =−−≤>，若A B 中恰含有一个整数，则实数a 的取值范围是( )A ．34,43B ．41,3C ．3,4 +∞D ．(1,)+∞12．在直角坐标系内，已知(3,3)A 是C 上一点，折叠该圆两次使点A 分别与圆上不相同的两点（异于点A ）重合，两次的折痕方程分别为xx −yy +1=0和xx +yy −7=0，若C 上存在点P ，使90MPN ∠=°，其中M 、N 的坐标分别为(,0)m −、(,0)m ，则m 的最大值为( )A ． 4B ． 5C ． 6D ． 7第II 卷（非选择题）二、填空题13．已知过点(1,)A m −和(,5)B m 的直线与310x y −−=平行，则m 的值为______. 14．给定下列四个命题：①过直线外一点可作无数条直线与已知直线平行;②如果一条直线不在这个平面内，那么这条直线就与这个平面平行; ③垂直于同一直线的两条直线可能相交、可能平行也可能异面; ④若两个平面分别经过两条垂直直线，则这两个平面互相垂直。

寒假作业(一)一、选择题1．下列各项中，不可以组成集合的是（ ） A ．所有的正数 B ．等于2的数 C ．接近于0的数 D ．不等于0的偶数 2．下列表示图形中的阴影部分的是（ ） A ．()()A C B C B ．()()A B A CC ．()()A B B CD ．()A B C 3．下面有四个命题： （1）集合N 中最小的数是1； （2）若a -不属于N ，则a 属于N ； （3）若,,N b N a ∈∈则b a +的最小值为2；（4）x x 212=+的解可表示为{}1,1； 其中正确命题的个数为（ ） A ．0个 B ．1个 C ．2个 D ．3个4．若集合{}c b a M ,,=中的元素是ABC ∆的三边长，则ABC ∆一定不是（ ） A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．等腰三角形 二、填空题 5．设集合{32}A x x =-≤≤,{2121}B x k x k =-≤≤+,且A B ⊇，则实数k 的取值范围是 。

A BC6．【选做】已知{}{}221,21A y y x xB y y x==-+-==+，则A B=_________。

三、解答题7．【选做】已知集合{}{}22,1,3,3,21,1A a aB a a a=+-=--+，若{}3A B=-，求实数a的值。

寒假作业(二)一、选择题1．若集合}1,1{-=A ，}1|{==mx x B ，且A B A =⋃，则m 的值为（ ） A ．1 B ．1- C ．1或1- D ．1或1-或0 2．若集合{}{}22(,)0,(,)0,,M x y x y N x y x y x R y R=+==+=∈∈，则有（ ）A ．MN M = B ． MN N = C ． MN M = D ．MN =∅3．方程组⎩⎨⎧=-=+9122y x y x 的解集是（ ） A ．()5,4 B ．()4,5- C ．(){}4,5- D ．(){}4,5-。

第3页 共9页
不同函数模型测试题二 1.某动物数量 y(只)与时间 x(年)的关系为 y=alog2(x+1)， 设第一年有 101 只，那么到第七年它们开展到() A.300 只 B.400 只 C.500 只 D.600 只 解析：选 A.由确定第一年有 101 只，得 a=101，将 a=101， x=7 代入 y=alog2(x+1)，得 y=300. 2.马先生于两年前购置了一部手机，此时此刻这款手机的价 格已降为 1010 元，设这种手机每年降价 20%，那么两年前这部手 机的价格为() A.1535.5 元 B.1440 元 C.1620 元 D.1562.5 元 解 析 ： 选 D. 设 这 部 手 机 两 年 前 的 价 格 为 a ， 那 么 有 a(1-0.2)2=1010，解得 a=1562.5 元，应选 D. 3.为了改善某地的生态环境，政府决心绿化荒山，打算第一 年先植树 0.5 万亩，以后每年比上年增加 1 万亩，结果第 x 年植 树亩数 y(万亩)是时间 x(年数)的一次函数，这个函数的图象是() 解析：选 A.当 x=1 时，y=0.5，且为递增函数. 4.某单位为鼓舞职工节约用水，作出了如下规定：每月用水 不超过 10m3，按每立方米 x 元收取水费;每月用水超过 10m3，超 过局部加倍收费，某职工某月缴费 16x 元，那么该职工这个月实
第6页 共9页
家发觉，两岁燕子的飞行速度可以表示为函数 v=5log2Q10，单位 是 m/s，其中 Q 表示燕子的耗氧量.
(1)试计算：燕子静止时的耗氧量是多少个单位? (2)当一只燕子的耗氧量是 80 个单位时，它的飞行速度是多 少? 解：(1)由题意知，当燕子静止时，它的速度为 0，代入题目 所给公式可得 0=5log2Q10，解得 Q=10， 即燕子静止时的耗氧量为 10 个单位. (2)将耗氧量 Q=80 代入公式得 v=5log28010=5log28=15(m/s)， 即当一只燕子耗氧量为 80 个单位时，它的飞行速度为 15m/s. 高一数学寒假作业及答案 5 集合的含义与表示练习一 1.对集合{1,5,9,13,17}用描述法来表示，其中正确的一个是 () A.{x|x 是小于 18 的正奇数} B.{x|x=4k+1，k∈Z，且 k0，所以 m<1. 答案：m<1 4. 用适当的方法表示以下集合： (1)全部被 3 整除的整数;

高一数学（必修二）寒假作业（立体几何）第Ⅰ卷（选择题，48分）一、选择题（本大题共12小题，每小题4分，共48分，在每小题给出的四个选项中，只有一项符合题目要求。

）1.若α、β是不重合的平面，a 、b 、c 是互不相同的空间直线，则下列命题中为真命题的是 （ ） ① 若α//a ，α//b ，则b a // ； ② 若α//c ，α⊥b ，则b c ⊥ ； ③ 若α⊥c ，β//c ，则βα⊥ ；④ 若α⊂b ，α⊂c 且b a ⊥，c a ⊥，则α⊥a A.③④ B. ①② C. ①④ D. ②③2.下列四个命题：①平行于同一平面的两条直线相互平行 ②平行于同一直线的两个平面相互平行 ③垂直于同一平面的两条直线相互平行 ④垂直于同一直线的两个平面相互平行 其中正确的有A ．4个 B.3个 C.2个 D.1个3.某几何体的三视图如图所示，则该几何体的体积为（ ）A 、163πB 、203πC 、403πD 、5π4.已知正四棱锥的各棱棱长都为23，则正四棱锥的外接球的表面积为( ) A ．π12B ．π36C ．π72D ．π1085.某几何体的三视图如图所示，则该几何体的体积为A.168π+B.88π+C.1616π+D.816π+6..a ，b 表示空间不重合两直线，α，β表示空间不重合两平面，则下列命题中正确的是（ ）A.若α⊂a ，β⊂b ，且b a ⊥，则βα⊥B.若βα⊥，α⊂a ，β⊂b 则b a ⊥C.若α⊥a ，β⊥b ，βα//则b a //D.若βα⊥，α⊥a ，β⊂b ，则b a //7.下列命题中为真命题的是（ ） A ．平行于同一条直线的两个平面平行 B ．垂直于同一条直线的两个平面平行C ．若—个平面内至少有三个不共线的点到另—个平面的距离相等，则这两个平面平行．D ．若三直线a 、b 、c 两两平行，则在过直线a 的平面中，有且只有—个平面与b ，c 均平行．8.如图是一个组合几何体的三视图，则该几何体的体积是 . A 36128π+ B 3616π+ C 72128π+ D 7216π+9.设l ，m 是两条不同的直线，α是一个平面，则下列命题正确的是（ ） A ．若l m ⊥，m α⊂，则l α⊥ B ．若l α⊥，l m //，则m α⊥ C ．若l α//，m α⊂，则l m // D ．若l α//，m α//，则l m //10.已知某几何体的三视图如右图所示，其中，主（正）视图，左（侧）视图均是由直角三角形与半圆构成，俯视图由圆与内接直角三角形构成，根据图中的数据可得此几何体的 体积为( )16+ (B) 4136π+12+ (D)2132π+11.已知圆柱1OO 底面半径为1，高为π，ABCD 是圆柱的一个轴截面．动点M 从点B 出发沿着圆柱的侧面到达点D ，其距离最短时在侧面留下的曲线Γ如图所示．现将轴截面ABCD 绕着轴1OO 逆时针旋转 (0)θθπ<≤后，边11B C 与曲线Γ相交于点P ，设BP 的长度为()f θ，则()y f θ=的图象大致为（ ）12.某三棱锥的侧视图和俯视图如图--1所示，则该三棱锥的体积为( )A ．4 3B ．8 3C ．12 3D ．243第Ⅱ卷（非选择题，共72分）二、填空题（本大题共4个小题，每小题4分，共16分）13.如图,在三棱柱ABC C B A -111中, F E D ，，分别是1AA AC AB ，，的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V _____.14. 已知圆的方程为22680x y x y +--=．设该圆过点(3，5)的最长弦和最短弦分别为AC 和BD ，则四边形ABCD 的面积为 ．15.如右图为长方体积木块堆成的几何体的三视图，此几何体共由________块木块堆成..ABC1ADE F1B1C16.已知某个几何体的三视图如图（正视图中的弧线是半圆），图中标出的尺（单位：㎝）， 可得这个几何体表面是 cm 2。

寒假作业（十一）一、选择题:1. 算法的三种基本结构是 ( )A. 依次结构、模块结构、条件结构B. 依次结构、循环结构、模块结构C. 依次结构、条件结构、循环结构D. 模块结构、条件结构、循环结构2. 给出以下四个问题,①输入一个数x,输出它的相反数.②求面积为6的正方形的周长.③求三个数a,b,c中的最大数.④求函数.1.2{)(≥-<+=　xx　xxxf的函数值. 其中不须要用条件语句来描述其算法的有( )A. 1个B. 2个C. 3个D. 4个3．要从已编号(1－50)的50枚最新研制的某型号导弹中随机抽取5枚来进行放射试验，用每部分选取的号码间隔一样的系统抽样方法确定所选取的5枚导弹的编号可能是( ).A．5，10，15，20，25 B．3，13，23，33，43C．1，2，3，4，5 D．2，4，8，16，324．某单位有老年人27人，中年人54人，青年人81人，为了调查他们身体状况的某项指标，需从他们中抽取一个容量为36的样本，适合抽取样本的方法是( ).A．抽签法 B．系统抽样C．随机数表法D．分层抽样二、填空题：5．某工厂生产 A，B，C 三种不同型号的产品，产品数量之比依次为2∶3∶5．现用分层抽样方法抽出一个容量为n的样本，样本中A种型号的产品有16件，那么此样本的容量n＝___________．6．已知x，y之间的一组数据：x 1.08 1.12 1.19 1.28y 2.25 2.37 2.40 2.55 y与x之间的线性回来方程yˆ＝bx＋a 必过定点_________．三、解答题7．【选做】(统计)某校100位学生期中考试语文成果的频率分布直方图如图4所示,其中成果分组区间是:[)50,60、[)60,70、[)70,80、[)80,90、[]90,100.(Ⅰ)求图中a 的值;(Ⅱ)依据频率分布直方图,估计这100名学生语文成果的平均分;(Ⅲ)若这100名学生的语文成果某些分数段的人数(x )与数学成果相应分数段的人数(y )之比如下表所示,求数学成果在[)50,90之外的人数.分数段[)50,60 [)60,70 [)70,80 [)80,90 :x y 1:1 2:1 3:4 4:5寒假作业(十一)答案:1.C2.B3．B 解析：依据系统抽样的规则，1到10一段，11到20一段，如此类推，每段10个号码，那么每一段上都应当有号码．4．D解析：总体是由差异明显的几部分组成的．16×(2＋3＋5)＝80．5．答案：80．解析：n＝26．答案：(1.167 5，2.392 5)．解析：必过四组数据的平均数，即(1.167 5，2.392 5)．7.解析:(Ⅰ)由()a+++⨯=,解得0.00520.020.030.04101a=.(Ⅱ)0.05550.4650.3750.2850.059573⨯+⨯+⨯+⨯+⨯=.(Ⅲ)这100位学生语文成果在[)80,90的分别有570,80、[)50,60、[)60,70、[)人、40人、30人、20人,依据表中所给比例,数学成果在[)70,80、50,60、[)60,70、[) [)50,90之80,90的分别有5人、20人、40人、25人,共90人,所以数学成果在[)外的人数有10人.。

2019 学年高一数学寒假作业答案参照以下是由查词典数学网为您整理供给的高一数学寒假作业答案参照，希望可以对您有所帮助，欢迎阅读与借鉴。

题号答案 DDDADDBCACBC13.14.415.16.②③17.(1) ∵A中有两个元素，对于的方程有两个不等的实数根，，且，即所求的范围是，且 6 分(2)当时，方程为，会合 A=当时，若对于的方程有两个相等的实数根，则 A 也只有一个元素，此时若对于的方程没有实数根，则A没有元素，此时，综合知此时所求的范围是，或.13 分18解：(1)，得(2)，得此时，因此方向相反19.解: ⑴由题义整理得 , 解方程得即的不动点为 -1 和 2.6 分⑵由 =得第 1页这样方程有两解, 则有△=把看作是对于的二次函数, 则有解得即为所求 .12 分20. 解： (1) 常数 m=14分(2)当 k0 时，直线 y=k 与函数的图象无交点 , 即方程无解 ; 当 k=0 或 k1 时 , 直线 y=k 与函数的图象有独一的交点，因此方程有一解;当 0因此方程有两解.12 分21.解： (1) 设，有， 2取，则有是奇函数4(2)设，则，由条件得在 R 上是减函数，在[-3 ，3] 上也是减函数。

6当 x=-3 时有最大值当 x=3 时有最小值，由，，当 x=-3 时有最大值 6; 当 x=3 时有最小值 -6.8(3)由，是奇函数原不等式就是 10由 (2) 知在 [-2 ， 2] 上是减函数第 2页原不等式的解集是1222.解： (1) 由数据表知，(3) 因为船的吃水深度为7 米，船底与海底的距离许多于 4.5米，故在船航行时水深米，令，得.解得 .取，则取，则 .第 3页。

寒假作业(八)一、选择题1．若函数)10(log )(<<=a x x f a 在区间]2,[a a 上的最大值是最小值的3倍，则a 的值为( )A ．42B ．22C ．41D ．212．若函数)1,0)((log ≠>+=a a b x y a 的图象过两点(1,0)-和(0,1)，则( )A ．2,2a b ==B ．2a b ==C ．2,1a b ==D ．a b ==3．已知x x f 26log )(=，那么)8(f 等于（ ）A ．34B ．8C ．18D ．214．【选做】函数lg y x =( )A.是偶函数，在区间(,0)-∞ 上单调递增B.是偶函数，在区间(,0)-∞上单调递减C.是奇函数，在区间(0,)+∞ 上单调递增D.是奇函数，在区间(0,)+∞上单调递减二、填空题5.若a x f x x lg 22)(-+=是奇函数，则实数a =_________。

6.函数()212()log 25f x x x =-+的值域是__________.三、解答题7.比较下列各组数值的大小：（1）3.37.1和1.28.0；（2）7.03.3和8.04.3；（3）25log ,27log ,2398寒假作业(八)答案:1. A 132311log 3log (2),log (2),2,8,,38a a a a a a a a a a a a ======2. A log (1)0,a b -=且log 1,2a b a b ===3. D 令1666228(0),8(8)()log log x x x f f x x =>=====4. B 令()lg ,()lg lg ()f x x f x x x f x =-=-==，即为偶函数 令,0u x x =<时，u 是x 的减函数，即lg y x =在区间(,0)-∞上单调递减 5． 110()()22lg 22lg x x x x f x f x a a --+-=+++ 1(lg 1)(22)0,lg 10,10x x a a a -=++=+== （另法）：x R ∈，由()()f x f x -=-得(0)0f =，即1lg 10,10a a +==6. (],2-∞-2225(1)44,x x x -+=-+≥而101,2<<()21122log 25log 42x x -+≤=- 7．解：（1）∵ 3.301.7 1.71,>= 2.100.80.81<=，∴ 3.31.7>1.28.0（2）∵0.70.80.80.83.3 3.3,3.3 3.4<<，∴0.73.3<8.04.3 （3）8293log 27log 3,log 25log 5,==332222233333log 2log log 3,log 3log log 5,22==<==> ∴983log 25log 27.2<<。