北京市海淀外国语实验学校2019-2020学年九年级第二学期直升三4月数学能力反馈练习(PDF版,无答案)

北京海淀实验中学2019-2020学年九年级下学期适应练习数学试题(word无答案)一、单选题(★) 1 . 随着“一带一路”的建设推进，北京丰台口岸进口货值业务量加速增长，2016年北京丰台口岸进口货值飙升至189 000 000美元，比上一年翻了三倍，创下历史新高．将189 000 000用科学记数法表示应（）A．189×106B．1.89×106C．18.9×107D．1.89×108(★★) 2 . 在数轴上，实数 a， b对应的点的位置如图所示，且这两个点到原点的距离相等，下列结论中，正确的是（）A．B．C．D．(★) 3 . 如图是某几何体的三视图，该几何体是（）A．三棱柱B．长方体C．圆锥D．圆柱(★) 4 . 如图，AB∥CD，直线EF分别交AB，CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB＝75°，则∠PNM等于( )A．15°B．25°C．30°D．45°(★) 5 . 一个多边形的内角和是720°，这个多边形是（）A．五边形B．六边形C．七边形D．八边形(★★) 6 . 如果x+y=4，那么代数式的值是（）A．﹣2B．2C．D．(★★)7 . 在“校园读书月”活动中，小华调查了班级里名同学本学期购买课外书的花费情况，并将结果绘制成如图所示的统计图．下面有四个推断：这次调查获取的样本数据的众数是元这次调查获取的样本数据的中位数是元若该校共有学生人，根据样本数据，估计本学期计划购买课外书花费元的学生有人花费不超过元的同学共有人．其中合理的是（）A．B．C．D．(★) 8 . 如图，小宇计划在甲、乙、丙、丁四个小区中挑选一个小区租住，附近有东西向的交通主干道 a和南北向的交通主干道 b，若他希望租住的小区到主干道 a和主干道 b的直线距离之和最小，则图中符合他要求的小区是（）A．甲B．乙C．丙D．丁二、填空题(★★) 9 . 如图，测量小玻璃管口径的量具ABC上，AB的长为10毫米，AC被分为60等份，如果小管口中DE正好对着量具上20份处（DE∥AB），那么小管口径DE的长是 _____ 毫米．(★) 10 . 已知，一次函数y=kx+b（k≠0）的图象经过点（0，2），且y随x的增大而减小，请你写出一个符合上述条件的函数关系式： __ ．(★★) 11 . 如图是的正方形网格，每个小正方形的边长均为1且顶点称为格点，点均在格点上.在网格中建立平面直角坐标系，且，.如果点也在此的正方形网格的格点上，且是等腰三角形，那么当的面积最大时，点的坐标为___．(★) 12 . 用一组的值说明命题“对于非零实数，若，则”是错误的，这组值可以是______，_____.(★★) 13 . 如图，为的直径，与相切于点，弦．若，则______ .(★) 14 . 京张高铁是2022年北京冬奥会的重要交通基础设施，考虑到不同路段的特殊情况，将根据不同的运行区间设置不同的时速．其中，北京北站到清河段全长11千米，分为地下清华园隧道和地上区间两部分，运行速度分别设计为80千米/小时和120千米/小时．按此运行速度，地下隧道运行时间比地上大约多2 分钟（小时），求清华园隧道全长为多少千米．设清华园隧道全长为 x千米，依题意，可列方程为__________．(★★) 15 . 某校初一年级68名师生参加社会实践活动，计划租车前往，租车收费标准如下：车型大巴车（最多可坐55人）中巴车（最多可坐39人）小巴车（最多可坐26人）每车租金900800550（元∕天）则租车一天的最低费用为 ____ 元.(★) 16 . 某实验室对150款不同型号的保温杯进行质量检测，其中一个品牌的30款保温杯的保温性、便携性与综合质量在此检测中的排名情况如图所示，可以看出其中 A型保温杯的优势是_____．三、解答题(★★) 17 . 计算：4sin60°+ （3﹣π）0．(★) 18 . 解不等式组：(★) 19 . 如图，在中，，点是边上一点，垂直平分，交于点，交于点，连结，求证：．(★★) 20 . 已知：关于 x的一元二次方程 x 2-4 x+2 m=0有两个不相等的实数根．（1）求 m的取值范围；（2）如果 m为非负整数，且该方程的根都是整数，求 m的值．(★★) 21 . 如图，平行四边形ABCD中，对角线AC，BD交于点O，且AC⊥BC，点E是BC延长线上一点，，连接DA．(1)求证：四边形ACED为矩形；(2)连接OE，如果BD=10，求OE的长.(★★) 22 . 如图，直线与反比例函数的图象交于点，与轴交于点，与y轴交于点．（1）求的值和反比例函数的表达式；（2）在 y轴上有一动点 P（0， n），过点 P作平行于轴的直线,交反比例函数的图象于点，交直线于点，连接．若，求的值．(★★) 23 . 如图，为上一点，点在直径的延长线上，求证：是的切线；过点作的切线交的延长线于点．若依题意补全图形并求的长(★★) 24 . 为了了解某区的绿化进程，小明同学查询了园林绿化政务网，根据网站发布的近几年该城市城市绿化资源情况的相关数据，绘制了如下统计图（不完整）请根据以上信息解答下列问题：求2018年该市人均公共绿地面积是多少平方米(精确到 ？补全条形统计图；小明同学还了解到自己身边的许多同学都树立起了绿色文明理念，从自身做起，多种树，为提高人均公共绿地面积做贡献，他对所在班级的多 名同学2019年参与植树的情况做了调查，并根据调查情况绘制出如下统计表：种树棵数（棵）人数如果按照小明的统计数据，请你通过计算估计，他所在学校的 名同学在2019年共植树多少棵？(★★) 25 . 如图，半圆 O 的直径 AB ＝5 cm ，点 M 在 AB 上且 AM ＝1 cm ，点 P 是半圆 O 上的动点，过点 B 作 BQ⊥ PM 交 PM （或 PM 的延长线）于点 Q ．设 PM ＝ xcm ， BQ ＝ ycm ．（当点 P 与点 A 或点 B 重合时， y 的值为0）小石根据学习函数的经验，对函数 y 随自变量 x 的变化而变化的规律进行了探究．下面是小石的探究过程，请补充完整：（1）通过取点、画图、测量，得到了 x 与 y 的几组值，如下表：x/cm1 1.52 2.53 3.54y/cm0 3.7______ 3.8 3.3 2.5______（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当BQ与直径AB所夹的锐角为60°时，PM的长度约为______ cm．(★★★★) 26 . 已知抛物线．求出抛物线的对称轴方程以及与轴的交点坐标当时，求出抛物线与轴的交点坐标已知三点构成三角形，当抛物线与三角形的三条边一共有个交点时，直接写出的取值范围．(★★★★★) 27 . 问题：如图1，在中，，点是射线上任意一点，是等边三角形，且点在的内部，连接．探究线段与之间的数量关系．请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．当点与点重合时(如图2)，请你补全图形．由的度数为_______________，点落在_______________，容易得出与之间的数量关系为_______________当是的平分线时，判断与之间的数量关系并证明当点在如图3的位置时，请你画出图形，研究三点是否在以为圆心的同一个圆上，写出你的猜想并加以证明．(★★★★★) 28 . 在平面直角坐标系中，点的坐标为，点的坐标为，且，，若为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直．则称该矩形为点的相关矩形"．下图为点的“相关矩形”的示意图．已知点的坐标为．若点的坐标为，求点的“相关矩形”的周长；点在直线上，若点的“相关矩形”为正方形，已知抛物线经过点和点，求抛物线与轴的交点的坐标；的半径为，点是直线上的从左向右的一个动点．若在上存在一点使得点的“相关矩形”为正方形，直接写出动点的横坐标的取值范围．。

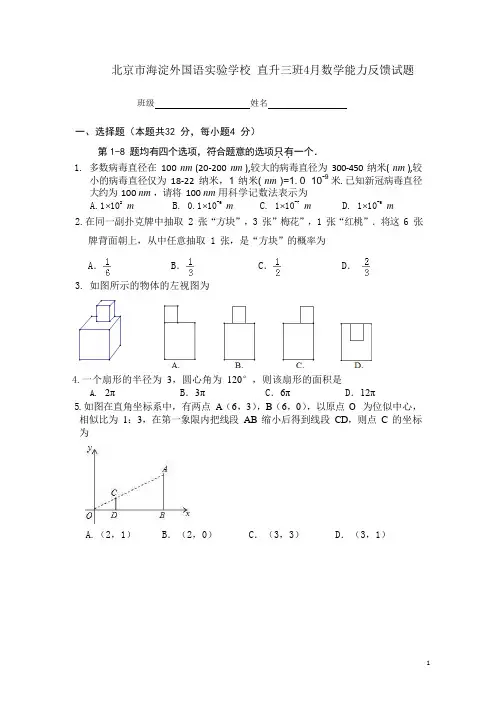
北京市海淀外国语实验学校直升三班4月数学能力反馈试题班级姓名一、选择题（本题共32 分，每小题4 分）第1-8 题均有四个选项，符合题意的选项只．有．一个．1. 多数病毒直径在100 nm (20-200 nm ),较大的病毒直径为300-450 纳米( nm ),较小的病毒直径仅为18-22 纳米，1 纳米( nm )=1.0×10-9 米.已知新冠病毒直径大约为100 nm ，请将100 nm 用科学记数法表示为A.1⨯102 mB. 0.1⨯10-6 mC. 1⨯10-7 mD. 1⨯10-6 m2.在同一副扑克牌中抽取 2 张“方块”，3 张”梅花”，1 张“红桃”．将这 6 张牌背面朝上，从中任意抽取 1 张，是“方块”的概率为A．B．C．D．3.如图所示的物体的左视图为4.一个扇形的半径为3，圆心角为120°，则该扇形的面积是A.2πB．3πC．6πD．12π5.如图在直角坐标系中，有两点A（6，3），B（6，0），以原点O为位似中心，相似比为1：3，在第一象限内把线段AB 缩小后得到线段CD，则点C 的坐标为A .（2，1）B．（2，0）C．（3，3）D．（3，1）OD6.已知抛物线y = -x 2+ bx + 4 经过(-2，n ) 和(4，n ) 两点，则n 的值为 A.2 B. 4 C. -2 D. -47.如图，已 AB 是⊙ O 的直径，点 C 、D 在⊙ O 上，∠ABC =50°，则∠D 为A ．50°B ．45°C ．40°D ．30°8.如图，在矩形 ABCD 中，E 为 AB 中点，以 BE 为边作正方形 BEFG ，边 EF 交 CD 于点 H ，在边 BE 上取点 M 使 BM ＝BC ，作 MN ∥BG 交 CD 于点 L ， 交 F G 于点 N ，欧几里得在《几何原本》中利用该图解释了（a +b ）（a ﹣b ） ＝a 2﹣b 2，现以点 F 为圆心，FE 为半径作圆弧交线段 DH 于点 P ，连接 EP ， 记△EPH 的面积为 S 1，图中阴影部分的面积为 S 2．若点 A 、L 、G 在同一直线上， 的值为CAB第 7 题图第 8 题图D. 二、填空题（本题共 28分，每小题 4 分）9. 分 解 因 式 ：4m 2+4m +1＝ ．10. 已知一个正比例函数的图象与一个反比例函数的图象的一个交点坐标为 （1,3），则另一个交点坐标是 11. 若a 2 - 3b = 5 ，则6b - 2a 2 + 2030 =12.抗疫期间，甲、乙两工厂分别承接了 160 万、200 万的医用口罩生产任务， 已知乙工厂比甲工厂每天多生产 5 万个，甲、乙完成生成任务的时间相同， 问甲每天生产多少万个？设甲每天生产 m 万个，根据题意可列出方程： ． 13.如图，⊙O 分别切∠BAC 的两边 AB 、AC 于点 E 、F ，点 P 在优弧（ ）上，若∠BAC ＝68°，则∠EPF 等于A ．B ．C ．2x + 3 14．描金又称泥金画漆，是一种传统工艺美术技艺．起源于战国时期，在漆器表面， 用金色描绘花纹的装饰方法，常以黑漆作底，也有少数以朱漆为底．描金工作分为两道工 序，第一道工序是上漆，第二道工序是描绘花纹．现甲、乙两位工匠要完成 A 、B 、 C 三件原料的描金工作，每件原料先由甲上漆，再由乙描绘花纹．每道工序所需原料 时间工序 原料 A 原料 B 原料 C 上漆 9 14 12 描绘花纹 13 8 10 则完成这三件原料的描金工作最少需要 小时.15. 已知集合 A ={x x 2 + 三、解答题mx +1 = 0}, 若 A ⋂ R = ∅,则实数m 的取值范围是 . 16.（6分）求下列函数的定义域 （1） y = ； （2） y =1(1 - 2x )(x + 1)； 17.（5分）已知函数 f (x ) = 1 x + 3, 求使f (x ) ∈(9, 4) 的 x 的取值范围2 818.（5分）设集合 A = {1, 2, a }, B = {1, a 2 - a },若 A ⊇ B 求实数a 的值.19．（8分）确定函数y ＝x ＋ 1（x ＞0）的单调区间，并用定义证明。

北京市海淀外国语实验学校初三 3 月份月考数学试题2020.3.17班级姓名考生须知1．本试卷共8 页，共三道大题，28 道小题。

满分100 分。

考试时间120 分钟。

2．在试卷和答题卡上准确填写班级和姓名。

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4．在答题卡上，作图题用2B 铅笔作答，其他题用黑色字迹签字笔作答。

一、选择题（本题共16 分，每小题2 分）第1-8 题均有四个选项，符合题意的选项只．有．一个．1．响应党中央号召，连日来，全国广大共产党员继续踊跃捐款，表达对新冠肺炎疫情防控工作的支持。

据统计，截至 3 月 10 日，全国已有 7436 万多名党员自愿捐款，共捐款 76.8 亿元，则 76.8 亿元用科学记数法可表示为A．7.68 ⨯109 元B．7.68 ⨯1010 元C．76.8 ⨯108 元D．0.768 ⨯1010 元2．某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“点”字所在面相对的面上的汉字是A.青B.春C.梦D.想3．如图，在△ABC 中，AB=AC，∠A=30°，直线a∥b，顶点C 在直线b 上，直线a 交AB 于点D，交AC 于点E，若∠1=145°，则∠2 的度数是A.30°B.35°C.40°D.45°4．下列运算正确的是5．如图1，该大桥由五个高度不同，跨径也不同的抛物线型钢拱通过吊桥，拉锁与主梁相连，最高的钢拱如图2 所示，此钢拱（近似看成二次函数的图象-抛物线）在同一竖直平面内，与拱脚所在的水平面相交于A，B 两点，拱高为78 米（即最高点O 到AB 的距离为78 米），跨径为90 米（即AB=90 米），以最高点O 为坐标原点，以平行于AB 的直线为x 轴建立平面直角坐标系，则此抛物线钢拱的函数表达式为图1 图26．如右上图，将△ABC 绕点C（0，1）旋转180°得到△A'B'C，设点A 的坐标为(a, b) ，则点A'的坐标为A. (-a, -b)B. (-a, -b + 1)C. (-a, -b - 1)D. (-a, -b + 2)7．如图，点A 的坐标是（﹣2，0），点B 的坐标是（0，6），C 为OB 的中点，将△ABC 绕点B 逆时针旋转90°后得到△A′B′C′．若反比例函数的图象恰好经过A′B 的中点D，则k 的值是A．9 B．12 C．15 D．188．宽与长的比是5 -1（约为0．618）的矩形叫做黄金矩形．黄金矩形蕴藏着丰富的美学2价值，给我们以协调和匀称的美感．我们可以用这样的方法画出黄金矩形：作正方形ABCD，分别取AD，BC 的中点E，F，连接EF；以点F 为圆心，以FD 为半径画弧，交BC 的延长线与点G；作GH ⊥AD ，交AD 的延长线于点H．则图中下列矩形是黄金矩形的是A．矩形DCGH B．矩形EFCD C．矩形EFGH D．矩形ABFE二、填空题（本题共16 分，每小题2 分）9．已知x＝1 是方程x2+bx﹣2＝0 的一个根，则方程的另一个根是．10．已知点P（x，y）位于第四象限，并且x≤y+4（x，y 为整数），写出一个符合上述条件的点P 的坐标．611．已知一次函数y =kx +b ( b ≠0)经过(2,-1),(-3,4)两点,则它的图象不经过第象限.12．世界文化遗产“三孔”景区已经完成5G 基站布设，“孔夫子家”自此有了5G 网络．5G 网络峰值速率为4G 网络峰值速率的10 倍，在峰值速率下传输500 兆数据，5G 网络比4G 网络快45 秒，求这两种网络的峰值速率．设4G 网络的峰值速率为每秒传输x 兆数据，依题意，可列方程是．13．如下图左，在△ABC 中，∠BAC=90°，AB=AC= 4 cm，点D 为△ABC 内一点，∠BAD=15°，AD=6cm，连接BD，将△ABD 绕点A 逆时针方向旋转，使AB 与AC 重合，点D 的对应点E，连接DE，DE 交AC 于点F，则CF 的长为cm.14．如上图中，抛物线y＝ax2+c 与直线y＝mx+n 交于A（﹣1，p），B（3，q）两点，则不等式ax2+mx+c＞n 的解集是．15．如上图右，四边形ABCD 内接于⊙O，AB 为⊙O 的直径，点C 为的中点．若∠A=40°，则∠B= 度．16．如图，在平面直角坐标系中，以为圆心，适当长为半径画弧，交轴于点，交轴于点，再分别以点，为圆心，大于的长为半径画弧，两弧在第二象限内交于点，则与的数量关系是．三、解答题（本题共68 分，第17-22 题，每小题5 分；第23-26 题，每小题6 分；第27-28题，每小题7 分）解答应写出文字说明、演算步骤或证明过程．17．计算：6sin60°﹣）0+| ﹣2020|．18．已知x +y =xy ，求代数式1+1- (1-x)(1-y) 的值.x yIM ID19．如图，在四边形ABCD 中，AB=BC，BF 平分∠ABC，AF∥DC，连接AC，CF. 求证：（1）AF=CF；（2）CA 平分∠DCF.20．去年某市为创评“全国文明城市”称号，周末团市委组织志愿者进行宣传活动．班主任梁老师决定从4 名女班干部（小悦、小文、小雅和小宇）中通过抽签方式确定2 名女生去参加．抽签规则：将4 名女班干部姓名分别写在4 张完全相同的卡片正面，把四张卡片背面朝上，洗匀后放在桌面上，梁老师先从中随机抽取一张卡片，记下姓名，再从剩余的 3 张卡片中随机抽取第二张，记下姓名．（1）该班男生“小安被抽中”是事件，“小悦被抽中”是事件（填“不可能”或“必然”或“随机”）；第一次抽取卡片“小文被抽中”的概率为；（2）试用画树状图或列表的方法表示这次抽签所有可能的结果，并求出“小雅被抽中”的概率．21．阅读以下材料，并按要求完成相应的任务：莱昂哈德·欧拉（Leonhard Euler）是瑞士数学家，在数学上经常见到以他的名字命名的重要常数、公式和定理，下面是欧拉发现的一个定理：在△ABC 中，R 和r 分别为外接圆和内切圆的半径，O和I 分别为其外心和内心，则OI 2 =R2 - 2Rr .下面是该定理的证明过程（借助了第(2)问的结论）：延长AI 交⊙O 于点D，过点I 作⊙O 的直径MN，连接DM，AN.∵∠D=∠N，∴∠DMI=∠NAI（同弧所对的圆周角相等），∴△MDI∽△ANI.∴=，∴IA⋅ID =IM ⋅IN ①IA IN如图②，在图1（隐去MD，AN）的基础上作⊙O 的直径DE，连接BE，BD，BI，IF∵DE 是⊙O 的直径，∴∠DBE=90°.∵⊙I 与AB 相切于点F，∴∠AFI=90°，∴∠DBE=∠IFA.∵∠BAD=∠E（同弧所对圆周角相等），∴△AIF∽△EDB.BF•∴2Rr = (R +d )(R -d ) ，∴R2 -d 2 = 2Rr∴d 2 =R2 - 2Rr任务：（1）观察发现：IM=R+d，IN =（用含R，d 的代数式表示）；（2）请判断BD 和ID 的数量关系，并说明理由.（请利用图1 证明）（3）应用：若△ABC 的外接圆的半径为6cm，内切圆的半径为2cm，则△ABC 的外心与内心之间的距离为cm.k22．如图，反比例函数y=x（k≠0）的图象与正比例函数y=2x 的图象相交于A（1，a），B 两点，点C 在第四象限，CA∥y 轴，∠ABC=90°．（1）求k 的值及点B 的坐标；（2）求tanC 的值．D EA C23．如上图右，菱形ABCD 中，对角线AC，BD 交于O 点，DE∥AC，CE∥BD．（1）求证：四边形OCED 为矩形；（2）在BC 上截取CF＝CO，连接OF，若AC＝16，BD＝12，求四边形OFCD 的面积．O24．如图，AB 是⊙O 的直径，C 是⊙O 上一点，D 的中点，E 为OD 延长线上一点，且∠CAE＝2∠C，AC 与BD 交于点H，与OE 交于点F．（1）求证：AE 是⊙O 的切线；（2）若，求直径AB 的长．25．阅读下面的材料：如果函数y＝f（x）满足：对于自变量x 的取值范围内的任意x1，x2，（1）若x1＜x2，都有f（x1）＜f（x2），则称f（x）是增函数；（2）若x1＜x2，都有f（x1）＞f（x2），则称f（x）是减函数．例题：证明函数（x＞0）是减函数．证明：设0＜x1＜x2，f（x1）﹣f（x2）＝﹣＝＝．∵0＜x1＜x2，∴x2﹣x1＞0，x1x2＞0．∴＞0．即f（x1）﹣f（x2）＞0．∴f（x1）＞f（x2）．∴函数f（x）= （x＞0）是减函数．根据以上材料，解答下面的问题：f（﹣1）＝+（﹣2）＝-1，f（﹣2）＝+（﹣4）＝-154 （1）计算：f（﹣3）＝，f（﹣4）＝；（3）请仿照例题证明你的猜想．26．已知抛物线y =-2x 2 +(m -2)x +(n -2020) (m，n 为常数)．（1）若抛物线的的对称轴为直线x=1,且经过点（0，-1），求m，n 的值；（2）若抛物线上始终存在不重合的两点关于原点对称，求n 的取值范围；1 1（3）在（1）的条件下，存在正实数a，b( a＜b)，当a≤x≤b 时，恰好有b请直接写出a，b 的值．≤y ≤，a 27．小明研究了这样一道几何题：如图 1，在∆ABC 中，把AB 点A 顺时针旋转α(00 <α<1800 )得到AB'，把AC绕点A逆时针旋转β得到AC'，连接B'C'.当α+β=1800 时，请问∆AB'C'边B'C'上的中线AD 与BC 的数量关系是什么？以下是他的研究过程：特例验证：（1）①如图2，当∆ABC 为等边三角形时，AD 与BC 的数量关系为AD =BC ；②如图3，当∠BAC = 900 , BC = 8 时，则AD 长为.猜想论证：（2）在图 1 中，当∆ABC 为任意三角形时，猜想AD 与BC 的数量关系，并给予证明.拓展应用（3）如图 4，在四边形ABCD ，是否存在点P ，使∆PDC 与∆PAB 之间满足小明探究的问题中的边角关系？若存在，请画出点 P 的位置（保留作图痕迹，不需要说明）并直接写出∆PDC 的边DC 上的中线PQ 的长度；若不存在，说明理由.28.定义：点P是△ABC内部或边上的点（顶点除外），在△PAB，△PBC，△PCA中，若至少有一个三角形与△ABC相似，则称点P是△ABC的自相似点．例如：如图1，点P在△ABC的内部，∠PBC＝∠A，∠BCP＝∠ABC，则△BCP∽△ABC，故点P是△ABC的自相似点．请你运用所学知识，结合上述材料，解决下列问题：在平面直角坐标系中，点M是曲线y＝（x＞0）上的任意一点，点N是x轴正半轴上的任意一点．（1）如图2，点P是OM上一点，∠ONP＝∠M，请判断点P是△MON的自相似点吗？（填是或不是）：当点M的坐标是（，3），点N的坐标是（，0）时，请直接写出点P的坐标（2）如图3，当点M的坐标是（3，），点N的坐标是（2，0）时，求△MON的自相似点的坐标；（3）是否存在点M和点N，使△MON无自相似点？若存在，请直接写出这两点的坐标；若不存在，请说明理由．。

2019-2020学年北京市海淀区八一学校九年级（下）月考数学试卷（4月份）一、选择题（本大题共12小题，共24.0分）1.下列立体图形中，主视图是圆的是()A. B. C. D.2.某种感冒病毒的直径约为120nm，1nm=10−9m，则这种感冒病毒的直径用科学记数法表示()A. 120×10−9mB. 1.2×10−6mC. 1.2×10−7mD. 1.×10−8m3.已知a，b两数在数轴上表示的点的位置如图所示，下列结论中正确的是()A. a>bB. |a|<|b|C. ab>0D. −a>b4.如图，将一张矩形纸片折叠，若∠1=80°，则∠2的度数是()A. 50°B. 60°C. 70°D. 80°5.随机闭合开关S1，S2，S3中的两个，则灯泡发光的概率是()A. 34B. 23C. 13D. 126.点A(x1,y1)，B(x2,y2)是反比例函数y=2的图象上的两点，如果x1<x2<0，那么xy1，y2的大小关系是()A. y2<y1<0B. y1<y2<0C. y2>y1>0D. y1>y2>07.若一个多边形的每个内角均为120°，则该多边形是()A. 四边形B. 五边形C. 六边形D. 七边形8.如果a2+3a+1=0，那么代数式(a2+9a +6)⋅2a2a+3的值为()A. 1B. −1C. 2D. −29.矩形、菱形、正方形都具有的性质是()A. 对角线相等B. 对角线互相平分C. 对角线互相垂直D. 对角线平分对角10.用配方法解方程x2−4x−1=0，方程应变形为()A. (x+2)2=3B. (x+2)2=5C. (x−2)2=3D. (x−2)2=511.定点投篮是同学们喜爱的体育项目之一，某位同学投出篮球的飞行路线可以看作是抛物线的一部分，篮球飞行的竖直高度y(单位：m)与水平距离x(单位：m)近似满足函数关系y=ax2+bx+c(a≠0).下表记录了该同学将篮球投出后的x与y的三组数据，根据上述函数模型和数据，可推断出篮球飞行到最高点时，水平距离为() x(单位：m)024y(单位：m) 2.25 3.45 3.05A. 1.5mB. 2mC. 2.5mD. 3m12.某市组织全民健身活动，有100名男选手参加由跑、跳、投等10个田径项目组成的“十项全能”比赛，其中25名选手的一百米跑成绩排名，跳远成绩排名与10项总成绩排名情况如图所示．甲、乙、丙表示三名男选手，下面有3个推断：①甲的一百米跑成绩排名比10项总成绩排名靠前；②乙的一百米跑成绩排名比10项总成绩排名靠后；③丙的一百米跑成绩排名比跳远成绩排名靠前．其中合理的是()A. ①B. ②C. ①②D. ①③二、填空题（本大题共8小题，共16.0分）13.说明：此大题结果中若含有无理数，“√”必须用汉字“根号下”表示．如“√34”必须写成“根号下34”．已知：m、n为两个连续的整数，且m<√11<n，则m+n=______．14.在平面直角坐标系xOy中，点A(a,b)(a>0,b>0)在双曲线y=k1x上，点A关于x轴的对称点B在双曲线y=k2x上，则k1+k2的值为______．15.如图，在矩形ABCD中，E是边AB中点，连接DE交AC于点F，若AB=12，AD=9，则CF的长为______．16.如图，点A，B，C，D在⊙O上，CB⏜=CD⏜，∠CAD=30°，∠ACD=50°，则∠ADB=______．17.如图，⊙O的半径为2.弦AB=2，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是______．18.计算：4sin60°+(π−1)0−√12+|1−√3|=______．19.不等式组{4(x−1)<x+2x+73>x的正整数解为x=______．20.如图，在△ABC中，∠ACB=90°，D为AB边上一点，连接CD，E为CD中点，连接BE并延长至点F，使得EF=EB，连接DF交AC于点G，连接CF.若∠A=30°，BC=2，CF=3，则CD=______．三、解答题（本大题共8小题，共60.0分）21.已知关于x的一元二次方程x2−3x+a−1=0有实数根．(1)求a的取值范围；(2)当a为符合条件的最大整数时，求此时方程的解．22.如图，点B为⊙O外一点，点A为⊙O上一点，点P为OB上一点且BP=BA，连接AP并延长交⊙O于点C，连接OC，OC⊥OB．(1)求证：AB是⊙O的切线；(2)若OB=10，⊙O的半径为8.求AP的长．(x>0)交于点23.如图，在平面直角坐标系xOy中，直线y=kx+k与双曲线y=4xA(1,a)．(1)求a，k的值；(2)已知直线l过点D(2,0)且平行于直线y=kx+k，点P(m,n)(m>3)是直线l上(x>0)于点M、N，双一动点，过点P分别作x轴、y轴的平行线，交双曲线y=4x曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为W.横、纵坐标都是整数的点叫做整点．①当m=4时，直接写出区域W内的整点个数；②若区域W内的整点个数不超过8个，结合图象，求m的取值范围．24.某公司的午餐采用自助的形式，并倡导员工“适度取餐，减少浪费”.该公司共有10个部门，且各部门的人数相同．为了解午餐的浪费情况，公司从这10个部门中随机抽取了A，B两个部门，进行了连续四周(20个工作日)的调查，得到这两个部门每天午餐浪费饭菜的重量，以下简称“每日餐余重量”(单位：千克)，并对这些数据进行了整理、描述和分析．下面给出了部分信息．a.A部门每日餐余重量的频数分布直方图如下(数据分成6组：0≤x<2，2≤x<4，4≤x<6，6≤x<8，8≤x<10，10≤x≤12)：b.A部门每日餐余重量在6≤x<8这一组的是：6.1 6.67.07.07.07.8c.B部门每日餐余重量如下：1.42.8 6.97.8 1.99.73.14.6 6.910.86.9 2.67.5 6.99.57.88.48.39.48.8d.A，B两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下：部门平均数中位数众数A 6.4m7.0B 6.67.2n根据以上信息，回答下列问题：(1)写出表中m，n的值，m=______，n=______；(2)在A，B这两个部门中，“适度取餐，减少浪费”做得较好的部门是______(填“A”或“B”)，理由是______；(3)结合A，B这两个部门每日餐余重量的数据，估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量．25.如图1，AB⏜是直径AB所对的半圆弧，点P是AB⏜与直径AB所围成图形的外部的一个定点，AB=8cm，点C是AB⏜上一动点，连接PC交AB于点D.小明根据学习函数的经验，对线段AD，CD，PD，进行了研究，设A，D两点间的距离为xcm，C，D两点间的距离为y1cm，P，D两点之间的距离为y2cm．小明根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整：(1)按照下表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值：x/cm0.001.002.003.003.204.005.006.006.507.008.00y1/cm0.001.042.093.113.304.004.413.462.501.530.00y2/cm6.245.294.353.463.302.642.00m 1.802.002.65补充表格；(说明：补全表格时，相关数值保留两位小数)(2)如图2，在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点，并画出函数y2的图象：(3)结合函数图象解决问题：当AD=2PD时，AD的长度约为______．26.在平面直角坐标系xOy中，抛物线y=ax2+bx经过点(3,3)．(1)用含a的式子表示b；(2)直线y=x+4a+4与直线y=4交于点B，求点B的坐标(用含a的式子表示)；(3)在(2)的条件下，已知点A(1,4)，若抛物线与线段AB恰有一个公共点，直接写出a(a<0)的取值范围．27.如图，在正方形ABCD中，P是边BC上的一动点(不与点B，C重合)，点B关于直线AP的对称点为E，连接AE.连接DE并延长交射线AP于点F，连接BF．(1)若∠BAP=α，直接写出∠ADF的大小(用含α的式子表示)；(2)求证：BF⊥DF；(3)连接CF，用等式表示线段AF，BF，CF之间的数量关系，并证明．28.如图1，在平面直角坐标系xOy中，过⊙T外一点P引它的两条切线，切点分别为M，N，若60°≤∠MPN<180°，则称P为⊙T的环绕点．(1)当⊙O半径为1时，①在P1(−2,0)，P2(0,1)，P3(1,1)中，⊙O的环绕点是______；②直线y=12x+b与x轴交于点A，y轴交于点B，若线段AB上存在⊙O的环绕点，求b的取值范围；(2)⊙T的半径为1，圆心为(0,t)，以(m,−√33m)(m>0)为圆心，√33m为半径的所有圆构成图形H，若在图形H上存在⊙T的环绕点，直接写出t的取值范围．答案和解析1.【答案】D【解析】解：A、圆锥的主视图是三角形，故A不符合题意；B、圆柱的主视图是矩形，故B不符合题意；C、圆台的主视图是梯形，故C不符合题意；D、球的主视图是圆，故D正确；故选：D．根据从正面看得到的图形是主视图，可得答案．本题考查了简单几何体的三视图，熟记常见几何体的三视图是解题关键．2.【答案】C【解析】解：∵1nm=10−9m，∴120nm=120×10−9m=1.2×10−7m.故选：C．科学记数法的表示形式为a×10n的形式，其中0<|a|≤1，n为整数．当原数为较大数时，n为整数位数减1；当原数为较小数(大于0小于1的小数)时，n为第一个非0数字前面所有0的个数的相反数．用科学记数法表示一个数的方法是：(1)确定a：a是只有一位整数的数；(2)确定n：当原数的绝对值≥10时，n为正整数，n等于原数的整数位数减1；当原数的绝对值<1时，n为负整数，n的绝对值等于原数中左起第一个非零数前零的个数(含整数位数上的零)．此题需要先换算单位把米换算成纳米，然后再根据科学记数法的方法表示．3.【答案】D【解析】解：∵由图可知，a<0<b，|a|>|b|，∴选项A、B错误；由于a、b异号，所以ab<0，故选项C错误；因为|a|>b，a<0，所以−a>b.故选项D正确．故选：D．先根据各点在数轴山上的位置判断出a、b的符号，进而可得出结论．此题主要考查了数轴，关键是掌握当数轴方向朝右时，右边的数总比左边的数大，原点左边的数为负数，右边的数为正数．4.【答案】A【解析】解：∵a//b，∴∠1=∠3=80°，(180°−80°)=由翻折不变性可知：∠2=∠4=1250°，故选：A．利用平行线的性质解决问题即可．本题考查平行线的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．5.【答案】B【解析】【分析】本题主要考查列表法求概率，属于简单题．采用列表法列出所有情况，再根据能让灯泡发光的情况利用概率公式进行计算即可求解．【解答】解：闭合的开关列表如下：除去重复情况，共有3种情况，必须闭合开关S3灯泡才亮，，即能让灯泡发光的概率是23故选：B．6.【答案】A【解析】解：∵反比例函数y=2x的图象在一，三象限，在每一象限内y随x的增大而减小，∵x1<x2<0，∴A(x1,y1)、B(x2,y2)两点均位于第三象限，∴y2<y1<0．故选：A．根据k的值判断此函数图象所在的象限，再根据x1<x2<0判断出A(x1,y1)、B(x2,y2)所在的象限，根据此函数的增减性即可解答．本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数的性质是解答此题的关键．7.【答案】C【解析】【解答】解：180°−120°=60°，360°÷60°=6．故选：C．【分析】本题主要考查的是正多边形的内角和与外角和．首先可求得每个外角为60°，然后根据外角和为360°即可求得多边形的边数．8.【答案】D【解析】解：(a2+9a +6)⋅2a2a+3=a2+9+6aa⋅2a2a+3=(a+3)2a⋅2a2a+3=2a(a+3)=2(a2+3a)，∵a2+3a+1=0，∴a 2+3a =−1，∴原式=2×(−1)=−2，故选：D ．根据分式的加法和乘法可以化简题目中的式子，然后根据a 2+3a +1=0，即可求得所求式子的值．本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．9.【答案】B【解析】解：矩形、菱形、正方形都具有的性质是对角线互相平分．故选：B ．利用特殊四边形的性质进而得出符合题意的答案．此题主要考查了多边形，正确掌握多边形的性质是解题关键．10.【答案】D【解析】解：∵x 2−4x =1，∴x 2−4x +4=1+4，即(x −2)2=5，故选：D ．常数项移到方程的右边后，两边配上一次项系数一半的平方，写成完全平方式即可得． 本题主要考查配方法解一元二次方程的能力，熟练掌握完全平方公式和配方法的基本步骤是解题的关键．11.【答案】C【解析】解：设二次函数的解析式为y =ax 2+bx +c ，根据表可得：{c =2.254a +2b +c =3.4516a +4b +c =3.05，解得：{a =−0.2b =1c =2.25，∴y =−0.2x 2+x +2.25=−0.2(x −2.5)2+3.5，∴可推断出篮球飞行到最高点时，水平距离为2.5米，故选：C．首先根据提供数据列出函数解析式，然后确定其顶点坐标的横坐标即为本题答案．考查了二次函数的应用，解题的关键是正确的求得解析式，难度不大．12.【答案】D【解析】解：由折线统计图可知：①甲的一百米跑成绩排名比10项总成绩排名靠前；结论正确；②乙的一百米跑成绩排名比10项总成绩排名靠前；故原说法错误；③由图2中10项总成绩的位置可知丙的一百米跑成绩排名比跳远成绩排名靠前；结论正确．所以合理的是①③．故选：D．解决本题需要从由统计图获取信息，由此关键是明确图表中数据的来源及所表示的意义，依据所示的实际意义获取正确的信息．本题考查折线统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．13.【答案】7【解析】解：∵9<11<16，∴3<√11<4，∴m=3，n=4，∴m+n=3+4=7．故答案为：7．先估算√11的取值范围，得出m、n的值，进而可得出结论．本题考查的是估算无理数的大小，先根据题意估算出√11的取值范围是解答此题的关键．14.【答案】0上，【解析】解：∵点A(a,b)(a>0,b>0)在双曲线y=k1x∴k1=ab；又∵点A与点B关于x轴对称，∴B(a,−b)∵点B在双曲线y=k2x上，∴k2=−ab；∴k1+k2=ab+(−ab)=0；故答案为：0．由点A(a,b)(a>0,b>0)在双曲线y=k1x上，可得k1=ab，由点A与点B关于x轴对称，可得到点B的坐标，进而表示出k2，然后得出答案．本题考查反比例函数图象上的点坐标的特征，关于x轴对称的点的坐标的特征以及互为相反数的和为0的性质．15.【答案】10【解析】解：∵四边形ABCD是矩形，∴AD=BC=9，AB=CD=12，∠B=90°，∴AC=√AB2+BC2=√144+81=15，∵E是边AB中点，∴AE=6，∵AB//CD，∴△AEF∽△CDF，∴AECD =AFCF=12，∴CF=2AF，∵AF+CF=AC=15，∴AF=5，∴CF=10，故答案为：10．由勾股定理可求AC的长，通过证明△AEF∽△CDF，可得AECD =AFCF=12，可得CF=2AF，即可求解．本题考查了相似三角形的判定和性质，矩形的性质，勾股定理等知识，灵活运用这些性质解决问题是本题的关键．16.【答案】70°【解析】【试题解析】【分析】此题主要考查了圆周角定理以及三角形内角和定理有关知识，直接利用圆周角定理以及结合三角形内角和定理得出∠ACB=∠ADB=180°−∠CAB−∠ABC，进而得出答案．【解答】解：∵CB⏜=CD⏜，∠CAD=30°，∴∠CAD=∠CAB=30°，∴∠DBC=∠DAC=30°，∵∠ACD=50°，∴∠ABD=50°，∴∠ACB=∠ADB=180°−∠CAB−∠ABC=180°−50°−30°−30°=70°．故答案为70°．17.【答案】√3【解析】解：连结OA、OB，作△ABC的外接圆D，如图1，∵OA=OB=2，AB=2，∴△OAB为等边三角形，∴∠AOB=60°，∴∠APB=1∠AOB=30°，2∵AC⊥AP，∴∠C=60°，∵AB=2，要使△ABC的最大面积，则点C到AB的距离最大，∵∠ACB=60°，点C在⊙D上，∴∠ADB=120°，如图2，当点C优弧AB的中点时，点C到AB的距离最大，此时△ABC为等边三角形，且面积为√34AB2=√3，∴△ABC的最大面积为√3．故答案为：√3．连结OA、OB，如图1，由OA=OB=AB=2可判断△OAB为等边三角形，则∠AOB=60°，根据圆周角定理得∠APB=12∠AOB=30°，由于AC⊥AP，所以∠C=60°，因为AB=2，则要使△ABC的最大面积，点C到AB的距离要最大；由∠ACB=60°，可根据圆周角定理判断点C在⊙D上，且∠ADB=120°，如图2，于是当点C优弧AB的中点时，点C到AB的距离最大，此时△ABC为等边三角形，从而得到△ABC的最大面积．本题考查了圆的综合题：熟练掌握圆周角定理和等边三角形的判断与性质；记住等边三角形的面积公式．18.【答案】√3【解析】解：4sin60°+(π−1)0−√12+|1−√3|=4×√32+1−2√3+√3−1=2√3−√3=√3．故答案为：√3．首先计算乘方、开方，然后计算乘法，最后从左向右依次计算，求出算式的值是多少即可．此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．正确化简各数是解题关键．19.【答案】1【解析】解：{4(x−1)<x+2①x+73>x②，由①得：x<2，由②得：x<72，∴不等式组的解集为x<2，则不等式组的正整数解为x=1．故答案为：1．求出不等式组的解集，确定出正整数解即可．此题考查了一元一次不等式组的整数解，求出不等式组的解集是解本题的关键．20.【答案】√7【解析】解：∵点E为CD中点，∴CE=DE．∵EF=BE，∴四边形DBCF是平行四边形．∴CF//AB，DF//BC．∴∠FCG=∠A=30°，∠CGF=∠CGD=∠ACB=90°．在Rt△FCG中，CF=3，∴FG=12CF=32，CG=32√3．∵DF=BC=2，∴DG=12．在Rt△DCG中，CD=√CG2+DG2=√7．故答案为：√7．证明四边形DBCF为平行四边形，由平行四边形的性质可得CF//AB，DF//BC，可得∠FCG=∠A=30°，∠CGF=∠CGD=∠ACB=90°，由直角三角形的性质可得FG，CG，GD的长，由勾股定理可求CD的长．本题考查了平行四边形的判定和性质，直角三角形的性质，勾股定理，利用直角三角形的性质求线段CG的长度是本题的关键．21.【答案】解：(1)∵关于x的一元二次方程x2−3x+a−1=0有实数根，∴△=(−3)2−4(a−1)=−4a+13≥0，，解得：a≤134；即a的取值范围是a≤134(2)∵a的取值范围是a≤13，4∴整数a的最大值是3，把a=3代入方程x2−3x+a−1=0得：x2−3x+2=0，解得：x1=1，x2=2．【解析】(1)先求出“△”的值，再根据根的判别式的内容判断即可；(2)求出a=3，把a=3代入方程，求出方程的解即可．本题考查了解一元二次方程和根的判别式，能根据根的判别式求出a的取值范围是解此题的关键．22.【答案】(1)证明：∵BP=BA，OA=OC，∴∠BAP=∠BPA，∠PAO=∠C，∵OC⊥OB，∴∠COP=90°，∴∠OPC+∠C=90°，∵∠OPC=∠BPA，∴∠BAP=∠OPC，∴∠BAP+∠OAP=90°，即∠BAO=90°，∴AB⊥OA，又∵OA为⊙O的半径，∴AB是⊙O的切线；(2)解：如图，作BD⊥AP于点D，∵⊙O的半径为8，∴CO=OA=8，由(1)得：∠BAO=90°，∴AB=√OB2−OA2=√102−82=6，∴BP=BA=6，∴OP=OB−BP=4，在Rt△CPO中，OP=4，CO=8，∴CP=√OP2+CO2=√42+82=4√5，∵BA=BP，BD⊥AP，∴AD=PD，∠BDP=90°=∠COP，∵∠BPD=∠CPO，∴△BPD∽△CPO，∴BPCP =PDPO，即64√5=PD4，解得：PD=6√55，∴AP=2PD=12√55．【解析】(1)由等腰三角形的性质可得∠BAP=∠BPA，可证∠BAO=90°，结论得证；(2)作BD⊥AP于点D，先求出AB，OP的长，再求出CP长，根据△BPD∽△CPO，得出比例线段，求出PD的长，则AP可求．本题考查了切线的判定与性质，等腰三角形的性质，相似三角形的判定和性质，勾股定理等知识；正确的作出辅助线是解题的关键．23.【答案】解：(1)∵点A(1,a)在双曲线y=4x上，∴a=41=4，∴点A的坐标为(1,4)，将A(1,4)代入y=kx+k，得：k+k=4，∴k=2．(2)①∵直线l过点D(2,0)且平行于直线y=2x+2，∴直线l的解析式为y=2x−4．当m=4时，n=2m−4=4，∴点P的坐标为(4,4)．依照题意画出图象，如图1所示．观察图形，可知：区域W内的整点个数是3．②如图2所示：当2x−4=4时，即x=4，此时线段PM和PN上有5个整点；当2x−4=5时，即x=4.5，此时线段PM上有整点．观察图形，可知：若区域W内的整点个数不超过8个，m的取值范围为3<m≤4.5．【解析】(1)利用反比例函数图象上点的坐标特征可求出a的值，进而可得出点A的坐标，根据点A的坐标，利用待定系数法可求出k值；(2)①由直线l过点D(2,0)且平行于直线y=2x+2可得出直线l的解析式，利用一次函数图象上点的坐标特征找出当m=4时点P的坐标，画出图形，观察后即可得出结论；②找出：当x=4时，线段PM和PN上有5个整点；当x=4.5时，线段PM上有整点．结合函数图象，即可求出当区域W内的整点个数不超过8个时m的取值范围．本题考查了反比例函数图象上点的坐标特征、待定系数法求一次函数解析式、平行的性质以及数形结合，解题的关键是：(1)根据点的坐标，利用待定系数法求出k值；(2)①②依照题意画出图形，利用数形结合找出结论．24.【答案】6.8 6.9A A部门的平均数较小，中位数也较小【解析】解：(1)A部门20个工作日的餐余重量从小到大排列后，处在中间位置的两个=6.8，因此中位数是6.8，即m=6.8，数的平均数为6.6+7.02B部门20个工作日的餐余重量出现次数最多的是6.9，共出现4次，故众数是6.9，即n= 6.9，故答案为：6.8，6.9；(2)从中位数、平均数上看，A部门的中位数较小，平均数也较小，说明浪费的少，因此，做得较好的是A部门，理由：A部门的中位数较小，平均数也较小，故答案为：A；A部门的中位数较小，平均数也较小；×240×10=15600(千克)，(3)6.4+6.62答：该公司(10个部门)一年(按240个工作日计算)的餐余总重量为15600千克．(1)根据中位数、众数的意义可求出m、n的值；(2)从平均数、中位数方面得出结论及相应的理由；(3)计算出平均一个工作日餐余重量的平均数，再计算该公司(10个部门)一年(按240个工作日计算)的餐余总重量．本题考查频数分布直方图的意义和制作方法、理解平均数、中位数、众数的意义和计算方法是正确计算的前提．25.【答案】4.54【解析】解：(1)通过取点、画图、测量，可得m=1.73，(2)如图(3)∵当AD=2PD，AD，∴PD=12x的图象，并测量两个函数图象交点得：AD=4.54，在(2)中图象中作出y=12故答案为：4.54．(1)通过取点、画图、测量可求解；(2)根据题意作图即可；(3)由题意可得PD=12AD，画出y=12x，交曲线AD的值为所求，即可求解．本题是圆的综合题，以几何动点问题为背景，考查了函数思想和数形结合思想．在(3)中将线段的数量转化为函数问题，设计到了转化的数学思想．26.【答案】解：(1)将点(3,3)代入y=ax2+bx，得9a+3b=3．∴b=−3a+1．(2)令x+4a+4=4，得x=−4a．∴B(−4a,4)．(3)∵a<0，∴抛物线开口向下，抛物线与线段AB恰有一个公共点，∵A(1,4)，B(−4a,4)∴点A、B所在的直线为y=4，由(1)得b=1−3a，则抛物线可化为：y=ax2+(1−3a)x，分两种情况讨论：①当抛物线y=ax2+(1−3a)x与直线y=4只有一个公共点时，且抛物线的顶点在点A、B之间，则1≤3a−12a≤−4a或−4a≤3a−12a≤1，方程ax2+(1−3a)x=4的根的判别式：△=0，即(1−3a)2+16a=0，解得a1=−19，a2=−1，当a1=−19时，3a−12a=6(不符合题意)，当a2=−1时，3a−12a=2，则1≤3a−12a≤−4a成立．②当抛物线经过点A时，即当x=1，y=4时，a+1−3a=4，解得a=−32；∴a<−32时，抛物线与线段AB恰有一个公共点，综上：a的取值为：a=−1或a<−32时，抛物线与线段AB恰有一个公共点．【解析】(1)将点(3,3)代入解析式即可求得；(2)把y=4代入y=x+4a+4得到关于x的方程，解方程即可求得；(3)根据抛物线与线段AB恰有一个公共点，分两种情况讨论，即可得结论．本题考查了二次函数的性质、二次函数和一次函数图象上的点的坐标特征，解决本题的关键是理解抛物线与线段AB恰有一个公共点的含义．27.【答案】(1)解：由轴对称的性质得：∠EAP=∠BAP=α，AE=AB，∵四边形ABCD是正方形，∴∠BAD=90°，AB=AD，∴∠DAE=90°−2α，AD=AE，∴∠ADF=∠AED=12(180°−∠DAE)=12(90°+2α)=45°+α；(2)证明：∵四边形ABCD是正方形，∴∠BAD=90°，AB=AD，∵点E与点B关于直线AP对称，∴∠AEF=∠ABF，AE=AB．∴AE=AD．∴∠ADE=∠AED．∵∠AED+∠AEF=180°，∴在四边形ABFD中，∠ADE+∠ABF=180°，∴∠BFD+∠BAD=180°，∴∠BFD=90°∴BF⊥DF；(3)解：线段AF，BF，CF之间的数量关系为AF=√2BF+CF，理由如下：过点B作BM⊥BF交AF于点M，如图所示：∵四边形ABCD是正方形，∴AB =CB ，∠ABC =90°，∴∠ABM =∠CBF ，∵点E 与点B 关于直线AP 对称，∠BFD =90°，∴∠MFB =∠MFE =45°，∴△BMF 是等腰直角三角形，∴BM =BF ，FM =√2BF ，在△AMB 和△CFB 中，{AB =CB∠ABM =∠CBF BM =BF，∴△AMB≌△CFB(SAS)，∴AM =CF ，∵AF =FM +AM ，∴AF =√2BF +CF ．【解析】(1)由轴对称的性质得出∠EAP =∠BAP =α，AE =AB ，由正方形的性质得出∠BAD =90°，AB =AD ，得出∠DAE =90°−2α，AD =AE ，由等腰三角形的性质即可得出答案；(2)由轴对称的性质得出∠AEF =∠ABF ，AE =AB.得出AE =AD.由等腰三角形的性质得出∠ADE =∠AED.证出∠BFD +∠BAD =180°，得出∠BFD =90°即可；(3)过点B 作BM ⊥BF 交AF 于点M ，证明△BMF 是等腰直角三角形，得出BM =BF ，FM =√2BF ，证明△AMB≌△CFB(SAS)，得出AM =CF ，即可得出结论．本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质、轴对称的性质、等腰三角形的性质、等腰直角三角形的判定与性质等知识；熟练掌握正方形的性质和等腰三角形的性质，证明三角形全等是解题的关键．28.【答案】P 1，P 3【解析】解：(1)①如图，PM，PN是⊙T的两条切线，M，N为切点，连接TM，TN．当∠MPN=60°时，∵PT平分∠MPN，∵∠TPM=∠TPN=30°，∵TM⊥PM，TN⊥PN，∴∠PMT=∠PNT=90°，∴TP=2TM，以T为圆心，TP为半径作⊙T，观察图象可知：当60°≤∠MPN<180°时，⊙T的环绕点在图中的圆环内部(包括大圆上的点不包括小圆上的点)．如图1中，以O为圆心2为半径作⊙O，观察图象可知，P1，P3是⊙O的环绕点，故答案为P1，P3；②如图3中，设小圆交y轴的正半轴与于E．当直线y=12x+b经过点E时，b=1．当直线y=12x+b与大圆相切于K(在第二象限)时，连接OK，由题意B(0,b)，A(−2b,0)，∴OB=b，OA=2b，AB=√AO2+OB2=√5b，∵OK=2，12⋅AB⋅OK=12⋅OA⋅OB，∴S△ABO=12×AB⋅OK=12×OA⋅OB，即12×√5b×2=12×b×2b，解得b=√5，观察图象可知，当1<b≤√5时，线段AB上存在⊙O的环绕点，根据对称性可知：当−√5≤b<−1时，线段AB上存在⊙O的环绕点，综上所述，满足条件的b的值为1<b≤√5或−√5≤b<−1；(2)如图4中，不妨设E(m,−√33m)，则点E在直线y=−√33x时，∵m>0，∴点E在射线OE上运动，作EM⊥x轴，∵E(m,−√33m)，∴OM=m，EM=√33m，∴以E(m,−√33m)(m>0)为圆心，√33m为半径的⊙E与x轴相切，作⊙E的切线ON，观察图象可知，以E(m,−√33m)(m>0)为圆心，√33m为半径的所有圆构成图形H，图形H即为∠MON的内部，包括射线OM，ON上．当⊙T的圆心在y轴的正半轴上时，假设以T为圆心，2为半径的圆与射线ON相切于D，连接TD．∵tan∠EOM=EMOM =√33，∴∠EOM=30°，∵ON，OM是⊙E的切线，∴∠EON=∠EOM=30°，∴∠TOD=30°，∴OT=2DT=4，∴T(0,−4)，当⊙T的圆心在y轴的负半轴上时，且经过点O(0,0)时，T(0,2)，观察图象可知，当−4≤t≤2时，在图形H上存在⊙T的环绕点．(1)①如图，PM，PN是⊙T的两条切线，M，N为切点，连接TM，TN.当∠MPN=60°时，可证TP=2TM，以T为圆心，TP为半径作⊙T，首先说明：当60°≤∠MPN<180°时，⊙T的环绕点在图中的圆环内部(包括大圆设的点不包括小圆上的点)，利用这个结论解决问题即可；②如图2中，设小圆交y轴的正半轴与于E.求出两种特殊位置b的值，结合图形根据对称性解决问题即可；(2)如图3中，不妨设E(m,−√33m)，则点E在直线y=−√33x时，以E(m,−√33m)(m>0)为圆心，√33m为半径的⊙E与x轴相切，作⊙E的切线ON，观察图象可知，以为圆心，√33m为半径的所有圆构成图形H，图形H即为∠MON的内部，包括射线OM，ON上．利用(1)中结论，画出圆环，当圆环与∠MON的内部有交点时，满足条件，求出两种特殊位置t的值即可解决问题．本题属于圆综合题，考查了切线长定理，直线与圆的位置关系，一次函数的性质等知识，解题的关键是理解题意，学会用转化的思想问题，学会利用特殊位置解决数学问题，属于中考压轴题．。

海淀实验中学九年级第二学期适应练习数 学2020．04学校 姓名 准考证号1．本试卷共 8 页，共三道大题，28 道小题。

满分 100 分。

考试时间 120 分钟。

考 2．在试卷和答题卡上准确填写学校名称、姓名和准考证号。

生 3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

须 4．在答题卡上，选择题、作图题用 2B 铅笔作答，其他题用黑色字迹签字笔作 知答。

5．考试结束，将本试卷、答题卡和草稿纸一并交回。

一、选择题（本题共 16 分，每小题 2 分）第 1-8 题均有四个选项，符合题意的选项只．有．一个． 1. 随着“一带一路”的建设推进，北京某区口岸进口货值业务量加速增长，进口货值飙升至 189 000 000 美元，比上一年翻了三倍，创下历史新高．将 189 000 000 用科学记数法表 示应为A ．189 ⨯106B ．1.89 ⨯106C ．18.9 ⨯107D ．1.89 ⨯1082. 在数轴上，实数 a ，b 对应的点的位置如图所示，且这两 个点关于原点对称，下列结论中，正确的是(A) a + b = 0 (B) a − b = 0 (C) a b < (D) ab > 03. 右图是某几何体的三视图，该几何体是(A) 三棱柱 (B) 长方体 (C) 圆锥(D) 圆柱4. 如图，AB ∥CD ，直线 EF 分别交 AB ，CD 于 M ，N 两点，将一个含有 45°角的直角三角尺按如图所示的方式摆放，若∠E MB =75°，则 ∠P N M 等于 A ．15° B ．25°C ．30°D ．45°5. 如果一个多边形的内角和为 720°，那么这个多边形是 A ．五边形 B ．六边形 C ．七边形D ．八边形6. 如果 x+y =4，那么代数式222222x yx y x y---的值是A ． ﹣2B ． 2 C．12 D ．-127.在“校园读书月”活动中，小华调查了班级里 40 名同学本学期购买课外书的花费情况，并将 结果绘制成如图所示的统计图.下面有四个推断： ①这次调查获取的样本数据的众数是 30 元 ②这次调查获取的样本数据的中位数是 40 元 ③若该校共有学生 1200 人，根据样本 数据，估计本学期计划购买课外书花 费 50 元的学生有 300 人④花费不超过 50 元的同学共有 18 人其中合理的是 (A) ①② (B) ②④(C) ①③(D) ①④8. 如图，小宇计划在甲、乙、丙、丁四个小区中挑选一个小区租住，附近有东西向的交通主干道 a 和南北向的交通主干道 b ，若他希望租住的小区到主干道 a 和主干道 b 的直线距离之 和最小，则下图中符合他要求的小区是A ．甲B ．乙C ．丙D ．丁二、填空题（本题共 16 分，每小题 2 分）9. 如图，测量小玻璃管口径的量具 ABC 上，AB 的长为 10 毫米，AC 被分为 60 等份，如果小管口中 DE 正好对着量具上 20 份处（DE ∥AB ）， 那么小管口径 DE 的长是毫米．10. 一次函数 y = kx + b (k ≠ 0) 的图象过点 (0, 2) ，且 y 随 x 的增大而减小，请写出一个符 合条件的函数表达式：．11. 如图是 4×4 的正方形网格，每个小正方形的边长均为 1 且顶点称为格点，点 A ，B 均在格点上.在网格中建立平面直角坐 标系，且 A （-1，1），B （1，2）.如果点 C 也在此 4×4 的正 方形网格的格点上，且△A BC 是等腰三角形，那么当△AB C 的面积最大时，点 C 的坐标为．12 用一组 a ，b 的值说明命题“对于非零实数 a ，b ，若 a < b ，则11a b>是错误的，这组值 可以是 a =，b = ．13. 如图，AB 为⊙O 的直径，AC 与⊙O 相切于点 A ，弦 BD ∥OC .若 ∠C = 36︒ ，则∠D O C =︒ ．14. 京张高铁是 2022 年北京冬奥会的重要交通基础设施，考虑到不同路段的特殊情况，将根据不同的运行区间设置不同的时速．其中，北京北站到清河段全长 11 千米，分为地 下清华园隧道和地上区间两部分，运行速度分别设计为 80 千米/小时和 120 千米/小时．按此运行速度，地下隧道运行时间比地上大约多 2 分．钟．（130小时），求清华园隧道 全长为多少千米．设清华园隧道全长为 x 千米，依题意，可列方程为15. 某校初三年年级 68 名师生参加社会实践活动，计划租车前往，租车收费标准如下：车型 大巴车（最多可坐 55 人）中巴车（最多可坐 39 人）小巴车（最多可坐 26 人）每车租金 （元/天）90080055016. 某实验室对 150 款不同型号的保温杯进行质量检测，其中一个品牌的 30 款保温杯的保 温性、便携性与综合质量在此次检测中的排名情况如下图所示，可以看出其中 A 型保温杯 的优势是．三、解答题（本题共 68 分，第 17-22 题，每小题 5 分；第 23-26 题，每小题 6 分；第 27-28 题，每小题 7 分）解答应写出文字说明、演算步骤或证明过程．17．计算：04sin 60(3)π+-18．解不等式组：3(1)1342x x x -<+⎧⎪⎨-≥-⎪⎩19．如图，在△AB C 中，AB=AC ，点 D 是 BC 边上一点，EF 垂直平分 CD ，交 AC 于点 E ， 交 BC 于点 F ，连结 DE ，求证：DE ∥AB ．20．已知：关于 x 的一元二次方程 x 2 - 4x + 2m = 0 有两个不相等的实数根．（1）求 m 的取值范围；（2）如果 m 为非．负．整．数．，且该方程的根都是整．数．，求 m 的值．21．如图，平行四边形 ABCD 中，对角线 AC ，BD 交于点 O ，且 AC ⊥BC ，点 E 是 BC 延长 线上一点，AD BE =12，连接 DE ． （1）求证：四边形 ACED 为矩形；（2）连接 OE ，如果 BD=10，求 OE 的长．22 如图，直线 y = 2x + 6 与反比例函数 y = kx( x > 0) 的图象交于点 A (1, m )，与 x 轴交于 点 B ，与 y 轴交于点 D ．（1）求 m 的值和反比例函数的表达式；（2）在 y 轴上有一动点 P （0，n ） ( 0 < n < 6 ) ，过点 P 作平行于 x 轴的直线,交反比例函数的图象于点 M ，交直线 AB 于点 N ，连接 BM ．若S △BMN = 12S △BOD ，求 n 的值．23．如图， D 为 ⊙O 上一点，点 C 在直径 BA 的延长线上， ∠CDA = ∠CBD ． （1）求证： CD 是⊙O 的切线； （2）过点 B 作⊙O 的切线交 CD 的延长线于点 E ，若 AB =6，tan ∠CDA =23，依题意补全图形并求 DE 的长24. 为了了解某区的绿化进程，小明同学查询了园林绿化政务网，根据网站发布的近几年该 城市城市绿化资源情况的相关数据，绘制了如下统计图（不完整）某市 2015-2019 年人均公共绿地面积年增长率统计图 某市 2015-2019 年人均公共绿地面积统计图②补全条那统计图：（2）小明同学还了解到自己身边的许多同学都树立起了绿色文明理念，从自身做起，多种树，为提高人均公共绿地面积做贡献，他对所在班级的40 多名同学2019 年参与植树的情况做了调查，并根据调查情况绘制出如下统计表：种树棵数（棵）012345人数1056946如果按照小明的统计数据，请你通过计算估计，他所在学校的300 名同学在2019 年共植树多少棵？25.如图，半圆O 的直径AB＝5cm，点M 在AB 上且AM＝1cm，点P 是半圆O 上的动点，过点B 作BQ⊥PM 交PM（或PM 的延长线）于点Q．设PM＝xcm，BQ＝ycm．（当点P 与点A 或点B 重合时，y 的值为0）小石根据学习函数的经验，对函数y 随自变量x 的变化而变化的规律进行了探究．下面是小石的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x 与y 的几组值，如下表：（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当BQ 与直径AB 所夹的锐角为60°时，PM 的长度约为cm．26、已知抛物线y=mx2-4mx+3(m>0)，（1）求出抛物线的对称轴方程以及与y 轴的交点坐标（2）当m=2 时.求出抛物线与x 轴的交点坐标（3）已知A（1,0）B（4,0）C（3,3）三点构成三角形ABC，当抛物线与三角形ABC 的三条边一共有2 个交点时，直接写出m 的取值范围。

北京市海淀区2019-2020学年中考第四次大联考数学试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．PM2.5是大气压中直径小于或等于0.0000025m 的颗粒物，将0.0000025用科学记数法表示为（ ） A ．0.25×10﹣5 B ．0.25×10﹣6 C ．2.5×10﹣5 D ．2.5×10﹣62．点A 为数轴上表示-2的动点，当点A 沿数轴移动4个单位长到B 时，点B 所表示的实数是（ ） A ．1 B ．-6 C ．2或-6 D ．不同于以上答案3．如图，矩形ABCD 中，12AB =，13BC =，以B 为圆心，BA 为半径画弧，交BC 于点E ，以D 为圆心，DA 为半径画弧，交BC 于点F ，则EF 的长为（ ）A ．3B ．4C ．92D ．54．在国家“一带一路”倡议下，我国与欧洲开通了互利互惠的中欧专列．行程最长，途经城市和国家最多的一趟专列全程长13000 km ，将13000用科学记数法表示应为( )A ．0.13×105B ．1.3×104C ．1.3×105D ．13×1035．下列二次函数的图象，不能通过函数y=3x 2的图象平移得到的是（ ）A ．y=3x 2+2B ．y=3（x ﹣1）2C ．y=3（x ﹣1）2+2D ．y=2x 26．如图是一个几何体的主视图和俯视图，则这个几何体是（ ）A ．三棱柱B ．正方体C ．三棱锥D ．长方体7．在一个口袋中有4个完全相同的小球，把它们分别标号为 1，2，3，4，随机地摸出一个小球然后放回，再随机地摸出一个小球．则两次摸出的小球的标号的和等于6的概率为（ ）A ．116B ．18C ．316D ．148．已知一个多边形的内角和是外角和的3倍，则这个多边形是（ ）A ．五边形B ．六边形C ．七边形D ．八边形9．如图，已知△ABC，按以下步骤作图：①分别以B，C 为圆心，以大于12BC 的长为半径作弧，两弧相交于两点M，N；②作直线MN 交AB 于点D，连接CD．若CD=AC，∠A=50°，则∠ACB 的度数为（）A．90°B．95°C．105°D．110°10．已知a,b为两个连续的整数,且a<11<b,则a+b的值为()A．7 B．8 C．9 D．1011．观察图中的“品”字形中个数之间的规律，根据观察到的规律得出a的值为A．75 B．89 C．103 D．13912．下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．二、填空题：（本大题共6个小题，每小题4分，共24分．）13．分解因式：2288a a-+=_______14．如图，▱ABCD中，AC⊥CD，以C为圆心，CA为半径作圆弧交BC于E，交CD的延长线于点F，以AC上一点O为圆心OA为半径的圆与BC相切于点M，交AD于点N．若AC=9cm，OA=3cm，则图中阴影部分的面积为_____cm1．15．已知21xy=⎧⎨=⎩是方程组ax5{1bybx ay+=+=的解，则a﹣b的值是___________16．△ABC的顶点都在方格纸的格点上，则sinA＝_ ▲ ．17．用正三角形、正四边形和正六边形按如图所示的规律拼图案，即从第二个图案开始，每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个，则第n个图案中正三角形的个数为（用含n 的代数式表示）．18．将一个底面半径为2，高为4的圆柱形纸筒沿一条母线剪开，所得到的侧面展开图形面积为_____．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）一辆汽车在某次行驶过程中，油箱中的剩余油量y （升）与行驶路程x （千米）之间是一次函数关系，其部分图象如图所示．求y 关于x 的函数关系式；（不需要写定义域）已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时，司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？20．（6分）解不等式组：426113x x x x >-⎧⎪+⎨-≤⎪⎩，并写出它的所有整数解． 21．（6分）如图，抛物线2y ax bx c =++()0a ≠与x 轴交于点A 和点B （1，0），与y 轴交于点C （0，3），其对称轴l 为x =–1，P 为抛物线上第二象限的一个动点．（1）求抛物线的解析式并写出其顶点坐标；（2）当点P 的纵坐标为2时，求点P 的横坐标；（3）当点P 在运动过程中，求四边形PABC 面积最大时的值及此时点P 的坐标．22．（8分）如图1，矩形ABCD 中，E 是AD 的中点，以点E 直角顶点的直角三角形EFG 的两边EF ，EG 分别过点B ，C ，∠F ＝30°.（1）求证：BE ＝CE（2）将△EFG 绕点E 按顺时针方向旋转，当旋转到EF 与AD 重合时停止转动.若EF ，EG 分别与AB ，BC 相交于点M ，N.（如图2）①求证：△BEM ≌△CEN ；②若AB ＝2，求△BMN 面积的最大值；③当旋转停止时，点B 恰好在FG 上（如图3），求sin ∠EBG 的值.23．（8分）如图在由边长为1个单位长度的小正方形组成的12×12网格中，已知点A ，B ，C ，D 均为网格线的交点在网格中将△ABC 绕点D 顺时针旋转90°画出旋转后的图形△A 1B 1C 1；在网格中将△ABC 放大2倍得到△DEF ，使A 与D 为对应点．24．（10分）列方程或方程组解应用题：去年暑期，某地由于暴雨导致电路中断，该地供电局组织电工进行抢修．供电局距离抢修工地15千米．抢修车装载着所需材料先从供电局出发，10分钟后，电工乘吉普车从同一地点出发，结果他们同时到达抢修工地．已知吉普车速度是抢修车速度的1.5倍，求吉普车的速度．25．（10分）（1）计算：20(2)(3)12sin 60π︒-++-；（2）化简：2121()a a a a a--÷-． 26．（12分）如图1，在等边三角形ABC 中，CD 为中线，点Q 在线段CD 上运动，将线段QA 绕点Q 顺时针旋转，使得点A 的对应点E 落在射线BC 上，连接BQ ，设DAQ α∠=（060α<<o o 且30α≠o ）．（1）当030α<<o o 时，①在图1中依题意画出图形，并求BQE ∠（用含α的式子表示）；②探究线段CE ，AC ，CQ 之间的数量关系，并加以证明；（2）当3060α<<o o 时，直接写出线段CE ，AC ，CQ 之间的数量关系．27．（12分）每年的6月5日为世界环保日，为了提倡低碳环保，某公司决定购买10台节省能源的新设备，现有甲、乙两种型号的设备可供选购，经调查：购买了3台甲型设备比购买2台乙型设备多花了16万元，购买2台甲型设备比购买3台乙型设备少花6万元.求甲、乙两种型号设备的价格；该公司经预算决定购买节省能源的新设备的资金不超过110万元，你认为该公司有几种购买方案；在（2）的条件下，已知甲型设备的产量为240吨/月，乙型设备的产量为180吨/月，若每月要求总产量不低于2040吨，为了节约资金，请你为该公司设计一种最省钱的购买方案.参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．D【解析】【分析】根据科学记数法的定义，科学记数法的表示形式为a×10n ，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．在确定n 的值时，看该数是大于或等于1还是小于1．当该数大于或等于1时，n 为它的整数位数减1；当该数小于1时，－n 为它第一个有效数字前0的个数（含小数点前的1个0）．【详解】解： 0.0000025第一个有效数字前有6个0（含小数点前的1个0），从而60.0000025 2.510-=⨯． 故选D ．2．C【解析】解：∵点A 为数轴上的表示-1的动点，①当点A 沿数轴向左移动4个单位长度时，点B 所表示的有理数为-1-4=-6；②当点A 沿数轴向右移动4个单位长度时，点B 所表示的有理数为-1+4=1．故选C ．点睛：注意数的大小变化和平移之间的规律：左减右加．与点A 的距离为4个单位长度的点B 有两个，一个向左，一个向右．3．B【解析】【分析】连接DF ，在Rt DCF △中，利用勾股定理求出CF 的长度，则EF 的长度可求．【详解】连接DF ，∵四边形ABCD 是矩形∴12,13AB CD BE AD BC DF ======在Rt DCF △中，90C ∠=︒222213125CF DF CD ∴-=-=13121EC BC BE =-=-=Q514EF CF EC ∴=-=-=故选：B ．【点睛】本题主要考查勾股定理，掌握勾股定理的内容是解题的关键．4．B【解析】试题分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．将13000用科学记数法表示为：1.3×1．故选B．考点：科学记数法—表示较大的数5．D【解析】分析：根据平移变换只改变图形的位置不改变图形的形状与大小对各选项分析判断后利用排除法求解：A、y=3x2的图象向上平移2个单位得到y=3x2+2，故本选项错误；B、y=3x2的图象向右平移1个单位得到y=3（x﹣1）2，故本选项错误；C、y=3x2的图象向右平移1个单位，向上平移2个单位得到y=3（x﹣1）2+2，故本选项错误；D、y=3x2的图象平移不能得到y=2x2，故本选项正确．故选D．6．A【解析】【分析】根据三视图的知识使用排除法即可求得答案.【详解】如图，由主视图为三角形，排除了B、D，由俯视图为长方形，可排除C，故选A．【点睛】本题考查了由三视图判断几何体的知识，做此类题时可利用排除法解答．7．C【解析】列举出所有情况，看两次摸出的小球的标号的和等于6的情况数占总情况数的多少即可．解：共16种情况，和为6的情况数有3种，所以概率为．故选C．8．D【解析】【分析】根据多边形的外角和是360°，以及多边形的内角和定理即可求解．【详解】设多边形的边数是n，则(n−2)⋅180=3×360，解得：n=8.故选D.【点睛】此题考查多边形内角与外角，解题关键在于掌握其定理.9．C【解析】【分析】根据等腰三角形的性质得到∠CDA=∠A=50°，根据三角形内角和定理可得∠DCA=80°，根据题目中作图步骤可知，MN垂直平分线段BC，根据线段垂直平分线定理可知BD=CD，根据等边对等角得到∠B=∠BCD，根据三角形外角性质可知∠B+∠BCD=∠CDA，进而求得∠BCD=25°，根据图形可知∠ACB=∠ACD+∠BCD，即可解决问题.【详解】∵CD=AC，∠A=50°∴∠CDA=∠A=50°∵∠CDA+∠A+∠DCA=180°∴∠DCA=80°根据作图步骤可知，MN垂直平分线段BC∴BD=CD∴∠B=∠BCD∵∠B+∠BCD=∠CDA∴2∠BCD=50°∴∠BCD=25°∴∠ACB=∠ACD+∠BCD=80°+25°=105°故选C【点睛】本题考查了等腰三角形的性质、三角形内角和定理、线段垂直平分线定理以及三角形外角性质，熟练掌握各个性质定理是解题关键.10．A【解析】∵9<11<16，<<，即34<<，∵a ，b 为两个连续的整数，且a b <<，∴a=3，b=4，∴a+b=7，故选A.11．A【解析】观察可得，上边的数为连续的奇数1，3，5，7，9，11，左边的数为21，22，23，…，所以b=26=64，又因上边的数与左边的数的和正好等于右边的数，所以a=11+64=75，故选B ．12．B【解析】分析：根据轴对称图形与中心对称图形的概念求解即可．详解：A ．是轴对称图形，不是中心对称图形；B ．是轴对称图形，也是中心对称图形；C ．是轴对称图形，不是中心对称图形；D ．是轴对称图形，不是中心对称图形．故选B ．点睛：本题考查了中心对称图形和轴对称图形的知识，关键是掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180°后与原图重合．二、填空题：（本大题共6个小题，每小题4分，共24分．）13．22(2)a -【解析】22a 8a 8-+=2（2a 4a 4-+）=()22a 2-.故答案为()22a 2-.14．11π． 【解析】【分析】 阴影部分的面积=扇形ECF 的面积-△ACD 的面积-△OCM 的面积-扇形AOM 的面积-弓形AN 的面积．【详解】解：连接OM ，ON.∴OM=3，OC=6，∴30ACM ∠=o ， ∴33CD AB ==，∴扇形ECF 的面积2120π927π360⋅==； △ACD 的面积2732AC CD =⨯÷= 扇形AOM 的面积2120π33π360⋅==； 弓形AN 的面积2120π31393333π360224⋅=-⨯⨯=- △OCM 的面积1933332=⨯⨯= ∴阴影部分的面积=扇形ECF 的面积−△ACD 的面积−△OCM 的面积−扇形AOM 的面积−弓形AN 的面积2633(21π.= 故答案为63321π． 【点睛】考查不规则图形的面积的计算，掌握扇形的面积公式是解题的关键.15．4;【解析】试题解析：把21x y =⎧⎨=⎩代入方程组得：25{21a b b a ++＝①＝②， ①×2-②得：3a=9，即a=3，把a=3代入②得：b=-1，则a-b=3+1=4，16．5 5【解析】【分析】在直角△ABD中利用勾股定理求得AD的长，然后利用正弦的定义求解．【详解】在直角△ABD中，BD=1，AB=2，则AD=22AB BD+=2221+=5，则sinA=BDAD=5=5.故答案是：5 .17．4n+1【解析】【分析】分析可知规律是每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个．【详解】解：第一个图案正三角形个数为6=1+4；第二个图案正三角形个数为1+4+4=1+1×4；第三个图案正三角形个数为1+1×4+4=1+3×4；…；第n个图案正三角形个数为1+（n﹣1）×4+4=1+4n=4n+1．故答案为4n+1．考点：规律型：图形的变化类．18．【解析】试题分析：先根据勾股定理求得圆锥的母线长，再根据圆锥的侧面积公式求解即可.由题意得圆锥的母线长则所得到的侧面展开图形面积.考点：勾股定理，圆锥的侧面积公式点评：解题的关键是熟记圆锥的侧面积公式：圆锥的侧面积底面半径母线.三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（1）该一次函数解析式为y=﹣x+1．（2）在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是10千米．【解析】【分析】（1）根据函数图象中点的坐标利用待定系数法求出一次函数解析式；（2）根据一次函数图象上点的坐标特征即可求出剩余油量为8升时行驶的路程，即可求得答案.【详解】（1）设该一次函数解析式为y=kx+b ，将（150，45）、（0，1）代入y=kx+b 中，得 ，解得：，∴该一次函数解析式为y=﹣x+1；（2）当y=﹣x+1=8时，解得x=520，即行驶520千米时，油箱中的剩余油量为8升．530﹣520=10千米，油箱中的剩余油量为8升时，距离加油站10千米，∴在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是10千米．【点睛】本题考查了一次函数的应用，熟练掌握待定系数法，弄清题意是解题的关键.20．﹣2，﹣1，0，1，2；【解析】【分析】首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集；再确定解集中的所有整数解即可．【详解】解：解不等式（1），得x 3>-解不等式（2），得x≤2所以不等式组的解集：－3＜x≤2它的整数解为：－2，－1，0，1，221．（1）二次函数的解析式为223y x x =--+，顶点坐标为（–1，4）；（2）点P 横坐标为2–1；（3）当3x 2=-时，四边形PABC 的面积有最大值758，点P （31524-，）． 【解析】试题分析: （1）已知抛物线2y ax bx c =++ ()0a ≠与x 轴交于点A 和点B （1，0），与y 轴交于点C（0，3），其对称轴l 为x =﹣1，由此列出方程组，解方程组求得a 、b 、c 的值，即可得抛物线的解析式，把解析式化为顶点式，直接写出顶点坐标即可；（2）把y=2代入解析式，解方程求得x 的值，即可得点P 的横坐标，从而求得点P 的坐标；（3）设点Ｐ（x ，y ），则2--23y x x =+ ,根据 OBC OAP OPC BCPA S S S S ∆∆∆=++四边形得出四边形PABC 与x 之间的函数关系式，利用二次函数的性质求得x 的值，即可求得点P 的坐标.试题解析:（1）∵抛物线2y ax bx c =++ ()0a ≠与x 轴交于点A 和点B （1，0），与y 轴交于点C （0，3），其对称轴l 为x =﹣1，∴0312a b c c b a⎧⎪++=⎪=⎨⎪⎪-=-⎩ ， 解得：123a b c =-⎧⎪=-⎨⎪=⎩，∴二次函数的解析式为2--23y x x =+ =()214x -++，∴顶点坐标为（﹣1，4）（2）设点P （x ，2），即2--23y x x =+=2，解得1x1（舍去）或2x =﹣1，∴点P1，2）.（3）设点Ｐ（x ，y ），则2--23y x x =+ , OBC OAP OPC BCPA S S S S ∆∆∆=++四边形,∴ 2339332222BCPAS x x x =--+-四边形＝23375228x ⎛⎫-++ ⎪⎝⎭ ∴当32x =-时，四边形PABC 的面积有最大值758. 所以点P （315,24-）. 点睛：本题是二次函数综合题，主要考查学生对二次函数解决动点问题综合运用能力，动点问题为中考常考题型，注意培养数形结合思想，培养综合分析归纳能力，解决这类问题要会建立二次函数模型，利用二次函数的性质解决问题.22．（1）详见解析；（1）①详见解析；②1；③62 4.【解析】【分析】（1）只要证明△BAE≌△CDE即可；（1）①利用（1）可知△EBC是等腰直角三角形，根据ASA即可证明；②构建二次函数，利用二次函数的性质即可解决问题；③如图3中，作EH⊥BG于H．设NG=m，则BG=1m，BN=EN=3m，EB=6m．利用面积法求出EH，根据三角函数的定义即可解决问题.【详解】（1）证明：如图1中，∵四边形ABCD是矩形，∴AB=DC，∠A=∠D=90°，∵E是AD中点，∴AE=DE，∴△BAE≌△CDE，∴BE=CE．（1）①解：如图1中，由（1）可知，△EBC是等腰直角三角形，∴∠EBC=∠ECB=45°，∵∠ABC=∠BCD=90°，∴∠EBM=∠ECN=45°，∵∠MEN=∠BEC=90°，∴∠BEM=∠CEN，∵EB=EC，∴△BEM≌△CEN；②∵△BEM≌△CEN，∴BM=CN，设BM=CN=x，则BN=4-x，∴S△BMN=1 2•x（4-x）=-12（x-1）1+1，∵-12＜0，∴x=1时，△BMN的面积最大，最大值为1．③解：如图3中，作EH⊥BG于H．设NG=m，则BG=1m，BN=EN=3m，EB=6m．∴3（3m，∵S△BEG=12•EG•BN=12•BG•EH，∴EH=3?(13)m m+3+3m，在Rt△EBH中，sin∠EBH=3+362246EHEB m==．【点睛】本题考查四边形综合题、矩形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质、旋转变换、锐角三角函数等知识，解题的关键是准确寻找全等三角形解决问题，学会添加常用辅助线，学会利用参数解决问题，23．（1）见解析（2）见解析【解析】【分析】（1）根据旋转变换的定义和性质求解可得；（2）根据位似变换的定义和性质求解可得．【详解】解：（1）如图所示，△A 1B 1C 1即为所求；（2）如图所示，△DEF 即为所求．【点睛】本题主要考查作图﹣位似变换与旋转变换，解题的关键是掌握位似变换与旋转变换的定义与性质． 24．吉普车的速度为30千米/时.【解析】【分析】先设抢修车的速度为x 千米/时，则吉普车的速度为1.5x 千米/时，列出方程求出x 的值，再进行检验，即可求出答案．【详解】解：设抢修车的速度为x 千米/时，则吉普车的速度为15x 千米/时. 由题意得：1515151.560x x -=. 解得，x=20经检验，x=20是原方程的解，并且x=20,1.5x=30都符合题意.答：吉普车的速度为30千米/时.点评：本题难度中等，主要考查学生对分式方程实际应用的综合运用．为中考常见题型，要求学生牢固掌握．注意检验．25．（1）3（2）11a a +-. 【解析】【分析】（1）根据幂的乘方、零指数幂、特殊角的三角函数值和绝对值可以解答本题；（3）根据分式的减法和除法可以解答本题．【详解】（1）())0223π12sin60︒-+-+-=4+1+|1﹣2×3=4+1+|11（2）2a 12a 1a a a --⎛⎫÷- ⎪⎝⎭ =()()2a 1a 1a 2a 1a a+--+÷ =()()()2a 1a 1a ·a a 1+-- =a 1a 1+-． 【点睛】本题考查分式的混合运算、实数的运算、零指数幂、特殊角的三角函数值和绝对值，解答本题的关键是明确它们各自的计算方法．26．（1）①602α+o ；②CE AC +=；（2）AC CE -=【解析】【分析】（1）①先根据等边三角形的性质的QA QB =，进而得出QB QE =，最后用三角形的内角和定理即可得出结论；②先判断出QAF QEC ∆≅∆，得出QF QC =，再判断出QCF ∆是底角为30度的等腰三角形，再构造出直角三角形即可得出结论；（2）同②的方法即可得出结论．【详解】（1）当030α<<o o 时，①画出的图形如图1所示，∵ABC ∆为等边三角形，∴60ABC ∠=o ．∵CD 为等边三角形的中线∴CD 是AB 的垂直平分线，∵Q 为线段CD 上的点，∴QA QB =．∵DAQ α∠=，∴ABQ DAQ α∠=∠=，60QBE α∠=-o ．∵线段QE 为线段QA 绕点Q 顺时针旋转所得，∴QE QA =．∴QB QE =．∴60QEB QBE α∠=∠=-o ，∴()1802180260BQE QBE α∠=-∠=--o o o 602α=+o ；②3CE AC CQ +=；如图2，延长CA 到点F ，使得AF CE =，连接QF ，作QH AC ⊥于点H ．∵602BQE α∠=+o ，点E 在BC 上，∴()()60260QEC BQE QBE αα∠=∠+∠=++-o o 120α=+o ．∵点F 在CA 的延长线上，DAQ α∠=，∴120QAF BAF DAQ α∠=∠+∠=+o ．∴QAF QEC ∠=∠．又∵AF CE =，QA QE =，∴QAF QEC ∆≅∆．∴QF QC =．∵QH AC ⊥于点H ，∴FH CH =，2CF CH =．∵在等边三角形ABC 中，CD 为中线，点Q 在CD 上， ∴1302ACQ ACB ∠=∠=o ， 即QCF ∆为底角为30o 的等腰三角形．∴3cos cos302CH CQ QCH CQ CQ =⋅∠=⋅=o ． ∴23CE AC AF AC CF CH CQ +=+===．（2）如图3，当3060α<<o o 时，在AC 上取一点F 使AF CE =，∵ABC ∆为等边三角形，∴60ABC ∠=o ．∵CD 为等边三角形的中线，∵Q 为线段CD 上的点，∴CD 是AB 的垂直平分线，∴QA QB =．∵DAQ α∠=，∴ABQ DAQ α∠=∠=，60QBE α∠=-o ．∵线段QE 为线段QA 绕点Q 顺时针旋转所得，∴QE QA =．∴QB QE =．∴60QEB QBE QAF α∠=∠=-=∠o ，又∵AF CE =，QA QE =，∴QAF QEC ∆≅∆．∴QF QC =．∵QH AC ⊥于点H ，∴FH CH =，2CF CH =．∵在等边三角形ABC 中，CD 为中线，点Q 在CD 上， ∴1302ACQ ACB ∠=∠=o ， ∴3cos cos30CH CQ HCQ CQ CQ =⋅∠=⋅=o ． ∴23AC CE AC AF CF CH CQ -=-===．【点睛】此题是几何变换综合题，主要考查了等边三角形的性质，三角形的内角和定理，全等三角形的判定和性质，等腰三角形的判定和性质，锐角三角函数，作出辅助线构造出全等三角形是解本题的关键．27．（1）甲，乙两种型号设备每台的价格分别为12万元和10万元．（2）有6种购买方案．（3）最省钱的购买方案为，选购甲型设备4台，乙型设备6台．【解析】【分析】(1)设甲、乙两种型号设备每台的价格分别为x 万元和y 万元，根据购买了3台甲型设备比购买2台乙型设备多花了16万元，购买2台甲型设备比购买3台乙型设备少花6万元可列出方程组，解之即可；(2)设购买甲型设备m 台，乙型设备()10m -台，根据购买节省能源的新设备的资金不超过110万元列不等式，解之确定m 的值，即可确定方案；(3)因为公司要求每月的产量不低于2040吨，据此可得关于m 的不等式，解之即可由m 的值确定方案，然后进行比较，做出选择即可．【详解】(1)设甲、乙两种型号设备每台的价格分别为x 万元和y 万元，由题意得：3216263x y x y-=⎧⎨+=⎩， 解得：1210x y =⎧⎨=⎩， 则甲，乙两种型号设备每台的价格分别为12万元和10万元；(2)设购买甲型设备m 台，乙型设备()10m -台，则()121010110m m +-≤，∴5m ≤,∵m 取非负整数，∴0,1,2,3,4,5m =，∴有6种购买方案；(3)由题意：()240180102040m m +-≥，∴4m ≥，∴m 为4或5，当4m =时，购买资金为：124106108⨯+⨯=(万元)，当5m =时，购买资金为：125105110⨯+⨯=(万元)，则最省钱的购买方案是选购甲型设备4台，乙型设备6台.【点睛】本题考查了二元一次方程组的应用，一元一次不等式的应用，弄清题意，找准等量关系、不等关系列出方程组与不等式是解题的关键.。

北京市海淀外国语实验学校2019-2020-2 直升三班4 月英语学科能力反馈练习满分：100 考试时长：60 分钟一、单项填空（共28 分，每小题 2 分）。

1.Mother's Day is May 10th this year.A.inB. ofC. onD. at2.Gary and his brother graduated from high school three years ago. But the memories are still new to .A. themB. usC. herD. you3.—Many boy students think English is math. —I agree. I'm also weak in English.A. much difficult thanB. as difficult asC. more difficult thanD. less difficult than4.— I had a quarrel with my classmates this morning. What should I do now, Mum?— You should think more of others if you want to them.A. run out ofB. show offC. come up withD. get on well with5.The Dragon Boat Festival the fifth day of the fifth month of the lunar year.A. falls onB. goes onC. is toD. to be6.My classmate, Tom, often English after lunch every week.A. readB. is readingC. was readingD. reads7.Mike the piano when his father came back home at 8 p. m. yesterday.A. playsB. playedC. was playingD. is playing8.We the Science Museum yesterday and we did many interesting experiments.A. visitedB. visitC. will visitD. have visited9.—The Great Wall is so famous that a lot of foreigners visit it every year.—I can’t agree more. I there twice since I came here.A. will beB. will goC. have goneD. have been10.Our school library a year ago. It’s very nice and there are lots of new books.A. buildsB. builtC. was builtD. is built11.The Mid-Autumn Festival is important because it is a special for family.A. occasionB. opportunityC. chanceD. choice12.My bike was broken on the way, I was late for school.A. butB. forC. soD. or13.. Millions of people the Great Wall every year.A. visitedB. visitC. will visitD. are visiting14.—Do you know the new mobile phone last week?—Maybe 2000 yuan. I'm not quite sure.A. how much she paid forB. how much will she pay forC. how much did she pay forD. how much she will pay for二．课内完型：（每题2 分，共10 分）The Lantern Festival falls on the fifteenth day of the first lunar month. It 15 the end of the Chinese New Year celebrations.There are many stories about how the Lantern Festival started. In one story, lanterns were 16 to celebrate the power of light over darkness. In another story, a town was almost destroyed but the light from many lanterns saved it. The story was about a god who wanted to 17 the town. He was fooled when he saw 18 lanterns. He thought the town was already burning.In the past, lanterns were usually lit by candles and decorated with pictures of birds, animals and flowers, etc.. Nowadays, most lanterns are made with light bulbs and batteries, and they come in many shapesand 19 . In the north-eastern part of China, there are even ice-lanterns.The special food for the Lantern Festival is the sweet dumpling. Sweet dumplings are boiled and served in hot water.15. A. marks B. light C. remark D. on16. A. lit B. light C. let D. lighted17.A. burn B. burn down C. burn off D. light off18. A. thousands of B. thousand of C. hundreds D. hundred of19.A. pictures B. patterns C. size D. sizes三、完型填空（12 分，每个 1.5 分）Rob tapped his foot on the ground impatiently（不耐烦地）. His friend, Steve, should meet him in five minutes. They were going to meet and watch a movie together, and Rob didn't want to miss a single minute of the show.Both of them really liked 20 and tried to see one almost every week, but lately Steve had been arriving later and later. Rob complained about late friends in a low voice while he waited.Rob began pacing（踱步）back and forth. When pacing didn't 21 him, he started to look at his watch from time to time. There were only three minutes left before he went in without his friend, Rob decided. Pacing was making him more impatient.He wondered why Steve couldn't be on time. He wondered what 22 Steve would have this time. Last time Steve had said it was because his dad needed help in the garden. What would be this time?There was only one minute Left. Then he heard a familiar voice, " Rob, I 23 it! "Rob turned around and saw Steve. "You made it, and you are on time, too! " Rob said excitedly."Of course, " Steve replied, "I really wanted to see this movie.""Well let's go then." Rob suggested. He 24 for his wallet, so he could buy a ticket. Where was his wallet?"What's wrong?" Steve asked."I don't have my wallet." Rob replied 25 ."Go check in your car.""I might be late then." Rob answered, feeling foolish. Here he'd been standing around waiting, and he was going to be the late one now. He ran across the parking lot.By the time he got his wallet from his car and bought a ticket, he'd already 26 the beginning and he didn't have time to get popcorn or a drink. Steve shared his popcorn, but Rob could hardly eat it. He felt guilty （内疚的）during the whole movie.When the movie was over, he apologized to Steve. "I'm sorry, Steve. I was complaining about you being late, but then I was the one who was late."Steve said. "Don't worry. It happens to all of us.""I see that now. Thanks for 27 . ""That's what friends for." Steve replied.20.A. cars21.A. calm22.A. plan B. friendsB. beatB. adviceC. walletsC. interestC. excuseD. moviesD. warmD. example23. A. had B. made C. saw D. bought24. A. reached B. asked C. cared D. left25. A. worriedly B. excitedly C. rudely D. confidently26. A. enjoyed B. guessed C. known D. missed27. A. helping B. driving C. understanding D. waiting四．阅读理解（30 分，每题 3 分）you want to do in the future? Here are some answers from some students.urent came to the UK from .A. ItalyB. RussiaC. ChinaD. Africa29.Rosie is going to be .A. a writerB. a teacherC. a doctorD. a traveler30.Kevin wants to .A. travel abroadB. go to universityC. teach in schoolsD. work in hospitalsBA dog on a surfboard is something you might enjoy seeing in a funny video. Butwould you believe that a real surfing dog could help raise money for those in need? Adog named Lucky is using her special talents to do just that.Lucky’s trainer started coaching her to become a service dog when she was a puppy. Lucky did well during training. She learned how to turn on lights, open doors,and do other jobs. These skills would be useful for her to help a person with specialneeds.Judy, the dog’s trainer, concentrated ( 关注) on Lucky’s positive qualities. Like most dogs, Lucky loved water, so Judy took her to the beach. Lucky quickly became good at surfing. Her talent got people’s attention. Judy dec ided that instead of being a service dog, Lucky would become a “surfing” dog. The idea was that Lucky could use her surfing talent to raise money to help people.Lucky’s first charity event was in 2009. She starred at an activity to help a teenager named Patrick. Patrick was unable to walk, but he had always dreamed of surfing. At the event, Patrick and Lucky were supposed to use their own surfboards. Lucky decided to jump on Patrick’s board, however. They surfed together and raised $10,000. The money helpe d pay for Patrick’s medical treatment and his own service dog.Encouraged by this event, Judy started the organization named Surfing for Paws-abilities. Lucky now travels to different places and surfs at events to raise money for the organization that helps people in need.Not only does Lucky raise money, but also what she has done inspires many other organizations to help both people and animals. She’s surfed to make money to buy pet masks for fire departments. She’s surfed at charity events to help fight human and animal cancer. She’s even shown off her surfing skills to raise money to buy teddy bears for children in hospitals and people in nursing homes. As of 2012, this amazing dog has raised $250,000 to help those in need.31.What is Lucky’s special talent?A. Surfing on a board.B. Turning on lights.C. Making a video.D. Opening doors.32.We can know from the passage that .A.Lucky is Patrick’s service dogB.Lucky looks after sick childrenC.Lucky helps both people and animalsD.Lucky visits old people in nursing homes33.Which of the following would be the best title for the passage?A.Dogs are humans’ good friendsB.The person who trains dogs wellC.Charity needs great dog helpersD.The dog who surfs to raise moneyCWhen it comes to days of the week, Monday gets little expectation. I surveyed friends, and the results were very clear. When asked which day of the week they like the least, 90 percent of my friends chose Monday. Not one person thought of Monday as his or her favorite day. Songwriters have even written a song about horrible Mondays. In the 1960s, a musical group had a hit titled “Monday, Monday.” They sang, “Every other day of the week is fine, yeah. But whenever Monday comes, you can find me crying all of the time.” I don’t agree with all these ideas. In fact, I think that Monday is actually the best day of the week.First of all, consider all the good things that happen on Mondays. If you are a sports fan, you may get towatch Monday Night Football in the fall. Furthermore, quite a few public holidays, including Memorial Day, Labor Day, and Columbus Day, are celebrated on Mondays. That means that several times a year, a Monday provides a three-day weekend. And according to consumer (消费者) websites, Monday is the best day to get a good deal on a car because there aren’t as many people shopping on the first day of the workweek. Experts say that you can also get the best online deals on Mondays. This is especially true for electronics, such as computers, TVs, and video games.To me, however, there’s something even more important about Mondays. Each Monday stands for a new beginning. For example, last week I got behind on my homework and had to spend the weekend catching up. But as soon as Monday arrived, I had a clean slate. Another week I forgot to do some of my chores, so I had to give up going to a movie with my friends on the weekend.I also love Mondays because we frequently start new lessons at school at the beginning of the week. While last week’s topics may have been boring, Monday can bring a new book to read, more experiments to conduct, or math problems to work out.I realize that I am probably not going to persuade everyone that Monday is the best day of the week, but hopefully I can encourage a few people to change their attitude. The next time a Monday comes, think about all the good things that could happen and look forward to the day instead of fearing it.There’s no way to avoid Mondays, so join me in making the best of them. Who knows? You might even start liking the first day of the workweek.34.Why does the writer mention the song “Monday, Monday. ” in Paragraph 1?A.Because it was a very popular song in the 1960s.B.Because it shows most people don’t like Monday.C.Because songwriters like to write songs about Monday.D.Because the musical group often performed on Monday.35.The words “a clean slate” in Paragraph 3 probably mean “”.A. a fresh startB. a sudden stopC. a tiring endD. a near future36.What can we learn from the passage?A.People don’t like to go shopping online on weekdays.B.The writer likes doing chores instead of going to a movie.C.The lesson topics on weekdays are always interesting.D.Some public holidays on Mondays make three-day weekends.37.What does the passage mainly talk about?A.What makes Monday the worst day.B.Why some people like Monday the least.C.Why Monday is the best day of the week.D.How we can make good use of Mondays.五、阅读短文，根据短文内容回答问题。

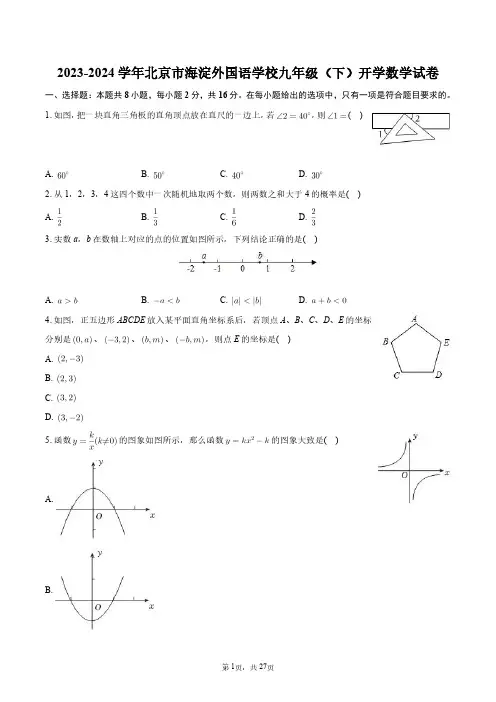
2023-2024学年北京市海淀外国语学校九年级（下）开学数学试卷一、选择题：本题共8小题，每小题2分，共16分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.如图，把一块直角三角板的直角顶点放在直尺的一边上，若，则()A. B. C. D.2.从1，2，3，4这四个数中一次随机地取两个数，则两数之和大于4的概率是()A. B. C. D.3.实数a，b在数轴上对应的点的位置如图所示，下列结论正确的是()A. B. C. D.4.如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A、B、C、D、E的坐标分别是、、、，则点E的坐标是()A.B.C.D.5.函数的图象如图所示，那么函数的图象大致是()A.B.C.D.6.点，在反比例函数的图象上，下列推断正确的是()A.若，则B.若，则C.若，则D.存在，使得7.如图，矩形OABC的对角线OB与反比例函数相交于点D，且，则矩形OABC的面积为()A.50B.25C.15D.8.如图，将一圆柱形水杯杯底固定在大圆柱形容器底面中央，现用一个注水管沿大容器内壁匀速注水，则水杯内水面的高度单位：与注水时间单位：的函数图象大致为() A.B.C.D.二、填空题：本题共8小题，每小题2分，共16分。

9.若式子在实数范围内有意义，则x的取值范围是______.10.若，则代数式的值是______.11.如图，AC，BC是的弦，PA，PB是的切线，若，则__________.12.北京冬奥会雪上项目竞赛场地“首钢滑雪大跳台”巧妙地融入了敦煌壁画“飞天”元素．如图，赛道剖面图的一部分可抽象为线段已知坡AB的长为30m，坡角约为，则坡AB的铅直高度AH约为__________参考数据：，，13.如图，在菱形ABCD中，E是BC边上的点，连接AE交BD于点F，若，______.14.如图，小军在A时测量某树的影长时，日照的光线与地面的夹角恰好是，当他在B时测量该树的影长时，日照的光线与地面的夹角是，若两次测得的影长之差DE为3m，则树的高度为______结果精确到，参考数据：，15.如图，一扇形纸扇完全打开后，外侧两竹条AB和AC的夹角为，AB长为25cm，贴纸部分的宽BD为15cm，若纸扇两面贴纸，则贴纸的面积为______结果保留16.尊老敬老是中华民族的传统美德，某校文艺社团的同学准备在“五一”假期去一所敬老院进行慰问演出，他们一共准备了6个节目，全体演员中有8人需参加两个或两个以上的节目演出，情况如表：演员1演员2演员3演员4演员5演员6演员7演员8节目A√√√√√节目B√√√节目C√√√节目D√√节目E√√节目F√√从演员换装的角度考虑，每位演员不能连续参加两个节目的演出，从节目安排的角度考虑，首尾两个节目分别是A，F，中间节目的顺序可以调换，请写出一种符合条件的节目先后顺序__________只需按演出顺序填写中间4个节目的字母即可三、计算题：本大题共1小题，共5分。

北京市海淀外国语实验学校2019-2020学年度第二学期初二数学期末练习考试时间90分钟 满分100分一、选择题（每题3分，本大题共30分） 1．下列二次根式中，最简二次根式是（ ） A ．8 B ．19C ．2a D ． 23a2. 下列四组线段中，不能作为直角三角形三条边的是（ ）A. 3，4，5B. 2，2，22C. 2，5，6D. 5，12，13 3. 已知P 1（－1，y 1），P 2（2，y 2）是一次函数1y x =-+图象上的两个点，则y 1，y 2的大小关系是（ ） A ．12y y = B ．12y y < C ．12y y > D ．不能确定 4. 下图中，不是函数图象的是（ ）A B C D5. 平行四边形所具有的性质是（ ）A. 对角线相等B.邻边互相垂直C. 每条对角线平分一组对角D. 两组对边分别相等 6．下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差：甲 乙 丙 丁 平均数（分）92 95 95 92 方差3.63.67.48.1要选择一名成绩好且发挥稳定的同学参加数学比赛，应该选择（ ） A ．甲 B ．乙 C ．丙 D ．丁7. 将正比例函数2y x =的图象向下平移2个单位长度，所得图象对应的函数解析式是（ ） A ．21y x =- B ．22y x =+ C ．22y x =- D ．21y x =+8. 在一次为某位身患重病的小朋友募捐过程中，某年级有50师生通过微信平台奉献了爱心.小东对他们的捐款金额进行统计，并绘制了如下统计图. 师生捐款金额的中位数和众数分别是（ ） A ．20，20 B ．30，30 C ．30，20 D ．20，30xS612OxS612OxS124OABC DEFA B C DE 9.如图，在正方形ABCD 的外侧，作等边三角形ADE ，AC 、BE 相交于点F ，则∠BFC 为（ ） A ．75︒ B ．60︒ C ．55︒ D ．45︒10．点P （x ，y ）在第一象限内，且x+y=6，点A 的坐标为（4，0）．设△OP A 的面积为S ，则下列图象中，能正确反映S 与x 之间的函数关系式的是（ ）xS66OA B C D 二、填空题（每题3分，本大题共24分）11.函数23=-y x 中，自变量x 的取值范围为 ． 12. 如果3+20x y -+=，那么xy 的值为 ．13. 请写出一个过点（0,1），且y 随着x 的增大而减小的一次函数解析式 ．14. 在湖的两侧有A ，B 两个消防栓，为测定它们之间的距离，小明在岸上任选一点C ，并量取了AC 中点D 和BC 中点E 之间的距离为16米，则A ，B 之间的距离应为 米．15. 如图，直线y ＝x ＋b 与直线y ＝kx ＋6交于点P (3，5)，则关于x 的不等式kx ＋6＞x ＋b 的解集是_____________．16. 在菱形ABCD 中，∠A =60°，其所对的对角线长为2，则菱形ABCD 的面积是 ．17. 如图，在平行四边形ABCD 中，2=AD AB ，CE 平分∠BCD 交AD 边于点E ，且AE=2，则AB 的长为 ．第13题图 第14题图18. 在一节数学课上，老师布置了一个任务： 已知，如图1，在Rt ABC △中，∠B =90°，用尺规作图作矩形ABCD .图1 图2同学们开动脑筋，想出了很多办法，其中小亮作了图2，他向同学们分享了作法： ① 分别以点A ，C 为圆心，大于12AC 长为半径画弧，两弧分别交于点E ，F ，连接EF 交AC 于点O ； ② 作射线BO ，在BO 上取点D ，使OD OB =； ③ 连接AD ，CD .则四边形ABCD 就是所求作的矩形. 老师说：“小亮的作法正确.”小亮的作图依据是 .三、解答题（19—23题，每题6分，24、25题每题8分，本大题共46分） 19．计算．（1(2032522-（2）()227284-20．老李家有一块草坪如图所示，家里想整理它，需要知道其面积．老李测量了草坪各边得知：3=AB 米，4=BC 米，12=AD 米，13=CD 米，且⊥AB CB ．请同学们帮老李家计算一下这块草坪的面积．AB CD21．在平面直角坐标系中，一条直线经过5( 1 ) -，A ，与 (33) -，B 两点． （1）求这条直线与坐标轴围成的图形的面积．（2）若这条直线与1=-+y x 交于点C ，求点C 的坐标．22. 如图，平行四边形ABCD 中，AB=6cm ，BC=10cm ，60=︒∠B ，G 是CD 的中点，E 是边AD 上的动点，EG 的延长线与BC 的延长线交于点F ，连接CE ，DF ．GFE DCBAD B A D B A （1）求证：四边形CEDF 是平行四边形． （2）以下两问二选一进行求解①当=AE cm 时，四边形CEDF 是矩形； ②当=AE cm 时，四边形是CEDF 菱形．23.四川雅安发生地震后，某校学生会向全校700名学生发起了爱心捐款活动，为了解捐款情况，随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列是问题：（Ⅰ）本次随机抽样调查的学生人数为______，图①中m 的值是______； （Ⅱ）求本次调查获取的样本数据的众数和中位数；（Ⅲ）根据样本数据，估计该校本次活动捐款为10元的学生人数．24. 如图，在△ABD 中，AB =AD , 将△ABD 沿BD 翻折，使点A 翻折到点C ，E 是BD 上一点，且BE >DE ，连结CE 并延长交AD 于F ，连结AE . （1）依题意补全图形；（2）判断∠DFC 与∠BAE 的大小关系并加以证明；（3）若∠BAD =120°，AB =2，取AD 的中点G ，连结EG ，求EA+EG 的最小值.备用图 25. 在平面直角坐标系xOy 中，已知点(),M a b 及两个图形1W 和2W ，若对于图形1W 上任意一点(),P x y ，在图形2W 上总存在点(),P x y '''，使得点P '是线段PM 的中点，则称点P '是点P 关于点M 的关联点，图形2W 是图形1W 关于点M 的关联图形，此时三个点的坐标满足2x a x +'=，2y by +'=.（1）点()2,2P '-是点P 关于原点O 的关联点，则点P 的坐标是 ； （2）已知，点()4,1A -，()2,1B -，()2,1C --，()4,1D --以及点()3,0M①画出正方形ABCD 关于点M 的关联图形；②在y轴上是否存在点N,使得正方形ABCD关于点N=-分成面积相等的两部分？若存的关联图形恰好被直线y x在，求出点N的坐标；若不存在，说明理由.。

武汉海淀外国语实验学校4月考试一、选择题（共10小题，每小题3分，共30分）1．《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数若其意义相反，则分别叫做正数与负数．如果水位上升2米记为+2米，则水位下降3米记为（）A．+3米B．﹣3米C．+2米D．﹣2米在实数范围内有意义，则x 的取值范围是（）A．x ≤12B．x ≥12C．x ≤2D．x ≥23.一组数据：1，2，3，4，1.这组数据的众数与中位数分别为（）A．1，3B．2，2.5C．1，2D．2，24．下列四个图案中，是轴对称图形的是（）A．B．C．D5.五个相同的小正方体摆成了如图所示的几何体，它的左视图为（）6.在不透明的袋中装有红、白两种颜色的小球共20个，这些小球除了颜色不同外其它特质均相同，小明进行了摸球试验，每次摸出一个小球记下颜色，然后放回袋中搅拌均匀，再从中摸出一个，…，如此重复，经大量的试验发现摸到红球的频率稳定在0.6，由此可以估计袋中红球的个数为（）A．6B．8C．10D．127．反比例函数xk y 12+=图象上有三个点（－2，y 1），（－1，y 2），（1，y 3），则y 1、y 2、y 3的大小关系是（）A.y 1＜y 2＜y 3 B.y 2＜y 1＜y 3C.y 3＜y 1＜y 2D.y 3＜y 2＜y 18.如图，某小区有东西方向的街道3条，南北方向的街道4条，从位置A 出发沿街道行走到达位置B，要求路程最短，研究有多少种不同的走法.小聪是这样思考的：要使路程最短，就不能走“回头路”，只能分五步来完成，其中三步向右行进，两步向上行进，如果用数字“1”表示向右行走一格，数字“2”表示向上行走一格，如“11221”与“11212”就表示两种符合要求的不同走法.那么符合要求的不同走法的种数为（）A．6种B．8种C．10种D．12种9.已知关于x 的二次函数y =x 2+(2－a )x +5，当1≤x ≤3时，y 在x =1时取得最大值，则实数a 的取值范围是（）A．a ≥2B．a ≤－2C．a ≥6D．a ＜010．如图，Rt△ABC 中，∠BAC =90°，AC =6，AB =8，O 为Rt△ABC 的外心，I 为Rt△ABC 的内心，延长AI 交⊙O 于点D .连接OI ，则cos∠OID 的值为（）A.35B.552C.510 D.10103二、填空题（本大题共6个小题，每小题3分，共18分）11．将二次根式化为最简二次根式_____．12．为调查某班学生每天使用零花钱的情况，子康同学随机调查了4名同学，结果如下20元25元18元20元，则这4名同学每天使用的零花钱中位数分别是13．计算：261a a 3－－9－＝_____．14.如图，E 是矩形ABCD 的边DC 上一点，AB =AE =4，BC =2，则∠BEC的度数为___________.15．抛物线y ＝(a 2+1)x 2+bx +c 经过点A （﹣3，t）、B （4，t）两点，则不等式(a 2+1)（x-2)2+bx<2b-c+t 的解集是_____________________．16．如图，⊙O 的半径为2，弦AB 的长为2，点C 是优弧AB 上的一动点，BD ⊥BC 交直线AC 于点D ，当点C 从△ABC 面积最大时运动到BC 最长时，点D 所经过的路径长为．三、解答题（共8题，共72分）17．（8分）计算：x 2•（﹣x ）2•（﹣x ）2+（﹣x 2）318.（本题8分）如图，AB ∥CD ，∠B =∠D.求证：AD ∥BE .19.（本题8分）为了解学生自主学习的具体情况，黄老师随机对部分学生进行了跟踪调查，并将调查结果分成四类，A ：特别好；B ：好；C ：一般；D ：较差.绘制成了以下两幅不完整的统计图（每位学生只属于一类），请你解答下列问题：（1）本次调查的样本容量为________；（2）将条形统计图补充完整；（3）D 类所占扇形角的度数为；（4）学校共有2000名学生，其中自主学习情况特别好的约有多少人？20．（8分）横、纵坐标均为整数的点叫做格点，例如A （1,4），B （1,1），C （4,1），D （4,4），E（2,1）都是格点。

北京市海淀外国语实验学校2019-2020-2 直升三班4 月英语学科能力反馈练习满分：100 考试时长：60 分钟一、单项填空（共28 分，每小题 2 分）。

1.Mother's Day is May 10th this year.A.inB. ofC. onD. at2.Gary and his brother graduated from high school three years ago. But the memories are still new to .A. themB. usC. herD. you3.—Many boy students think English is math. —I agree. I'm also weak in English.A. much difficult thanB. as difficult asC. more difficult thanD. less difficult than4.— I had a quarrel with my classmates this morning. What should I do now, Mum?— You should think more of others if you want to them.A. run out ofB. show offC. come up withD. get on well with5.The Dragon Boat Festival the fifth day of the fifth month of the lunar year.A. falls onB. goes onC. is toD. to be6.My classmate, Tom, often English after lunch every week.A. readB. is readingC. was readingD. reads7.Mike the piano when his father came back home at 8 p. m. yesterday.A. playsB. playedC. was playingD. is playing8.We the Science Museum yesterday and we did many interesting experiments.A. visitedB. visitC. will visitD. have visited9.—The Great Wall is so famous that a lot of foreigners visit it every year.—I can’t agree more. I there twice since I came here.A. will beB. will goC. have goneD. have been10.Our school library a year ago. It’s very nice and there are lots of new books.A. buildsB. builtC. was builtD. is built11.The Mid-Autumn Festival is important because it is a special for family.A. occasionB. opportunityC. chanceD. choice12.My bike was broken on the way, I was late for school.A. butB. forC. soD. or13.. Millions of people the Great Wall every year.A. visitedB. visitC. will visitD. are visiting14.—Do you know the new mobile phone last week?—Maybe 2000 yuan. I'm not quite sure.A. how much she paid forB. how much will she pay forC. how much did she pay forD. how much she will pay for二．课内完型：（每题2 分，共10 分）The Lantern Festival falls on the fifteenth day of the first lunar month. It 15 the end of the Chinese New Year celebrations.There are many stories about how the Lantern Festival started. In one story, lanterns were 16 to celebrate the power of light over darkness. In another story, a town was almost destroyed but the light from many lanterns saved it. The story was about a god who wanted to 17 the town. He was fooled when he saw 18 lanterns. He thought the town was already burning.In the past, lanterns were usually lit by candles and decorated with pictures of birds, animals and flowers, etc.. Nowadays, most lanterns are made with light bulbs and batteries, and they come in many shapesand 19 . In the north-eastern part of China, there are even ice-lanterns.The special food for the Lantern Festival is the sweet dumpling. Sweet dumplings are boiled and served in hot water.15. A. marks B. light C. remark D. on16. A. lit B. light C. let D. lighted17.A. burn B. burn down C. burn off D. light off18. A. thousands of B. thousand of C. hundreds D. hundred of19.A. pictures B. patterns C. size D. sizes三、完型填空（12 分，每个 1.5 分）Rob tapped his foot on the ground impatiently（不耐烦地）. His friend, Steve, should meet him in five minutes. They were going to meet and watch a movie together, and Rob didn't want to miss a single minute of the show.Both of them really liked 20 and tried to see one almost every week, but lately Steve had been arriving later and later. Rob complained about late friends in a low voice while he waited.Rob began pacing（踱步）back and forth. When pacing didn't 21 him, he started to look at his watch from time to time. There were only three minutes left before he went in without his friend, Rob decided. Pacing was making him more impatient.He wondered why Steve couldn't be on time. He wondered what 22 Steve would have this time. Last time Steve had said it was because his dad needed help in the garden. What would be this time?There was only one minute Left. Then he heard a familiar voice, " Rob, I 23 it! "Rob turned around and saw Steve. "You made it, and you are on time, too! " Rob said excitedly."Of course, " Steve replied, "I really wanted to see this movie.""Well let's go then." Rob suggested. He 24 for his wallet, so he could buy a ticket. Where was his wallet?"What's wrong?" Steve asked."I don't have my wallet." Rob replied 25 ."Go check in your car.""I might be late then." Rob answered, feeling foolish. Here he'd been standing around waiting, and he was going to be the late one now. He ran across the parking lot.By the time he got his wallet from his car and bought a ticket, he'd already 26 the beginning and he didn't have time to get popcorn or a drink. Steve shared his popcorn, but Rob could hardly eat it. He felt guilty （内疚的）during the whole movie.When the movie was over, he apologized to Steve. "I'm sorry, Steve. I was complaining about you being late, but then I was the one who was late."Steve said. "Don't worry. It happens to all of us.""I see that now. Thanks for 27 . ""That's what friends for." Steve replied.20.A. cars21.A. calm22.A. plan B. friendsB. beatB. adviceC. walletsC. interestC. excuseD. moviesD. warmD. example23. A. had B. made C. saw D. bought24. A. reached B. asked C. cared D. left25. A. worriedly B. excitedly C. rudely D. confidently26. A. enjoyed B. guessed C. known D. missed27. A. helping B. driving C. understanding D. waiting四．阅读理解（30 分，每题 3 分）you want to do in the future? Here are some answers from some students.urent came to the UK from .A. ItalyB. RussiaC. ChinaD. Africa29.Rosie is going to be .A. a writerB. a teacherC. a doctorD. a traveler30.Kevin wants to .A. travel abroadB. go to universityC. teach in schoolsD. work in hospitalsBA dog on a surfboard is something you might enjoy seeing in a funny video. Butwould you believe that a real surfing dog could help raise money for those in need? Adog named Lucky is using her special talents to do just that.Lucky’s trainer started coaching her to become a service dog when she was a puppy. Lucky did well during training. She learned how to turn on lights, open doors,and do other jobs. These skills would be useful for her to help a person with specialneeds.Judy, the dog’s trainer, concentrated ( 关注) on Lucky’s positive qualities. Like most dogs, Lucky loved water, so Judy took her to the beach. Lucky quickly became good at surfing. Her talent got people’s attention. Judy dec ided that instead of being a service dog, Lucky would become a “surfing” dog. The idea was that Lucky could use her surfing talent to raise money to help people.Lucky’s first charity event was in 2009. She starred at an activity to help a teenager named Patrick. Patrick was unable to walk, but he had always dreamed of surfing. At the event, Patrick and Lucky were supposed to use their own surfboards. Lucky decided to jump on Patrick’s board, however. They surfed together and raised $10,000. The money helpe d pay for Patrick’s medical treatment and his own service dog.Encouraged by this event, Judy started the organization named Surfing for Paws-abilities. Lucky now travels to different places and surfs at events to raise money for the organization that helps people in need.Not only does Lucky raise money, but also what she has done inspires many other organizations to help both people and animals. She’s surfed to make money to buy pet masks for fire departments. She’s surfed at charity events to help fight human and animal cancer. She’s even shown off her surfing skills to raise money to buy teddy bears for children in hospitals and people in nursing homes. As of 2012, this amazing dog has raised $250,000 to help those in need.31.What is Lucky’s special talent?A. Surfing on a board.B. Turning on lights.C. Making a video.D. Opening doors.32.We can know from the passage that .A.Lucky is Patrick’s service dogB.Lucky looks after sick childrenC.Lucky helps both people and animalsD.Lucky visits old people in nursing homes33.Which of the following would be the best title for the passage?A.Dogs are humans’ good friendsB.The person who trains dogs wellC.Charity needs great dog helpersD.The dog who surfs to raise moneyCWhen it comes to days of the week, Monday gets little expectation. I surveyed friends, and the results were very clear. When asked which day of the week they like the least, 90 percent of my friends chose Monday. Not one person thought of Monday as his or her favorite day. Songwriters have even written a song about horrible Mondays. In the 1960s, a musical group had a hit titled “Monday, Monday.” They sang, “Every other day of the week is fine, yeah. But whenever Monday comes, you can find me crying all of the time.” I don’t agree with all these ideas. In fact, I think that Monday is actually the best day of the week.First of all, consider all the good things that happen on Mondays. If you are a sports fan, you may get towatch Monday Night Football in the fall. Furthermore, quite a few public holidays, including Memorial Day, Labor Day, and Columbus Day, are celebrated on Mondays. That means that several times a year, a Monday provides a three-day weekend. And according to consumer (消费者) websites, Monday is the best day to get a good deal on a car because there aren’t as many people shopping on the first day of the workweek. Experts say that you can also get the best online deals on Mondays. This is especially true for electronics, such as computers, TVs, and video games.To me, however, there’s something even more important about Mondays. Each Monday stands for a new beginning. For example, last week I got behind on my homework and had to spend the weekend catching up. But as soon as Monday arrived, I had a clean slate. Another week I forgot to do some of my chores, so I had to give up going to a movie with my friends on the weekend.I also love Mondays because we frequently start new lessons at school at the beginning of the week. While last week’s topics may have been boring, Monday can bring a new book to read, more experiments to conduct, or math problems to work out.I realize that I am probably not going to persuade everyone that Monday is the best day of the week, but hopefully I can encourage a few people to change their attitude. The next time a Monday comes, think about all the good things that could happen and look forward to the day instead of fearing it.There’s no way to avoid Mondays, so join me in making the best of them. Who knows? You might even start liking the first day of the workweek.34.Why does the writer mention the song “Monday, Monday. ” in Paragraph 1?A.Because it was a very popular song in the 1960s.B.Because it shows most people don’t like Monday.C.Because songwriters like to write songs about Monday.D.Because the musical group often performed on Monday.35.The words “a clean slate” in Paragraph 3 probably mean “”.A. a fresh startB. a sudden stopC. a tiring endD. a near future36.What can we learn from the passage?A.People don’t like to go shopping online on weekdays.B.The writer likes doing chores instead of going to a movie.C.The lesson topics on weekdays are always interesting.D.Some public holidays on Mondays make three-day weekends.37.What does the passage mainly talk about?A.What makes Monday the worst day.B.Why some people like Monday the least.C.Why Monday is the best day of the week.D.How we can make good use of Mondays.五、阅读短文，根据短文内容回答问题。

北京市海淀区2019-2020学年中考数学四模试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．如图，在△ABC 中，∠ACB=90°，∠A=30°，BC=4，以点C 为圆心，CB 长为半径作弧，交AB 于点D ；再分别以点B 和点D 为圆心，大于12BD 的长为半径作弧，两弧相交于点E ，作射线CE 交AB 于点F ，则AF 的长为（ ）A ．5B ．6C ．7D ．82．随着服装市场竞争日益激烈，某品牌服装专卖店一款服装按原售价降价20%，现售价为a 元，则原售价为（ ）A ．（a ﹣20%）元B ．（a+20%）元C ．a 元D ． a 元3．计算（﹣ab 2）3的结果是（ ）A ．﹣3ab 2B ．a 3b 6C ．﹣a 3b 5D ．﹣a 3b 6 4．已知方程组2728x y x y +=⎧⎨+=⎩，那么x+y 的值（ ） A ．-1 B ．1 C ．0 D ．55．如图，在⊙O 中，直径CD ⊥弦AB ，则下列结论中正确的是( )A ．AC=AB B ．∠C=12∠BODC ．∠C=∠BD ．∠A=∠B0D6．下列说法中不正确的是（ ）A ．全等三角形的周长相等B ．全等三角形的面积相等C ．全等三角形能重合D ．全等三角形一定是等边三角形7．如图，在平行四边形ABCD 中，F 是边AD 上的一点，射线CF 和BA 的延长线交于点E ，如果12C EAF C CDF =V V ，那么S EAF S EBCV V 的值是（ ）A．12B．13C．14D．198．如图，△ABC是等腰直角三角形，∠A=90°，BC=4，点P是△ABC边上一动点，沿B→A→C的路径移动，过点P作PD⊥BC于点D，设BD=x，△BDP的面积为y，则下列能大致反映y与x函数关系的图象是（）A．B．C．D．9．下列各式中，正确的是（）A．t5·t5 = 2t5B．t4+t2 = t 6C．t3·t4 = t12D．t2·t3 = t510．如图,E为平行四边形ABCD的边AB延长线上的一点,且BE:AB=2：3,△BEF的面积为4,则平行四边形ABCD的面积为()A．30 B．27 C．14 D．3211．不等式组1030xx+>⎧⎨->⎩的解集是()A．x＞－1 B．x＞3C．－1＜x＜3 D．x＜312．如图，△ABC中，AB＝4，AC＝3，BC＝2，将△ABC绕点A顺时针旋转60°得到△AED，则BE 的长为（）A．5 B．4 C．3 D．2二、填空题：（本大题共6个小题，每小题4分，共24分．）13．如图，扇形OAB的圆心角为30°，半径为1，将它沿箭头方向无滑动滚动到O′A′B′的位置时，则点O 到点O′所经过的路径长为_____．14．如图1，点P从扇形AOB的O点出发，沿O→A→B→0以1cm/s的速度匀速运动，图2是点P运动时，线段OP的长度y随时间x变化的关系图象，则扇形AOB中弦AB的长度为______cm．15．已知双曲线k1yx+=经过点（－1，2），那么k的值等于_______.16．已知x=2是一元二次方程x2﹣2mx+4=0的一个解，则m的值为．17．如图是一个几何体的三视图（图中尺寸单位：cm），根据图中数据计算，这个几何体的表面积为__________2cm．18．已知扇形AOB的半径OA=4，圆心角为90°，则扇形AOB的面积为_________.三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）已知△OAB在平面直角坐标系中的位置如图所示．请解答以下问题：按要求作图：先将△ABO 绕原点O逆时针旋转90°得△OA1B1，再以原点O为位似中心，将△OA1B1在原点异侧按位似比2：1进行放大得到△OA2B2；直接写出点A1的坐标，点A2的坐标．20．（6分）已知，关于x的一元二次方程（k﹣1）x2+2k x+3＝0 有实数根，求k的取值范围．21．（6分）如图，抛物线y＝ax2+bx﹣2经过点A（4，0），B（1，0）．（1）求出抛物线的解析式；（2）点D是直线AC上方的抛物线上的一点，求△DCA面积的最大值；（3）P是抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．22．（8分）计算:2344 (1)11x xxx x++-+÷++.23．（8分）2018年4月份，郑州市教育局针对郑州市中小学参与课外辅导进行调查，根据学生参与课外辅导科目的数量，分成了：1科、2科、3科和4科，以下简记为：1、2、3、4，并根据调查结果绘制成如图所示的条形统计图和扇形统计图（未完成），请结合图中所给信息解答下列问题：（1）本次被调查的学员共有人；在被调查者中参加“3科”课外辅导的有人．（2）将条形统计图补充完整；（3）已知郑州市中小学约有24万人，那么请你估计一下参与辅导科目不多于2科的学生大约有多少人．24．（10分）计算：（﹣3）0﹣|﹣3|+（﹣1）2015+（12）﹣1．25．（10分）如图，二次函数y=ax2+2x+c的图象与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，3）．（1）求该二次函数的表达式；（2）过点A的直线AD∥BC且交抛物线于另一点D，求直线AD的函数表达式；（3）在（2）的条件下，请解答下列问题：①在x轴上是否存在一点P，使得以B、C、P为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，请说明理由；②动点M以每秒1个单位的速度沿线段AD从点A向点D运动，同时，动点N以每秒135个单位的速度沿线段DB从点D向点B运动，问：在运动过程中，当运动时间t为何值时，△DMN的面积最大，并求出这个最大值．26．（12分）（11分）阅读资料：如图1，在平面之间坐标系xOy中，A，B两点的坐标分别为A（x1，y1），B（x1，y1），由勾股定理得AB1=|x1﹣x1|1+|y1﹣y1|1，所以A，B两点间的距离为AB=．我们知道，圆可以看成到圆心距离等于半径的点的集合，如图1，在平面直角坐标系xoy中，A（x，y）为圆上任意一点，则A到原点的距离的平方为OA1=|x﹣0|1+|y﹣0|1，当⊙O的半径为r时，⊙O的方程可写为：x1+y1=r1．问题拓展：如果圆心坐标为P（a，b），半径为r，那么⊙P的方程可以写为．综合应用：如图3，⊙P与x轴相切于原点O，P点坐标为（0，6），A是⊙P上一点，连接OA，使tan∠POA=，作PD⊥OA，垂足为D，延长PD交x轴于点B，连接AB．①证明AB是⊙P的切点；②是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以Q为圆心，以OQ 为半径的⊙O的方程；若不存在，说明理由．27．（12分）如图，已知：AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D，E 是AB延长线上一点，CE交⊙O于点F，连接OC、AC．（1）求证：AC平分∠DAO．（2）若∠DAO=105°，∠E=30°①求∠OCE的度数；②若⊙O的半径为22，求线段EF的长．参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．B【解析】试题分析：连接CD，∵在△ABC中，∠ACB=90°，∠A=30°，BC=4，∴AB=2BC=1．∵作法可知BC=CD=4，CE是线段BD的垂直平分线，∴CD是斜边AB的中线，∴BD=AD=4，∴BF=DF=2，∴AF=AD+DF=4+2=2．故选B．考点：作图—基本作图；含30度角的直角三角形．2．C【解析】【分析】根据题意列出代数式，化简即可得到结果．【详解】根据题意得：a÷(1−20%)=a÷= a(元)，故答案选：C.【点睛】本题考查的知识点是列代数式，解题的关键是熟练的掌握列代数式.3．D【解析】【分析】根据积的乘方与幂的乘方计算可得．【详解】解：（﹣ab2）3=﹣a3b6，故选D．【点睛】本题主要考查幂的乘方与积的乘方，解题的关键是掌握积的乘方与幂的乘方的运算法则．4．D【解析】【详解】解：2728x yx y+=⎧⎨+=⎩①②，①+②得：3(x+y)=15，则x+y=5，故选D5．B 【解析】【分析】先利用垂径定理得到弧AD=弧BD，然后根据圆周角定理得到∠C=12∠BOD，从而可对各选项进行判断．【详解】解：∵直径CD⊥弦AB，∴弧AD =弧BD，∴∠C=12∠BOD．故选B．【点睛】本题考查了垂径定理和圆周角定理，垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．6．D【解析】【详解】根据全等三角形的性质可知A，B，C命题均正确，故选项均错误；D.错误，全等三角也可能是直角三角，故选项正确.故选D.【点睛】本题考查全等三角形的性质，两三角形全等，其对应边和对应角都相等.7．D【解析】分析：根据相似三角形的性质进行解答即可．详解：∵在平行四边形ABCD中，∴AE∥CD，∴△EAF∽△CDF，∵12EAFCDFCCVV，=∴12 AFDF=，∴11123 AFBC==+，∵AF∥BC，∴△EAF∽△EBC，∴21139 EAFEBCSS⎛⎫==⎪⎝⎭VV，故选D.点睛：考查相似三角形的性质：相似三角形的面积比等于相似比的平方.8．B【解析】解：过A点作AH ⊥BC于H，∵△ABC是等腰直角三角形，∴∠B=∠C=45°，BH=CH=AH=BC=2，当0≤x≤2时，如图1，∵∠B=45°，∴PD=BD=x，∴y=•x•x=；当2＜x≤4时，如图2，∵∠C=45°，∴PD=CD=4﹣x，∴y=•（4﹣x）•x=，故选B．9．D【解析】选项A，根据同底数幂的乘法可得原式=t10；选项B，不是同类项，不能合并；选项C，根据同底数幂的乘法可得原式=t7；选项D，根据同底数幂的乘法可得原式=t5，四个选项中只有选项D正确，故选D.10．A【解析】∵四边形ABCD是平行四边形，∴AB//CD，AB=CD，AD//BC，∴△BEF∽△CDF，△BEF∽△AED，∴22BEF BEFCDF AEDS SBE BES CD S AE∆∆∆∆⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭，，∵BE：AB=2：3，AE=AB+BE，∴BE：CD=2：3，BE：AE=2：5，∴44925BEF BEF CDF AED S S S S ∆∆∆∆==， ， ∵S △BEF =4，∴S △CDF =9，S △AED =25，∴S 四边形ABFD =S △AED -S △BEF =25-4=21，∴S 平行四边形ABCD =S △CDF +S 四边形ABFD =9+21=30，故选A.【点睛】本题考查了平行四边形的性质，相似三角形的判定与性质等，熟记相似三角形的面积等于相似比的平方是解题的关键.11．B【解析】【分析】根据解不等式组的方法可以求得原不等式组的解集．【详解】1030x x +>⎧⎨->⎩①②， 解不等式①，得x ＞-1，解不等式②，得x ＞1，由①②可得，x ＞1，故原不等式组的解集是x ＞1．故选B ．【点睛】本题考查解一元一次不等式组，解题的关键是明确解一元一次不等式组的方法．12．B【解析】【分析】根据旋转的性质可得AB=AE ，∠BAE=60°，然后判断出△AEB 是等边三角形，再根据等边三角形的三条边都相等可得BE=AB ．【详解】解：∵△ABC 绕点A 顺时针旋转 60°得到△AED ，∴AB=AE ，∠BAE=60°，∴△AEB 是等边三角形，∴BE=AB ，∴BE=1．故选B．【点睛】本题考查了旋转的性质，等边三角形的判定与性质，主要利用了旋转前后对应边相等以及旋转角的定义．二、填空题：（本大题共6个小题，每小题4分，共24分．）13．7 6π【解析】【分析】点O到点O′所经过的路径长分三段，先以A为圆心，1为半径，圆心角为90度的弧长，再平移了AB弧的长，最后以B为圆心，1为半径，圆心角为90度的弧长．根据弧长公式计算即可．【详解】解：∵扇形OAB的圆心角为30°，半径为1，∴AB弧长=30π1π, 1806⋅⋅=∴点O到点O′所经过的路径长=90π1π72π. 18066⋅⋅⨯+=故答案为:7π. 6【点睛】本题考查了弧长公式：π180n Rl⋅⋅=．也考查了旋转的性质和圆的性质．14．【解析】【分析】由图2可以计算出OB的长度，然后利用OB＝OA可以计算出通过弦AB的长度. 【详解】由图2得通过OB所用的时间为4442233ππ⎛⎫++⎪⎝⎭－＝s，则OB的长度为1×2＝2cm,则通过弧AB的时间为4442233ππ+⨯－＝s，则弧长AB为44133ππ⨯＝，利用弧长公式180n rlπ＝,得出∠AOB＝120°,即可以算出AB为【点睛】本题主要考查了从图中提取信息的能力和弧长公式的运用及转换,熟练运用公式是本题的解题关键. 15．－1【解析】分析：根据点在曲线上点的坐标满足方程的关系，将点（－1,2）代入k1yx+=，得：k121+=-，解得：k＝－1．16．1．【解析】试题分析：直接把x=1代入已知方程就得到关于m的方程，再解此方程即可．试题解析：∵x=1是一元二次方程x1-1mx+4=0的一个解，∴4-4m+4=0，∴m=1．考点：一元二次方程的解．17．16π【解析】分析：由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状，确定圆锥的母线长和底面半径，从而确定其表面积．详解：由主视图和左视图为三角形判断出是锥体，由俯视图是圆形可判断出这个几何体应该是圆锥；根据三视图知：该圆锥的母线长为6cm，底面半径为2cm，故表面积=πrl+πr2=π×2×6+π×22=16π（cm2）．故答案为：16π．点睛：考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．18．4π【解析】根据扇形的面积公式可得：扇形AOB的面积为29044360ππ⨯=，故答案为4π.三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．(1)见解析；（2）点A1的坐标为：（﹣1，3），点A2的坐标为：（2，﹣6）．【解析】【分析】（1）直接利用位似图形的性质得出对应点位置进而得出答案；（2）利用（1）中所画图形进而得出答案．【详解】（1）如图所示：△OA1B1，△OA2B2，即为所求；（2）点A1的坐标为：（﹣1，3），点A2的坐标为：（2，﹣6）．【点睛】此题主要考查了位似变换以及旋转变换，正确得出对应点位置是解题关键．20．0≤k≤65且k≠1．【解析】【分析】根据二次项系数非零、被开方数非负及根的判别式△≥0，即可得出关于k 的一元一次不等式组，解之即可求出k 的取值范围．【详解】解：∵关于x 的一元二次方程（k﹣1）x2+x+3＝0 有实数根，∴2k≥0，k-1≠0，2k2-4 3(k-1)≥0，解得：0≤k≤65且k≠1．∴k 的取值范围为0≤k≤65且k≠1．【点睛】本题考查了根的判别式、二次根式以及一元二次方程的定义，根据二次项系数非零、被开方数非负及根的判别式△≥0，列出关于k 的一元一次不等式组是解题的关键．当∆>0时，一元二次方程有两个不相等的实数根；当∆=0时，一元二次方程有两个相等的实数根；当∆<0时，一元二次方程没有实数根.21．（1）y=﹣12x2+52x﹣2；（2）当t=2时，△DAC面积最大为4；（3）符合条件的点P为（2，1）或（5，﹣2）或（﹣3，﹣14）．【解析】【分析】（1）把A与B坐标代入解析式求出a与b的值，即可确定出解析式；（2）如图所示，过D作DE与y轴平行，三角形ACD面积等于DE与OA乘积的一半，表示出S与t的二次函数解析式，利用二次函数性质求出S的最大值即可；（3）存在P点，使得以A，P，M为顶点的三角形与△OAC相似，分当1＜m＜4时；当m＜1时；当m＞4时三种情况求出点P坐标即可．【详解】（1）∵该抛物线过点A（4，0），B（1，0），∴将A与B代入解析式得：，解得：，则此抛物线的解析式为y=﹣x2+x﹣2；（2）如图，设D点的横坐标为t（0＜t＜4），则D点的纵坐标为﹣t2+t﹣2，过D作y轴的平行线交AC于E，由题意可求得直线AC的解析式为y=x﹣2，∴E点的坐标为（t，t﹣2），∴DE=﹣t2+t﹣2﹣（t﹣2）=﹣t2+2t，∴S△DAC=×（﹣t2+2t）×4=﹣t2+4t=﹣（t﹣2）2+4，则当t=2时，△DAC面积最大为4；（3）存在，如图，设P点的横坐标为m，则P点的纵坐标为﹣m2+m﹣2，当1＜m ＜4时，AM=4﹣m ，PM=﹣m 2+m ﹣2，又∵∠COA=∠PMA=90°， ∴①当==2时，△APM ∽△ACO ，即4﹣m=2（﹣m 2+m ﹣2），解得：m=2或m=4（舍去），此时P （2，1）； ②当==时，△APM ∽△CAO ，即2（4﹣m ）=﹣m 2+m ﹣2，解得：m=4或m=5（均不合题意，舍去）∴当1＜m ＜4时，P （2，1）；类似地可求出当m ＞4时，P （5，﹣2）；当m ＜1时，P （﹣3，﹣14），综上所述，符合条件的点P 为（2，1）或（5，﹣2）或（﹣3，﹣14）．【点睛】本题综合考查了抛物线解析式的求法，抛物线与相似三角形的问题，坐标系里求三角形的面积及其最大值问题，要求会用字母代替长度，坐标，会对代数式进行合理变形,解决相似三角形问题时要注意分类讨论．22．22x x -+ 【解析】【分析】括号内先进行通分，进行分式的加减法运算，然后再与括号外的分式进行分式乘除法运算即可.【详解】原式=()22311112x x x x x ⎛⎫-+-⨯ ⎪+++⎝⎭ =()()()2x 22112x x x x +-+⨯++ =22x x -+. 【点睛】本题考查了分式的混合运算，熟练掌握有关分式的运算法则是解题的关键.23．（1）50,10；（2）见解析.（3）16.8万【解析】【分析】（1）结合条形统计图和扇形统计图中的参加“3科”课外辅导人数及百分比，求得总人数为50人；再由总人数减去参加“1科”，“2科”，“4科”课外辅导人数即可求出答案.（2）由（1）知在被调查者中参加“3科”课外辅导的有10人，由扇形统计图可知参加“4科”课外辅导人数占比为10%，故参加“4科”课外辅导人数的有5人.（3）因为参加“1科”和“2科”课外辅导人数占比为152050+，所以全市参与辅导科目不多于2科的人数为24×152050+ ＝16.8（万）. 【详解】解：（1）本次被调查的学员共有：15÷30%＝50（人），在被调查者中参加“3科”课外辅导的有：50﹣15﹣20﹣50×10%＝10（人）， 故答案为50，10；（2）由（1）知在被调查者中参加“3科”课外辅导的有10人，在被调查者中参加“4科”课外辅导的有：50×10%＝5（人），补全的条形统计图如右图所示；（3）24×152050+ ＝16.8（万）， 答：参与辅导科目不多于2科的学生大约有16.8人．【点睛】本题考察了条形统计图和扇形统计图，关键在于将两者结合起来解题. 24．-1【解析】分析：根据零次幂、绝对值以及负指数次幂的计算法则求出各式的值，然后进行求和得出答案． 详解：解：30﹣|﹣3|+（﹣1）2015+（12）﹣1=1﹣3+（﹣1）+2=﹣1． 点睛：本题主要考查的是实数的计算法则，属于基础题型．理解各种计算法则是解决这个问题的关键． 25．（1）y=﹣x 2+2x+3；（2）y=﹣x ﹣1；（3）P （3,05）或P （﹣4.5，0）；当t=522时，S △MDN 的最大值为52． 【解析】【分析】（1）把A （-1，0），C （0，3）代入y=ax 2+2x+c 即可得到结果；（2）在y=-x 2+2x+3中，令y=0，则-x 2+2x+3=0，得到B （3，0），由已知条件得直线BC 的解析式为y=-x+3，由于AD ∥BC ，设直线AD 的解析式为y=-x+b ，即可得到结论；（3）①由BC ∥AD ，得到∠DAB=∠CBA ，全等只要当BC PB AD AB =或BC PB AB AD=时，△PBC ∽△ABD ，解方程组2231y x x y x ⎧=-++⎨=--⎩得D(4,−5)，求得AD =4,AB =BC =设P 的坐标为（x ，0），代入比例式解得35x =或x=−4.5,即可得到3,05P ⎛⎫ ⎪⎝⎭或P(−4.5,0)； ②过点B 作BF ⊥AD 于F ，过点N 作NE ⊥AD 于E ，在Rt △AFB 中，∠BAF=45°，于是得到sin ∠BAF BF AB =，求得42BF BD =⨯==求得sin 13BF ADB BD ∠=== 由于,DM t DN ==，于是得到12MDN S DM NE =⋅V ()1225t t =⋅215t =-+21()5t =--215522t ⎛=--+ ⎝⎭，即可得到结果．【详解】(1)由题意知：023a c c =-+⎧⎨=⎩， 解得13a c =-⎧⎨=⎩， ∴二次函数的表达式为223y x x =-++；(2)在2y x 2x 3=-++ 中,令y=0,则2230x x -++=，解得：121,3x x ，=-= ∴B(3,0)，由已知条件得直线BC 的解析式为y=−x+3，∵AD ∥BC ，∴设直线AD 的解析式为y=−x+b ，∴0=1+b ，∴b=−1，∴直线AD 的解析式为y=−x−1；(3)①∵BC ∥AD ，∴∠DAB=∠CBA ， ∴只要当：BC PB AD AB =或BC PB AB AD=时,△PBC ∽△ABD ，解2231y x x y x ⎧=-++⎨=--⎩得D(4,−5)， ∴52,4,32AD AB BC ===，设P 的坐标为(x,0)， 即323452x -=或32452=， 解得35x =或x=−4.5, ∴3,05P ⎛⎫ ⎪⎝⎭或P(−4.5,0)， ②过点B 作BF ⊥AD 于F ，过点N 作NE ⊥AD 于E ，在Rt △AFB 中,45BAF ∠=o ， ∴sin ∠BAF BF AB=， ∴242,262BF BD =⨯==， ∴22213sin 26BF ADB BD ∠=== ∵1352,DM t DN ==， 又∵132132sin ,5135NE ADB NE t t DN ∠==⋅=， ∴1,2MDN S DM NE =⋅V ()125225t t =⋅215t =-21(),5t =-- 215522t ⎛⎫=--+ ⎪ ⎪⎝⎭，∴当2t =时,MDN S V 的最大值为5.2 【点睛】属于二次函数的综合题，考查待定系数法求二次函数解析式，锐角三角形函数，相似三角形的判定与性质，二次函数的最值等，综合性比较强，难度较大.26．问题拓展：（x ﹣a ）1+（y ﹣b ）1=r 1综合应用：①见解析②点Q 的坐标为（4，3），方程为（x ﹣4）1+（y ﹣3）1=15．【解析】试题分析：问题拓展：设A （x ，y ）为⊙P 上任意一点，则有AP=r ，根据阅读材料中的两点之间距离公式即可求出⊙P 的方程；综合应用：①由PO=PA ，PD ⊥OA 可得∠OPD=∠APD ，从而可证到△POB ≌△PAB ，则有∠POB=∠PAB ．由⊙P 与x 轴相切于原点O 可得∠POB=90°，即可得到∠PAB=90°，由此可得AB 是⊙P 的切线；②当点Q 在线段BP 中点时，根据直角三角形斜边上的中线等于斜边的一半可得QO=QP=BQ=AQ ．易证∠OBP=∠POA ，则有tan ∠OBP==．由P 点坐标可求出OP 、OB ．过点Q 作QH ⊥OB 于H ，易证△BHQ ∽△BOP ，根据相似三角形的性质可求出QH 、BH ，进而求出OH ，就可得到点Q 的坐标，然后运用问题拓展中的结论就可解决问题．试题解析：解：问题拓展：设A （x ，y ）为⊙P 上任意一点，∵P （a ，b ），半径为r ，∴AP 1=（x ﹣a ）1+（y ﹣b ）1=r 1．故答案为（x ﹣a ）1+（y ﹣b ）1=r 1；综合应用：①∵PO=PA ，PD ⊥OA ，∴∠OPD=∠APD ．在△POB 和△PAB 中，，∴△POB ≌△PAB ，∴∠POB=∠PAB．∵⊙P与x轴相切于原点O，∴∠POB=90°，∴∠PAB=90°，∴AB是⊙P的切线；②存在到四点O，P，A，B距离都相等的点Q．当点Q在线段BP中点时，∵∠POB=∠PAB=90°，∴QO=QP=BQ=AQ．此时点Q到四点O，P，A，B距离都相等．∵∠POB=90°，OA⊥PB，∴∠OBP=90°﹣∠DOB=∠POA，∴tan∠OBP==tan∠POA=．∵P点坐标为（0，6），∴OP=6，OB=OP=3．过点Q作QH⊥OB于H，如图3，则有∠QHB=∠POB=90°，∴QH∥PO，∴△BHQ∽△BOP，∴===，∴QH=OP=3，BH=OB=4，∴OH=3﹣4=4，∴点Q的坐标为（4，3），∴OQ==5，∴以Q为圆心，以OQ为半径的⊙O的方程为（x﹣4）1+（y﹣3）1=15．考点：圆的综合题；全等三角形的判定与性质；等腰三角形的性质；直角三角形斜边上的中线；勾股定理；切线的判定与性质；相似三角形的判定与性质；锐角三角函数的定义．27．（1）证明见解析；（2）①∠OCE=45°；②EF =23-2.【解析】【试题分析】（1）根据直线与⊙O相切的性质，得OC⊥CD.又因为AD⊥CD，根据同一平面内，垂直于同一条直线的两条直线也平行，得：AD//OC. ∠DAC=∠OCA.又因为OC=OA，根据等边对等角，得∠OAC=∠OCA.等量代换得：∠DAC=∠OAC.根据角平分线的定义得：AC平分∠DAO.（2）①因为AD//OC，∠DAO=105°，根据两直线平行，同位角相等得，∠EOC=∠DAO=105°，在OCE 中，∠E=30°，利用内角和定理，得：∠OCE=45°.②作OG⊥CE于点G，根据垂径定理可得FG=CG，因为OC=22，∠OCE=45°.等腰直角三角形的斜边是腰长的2倍，得CG=OG=2. FG=2.在Rt△OGE中，∠E=30°，得GE=23，则EF=GE-FG=23-2. 【试题解析】（1）∵直线与⊙O相切，∴OC⊥CD.又∵AD⊥CD，∴AD//OC.∴∠DAC=∠OCA.又∵OC=OA，∴∠OAC=∠OCA.∴∠DAC=∠OAC.∴AC平分∠DAO.（2）解：①∵AD//OC，∠DAO=105°，∴∠EOC=∠DAO=105°∵∠E=30°，∴∠OCE=45°.②作OG⊥CE于点G，可得FG=CG∵OC=22，∠OCE=45°.∴CG=OG=2.∴FG=2.∵在Rt△OGE中，∠E=30°，∴GE=23.∴EF=GE-FG=23-2.【方法点睛】本题目是一道圆的综合题目，涉及到圆的切线的性质，平行线的性质及判定，三角形内角和，垂径定理，难度为中等.。

北京市海淀区2019-2020学年中考数学四模考试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．已知a ，b ，c 在数轴上的位置如图所示，化简|a+c|-|a-2b|-|c+2b|的结果是（ ）A ．4b+2cB ．0C ．2cD ．2a+2c2．一元二次方程x 2﹣2x ＝0的根是（ ）A ．x ＝2B ．x ＝0C ．x 1＝0，x 2＝2D ．x 1＝0，x 2＝﹣23．如图，AB 是O e 的直径，弦CD AB ⊥，垂足为点E ，点G 是AC 上的任意一点，延长AG 交DC 的延长线于点F ，连接,,GC GD AD .若25BAD ∠=︒，则AGD ∠等于（ ）A ．55︒B ．65︒C ．75︒D ．85︒4．如图，某小区计划在一块长为31m ，宽为10m 的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m 1．若设道路的宽为xm ，则下面所列方程正确的是（ ）A ．（31﹣1x ）（10﹣x ）=570B ．31x+1×10x=31×10﹣570C ．（31﹣x ）（10﹣x ）=31×10﹣570D ．31x+1×10x ﹣1x 1=5705．人的大脑每天能记录大约8 600万条信息，数据8 600用科学记数法表示为（ ）A ．0.86×104B ．8.6×102C ．8.6×103D ．86×1026．一副直角三角板如图放置，其中C DFE 90∠=∠=o ，45A ∠=︒，60E ∠=︒，点F 在CB 的延长线上若//DE CF ，则BDF ∠等于（ ）A ．35°B ．25°C ．30°D ．15°7．如图，一把带有60°角的三角尺放在两条平行线间，已知量得平行线间的距离为12cm ，三角尺最短边和平行线成45°角，则三角尺斜边的长度为（ ）A ．12cmB ．122cmC ．24cmD ．242cm8．二次函数2y ax bx c =++的图象如图所示，则反比例函数a y x=与一次函数y bx c =+在同一坐标系中的大致图象是( )A ．B ．C ．D ．9．如图，△ABC 中，DE 垂直平分AC 交AB 于E ，∠A=30°，∠ACB=80°，则∠BCE 等于（ ）A ．40°B ．70°C ．60°D ．50°10．如图，在5×5的方格纸中将图①中的图形N 平移到如图②所示的位置，那么下列平移正确的是( )A ．先向下移动1格，再向左移动1格B ．先向下移动1格，再向左移动2格C ．先向下移动2格，再向左移动1格D ．先向下移动2格，再向左移动2格 11．关于x 的方程=无解，则k 的值为（ ）A ．0或B ．﹣1C ．﹣2D ．﹣312．如图，二次函数y=ax 2+bx+c （a≠0）的图象与x 轴的正半轴相交于A ，B 两点，与y 轴相交于点C ，对称轴为直线x=2，且OA=OC ．有下列结论：①abc ＜0；②3b+4c ＜0；③c ＞﹣1；④关于x 的方程ax 2+bx+c=0有一个根为﹣1a，其中正确的结论个数是（ ）A ．1B ．2C ．3D ．4二、填空题：（本大题共6个小题，每小题4分，共24分．）13．如图，AB 是⊙O 的直径，且经过弦CD 的中点H ，过CD 延长线上一点E 作⊙O 的切线，切点为F ．若∠ACF=65°，则∠E= ．14．分式方程32xx 2--+22x-=1的解为________. 15．不等式组4342x x ->-⎧⎨>⎩的解集为____． 16．如图，矩形OABC 的边OA ，OC 分别在x 轴，y 轴上，点B 在第一象限，点D 在边BC 上，且∠AOD ＝30°，四边形OA′B′D 与四边形OABD 关于直线OD 对称（点A′和A ，点B′和B 分别对应）．若AB ＝2，反比例函数y ＝k x（k≠0）的图象恰好经过A′，B ，则k 的值为_____．17．已知扇形AOB的半径OA=4，圆心角为90°，则扇形AOB的面积为_________.18．已知二次函数y=ax2+bx（a≠0）的最小值是﹣3，若关于x的一元二次方程ax2+bx+c=0有实数根，则c的最大值是_____．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x 元，每星期的销售量为y件．(1)求y与x之间的函数关系式；(2)当每件售价定为多少元时，每星期的销售利润最大，最大利润是多少元？(3)若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？20．（6分）如图，在平面直角坐标系中，一次函数y＝﹣13x+2的图象交x轴于点P，二次函数y＝﹣1 2x2+32x+m的图象与x轴的交点为（x1，0）、（x2，0），且21x+22x＝17（1）求二次函数的解析式和该二次函数图象的顶点的坐标．（2）若二次函数y＝﹣12x2+32x+m的图象与一次函数y＝﹣13x+2的图象交于A、B两点（点A在点B的左侧），在x轴上是否存在点M，使得△MAB是以∠ABM为直角的直角三角形？若存在，请求出点M 的坐标；若不存在，请说明理由．21．（6分）如图抛物线y=ax2+bx，过点A（4，0）和点B（6，3，四边形OCBA是平行四边形，点M（t，0）为x轴正半轴上的点，点N为射线AB上的点，且AN=OM，点D为抛物线的顶点．（1）求抛物线的解析式，并直接写出点D的坐标；（2）当△AMN的周长最小时，求t的值；（3）如图②，过点M作ME⊥x轴，交抛物线y=ax2+bx于点E，连接EM，AE，当△AME与△DOC 相似时．请直接写出所有符合条件的点M坐标．22．（8分）如图，△ABC内接于⊙O，且AB为⊙O的直径，OD⊥AB，与AC交于点E，与过点C的⊙O 的切线交于点D．若AC=4，BC=2，求OE的长．试判断∠A与∠CDE的数量关系，并说明理由．23．（8分）如图，可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域，其中标有数字“1”的扇形圆心角为120°．转动转盘，待转盘自动停止后，指针指向一个扇形的内部，则该扇形内的数字即为转出的数字，此时，称为转动转盘一次（若指针指向两个扇形的交线，则不计转动的次数，重新转动转盘，直到指针指向一个扇形的内部为止）(1)转动转盘一次，求转出的数字是－2的概率；(2)转动转盘两次，用树状图或列表法求这两次分别转出的数字之积为正数的概率．24．（10分）如图在由边长为1个单位长度的小正方形组成的12×12网格中，已知点A，B，C，D均为网格线的交点在网格中将△ABC绕点D顺时针旋转90°画出旋转后的图形△A1B1C1；在网格中将△ABC放大2倍得到△DEF，使A与D为对应点．25．（10分）目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利，初二数学小组在校内对“你最认可的四大新生事物”进行调查，随机调查了m 人（每名学生必选一种且只能从这四种中选择一种）并将调查结果绘制成如下不完整的统计图．根据图中信息求出m= ，n= ；请你帮助他们将这两个统计图补全；根据抽样调查的结果，请估算全校2000名学生中，大约有多少人最认可“微信”这一新生事物？已知A 、B 两位同学都最认可“微信”，C 同学最认可“支付宝”D 同学最认可“网购”从这四名同学中抽取两名同学，请你通过树状图或表格，求出这两位同学最认可的新生事物不一样的概率．26．（12分）先化简，再求代数式（222311a a a --+-）÷11a +的值，其中a=2sin45°+tan45°． 27．（12分）如图，抛物线y=x 2﹣2mx （m ＞0）与x 轴的另一个交点为A ，过P （1，﹣m ）作PM ⊥x 轴于点M ，交抛物线于点B ，点B 关于抛物线对称轴的对称点为C（1）若m=2，求点A 和点C 的坐标；（2）令m ＞1，连接CA ，若△ACP 为直角三角形，求m 的值；（3）在坐标轴上是否存在点E ，使得△PEC 是以P 为直角顶点的等腰直角三角形？若存在，求出点E 的坐标；若不存在，请说明理由．参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．A【解析】由数轴上点的位置得：b<a<0<c，且|b|>|c|>|a|，∴a+c>0，a−2b>0，c+2b<0，则原式=a+c−a+2b+c+2b=4b +2c.故选：B.点睛：本题考查了整式的加减以及数轴，涉及的知识有：去括号法则以及合并同类项法则，熟练掌握运算法则是解本题的关键.2．C【解析】【分析】方程左边分解因式后，利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．【详解】方程变形得：x（x﹣1）＝0，可得x＝0或x﹣1＝0，解得：x1＝0，x1＝1．故选C．【点睛】考查了解一元二次方程﹣因式分解法，熟练掌握因式分解的方法是解本题的关键．3．B【解析】【分析】连接BD，利用直径得出∠ABD=65°，进而利用圆周角定理解答即可．【详解】连接BD，∵AB是直径，∠BAD=25°，∴∠ABD=90°-25°=65°，∴∠AGD=∠ABD=65°，故选B．【点睛】此题考查圆周角定理，关键是利用直径得出∠ABD=65°．4．A【解析】六块矩形空地正好能拼成一个矩形，设道路的宽为xm，根据草坪的面积是570m1，即可列出方程:(31−1x)(10−x)=570，故选A.5．C【解析】【分析】科学记数法就是将一个数字表示成a×10的n次幂的形式，其中1≤|a|＜10，n表示整数．n为整数位数减1，即从左边第一位开始，在首位非零的后面加上小数点，再乘以10的n次幂．【详解】数据8 600用科学记数法表示为8.6×103故选C．【点睛】用科学记数法表示一个数的方法是（1）确定a：a是只有一位整数的数；（2）确定n：当原数的绝对值≥10时，n为正整数，n等于原数的整数位数减1；当原数的绝对值＜1时，n为负整数，n的绝对值等于原数中左起第一个非零数前零的个数（含整数位数上的零）．6．D【解析】【分析】直接利用三角板的特点，结合平行线的性质得出∠BDE=45°，进而得出答案．【详解】解：由题意可得：∠EDF=30°，∠ABC=45°，∵DE∥CB，∴∠BDE=∠ABC=45°，∴∠BDF=45°-30°=15°．故选D．【点睛】此题主要考查了平行线的性质，根据平行线的性质得出∠BDE的度数是解题关键．7．D【解析】【分析】过A 作AD ⊥BF 于D,根据45°角的三角函数值可求出AB 的长度，根据含30°角的直角三角形的性质求出斜边AC 的长即可.【详解】如图，过A 作AD ⊥BF 于D ，∵∠ABD=45°，AD=12， ∴sin 45AD AB ︒==122， 又∵Rt △ABC 中，∠C=30°，∴AC=2AB=242，故选：D ．【点睛】本题考查解直角三角形，在直角三角形中，30°角所对的直角边等于斜边的一半，熟记特殊角三角函数值是解题关键.8．D【解析】【分析】根据抛物线和直线的关系分析.【详解】由抛物线图像可知，所以反比例函数应在二、四象限，一次函数过原点，应在二、四象限.故选D【点睛】考核知识点：反比例函数图象.9．D【解析】【分析】根据线段垂直平分线性质得出AE=CE，推出∠A=∠ACE=30°，代入∠BCE=∠ACB-∠ACE求出即可．【详解】∵DE垂直平分AC交AB于E，∴AE=CE，∴∠A=∠ACE，∵∠A=30°，∴∠ACE=30°，∵∠ACB=80°，∴∠BCE=∠ACB-∠ACE=50°，故选D．【点睛】本题考查了等腰三角形的性质，线段垂直平分线性质的应用，注意：线段垂直平分线上的点到线段两个端点的距离相等．10．C【解析】【分析】根据题意,结合图形,由平移的概念求解.【详解】由方格可知，在5×5方格纸中将图①中的图形N平移后的位置如图②所示，那么下面平移中正确的是：先向下移动2格，再向左移动1格，故选C．【点睛】本题考查平移的基本概念及平移规律,是比较简单的几何图形变换.关键是要观察比较平移前后物体的位置.11．A【解析】方程两边同乘2x(x+3)，得x+3=2kx，（2k-1）x=3，∵方程无解，∴当整式方程无解时，2k-1=0，k=，当分式方程无解时，①x=0时，k无解，②x=-3时，k=0，∴k=0或时，方程无解，故选A.12．B【解析】【分析】由二次函数图象的开口方向、对称轴及与y 轴的交点可分别判断出a 、b 、c 的符号，从而可判断①；由对称轴2b a -=2可知a=14b -，由图象可知当x=1时，y ＞0，可判断②；由OA=OC ，且OA ＜1，可判断③；把-1a代入方程整理可得ac 2-bc+c=0，结合③可判断④；从而可得出答案． 【详解】解：∵图象开口向下，∴a ＜0，∵对称轴为直线x=2，∴2b a-＞0，∴b ＞0， ∵与y 轴的交点在x 轴的下方，∴c ＜0，∴abc ＞0，故①错误.∵对称轴为直线x=2，∴2b a -=2，∴a=14b -， ∵由图象可知当x=1时，y ＞0， ∴a+b+c ＞0，∴4a+4b+4c>0，∴4⨯(14b -)+4b+4c>0，∴3b+4c>0，故②错误.∵由图象可知OA ＜1，且OA=OC ，∴OC ＜1，即-c ＜1，∴c ＞-1，故③正确.∵假设方程的一个根为x=-1a ，把x=-1a 代入方程可得1b a a-+c=0， 整理可得ac-b+1=0，两边同时乘c 可得ac 2-bc+c=0，∴方程有一个根为x=-c ，由③可知-c=OA ，而当x=OA 是方程的根，∴x=-c 是方程的根，即假设成立，故④正确.综上可知正确的结论有三个：③④.故选B.【点睛】本题主要考查二次函数的图象和性质．熟练掌握图象与系数的关系以及二次函数与方程、不等式的关系是解题的关键．特别是利用好题目中的OA=OC ，是解题的关键.二、填空题：（本大题共6个小题，每小题4分，共24分．）13．50°．【解析】【分析】【详解】解：连接DF ，连接AF 交CE 于G ，∵EF 为⊙O 的切线，∴∠OFE=90°，∵AB 为直径，H 为CD 的中点∴AB ⊥CD ，即∠BHE=90°，∵∠ACF=65°，∴∠AOF=130°，∴∠E=360°-∠BHE-∠OFE-∠AOF=50°，故答案为：50°. 14．x 1=【解析】【分析】根据解分式方程的步骤，即可解答．【详解】方程两边都乘以x 2-，得：32x 2x 2--=-，解得：x 1=，检验：当x 1=时，x 21210-=-=-≠，所以分式方程的解为x 1=，故答案为x 1=．【点睛】考查了解分式方程，()1解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解().2解分式方程一定注意要验根．15．x>1【解析】【分析】分别解出两不等式的解集再求其公共解．【详解】4342x x ->-⎧⎨>⎩①②由①得：x ＞1由②得：x ＞12∴不等式组4342x x ->-⎧⎨>⎩的解集是x ＞1． 【点睛】 求不等式的解集须遵循以下原则：同大取较大，同小取较小．小大大小中间找，大大小小解不了． 16．3【解析】【分析】【详解】解：∵四边形ABCO 是矩形，AB=1，∴设B （m ，1），∴OA=BC=m ，∵四边形OA′B′D 与四边形OABD 关于直线OD 对称，∴OA′=OA=m ，∠A′OD=∠AOD=30°∴∠A′OA=60°，过A′作A′E ⊥OA 于E ，∴OE=12m ，， ∴A′（12m）， ∵反比例函数k y x=（k≠0）的图象恰好经过点A′，B ， ∴12m•2m=m ，∴故答案为317．4π【解析】根据扇形的面积公式可得：扇形AOB的面积为29044360ππ⨯=，故答案为4π.18．3【解析】【分析】由一元二次方程ax2+bx+c=0有实数根，可得y=ax2+bx（a≠0）和y=-c有交点，由此即可解答.【详解】∵一元二次方程ax2+bx+c=0有实数根，∴抛物线y=ax2+bx（a≠0）和直线y=-c有交点，∴-c≥-3，即c≤3，∴c的最大值为3.故答案为：3.【点睛】本题考查了一元二次方程与二次函数，根据一元二次方程有实数根得到抛物线y=ax2+bx（a≠0）和直线y=-c 有交点是解决问题的关键.三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（1）y=﹣30x+1；（2）每件售价定为55元时，每星期的销售利润最大，最大利润2元；（3）该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装360件．【解析】【分析】(1) 每星期的销售量等于原来的销售量加上因降价而多销售的销售量, 代入即可求解函数关系式;(2) 根据利润=销售量⨯(销售单价-成本) , 建立二次函数, 用配方法求得最大值.(3) 根据题意可列不等式, 再取等将其转化为一元二次方程并求解, 根据每星期的销售利润所在抛物线开口向下求出满足条件的x的取值范围, 再根据(1) 中一元一次方程求得满足条件的x的取值范围内y的最小值即可.【详解】（1）y ＝300+30（60﹣x ）＝﹣30x+1．（2）设每星期利润为W 元，W ＝（x ﹣40）（﹣30x+1）＝﹣30（x ﹣55）2+2．∴x ＝55时，W 最大值＝2．∴每件售价定为55元时，每星期的销售利润最大，最大利润2元．（3）由题意（x ﹣40）（﹣30x+1）≥6480，解得52≤x≤58，当x ＝52时，销售300+30×8＝540， 当x ＝58时，销售300+30×2＝360， ∴该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装360件．【点睛】本题主要考查一次函数的应用和二次函数的应用,注意综合运用所学知识解题.20．（1）y ＝﹣12x 2+32x+2＝（x ﹣32）2+258，顶点坐标为（32，258）；（2）存在，点M （9227，0）．理由见解析．【解析】【分析】（1）由根与系数的关系，结合已知条件可得9+4m ＝17，解方程求得m 的值，即可得求得二次函数的解析式，再求得该二次函数图象的顶点的坐标即可；（2）存在，将抛物线表达式和一次函数y ＝﹣13x+2联立并解得x ＝0或113，即可得点A 、B 的坐标为（0，2）、（113，79），由此求得PB=9， ，过点B 作BM ⊥AB 交x 轴于点M ，证得△APO ∽△MPB ，根据相似三角形的性质可得AP OP MP PB ，代入数据即可求得MP ＝7027，再求得OM ＝9227，即可得点M 的坐标为（9227，0）． 【详解】 （1）由题意得：x 1+x 2＝3，x 1x 2＝﹣2m ，x 12+x 22＝（x 1+x 2）2﹣2x 1x 2＝17，即：9+4m ＝17，解得：m ＝2，抛物线的表达式为：y ＝﹣12x 2+32x+2＝（x ﹣32）2+258， 顶点坐标为（32，258）； （2）存在，理由：将抛物线表达式和一次函数y ＝﹣13x+2联立并解得：x ＝0或113， ∴点A 、B 的坐标为（0，2）、（113，79）， 一次函数y ＝﹣13x+2与x 轴的交点P 的坐标为（6，0）， ∵点P 的坐标为（6，0），B 的坐标为（113，79），点B 的坐标为（0，2）、 ∴PB ＝221176039()()-+-=7109， AP=2262+=210过点B 作BM ⊥AB 交x 轴于点M ，∵∠MBP ＝∠AOP ＝90°，∠MPB ＝∠APO ，∴△APO ∽△MPB ，∴AP OP MP PB = ，∴210710MP = ， ∴MP ＝7027， ∴OM ＝OP ﹣MP ＝6﹣7027＝9227， ∴点M （9227，0）． 【点睛】 本题是一道二次函数的综合题，一元二次方程根与系数的关系、直线与抛物线的较大坐标．相似三角形的判定与性质，题目较为综合，有一定的难度，解决第二问的关键是求得PB 、AP 的长，再利用相似三角形的性质解决问题．21．（1）3223，点D 的坐标为（223）；（2）t=2；（3）M 点的坐标为（2，0）或（6，0）．【解析】【分析】（1）利用待定系数法求抛物线解析式；利用配方法把一般式化为顶点式得到点D的坐标；（2）连接AC，如图①，先计算出AB=4，则判断平行四边形OCBA为菱形，再证明△AOC和△ACB都是等边三角形，接着证明△OCM≌△ACN得到CM=CN，∠OCM=∠ACN，则判断△CMN为等边三角形得到MN=CM，于是△AMN的周长=OA+CM，由于CM⊥OA时，CM的值最小，△AMN的周长最小，从而得到t的值；（3）先利用勾股定理的逆定理证明△OCD为直角三角形，∠COD=90°，设M（t，0），则E（t，3t2-23t），根据相似三角形的判定方法，当AM MEOC OD=时，△AME∽△COD，即|t-4|：4=|36t2-233t |：433，当AM MEOD OC=时，△AME∽△DOC，即|t-4|：433=|36t2-233t |：4，然后分别解绝对值方程可得到对应的M点的坐标．【详解】解：（1）把A（4，0）和B（6，23）代入y=ax2+bx得164036623a ba b+⎧⎪⎨+⎪⎩＝＝，解得323ab⎧=⎪⎪⎨⎪=-⎪⎩，∴抛物线解析式为y=3x2-23x；∵y=3x2-23x =3(x-2) 2-23；∴点D的坐标为（2，-23）；（2）连接AC，如图①，()2246(23)-+，而OA=4，∴平行四边形OCBA 为菱形，∴OC=BC=4，∴C （2，，∴，∴OC=OA=AC=AB=BC ，∴△AOC 和△ACB 都是等边三角形，∴∠AOC=∠COB=∠OCA=60°，而OC=AC ，OM=AN ，∴△OCM ≌△ACN ，∴CM=CN ，∠OCM=∠ACN ，∵∠OCM+∠ACM=60°，∴∠ACN+∠ACM=60°，∴△CMN 为等边三角形，∴MN=CM ，∴△AMN 的周长=AM+AN+MN=OM+AM+MN=OA+CM=4+CM ，当CM ⊥OA 时，CM 的值最小，△AMN 的周长最小，此时OM=2，∴t=2；（3）∵C （2，，D （2，），∴，∵3=，OC=4， ∴OD 2+OC 2=CD 2，∴△OCD 为直角三角形，∠COD=90°，设M （t ，0），则E （t ，6t 2-3t ）， ∵∠AME=∠COD ，∴当AM ME OC OD =时，△AME ∽△COD ，即|t-4|：2t |， 整理得|16t 2-23t|=13|t-4|，解方程16t 2-23t =13（t-4）得t 1=4（舍去），t 2=2，此时M 点坐标为（2，0）； 解方程16t 2-23t =-13（t-4）得t 1=4（舍去），t 2=-2（舍去）；当AM ME OD OC =时，△AME ∽△DOC ，即|t-4|2t |：4，整理得|16t 2-23t |=|t-4|， 解方程16t 2-23t =t-4得t 1=4（舍去），t 2=6，此时M 点坐标为（6，0）； 解方程16t 2-23t =-（t-4）得t 1=4（舍去），t 2=-6（舍去）； 综上所述，M 点的坐标为（2，0）或（6，0）．【点睛】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质、平行四边形的性质和菱形的判定与性质；会利用待定系数法求函数解析式；理解坐标与图形性质；熟练掌握相似三角形的判定方法；会运用分类讨论的思想解决数学问题．22．（1；（2）∠CDE=2∠A ． 【解析】【分析】（1）在Rt △ABC 中，由勾股定理得到AB 的长，从而得到半径AO ．再由△AOE ∽△ACB ，得到OE 的长；（2）连结OC ，得到∠1=∠A ，再证∠3=∠CDE ，从而得到结论．【详解】（1）∵AB 是⊙O 的直径，∴∠ACB=90°，在Rt △ABC 中，由勾股定理得：==∴AO=12 ∵OD ⊥AB ，∴∠AOE=∠ACB=90°，又∵∠A=∠A ，∴△AOE ∽△ACB ， ∴OE AO BC AC=，∴OE=BC AO AC ⋅==5.（2）∠CDE=2∠A．理由如下：连结OC，∵OA=OC，∴∠1=∠A，∵CD是⊙O的切线，∴OC⊥CD，∴∠OCD=90°，∴∠2+∠CDE=90°，∵OD⊥AB，∴∠2+∠3=90°，∴∠3=∠CDE．∵∠3=∠A+∠1=2∠A，∴∠CDE=2∠A．考点：切线的性质；探究型；和差倍分．23．（1）13；（2）59.【解析】【分析】（1）根据题意可求得2个“－2”所占的扇形圆心角的度数，再利用概率公式进行计算即可得；（2）由题意可得转出“1”、“3”、“－2”的概率相同，然后列表得到所有可能的情况，再找出符合条件的可能性，根据概率公式进行计算即可得.【详解】（1）由题意可知：“1”和“3”所占的扇形圆心角为120°，所以2个“－2”所占的扇形圆心角为360°－2×120°＝120°，∴转动转盘一次，求转出的数字是－2的概率为120360︒︒＝13；（2）由（1）可知，该转盘转出“1”、“3”、“－2”的概率相同，均为13，所有可能性如下表所示：第一次第二次1 －2 31 (1，1) (1，－2) (1，3)－2 (－2，1) (－2，－2) (－2，3)3 (3，1) (3，－2) (3，3)由上表可知：所有可能的结果共9种，其中数字之积为正数的的有5种，其概率为9.【点睛】本题考查了列表法或树状图法求概率，用到的知识点为：概率=所求情况数与总情况数之比．24．（1）见解析（2）见解析【解析】【分析】（1）根据旋转变换的定义和性质求解可得；（2）根据位似变换的定义和性质求解可得．【详解】解：（1）如图所示，△A1B1C1即为所求；（2）如图所示，△DEF即为所求．【点睛】本题主要考查作图﹣位似变换与旋转变换，解题的关键是掌握位似变换与旋转变换的定义与性质．25．（1）100、35；（2）补图见解析；（3）800人；（4）5 6【解析】分析：（1）由共享单车人数及其百分比求得总人数m，用支付宝人数除以总人数可得其百分比n的值；（2）总人数乘以网购人数的百分比可得其人数，用微信人数除以总人数求得其百分比即可补全两个图形；（3）总人数乘以样本中微信人数所占百分比可得答案；（4）列表得出所有等可能结果，从中找到这两位同学最认可的新生事物不一样的结果数，根据概率公式计算可得．详解：（1）∵被调查的总人数m=10÷10%=100人，（2）网购人数为100×15%=15人，微信对应的百分比为40100×100%=40%， 补全图形如下：（3）估算全校2000名学生中，最认可“微信”这一新生事物的人数为2000×40%=800人； （4）列表如下：共有12种情况，这两位同学最认可的新生事物不一样的有10种， 所以这两位同学最认可的新生事物不一样的概率为105126=． 点睛：本题考查的是用列表法或画树状图法求概率以及扇形统计图与条形统计图的知识．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比． 26．11a -2． 【解析】 【分析】先把小括号内的通分，按照分式的减法和分式除法法则进行化简，再把字母的值代入运算即可． 【详解】解：原式()()()()()()21231,1111a a a a a a a ⎡⎤--=-⋅+⎢⎥+-+-⎢⎥⎣⎦()()()22231,11a a a a a --+=⋅++-当2sin45tan45a =︒+︒22121,2=⨯+=+时 原式2.22112===+-【点睛】考查分式的混合运算，掌握运算顺序是解题的关键． 27．（1）A （4，0），C （3，﹣3）;(2) m=32;(3) E 点的坐标为（2，0）或（43，0）或（0，﹣4）；【解析】 【分析】方法一：(1)m=2时,函数解析式为y=24x x -,分别令y=0,x=1,即可求得点A 和点B 的坐标, 进而可得到点C 的坐标；(2) 先用m 表示出P, A C 三点的坐标,分别讨论∠APC=90o ,∠ACP=90o ,∠PAC=90o 三种情况, 利用勾股定理即可求得m 的值；(3) 设点F （x ，y ）是直线PE 上任意一点，过点F 作FN ⊥PM 于N ，可得Rt △FNP ∽Rt △PBC ， NP ：NF=BC ：BP 求得直线PE 的解析式，后利用△PEC 是以P 为直角顶点的等腰直角三角形求得E 点坐标.方法二：（1）同方法一.(2) 由△ACP 为直角三角形, 由相互垂直的两直线斜率相乘为-1，可得m 的值；（3）利用△PEC 是以P 为直角顶点的等腰直角三角形，分别讨论E 点再x 轴上，y 轴上的情况求得E 点坐标． 【详解】 方法一：解：（1）若m=2，抛物线y=x 2﹣2mx=x 2﹣4x ， ∴对称轴x=2， 令y=0，则x 2﹣4x=0，∵P（1，﹣2），令x=1，则y=﹣3，∴B（1，﹣3），∴C（3，﹣3）．（2）∵抛物线y=x2﹣2mx（m＞1），∴A（2m，0）对称轴x=m，∵P（1，﹣m）把x=1代入抛物线y=x2﹣2mx，则y=1﹣2m，∴B（1，1﹣2m），∴C（2m﹣1，1﹣2m），∵PA2=（﹣m）2+（2m﹣1）2=5m2﹣4m+1，PC2=（2m﹣2）2+（1﹣m）2=5m2﹣10m+5，AC2=1+（1﹣2m）2=2﹣4m+4m2，∵△ACP为直角三角形，∴当∠ACP=90°时，PA2=PC2+AC2，即5m2﹣4m+1=5m2﹣10m+5+2﹣4m+4m2，整理得：4m2﹣10m+6=0，解得：m=，m=1（舍去），当∠APC=90°时，PA2+PC2=AC2，即5m2﹣4m+1+5m2﹣10m+5=2﹣4m+4m2，整理得：6m2﹣10m+4=0，解得：m=，m=1，和1都不符合m＞1，故m=32．（3）设点F（x，y）是直线PE上任意一点，过点F作FN⊥PM于N，∵∠FPN=∠PCB，∠PNF=∠CBP=90°，∴Rt△FNP∽Rt△PBC，∴NP：NF=BC：BP，即=，∴y=2x﹣2﹣m，∴直线PE的解析式为y=2x﹣2﹣m．令y=0，则x=1+，∴E（1+m，0），∴PE2=（﹣m）2+（m）2=，∴E（2，0）或E（，0），∴在x轴上存在E点，使得△PEC是以P为直角顶点的等腰直角三角形，此时E（2，0）或E（，0）；令x=0，则y=﹣2﹣m，∴E（0，﹣2﹣m）∴PE2=（﹣2）2+12=5∴5m2﹣10m+5=5，解得m=2，m=0（舍去），∴E（0，﹣4）∴y轴上存在点E，使得△PEC是以P为直角顶点的等腰直角三角形，此时E（0，﹣4），∴在坐标轴上是存在点E，使得△PEC是以P为直角顶点的等腰直角三角形，E点的坐标为（2，0）或（43，0）或（0，﹣4）；方法二：（1）略．（2）∵P（1，﹣m），∴B（1，1﹣2m），∵对称轴x=m，∴C（2m﹣1，1﹣2m），A（2m，0），∵△ACP为直角三角形，∴AC⊥AP，AC⊥CP，AP⊥CP，①AC⊥AP，∴K AC×K AP=﹣1，且m＞1，∴，m=﹣1（舍）②AC⊥CP，∴K AC×K CP=﹣1，且m＞1，∴=﹣1，∴m=，③AP⊥CP，∴K AP×K CP=﹣1，且m＞1，∴=﹣1，∴m=（舍）（3）∵P（1，﹣m），C（2m﹣1，1﹣2m），∴PE ⊥PC ，∴K PE ×K CP =﹣1，∴K PE =2， ∵P （1，﹣m ）， ∴l PE ：y=2x ﹣2﹣m ， ∵点E 在坐标轴上， ∴①当点E 在x 轴上时， E （，0）且PE=PC ，∴（1﹣）2+（﹣m ）2=（2m ﹣1﹣1）2+（1﹣2m+m ）2，∴m2=5（m ﹣1）2， ∴m 1=2，m 2=，∴E 1（2，0），E 2（，0），②当点E 在y 轴上时，E （0，﹣2﹣m ）且PE=PC ，∴（1﹣0）2+（﹣m+2+m ）2=（2m ﹣1﹣1）2+（1﹣2m+m ）2， ∴1=（m ﹣1）2， ∴m 1=2，m 2=0（舍）， ∴E （0，4），综上所述，（2，0）或（，0）或（0，﹣4）． 【点睛】本题主要考查二次函数的图象与性质. 扩展:设坐标系中两点坐标分别为点A(11,x y ), 点B(22,x y ), 则线段AB 的长度为: 221212()()x x y y --设平面内直线AB 的解析式为:111y k x b =+,直线CD 的解析式为:222y k x b =+ (1)若AB//CD,则有:12k k =; (2)若AB ⊥CD,则有:121k k ?-.。

2020年海淀外国语实验学校中考数学模拟试卷(3月份)一、选择题（本大题共8小题，共16.0分）1.小明给希望工作捐款15000元，15000用科学记数法表示为()A. 15×103B. 1.5×103C. 1.5×104D. 1.5×1052. 3.下列正方体展开图中，与“治”字相对面的字为()A. 乱B. 扫C. 黑D. 除3.如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE//BD交CB的延长线于点E.若∠E=35°，则∠BAC的度数为()A. 40°B. 45°C. 60°D. 70°4.下列运算正确的是()A. (−x2)3=−x5B. xy2÷12y=2xy(y≠0)C. 2√x+3√y=5√xyD. −6a6÷2a2=−3a45.如图(1)是一座横断面为抛物线形状的拱桥，当水面在直线l时，拱顶(拱桥洞的最高点)离水面2m，水面宽4m.如图(2)建立平面直角坐标系，则抛物线的表达式是()A. y=−2x2B. y=2x2C. y=−12x2 D. y=12x26.如图，△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1)，如果将△ABC绕点C按逆时针方向旋转90°，得到△A′B′C，那么点A、B的对应点A′、B′的坐标分别是()A. (−3,3)、(−2,4)B. (3,−3)、(1,4)C. (3,−3)、(−2,4)D. (−3,3)、(1,4)7.如图，在平面直角坐标系中，将△OAB(顶点为网格线交点)绕原的图像点O顺时针旋转90∘，得到△OA′B′，若反比例函数y=kx经过点A的对应点A′，则k的值为()A. 6B. −3C. 3D. 68.矩形的两相邻边长分别为a、b，下列数据能构成黄金矩形的是()A. a=4，b=√5+1B. a=4，b=√5−2C. a=2.b=√5+1D. a=2.b=√5−1二、填空题（本大题共8小题，共16.0分）9.已知关于x的方程x2+kx−3=0的一个根是x=−1，则另一根为_____．10.如果点P(6,1+m)在第四象限，写出一个符合条件的m的值：m=______．11.已知一次函数y=kx+2，若y随x的增大而减小，则它的图象不经过第_________象限．12.A、B两地相距10千米，甲、乙二人同时从A地出发去B地，甲的速度是乙的速度的3倍，结小时．设乙的速度为x千米/时，可列方程为______ ．果甲比乙早到1313.如图，已知△ABC中，∠C=90°，∠BAC=45°，AC=√2，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B，则C′B的长为_______．14.如图，直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2)，不等式x2+bx+c>x+m的解集为______ ．15.如图，四边形ABCD是半圆的内接四边形，AB是直径，DC⏜=CB⏜，若∠C=110°，则∠ABC的度数等于______.16.已知点P(a,3)，点Q(−2,b)分别在第二、三象限的角平分线上，则a=______，b=__________．三、解答题（本大题共12小题，共68.0分）17.计算：2sin60°+2−1−20190−|1−√3|18.已知2x+3y=2014，求代数式2(3x−2y)−(x−y)+(−x+9y)的值．19.已知：如图，AB//CD，E是AB的中点，CE=DE.求证：(1)∠AEC=∠BED;(2)AC=BC．20.2019年春节，小娜家购买了4个灯笼，灯笼上，灯笼上分别写有“欢”、“度”、“春”、“节”(外观完全一样)．(1)小娜抽到“2019年”是______事件，“欢”字被抽中的是______事件；(填“不可能”或“必然”或“随机”).小娜从四个灯笼中任取一个，取到“春”的概率是______．(2)小娜从四个灯笼中先后取出两个灯笼，请用列表法或画树状图法求小娜恰好取到“春”、“节”两个灯笼的概率．21.如图，在直角三角形ABC中，∠ACB=90°，点H是△ABC的内心，AH的延长线和三角形ABC的外接圆O相交于点D，连结DB．(1)求证：DH=DB；(2)过点D作BC的平行线交AC、AB的延长线分别于点E、F，已知CE=1，圆O的直径为5．①求证：EF为圆O的切线；②求DF的长．22.已知正比例函数y=kx(k≠0)和反比例函数y=m的图象都经过点(4,2)．x(1)求这两个函数的解析式；(2)这两个函数图象还有其他交点吗⋅若有，请求出交点的坐标；若没有，请说明理由．23.如图，在菱形ABCD中，对角线AC、BD相交于点O，DE//AC，AE//BD．(1)求证：四边形AODE是矩形；(2)若AB=2√5，AC=2，求四边形AODE的周长．24.如图，AB是⊙O的直径，AC为⊙O的弦，OD⊥AB，OD与AC的延长线交于点D，点E在OD上，且∠ECD=∠B．(1)求证：EC 是⊙O 的切线；(2)若OA =3，AC =2，求线段CD 的长．25. 若一个四位自然数n 满足千位与个位相同，百位与十位相同，我们称这个数为“天平数”.将“天平数”n 的前两位与后两位交换位置得到一个新的“天平数”n′，记F(n)=n−n′99，例如n =2112，n′=1221，F(2112)=2112−122199=9(1)计算F(5335)=______；若“天平数”n 满足F(n)是一个完全平方数，求F(n)的值；(2)s 、t “天平数“，其中s =abba −，t =xyyx −(1≤b <a ≤9,1≤x <y ≤9且a ，b ，xy 为整数)，若F(s)能被8整除，且F(s)+F(t)−9(y +1)=0，规定：K(s,t)=s−t s ，求K(s,t)的所有结果的值．26.已知P(−5,m)和Q(3,m)是二次函数y=2x2+bx+1图象上的两点．(1)求b的值；(2)将二次函数y=2x2+bx+1的图象进行一次平移，使图象经过原点.(写出一种即可)27.(1)问题发现：如图①，在△ABC中，∠BAC=90°，AB=AC，点D是BC的中点，以点D为顶点作正方形DFGE，使点A、C分别在DE和DF上，连接BE、AF.则线段BE和AF数量关系______．(2)类比探究：如图②，保持△ABC固定不动，将正方形DFGE绕点D旋转α(0°<α≤360°)，则(1)中的结论是否成立？如果成立，请证明；如果不成立，请说明理由．(3)解决问题：若BC=DF=2，在(2)的旋转过程中，连接AE，请直接写出AE的最大值．28.如图，在平面直角坐标系xOy中，已知△ABC的∠ACB=90°，A(−3,0)，C(1,0)，tan∠BAC=3，4 P是AB的中点．(1)点B的坐标是____，点P的坐标是____；(2)在x轴上找一点D，连接DB，使得△ADB与△ABC相似(不含全等)，求点D的坐标；(3)在x轴上找一点Q，使以A，P，Q为顶点的三角形与△ABC相似，求Q的坐标．【答案与解析】1.答案：C解析：科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数.确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n 是正数；当原数的绝对值小于1时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n 为整数，表示时关键要正确确定a的值以及n的值．解：15000=1.5×104．故选C．2.答案：A解析：根据正方体的表面展开图，相对的面之间一定相隔一个正方形，从而分析判断即可．【详解】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，与“治”字相对面的字为乱．故选A．本题主要考查了正方体的展开图，熟练掌握正方体展开图的特点是解题的关键．3.答案：A解析：解：∵AE//BD，∴∠CBD=∠E=35°，。

北京市海淀区2019-2020学年中考第四次质量检测数学试题一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．已知二次函数y=x2+bx﹣9图象上A、B两点关于原点对称，若经过A点的反比例函数的解析式是y=8 x，则该二次函数的对称轴是直线（）A．x=1 B．x=49C．x=﹣1 D．x=﹣492．用加减法解方程组323415x yx y-=⎧⎨+=⎩①②时，如果消去y，最简捷的方法是（）A．①×4﹣②×3 B．①×4+②×3 C．②×2﹣①D．②×2+①3．如图是我国南海地区图，图中的点分别代表三亚市，永兴岛，黄岩岛，渚碧礁，弹丸礁和曾母暗沙，该地区图上两个点之间距离最短的是（）A．三亚﹣﹣永兴岛B．永兴岛﹣﹣黄岩岛C．黄岩岛﹣﹣弹丸礁D．渚碧礁﹣﹣曾母暗山4．下列图形中，是中心对称图形，但不是轴对称图形的是( )A．B．C．D．5．在平面直角坐标系中，将点P（﹣2，1）向右平移3个单位长度，再向上平移4个单位长度得到点P′的坐标是（）A．（2，4）B．（1，5）C．（1，-3）D．（-5，5）6．如图是一个由4个相同的正方体组成的立体图形，它的左视图为（）A．B．C．D．7．方程x2+2x﹣3=0的解是（）A．x1=1，x2=3 B．x1=1，x2=﹣3C．x1=﹣1，x2=3 D．x1=﹣1，x2=﹣38．如图，等腰直角三角形纸片ABC中，∠C=90°，把纸片沿EF对折后，点A恰好落在BC上的点D处，点CE=1，AC=4，则下列结论一定正确的个数是（）①∠CDE=∠DFB；②BD＞CE；③BC=2CD；④△DCE与△BDF的周长相等．A．1个B．2个C．3个D．4个9．计算1211x xx x+---的结果是（）A．1 B．﹣1 C．1﹣x D．311 xx+ -10．如图，在正八边形ABCDEFGH中，连接AC，AE，则AEAC的值是（）A．1 B．2C．2 D．3 11．如图是某个几何体的三视图，该几何体是（）A．圆锥B．四棱锥C．圆柱D．四棱柱12．下列运算结果正确的是()A．x2+2x2＝3x4B．(﹣2x2)3＝8x6C．x2•(﹣x3)＝﹣x5D．2x2÷x2＝x二、填空题：（本大题共6个小题，每小题4分，共24分．）13．已知：如图，AB是⊙O的直径，弦EF⊥AB于点D，如果EF＝8，AD＝2，则⊙O半径的长是_____．14．我国自主研发的某型号手机处理器采用10 nm工艺，已知1 nm=0.000000001 m，则10 nm用科学记数法可表示为_____m．15．在△ABC中，∠BAC＝45°，∠ACB＝75°，分别以A、C为圆心，以大于12AC的长为半径画弧，两弧交于F、G作直线FG，分别交AB，AC于点D、E，若AC的长为4，则BC的长为_____．16．2017年5月5日我国自主研发的大型飞机C919成功首飞，如图给出了一种机翼的示意图，用含有m、n的式子表示AB的长为______．17．如图，在矩形ABCD中，过点A的圆O交边AB于点E，交边AD于点F，已知AD=5，AE=2，AF=1．如果以点D为圆心，r为半径的圆D与圆O有两个公共点，那么r的取值范围是______．18．不等式组2012xxx-≤⎧⎪⎨-<⎪⎩的最大整数解是__________.三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）某校对学生就“食品安全知识”进行了抽样调查（每人选填一类），绘制了如图所示的两幅统计图（不完整）。