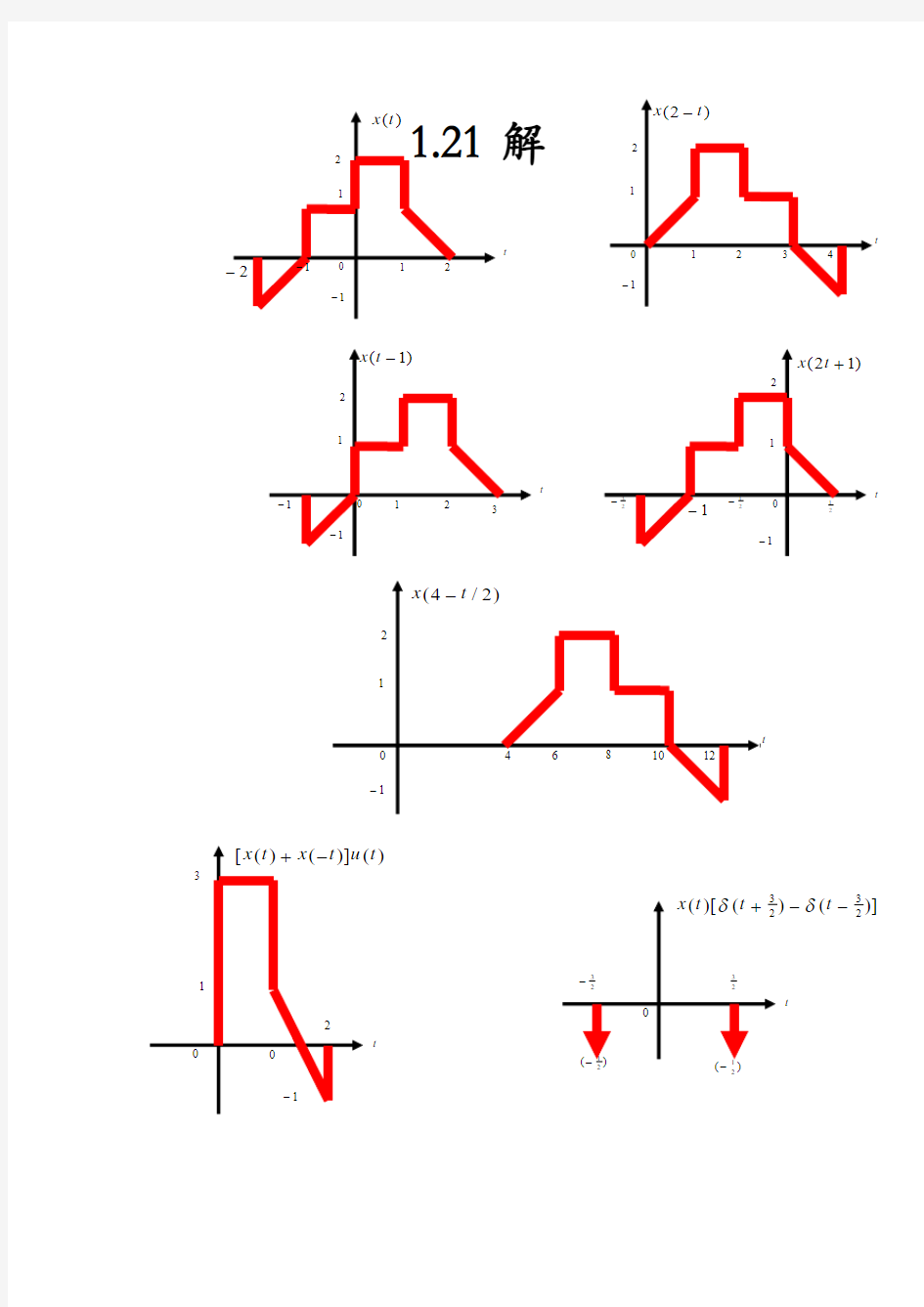
当前位置：文档之家› 信号与系统作业答案

信号与系统作业答案

)

t t

)](

--t δt

解

1.27

（a ）)2()2()(t x t x t y -+-=

① 因为)2()2()0(x x y +-=

，在0=t 的输出与前后时刻的输入都有关，所以系统是记

忆的。

② 已知)2()2()(111t x t x t y -+-=，)2()2()(222t x t x t y -+-=。当

)()(012t t x t x -=时，

)2()2()(01012t t x t t x t y --+--=，而)2()2()(010101t t x t t x t t y +-+--=-，

所以：)()(012t t y t y -≠。因而系统是时变的。

③已知)2()2()(111t x t x t y -+-=，)2()2()(222t x t x t y -+-=，

)2()2()(333t x t x t y -+-=，

当)()()(213t x t x t x +=时，)]2()2([)]2()2([)(21213t x t x t x t x t y -+-+-+-= 所以)()()(213t y t y t y +=，因而系统是可加的。

当)()(12t ax t x =时，)()2()2()(1112t ay t ax t ax t y =-+-=，因而系统是齐次的。

综合系统的可加性与齐次性，所以系统是线性的。

④因为)2()2()0(x x y +-=

，在0=t 的输出与2=t 的输入也有关，所以系统是非因果

的。

⑤若+∞

<≤B t x )

(，即输入有界，则：

+∞

<≤-+-≤-+-=B t x t x t x t x t y 2)2()2()2()2()(，即输出有界。

所以系统是稳定的。

（d ）

?≥-+<=0),2()(0

,0)(t t x t x t t y

①)2()0()0(-+=x x y ，即)0(y 与2,0-==t t 的输入有关， ∴系统是记忆系统。

②令)

()(01t t x t x -=

，则

?≥--+-<=???≥-+<=0),2()(0,00),2()(0

,0)(00111t t t x t t x t t t x t x t t y

而

?≥--+-<=???≥---+-<-=-0000

00000),2()(,00),2()(0,0)(t t t t x t t x t t t t t t x t t x t t t t y

)

()(01t t y t y -≠∴，系统是时变的。

③令)()(1t ax t x =，则)

(0),2()(0

,0)(1t ay t t ax t ax t t y =???≥-+<=，所以，系统是齐次的。

已知

???≥-+<=0),2()(0,0)(111t t x t x t t y ，??

?≥-+<=0),2()(0

,0)(222t t x t x t t y

当)()()(213t x t x t x +=时，

)()(0

),2()(0,00),2()(0,00),2()2()()(0

,00),2()(0,0)(2122112121333t y t y t t x t x t t t x t x t t t x t x t x t x t t t x t x t t y +=???≥-+<+???≥-+<=??

?≥-+-++<=???≥-+<=

综上，所以，系统是线性的。

④考察0

t t

=点，

若00

若00≥t ，则)2()()(000-+=t x t x t y ，满足因果的定义，所以系统是因果的。

⑤若∞

<≤B t x )

(，即输入有界，则：

∞

<≤???≥+<=B t t x t x t t y 20,)2()(0

,0)(，有界，所以系统是稳定的。

2.23 解：

∑∑∑+∞

-∞

=+∞

-∞

=+∞

-∞

=-=-=-==k k k kT t h kT t t h kT t t h t h t x t y )

()(*)()(*

)()(*)()(δδ

(a) 当4=T 时，

)

2()()(112--=t x t x t x 解

31.1.

的系统是又LTI )

2()()(112--=∴t y t y t y

)

()1()(113t x t x t x ++= .

的系统是又LTI )

()1()(113t y t y t y ++=∴

)8()4()()4()8()4()(-+-++++++=-=

∑+∞

-∞

=t h t h t h t h t h k t h t y k a

(b) 当2=T 时，

)4()2()()2()4

()2()(-+-++++++=-=

∑+∞

-∞

=t h t h t h t h t h k t h t y k b

T 时，

)2()()()()2()()(2

323232323?-+-++++?++=-

∑+∞

t h t h t h t h t h k t h t y c

(d) 当1=T 时，

)2()1()()1()2()()(=-+-++++++=-=

∑+∞

-∞

= t h t h t h t h t h k t h t y k d

2.40

解：依题意)()(t y t x LTI ?→?，

∞

----=

t d x e

t y τ

ττ)2()()

(。

(a) 而)()()()(t h t y t t x LTI

=??

→?=δ， ∴

)

2()2()2()()

2()

(-=-=-=

--∞

---∞

---?

t u e

d e

t h t t

t t

t ττδττδτ

(b) )(t x )2()1()('--+=t t t x δδ波形如图。

令)()(t u e t w t

-=，则)2(*)()2()(-=-=t t w t w t h δ，

x'(t)

-1 -1

而

)

()1()()()()(0)

1(t u e t u d e d u e

d w t w

--∞

---=??????==

λλλλλλλ

，所以

)

4(]1[)]1()1[)4()1()]

4()1([*)()2(*)]2()1([*)()

2(*)('*)()2(*)(*)()(*)()()

4()

1()

1()1()

1(-----=---=---=---+=-=-==---------t u e t u e

t w

t t t w t t t t w t t x t w

t t w t x t h t x t y t t δδδδδδδ

3.34解：

168

)()(,)(2

|4+=

∴=?

+∞

∞

---ωωωdt e

t h j H e

t h t

j t (a)

πωδω22,)()(00

==∑=-∑=-+∞

-∞

=+∞

-∞

a n t t x t

jk k k n

)(10==

dt e

t x T

a t

jk T

k ω

jk k e

t x 0)(ω+∞

-∞

=∑=∴

则kt

j k kt

j k t

jk k k e

k e

jk H a t y ππωπ

πω22

04216

)2(8)()(0+∑

=+∑

=∑=+∞

-∞

=+∞

-∞

=+∞

-∞=。

(b)

jk k k n

k e a n t t x 0)()1()(ωδ+∞-∞

=+∞-∞

=∑=--∑=，

ππω==

20 []??

??--=

-5

.15.0)1()(21)(10dt e t t dt e

t x T

a t

jk t

jk T

k πωδδ

???±±=+=???????±±===--=

......

2,1,0,12,12,1,0,2,0])1(1[21

)1(2

1m m k m m k e

jk π

m j m m t

jk k k e

m j H a e

jk H a t y ππωππω22)12(120)2(])12([)()(0+∞

-∞

=+++∞

-∞

=+∞

-∞

=∑++∑=∑=∴

k j k t

m j m e

k e

m ππππ)12(2

)12(2

])12[(8

++∞

-∞

=++∞

-∞=++∑

=++∑

(c)

jk k k e

a t x 0)(ω+∞

-∞

=∑=，

πω220==

)

1sin

][21)(12

120k Sa k

j dt e

dt e t x T

a k

j t

jk T

k ππππ

πω=

--==

----?

j k kt

j k t

jk k k e

k k k e

k k

k e

jk H a t y ππ

ππ

ωππππω22

4()

sin(

416

)2(8)sin()()(0+∑

=+∑

=∑=∴+∞

-∞

=+∞

-∞

=+∞

-∞

3.35解：

j k k t

jk k k e

a e

a t x 140)(+∞

-∞

=+∞

-∞

=∑=∑=ω，

227

0==

πωT

，

?≥=other

j H ,0250

||,1)(ωω

j k k kt

j k k t

jk k k e

a e

k j H a e

jk H a t y 1418

||140)14()()(0≥+∞

-∞

=+∞

-∞

=∑=∑=∑=∴ωω 要使)()()(t x t y t x S

=?→?

，则要求k a 满足：??

?≥=other k a a k k ,018,

4.21解： (a)

[

]

0),(cos )(0>=-a t u t e

t x at

j a FT

t u e +-?→

←1

)( ；)()(cos 000ωωπδωωπδω-++??

→←FT

t ()2

0200][)]()([)()

)

21001

21ωωω

ωωω

ωπωωπδωωπδω+++-++++=

=-++*=

∴j a j a j a j a j a j X

(h)

)(1t x 如图所示：

则

111)(=

?→←T

k FS

a t x ；

∑∑+∞

-∞

=+∞

-∞

=-=-=

??→←k k T

k k

j X t x )

()(2)()(211πωδπ

ωδπωπ

而)1()(2)(11-+=t x t x t x

∑∑+∞

-∞

=+∞

-∞

=----+=-+=+=∴k k

k j j k k e

j X j X j X )

(])

1(2[)()2()()(2)(11πωδπ

πω

δπ

ωωωω

4.22解：

（c ）令: )()()(11ωωj X j X t x FT

=?→←，则：

????

-+∞

∞

-1

111)cos(1

][21)(21)(ωωωπ

ωωωωπ

ωωπ

ωωωd t d e

d e

j X t x t

j t

cos sin ]cos 1[sin 1

])sin()sin([1

t t

d t t t

ππωπωωωωπ-+

而

)

3(1)

()()()(ωωωωω-∠?==j j X j e

j X e j X j X ，

1)3(1

)3cos()3()

3sin()3()(---+

--=

-=∴t t t t t x t x ππ

（d ）)]2()2([3)]1()1([2)(πωδπωδωδωδω++-++--=j X

)]}

2()2([{3

)]}1()1([{2πωδπωδππ

ωδωδππ

-+++

--+=

j j

t j

t x ππ

2cos 3sin 2)(+

∴

4.25 解：

（a ）令)(1t x 如图所示，

)(1111

)()()(ωωωj X j FT

e j X j X t x ∠=?→←。因为)(1t x 为实偶

信号，所以)(1ωj X 也为实偶信号。

0)(1=∠∴ωj X ，或πω=∠)(1j X

而

)

()()()(ωωωj X j FT e

j X j X t x ∠?=?→←，

]

)([1)

(111)()()()1()(ωωωωωω-∠-?=?=?→←-=j X j j FT

j X e j X j X t x t x

ωωω-∠=∠∴)()(1j X j X 。即：ωω-=∠)(j X ，ωπω-=∠)(j X

（b ）?

+∞

∞--=

t x j X t

j ωω)()( ，

)()0(===

∴?

+∞

∞

-图形S dt t x j X

（c ）

+∞

∞

ωπ

ωd e

j X t x t

j )(21)( ，

πωω4)0(2)(=?=∴?

+∞

∞

-x d j X

（d ）令

ω2sin 2)(j e

j Y =

，则)1()3()(+-+=t u t u t y

{}π

πωωωωω

ωω

7)()(2)()(sin 2)

(02=*=?=

∴

=+∞

∞

-+∞

∞

t j t y t x d j Y j X d e j X

（e ）π

πωω3

762

)(2)(==?

?+∞

∞

-+∞

∞

-dt t x d j X （

）

)

()()()(t x t x t x t x o e +==*

，

)

()()()(t x t x t x t x e e -+=

，

)

()()()(t x t x t x t x o o --=

)}(Im{)}(Re{)()(ωωωj X j j X j X t x FT

+=??→←，)}(Re{)(ωj X t x FT

e ??→←

所以，)}(Re{ωj X 的反变换为

)

()()(t x t x t x e -+=

。)(t x e 图示为：

4.28 解：

（a ） )()(ωj X t x FT

→←，∑∑+∞

-∞

=+∞

-∞

=-=

??→←=

n n

n t

jn n

n a

j P e

t p o )

(2)()(0ωωδπωω

又)()()(t p t x t y ?=

∴

∑∑+∞

-∞

=+∞

-∞

=-=

n n

n j X a

n a

j X j P j X j Y )]

([)(2*

)(21)(*)(21)(00ωωωωδπωπ

ωωπ

4.33 解：方程两边取FT ，得

)

(2)(8)(6)()(2

ωωωωωωj X j Y j Y j j Y j =++，

86)(2

)

()()(2

++=

ωωωωωj j j X j Y j H （a ）

2186)(2)(2

+-++=++=ωωωωωj j j j j H ，∴)()()(42t u e e t h t t ?-=-- （b ）

2)2(1)()()(+=

?→←=-ωωj j X t u te

t x FT

， 4

)

2(1)

2(2

6)(2

)

2(1

)()()(4

++?

?=ωωωωωωωωωωj j j j j j j j H j X j Y

∴

)

()412141()(422

22t u e

t te

t y t

t t

?-+-

=----

（c ）方程两边取FT ，可得：

)1(2)1(221

2)(2)(2)

()()(j j j j j j j j j j X j Y j H --+--

--+

+-+

=++

ωωωωωωωω

∴

)

()sin(

4)(2)()1(2)()1(2)(2)(4

1t u t e

t t u e

j t u e

j t t y t

j j

?-=--+-=---+-π

δδ

4.34 解：

（a ）

)()

5)(4564)(2

ωωωωωω

ωωωj X j Y j j j j j j H =

+++=

+-+=

，描述的微分方程为：

)(4)()(6)(5)('

't x t x t y t y t y +=++

（b ） 31

2564)(2

+-+

+-+=

ωωωωωωj j j j j H ，∴)

()2()(32t u e

t h t

---=

（c ）

244)4(3)

4(14

1)()()()(++=

??→←-=--ωωωωωj j j j j X t u te

t u e t x FT

t t

∴42)4(3

)3)(2(4

)()()(2

++=++?+++=

?=ωωωωωωωωωωj j j j j j j j H j X j Y

∴

)

()(21)(42t u e

t y t

---=

4.36 解：

)3)(1()

2(23

1)()()()(3+++=

?→←+=--ωωωωωωj j j j j j X t u e

t x FT

)4)(1(64212)()()22()(4++=

+-+=?→←-=--ωωωωωj j j j j Y t u e e t y FT t

（a ）

)4)(2()

3(3)2(2)3)(1()4)(1(6)()()(+++=

+++?++==ωωωωωωωωωωωj j j j j j j j j X j Y j H （b ）42

)

4)(2()3(3)(2

+++=ωωωωωωj j j j j j H ，∴

)

()(2

3)(42t u e

t h t

--+=

（c ）86)(9

4)(2()3(3)(2

+++=

ωωωωωωωj j j j j j j H ，描述该系统的微分方程为：

)(9)(3)(8)(6)('

't x t x t y t y t y +=++

6.23 解：

?<=other j H C

,0,1)(ωωω，

)

()()(ωωωj H j e

j H j H ∠?=

（a ） 0)(=∠ωj H ，∴

?<==other j H j H C

,0,1)()(ωωωω，∴

t h c πωsin )(=

（b ） T j H ωω=∠)(，∴T

j e

j H j H ωωω?=)()(，∴

)

()

(sin )(T t T t t h c ++=

πω

（c ） )sgn(20,0,)(22

ωπωωωππ=???<->=∠j H ，∴

?<=other j j H c ,0,sgn )(ωωωω，

∴

+∞

∞

-+∞

∞

-+∞

∞

ωπ

ωωπ

ωωd t d e

j d e

j H t h t

j t

j )sin(1

)sgn(21)(21)(

t t t c

c ππωω)

(

sin 21

)cos(2

7.21 解：

)()(ωj X t x FT

?→←

，

)

()(ωj X t x p FT

p ?→←

∑∑+∞

-∞

=+∞

-∞

=-=

-=?=n n T p nT t nT x nT t t x t t x t x )

()()().()()()(δδδ

∴

πωωωπ200002,)]([1)(2==

∑+∞

-∞

j X T

j X s n T p 。根据采样定理，要

保证)(t x 可完全从)(t x p 中恢复，要求信号)(t x 的最高频率满足：

ωω100002

（a ）

?>=other j X j X ),(5000,0)(ωπ

ωω，

25000s

M ωπω<

=，能恢复。

（b ）

?>=other j X j X ),(15000,0)(ωπ

ωω，

215000s

M ωπω>

=，不能恢复。

（c ）

虽然

?>=o t h

e r

j X j X )}

e {5000,

0)}(Re{ωπ

ωω，然而

)}(Im{)}(Re{)(ωωωj X j j X j X +=，由于其虚部未知，所以M

ω不能确定满

足

M ωω<

。故，不能恢复。

（d ） )()()()(ωωj X j X t x t x FT

-=?→←=*

，∴)

()(ωωj X j X *

=-。

又 πωω5000,0)(>=j X ，∴πωω5000,0)(-<=j X

x p (t)

∴

?>=other j X j X ),(5000,0)(ωπ

ωω，

25000s

M ωπω<

=，能恢复。

（e ） )()()()(ωωj X j X t x t x FT

-=?→←=*

，∴)

()(ωωj X j X *

=-。

又

ωω15000,0)(-<=j X ，

则

πωω1

5000,0)(*

-<=j X ∴πωω1500

,0)(>=j X ∴??

?>=other j X j X ),(15000,0)(ωπ

ωω，

215000s

ωπω>=，不能恢复。（f ）

?>*=*????>=1

12,0),()()()(,0),()(ωωωωωωωωωωother

j X j X j X j X other j X j X

∴

?>=????>*=*πωωωπωωωωω7500,0),()(15000,0),()()()(other

j X j X other j X j X j X j X

∴

27500s

M ωπω<

=，能恢复。

（g ）

?>=????>=πωωωπ

ωωω5000,0),()(5000,0,)()(other

j X j X other j X j X

不能确定

M ωω<

，不能恢复。

7.22解：

?>=?→←πωωω1000,

0),()()(111other

j X j X t x FT

，

?>=?→←πωωω2000,

0),()()(222other

j X j X t x FT

∴

?>==?→←=π

ωωωωω1000,0),()().()()(*)()(2121other

j Y j X j X j Y t x t x t y FT

，

πω1000=∴M

)()(ωj Y t y FT

?→←

，

)

()(ωj Y t y p FT

p ?→←

∑

∑+∞

-∞

=+∞

-∞

=-=

-=?=n n T p nT t nT y nT t t y t t y t y )

()()().()()()(δδδ

y p (t)

∴

j Y T

j Y s n T p πωωωπ2,)]([1)(2=

∑+∞

-∞

=。根据采样定理，要保证)(t y 可

完全从

)

(t y p 中恢复，采样频率满足：π

ωωπ200022=>=

M T

s 。

∴001.0

7.27解：

（a ）

令)(1t x 、)(2t x 如图中标注。

)]

([)()()(0110ωωωω+=?→←?=-j X j X e

t x t x FT

j ，)(2121

0ωωω+=

其中：

()(1221

0102ωωωωωω-=--=-而)()()(

ωωωj H j X j X ?=∑-=?→←?=?=T

p FT

T p n

j X j X t t x t p t x t x )]

([)()()()()()(2222πωωδ

（b ）要使)(t x 可完全从)(t x p 中恢复，由（a ）的)(ωj X p 图中可得到：

01202ωωωωπ

-+<

-T

，即：

122ωωπ

（c ）构建如下图所示系统：

x p (t)

)

()()()(213ωωωωj X j TH j X j X p =?=

)]([)()

()(0

34340ωωωω-=?→←?=j X j X e t x t x FT

j ，)(2

0ωωω+=

)()()()()()(44441

t x t x t x j X j X j X FT

-+=??→←-+=-ωωω )}({2)(4t x Ev t x =∴

8.22 解：

)]5([)]5([)()5cos()()(02

102

110ωωωωωω++

?→←?=j X j X j X t t x t x FT

)().()(112ωω

ωj H j X j X = )]

3([)]3([)()3cos()()(11

ωωωωωω++-=?→←?=j X j X j X t t x t x FT

)().()(23ωωωj H j X j Y =

x(t)

解：

)]([)]([)()cos()()(11FT

j X j X j Y t t x t y ωωωωωω-+

+=?→←?=)

()()(ωωωj H j X j X p ?=；

)]([)]([)()sin()()(122j FT j X j X j Y t t x t y ωωωωωω--+=

?→←?=)()(1t y t y FT

=（b ）

)]([)]([)()cos()()(11

c j X j X j Y t t x t y ωωωωωω-+

?→←?=)

()()(ωωωj H j X j X p ?=；

)]([)]([)()sin()()(2

22c p c p j FT

c p j X j X j Y t t x t y ωωωωωω--+=?→←?=

)(1j Y j Y j Y t y t y t y FT

+=?→←+=

10.21 解：

（a ）5

)(]5[][z z X n n x ZT =?→←+=δ，

零点：0=z 为5阶零点；极点：∞=z ；收敛域ROC 为整个z 平面，不含无穷远点。

收敛域ω

ω5)(j j e

e X =。（c ）1,11)1(11)(][)1(][1

>+=

--=?→

←-=--z z

z X n u n x ZT

n ，

零点：0=z ；极点：1-=z ；收敛域ROC ：1>z 。

收敛域

10.22 解：

（a ）]}5[]4[{)(][2

1--+=n u n u n x n

， )

()

(161221)

()

()(][)(2

5441

--=

---------=-+∞-∞

=-∑

∑

z z z z

z z

z z z

n x z X n n

n n n

][n x 为有限长序列，∴ROC 为整个z 平面，但不含0=z 点。

令：8,,1,0,029

199 ==?=--k e z z k j k π

∴零点：8,,2,1,9

==k e z k j k π

；极点：0=z 为4阶极点。

收敛域ROC 包含1=z 单位圆，∴其傅里叶变换存在。

j j j j e

X ----

1532

14116)(

（d

）

]1[)4(]1[)4(]1[)cos(

4][3

146

2--+--=

--+=--n u e

n u e

n u n n x n

j j

ππ

πππ

411

411)(1

<--+--=

----z z

z X j

ππππ

)

4)(4()]cos(24)[cos()

41)(41()cos(4)cos(3

4πππππ

ππ

πj

z e

z z z z e z

z -------?--=

--?+-=

∴零点：01=z z ，12

2cos 24π=z z ；极点：3

41πj

p e

z =，3

42πj

p e

z -=。

收敛域

ROC 包含1=z 单位圆，∴其傅里叶变换存在。

)

4)(4()]cos(

24)[cos()(3

ππω

πω

j j

j j j j e

e e

X ---?--=

10.28 解：

（a ）]6[95.0][][--=n n n x δδ

95.01)(--=z

z X ，ROC 为整个z 平面，不包含0=z 原点。

（b ）6

.0)(z

z z X -=

令：5

,.1,0,95.0095.06

=?=?=-k e

z z k j

k π。

∴零点：5,.1,0,95.06

261

=?=k e

z k j

k π；极点：0

=z 为6阶极点。

ROC 为整个

（c ）65

)

.0(95

.0)(3

z z

z z X k j k ∏=?-=

∴ω

)

95.0()(3

1j k j j j e

e e

X k ∏=?-=

，∏

=?-=

195.0)(k j j j k e

e X π

在ππωπππ

π2,,,,,,035343

23=3

ω=

10.31 解：

由事实2与事实3，可得)(z X 的表达式形如：)

)(()(212

p p z z z z z

K z X --?=

。

由事实1，可得：*21)(p p z z =，且收敛域ROC ：21p p z z z =>。

由事实

4，可得：3

/12

1πj p e

z =

，3

/22

1πj p e

z -=

。则：

)

)(()(3

ππj j e

z e z z

K z X ---

，2

z 。

由事实5，3

4cos

1)(1()1(4

--=

-K K e e

X j j π

ππ，得2=K 。

∴)

)((2)(3

ππj j e

z e

z z

z X ---

，ROC ：2

z 。

10.32 解：

（a ）∑+∞

-∞

=-=

=k k n h k x n h n x n y ][][][*][][，而：

???-≤≤=other N k k x ,010,1][，][0

,00,][k n u a k n k n a k n h k

n k n -=??

?<-≥-=---，则当1≠a 时：

]

[11][111,110,10,0][][1][1

010N n u a

n u a

N n a a a a a N n a a a a a n k n u a a k n u a n y N n n N n n N k k

n n n k k n N k k

n N k k n ---+

--=??????

???

->--=-≤≤--=<=-=-?=------=---=--=--=-∑∑∑∑

当1=a 时：

]

[)1(][)1(1,11

0,110,0][][11][1

010N n u N n n u n N n N N n n n k n u k n u n y N k n k N k N k k

n -+--+=??????

???

->=-≤≤+=<=-=-?=∑∑∑∑-==-=-=- （b ）对][n x 、][n h 分别求ZT 变换，得：

)1(111111)(][][][1

z X N n u n u n x -------=

?→←--=，ROC ：

整个z 平面；

z az

z H n u a n h ZT

>-=?→←=-,11)(][][1

。

z az

z z

z H z X z Y N

>-?

--=

?=∴---,11

)1(11)()()(1

。

当1≠a 时：

a a z

a az

a a z

a z

az a a z

a az

z z

z Y ---------------+

--+

---+

--=

----+

--=-?

--=

1(1)1/(11)1(1)1/(1)

1](1)1(1)1/(1[

11)1(11)(，a z >。

可得

]

[11][11]

[1][11][1][11][1

N n u a

n u a

N n u a

a N n u a

n u a a

a n u a n y N n n N

n n

---+

--=

---+

--+

----

当1=a 时：

()

z z z

z z Y -------

--=

111

)1(11

)(，1>z 。可得

]1[)(][)1(][+---+=N n u N n n u n n y )

1)(1()()(1111

111

---------+-+=-+

-az z z B aA B A az B

A az

，可得

=????=+=+---a

a a B A B aA B A 11101，∴

1)1(1)1/(111

-------+

--=

-az

a a z

a az

信号与系统课后答案.doc

1-1 （2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 1-3 1-5 判别下列各序列是否为周期性的。如果是，确定其周期。（2）)6 3cos()443cos()(2π πππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+= ：

1-9 已知信号的波形如图1-11所示，分别画出 )(t f和 dt t df)( 的波形。解：由图1-11知，) 3(t f-的波形如图1-12(a)所示（) 3(t f-波形是由对) 2 3(t f- 的波形展宽为原来的两倍而得）。将) 3(t f-的波形反转而得到)3 (+ t f的波形，如图1-12(b)所示。再将)3 (+ t f的波形右移3个单位，就得到了)(t f，如图1-12(c)所示。dt t df)(的波形如图1-12(d)所示。 1-23 设系统的初始状态为)0(x，激励为)(? f，各系统的全响应)(? y与激励和初始状态的关系如下，试分析各系统是否是线性的。（1）?+ =-t t dx x xf x e t y ) ( sin )0( )(（2）?+ =t dx x f x t f t y ) ( )0( )( )( （3）?+ =t dx x f t x t y ) ( ])0( sin[ )(（4）)2 ( ) ( )0( )5.0( ) (- + =k f k f x k y k （5）∑=+ = k j j f kx k y ) ( )0( ) (

信号与系统作业作业答案

信号与系统作业作业答案 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-

第二章作业答案 2–1 已知描述某LTI 连续系统的微分方程和系统的初始状态如下，试求此系统的零输入响应。（1）)()(2)(2)(3)(t e t e t y t y t y +'=+'+'' 2)0(=-y ，1)0(-='-y 解：根据微分方程，可知特征方程为： 0)2)(1(0232=++?=++λλλλ 所以，其特征根为： 1,221-=-=λλ 所以，零输入响应可设为：0)(221≥+=--t e C e C t y t t zi 又因为 ?? ?=-=????-=--='=+=--31 12)0(2)0(2 12121C C C C y C C y 所以，03)(2≥-=--t e e t y t t zi （2）)(2)()(6)(5)(t e t e t y t y t y -'=+'+'' 1)0()0(=='--y y 。解：根据微分方程，可知特征方程为： 0)3)(2(0652=++?=++λλλλ 所以，其特征根为： 3,221-=-=λλ 所以，零输入响应可设为：0)(3221≥+=--t e C e C t y t t zi

又因为 ???-==??? ?=--='=+=--3 4 132)0(1)0(21 2121C C C C y C C y 所以，034)(32≥-=--t e e t y t t zi 2–2 某LTI 连续系统的微分方程为 )(3)()(2)(3)(t e t e t y t y t y +'=+'+'' 已知1)0(=-y ，2)0(='-y ，试求：（1）系统的零输入响应)(t y zi ；（2）输入)()(t t e ε=时，系统的零状态响应)(t y zs 和全响应)(t y 。解：（1）根据微分方程，可知特征方程为： 0)2)(1(0232=++?=++λλλλ 所以，其特征根为： 1,221-=-=λλ 所以，零输入响应可设为：0)(221≥+=--t e C e C t y t t zi 又因为 ???=-=??? ?=--='=+=--43 22)0(1)0(2 12121C C C C y C C y 所以，034)(2≥-=--t e e t y t t zi （2）可设零状态响应为：0)(221>++=--t p e C e C t y t x t x zs 其中p 为特解，由激励信号和系统方程确定。因为)()(t t e ε= 所以，p 为常数，根据系统方程可知，23=p 。

汕头大学信号与系统历年真题(2008~2011)

汕头大学2010 科目代码：829 科目名称：信号与系统电子与通信工程

汕头大学2009年攻读硕士学位研究生入学考试试题科目代码：829 科目名称：信号与系统适用专业：通信与信息系统，信号与信息处理一、（60分）简要回答下列问题 1.从增量线性系统的角度说明常系数差分方程因果系统响应由哪两部分构成（2分）？每部分响应分别是由什么样的输入引起的（2分）？在什么条件下常系数差分方程系统为线性时不变（LTI ）系统（2分）？ 2.连续时间（LTI ）系统在时域、频域及复频域分别如何表征（3分）？各种表征形式之间有何关系？（3分） 3.若把地面无线信道用连续时间因果LTI 系统等效，窄带信道可视为无记忆LTI 系统，宽带信道可视为有记忆LTI 系统。那么，窄带信道连续时间单位冲激响应（Unit impulse response ）有何特点(2分)？宽带信道单位冲激响应有何特点（2分）？其幅频特性（或称幅度响应）又有何特点（2分）？ 4．一工程师试图用LTI 系统产生输入信号以外的频率成份。试从理论上解释他这种做法行不通的原因（8分）。（提示：推导频率分量通过LTI 系统的输出结果，并加以分析） 5.若把地面无线信道用连续时间因果LTI 系统等效，那么把接收端的部分信号处理前置到发射端进行预先处理可达到同样效果。试从LTI 系统级联（或称串联）特性解释这样做的合理性，写出相应的卷积（Convolution ）特性公式（6分）。 6.连续时间信号ⅹ(t)的傅氏变换算法：X(j ω)= ()jwt x t e dt -+∞-∞?。证明：X(j ω)收敛的必要条件是()x t dt +∞-∞<∞?（4分）。当()x t 不满足条件()x t dt +∞ -∞<∞?时，从连续时间傅氏变换推广的角度解释拉普拉斯变换的定义：()()st X s x t e dt +∞--∞= ?（5分）。 7.连续时间信号的理想抽样信号用()() ()p n x t x t t nT σ+∞=-∞=-∑表示（注：()t σ为连续时间冲激函数），而实际上对()x t 均匀抽样得到的离散时间信号[]()d x n x nT =。推导给出()p x t 的连续时间傅氏变换()P X jw 的两种表达形式（9分）。从其中一种表达形式说明()P X jw 与 ()x t 连续时间傅氏变换X(j ω)的关系（3分）；从另外一种表达形式说明()P X jw 与[] d x n 离散时间傅氏变换()j d X e Ω的关系（3分）。最后分析用()j d X e Ω估计X(j ω)可能存在的误差（2分）。二、（25分）离散时间LTI 系统的单位冲激响应用h[n]表示，系统对输入信号x[n]的响应用y[n]表示。 1．利用系统的线性时不变性质，推导给出y[n]的卷积和（Convolution Sum ）表达式（8

武汉理工大学信号与系统历年试题

武汉理工大学考试试题纸（A 卷）课程名称信号与系统专业班级信息工程学院05级题号一二三四五六七八九十总分题分 6 10 34 50 100 备注: 学生不得在试题纸上答题(含填空题、选择题等客观题) 一、选择题（共2小题，每题3分，共6分） 1. 已知()f t 的付里叶变换为()F j ω，则信号)52(-t f 的付里叶变换为（） A. 1225F j e j ()ωω- B. F j e j ()ωω25- C. F j e j ()ωω25 2- D. 122 5 2F j e j ()ωω- 2. 信号f t t t ()sin ()()=--ωε022的拉普拉斯变换为（） A. s s e s 2022+-ω B. s s e s 2022+ω C. ωω02 22s e s + D. ωω02022s e s +- 二、填空题（共2小题，每空2分，共10分） 1. 对带宽为0～40KHz 的信号()f t 进行抽样，其奈奎斯特间隔T ＝ s μ；信号()2 t f 的带宽为 KHz ，奈奎斯特频率为 KHz 。 2. 设)()(ωj F t f 的付里叶变换为，则F (0)= _________；f (0)= _________。三、简答题（6小题，共34分） 1．（4分）试画出函数 )(cos t πδ的波形。 2．（6分）求象函数)4(1)(222+-=-s s e s F S 的原函数)(t f ；并求其初值和终值。 ) ()]([)(t te t e T t r ==

3. 判断并说明理由： (1) （2分）)()]([)(t te t e T t r == 是否为非时变系统？ (2) （2分）)()]([)(t ae t e T t r ==（a 为常数）是否为线性系统？ (3) （2分）()[()]()sin r t T e t e t t ω==是否为稳定系统？ (4) （2分）)2()]([)(+==t e t e T t r 是否为因果系统？ 4. （5分）)(1t f 与()t f 2波形如下图所示，试利用卷积的性质，画出)()(21t f t f *的波形。 02 1 -1 ) (1t f () t f 2t t 12 1 3 5. （6分）求收敛域为13z <<，2 2()43 z F z z z =-+的原序列)(k f 。 6. （5分）说明系统函数为 2 2331 )(234523++++++++=s s s s s s s s s H 的系统的稳定性。四、计算题（4小题，共50分） 1. （10分）一线性时不变具有非零的初始状态，已知当激励为)(t e 时全响应为 )cos(2)(1t e t r t π+=-，0>t ；若在初始状态不变，激励为)(2t e 时系统的全响应为)cos(3)(2t t r π=，0>t 。求在初始状态扩大一倍的条件下，如激励为)(30t t e -时，求系统的全响应)(3t r 。

信号与系统课后习题与解答第三章

3-1 求图3-1所示对称周期矩形信号的傅利叶级数（三角形式和指数形式）。图3-1 解由图3-1可知，)(t f 为奇函数，因而00==a a n 2 1120 11201)cos(2)sin(242,)sin()(4T T T n t n T n E dt t n E T T dt t n t f T b ωωωπωω-== = =?? 所以，三角形式的傅利叶级数（FS ）为 T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=?? ? ???+++= Λ 指数形式的傅利叶级数（FS ）的系数为??? ??±±=-±±==-=ΛΛ,3,1,0,,4,2,0, 021n n jE n jb F n n π 所以，指数形式的傅利叶级数为 T e jE e jE e jE e jE t f t j t j t j t j π ωπππ π ωωωω2,33)(11111= ++- + -=--Λ 3-2 周期矩形信号如图3-2所示。若：

图3-2 2 T -2- 重复频率kHz f 5= 脉宽 s μτ20= 幅度 V E 10= 求直流分量大小以及基波、二次和三次谐波的有效值。解对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数（FS ）的系数 ?? ? ??=??? ??== = =??--22 sin 12,)(1112212211τωττωππωτ τ ωωn Sa T E n n E dt Ee T T dt e t f T F t jn T T t jn n 则的指数形式的傅利叶级数（FS ）为 ∑∑∞ -∞ =∞ -∞ =?? ? ? ?== n t jn n t jn n e n Sa T E e F t f 112 )(1ωωτωτ 其直流分量为T E n Sa T E F n ττωτ=?? ? ??=→2lim 100 基波分量的幅度为??? ? ? ?= +-2sin 2111τωπE F F 二次谐波分量的幅度为??? ? ? ?= +-22sin 122τωπE F F 三次谐波分量的幅度为??? ? ? ?=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得

信号与系统习题答案

《信号与系统》复习题 1．已知f(t)如图所示，求f(-3t-2)。 2．已知f(t)，为求f(t0-at)，应按下列哪种运算求得正确结果？（t0和a 都为正值） 3．已知f(5-2t)的波形如图，试画出f(t)的波形。解题思路：f(5-2t)?????→?=倍展宽乘22/1a f(5-2×2t)= f(5-t) ??→?反转f(5+t)??→?5 右移 f(5+t-5)= f(t) 4．计算下列函数值。（1） dt t t u t t )2(0 0--?+∞ ∞-）（δ （2） dt t t u t t )2(0 --?+∞ ∞-）（δ （3） dt t t e t ?+∞ ∞ --++）（2)(δ

5．已知离散系统框图，写出差分方程。解：2个延迟单元为二阶系统，设左边延迟单元输入为x(k) 左○ ∑:x(k)=f(k)-a 0*x(k-2)- a 1*x(k-1)→ x(k)+ a 1*x(k-1)+ a 0*x(k-2)=f(k) (1) 右○ ∑: y(k)= b 2*x(k)- b 0*x(k-2) (2) 为消去x(k)，将y(k)按（1）式移位。 a 1*y(k-1)= b 2* a 1*x(k-1)+ b 0* a 1*x(k-3) (3) a 0*y(k-2)= b 2* a 0*x(k-2)-b 0* a 0*x(k-4) (4) (2)、（3）、（4）三式相加：y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b 2*[x(k)+ a 1*x(k-1)+a 0*x(k-2)]- b 0*[x(k-2)+a 1*x(k-3)+a 0*x(k-4)] ∴ y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b 2*f(k)- b 0*f(k-2)═>差分方程 6．绘出下列系统的仿真框图。 )()()()()(10012 2t e dt d b t e b t r a t r dt d a t r dt d +=++ 7．判断下列系统是否为线性系统。（2） 8．求下列微分方程描述的系统冲激响应和阶跃响应。 )(2)(3)(t e dt d t r t r dt d =+

2021《信号与系统》考研奥本海姆2021考研真题库

2021《信号与系统》考研奥本海姆2021 考研真题库一、考研真题解析下列关于冲激函数性质的表达式不正确的是（）。[西安电子科技大学2012研] A．f（t）δ′（t）＝f（0）δ′（t） B．f（t）δ（t）＝f（0）δ（t） C． D．【答案】A查看答案【解析】A项，正确结果应该为f（t）δ′（t）＝f（0）δ′（t）－f′（0）δ（t）。 2x（t）＝asint－bsin（3t）的周期是（）。[西南交通大学研] A．π/2 B．π C．2π D．∞ 【答案】C查看答案【解析】因为asint的周期为T1＝2π/1＝2π，bsin（3t）的周期为T2＝2π/3，因为T1/T2＝3/1为有理数，因此x（t）是周期信号，且x（t）＝asint－bsin （3t）的周期是3T2＝T1＝2π。

3序列f（k）＝e j2πk/3＋e j4πk/3是（）。[西安电子科技大学2012研] A．非周期序列 B．周期N＝3 C．周期N＝6 D．周期N＝24 【答案】B查看答案【解析】f1（k）＝e j2πk/3的周期N1＝2π/（2π/3）＝3，f2（k）＝e j4πk/3的周期N2＝2π/（4π/3）＝3/2，由于N1/N2＝2为有理数，因此f（k）为周期序列，周期为2N2＝N1＝3。 4积分[西安电子科技大学2011研] A．2 B．1 C．0 D．4 【答案】A查看答案【解析】一电路系统H（s）＝（10s＋2）/（s3＋3s2＋4s＋K），试确定系统稳定时系数K 的取值范围（）。[山东大学2019研]

A．K＞0 B．0＜K＜12 C．K＞－2 D．－2＜K＜2 【答案】B查看答案【解析】H（s）＝（10s＋2）/（s3＋3s2＋4s＋K）＝B（s）/A（s），其中A（s）＝s3＋3s2＋4s＋K，系统稳定需要满足K＞0，3×4＞K，因此0＜K＜12。7信号f（t）＝6cos[π（t－1）/3]ε（t＋1）的双边拉普拉斯变换F（s）＝（）。[西安电子科技大学2012研] A． B． C． D．【答案】C查看答案【解析】信号f（t）变形为

18年西南大学网络教育[1073]《信号与系统》作业参考答案

单项选择题 1、连续系统的结构图如图所示，系统的系统函数为（）。 H1(s) H2(s) - H3(s) h1(t) *h2(t)+h3(t) H1(s) H2(s) + H3(s) h1(t) *h2(t)-h3(t) 2、已知离散系统的结构图如图所示，则该系统的冲激响应为（）。 h1(k)+h2(k) h1(k)*h2(k) h1(k)*h2(k)+1 h1(k)*h2(k)+δ(k) 3、设是信号的傅里叶变换，的波形如图所示，则等于（）。 4pi 2pi 6pi

4、已知输入，系统频率，则系统的输出的幅值为() 3 1/2 2 1 5、某滤波器的幅频特性曲线如图，则20dB阻带起始频率约为（）rad/s。 3 0.5 1 2 6、若数字滤波器在两点处的幅值为（1，1），则该滤波器为（） A. lp bp bs hp 7、已知信号x(t)的傅里叶变换为，则信号y(t)的频谱为（）。 R(w)cos(w) R(w)/2 R(w/2) R(w)

8、利用Matlab求取系统的冲激响应，调用的函数是（） step impulse initial lism 9、已知，设抽样频率为100Hz，则所得序列的数字频率为() 0.4pi 0.3pi 0.2pi 0.1pi 10、共轭对称的信号，其幅值与相位分别为（） C. 偶、偶函数奇、偶函数偶、奇函数奇、奇函数 11、（） B. -1 2 1

12、(） f'(t) １ f(0) f(t) 13、序列，其周期为（） 7 2 不是周期序列 14 14、对信号进行采样，最大采样间隔为() 0.001 0.005 0.05 0.01 15、周期信号的波形如图所示，则其傅里叶级数中含有（）。正弦分量与余弦分量直流分量与正弦分量奇次谐波分量直流分量与余弦分量

信号与系统期末复习作业4及答案

第四章答案 4-1．拉氏变换法和算子符号法在求解微分方程时的区别和联系？解：拉氏变换法和算子符号法都能求解微分方程。拉氏变换法可以把初始条件的作用计入，这就避免了算子法分析过程中的一些禁忌，便于把微分方程转为代数方程，简化求解过程。但拉氏变换法得到的系统函数可能丢失零输入响应的极点故无法用来求零输入响应，而算子符号法得到的传输算子则能反映出所有零输入响应极点。 4-2．判断下列说法的正误。（1）非周期信号的拉氏变换一定存在；错（2）有界周期信号的收敛域为整个右半平面；对（3）能量信号的收敛域为整个s 平面；错（4）信号2 t e 的拉氏变换不存在。错 4-3．求如下信号的拉氏变换。（1）)sinh(at ；（2）)cosh(at ；（3）t t ωcos ；（4）t t ωsin 。解：（1）22 111sinh()22at at e e a at s a s a s a --??=?-= ?-+-?? （2）2 2 111cosh()22at at e e s at s a s a s a -+??=?+= ?-+-?? （3）2222222cos () d s s t t ds s s ωωωω-???-=??++?? （4）22222 2sin () d s t t ds s s ωωωωω???-=??++?? 4-4．求图示信号)(t f 的拉氏变换)(s F 。标明其零点和极点。解：22242(2)()()(2)()(2)t t t t f t e u t e u t e u t e e u t ------=--=-- t

(完整版)信号与系统习题答案.docx

《信号与系统》复习题 1．已知 f(t) 如图所示，求f(-3t-2) 。 2．已知 f(t) ，为求 f(t0-at) ，应按下列哪种运算求得正确结果？（t0 和 a 都为正值）

3．已知 f(5-2t) 的波形如图，试画出f(t) 的波形。解题思路：f(5-2t)乘a 1 / 2展宽 2倍f(5-2 × 2t)= f(5-t)

反转右移 5 f(5+t) f(5+t-5)= f(t) 4．计算下列函数值。（ 1）（ 2）（ t ） t 0 )dt t 0 u(t 2 （t t 0）u(t 2t 0 )dt （ 3） (e t t ) （t 2）dt 5．已知离散系统框图，写出差分方程。解： 2 个延迟单元为二阶系统，设左边延迟单元输入为 x(k) ∑ 0 1 1) → 左○ :x(k)=f(k)-a *x(k-2)- a*x(k- x(k)+ a 1*x(k-1)+ a 0*x(k-2)=f(k) (1) ∑ y(k)= b 2*x(k)- b 0*x(k-2) (2) 右○ : 为消去 x(k) ，将 y(k) 按（ 1）式移位。 a 1*y(k-1)= b 2 * a 1*x(k-1)+ b * a 1*x(k-3) (3) a 0*y(k-2)= b 2 * a 0*x(k-2)-b 0* a 0*x(k-4) (4) (2) 、（ 3）、（ 4）三式相加： y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b *[x(k)+ a 1 *x(k-1)+a *x(k-2)]- b *[x(k-2)+a 1*x(k-3)+a *x(k-4)] 2 0 0 0 ∴ y(k)+ a 1 *y(k-1)+ a *y(k-2)= b 2 *f(k)- b *f(k-2) ═ >差分方程

信号系统习题解答3版-3

第3章习题答案 3-1 已知周期矩形脉冲信号的重复频率 5 kHz f =，脉宽20 s τ=μ，幅度10V E =，如图题 3-1所示。用可变中心频率的选频回路能否从该周期矩形脉冲信号中选取出5，12，20，50，80及100 kHz 频率分量来？要求画出图题3-1所示信号的频谱图。图题3-1 解：5kHz f =，20μs τ=，10V E =，1 1 200T s f μ= =，41210f ππΩ== 频谱图为从频谱图看出，可选出5、20、80kHz 的频率分量。 3-3 求图题3-3 所示周期锯齿信号指数形式的傅里叶级数，并大致画出频谱图。图题3-3 解： ()f t 在一个周期（0，T 1）内的表达式为： 11 ()()E f t t T T =- - 111110011111()()(1,2,3)2T T jn t jn t n E jE F f t e dt t T e dt n T T T n π -Ω-Ω==--=- =±±±??L 11010011111()()2 T T E E F f t dt t T dt T T T ==--=?? 傅氏级数为： n c 1 2(kHz) f 5205010015080

111122()22244j t j t j t j t E jE jE jE jE f t e e e e ππππ Ω-ΩΩ-Ω=-+-+-L (1,2,3)2n E F n n π = =±±±L (0)2 (0)2 n n n π?π?->??=? ??? 其中：112T πΩ= 111124 01112411()cos T T T T E a f t dt E tdt T T π --==Ω=?? n F 2E π 6E π 10E π1 Ω13Ω1 5Ω1-Ω13-Ω15-ΩL L 4E π 12Ω14Ω8E π 2E 12-Ω14-Ω2 π- 2 πn ?15-Ω13-Ω1 -Ω1 Ω1 3Ω1 5ΩL L 1 2Ω12-Ω14-Ω14Ω

信号系统习题解答版-

第8章习题答案 8-2 列出图题8-2所示系统的差分方程，指出其阶次。图题8-2 解： 1201[][1][2][][1]y n b y n b y n a x n a x n ----=+- 二阶 8-3 列出图题8-3所示系统的差分方程，已知边界条件y [-1] = 0，分别求以下输入序列时的输出y [n ]，并绘出其图形（用逐次迭代方法求）。（1）[][]x n n δ= （2）[][]x n u n = 图题8-3 解：1 [][1][]3 y n y n x n --= （1） 1[][]3n y n u n ?? = ??? （2）311[](())[]223n y n u n =- 8-7 求解下列差分方程的完全解。（1）[]2[1]2, [0]1y n y n n y +-=-= （2）[]5[1],y n y n n =--+ [1]0y -= 解：（1）方程齐次解为：h [](2)n y n C =-，特解为：p 12[]y n D n D =+，代入原方程 121212142(1)2 2 , 39 D n D D n D n D D ++-+=-→==- 完全响应为：()14[]239n y n C n =-+-，代入1]0[=y 得：9 13=C ()1314[]2939 n y n n ∴=-+- （2）方程齐次解为：h [](5)n y n C =-，特解为：p 12[]y n D n D =+，代入原方程 0234

12121215 5(1)5 , 636D n D D n D n D D +=---+→== 完全响应为：()1 5 []5636 n y n C n =-++ ，代入0]1[=-y 得：36 5-=C ()1 1[][565]36 n y n n += -++ 8-12 用单边z 变换解下列差分方程。（1）y [n ] + 0.1y [n -1] - 0.02y [n -2] = 10 u [n ]，y [-1] = 4，y [-2] = 6 （2）y [n ] - 0.9y [n -1] = 0.05 u [n ]，y [-1] = 1 （3）y [n ] + 2y [n -1] = (n -2) u [n ]，y [0] = 1 解：（2）差分方程两边同时进行z 变换： 1 1 211 ()0.9[()[1]]0.05 1 (){10.9}0.050.9[1] 1 0.050.90.050.9()(1)(0.9)(0.9) (1)(10.9)(10.9)()0.50.45 10.910.9 0.50.45[][]0.10.9 z Y z z Y z y z z z Y z z y z z z z Y z z z z z z z Y z A B z z z z z z z y n z z -----+-=--=+--=+=+------=+=+----=+=---1Z 5[]0.45(0.9)[] n u n u n +（3）由差分方程得： 2(0)3(0)2(1)2(1)22 y y y y --+-=-∴-==- 差分方程两边同时进行z 变换： 1 2 211 1222 2 ()2[()(1)]21(1) 22(1) ()(1)(12)(1)(12)(12) ()33(1)2(1)(2)(1) 3949139(1)2(1)z z Y z z Y z y z z z z z y Y z z z z z z Y z z z A B C z z z z z z z z z ----++-=----=---+-++-+==++-+-+--=++ -+-

信号与系统西安邮电习题答案

第一次 1.1 画出下列各个信号的波形[式中()()r t t t ε=为斜升函数] 知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。解题方法：①首先考虑各信号中普通函数的波形特点，再考虑与()t ε或()k ε结合时的变化情况； ②若()t f 只是普通信号与阶跃信号相乘，则可利用()t ε或()k ε的性质直接画出 0>t 或0≥k 部分的普通函数的波形； ③若()t f 是普通函数与阶跃信号组合成的复合信号，则需要考虑普通函数值域及其对应的区间。 (1) ()()()t t t f εsin = 解：正弦信号周期ππ ω π 21 22== = T 1 -1 2ππ t () f t (2) ()()sin f t t επ= 解：()0 sin 0 1 sin 0 t f t t ππ?，

正弦信号周期22== π π T 10-1-1 -212 -1 -2 12 1 () f t t t () sin t π (3) ()()cos f t r t = 解：()0 cost 0 cos cos 0f t t t ?，正弦信号周期221 T π π= = 1 0-1t () cos t π 2π π -2π -1 () f t 0 t π 2π π -2π -

(4) ()()k k k f ε)12(+= -1 -2 1 2 k 3 13 5() f k …… …… (5) ()()()1 11k f k k ε+??=+-? ? -2 -4 1 2 k 3 12 () f k …… …… 4 5 -1 -3 1.2 画出下列各信号的波形[式中()()r t t t ε=为斜升函数] 知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。解题方法：①首先考虑各信号中普通函数的波形特点，再考虑与()t ε或()k ε结合时的变化情况； ②若()t f 只是普通信号与阶跃信号相乘，则可利用()t ε或()k ε的性质直接画出 0>t 或0≥k 部分的普通函数的波形；

信号系统习题解答版

第5章习题答案 5-1 图题5-1所示RC 电路中，当t = 0时，开关S 闭合，求输出信号R ()v t 。输入信号分别为以下几种情况。（1）()()x t Eu t = （3） 0≤≤()0 < 0, > E t x t t t τ τ ?=?? （4）()sin ()x t t u t Ω=? 图题5-1 解： ()()()11R R s V s X s X s R s sC RC = = + + （1） ()E X s s = ()11R s E E V s s s s RC RC = ? =++ 1 ()()t RC R v t Ee u t -= （3） ()(1)s E X s e s τ -=- ()(1)(1)11s s R s E E V s e e s s s RC RC ττ --=?-=-++ 11 ()()()()t t RC RC R v t E e u t e u t ττ---??=--???? （4） 22()X s s Ω= +Ω

22()1R s V s s s RC Ω= ? + Ω + 2 222 111()RC s RC RC s s RC ?? ??Ω+Ω=-??+Ω+Ω??+ ? ? 12 ()cos sin ()1() t RC R RC v t t RC t e u t RC -??Ω =Ω+ΩΩ-??+Ω?? 5-3 电路如图题5-3所示，当t < 0时，电路元件无储能，当t = 0时，开关闭合。求电压2()v t 的表达式，并画出2()v t 的波形。图题5-3 解：电流源电流为：s s 11/1= )12(11.09.01111.09.01 1)(2++=++ +++?=s s s s s s s s s s I

信号与系统课后习题答案—第1章

第1章习题答案 1－1 题1－1图所示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？解： ① 连续信号：图（a ）、（c ）、（d ）； ② 离散信号：图（b ）； ③ 周期信号：图（d ）； ④ 非周期信号：图（a ）、（b ）、（c ）； ⑤有始信号：图（a ）、（b ）、（c ）。 1－2 已知某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|，试判定该系统是否为线性时不变系统。解：设T 为此系统的运算子，由已知条件可知： y(t)=T[f(t)]=|f(t)|，以下分别判定此系统的线性和时不变性。 ① 线性 1）可加性不失一般性，设f(t)=f 1(t)+f 2(t)，则 y 1(t)=T[f 1(t)]=|f 1(t)|，y 2(t)=T[f 2(t)]=|f 2(t)|，y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|，而 |f 1(t)|＋|f 2(t)|≠|f 1(t)+f 2(t)| 即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下，不存在f 1(t)＋f 2(t)→y 1(t)＋y 2(t)，因此系统不具备可加性。由此，即足以判定此系统为一非线性系统，而不需在判定系统是否具备齐次性特性。 2）齐次性由已知条件，y(t)=T[f(t)]=|f(t)|，则T[af(t)]=|af(t)|≠a|f(t)|=ay(t) （其中a 为任一常数）即在f(t)→y(t)前提下，不存在af(t)→ay(t),此系统不具备齐次性，由此亦可判定此系统为一非线性系统。 ② 时不变特性由已知条件y(t)=T[f(t)]=|f(t)|，则y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|，即由f(t)→y(t)，可推出f(t-t 0)→y(t-t 0)，因此，此系统具备时不变特性。依据上述①、②两点，可判定此系统为一非线性时不变系统。 1－3 判定下列方程所表示系统的性质： )()()]([)()(3)(2)(2)()()2()()(3)(2)()()()()() (2''''''''0t f t y t y d t f t y t ty t y c t f t f t y t y t y b dx x f dt t df t y a t =+=++-+=+++=? 解：（a ）① 线性 1）可加性由 ?+=t dx x f dt t df t y 0)()()(可得?????→+=→+=??t t t y t f dx x f dt t df t y t y t f dx x f dt t df t y 01122011111)()()()()()()()()()(即即则 ???+++=+++=+t t t dx x f x f t f t f dt d dx x f dt t df dx x f dt t df t y t y 0212102201121)]()([)]()([)()()()()()( 即在)()()()()()()()(21212211t y t y t f t f t y t f t y t f ＋＋前提下，有、→→→，因此系统具备可加性。 2）齐次性由)()(t y t f →即?+=t dx x f dt t df t y 0)()()(，设a 为任一常数，可得 )(])()([)()()]([)]([000t ay dx x f dt t df a dx x f a dt t df a dx x af t af dt d t t t =+=+=+??? 即)()(t ay t af →，因此，此系统亦具备齐次性。由上述1）、2）两点，可判定此系统为一线性系统。

信号与系统课后习题答案汇总

第一章习题参考解答 1.1 绘出下列函数波形草图。 (1) | |3)(t e t x -= (2) ()? ???<≥=02021)(n n n x n n (3) )(2sin )(t t t x επ= (5) )]4()([4cos )(--=-t t t e t x t εεπ (7) t t t t x 2 cos )]2()([)(π δδ--= (9) )2()1(2)()(-+--=t t t t x εεε )5- (11) )]1()1([)(--+=t t dt d t x εε (12) )()5()(n n n x --+-=εε (13) ?∞--= t d t x ττδ)1()( (14) )()(n n n x --=ε 1.2 确定下列信号的能量和功率，并指出是能量信号还是功率信号，或两者均不是。 (1) | |3)(t e t x -= 解能量有限信号。信号能量为： (2) ()?????<≥=0 2 021)(n n n x n n 解能量有限信号。信号能量为： (3) t t x π2sin )(= 解功率有限信号。周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率，t π2sin 的周期为1。 (4) n n x 4 sin )(π = 解功率有限信号。n 4 sin π 是周期序列，周期为8。 (5) )(2sin )(t t t x επ= 解功率有限信号。由题(3)知，在),(∞-∞区间上t π2sin 的功率为1/2，因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。如果考察)(2sin t t επ在),0(∞区间上的功率，其功率为1/2。 (6) )(4 sin )(n n n x επ = 解功率有限信号。由题(4)知，在),(∞-∞区间上n 4 sin π 的功率为1/2，因此)(4 sin n n επ 在),(∞-∞区间上的功率为1/4。如果考察)(4 sin n n επ 在),0(∞区间上的功率，其功率为1/2。 (7) t e t x -=3)( 解非功率、非能量信号。考虑其功率：上式分子分母对T 求导后取极限得∞→P 。 (8) )(3)(t e t x t ε-= 解能量信号。信号能量为： 1.3 已知)(t x 的波形如题图1.3所示，试画出下列函数的波形。 (3) )2(t x (4) ( x (5) )(t x - (6) )2(+-t x 1 1 -1/ 2 0 1 1 -2 -1 0 1 2 3 4

西南交大考研试题(信号与系统)

2000年一、选择题（每小题3分，共30分） 1、已知y (t )=x (t )*h (t )，g (t )=x (3t )*h (3t )，x (t )?X (j ω)，h (t )?H (j ω)，则g (t ) = ( )。（a ）?? ? ??33t y （b ） ?? ? ??331t y （c ） ()t y 33 1 （d ） ()t y 39 1 2、差分方程)()2()5()3(6)(k f k f k y k y k y --=+++-所描述的系统是（）的线性时不变系统。（a ）五阶（b ）六阶（c ）三阶（d ）八阶 3、已知信号f 1(t )，f 2(t )的频带宽度分别为?ω1和?ω2，且?ω2>?ω1，则信号y (t )= f 1(t )*f 2(t )的不失真采样间隔（奈奎斯特间隔）T 等于（）。（a ） 2 1π ωω?+? （b ） 1 2π ωω?-? （c ） 2 πω? （d ） 1 πω? 4、已知f (t )?F (j ω)，则信号y (t )= f (t )δ (t -2)的频谱函数Y (j ω)=（）。（a ）ωω2j e )j (F （b ）ω2-j e )2(f （c ）)2(f （d ）ω2j e )2(f 5、已知一线性时不变系统的系统函数为) 2)(1(1 -)(-+=s s s s H ，若系统是因果的，则系统函数H (s )的收敛域ROC 应为（）。（a ）2]Re[>s （b ）1]Re[-0，则此系统的幅频特性|H (j ω)|= （）。（a ） 2 1 （b ）1 （c ）??? ??-a ω1 tan （d ）?? ? ??-a ω1tan 2 7、已知输入信号x (n )是N 点有限长序列，线性时不变系统的单位函数响应h (n )是M 点有限长序列，且M >N ，则系统输出信号为y (n )= x (n )*h (n )是（）点有限长序列。（a ）N +M （b ）N +M -1 （c ）M （d ）N 8、有一信号y (n )的Z 变换的表达式为113 112 4111)(---+-= z z z Y ，如果其Z 变换的收敛域为3 1 ||41<

相关主题

信号与系统课后答案

信号与系统历年真题

信号系统作业答案

邮电大学信号与系统

清华大学信号与系统

西南大学信号与系统

~~文本预览~~

相关文档

(完整版)信号与系统习题答案.docx

(完整版)信号与系统习题答案

信号与系统课后习题答案汇总

信号与系统课后答案

第二章1信号与系统-课后答案

信号与系统课后答案.doc

信号与系统(郑君里)习题答案

信号与系统课后习题答案—第1章

信号与系统_陈后金_第二版_课后答案

信号与系统课后习题答案

信号与系统课后习题参考答案

信号与系统课后答案

信号与系统习题答案

郑君里信号与系统习题答案

信号与系统课后习题与解答第一章

《信号与系统》课后习题答案.ppt

信号与系统习题答案(7-10)

信号与系统课后答案

信号与系统西安邮电习题答案

信号与系统课后习题答案—第章

最新文档

幼儿园小班科学《小动物过冬》PPT课件教案

2021年春新青岛版(五四制)科学四年级下册 20.《露和霜》教学课件

自然教育课件

小学语文优质课火烧云教材分析及课件

(超详)高中语文知识点归纳汇总

高中语文基础知识点总结(5篇)

高中语文基础知识点总结(最新)

高中语文知识点整理总结

高中语文知识点归纳

高中语文基础知识点总结大全

超详细的高中语文知识点归纳

高考语文知识点总结高中

高中语文知识点总结归纳

高中语文知识点整理总结

高中语文知识点归纳

高中语文知识点归纳(大全)

高中语文知识点总结归纳(汇总8篇)

高中语文基础知识点整理

化工厂应急预案

化工消防应急预案(精选8篇)