下载文档原格式
2024高中三角函数公式大全
1、三角函数的定义
三角函数是建立在三角形中的特殊关系上，用于表示角度和边长之间的函数。
三角函数的基本定义如下：
（1）正弦函数sinθ：表示角θ的对边和斜边的比值，即sinθ = y/r。
（2）余弦函数cosθ：表示角θ的邻边和斜边的比值，即cosθ = x/r。
（3）正切函数tanθ：表示角θ的对边和邻边的比值，即tanθ = y/x。
（4）反正弦函数arcsinα：表示α对应的角度θ，即arcsinα = θ。
（5）反余弦函数arccosα：表示α对应的角度θ，即arccosα = θ。
（6）反正切函数arctanα：表示α对应的角度θ，即arctanα = θ。
2、三角函数的基本公式
（1）正弦定理：（a，b，C）为θ对应的三边，则
a/sinθ=b/sinθ=c/sinθ。
（2）余弦定理：（a，b，C）为θ对应的三边，则a^2=b^2+c^2-
2bc*cosθ。
（3）正切定理：（a，b，C）为θ对应的三边，则tanθ=b/a=c/b。
（4）反正弦定理：arcsinα=θ，其中θ的范围在（-π/2，π/2）
之间。
（5）反余弦定理：arccosα=θ，其中θ的范围在（0，π）之间。
（6）反正切定理：arctanα=θ，其中θ的范围在（-π/2，π/2）
之间。
3、三角函数的关系和性质
（1）正弦定理：sin2θ+cos2θ=1
（2）正弦定理的奇偶周期性：sin(-θ)= -sinθ；cos(-θ)= cosθ。
高一数学知识点总结三角一、三角函数的定义在一个直角三角形中，对于一个锐角θ（0 < θ < 90°），定义以下三个比率：1. 正弦（sine）：sinθ = 对边/斜边2. 余弦（cosine）：cosθ = 邻边/斜边3. 正切（tangent）：tanθ = 对边/邻边二、三角恒等式1. 余弦的平方 + 正弦的平方等于1：sin²θ + cos²θ = 12. 余切和正切的关系：tanθ = 1/cotθ3. 余割和正弦的关系：cscθ = 1/sinθ4. 正割和余弦的关系：secθ = 1/cosθ5. 三角函数的倒数关系：sinθ = 1/cscθ，cosθ = 1/secθ，tanθ = 1/cotθ6. 双角公式：- sin2θ = 2sinθcosθ- cos2θ = cos²θ - sin²θ = 2cos²θ - 1 = 1 - 2sin²θ - tan2θ = 2tanθ/1 - tan²θ三、三角函数的图像与性质1. 正弦函数：- 定义域：(-∞, ∞)- 值域：[-1, 1]- 周期：2π（或360°）- 对称性：奇函数，关于原点对称2. 余弦函数：- 定义域：(-∞, ∞)- 值域：[-1, 1]- 周期：2π（或360°）- 对称性：偶函数，关于y轴对称3. 正切函数：- 定义域：(-∞, ∞)，除去所有cosθ = 0的点 - 值域：(-∞, ∞)- 周期：π（或180°）- 对称性：奇函数，关于原点对称，对称轴为x = π/2（或90°）4. 余切函数：- 定义域：(-∞, ∞)，除去所有sinθ = 0的点- 值域：(-∞, ∞)- 周期：π（或180°）- 对称性：奇函数，关于原点对称，对称轴为x = 05. 正割函数：- 定义域：(-∞, ∞)，除去所有cosθ = 0的点- 值域：(-∞, -1] ∪ [1, ∞)- 周期：2π（或360°）- 对称性：无6. 余割函数：- 定义域：(-∞, ∞)，除去所有sinθ = 0的点- 值域：(-∞, -1] ∪ [1, ∞)- 周期：2π（或360°）- 对称性：无四、三角函数的基本关系1. 正弦定理：在任意三角形ABC中，边长分别为a，b，c，角度分别为A，B，C，则有：a/sinA = b/sinB = c/sinC2. 余弦定理：在任意三角形ABC中，边长分别为a，b，c，角度分别为A，B，C，则有：c² = a² + b² - 2abcosC3. 正弦定理：在任意三角形ABC中，边长分别为a，b，c，角度分别为A，B，C，则有：sinA/a = sinB/b = sinC/c五、特殊角的三角函数值1. 30°特殊角：- sin30° = 1/2, cos30° = √3/2, tan30° = 1/√32. 45°特殊角：- sin45° = √2/2, cos45° = √2/2, tan45° = 13. 60°特殊角：- sin60° = √3/2, cos60° = 1/2, tan60° = √3六、三角函数的应用1. 三角函数在几何中的应用：- 利用正弦定理、余弦定理等求解三角形的边长和角度 - 利用三角函数计算三角形的面积2. 三角函数在物理中的应用：- 载荷的力分析- 物体在斜面上的运动- 振动和波动现象的分析- 电流、电压的分析总结：通过本文，我们对高中一年级数学中的三角函数知识点进行了总结。
三角函数知识点总结高一三角函数知识点总结在高中数学学习中，三角函数是一个重要的知识点。
它涉及到正弦、余弦、正切等函数的定义、性质和应用。
下面是对三角函数的知识点进行总结。
一、三角函数的定义三角函数中最常用的三个函数是正弦函数、余弦函数和正切函数。
它们的定义如下：1. 正弦函数（sine function）：在直角三角形中，对于一个锐角A，正弦函数的值等于A的对边与斜边的比值，记作sin(A)。
2. 余弦函数（cosine function）：在直角三角形中，对于一个锐角A，余弦函数的值等于A的邻边与斜边的比值，记作cos(A)。
3. 正切函数（tangent function）：在直角三角形中，对于一个锐角A，正切函数的值等于A的对边与邻边的比值，记作tan(A)。
二、三角函数的性质三角函数具有以下一些重要的性质：1. 周期性：正弦函数和余弦函数的周期都是2π，即在一个周期内，函数的值会重复。
2. 奇偶性：正弦函数是奇函数，即sin(-A)=-sin(A)，余弦函数是偶函数，即cos(-A)=cos(A)。
3. 互余关系：正弦函数和余弦函数有互余关系，即sin(A)=cos(90°-A)，cos(A)=sin(90°-A)。
4. 基本关系式：正弦函数和余弦函数之间有基本关系式sin²(A)+cos²(A)=1。
5. 正切函数的性质：正切函数在每个周期内有一个渐近线，tan(A)=sin(A)/cos(A)。
三、三角函数的应用三角函数在很多实际问题中有广泛的应用，以下是一些常见的应用：1. 角度的求解：利用三角函数可以求解未知角度的大小。
通过已知边长和角度的关系，可以利用三角函数求解未知角度的值。
2. 三角恒等式：三角函数之间有一些重要的恒等式，如和差化积、倍角公式、半角公式等，可以简化复杂的三角运算。
3. 三角函数图像的分析：通过对三角函数图像的分析，可以得到函数的周期、最大最小值等信息，进而解决函数相关的问题。
高一数学中的三角函数公式整理三角函数是高一数学中的重要内容，它们在解决各种三角形和角度相关问题时起到关键作用。
为了更好地掌握三角函数，以下是一些常用的三角函数公式整理。
正弦函数公式1. 三角函数的定义：对于任意角θ，正弦函数的值可以由一个比率给出：$\sin(\theta) = \frac{\text{对边}}{\text{斜边}}$。
2. 余弦函数的定义：对于任意角θ，余弦函数的值可以由一个比率给出：$\cos(\theta) = \frac{\text{邻边}}{\text{斜边}}$。
3. 正弦函数的基本关系：$\sin^2(\theta) + \cos^2(\theta) = 1$。
4. 正弦函数的诱导公式：$\sin(\theta + \alpha) =\sin(\theta)\cos(\alpha) + \cos(\theta)\sin(\alpha)$。
5. 正弦函数的周期性：$\sin(\theta + 360^\circ) = \sin(\theta)$。
余弦函数公式1. 余弦函数的基本关系：$\sin^2(\theta) + \cos^2(\theta) = 1$。
2. 余弦函数的诱导公式：$\cos(\theta + \alpha) =\cos(\theta)\cos(\alpha) - \sin(\theta)\sin(\alpha)$。
3. 余弦函数的周期性：$\cos(\theta + 360^\circ) = \cos(\theta)$。
正切函数公式1. 正切函数的定义：对于任意角θ，正切函数的值可以由一个比率给出：$\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}$。
2. 正切函数的诱导公式：$\tan(\theta + \alpha) = \frac{\tan(\theta) + \tan(\alpha)}{1 - \tan(\theta)\tan(\alpha)}$。
高一三角函数知识点归纳总结公式三角函数是高中数学中的一个重要内容，它在数学和物理等学科中有着广泛的应用。
下面我将对高一阶段学习的三角函数的知识点进行归纳总结，并给出相应的公式。
1. 正弦函数（sin）正弦函数是三角函数中最基本的函数之一，它表示一个角的正弦值与其对边和斜边的比值。
其公式为：sinθ = 对边 / 斜边2. 余弦函数（cos）余弦函数是三角函数中另一个基本的函数，它表示一个角的余弦值与其邻边和斜边的比值。
其公式为：cosθ = 邻边 / 斜边3. 正切函数（tan）正切函数是三角函数中较为复杂的函数，它表示一个角的正切值与其对边和邻边的比值。
其公式为：tanθ = 对边 / 邻边4. 余切函数（cot）余切函数是正切函数的倒数，表示一个角的余切值与其邻边和对边的比值。
其公式为：cotθ = 邻边 / 对边5. 正割函数（sec）正割函数是余弦函数的倒数，表示一个角的正割值与其斜边和邻边的比值。
其公式为：secθ = 斜边 / 邻边6. 余割函数（csc）余割函数是正弦函数的倒数，表示一个角的余割值与其斜边和对边的比值。
其公式为：cscθ = 斜边 / 对边除了以上的基本三角函数，还有一些与三角函数相关的公式：7. 和差角公式sin(A±B) = sinAcosB ± cosAsinBcos(A±B) = cosAcosB ∓ sinAsinBtan(A±B) = (tanA ± tanB) / (1 ∓ tanAtanB)8. 二倍角公式sin2θ = 2sinθcosθcos2θ = cos^2θ - sin^2θtan2θ = (2tanθ) / (1 - tan^2θ)9. 半角公式sin(θ/2) = ± √((1 - cosθ) / 2)cos(θ/2) = ± √((1 + cosθ) / 2)tan(θ/2) = ± √((1 - cosθ) / (1 + cosθ))10. 诱导公式sin(A ± π/2) = ± cosAcos(A ± π/2) = ∓ sinAtan(A ± π/2) = -cotA这些公式是高一阶段学习三角函数时需要掌握和应用的重要工具，通过熟练掌握这些公式，可以帮助我们解决各种与三角函数相关的问题。
高一数学三角函数公式汇总三角函数通常定义为包含这个角的直角三角形的两个边的比率，也可以等价的定义为单位圆上的各种线段的长度。
下面是小编整理的三角函数公式，一起来看看吧!两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB tan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A)ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=((1-cosA)/2)sin(A/2)=-((1-cosA)/2)cos(A/2)=((1+cosA)/2)cos(A/2)=-((1+cosA)/2)tan(A/2)=((1-cosA)/((1+cosA))tan(A/2)=-((1-cosA)/((1+cosA))ctg(A/2)=((1+cosA)/((1-cosA))ctg(A/2)=-((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B) 2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B) sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosBtanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB-ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9++n=n(n+1)/21+3+5+7+9+11+13 +15++(2n-1)=n22+4+6+8+10+12+14++(2n)=n(n+1)12+22+32+42+52+62 +72+82++n2=n(n+1)(2n+1)/613+23+33+43+53+63+n3=n2(n+1)2/41*2+2*3+3*4+4*5+ 5*6+6*7++n(n+1)=n(n+1)(n+2)/3判别式b2-4ac=0注：方程有两个相等的实根b2-4ac0注：方程有两个不等的实根b2-4ac0注：方程没有实根，有共轭复数根降幂公式(sin^2)x=1-cos2x/2(cos^2)x=i=cos2x/2万能公式令tan(a/2)=tsina=2t/(1+t^2)cosa=(1-t^2)/(1+t^2)tana=2t/(1-t^2)。
高中数学三角函数知识点总结精品版资料高中数学中，三角函数是一个重要的章节，它是数学的基础，在其他学科中也有广泛的应用。
以下是关于高中数学三角函数的知识点总结。
一、三角函数的定义1. 正弦函数 sin(x)：在直角三角形中，对于角度x对应的角的正弦值定义为：正弦值 = 对边/斜边。
2. 余弦函数 cos(x)：在直角三角形中，对于角度x对应的角的余弦值定义为：余弦值 = 邻边/斜边。
3. 正切函数 tan(x)：在直角三角形中，对于角度x对应的角的正切值定义为：正切值 = 对边/邻边。
二、三角函数的基本关系1. 正弦函数、余弦函数、正切函数的基本关系：sin(x)² + cos(x)² = 12. 正切函数与正弦函数、余弦函数的关系：tan(x) =sin(x)/cos(x)。
三、三角函数的性质1. 周期性：sin(x + 2π) = sin(x)，cos(x + 2π) = cos(x)，tan(x + π) = tan(x)。
2. 奇偶性：sin(-x) = -sin(x)，cos(-x) = cos(x)，tan(-x) = -tan(x)。
3. 正负性：sin(x)在0 < x < π范围内为正，余弦函数cos(x)在0 < x < π范围内为负，正切函数tan(x)在0 < x < π范围内为正。
4. 三角函数的特殊值：sin(0) = 0，cos(0) = 1，tan(0) = 0。
四、三角函数的图像1. 正弦函数的图像：y = sin(x)的图像在[0, 2π]区间内的图像是一条连续的波浪曲线，振幅为1，周期为2π。
2. 余弦函数的图像：y = cos(x)的图像在[0, 2π]区间内的图像是一条连续的波浪曲线，振幅为1，周期为2π。
3. 正切函数的图像：y = tan(x)的图像在(-π/2, π/2)区间内是一条连续的曲线，具有无穷多个渐近线。
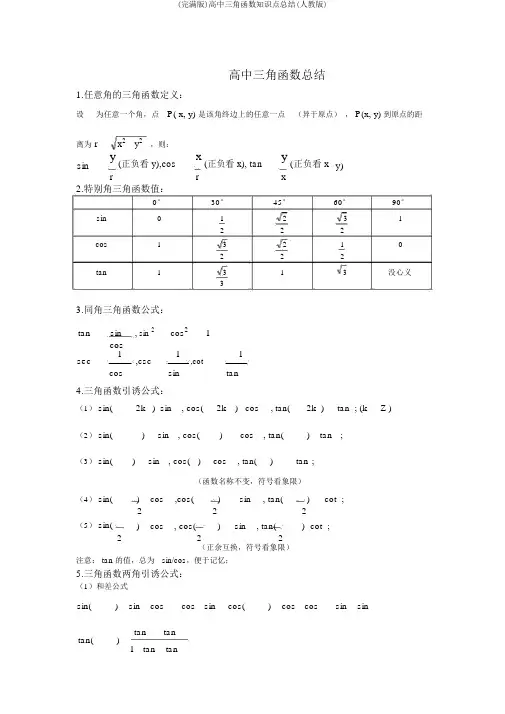
高中三角函数总结1.任意角的三角函数定义：设 为任意一个角，点 P( x, y) 是该角终边上的任意一点 （异于原点） ， P(x, y) 到原点的距离为 rx 2 y 2 ，则：siny(正负看 y),cosx(正负看 x), tany(正负看 x y)rrx2.特别角三角函数值：0° 30° 45°60°90° sin0 12 3 122 2cos1 32 1 02 22tan13 13没心义33.同角三角函数公式：tansin , sin 2cos 21cossec1,csc 11cos,cottansin4.三角函数引诱公式：（1） sin( 2k ) sin , cos( 2k ) cos , tan( 2k ) tan ; (kZ )（2） sin( ) sin , cos( )cos , tan() tan ;（3） sin()sin , cos( )cos , tan()tan ;（函数名称不变，符号看象限）（4） sin() cos ,cos( )sin, tan() cot ;222（5） sin() cos , cos()sin , tan() cot ;222（正余互换，符号看象限）注意： tan 的值，总为 sin/cos ，便于记忆；5.三角函数两角引诱公式：（1）和差公式sin( ) sin coscos sin cos( ) cos cos sin sintantantan( )1 tan tan（2）倍角公式令上面的可得： sin( 2 ) 2 sin coscos(2 ) cos2 sin 22 tan 2 cos2 1 tan(2 )1 2sin 21 tan2 6.正弦定理：△ABC 中三边分别为a,b, c ,外接圆半径为R ，则有：a b cR sin A sin B27.余弦定理：sin C△ABC 中三边分别为a,b, c ,则有： cosC a2 b2 c22ab8.面积公式：1ab sinC(两边与夹角正弦值 ) △ABC 中三边分别为a,b, c ,面积为S，则有：S2三角函数图象：9.函数名图像单调区间y=sinx递加区间：[ 2k ,2k ]2 2递减区间：[ 2k ,2k 3], k Z2 2y=cosx递加区间：[ 2k,2k ]递减区间：[ 2k ,2k], k Zy=tanx递加区间：(k, k), k Z2 2定义域非R，为：{ x | x k}210.关于y Asin( x ) B 的性质：（1）最大值为| A | B ，最小值为| A | B （ sin( x )1时 ,得最大最小）（2）周期2 1 | |x ，初相是T ，频率 f ，相位是| | T 2（3）图像的对称轴是直线：（4）图像的对称中心为：x k (k Z ) ，可化简为x=的形式；2y A sin( x ) B B 时获取的所有交点（x，B ）（5）单调区间求取：一利用引诱公式将变为正，如变为cos 等，此处假设0 ，二求出 y Asin x 的单调区间，令x分别位于单调区间地域，反解x 范围；11.图像变换：y Asin( x) B ：y sin x沿x轴左移个单位y sin(x )横坐标x变为原来的1 倍xy sin( ) sin( x )1纵坐标 y变为原来的 A倍y ) y Asin( x )sin( xA沿y轴下移 B个单位y B Asin( x ) y Asin( x ) B 要点点：上 +下 -（ y），左 +右 -（ x），倍数相除（变为原来的n 倍，则对应的坐标都除以n）。
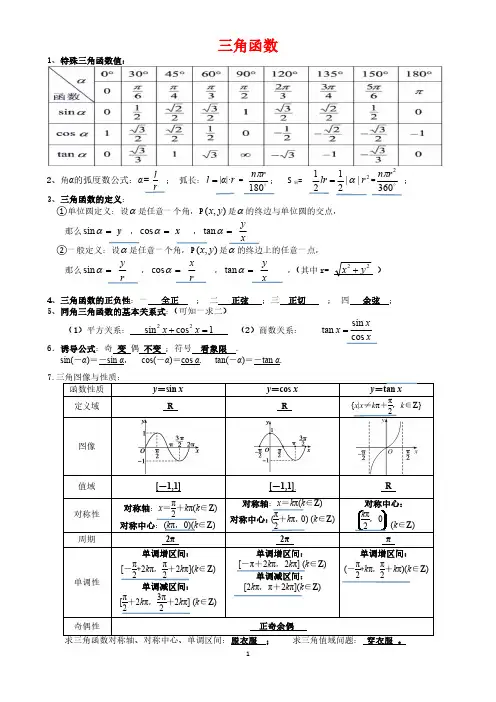
1三角函数1、特殊三角函数值：2、角α的弧度数公式：α=lr ；弧长：=l |α|·r =180r n π；S 扇=211||22lr r α== 3602r n π；3、三角函数的定义：①单位圆定义：设α是任意一个角，P (,)x y 是α的终边与单位圆的交点，那么=αsin y，=αcos x，=αtan yx②一般定义：设α是任意一个角，P (,)x y 是α的终边上的任意一点，那么=αsin y r，=αcos x r，=αtan y x，（其中r=22y x +）4、三角函数的正负性：一全正；二正弦；三正切；四余弦；5、同角三角函数的基本关系式：（可知一求二）（1）平方关系：22sin cos 1x x +=（2）商数关系：sin tan cos x x x=6．诱导公式：奇变偶不变；符号看象限.sin(－α)＝－sin α，cos(－α)＝cos α.tan(－α)＝－tan α.21,1]π(求三角函数对称轴、对称中心、单调区间：脱衣服；求三角值域问题：穿衣服。
28.和差公式：sin(α＋β)＝s in αcos β＋cos αsin β;sin(α－β)＝sin αcos β－cos αsin βcos(α＋β)＝cos αcos β－sin αsin β；cos(α－β)＝cos αcos β＋sin αsin βtan(α＋β)＝；tan(α－β)＝.9、二倍角公式：sin 2α＝2sin αcos αcos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2αtan 2α＝.10、降次公式：cos 2α＝；sin 2α＝；＝；tan 2α＝ αα2cos 12cos 1+-11、辅助角公式：a sin α＋b cos α＝(其中tan θ＝)注意：①使sin 系数为正；②a 与b 都取正。
12、正弦型函数y ＝A sin(ωx ＋ϕ)+B 参数的求法：求A 看最值：A=2min -max ；求ω看周期：Tπω2=；求ϕ：代点；求B 看最值：B =2minmax +13、正弦函数y ＝sin x 的特殊5点坐标：） （0,0） （1,2π） （0,π） （1,23-π） （0,2π余弦函数y ＝cos x 的特殊5点坐标：） （1,0） （0,2π） （1,-π） （0,23π） （1,2π。
三角函数的定义及常用公式三角函数是数学中研究角度和三角形的函数关系的一门学科。
它以正弦函数、余弦函数和正切函数为代表，是数学分析和几何学等领域的重要内容。
本文将介绍三角函数的定义及其常用公式，并探讨其在数学和实际应用中的意义。
一、正弦函数（sin）的定义及常用公式正弦函数是以单位圆上的点坐标的y值来定义的。
在直角三角形中，正弦函数是对边与斜边的比值。
正弦函数的定义域为实数集，其值域在-1至1之间。
正弦函数的常用公式：1. 正弦函数的周期性公式：sin(x + 2π) = sin(x)2. 正弦函数的奇偶性公式：sin(-x) = -sin(x)3. 正弦函数的和差公式：sin(x + y) = sin(x)cos(y) + cos(x)sin(y)4. 正弦函数的积化和差公式：2sin(x)sin(y) = cos(x-y)-cos(x+y)5. 正弦函数的半角公式：sin(x/2) = ±√[(1 - cos(x))/2]二、余弦函数（cos）的定义及常用公式余弦函数是以单位圆上的点坐标的x值来定义的。
在直角三角形中，余弦函数是邻边与斜边的比值。
余弦函数的定义域为实数集，其值域在-1至1之间。
余弦函数的常用公式：1. 余弦函数的周期性公式：cos(x + 2π) = cos(x)2. 余弦函数的奇偶性公式：cos(-x) = cos(x)3. 余弦函数的和差公式：cos(x + y) = cos(x)cos(y) - sin(x)sin(y)4. 余弦函数的积化和差公式：2cos(x)cos(y) = cos(x-y) + cos(x+y)5. 余弦函数的半角公式：cos(x/2) = ±√[(1 + cos(x))/2]三、正切函数（tan）的定义及常用公式正切函数是以正弦函数与余弦函数的比值来定义的。
在直角三角形中，正切函数是对边与邻边的比值。
正切函数的定义域为实数集，其值域为全体实数。
----------三角函数的定义及三角公式◇知识归纳：1、三角函数的概念 （1）、按旋转方向，角可以分为三类： （2）、终边在射线y=x 上的角的集合为 ，终边在直线y=x 上的角的集合为 （3）、象限角的概念：如果角的终边在坐标轴上，就认为这个角 任何象限． （4）、弧长公式： ，扇形面积公式： ，1弧度(1rad )等于 度. （5）、任意角的三角函数的定义：设α是任意一个角，P (,)x y 是α的终边上的任意一点（异于原点），它与原点的距离是0r =>，那么sin α= cos α= tan α=三角函数符号规律记忆口诀：一全正， （6）、三角函数线的特征是：正弦线 “站在x 轴上(起点在x 轴上)”、余弦线 “躺在x 轴上(起点是原点)”、正切线 “站在点(1,0)A 处(起点是A )”. （7）、三角函数值的大小和解三角不等式．若(0,)2x π∈，则x 、sinx 、tanx 的大小关系为： ；2、三角公式：（1）同角三角函数的基本关系式平方关系： ； 商数关系： （2）诱导公式“奇变偶不变，符号看象限”．sin(90°+α)= cos(-α)= tan(180°-α)= cos(270°-α)= （3）、两角和（差）的正弦、余弦及正切（4）、二倍角的正弦、余弦及正切（5）、万能公式：（6）、降次公式：（7）、半角公式：（8）、辅助角公式：()sin cos a x b x x θ+=+(其中θ角所在的象限由,a b 的符号确定，θ角的值由tan baθ=确定)，在求最值、化简时起着重要作用.注：三角函数的恒等变形的基本思路：一角二名三结构.即首先观察角与角之间的关系，注意角的一些常用变式，角的变换是三角函数变换的核心！第二看函数名称之间的关系，通常“切化弦”；第三观察代数式的结构特点.基本的技巧有:(1)巧变角(配角)；(2)三角函数名互化(切化弦)；(3)公式变形使用；(4)三角函数次数的降升；(5)式子结构转化(对角、函数名、式子结构化同)；(6)常值变换主要指“1”的变换；(7)正余弦“三兄妹——sin cos sin cos x x x x ±、”的内在联系――“知一求二”. 求角的方法：先确定角的范围，再求出关于此角的某一个三角函数（要注意选择，其标准有二：一是此三角函数在角的范围内具有单调性；二是根据条件易求出此三角函数值）.◇基础演练：1、若一个6000的角的终边上有一点P (－4 , a )，则a 的值为 .2、 sin1100sin200cos 21550－sin 21550 = .3、1 + tan1501－tan150 = .4、cos α + 3 sin α5、tan200 + tan4000= .6、(1 + tan α其中α + β = 45 0).7、已知tan α = 12，则sin2α + sin 2α = __________.8、一段圆弧的长度等于其圆内接正三角形的边长，则其圆心角的弧度数为( )A.π3B.2π3C. 3D. 2 9、如图，三个相同的正方形相接，则α +β = . ◇能力提升：1、已知sin α是方程5x 2－7x －6＝0的根，且α是第三象限角，则sin ⎝⎛⎭⎫－α－3π2cos ⎝⎛⎭⎫3π2－αt a n 2(π－α)cos ⎝⎛⎭⎫π2－αsin ⎝⎛⎭⎫π2＋α＝( )A.916 B ．－916 C ．－34 D.342、(2012·开封调研)若α为三角形的一个内角，且sin α＋cos α＝23，则这个三角形是( )A ．正三角形B ．直角三角形C ．锐角三角形D ．钝角三角形 3、tan70°·cos10°(3tan20°－1)等于( )A ．1B ．2C ．－1D ．－24、已知A 为锐角，sinA ＝35，t a n A －t a n B 1＋t a n A ·t a n B＝－12，则tan B=_____.5、已知角α的终边上一点的坐标为⎝⎛⎭⎫sin 2π3，cos 2π3，则角α的最小正值为________． 6、点P 从(1,0)出发，沿单位圆x 2＋y 2＝1按逆时针方向运动2π3弧长到达点Q ，则点Q 的坐标为________．7、证明：sin(2)sin 2cos()sin sin A B BA B A A+-+=．8、已知,)cos(,cos 141371=-=βαα且,20παβ<<<（1）求tan2α求的值；（2）、求β9、在平面直角坐标系xOy 中，点P (12，cos 2θ)在角α的终边上，点Q (sin 2θ，－1)在角β的终边上，且OP →·OQ→＝－12. (1)求cos2θ的值 (2)求sin(α＋β)的值．◇课外练习：（第一天）1．已知sin ⎝⎛⎭⎫π2－α＝35，则1－2cos 2α＝( ) A.725 B.2425 C ．－725 D ．－2425 2．已知sin (2π＋θ)t a n (π＋θ)t a n (3π－θ)cos (π2－θ)t a n (－π－θ)＝1，则sin 2θ＋3sin θcos θ＋2cos 2θ的值是( )A ．1B ．2C ．3D ．63．化简sin 235°－12cos10°cos80°＝( )A ．－2B ．－12C ．－1D ．14．sin 29π6＋cos ⎝⎛⎭⎫－29π3－tan ⎝⎛⎭⎫25π4＝________. 5.一个半径为2的扇形，若它的周长等于弧所在的半圆的弧长，那么这个扇形的面积为________.6．已知sin θ＝45，π2＜θ＜π. (1)求tan θ的值； (2)求sin 2θ＋2sin θcos θ3sin 2θ＋cos 2θ的值．7、化简：（1）tan15cot15︒+︒；（2）1sin10 （3）001tan10cos50+◇课外练习：（第二天）1．点A(sin2013°，cos2013°)在直角坐标平面上位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．(2011·高考福建卷)若tan α＝3，则sin2αcos 2α的值等于( )A ．2B ．3C ．4D ．63．若sin θ＝－45，tan θ＞0，则cos θ＝________.4．(2012·洛阳调研)已知角α＝45°，在区间[－720°，0°]内与角α有相同终边的角β＝________. 5、若tan α、tan β是方程2330x x --=的两根，求)cos()sin(βαβα-+的值．6、已知2 1sin2sin 2,(,),2sin tan cot 144442ππππαα=α∈ααα（＋）（－）求＋－－的值；7．已知角A 、B 、C 为△A BC 的三个内角，OM →＝(sin B ＋cos B ，cos C )，ON →＝(sin C ，sin B －cos B )，OM →·ON→＝－15. (1)求tan2A 的值； (2)求2cos 2A2－3sin A －12sin ⎝⎛⎭⎫A ＋π4的值．◇选作题：1．(2012·秦皇岛质检)若cos(3π－x )－3cos ⎝⎛⎭⎫x ＋π2＝0，则tan ⎝⎛⎭⎫x ＋π4等于( ) A ．－12 B ．－2 C.12D ．22．在△ABC 中，若cos2B ＋3cos(A ＋C )＋2＝0，则sin B 的值是( )A.12B.22C.32D ．1 3．(2012·宜昌调研)已知角A 为△ABC 的内角，且sin2A ＝－34，则sin A －cos A ＝( )A.72 B ．－72 C ．－12 D.12 4．若sin ⎝⎛⎭⎫π6＋α＝35，则cos ⎝⎛⎭⎫π3－α＝________. 5．已知角α的终边上一点的坐标为⎝⎛⎭⎫sin 2π3，cos 2π3，则角α的最小正值为________． 6．f (x )＝asin(πx ＋α)＋b cos(πx ＋β)＋4(a 、b 、α、β均为非零实数)，若f (2012)＝6，则f (2013)＝________.8．函数()()b x A x f ++=ϕωs i n 的图象如下，则()()()201110f f f S +⋅⋅⋅++=等于（ ）9、函数2()6cos3(0)2xf x x ωωω=+->在一个周期内的图象如图所示,A 为图象的最高点,B 、C 为图象与x 轴的交点,且ABC ∆为正三角形.(Ⅰ)求ω的值及函数()f x 的值域;(Ⅱ)若0()f x =,且0102(,)33x ∈-,求0(1)f x +的值.10．将一块圆心角为120，半径为200cm 的扇形铁片截成一块矩形；如图有两种截法：让矩形一边在扇形的一条半径OA 上，或让矩形一边与弦AB 平行．请问哪种截法能得到最大面积的矩形，并求出这个最大值．专题（1）----三角函数的定义与三角公式答案----第一天1、A ；2、C ；3、B ；4、0；5、4+2π；6、（1）-4/3；（2）-8/57；7、（1）4；（2）4；（3）原式=0001sin10cos50cos10+0001sin10sin 40sin80=+02cos40cos80sin80︒+︒=（或40=60-20；80=60+20） =380sin 10cos 30cos 280sin 20cos 60cos 240cos 00=︒︒︒=︒+︒. 选作题：9、【解析】(Ⅰ)由已知可得:2()6cos 3(0)2x f x x ωωω=+-> =3cos ωx+)3sin(32sin 3πωω+=x x 又由于正三角形ABC 的高为23,则BC=4所以,函数482824)(πωωπ===⨯=，得，即的周期T x f 所以,函数]32,32[)(-的值域为x f(Ⅱ)因为，由538)(0=x f (Ⅰ)有 ，538)34(sin 32)(00=+=ππx x f 54)34(sin 0=+ππx 即 由x 0)2,2()34x (323100ππππ-∈+-∈），得，（ 所以,53)54(1)34(cos 20=-=+ππx 即故=+)1(0x f =++)344(sin 320πππx ]4)34(sin[320πππ++x)22532254(324sin)34cos(4cos)34([sin 320⨯+⨯=+++=ππππππx x 567=专题（1）----三角函数的定义与三角公式答案----第一天1、C ；2、D ；3、-3/5；4、-315度或-675度；5、-3/2；6、注意到）－）与（＋απαπ2424(互为余角， 由已知得 1sin 2sin 2444ππαα=（＋）（－）214cos 21)42sin(=⇔=+⇔ααπ ∵)2,4(ππα∈，∴)2,(4ππα∈∴125,354παπα＝即=∴原式＝）－）＋（－（αααc o t t a n 1s i n 22＝αααααcos sin cos sin 2cos 22－＋－＝αααsin22cos22cos －－＝）＋（－ααsin2212cos ＝）＋（－65sin 2165cos ππ=2354123）＝＋（ 7、解：(1)∵OM →·ON →＝(sin B ＋cos B )sin C ＋cos C (sin B －cos B )＝sin(B ＋C )－cos(B ＋C )＝－15，∴sinA ＋cosA ＝－15，①两边平方并整理得：2sinAcosA ＝－2425，∵－2425＜0，∴A ∈⎝⎛⎭⎫π2，π，∴sinA －cosA ＝1－2sin A cos A ＝75.②联立①②得：sinA ＝35，cosA ＝－45，∴tanA ＝－34，∴tan2A ＝2t a n A 1－t a n 2A＝－321－916＝－247. (2)∵tanA ＝－34，∴2cos 2A 2－3sin A －12sin ⎝⎛⎭⎫A ＋π4＝cos A －3sin A cos A ＋sin A ＝1－3t a n A 1＋t a n A ＝1－3×⎝ ⎛⎭⎪⎫－341＋⎝ ⎛⎭⎪⎫－34＝13. 选作题：10．【解析】 在方案一中，令∠AOM=θ，则0＜θ＜90°，在Rt △OMP 中，MP=200sin θ，OP=200cos θ， 所以，S OPMN =20000sin2θ，当2θ=90°，即θ=45°时，S OPMN 取得最大值20000 cm 2． 在方案二中，令∠AOM=θ，则0＜θ＜60°， 在Rt △OMS 中，MS=200sin θ，OS=200cos θ， 在Rt △MQS 中，∠MQS=60°，MQ MS θ==，12QS MQ θ==在Rt △OCQ 中，)CQ OS QS ==-(200cos )100sin θθθθ==-，所以，2sin )MNPQ S CQ MQ θθθ=⨯=-2sin )sin cos sin )θθθθθθ=-=-1cos 211(2)(2cos 2)22222θθθθ-=-=+-130)]2θ=+︒-，当2θ+30°=90°，即θ=30°时，S MNPQcm 2．比较两种方案的最大值可知，第二种截法能得到最大面积，最大面积为3cm 2一、基本知识（必做题部分）（五）平面向量（必修4第二章） 1、平面向量的概念（B ） （1）向量的概念：向量常用有向线段来表示，注意不能说向量就是有向线段，为什么？（向量可以平移）． （2）零向量：长度为0的向量叫零向量，记作：0，注意零向量的方向是任意的． （3）单位向量：长度为一个单位长度的向量 (与AB 共线的单位向量是||AB AB ±)．（4）相等向量：长度相等且方向相同的两个向量叫相等向量，相等向量有传递性．（5）平行向量（也叫共线向量）：方向相同或相反的非零向量a 、b 叫做平行向量，记作：a ∥b ，规定零向量和任何向量平行．提醒：①相等向量一定是共线向量，但共线向量不一定相等；②两个向量平行与与两条直线平行是不同的两个概念：两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合；③平行向量无传递性！（因为有0)；④三点A B C 、、共线⇔ AB AC 、共线． （6）相反向量：长度相等方向相反的向量叫做相反向量．的相反向量是－．2、平面向量的加法、减法及数乘运算（B ） 实数与向量的积的运算律：设λ、μ为实数 (1)结合律：()()a a λμλμ=；(2)第一分配律：()a a a λμλμ+=+； (3)第二分配律：()a b a b λλλ+=+.注：实数λ与向量a 的积是一个向量，记作a λ，它的长度和方向规定如下：(1)a a λλ=；(2)当λ>0时，a λ的方向与a 的方向相同，当0λ<时，a λ的方向与a 的方向相反，当0λ=时，0a λ=，注意：0a λ≠.3、平面向量的坐标表示（B ） 向量的表示方法：①几何表示法：用带箭头的有向线段表示，如AB ，注意起点在前，终点在后； ②符号表示法：用一个小写的英文字母来表示，如a ，b ，c 等；③坐标表示法：在平面内建立直角坐标系，以与x 轴、y 轴方向相同的两个单位向量i ，j 为基底，则平面内的任一向量a 可表示为(),a xi yj x y =+=，称(),x y 为向量a 的坐标，a ＝(),x y 叫做向量a 的坐标表示．如果向量的起点在原点，那么向量的坐标与向量的终点坐标相同． 平面向量的坐标运算：(1)设=11(,)x y ,=22(,)x y ，则+=1212(,)x x y y ++. (2)设a =11(,)x y ,b =22(,)x y ，则a -b =1212(,)x x y y --.(3)设11(,)A x y ，22(,)B x y ,则2121(,)AB OB OA x x y y =-=--. (4)设=(,),x y R λ∈，则λ=(,)x y λλ.(5)设=11(,)x y ,=22(,)x y ，则·=1212x x y y +.平面向量基本定理：如果1e 、2e 是同一平面内的两个不共线向量，那么对于这一平面内的任一向量，有且只有一对实数1λ、2λ，使得1122a e e λλ=+．不共线的向量1e 、2e 叫做表示这一平面内所有向量的一组基底．4、平面向量的数量积（C ）两个向量的夹角：对于非零向量，，作,OA a OB b ==，AOB θ∠=()0θπ≤≤称为向量，的夹角，当θ＝0时，a ，b 同向，当θ＝π时，a ，b 反向，当θ＝2π时，a ，b 垂直.当θ为锐角时，a ⋅b ＞0，且 a b 、不同向，0a b ⋅>是θ为锐角的必要非充分条件；当θ为钝角时，⋅＜0，且 a b 、不反向，0a b ⋅<是θ为钝角的必要非充分条件.向量的数量积的运算律： (1) a ·b = b ·a （交换律）；(2)（λa ）·b = λ（a ·b ）=λa ·b = a ·（λb ）； (3)（a +b ）·c = a ·c +b ·c . 平面向量数量积的坐标表示：（1）若11(,)a x y =，22(,)b x y =，则1212a b x x y y ⋅=+；(AB x =（2）若=(x,y)，则2=⋅=x 2+y 2,22y x a += ；cos θ=(=11(,)x y ,=22(,)x y ).9.平面两点间的距离公式(A 11(,)x y ，B 22(,)x y ).,A B d =||AB AB AB =⋅=5、平面向量的平行与垂直（B ）⑴两个向量平行的充要条件：设a =(x 1,y 1), b =(x 2,y 2),λ为实数.①向量式：a ∥b (b ≠0)⇔a =λb ；②坐标式：a ∥b (b ≠0)⇔x 1y 2－x 2y 1=0.⑵两个向量垂直的充要条件：设a =(x 1,y 1), b =(x 2,y 2), ①向量式：a ⊥b (b ≠0)⇔a ⋅b =0; ②坐标式：a ⊥b ⇔x 1x 2+y 1y 2=0. 6、平面向量的应用（A ）重要结论：⑴三角形的重心坐标公式：△ABC 三个顶点的坐标分别为11A(x ,y )、22B(x ,y )、33C(x ,y ),则△ABC 的重心的坐标是123123(,)33x x x y y y G ++++. ⑵设A （x 1,x 2）、B (x 2,y 2)，则S ⊿AOB ＝122121y x y x -. （3）三角形五“心”向量形式的充要条件：设O 为ABC ∆所在平面上一点，角,,A B C 所对边长分别为,,a b c ，则 ①O 为ABC ∆的外心222OA OB OC ⇔==.②O 为ABC ∆的重心0OA OB OC ⇔++=.③O 为ABC ∆的垂心OA OB OB OC OC OA ⇔⋅=⋅=⋅. 二、思想方法 （三）向量法向量法是运用向量知识解决问题的一种方法，解题常用下列知识： （1）向量的几何表示，两个向量共线的充要条件； （2）平面向量基本定理及其理论；（3）利用向量的数量积处理有关长度、角度和垂直的问题. 三、易题重现1、和向量a = (6,8)共线的单位向量是__________.2、已知向量m =(a,b )，向量m ⊥n 且,n m=则n的坐标可能的一个为__________. 3、将函数y=x+2的图象按a=(6,－2)平移后，得到的新图象的解析为__________. 4、若O 为平行四边形ABCD 的中心，AB =4e1, 2216,32BC e e e =-等于__________.5、若)2,1(),7,5(-=-=b a，且（b a λ+）b ⊥，则实数λ的值为__________.6、已知z 是虚数，则方程z 3 = | z | 的解是__________.7、已知复数z = (4－3i )2·(－1 + 3 i )10(1－i )12，则| z | =__________.8、已知 = (1,2)， = (－3,2)，当k 为何值时，(1)k +与－3垂直？(2) k +与→a －3平行？平行时它们是同向还是反向？ 9、已知 |a |＝1，|b |＝2。
