高一数学第7周周练

高一数学静校练习(第7周）时间：30分钟 满分：27分第1-3小题每题5分，第4题12分1．在ABC ∆中，已知2b =，c = 45B =，则C =A ．60B ．120C ．60或120D ．30或1502．在ABC ∆中,已知2b =，c =45B =，则___________a =3．设sin 2sin αα=-，(,)2παπ∈,则tan 2__________α=4．在ABC ∆中，内角,,A B C 所对的边分别是,,a b c ，已知14b c a -=， 2sin 3sin B C =，求cos A 的值．答案:1．C2．2a =34．解:由正弦定理及2sin 3sin B C =得， 32b c =， 代入14b c a -=可得，2a c = 由余弦定理, 22222229414cos 234c c c b c a A bc c +-+-===-尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文稿在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。

2021年春期高2021级数学周测试题7一、选择题：1．以下命题中，正确的选项是〔 〕b a >，dc >，那么bd ac >bc ac >，那么b a >22cbc a <，那么b a <b a >，d c >，那么d b c a ->- 2．n S 为等差数列{}n a 的前n 项和，15765=++a a a ，那么11S 为〔 〕 A.25 B.30 C3．在ABC ∆中，45B =︒，60C =︒，1c =，那么最短边的边长等于〔 〕(A ()2B ()12C (D4．假设,,a b c 为ABC ∆的内角A B C ，，，那么角C 等于〔 〕A ．030B ．045C ．060D ．0905．等比数列}{n a 的前n 项和为n S ，且14a ，22a ，3a 成等差数列，假设11=a ，那么=4S 〔 〕A ．7B ． 15C ．31D ．8 6．设,x y R +∈且191x y+=,那么x y +的最小值为〔 〕 13)(A 14)(B 15)(C 16)(D7．设00>>b a ，，假设3是a 3和b3的等比中项，那么ba 41+的最小值为〔 〕 A . 6 B ．24 C ．8 D ．9 8．设△ABC 的内角A,B,C 的对边分别为,,a b c 假设()cos ab c C ,那么△ABC 的形状是〔 〕A ．等腰三角形B ．等边三角形C ．直角三角形D ．锐角三角形9．假设等比数列{}n a 的前项和为n S ，且322010=s s ，那么=4020s s〔 〕 A.52 B. 54 C. 74D. 4310．{}n a 是等比数列，3a ，8a 是关于x 的方程22sin 3sin 0x x αα--=的两根，且23829()26a a a a +=+，那么锐角α的值是〔 〕A ．6π B ．4π C ．3π D ．512π11．在ABC ∆中，A 2sin ≤C B C B sin sin sin sin 22-+，那么A 的取值范围是( )．A.]60(π， B.),6[ππ C ]30(π，. D.)3[，ππ12．设等差数列{}n a 的前n 项和为n S ，假设20130S >，20140S <，那么20132014121220132014,,...,,S S S S a a a a 中最大的是〔 〕A.20132013S a B. 20142014S a C. 10081008S a D. 10071007Sa 二、填空题：13．在锐角ABC ∆中，c b a ,,分别为角C B A ,,所对的边，且A c a sin 23=，角C ＝________.14．不等式{}23802x ax x x c -+-><<的解集为，那么a c +=________。

卫星通信技术发展现状及对策河北省保定市某校高一（上）第七次周练数学试卷一、选择题（共9小题，每小题3分，满分27分）1. 若函数f(x)=x 3(x ∈R)，则函数y =f(−x)在其定义域上是（ ） A.单调递减的偶函数 B.单调递减的奇函数 C.单调递增的偶函数 D.单调递增的奇函数2. 函数y =1x+2的大致图象只能是（ ）A. B.C. D.3. 若函数f(x)=3x +3−x 与g(x)=3x −3−x 的定义域均为R ，则（ ） A.f(x)与g(x) 均为偶函数 B.f(x )为偶函数，g(x)为奇函数 C.f(x)与g(x) 均为奇函数 D.f(x)为奇函数，g(x)为偶函数4. 函数f(x)=4x +12x的图象（ ）A.关于原点对称B.关于直线y =x 对称C.关于x 轴对称D.关于y 轴对称5. 如果f(x)是定义在R 上的偶函数，它在[0, +∞)上是减函数，那么下述式子中正确的是（ ）A.f(−34)≤f(a 2−a +1) B.f(−34)≥f(a 2−a +1)6. 已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=a x−a−x+2(a>0，且a≠1)，若g(2)=a，则f(2)=()A.2B.174C.154D. {x∈R|−2<x<2}7. 设函数f(x)和g(x)分别是R上的偶函数和奇函数，则下列结论恒成立的是()A.f(x)+|g(x)|是偶函数B.f(x)−|g(x)|是奇函数C.|f(x)|+g(x)是偶函数D.|f(x)|−g(x)是奇函数8. 已知函数f(x)=ax2+bx+ba+b是偶函数且其定义域为[a−1, 2a]，则（）A.a=13，b=0 B.a=−1，b=0 C.a=1，b=0 D.a=3，b=09. 如果奇函数f(x)在区间[3, 7]上是增函数且最小值为5，那么f(x)在区间[−7, −3]上是()A.增函数且最小值为−5B.增函数且最大值为−5C.减函数且最小值为−5D.减函数且最大值为−5二、填空题（共6小题，每小题3分，满分18分）函数①y=|x|；②y=|x|x ；③y=x2|x|；④y=x+x|x|在(−∞, 0)上为增函数的有________（填序号）．已知f(x)是R上的奇函数，当x>0时，f(x)=x(x−1)，则当x<0时，f(x)=________．若函数f(x)=x(2x+1)(x−a)为奇函数，则a＝________．若函数f(x)=(k−2)x2+(k−1)x+3是偶函数，则f(x)的递减区间是________．给定四个函数：①y =x 3+√x 3；②y =1x (x >0 )；③y =x 3+1；④y =x 2+1x．其中是奇函数的有________ （填序号）． 三、解答题（共3小题，满分0分）判断 函数f(x)={x 2−2x +3，x >00,x =0−x 2−2x −3，x <0的奇偶性．定义在(−1, 1)上的函数f(x)满足：对任意x ，y ∈(−1, 1)，都有f(x)+f(y)=f(x+y 1+xy)，求证：f(x)为奇函数．f(x)是定义在[−2, 2]上的偶函数，且f(x)在[0, 2]上单调递减，若f(1−m)<f(m)成立，求实数m 的取值范围．参考答案与试题解析河北省保定市某校高一（上）第七次周练数学试卷一、选择题（共9小题，每小题3分，满分27分） 1.【答案】 B【考点】函数奇偶性的判断函数单调性的判断与证明【解析】先有f(−x)=−f(−x)得y =f(−x)是奇函数，再利用f(x)=x 3的单调性求出y =f(−x)的单调性即可． 【解答】解：∵ f(x)=x 3(x ∈R)，则函数y =f(−x)=−x 3=−f(−x)(x ∈R)，得y =f(−x)是奇函数．又因为函数f(x)=x 3在定义域内为增函数，所以y =f(−x)在其定义域上是减函数； 所以y =f(−x)在其定义域内是单调递减的奇函数． 故选：B 2.【答案】 B【考点】函数的图象变换 【解析】根据图象的平移即可得到答案 【解答】解：函数y =1x+2的大致图象是由y =1x 的图象向左平移2个单位得到， 故选：B 3.【答案】 B【考点】函数奇偶性的判断 【解析】根据函数奇偶性的定义进行判断即可． 【解答】解：f(−x)=3−x +3x =3x +3−x =f(x)，则f(x)是偶函数， g(−x)=3−x −3x =−(3x −3−x )=−g(x)，则g(x)是奇函数， 故选：B ． 4. 【答案】函数奇偶性的判断 【解析】 由f(x)=4x +12x=2x +2−x，得函数f(x)=4x +12x的图象关于y 轴对称．【解答】 解：∵ f(x)=4x +12x=2x +2−x ，∴ f(−x)=2−x +2x =f(x)， ∴ f(x)是偶函数， ∴ 函数f(x)=4x +12x的图象关于y 轴对称，故选：D ． 5.【答案】 B【考点】奇偶性与单调性的综合 奇偶函数图象的对称性 【解析】利用二次函数的性质比较较a 2−a +1与34的大小关系，利用函数的奇偶性和单调性中之间的关系即可得到结论． 【解答】解：a 2−a +1=(a −12)2+34≥34，∵ f(x)是定义在R 上的偶函数，它在[0, +∞)上是减函数， ∴ f(a 2−a +1)≤f(34)=f(−34)，故选：B ． 6.【答案】 C【考点】函数奇偶性的性质 【解析】根据条件构造关于g(2)和f(2)的方程组来求解． 【解答】解：因为f(x)+g(x)=a x −a −x +2， 所以{f(2)+g(2)=a 2−a −2+2f(−2)+g(−2)=a −2−a 2+2，因为f(x)为奇函数，g(x)为偶函数， 所以{f(2)+g(2)=a 2−a −2+2−f(2)+g(2)=a −2−a 2+2，上述方程组中两式相加得：2g(2)=4，即g(2)=2， 因为g(2)=a ，所以a =2，故选C．7.【答案】A【考点】函数奇偶性的判断【解析】由设函数f(x)和g(x)分别是R上的偶函数和奇函数，我们易得到|f(x)|、|g(x)|也为偶函数，进而根据奇+奇=奇，偶+偶=偶，逐一对四个结论进行判断，即可得到答案．【解答】解：∵函数f(x)和g(x)分别是R上的偶函数和奇函数，则|g(x)|也为偶函数，则f(x)+|g(x)|是偶函数，故A满足条件；f(x)−|g(x)|是偶函数，故B不满足条件；|f(x)|也为偶函数，则|f(x)|+g(x)与|f(x)|−g(x)的奇偶性均不能确定.故选A.8.【答案】A【考点】函数奇偶性的性质【解析】因为函数的偶函数的定义域关于原点对称，可求a，然后利用函数偶函数的定义解b即可．【解答】解：因为f(x)=ax2+bx+ba+b是偶函数，所以定义域关于原点对称，所以a−1+ 2a=0，解得a=13．所以f(x)=13x2+bx+13b+b，因为函数为偶函数，所以f(−x)=f(x)，即）13x2−bx+13b+b=13x2+bx+13b+b，所以2bx=0，解得b=0．故选A．9.【答案】B【考点】函数奇偶性的性质函数的最值及其几何意义函数单调性的判断与证明【解析】由奇函数在关于原点对称的区间上单调性一致及奇函数定义可选出正确答案．【解答】所以f(x)在区间[−7, −3]上也是增函数，且奇函数f(x)在区间[3, 7]上有最小值为f(3)=5，则f(x)在区间[−7, −3]上有最大值为f(−3)=−f(3)=−5.故选B．二、填空题（共6小题，每小题3分，满分18分）【答案】④【考点】函数单调性的判断与证明【解析】对每个函数去绝对值，根据一次函数及常数函数的单调性即可得到答案．【解答】解：①y=|x|={x x≥0−x x<0，所以该函数在(−∞, 0)上单调递减；②y=|x|x ={1x>0−1x<0，所以该函数在(−∞, 0)上是常数函数，不具有单调性；③y=x2|x|={x x>0−x x<0，所以该函数在(−∞, 0)上单调递减；④y=x+x|x|={x+1x>0x−1x<0，所以该函数在(−∞, 0)上为增函数；∴在(−∞, 0)上为增函数的有④．故答案为：④．【答案】−x(x+1)【考点】奇函数函数解析式的求解及常用方法【解析】根据x>0时函数的表达式，可得x<0时f(−x)=−x(−x−1)，再利用奇函数的定义，即可算出当x<0时函数f(x)的表达式．【解答】解：设x<0，则−x>0，∵当x>0时，f(x)=x(x−1)，∴当x<0时，f(−x)=−x(−x−1)=x(x+1)，又∵f(x)是R上的奇函数，∴f(x)=−f(−x)，∴当x<0时，f(x)=−f(−x)=−x(x+1)，故答案为：−x(x+1)．【答案】12【考点】函数奇偶性的性质与判断【解析】由函数f(x)=x为奇函可得，可得f(−x)＝−f(x)，代入整理可求a由函数f(x)=x(2x+1)(x−a)为奇函可得，f(−x)＝−f(x) ∴−x (−2x+1(−x−a)=−x (2x+1)(x−a)∴ −x(2x +1)(x −a)＝−x(2x −1)(x +a)∴ −x(2x 2−2ax +x −a)＝−x(2x 2+2ax −x −a) 即(2a −1)x 2＝0 ∴ 2a −1＝0即a =12【答案】 [0, +∞) 【考点】函数奇偶性的性质 【解析】利用偶函数的定义f(−x)=f(x)，解出k 的值，化简f(x)的解析式，通过解析式求出f(x)的递减区间． 【解答】解：∵ 函数f(x)=(k −2)x 2+(k −1)x +3是偶函数， ∴ f(−x)=f(x)，即(k −2)x 2−(k −1)x +3=(k −2)x 2+(k −1)x +3， ∴ k =1，∴ f(x)=−x 2+3，f(x)的递减区间是[0, +∞)． 故答案为：[0, +∞)． 【答案】[−12，0]和[12，+∞),14【考点】函数的最值及其几何意义 函数的单调性及单调区间【解析】利用函数是个偶函数，图象关于y 轴对称，化简函数的解析式，结合图象特征写出函数的单调递减区间及最大值． 【解答】解：函数y =−x 2+|x|是个偶函数，图象关于y 轴对称，当x ≥0时，函数y =−x 2+x =−(x −12)2+14，当x <0时，函数y =−x 2−x =−(x +12)2+14，结合图象可得函数y 的单调递减区间为[−12, 0]和[12, +∞)，最大值是14，故答案为[−12, 0]和[12, +∞)，14． 【答案】函数奇偶性的判断【解析】根据函数奇偶性的定义进行判断即可．【解答】解：：①函数的定义域为R，则f(−x)=−(x3+√x3)=−f(x)，则函数f(x)是奇函数；②函数的定义域关于原点不对称，则函数f(x)为非奇非偶函数；③函数的定义域为R，f(0)=0+1=1≠0，则函数f(x)为非奇非偶函数；④函数的定义域为(−∞, 0)∪(0, +∞)，f(−x)=x2+1−x =−x2+1x=−f(x)，则函数f(x)是奇函数，故答案为：①④三、解答题（共3小题，满分0分）【答案】解：若x>0，则−x<0，则f(−x)=−(−x)2−2(−x)−3=−x2+2x−3=−(x2−2x+3)=−f(x)，若x<0，则−x>0，则f(−x)=x2−2(−x)+3=x2+2x+3=−(−x2−2x−3)=−f(x)，∵f(0)=0∴综上f(−x)=−f(x)，即f(x)为奇函数．【考点】函数奇偶性的判断【解析】根据函数奇偶性的定义进行判断即可．【解答】解：若x>0，则−x<0，则f(−x)=−(−x)2−2(−x)−3=−x2+2x−3=−(x2−2x+3)=−f(x)，若x<0，则−x>0，则f(−x)=x2−2(−x)+3=x2+2x+3=−(−x2−2x−3)=−f(x)，∵f(0)=0∴综上f(−x)=−f(x)，即f(x)为奇函数．【答案】证明：由x=y=0得f(0)+f(0)=f(0+01+0)=f(0)，∴f(0)=0，任取x∈(−1, 1)，则−x∈(−1, 1)，f(x)+f(−x)=f(x−x1−x2)=f(0)=0．∴f(x)+f(−x)=0，即f(x)=−f(−x)．∴f(x)在(−1, 1)上为奇函数．【考点】抽象函数及其应用函数奇偶性的判断【解析】利用赋值法，x=y=0求出f(0)的值，结合y=−x，利用已知条件，推出函数是奇函证明：由x=y=0得f(0)+f(0)=f(0+01+0)=f(0)，∴f(0)=0，任取x∈(−1, 1)，则−x∈(−1, 1)，f(x)+f(−x)=f(x−x1−x2)=f(0)=0．∴f(x)+f(−x)=0，即f(x)=−f(−x)．∴f(x)在(−1, 1)上为奇函数．【答案】解：因为函数是偶函数，∴f(1−m)=f(|1−m|)，f(m)=f(|m|)，又f(x)在[0, 2]上单调递减，故函数在[−2, 0]上是增函数∵f(1−m)<f(m)∴{|1−m|>|m|−2≤1−m≤2−2≤m≤2，得−1≤m<12．实数m的取值范围是−1≤m<12．【考点】抽象函数及其应用【解析】由题条件知函数在[0, 2]上是减函数，在[−2, 0]上是增函数，其规律是自变量的绝对值越小，其函数值越大，由此可直接将f(1−m)<f(m)转化成一般不等式，再结合其定义域可以解出m的取值范围．【解答】解：因为函数是偶函数，∴f(1−m)=f(|1−m|)，f(m)=f(|m|)，又f(x)在[0, 2]上单调递减，故函数在[−2, 0]上是增函数∵f(1−m)<f(m)∴{|1−m|>|m|−2≤1−m≤2−2≤m≤2，得−1≤m<12．实数m的取值范围是−1≤m<12．。

高一数学周练二十六1．在等比数列{}n a 中，3620,160a a ==，那么n a = ．2.等比数列中，首项为98，末项为13，公比为23，那么项数n 等于 .3.在等比数列中，n a >0，且21n n n a a a ++=+，那么该数列的公比q 等于 .4.在等比数列{an}中，已知Sn=3n+b ，那么b 的值为_______．5.等比数列{}n a 中，已知12324a a +=，3436a a +=，那么56a a +=6.数列{an}中，a1，a2－a1，a3－a2，…，an －an －1…是首项为一、公比为31的等比数列，那么an 等于 。

7.等比数列,8,4,2,132a a a 的前n 项和Sn= . 8. 已知等比数列{}n a 的首项为8，n S 是其前n 项和，某同窗经计算得224S =，338S =，465S =，后来该同窗发觉其中一个数算错了，那么算错的那个数是__________，该数列的公比是________.9.一个等比数列{}n a 中，701333241=+=+a a a a ，，求那个数列的通项公式。

10.设等比数列{}n a 的前n 项和为Sn,S4=1,S8=17,求通项公式an. 11.已知数列{}2log n x 是公差为1 的等差数列，数列{}n x 的前100项的和等于100，求数列{}n x 的前200项的和。

12.设数列{}n a 的前n 项和为n S ，其中0n a ≠，1a 为常数，且1a -、n S 、1n a +成等差数列．（Ⅰ）求{}n a 的通项公式；（Ⅱ）设1n n b S =-，问：是不是存在1a ，使数列{}n b 为等比数列？假设存在，求出1a 的值；假设不存在，请说明理由． 13.设数列{an}的前项的和Sn=31（an-1） (n ∈N +),（1）求a1;a2;(2)求证数列{an}为等比数列。

答案：1. 20×2n-32. 43.4. b=-15. 46. 23（1－n 31） 7.1,,21(2)1a 122n n n a S a a ⎧=⎪⎪=⎨-⎪≠⎪-⎩， 8. 2S ；32 9. 1125125852n n n n a a 或10. an=1215n -或an=1(1)25n n --⨯11. ()10010012⨯+12. （1）113n n a a -=⋅（n *∈N ）；（2）12a =-13. （1）412=a （2）{}n a 是首项21-,公比为21-的等比数列.。

高一数学周测题号一二三四总分得分一、单选题（本大题共6小题，共30.0分）1.如果a<0，b>0，那么，下列不等式中正确的是()A. 1a <1bB. √−a<√bC. a2<b2D. |a|>|b|2.如果a<0，b>0，则下列不等式中正确的是()A. a2<b2B. ab2<a2bC. √−a<√bD. |a|>|b|3.某生产厂商更新设备，已知在未来x年内，此设备所花费的各种费用总和y(万元)与x满足函数关系，若欲使此设备的年平均花费最低，则此设备的使用年限x为()A. 3B. 4C. 5D. 64.若f(x)=x+1x−2(x>2)在x=n处取得最小值，则n=()A. 52B. 3 C. 72D. 45.下列函数中，最小值为2的函数是()A. y=√x2+2√x2+2B. y=x2+1xC. y=x(2√2−x),(0<x<2√2)D. y=2√x2+16.已知∃x,y∈R+,若y2x +9x2y≤m2+2m恒成立，则实数m的取值范围是()A. {m|−3≤m≤1}B. {m|−1≤m≤3}C. {m|m≤−3,或 m≥1}D. {m|m≤−1,或 m≥3}二、多选题（本大题共3小题，共15.0分）7.下列说法正确的有()A. 不等式2x−13x+1>1的解集是(−2,−13)B. “a<1，b>1”是“ab>1”成立的充分条件C. 命题p：∀x∈R，x2>0，则￢p：∃x∈R，x2<0D. “a<5”是“a<3”的必要条件8.不等式mx2−ax−1>0(m>0)的解集不可能是()A. {x|x<−1或x>14} B. RC. {x|−13<x<32} D. ⌀9.下列说法中正确的有()A. 不等式a+b≥2√ab恒成立B. 存在a，使得不等式a+1a≤2成立C. 若a，b∈(0,+∞)，则ba +ab≥2D. 若正实数x，y满足x+2y=1，则2x +1y≥8三、单空题（本大题共3小题，共15.0分）10.某校要建造一个容积为8m3，深为2m的长方体无盖水池，池底和池壁的造价每平方米分别为240元和160元，那么水池的最低总造价为________元．11.已知A={x|x2+px+1=0}，M={x|x>0}，若A∩M=⌀，则实数p的取值范围为．12.已知关于x的方程mx2−3x+1=0(m∈R)的解集为{a,b}，则1a +1b=．四、解答题（本大题共2小题，共40分）13.已知关于x的一元二次不等式kx2−2x+6k<0(k≠0).(1)若不等式的解集是{x|x<−3或x>−2}，求k的值；(2)若不等式的解集是R，求k的取值范围．14.已知全集U=R，非空集合A={x|x−2x−3<0}，B={x|(x−a)(x−a2−2)<0}.(1)当a=12时，求(∁U B)∩A；(2)命题p:x∈A，命题q:x∈B，若q是p的必要条件，求实数a的取值范围．第3页，共1页。

河南省正阳县第二高级中学201７－20１8学年下期高一数学周练(七)一、选择题:1、角是( )A。

第一象限角 B、第二象限角 C。

第三象限角Ｄ、第四象限角2、若,与的夹角为,则( )A、 B、 C、 D、3。

的值等于( )A、B、 C、D、４、下列函数中最小正周期为且为偶函数的是( )A、B、Ｃ。

D。

５、方程在内( )A、没有根B、有且仅有一个根C、有且仅有两个根D、有无穷多个根6、要得到函数的图像,只需将函数的图像( )A。

向左平移个单位长度B、向右平移个单位长度C、向左平移个单位长度D、向右平移个单位长度7、已知taｎx=,则sin２x=( )A、 B。

C。

- D。

8、已知是所在平面内一点,向量满足条件,且,则是( )A、等腰三角形B、直角三角形 C。

等腰直角三角形 D。

等边三角形9、已知函数的最小正周期为,则该函数的图象( )Ａ。

关于直线对称 B、关于点对称Ｃ、关于直线对称Ｄ、关于点对称１０。

已知曲线,则下面结论正确的是 ( )A。

把上各点的横坐标缩短到原来的倍, 纵坐标不变,再把得到的曲线向左平移个单位长度, 得到曲线B、把上各点的横坐标缩短到原来的倍 ,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C。

把上各点的横坐标伸长到原来的倍 ,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线Ｄ、把上各点的横坐标伸长到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线1１、已知非零向量不共线,且,若,则满足的关系是( )A、 B、 C、D、12、已知向量,,则的取值范围是( )A。

B。

C、 D、１3。

已知函数,若,则、14、设向量满足,,,若,则的值是、15、假如向量与的夹角为,那么我们称为向量与的“向量积”,是一个向量,它的长度,假如,,,则、16、关于函数,有下列命题:①函数的表达式可改写为;②函数是以为最小正周期的周期函数;③函数的图像关于点对称;④函数的图像关于直线对称、其中正确的是、17、已知向量,,,(为常数)、(1)求;(2)若与平行,求实数的值。

高一数学周练七（满分100分）班别 ： 姓名：一、选择题（共50分，每道题5分）1、函数12log (32)y x =-的定义域是 （ ） （A ）[1,+∞] (B) (23,)+∞ (C) [23,1] (D) (23,1]2、下列四个函数中,在(0,+∞)上为增函数的是( )A. f (x )=3-xB. f (x )=x 2-3xC. f (x )=—11+x D. f (x )=-|x | 3、方程x 2-px +6=0的解集为M ,方程x 2+6x -q =0的解集为N ,且M ∩N ={2},那么p +q 等于( )A. 21B. 8C. 6D. 74、已知函数f(x)14x a -=+的图象恒过定点p ，则点p 的坐标是 （ ）（A ）（ 1，5 ） （B ）（ 1, 4） （C ）（ 0，4） （D ）（ 4，0）5、已知函数f (n )=⎩⎨⎧<+≥-),10)](5([),10(3n n f f n n 其中n ∈N ，则f (8)等于（ ）A. 2B. 4C. 6D. 76、某算法的程序框如图所示，若输出结果为12，则输入的实数x 的值是 （ ）A ．32-B ．2C ．52D ．4 7、设a,b,c 都是正数，且346a b c ==，则下列正确的是 （ ） (A)111c a b =+ (B) 221C a b=+ (C) 122C a b =+ (D) 212c a b =+ 8、已知偶函数()f x 在区间[0,)+∞单调递增，则满足)(x f ＜)1(f 的x 取值范围是( )A ．（-1，1）B ．(-1，0）C ．（0，1）D ．[-1，1)9、a y x y =-=与函数|1|2的图象有4个交点，则实数a 的取值范围是（ ）A ．（0，+∞）B ．(-1，1）C ．（0，1）D ．（1，+∞）10、下面四个结论：①偶函数的图象一定与y轴相交；②奇函数的图象一定通过原点；③偶函数的图象关于y轴对称；④既是奇函数又是偶函数的函数一定是()f x ＝0（x∈R），其中正确命题的个数是（）A 4B 3C 2D 1选择题答案：1 2 3 4 5 6 7 8 9 10二、填空题（共20分，每道题5分）11、已知集合}0=x-xA.若A中至多有一个元素，则a的取值范围ax+2{2=3|是12、按照程序框图(如右图)执行，第3个输出的数是.13、执行下图所示的程序，输出的结果为48，则判断框中应填入的条件为．(12题图) （13题图）14、函数f(x)＝a x＋log a(x＋1)在[0,1]上的最大值与最小值之和为a，则a的值为_________.三、解答题(共30分，每道题15分)15、（1）用辗转相除法和更相减损术求三个数 324 , 243 , 135 的最大公约数.（2）把“五进制”数)5(1234转化为“十进制”数，再把它转化为“八进制”数。

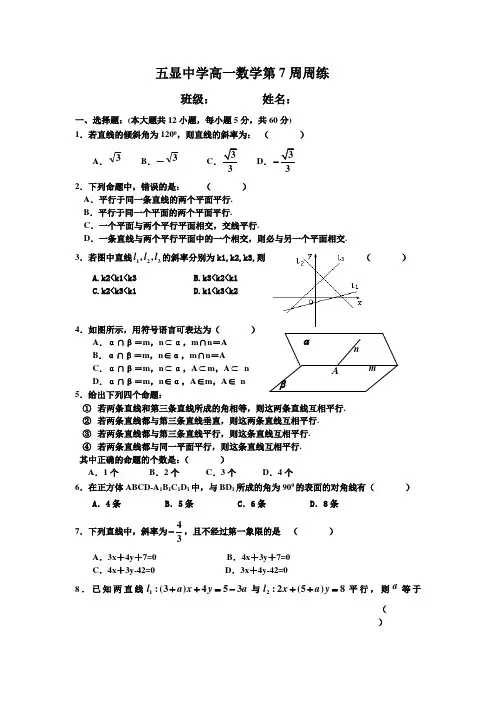
五显中学高一数学第7周周练班级： 姓名：一、选择题：(本大题共12小题，每小题5分，共60分)1．若直线的倾斜角为1200，则直线的斜率为： （ ）A ．3B ．－3 C．3 D．3- 2．下列命题中，错误的是： （ ）A ．平行于同一条直线的两个平面平行.B ．平行于同一个平面的两个平面平行.C ．一个平面与两个平行平面相交，交线平行.D ．一条直线与两个平行平面中的一个相交，则必与另一个平面相交.3．若图中直线123,,l l l 的斜率分别为k1,k2,k3,则 （ ） A.k2<k1<k3 B.k3<k2<k1 C.k2<k3<k1 D.k1<k3<k24．如图所示，用符号语言可表达为（ ） A ．α∩β＝m ，n ⊂α，m ∩n ＝A B ．α∩β＝m ，n ∈α，m ∩n ＝A C ．α∩β＝m ，n ⊂α，A ⊂m ，A ⊂ n D ．α∩β＝m ，n ∈α，A ∈m ，A ∈ n 5．给出下列四个命题：① 若两条直线和第三条直线所成的角相等，则这两条直线互相平行. ② 若两条直线都与第三条直线垂直，则这两条直线互相平行. ③ 若两条直线都与第三条直线平行，则这条直线互相平行.④ 若两条直线都与同一平面平行，则这条直线互相平行. 其中正确的命题的个数是：（ ） A ．1个 B ．2个 C ．3个 D ．4个6．在正方体ABCD-A 1B 1C 1D 1中，与BD 1所成的角为900的表面的对角线有（ ）A ．4条B ．5条C ．6条D ．8条 7．下列直线中，斜率为43-，且不经过第一象限的是 （ ） A ．3x ＋4y ＋7=0 B ．4x ＋3y ＋7=0 C ．4x ＋3y-42=0 D ．3x ＋4y-42=08．已知两直线1:(3)453l a x y a ++=-与2:2(5)8l x a y ++=平行，则a 等于（）A ． --71或B ．71或C ．-7D ．-19．下列命题中正确的是（其中a 、b 、c 为不相重合的直线，α为平面）（ ）①若b ∥a ，c ∥a ，则b ∥c②若b ⊥a ，c ⊥a ，则b ∥c ③若a ∥α，b ∥α，则a ∥b ④若a ⊥α，b ⊥α，则a ∥b A ．①、②、③、④ B ．①，④C ．①D ．④A10．已知三棱锥A BCD -的棱长都相等，,E F分别是棱,AB CD的中点，则EF BC 与所成的角是：（ ） A ．030 B ．45o C ．60oD ．90o11．过点(1,2),且在两坐标轴上的截距相等的直线有（ ） A. 1条 B. 2条 C. 3条 D. 4条12．设γβα,,为两两不重合的平面，n m l ,,为两两不重合的直线，给出下列四个命题： ①若γα⊥，γβ⊥，则//αβ；②若α⊂m ，α⊂n ，//m β，//n β，则//αβ；③若//αβ，α⊂l ，则//l β； ④若l =βα ，m =γβ ，n =αγ ，//l γ，则//m n 。

卜人入州八九几市潮王学校二零二零—二零二壹高一数学第七次周周练试题〔重点班，无答案〕一、选择题1．集合{}{}13,25A x x B x x A B =-≤<=<≤=,则()A.{x|2<x<3}B.{x|-1≤x ≤5}C.{x|-1<x<5}D.{x|-1<x ≤5}2．图中阴影局部表示的集合是()A.A ∩〔C U B 〕B 〔C U A 〕∩U (A ∩B)D.C U (A ∪B)3．集合A =B =R ,x ∈A ,y ∈B ,f :x →y =ax +b ,假设4和10的原象分别对应6和9，那么19在f 作用下的象为() A.18B.30 C.2274．集合{(,)|2},{(,)|4}M x y y x N x y x y ==-=-=，那么集合M N 为〔〕A 、3,1x y ==-B 、(3,1)-C 、{3,1}-D 、{(3,1)}-5．函数y =的值域为〔〕A 、[]0,2B 、[]0,4C 、(],4-∞D 、[)0,+∞6．)(x f 是定义在R 上的奇函数，以下结论中，不正确的选项是．．．．．．．()A 、()()0f x f x -+=B 、()()2()f x f x f x --=-C 、()()0f x f x -≤D 、()1()f x f x =--7．函数()()()2212(3)x x f x x f x ≥⎧+⎪=⎨<+⎪⎩，那么()()13ff -=()A ．－2B ．7C ．27D ．7-8、设集合{1,2}A =,那么满足{1,2,3}A B ⋃=的集合B 的个数是〔〕A ．1B.3 C.49、设集合32{|,},{|1,}S y y x x R T y y x x R ==∈==-∈，那么S T 是〔〕A 、∅B 、SC 、TD 、有限集10、二次函数2()45f x x mx =-+对任意(2)(2),(1)x f x f x f -+=--=满足则〔〕A 、7-B 、1C 、17D 、25二、填空题11、将二次函数22y x =-的顶点移到(3,2)-后，得到的函数的解析式为。

智才艺州攀枝花市创界学校正阳县第二高级二零二零—二零二壹下期高一数学周练〔七〕一.选择题：1.390-角是〔〕A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角 21,2==b a ，a 与b 的夹角为 60，那么=⋅b a 〔〕 A ．2B ．21C ．1D ．41 3. 240tan 600sin +的值等于〔〕A ．23-B ．23C ．321+-D ．321+ π且为偶函数的是〔〕A ．)22cos(π-=x yB ．)22sin(π+=x y C.)2sin(π+=x y D ．)2cos(π-=x y x x cos =在),(+∞-∞内〔〕A ．没有根B ．有且仅有一个根C.有且仅有两个根D ．有无穷多个根)32cos()(π+=x x f 的图像，只需将函数)32sin()(π+=x x g 的图像〔〕 A ．向左平移2π个单位长度B ．向右平移2π个单位长度 C.向左平移4π个单位长度D ．向右平移4π个单位长度 7.tanx=34,那么sin2x=() A.2425B.2425±2425D.4258.O 是ABC ∆所在平面内一点，向量321OP OP OP 、、满足条件0321=++OP OP OP ，且1321===OP OP OP ，那么ABC ∆是〔〕 A ．等腰三角形B ．直角三角形C.等腰直角三角形D ．等边三角形 )0)(4sin()(>+=ωπωx x f 的最小正周期为π，那么该函数的图象〔〕 A ．关于直线8π=x 对称B ．关于点)0,4(π对称4π=x 对称D ．关于点)0,8(π对称10.曲线122:sin ,:sin 23C y x C y x π⎛⎫==+ ⎪⎝⎭，那么下面结论正确的选项是〔〕 A ．把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变，再把得到的曲线向左平移23π个单位长度,得到曲线2CB ．把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移3π个单位长度，得到曲线2C C.把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变，再把得到的曲线向左平移23π个单位长度，得到曲线2C D ．把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变，再把得到的曲线向左平移3π个单位长度，得到曲线2C OB OA ,不一共线，且OB y OA x OP +=2，假设)(R AB PA ∈=λλ，那么y x ,满足的关系是〔〕A ．02=-+y xB ．012=-+y x C.022=-+y x D ．022=-+y x)0,1(=a ，]2,2[),sin ,(cos ππθθθ-∈=b ，那么b a +的取值范围是〔〕 A ．]2,0[B ．]2,0[ C.]2,1[D ．]2,2[x x x f tan 1tan )(+=，假设5)(=αf ，那么=-)(αf量c b a ,,满足0=++c b a ，0)(=⊥-c b a ，b a ⊥，假设1=a ，那么222c b a ++的值是1量a 与b 的夹角为θ，那么我们称b a ⨯为向量a 与b 的“向量积〞，b a ⨯是一个向量，它的长度θin s b a b a =⨯，假设4=a ，3=b ，2-b a =⋅，那么=⨯b a))(32sin(4)(R x x x f ∈+=π，有以下 ①函数)(x f y =的表达式可改写为)62cos(4π-=x y ；②函数)(x f y =是以π2为最小正周期的周期函数；③函数)(x f y =的图像关于点)0,6(π-对称；④函数)(x f y =的图像关于直线6π-=x 〔〕 17.向量)1,2(=a ，)1,1(=b ，)2,5(=c ，c b m +=λ〔λ为常数〕.〔1〕求b a +；〔2〕假设a 与m 平行，务实数λ的值.18.)sin()cos()23sin()2cos()3sin()(απαππααππαα----+---=f .〔1〕化简)(αf ；〔2〕假设α是第三象限的角，且51)23cos(=-πα，求)(αf 的值. 19.在平面直角坐标系中，)4,3(),2,1(---B A ，O 为坐标原点.〔1〕求OB OA ⋅；〔2〕假设点P 在直线AB 上，且AB OP ⊥，求OP 的坐标. 20.函数b a x a x f +++=)62sin(2)(π的定义域是]2,0[π，值域是]1,5[-，求b a ,值. 21.函数)0,0,(2)62sin()(>>∈+++=ωπωa R x b a x a x f 的最小正周期为π，函数)(x f 的最大值是47，最小值是43. 〔1〕求ω、a 、b 的值；〔2〕指出)(x f 的单调递增区间. 22.：a R a a x x f ,(1)62sin(2)(∈+++=π为常数). 〔1〕假设R x ∈，求)(x f 的最小正周期； 〔2〕假设)(x f 在]6,6[ππ-上最大值与最小值之和为3，求a 的值； 〔3〕求在〔2〕条件下)(x f 的单调减区间. 参考答案：1-6.DBBBCC7-12.ADABAD13.-51135①③ 17.(1)(3,2)(2)1λ=18.【答案】〔1〕cos α-〔2〕265- 19.【答案】〔1〕5〔2〕(1,2)OP =-20.【答案】a=2,b=-5或者a=-2,b=1.21.【答案】〔1〕1,1,12a b ω===〔2〕[,]36k k ππππ-+()k Z ∈ 22.【答案】〔1〕π〔2〕a=0〔3〕2[,]63k k ππππ++()k Z ∈。