
第13讲 正态分布
第四章 正态分布
§4.1 正态分布的概率密度与分布函数
在讨论正态分布之前,我们先计算积分()?
∞
+∞
---
dx e
x 2
2
221σ
μσ
π。
首先计算?∞
+∞
--dx e
x
2
2
。因为
πθσπ
20
2
20
2
2
2
2
2
2
22
2
==
=
??
?
??
??
∞
+-
+-
∞+∞
--
∞
+∞
--rdr e
d d e
dy e
dx e
r
R
x x y
x
(利用极坐标计算)
所以π22
2
=
?
∞
+∞
--
dx e
x
。
记
t
x =-σ
μ
,则利用定积分的换元法有
()12212121212
2
22
2
2
2
==
=
=
?
?
?
∞
+∞
--
∞
+∞
--
∞
+∞
---
ππ
π
π
σ
πσ
μdt e
dt e
dx e t
t
x
因为
()0212
2
2≥--
σ
μσ
πx e
,所以它可以作为某个连续随机变量的概率密度函数。
定义 如果连续随机变量X 的概率密度为
()(),,
212
2
2+∞<<∞-=
--
x e x f x σ
μσ
π
则称随机变量X 服从正态分布,记作()2
,~σμN X ,其中()0,>σ
σμ是正态分布的参
数。正态分布也称为高斯(Gauss )分布。
对于1,0==σμ的特殊情况,即如果()1,0~N X ,则称X 服从标准正态分布,它的概率密度记为()x ?,有()2
2
21x
e
x -
=
π
?。
函数()2
2
21x
e
x -
=
π
?的图象的特点:
令()022
2
=-=
'-
x
e
x x π
?,得驻点0=x 。根据()x ?'的正负性可知, 0=x 是()x ?的
极大值点,该点坐标为????
?
?
π21
,
0。 令()()0212
2
2
=-=
''-
x
e
x
x π
?,得1±=x ,根据()x ?''的正负性可知,函数()x ?在()
1,-∞-和()+∞,1内是凹的,在()1,1-内是凸的, ???
?
?
?
--
2
121,
1e
π
和???
?
??-
2
121,1e
π
是拐点。 因为021lim
2
2
=-
∞
→x
x e
π
,所以x 轴是该曲线的渐近线。
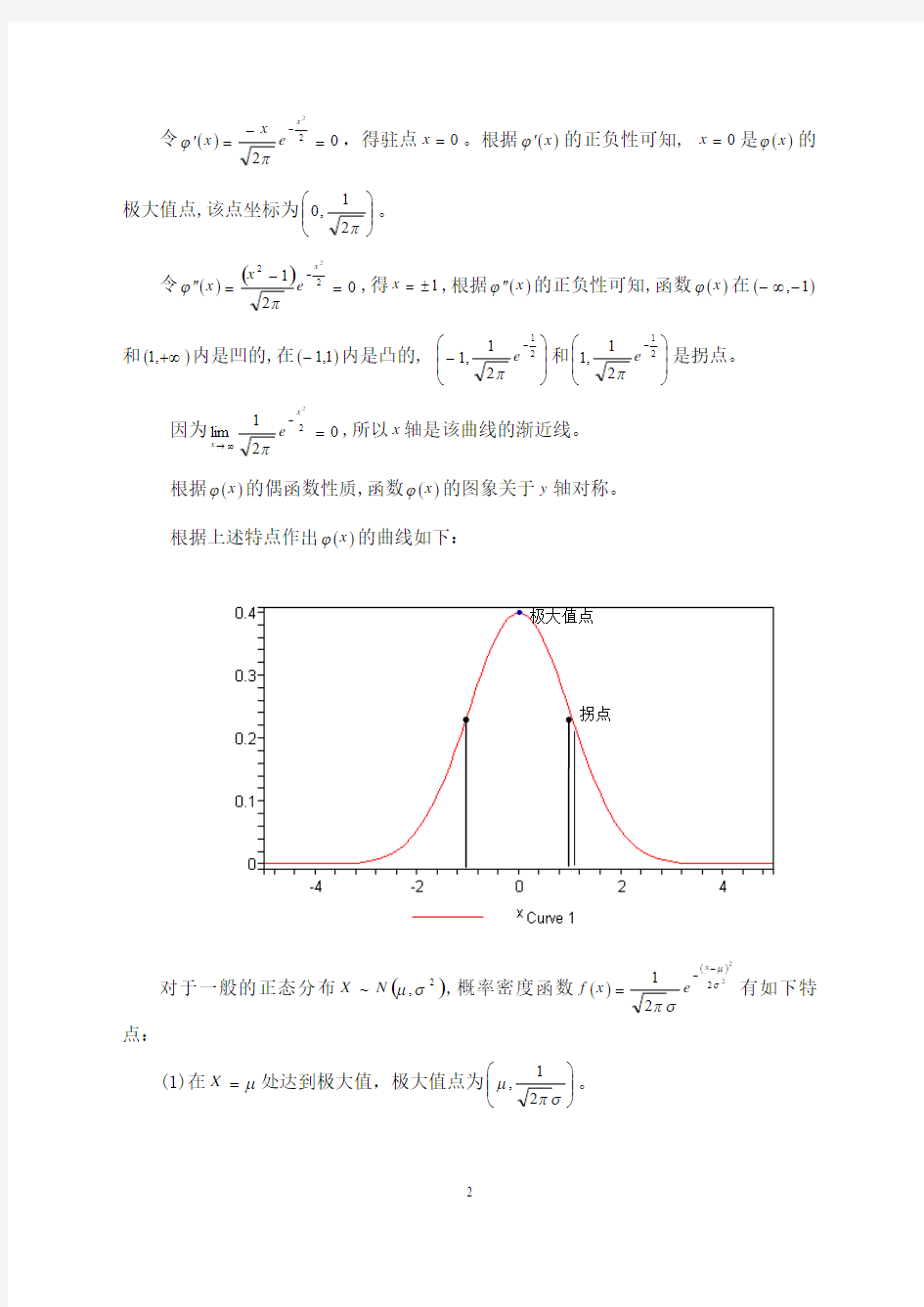
根据()x ?的偶函数性质,函数()x ?的图象关于y 轴对称。 根据上述特点作出()x ?的曲线如下:
对于一般的正态分布()2
,~σμN X ,概率密度函数()()2
2
221σ
μσ
π--
=
x e
x f 有如下特
点:
(1)在μ=X 处达到极大值,极大值点为????
??
σπμ21
,
。
极大值点
(2)在σμ±=X 处为图象的拐点,拐点坐标为???
? ?
?
±-
2
121,
e
σ
πσμ,在()
σμσμ+-,内是凸的,其它范围内是凹的。
(3)x 轴为渐近线。
(4)σ越大,最大值越小,拐点越偏离μ。 (5)图象关于直线μ=x 对称。 对于()2
,~σ
μN X ,它的分布函数为
()()()()?
?
∞
---
∞
---
=
=
≤=x
t x
t dt e
dt e x X P x F 2
2
2
2
222121σ
μσ
μσ
πσ
π
对于()1,0~N X ,记它的分布函数为()?
∞
--=
Φx
t dt e
x 2
2
21π
。
根据()()x x ?=Φ'以及()()x x ?'=Φ''的正负性质,得()x Φ在整个实数范围内单调递增。在0>x 范围内图象是凸的,在0 ()()1lim ,0lim =Φ=Φ+∞ →-∞ →x x x x ,得两条渐近线1=y 和x 轴。根据()x ?的对称性,得()2 10= Φ。 根据上述讨论作出()x Φ的图象如下: 根据()x ?的性质还可以得到()()x x Φ-=-Φ1。 ()x Φ的直接计算是比较困难的,但可以通过查表得到()x Φ在0>x 时的数值。对 于0 一般的正态分布()2 ,~σ μN X 的分布函数()x F 与()x Φ的关系如下: ()()().2121212 222 2 22 2 σ μ σ μ σ σ μσ μ π σ πμ σ π-∞ -- -∞ -- ∞ --- Φ == -== ? ? ? -x v u x u x t x dv e v du e t u dt e x F 记记 有了()x F 与()x Φ的关系,就可以求出任何正态随机变量X 落在某个区间内的概率。 对于()2 ,~σ μN X ,某两个数2 1 ,x x 满足21x x <,则有 ()()()()()121221x F x F X x P x X P x X x P -=≤-≤=≤< 又因为X 是连续随机变量,因此有 ()()()()()12212121x F x F x X x P x X x P x X x P -=<<=<≤=≤≤ 例1 已知()4,5.1~N X ,求()4- ()()()0030 .09970.0175.2175.225.144=-=Φ-=-Φ=?? ? ??--Φ=- ()()()()() ()()()()4414 .05981.09599.0225.075.1225.0175.125.12125.12212222=--=Φ-Φ-=Φ-+-Φ=??? ??-Φ-+??? ??--Φ=<-+-<=>+-<=>X P X P X P X P X P 例2 已知()2 ,~σμN X ,求()σμk X P -<-,()3,2,1=k 。 解 ()()()()()()()()?? ? ??==-Φ==-Φ==-Φ=-Φ=-Φ-Φ=??? ??--Φ-??? ??-+Φ== +<<-=<-. 3,9974.0132;2,9544.0122;1, 6826.011212k k k k k k k k k X k P k X P σμσμσμσμσμσμσμ 例3 已知()1,0~N X ,求随机变量2X Y =的概率密度函数。 解 因为()1,0~N X ,所以X 的密度函数()()()+∞∞-∈= =-,,212 2 x e x x f x X π ?,则Y 的分布函数()()()y X P y Y P y F Y ≤=≤=2。 显然当0≤Y 时,()0=y F Y ,此时()()0='=y F y f Y Y 。 对于0>Y 的情况有 ()()( ) ? ? - - - = = ≤- =≤=y x y y x Y dx e dx e y X y P y X P y F 0 2 2 2 2 2 2221π π 此时 ()()2 2 12 2 212 122 222 y y y x Y Y e y y e dx e dy d y F y f - - - - = ? =??? ? ? ?= '=? π π π 故随机变量Y 的概率密度函数为 ()?? ? ? ?≤>=- -0 , 00,212 2 1y y e y y f y Y π 注 称上述随机变量Y 服从自由度为1的2χ分布。 §4.2 正态分布的数字特征 我们首先讨论一般正态分布()2 ,σμN 与标准正态分布()1,0N 数字特征间的关系。 由一般正态分布()2 ,~σ μN X 的分布函数()x F 与标准正态分布的分布函数()x Φ的 关系可知,如果随机变量()2 ,~σμN X ,则()1,0~N X Y σ μ -= 。由期望与方差的线性性 质知()()()()()().,2Y D Y D X D Y E Y E X E σμσμσμσ=+=+=+=,因此,要研究正态分布的数字特征,只需研究标准正态分布的数字特征就可以了。 1. 正态分布的数学期望 对于()1,0~N Y ,().02121212 2 2 2 2 2 2 2 =- == ? =+∞ ∞ -- ∞ +∞ -- ∞ +∞ -- ? ? x x x x e d e dx e x Y E π π π 对于()2 ,~σ μN X ,()().μμ σ=+=Y E X E 2. 正态分布的方差 对于()1,0~N Y ,()()()[]2 2Y E Y E Y D -=,已知()0=Y E , (). 1221 021********* 2 2 2 2 2 2 2 2 2 2 2 2 2 =?+=+ - =??? ? ? ?-?= ?= ? =? ? ? ? ∞+∞ -- ∞ +∞ --∞ +∞ -- ∞ +∞ -- ∞ +∞ -- π π π ππ π πdx e xe e d x d e x dx e x Y E x x x x x x 所以()()()[]122=-=Y E Y E Y D 。 对于()2 ,~σ μN X ,()()2 2 σ σ ==Y D X D 。 综合上面的讨论知,正态分布()2 ,σμN 的期望值是μ,方差是2 σ 。 §4.3 正态分布的线性性质 1. 单个正态随机变量线性函数的分布 已知()2 ,~σμN X ,()0,≠∈b R b a ,记随机变量bX a Y +=,下面讨论Y 的性质。 因为 ( )2 ,~σ μN X b a Y =-, ()1,0~N X σ μ -,故有 ()1,0~N b b a Y b a Y σ μ σ μ --= -- 由此可见()2 2,~σ μb b a N Y +,既单个正态随机变量的线性函数仍然服从正态分布。 2. 两个正态随机变量和的分布 已知两个独立的随机变量Y X ,满足()2 11,~σμN X ,()2 2 2,~σμN Y ,则Y X Z +=仍然服从正态分布。由数字特征的线性性质可得 ()()()()()()22 2 121,σ σμμ+=+=+=+=Y D X D Z D Y E X E Z E 因此有()2 22 121,~σσμμ+++=N Y X Z 。 对于上述结论不予证明,其有更广泛的结论。 定理 设随机变量n X X X ,,,21 相互独立,都服从正态分布 ( ) n i N X i i i ,,2,1 ,,~2 =σμ 则它们的线性组合∑=n i i i X c 1 也服从正态分布,且有 ?? ? ??∑∑∑ ===n i i i n i i i n i i i c c N X c 122 1 1 ,~σ μ 其中n c c c ,,,21 为常数。 1 第一章 多元正态分布的参数估计 一、填空题 1.设X 、Y 为两个随机向量,对一切的u 、v ,有 ,则称X 与Y 相互独立。 2.多元分析处理的数据一般都属于 数据。 3.多元正态向量()' =p X X X ,,1 的协方差阵∑是 ,则X 的各分量是相互独立的随机变量。 4.一个p 元函数() p x x x f ,,,21 能作为p R 中某个随机向量的密度函数的主要条件是 和 。 5.若p 个随机变量1X ,2X , ,p X 的联合分布等于 ,则称1X , 2X , ,p X 是相互独立的。 6.多元正态分布的任何边缘分布为 。 7.若()∑,~μp N X ,A 为p s ?阶常数阵,d 为s 维常数向量,则~d AX + 。 8.多元正态向量X 的任何一个分量子集的分布称为X 的 。 9.多元样本中,不同样品的观测值之间一定是 。 10.多元正态总体均值向量和协差阵的极大似然估计量分别是 。 11.多元正态总体均值向量μ和协差阵∑的估计量X 、 S n 1 1-具有 、 和 。 12.设X 和S 分别是多元正态总体()∑,μp N 的样本均值向量和离差阵,则 ~X ,X 和S 。 13.若()()∑,~μαp N X ,n ,,2,1 =α且相互独立,则样本离差阵 ()()()()∑='--=n X X X X S 1~ααα 。 14.若()∑,~i p i n W S ,k i ,,1 =,且相互独立,则~21k S S S S +++= 。 二、判断题 1.多元分布函数()x F 是单调不减函数,而且是右连续的。 2.设X 是p 维随机向量,则X 服从多元正态分布的充要条件是:它的任何组合()p R X ∈'αα都是一元正态分布。 3.μ是一个P 维的均值向量,当A 、B 为常数矩阵时,具有如下性质: (1)E (AX )=AE (X ) (2)E (AXB )=AE (X )B 4.若P 个随机变量X 1,…X P 的联合分布等于各自边缘分布的乘积,则称X 1,… X P 是相互独立的。 5.一般情况下,对任何随机向量()'=X X X p ,,1 ,协差阵∑是对称阵,也 是正定阵。 6.多元正态向量()'=X X X p ,,1 的任意线性变换仍然服从多元正态分布。 7.多元正态分布的任何边缘分布为正态分布,反之一样。 8.多元样本中,不同样品之间的观测值一定是相互独立的。 9.多元正态总体参数均值μ的估计量X 具有无偏性、有效性和一致性。 10. S n 1是∑的无偏估计。 第二章多元正态分布及参数的估计 在多元统计分析中,多元正态分布占有相当重要的地位.这是因为许多实际问题涉及到的随机向量服从正态分布或近似服从正态分布;当样本量很大时,许多统计量的极限分布往往和正态分布有关;此外,对多元正态分布,理论与实践都比较成熟,已有一整套行之有效的统计推断方法.基于这些理由,我们在介绍多元统计分析的种种具体方法之前,首先介绍多元正态分布的定义、性质及多元正态分布中参 数的估计问题. 目录 §2.1 随机向量 §2.2 多元正态分布的定义与基本性质 §2.3 条件分布和独立性 §2.4 多元正态分布的参数估计 §2.1 随机向量 本课程所讨论的是多变量总体.把p个随机变量放在一起得X=(X1,X2,…,Xp)′为一个p维随机向量,如果同时对p维总体进行一次观测,得一个样品为p维数据.常把n个样品排成一个n×p矩阵,称为样本资料阵. ?? ? ? ?? ??'''= ?????? ??=)()2()1(2 1 2222111211n np n n p p X X X x x x x x x x x x X def =(X 1,X 2,…,X p ) 其中 X(i)( i =1,…,n)是来自p 维总体的一个样品. 在多元统计分析中涉及到的都是随机向量,或是多个随机向量放在一起组成的随机矩阵. 本节有关随机向量的一些概念(联合分布,边缘分布,条件分布,独立性;X 的均值向量,X 的协差阵和相关阵,X 与Y 的协差阵)要求大家自已复习. 三﹑ 均值向量和协方差阵的性质 (1) 设X ,Y 为随机向量,A ,B 为常数阵,则 E(AX )=A·E(X ), E(AXB )=A·E(X )·B D(AX)=A·D(X)·A' COV(AX,BY)=A·COV(X,Y)·B' (2) 若X,Y 相互独立,则COV(X,Y)=O;反之不成立. 若COV(X,Y)=O,我们称X 与Y 不相关.故有: 两随机向量若相互独立,则必不相关; 练习一 多元正态分布的参数估计 1.试叙述多元联合分布和边际分布之间的关系。 2.设二维随机向量12()X X '服从二元正态分布,写出其联合分布。 3.已知随机向量1 2()X X '的联合密度函数为 12121222 2[()()()()2()()] (,)()()d c x a b a x c x a x c f x x b a d c --+-----= -- 其中1a x b ≤≤,2c x d ≤≤。求 (1)随机变量1X 和2X 的边缘密度函数、均值和方差; (2)随机变量1X 和2X 的协方差和相关系数; (3)判断1X 和2X 是否相互独立。 4.设12(,,)p X X X X '= 服从正态分布,已知其协方差矩阵∑为对角阵,证明其分量是相互独立的随机变量。 5. 影响粮食产量的因素很多, 大致可分为三个层次:第一层次是宏观因素。主要有三种,一是制度创新, 如20世纪50年代初的土地改革、60年代初的“ 三自一包”和 80年代初的联产承包责任制和现行的粮食直补及税费改革等。二是政策导向, 如收购政策及价格、市场政策结构调整、储备政策、财政投人、政府抓粮食生产的力度等。三是科技进步,如良种的培育、播种技术的改进、机械化程度的提高等等, 特别是杂交水稻的发明, 是粮食生产的一次绿色革命, 大大地提高了粮食单位面积产量。第二层次是中观因素。主要有粮食播种面积、单位面积产量、受灾面积等等, 这些因素是影响粮食产量的直接因素。第三层次是微观因素, 主要有有效灌溉面积、化肥施用量、农业机械化程度、财政三项投入等。为了分析粮食产量的影响因素及其影响程度,将用1978一2007年的统计数据进行分析。其中:Y 是粮食产量(万吨),X1是农业化肥试用量(万吨),X2是粮食播种面积(千公顷),X3是成灾面积(千公顷),X4是农业劳动力(万人),X5是农业机械总动力(万千瓦)。 多元与一元正态分布及其应用 姓名:郭善禄班级:11-保险精算学号:10080104 摘要:正态分布又名高斯分布,是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。它概率论中最重要的一种分布,也是自然界最常见的一种分布。该分布由两个参数——平均值和方差决定。它是一种最常见的连续性随机变量的概率分布,其概率密度函数曲线以均值为对称中线,方差越小,分布越集中在均值附近。其曲线呈钟形,因此人们又经常称之为钟形曲线。无论从理论和实际应用的观点来看,正态分布毫无疑问是概率论和数理统计中的重要分布。它的重要性质是由于实际中遇到的随机变量有许多服从正态分布或近似服从正态分布的。本文简单的论述了一元正态分布,标准正态曲线,二元正态分布的定义, 关键字:一元正态分布标准正态曲线二元正态分布 一.一元正态分布 正态分布应用最广泛的连续概率分布,其特征是“钟”形曲线。 这种分布的概率密度函数为: ⒈正态分布:若已知的密度函数(频率曲线)为正态函数(曲线)则称已知曲线服从正态分布,记号~。其中μ、σ^2 是两个不确定常数,是正态分布的参数,不同的μ、不同的σ^2对应不同的正态分布。 2.正态分布的特征:服从正态分布的变量的频数分布由μ、σ完全决定。 集中性:正态曲线的高峰位于正中央,即均数所在的位置。对称性:正态曲线以均数为中心,左右对称,曲线两端永远不与横轴相交。 均匀变动性:正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降。 正态分布有两个参数,即均数μ和标准差σ,可记作N(μ,σ):均数μ决定正态曲线的中心位置;标准差σ决定正态曲线的陡峭或扁平程度。σ越小,曲线越陡峭;σ越大,曲线越扁平。 u变换:为了便于描述和应用,常将正态变量作数据转换。μ是正态分布的位置参数,描述正态分布的集中趋势位置。正态分布以X=μ为对称轴,左右完全对称。正态分布的均数、中位数、众数相同,均等于μ。 σ描述正态分布资料数据分布的离散程度,σ越大,数据分布越分散,σ越小,数据分布越集中。也称为是正态分布的形状参数,σ越大,曲线越扁平,反之,σ越小,曲线越瘦高。 二.标准正态曲线 第一章 多元正态分布的参数估计 一、填空题 1.设X 、Y 为两个随机向量,对一切的u 、v ,有 ,则称X 与Y 相互独立。 2.多元分析处理的数据一般都属于 数据。 3.多元正态向量),,(1'=p x x X 的协方差阵∑是 ,则X 的各分量是相互独立的随机变量。 4.一个p 元函数()p x x x f ,,,21 能作为p R 中某个随机向量的密度函数的主要条件是 和 。 5.若p 个随机变量1X ,2X , ,p X 的联合分布等于 ,则称1X ,2X , ,p X 是相互独立的。 6.多元正态分布的任何边缘分布为 。 7.若()∑,~μp N X ,A 为p s ?阶常数阵,d 为s 维常数向量,则~d AX + 。 8.多元正态向量X 的任何一个分量子集的分布称为X 的 。 9.多元样本中,不同样品的观测值之间一定是 。 10.多元正态总体均值向量和协差阵的极大似然估计量分别是 。 11.多元正态总体均值向量μ和协差阵∑的估计量X 、S n 1 1-具有 、 和 。 12.设X 和S 分别是多元正态总体()∑,μp N 的样本均值向量和离差阵,则 ~X ,X 和S 。 13.若()()∑,~μαp N X ,n ,,2,1 =α且相互独立,则样本离差阵 ()()()()∑='--=n X X X X S 1~ααα 。 14.若()∑,~i p i n W S ,k i ,,1 =,且相互独立,则~21k S S S S +++= 。 二、判断题 1.多元分布函数()x F 是单调不减函数,而且是右连续的。( ) 2.设X 是p 维随机向量,则X 服从多元正态分布的充要条件是:它的任何组合()p R X ∈'αα都是一元正态分布。 ( ) 3.μ 是一个P 维的均值向量,当A 、B 为常数矩阵时,具有如下性质: (1)E (AX )=AE (X ) (2)E (AXB )=AE (X )B ( ) 4.若P 个随机变量X 1,…X P 的联合分布等于各自边缘分布的乘积,则称X 1,… X P 是相互独立的。( ) 5.一般情况下,对任何随机向量()'=p X X X ,,1 ,协差阵∑是对称阵,也 是正定阵。 ( ) 6.多元正态向量()'=p X X X ,,1 的任意线性变换仍然服从多元正态分布。( ) 7.多元正态分布的任何边缘分布为正态分布,反之一样。( ) 8.多元样本中,不同样品之间的观测值一定是相互独立的。( ) 9.多元正态总体参数均值μ的估计量X 具有无偏性、有效性和一致性。( ) 10.S n 1是∑的无偏估计。( ) 11.Wishart 分布是2χ分布在p 维正态情况下的推广。( ) 12.若()()∑,~μαp N X ,n ,,1 =α,且相互独立,则样本离差阵 ()()()()()∑-'--=∑=,1~1n W X X X X S n p ααα。 ( ) 13.若()∑,~n W X p ,C 为奇异矩阵,则()c c n W C CX p '∑',~。( ) 三、简答题 1.多元正态分布有哪些基本性质? 2.均值向量和协差阵的最大似然估计量有哪些优良性质? 3.维希特分布有哪些基本性质? 四、证明题 1.样本均值向量和离差阵也可以用样本资料X 直接表示如下: n X n X 11'=,X n I X S n n n ?? ? ??'-'=111 其中:()'=1,,1,11 n ,???? ??????=1001 I 试分别给以证明。 五、计算题第1章 多元正态分布的参数估计
第二章 多元正态分布及参数的估计汇总
练习一多元正态分布的参数估计(精)
多元与一元正态分布及其应用
第1章 多元正态分布的参数估计