
平行四边形单元 期末复习自检题检测试卷
一、解答题
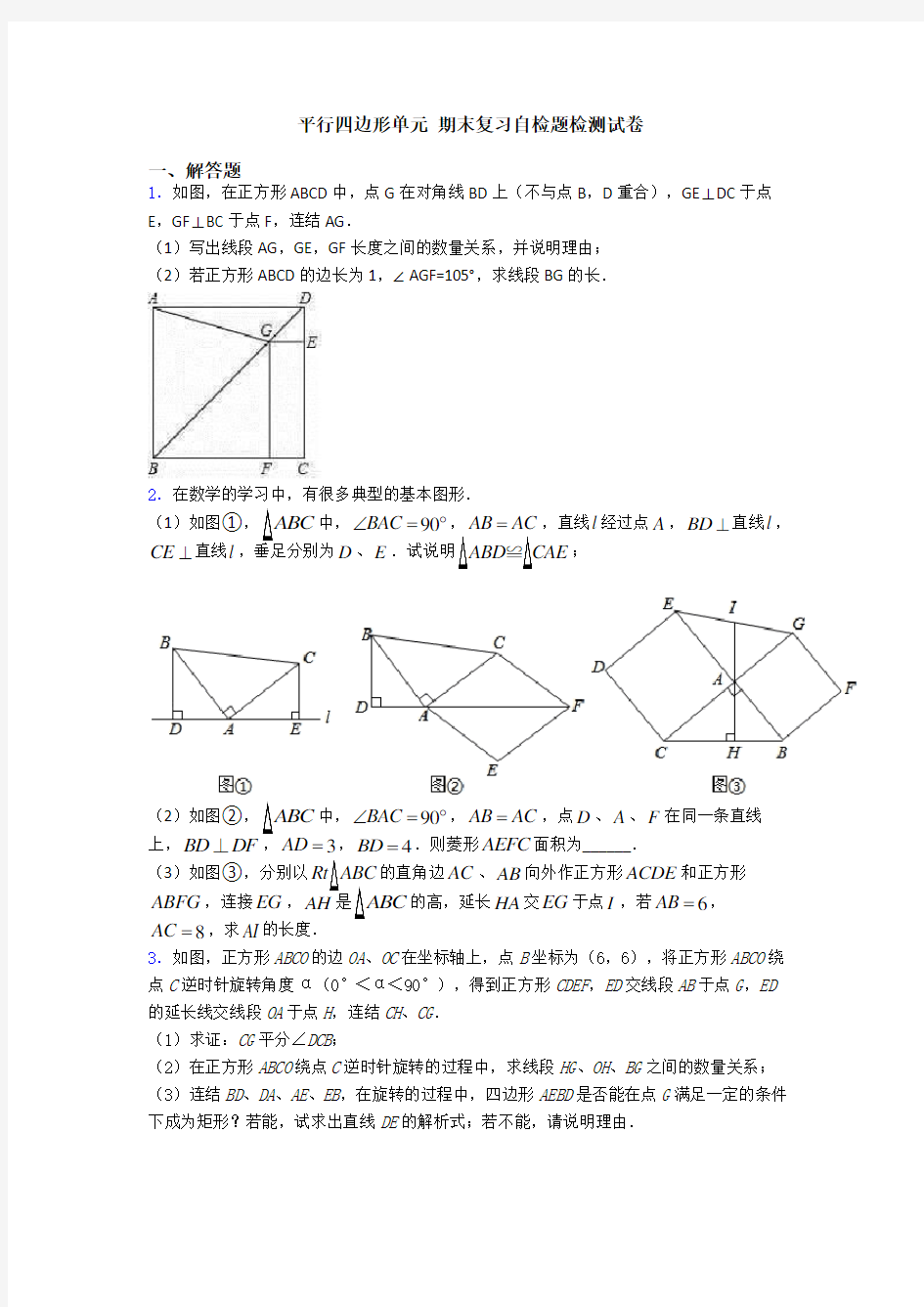
1.如图,在正方形ABCD 中,点G 在对角线BD 上(不与点B ,D 重合),GE ⊥DC 于点E ,GF ⊥BC 于点F ,连结AG .
(1)写出线段AG ,GE ,GF 长度之间的数量关系,并说明理由; (2)若正方形ABCD 的边长为1,∠AGF=105°,求线段BG 的长.
2.在数学的学习中,有很多典型的基本图形.
(1)如图①,ABC 中,90BAC ∠=?,AB AC =,直线l 经过点A ,BD ⊥直线l ,
CE ⊥直线l ,垂足分别为D 、E .试说明ABD CAE ≌;
(2)如图②,ABC 中,90BAC ∠=?,AB AC =,点D 、A 、F 在同一条直线上,BD DF ⊥,3AD =,4BD =.则菱形AEFC 面积为______.
(3)如图③,分别以Rt ABC 的直角边AC 、AB 向外作正方形ACDE 和正方形
ABFG ,连接EG ,AH 是ABC 的高,延长HA 交EG 于点I ,若6AB =,8AC =,求AI 的长度.
3.如图,正方形ABCO 的边OA 、OC 在坐标轴上,点B 坐标为(6,6),将正方形ABCO 绕点C 逆时针旋转角度α(0°<α<90°),得到正方形CDEF ,ED 交线段AB 于点G ,ED 的延长线交线段OA 于点H ,连结CH 、CG . (1)求证:CG 平分∠DCB ;
(2)在正方形ABCO 绕点C 逆时针旋转的过程中,求线段HG 、OH 、BG 之间的数量关系; (3)连结BD 、DA 、AE 、EB ,在旋转的过程中,四边形AEBD 是否能在点G 满足一定的条件下成为矩形?若能,试求出直线DE 的解析式;若不能,请说明理由.
4.如图1,在正方形ABCD 和正方形BEFG 中,点,,A B E 在同一条直线上,P 是线段
DF 的中点,连接,PG PC .
(1)求证:,PG PC PG PC ⊥=.
简析:由Р是线段DF 的中点,//DC CF ,不妨延长GP 交DC 于点M ,从而构造出一对全等的三角形,即_______?________.由全等三角形的性质,易证CMG 是_______三角形,进而得出结论;
(2)如图2,将原问题中的正方形ABCD 和正方形BEFG 换成菱形ABCD 和菱形BEFG ,且60ABC BEF ∠=∠=?,探究PG 与PC 的位置关系及
PG
PC
的值,写出你的猜想并加以证明;
(3)当6,2AB BE ==时,菱形ABCD 和菱形BEFG 的顶点都按逆时针排列,且
60ABC BEF ∠=∠=?.若点A B E 、、在一条直线上,如图2,则CP =________;若点
A B G 、、在一条直线上,如图3,则CP =________.
5.在矩形ABCD 中,连结AC ,点E 从点B 出发,以每秒1个单位的速度沿着B A →的路径运动,运动时间为t (秒).以BE 为边在矩形ABCD 的内部作正方形BEHG .
(1)如图,当ABCD 为正方形且点H 在ABC ?的内部,连结,AH CH ,求证:
AH CH =;
(2)经过点E 且把矩形ABCD 面积平分的直线有______条;
(3)当9,12AB BC ==时,若直线AH 将矩形ABCD 的面积分成1:3两部分,求t 的值.
6.如图,在矩形ABCD 中,E 是AD 的中点,将ABE ?沿BE 折叠,点A 的对应点为点
G .
图1 图2
(1)填空:如图1,当点G 恰好在BC 边上时,四边形ABGE 的形状是________; (2)如图2,当点G 在矩形ABCD 内部时,延长BG 交DC 边于点F . ①求证:BF AB DF =+. ②若3AD =
,试探索线段DF 与FC 的数量关系.
7.如图,在正方形ABCD 中,点M 是BC 边上任意一点,请你仅用无刻度的直尺,用连线的方法,分别在图(1)、图(2)中按要求作图(保留作图痕迹,不写作法).
(1)在如图(1)的AB 边上求作一点N ,连接CN ,使CN AM =; (2)在如图(2)的AD 边上求作一点Q ,连接CQ ,使CQ
AM .
8.如图,锐角ABC ?,AB AC =,点D 是边BC 上的一点,以AD 为边作ADE ?,使
AE AD =,EAD BAC ∠=∠.
(1)过点E 作//EF DC 交AB 于点F ,连接CF (如图①)
①请直接写出EAB ∠与DAC ∠的数量关系; ②试判断四边形CDEF 的形状,并证明;
(2)若60BAC ∠=,过点C 作//CF DE 交AB 于点F ,连接EF (如图②),那么(1)②中的结论是否任然成立?若成立,请给出证明,若不成立,请说明理由.
9.如图,在四边形OABC 是边长为4的正方形点P 为OA 边上任意一点(与点O A 、不重合),连接CP ,过点P 作PM CP ⊥,且PM CP =,过点M 作MN AO ∥,交BO 于点,N 联结BM CN 、,设OP x =.
(1)当1x =时,点M 的坐标为( , )
(2)设CNMB S y =四形边,求出y 与x 的函数关系式,写出函数的自变量的取值范围. (3)在x 轴正半轴上存在点Q ,使得QMN 是等腰三角形,请直接写出不少于4个符合条件的点Q 的坐标(用x 的式子表示)
10.如图①,在等腰Rt ABC 中,90BAC ∠=,点E 在AC 上(且不与点A 、C 重合
),在ABC 的外部作等腰Rt CED ,使90CED ∠=,连接AD ,分别以AB ,AD 为邻
边作平行四边形ABFD ,连接AF .
()1请直接写出线段AF ,AE 的数量关系;
()2①将CED 绕点C 逆时针旋转,当点E 在线段BC 上时,如图②,连接AE ,请判断
线段AF ,AE 的数量关系,并证明你的结论;
②若25AB =,2CE =,在图②的基础上将CED 绕点C 继续逆时针旋转一周的过
程中,当平行四边形ABFD 为菱形时,直接写出线段AE 的长度.
【参考答案】***试卷处理标记,请不要删除
一、解答题
1.(1)AG2=GE2+GF2,理由见解析;(2
【分析】
(1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在
Rt△GFC中,利用勾股定理即可证明;
(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.易证AM=BM=2x,
,在Rt△ABN中,根据AB2=AN2+BN2,可得1=x2+(x)2,解得
,推出BG=BN÷cos30°即可解决问题.
【详解】
解:(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2.
(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.
∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,
∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,
∴∠AMN=30°,
∴AM=BM=2x,
x,
在Rt△ABN中,∵AB2=AN2+BN2,
∴1=x
2+(x)2,
解得
∴
∴BG=BN÷cos30°=
.
6
【点睛】
本题考查正方形的性质,矩形的判定和性质,勾股定理,直角三角形30度的性质. 2.(1)见解析;(2)24;(3)5AI =. 【分析】
(1)证∠BDA =∠CEA =90°,∠CAE =∠ABD ,由AAS 证明△ABD ≌△CAE 即可; (2)连接CE ,交AF 于O ,由菱形的性质得∠COA =∠ADB =90°,同(1)得
△ABD ≌△CAO (AAS ),得OC =AD =3,OA =BD =4,由三角形面积公式求出S △AOC =6,即可得出答案;
(3)过E 作EM ⊥HI 的延长线于M ,过点G 作GN ⊥HI 于N ,同(1)得△ACH ≌△EAM (AAS ),△ABH ≌△GAN (AAS ),得EM =AH =GN ,证△EMI ≌△GNI (AAS ),得EI =GI ,证∠EAG =90°,由勾股定理求出EG =10,再由直角三角形的性质即可得出答案. 【详解】
(1)证明:∵BD ⊥直线l ,CE ⊥直线l , ∴∠BDA =∠CEA =90°, ∵∠BAC =90°, ∴∠BAD +∠CAE =90° ∵∠BAD +∠ABD =90°, ∴∠CAE =∠ABD 在△ABD 和△CAE 中,
ABD CAE BDA CEA AB AC ∠=∠??
∠=∠??=?
, ∴△ABD ≌△CAE (AAS );
(2)解:连接CE ,交AF 于O ,如图②所示: ∵四边形AEFC 是菱形, ∴CE ⊥AF ,
∴∠COA =∠ADB =90°,
同(1)得:△ABD ≌△CAO (AAS ), ∴OC =AD =3,OA =BD =4, ∴S △AOC =
12OA ?OC =1
2
×4×3=6, ∴S 菱形AEFC =4S △AOC =4×6=24,
故答案为:24;
(3)解:过E 作EM ⊥HI 的延长线于M ,过点G 作GN ⊥HI 于N ,如图③所示: ∴∠EMI =∠GNI =90°,
∵四边形ACDE 和四边形ABFG 都是正方形, ∴∠CAE =∠BAG =90°,AC =AE =8,AB =AG =6,
同(1)得:△ACH ≌△EAM (AAS ),△ABH ≌△GAN (AAS ), ∴EM =AH =GN , 在△EMI 和△GNI 中,
EIM GIH EMI GNI EM GN ∠=∠??
∠=∠??=?
, ∴△EMI ≌△GNI (AAS ), ∴EI =GI , ∴I 是EG 的中点,
∵∠CAE =∠BAG =∠BAC =90°, ∴∠EAG =90°,
在Rt △EAG 中, EG =22AE
AG +
=2286+=10, ∵I 是EG 的中点, ∴AI =
12EG =1
2
×10=5.
【点睛】
本题是四边形综合题目,考查了正方形的性质、菱形的性质、等腰直角三角形的性质、全等三角形的判定与性质、直角三角形斜边上的中线性质、勾股定理、三角形面积等知识;本题综合性强,熟练掌握正方形的性质和菱形的性质,证明三角形全等是解题的关键.
3.(1)见解析;(2)HG=OH+BG;(3)能成矩形,y
33 42
x
=-.
【分析】
(1)根据旋转和正方形的性质可得出CD=CB,∠CDG=∠CBG=90,根据全等直角三角形的判定定理(HL)即可证出Rt△CDG≌Rt△CBG,即∠DCG=∠BCG,由此即可得出CG平分∠DCB;
(2)由(1)的Rt△CDG≌Rt△CBG可得出BG=DG,根据全等直角三角形的判定定理(HL)即可证出Rt△CHO≌Rt△CHD,即OH=HD,再根据线段间的关系即可得出
HG=HD+DG=OH+BG;
(3)根据(2)的结论即可找出当G点为AB中点时,四边形AEBD为矩形,再根据正方形的性质以及点B的坐标可得出点G的坐标,设H点的坐标为(x,0),由此可得出
HO=x,根据勾股定理即可求出x的值,即可得出点H的坐标,结合点H、G的坐标利用待定系数法即可求出直线DE的解析式.
【详解】
(1)∵正方形ABCO绕点C旋转得到正方形CDEF,∴CD=CB,∠CDG=∠CBG=90°.在Rt△CDG和Rt△CBG中,
∵
CG CG
CD CB
=
?
?
=
?
,∴Rt△CDG≌Rt△CBG(HL),∴∠DCG=∠BCG,即CG平分∠DCB.
(2)由(1)证得:Rt△CDG≌Rt△CBG,∴BG=DG.在Rt△CHO和Rt△CHD中,
∵
CH CH
CO CD
=
?
?
=
?
,∴Rt△CHO≌Rt△CHD(HL),∴OH=HD,∴HG=HD+DG=OH+BG.
(3)假设四边形AEBD可为矩形.
当G点为AB中点时,四边形AEBD为矩形,如图所示.
∵G点为AB中点,∴BG=GA1
2
=AB,由(2)证得:BG=DG,则
BG=GA=DG
1
2
=AB
1
2
=DE=GE,又AB=DE,∴四边形AEBD为矩
形,∴AG=EG=BG=DG.
∵AG1
2
=AB=3,∴G点的坐标为(6,3).
设H点的坐标为(x,0),则HO=x,∴HD=x,DG=3.
在Rt△HGA中,HG=x+3,GA=3,HA=6﹣x,由勾股定理得:(x+3)2=32+(6﹣x)2,解得:x=2,∴H点的坐标为(2,0).
设直线DE的解析式为:y=kx+b(k≠0),将点H(2,0)、G(6,3)代入y=kx+b中,
得:
20
63
k b
k b
+=
?
?
+=
?
,解得:
3
4
3
2
k
b
?
=
??
?
?=-
??
,∴直线DE的解析式为:y33
42
x
=-.
故四边形AEBD能为矩形,此时直线DE的解析式为:y
33 42
x
=-.
【点睛】
本题考查了矩形的性质、旋转的性质、全等三角形的判定及性质、待定系数法求函数解析式以及勾股定理.解题的关键是:(1)证出Rt△CDG≌Rt△CBG;(2)找出
BG=DG、OH=HD;(3)求出点H、G的坐标.本题属于中档题,难度不大,解决该题型题目时,根据全等三角形的性质找出相等的边和角是关键.
4.(1)ΔDPM,ΔFPG;等腰直角;(2)线段PG与PC的位置关系是PG⊥PC;PG PC
=
3;(3)213
【分析】
(1)延长GP交DC于点M,由Р是线段DF的中点,//
DC CF,可得
∠MDP=∠GFP,DP=FP,利用ASA可证明△DPM≌△FPG;可得DM=GF,MP=GP,根据正方形的性质可得CM=CG,即可证明△CMG是等腰直角三角形,即可得答案;
(2)如图,延长GP交DC于点H,利用ASA可证明△GFP≌△HDP,可得GP=HP,GF=HD,进而根据菱形的性质可证明△CHG是等腰三角形,根据等腰三角形“三线合一”的性质可得PG⊥PC,∠HCP=∠GCP,由∠ABC=60°可得∠HCG=120°,进而可得∠CGP=30°,根据含30°角的直角三角形的性质及勾股定理即可得答案;
(3)利用线段的和差关系可求出图2中CG的长,由(2)可知∠CGP=30°,根据含30°角的直角三角形的性质即可求出CP的长;在图3中,延长GP到N,使GP=PN,连接DN、CN、CG,过N作NK⊥CD,交CD延长线于K,利用SAS可证明△FGP≌△DNP,可得
GF=DN,∠GFP=∠NDP,根据角的和差关系可得∠CDN=120°,根据平角的定义可得
∠GBC=120°,利用菱形的性质及等量代换可得DN=GB,利用SAS可证明△NDC≌△GBC,可得CN=CG,∠DCN=∠BCG,根据等腰三角形的性质可得PC⊥GN,根据角的和差关系可
得∠NCG=120°,进而可得出∠CNP=30°,可得PC=1
2
CG,根据平角的定义可得
∠KDN=60°,即可得出∠KND=30°,根据含30°角的直角三角形的性质可得得出KD的长,利用勾股定理可求出KN的长,再利用勾股定理可求出CN的长,根据含30°角的直角三角形的性质即可得出PC的长.
【详解】
(1)如图,延长GP交DC于点M,
∵Р是线段DF的中点,四边形ABCD、BEFG是正方形,点,,
A B E在同一条直线上,∴//
DC CF,DP=FP,CD=BC,FG=BG,
在△DPM和△FPG中,
MDP GFP DP FP
DPM FPG ∠=∠
?
?
=
?
?∠=∠
?
,
∴△DPM≌△FPG,
∴DM=FG,KP=GP,
∴CD-DM=BC-BC,即CM=CG,
∴△CMG是等腰直角三角形,
∴PG⊥PC,PG=PC.
故答案为:ΔDPM,ΔFPG;等腰直角
(2)猜想:线段PG与PC的位置关系是PG⊥PC;PG
PC
3.
如图,延长GP交DC于点H,
∵P是线段DF的中点,
∴FP=DP,
∵四边形ABCD和四边形BEFG是菱形,∴CD//AB,CF//BE,CD=CB,GF=GB,∵点A B E
、、在一条直线上,
∴DC∥GF,
∴∠GFP=∠HDP,
在△GFP和△HDP中,
GFP HDP FP DP
GPF HPD ∠=∠
?
?
=
?
?∠=∠
?
,
∴△GFP≌△HDP,
∴GP=HP,GF=HD,
∴CD-DH=CB-GB,即CG=CH,
∴△CHG是等腰三角形.
∴PG⊥PC,(三线合一),∠HCP=∠GCP,∵∠ABC=∠BEF=60°,
∴∠HCG=120°,
∴∠CGP=1
2
(180°-120°
)=30°,
∴CG=2PC,
∴PG=2222
(2)3
CG PC PC PC PC
-=-=,
∴
PG
PC
=3.
(3)如图2,∵AB=6,BE=2,
∴CG=AB-BE=4,
由(2)可知∠CGP=30°,PG⊥PC,
∴PC=
1
2
CG=2,
如图3,延长GP到N,使GP=PN,连接DN、CN、CG,过N作NK⊥CD,交CD延长线于K,
在△DNP和△FGP中,
DP FP
NPD GPF
PN PG
=
?
?
∠=∠
?
?=
?
,
∴△DNP≌△FGP,
∴DN=GF=BG=BE=2,∠NDP=∠GFP,
∵四边形ABCD和四边形BEFG是菱形,
∴CD//AB,EF//BC,
∵点A、B、G在一条直线上,
∴DC∥EF,
∴∠CDP=∠EFP,
∵∠ABC=∠BEF=60°,
∴∠EFG=∠CBG=120°,
∴∠NDP+CDP=∠GFP+∠EFP=∠EFG=120°,即∠NDC=120°,
∴∠KDN=60°,∠KND=30°,
∴KD=
1
2
DN=1,223
DN KD
-=,
∴CK=CD+KD=7,
∴22
CK NK
+213
在△CDN和△CBG中,
CD BC
CDN CBG ND BG
=
?
?
∠=∠
?
?=
?
,
∴CN=CG,∠DCN=∠BCG,
∴PC⊥GN,∠DCN+∠NCB=∠BCG+∠NCB=∠DCB=120°,即∠NCG=120°,
∴∠CNP=1 2
(180°-∠NCG)=30°,
∴PC=
1
2
CN=13.
故答案为:213
【点睛】
本题考查正方形的性质、菱形的性质、等腰直角三角形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质及勾股定理,正确作出辅助线、熟记30°角所对的直角边等于斜边的一半的性质及全等三角形的判定定理是解题关键.
5.(1)见解析;(2)1条;(3)
72
11
t=或
18
5
t=
【分析】
(1)证△AEH≌△CGH(SAS),即可得出AH=CH;
(2)连接BD交AC于O,作直线OE即可;
(3)分两种情况:①连接AH交BC于M,证出BM=CM=
1
2
BC=6,由题意得
BE=BG=EH=GH=t,则AE=9-t,GM=6-t,由三角形面积关系得出方程,解方程即可;
②连接AH交CD于M,交BC的延长线于K,证出DM=CM=
1
2
CD,证△KCM≌△ADM得CK=DA=12,则BK=BC+CK=24,且BE=BG=EH=GH=t,则AE=9-t,GK=24-t,由三角形面积关系得出方程,解方程即可.
【详解】
解:(1)四边形BEHG是正方形,
BE BG
∴=,90
BEH BGH
∠=∠=?,90
AEH CGH
∠=∠=?,
又AB BC
=,
AE CG
∴=,
又EH HG
=,
()
AEH CGH SAS
∴???,
AH CH
∴=.
(2)解:连接BD交AC于O,如图1所示:
作直线OE,则直线OE矩形ABCD面积平分,
即经过点E且把矩形ABCD面积平分的直线有1条,故答案为:1;
(3) 解:分两种情况:
①如图2所示:连接AH交BC于M,
∵四边形ABCD是矩形,
∴△ABC的面积=△ADC的面积,
∵直线AH将矩形ABCD的面积分成1:3两部分,∴△ABM的面积=△ACM的面积,
∴BM=CM=1
2
CD=6,
由题意得:BE=BG=EH=GH=t,则AE=9-t,GM=6-t,
∵△ABM的面积=△AEH的面积+正方形BEHG的面积+△GHM的面积,
∴1
2
×6×9=
1
2
t(9-t)+t2+
1
2
t(6-t),
解得:
18
5
t=;
②如图3所示:连接AH交CD于M,交BC的延长线于K,
∵四边形ABCD是矩形,
∴∠MCK=∠B=∠D=∠BCD=90°,AD=BC=12,CD=AB=9,△ABC 的面积=△ADC 的面积, ∵直线AH 将矩形ABCD 的面积分成1:3两部分, ∴△ADM 的面积=△ACM 的面积, ∴DM=CM=
1
2CD=92
, 在△KCM 和△ADM 中,∠=∠??
=??∠=∠?
D MCK
DM CM AMD KMC ,
∴△KCM ≌△ADM(ASA), ∴CK=DA=12, ∴BK=BC+CK=24,
由题意得:BE=BG=EH=GH=t ,则AE=9-t ,GK=24-t ,
∵△ABK 的面积=△AEH 的面积+正方形BEHG 的面积+△GHK 的面积, ∴
12×24×9=12t (9-t )+t 2+1
2
t (24-t ), 解得:72
11
t =
, 综上所述,7211t =或185t =, 故答案为:7211t =或185
t =. 【点睛】
本题是四边形综合题目,考查了正方形的性质、矩形的性质、全等三角形的判定与性质、三角形面积以及分类讨论等知识;本题综合性强,熟练掌握正方形的性质和矩形的性质,证明三角形全等是解题的关键.
6.(1)四边形ABGE 的形状是正方形;(2)①详见解析;②DF=3CF 【分析】
(1)由四边形ABCD 是矩形,可得90A ABC ?∠=∠=,由折叠得:
90BGE A ?∠=∠=,根据三个内角是直角可判断四边形ABGE 为矩形,由折叠得:
AB=BG ,根据一组邻边相等的矩形是正方形可判断矩形ABGE 为正方形;
(2)①如图,连结EF ,在矩形ABCD 中,AB=DC ,AD=BC ,∠A=∠C=∠D=90°,由△ABE 沿BE 折叠后得到△GBE ,可得BG=AB ,EG=AE=ED ,∠A=∠BGE=90°,故∠EGF=∠D=90°,由HL 可判断Rt △EGF ≌Rt △EDF ,得到DF=FG ,问题得证;
②设AB=DC=a ,则
,另设CF=x ,则DF=DC-CF=a-x ,由①得BF=AB+DF =2a-x ,在Rt △BCF 中,由勾股定理得:BF 2=BC 2+CF 2,代入数据运算可得:x=14a ,即CF=1
4
a ,DF=a-x=
3
4
a ,进而可得DF 与CF 关系.
(1)四边形ABGE 的形状是正方形. 理由是:∵四边形ABCD 是矩形, ∴90A ABC ?∠=∠=,
由折叠得:90BGE A ?∠=∠=, ∴四边形ABGE 为矩形, 由折叠得:AB=BG , ∴矩形ABGE 为正方形; 故答案为:正方形. (2)①如图,连结EF ,
在矩形ABCD 中,AB=DC ,AD=BC ,∠A=∠C=∠D=90°, ∵E 是AD 的中点, ∴AE=DE ,
∵△ABE 沿BE 折叠后得到△GBE , ∴BG=AB ,EG=AE=ED ,∠A=∠BGE=90°, ∴∠EGF=∠D=90°, Rt △EGF 和Rt △EDF 中,
EG ED
EF EF =??
=?
, ∴Rt △EGF ≌Rt △EDF (HL ), ∴DF=FG ,
∴BF=BG+GF=AB+DF ;
②不妨假设AB=DC=a ,则3,另设CF=x ,则DF=DC-CF=a-x , 由①得BF=AB+DF=a+a-x=2a-x , 在Rt △BCF 中,由勾股定理得: BF 2=BC 2+CF 2, 即(2a-x)23a)2+x 2, 整理得:x=1
4
a , ∴CF=
1
4
a ,DF=a-x=34a ,
∴DF=3CF .
本题主要考查了折叠的性质,正方形的判定,三角形全等的判定,勾股定理等内容,根据图形作出辅助线找出线段的等量关系列出方程是解题的关键.
7.(1)见解析;(2)见解析.
【分析】
(1)连接BD,BD与AM交于点O,连接CO并延长交于AB,则CO与AB的交点为点N.可先证明△AOD≌△COD,再证明△MOB≌NOB,从而可得NB=MB;
(2)连接MO并延长与AE交于点Q,连接QC,则CQ∥AM.理由如下:由正方形的性质以及平行线等分线段可证QO=MO,从而可知四边形AQCM为平行四边形,从而可得
CQ∥AM.
【详解】
解:(1)如图(1),
连接BD,BD与AM交于点O,连接CO并延长交于AB,则CO与AB的交点为点N,则CN 为所作.
理由:在△AOD与△COD中,
∵
AD CD
ADO CDO OD OD
?
?
∠∠
?
?
?
=
=
=
,
∴△AOD≌△COD(SAS),∴∠OAD=∠OCD,
∴∠BAM=∠BCN.
在△ABM与△CBN中,
∵
BAM BCN AB CB
ABM CBN ∠∠
?
?
?
?∠∠
?
=
=
=
,
∴△ABM≌△CBN(ASA),
∴CN=AM.
(2)如图2连接AC、BD交与O点,连接MO并延长与AE交于点Q,连接QC,则CQ为所求的线段.
在正方形ABCD 中,OA =OB =OC =OD ,AD ∥BC , ∴QO =MO
∴四边形AQCM 为平行四边形, ∴QC ∥AM 【点睛】
本题考查了作图-基本作图,解决此题的关键是利用正方形的性质求解.
8.(1)①EAB DAC ∠=∠; ② 平行四边形,证明见解析;(2)成立,证明见解析. 【分析】
(1)①根据EAD BAC ∠=∠,两角有公共角BAD ∠,可证EAB DAC ∠=∠; ②连接EB ,证明△EAB ≌△DAC ,可得,ABE ACD EB CD ∠=∠=,再结合平行线的性质和等腰三角形的判定定理可得EF=DC ,由此可根据一组对边平行且相等的四边形是平行四边形证明四边形CDEF 为平行四边形.
(2)根据60BAC ∠=?,可证明△AED 和△ABC 为等边三角形,再根据ED ∥FC 结合等边三角形的性质,得出∠AFC=∠BDA ,求证△ABD ≌△CAF ,得出ED=CF ,进而求证四边形EDCF 是平行四边形. 【详解】
解:(1)①EAB DAC ∠=∠,理由如下:
∵EAD BAC ∠=∠,EAD EAB BAD ∠=∠+∠,BAC BAD DAC ∠=∠+∠, ∴EAB BAD BAD DAC ∠+∠=∠+∠, ∴EAB DAC ∠=∠; ②证明:如下图,连接EB,
在△EAB 和△DAC 中
∵AE AD EAB DAC AB AC =??
∠=∠??=?
∴△EAB ≌△DAC (SAS ) ∴,ABE ACD EB CD ∠=∠=, ∵AB AC =, ∴ABC ACD ∠=∠, ∴ABE ABC ∠=∠, ∵//EF DC , ∴EFB ABC ∠=∠, ∴ABE EFB ∠=∠, ∴EB EF =, ∴DC EF =
∴四边形CDEF 为平行四边形; (2)成立;理由如下: 理由如下: ∵60BAC ∠=?,
∴=60EAD BAC ∠=∠?, ∵AE=AD ,AB=AC ,
∴△AED 和△ABC 为等边三角形, ∴∠B=60°,∠ADE=60°,AD=ED, ∵ED ∥FC , ∴∠EDB=∠FCB ,
∵∠AFC=∠B+∠BCF=60°+∠BCF ,∠BDA=∠ADE+∠EDB=60°+∠EDB , ∴∠AFC=∠BDA , 在△ABD 和△CAF 中,
60BDA AFC B BAC AB CA ∠=∠??
∠=∠=???=?
∴△ABD ≌△CAF (AAS ), ∴AD=FC , ∵AD=ED , ∴ED=CF , 又∵ED ∥CF ,
∴四边形EDCF 是平行四边形. 【点睛】
本题考查全等三角形的性质和判定,等腰三角形的性质和判定,等边三角形的性质和判定,平行四边形的判定定理,平行线的性质.在做本题时可先以平行四边形的判定定理进行分析,在后两问中已知一组对边平行,所以只需证明这一组对边相等即可,一般证明线段相等就是证明相应的三角形全等.本题中是间接证明全等,在证明线段相等的过程中还应用到等腰三角形的判定定理(第(1)小题的第②问)和等边三角形的性质(第(2)小
题),难度较大.
9.(1)点M 的坐标为(51),
;(2)()44y x =-()04x <<;(3)(
)224160Q x x ++-,,
()2
3
4160Q x x +--, ,()2
4
160Q x x +-,, ()2
5
160(224)Q x x x --<<,
【分析】
(1)过点M 作ME OA ⊥,由“AAS ”可证COP PEM ???,可得4CO PE ==,
1OP ME ==,即可求点M 坐标;
(2)由(1)可知COP PEM ???,设OP=x ,则可得M 点坐标为(4+x ,x ),由直线OB
解析式可得N (x ,x ),即可知MN=4,由一组对边平行而且相等的四边形是平行四边形即可证明四边形BCNM 是平行四边形,进而可求y 与x 的函数关系式;
(3)首先画出符合要求的点Q 的图形,共分三种情况,第一种情况:当MN 为底边时,第二种情况:当M 为顶点MN 为腰时,第三种情况:当N 为顶点MN 为腰时,然后根据图形特征结合勾股定理求出各种情况点的坐标即可解答. 【详解】
解:(1)如图,过点M 作ME OA ⊥,
CP PM ⊥
90CPO MPE ∴∠+∠=?,且90CPO PCO ∠+∠=?
PCO MPE ∴∠=∠,且CP PM =,90COP PEM ∠=∠=? ()COP PEM AAS ∴???
4CO PE ∴==,1OP ME == 5OE ∴=
∴点M 坐标为(5,1)
故答案为(5,1)
(2)由(1)可知COP PEM ???
4CO PE ∴==,OP ME x ==
∴点M 坐标为(4,)x x +
四边形OABC 是边长为4的正方形,