信息论与编码第二章课后习题答案

第二章习题解答2-1、试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍？ 解：四进制脉冲可以表示4个不同的消息，例如：{0, 1, 2, 3}八进制脉冲可以表示8个不同的消息，例如：{0, 1, 2, 3, 4, 5, 6, 7} 二进制脉冲可以表示2个不同的消息，例如：{0, 1} 假设每个消息的发出都是等概率的，则：四进制脉冲的平均信息量symbol bit n X H / 24log log )(1=== 八进制脉冲的平均信息量symbol bit n X H / 38log log )(2=== 二进制脉冲的平均信息量symbol bit n X H / 12log log )(0===所以：四进制、八进制脉冲所含信息量分别是二进制脉冲信息量的2倍和3倍。

2、 设某班学生在一次考试中获优（A ）、良（B ）、中（C ）、及格（D ）和不及格（E ）的人数相等。

当教师通知某甲：“你没有不及格”，甲获得了多少比特信息？为确定自己的成绩，甲还需要多少信息？ 解：根据题意，“没有不及格”或“pass”的概率为54511pass =-=P 因此当教师通知某甲“没有不及格”后，甲获得信息在已知“pass”后，成绩为“优”（A ），“良”（B ），“中”（C ）和“及格”（D ） 的概率相同：41score )pass |()pass |()pass |()pass |(=====D P C P B P A P P 为确定自己的成绩，甲还需信息bits 241loglog score score =-=-=P I 3、中国国家标准局所规定的二级汉字共6763个。

设每字使用的频度相等，求一个汉字所含的信息量。

设每个汉字用一个1616⨯的二元点阵显示，试计算显示方阵所能表示的最大信息。

显示方阵的利用率是多少？解：由于每个汉字的使用频度相同，它们有相同的出现概率，即67631=P 因此每个汉字所含的信息量为bits 7.1267631loglog =-=-=P I 字每个显示方阵能显示256161622=⨯种不同的状态，等概分布时信息墒最大，所以一个显示方阵所能显示的最大信息量是bits322.054log log passpass =-=-=P Ibits 25621loglog =-=-=P I 阵显示方阵的利用率或显示效率为0497.02567.12===阵字I I η 4、两个信源1S 和2S 均有两种输出：1 ,0=X 和1 ,0=Y ，概率分别为2/110==X X P P ，4/10=Y P ，4/31=Y P 。

《信息论与编码》-曹雪虹-课后习题答案 第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ，转移概率为：()11|1/2p u u =，()21|1/2p uu =，()31|0p u u =，()12|1/3p u u =，()22|0p u u =，()32|2/3p u u =，()13|1/3p u u =，()23|2/3p u u =，()33|0p u u =，画出状态图并求出各符号稳态概率。

解：状态图如下状态转移矩阵为：1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1，u 2，u 3稳定后的概率分别为W 1，W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0，1}组成的二阶马尔可夫链，其转移概率为：(0|00)p =0.8，(0|11)p =0.2，(1|00)p =0.2，(1|11)p =0.8，(0|01)p =0.5，(0|10)p =0.5，(1|01)p =0.5，(1|10)p =0.5。

画出状态图，并计算各状态的稳态概率。

解：(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p == (1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵：0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为：设各状态00，01，10，11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子，也就是各面呈现的概率都为1/6，求：(1) “3和5同时出现”这事件的自信息； (2) “两个1同时出现”这事件的自信息； (3) 两个点数的各种组合（无序）对的熵和平均信息量；(4) 两个点数之和（即2, 3, … , 12构成的子集）的熵；(5) 两个点数中至少有一个是1的自信息量。

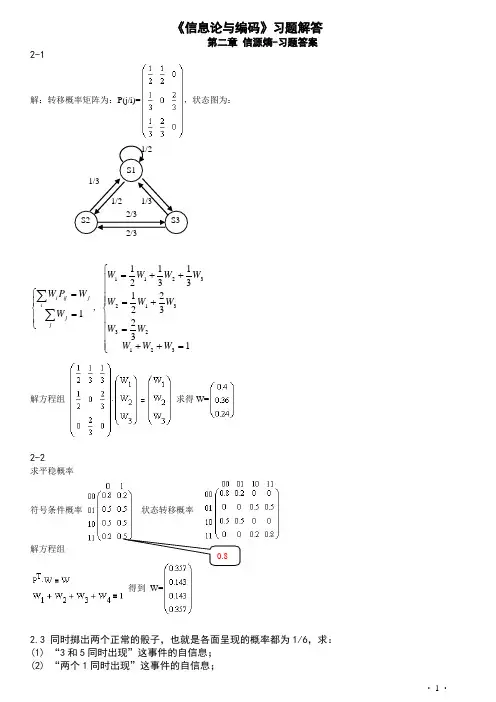
《信息论与编码》习题解答第二章 信源熵-习题答案2-1解：转移概率矩阵为：P(j/i)=，状态图为：⎪⎩⎪⎨⎧==∑∑j jj ij ii W W P W 1，⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=++=+=++=1323221313121321233123211W W W W W W W W W W W W 解方程组求得W=2-2求平稳概率符号条件概率状态转移概率解方程组得到 W=2.3 同时掷出两个正常的骰子，也就是各面呈现的概率都为1/6，求： (1) “3和5同时出现”这事件的自信息； (2) “两个1同时出现”这事件的自信息；(3) 两个点数的各种组合（无序）对的熵和平均信息量； (4) 两个点数之和（即2, 3, … , 12构成的子集）的熵； (5) 两个点数中至少有一个是1的自信息量。

解： (1)bitx p x I x p i i i 170.4181log )(log )(18161616161)(=-=-==⨯+⨯=(2)bitx p x I x p i i i 170.5361log )(log )(3616161)(=-=-==⨯=(3)共有21种组合：其中11，22，33，44，55，66的概率是3616161=⨯ 其他15个组合的概率是18161612=⨯⨯symbol bit x p x p X H ii i / 337.4181log 18115361log 3616)(log )()(=⎪⎭⎫ ⎝⎛⨯+⨯-=-=∑(4)参考上面的两个点数的排列，可以得出两个点数求和的概率分布如下：symbolbit x p x p X H X P Xii i / 274.3 61log 61365log 365291log 912121log 1212181log 1812361log 3612 )(log )()(36112181111211091936586173656915121418133612)(=⎪⎭⎫ ⎝⎛+⨯+⨯+⨯+⨯+⨯-=-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡∑(5)bit x p x I x p i i i 710.13611log)(log )(3611116161)(=-=-==⨯⨯=2-4(4)2.5 居住某地区的女孩子有25%是大学生，在女大学生中有75%是身高160厘米以上的，而女孩子中身高160厘米以上的占总数的一半。

第二章习题解答2-1、试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍？ 解：四进制脉冲可以表示4个不同的消息，例如：{0, 1, 2, 3} 八进制脉冲可以表示8个不同的消息，例如：{0, 1, 2, 3, 4, 5, 6, 7} 二进制脉冲可以表示2个不同的消息，例如：{0, 1} 假设每个消息的发出都是等概率的，则：四进制脉冲的平均信息量symbol bit n X H / 24log log )(1=== 八进制脉冲的平均信息量symbol bit n X H / 38log log )(2=== 二进制脉冲的平均信息量symbol bit n X H / 12log log )(0===所以：四进制、八进制脉冲所含信息量分别是二进制脉冲信息量的2倍和3倍。

2、 设某班学生在一次考试中获优（A ）、良（B ）、中（C ）、及格（D ）和不及格（E ）的人数相等。

当教师通知某甲：“你没有不及格”，甲获得了多少比特信息？为确定自己的成绩，甲还需要多少信息？ 解：根据题意，“没有不及格”或“pass”的概率为54511pass =-=P 因此当教师通知某甲“没有不及格”后，甲获得信息在已知“pass”后，成绩为“优”（A ），“良”（B ），“中”（C ）和“及格”（D ） 的概率相同：41score )pass |()pass |()pass |()pass |(=====D P C P B P A P P 为确定自己的成绩，甲还需信息bits 241loglog score score =-=-=P I 3、中国国家标准局所规定的二级汉字共6763个。

设每字使用的频度相等，求一个汉字所含的信息量。

设每个汉字用一个1616⨯的二元点阵显示，试计算显示方阵所能表示的最大信息。

显示方阵的利用率是多少？解：由于每个汉字的使用频度相同，它们有相同的出现概率，即67631=P 因此每个汉字所含的信息量为bits 7.1267631loglog =-=-=P I 字每个显示方阵能显示256161622=⨯种不同的状态，等概分布时信息墒最大，所以一个显示方阵所能显示的最大信息量是bits 322.054loglog passpass =-=-=P Ibits 25621loglog 256=-=-=P I 阵显示方阵的利用率或显示效率为0497.02567.12===阵字I I η 4、两个信源1S 和2S 均有两种输出：1 ,0=X 和1 ,0=Y ，概率分别为2/110==X X P P ，4/10=Y P ，4/31=Y P 。

第二章习题参考答案2-1解：同时掷两个正常的骰子，这两个事件是相互独立的，所以两骰子面朝上点数的状态共有6×6＝36种，其中任一状态的分布都是等概的，出现的概率为1/36。

(1)设“3和5同时出现”为事件A ，则A 的发生有两种情况：甲3乙5，甲5乙3。

因此事件A 发生的概率为p(A)=(1/36)*2=1/18 故事件A 的自信息量为I(A)=－log 2p(A)=log 218=4.17 bit(2)设“两个1同时出现”为事件B ，则B 的发生只有一种情况：甲1乙1。

因此事件B 发生的概率为p(B)=1/36 故事件B 的自信息量为I(B)=－log 2p(B)=log 236=5.17 bit (3) 两个点数的排列如下：因为各种组合无序，所以共有21种组合： 其中11，22，33，44，55，66的概率是3616161=⨯其他15个组合的概率是18161612=⨯⨯ symbol bit x p x p X H ii i / 337.4181log 18115361log 3616)(log )()(=⎪⎭⎫ ⎝⎛⨯+⨯-=-=∑(4) 参考上面的两个点数的排列，可以得出两个点数求和的概率分布：symbolbit x p x p X H X P X ii i / 274.3 61log 61365log 365291log 912121log 1212181log 1812361log 3612 )(log )()(36112181111211091936586173656915121418133612)(=⎪⎭⎫ ⎝⎛+⨯+⨯+⨯+⨯+⨯-=-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡∑(5)“两个点数中至少有一个是1”的组合数共有11种。

bit x p x I x p i i i 710.13611log)(log )(3611116161)(=-=-==⨯⨯=2-2解：(1)红色球x 1和白色球x 2的概率分布为⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡2121)(21x x x p X i 比特 12log *21*2)(log )()(2212==-=∑=i i i x p x p X H(2)红色球x 1和白色球x 2的概率分布为⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡100110099)(21x x x p X i 比特 08.0100log *100199100log *10099)(log )()(22212=+=-=∑=i i i x p x p X H (3)四种球的概率分布为⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡41414141)(4321x x x x x p X i ，42211()()log ()4**log 4 2 4i i i H X p x p x ==-==∑比特 2-5解：骰子一共有六面，某一骰子扔得某一点数面朝上的概率是相等的，均为1/6。

部分答案，仅供参考。

2.1信息速率是指平均每秒传输的信息量点和划出现的信息量分别为3log ,23log ，一秒钟点和划出现的次数平均为415314.0322.01=⨯+⨯一秒钟点和划分别出现的次数平均为45.410那么根据两者出现的次数，可以计算一秒钟其信息量平均为253log 4153log 4523log 410-=+2.3 解：(a)骰子A 和B ，掷出7点有以下6种可能：A=1,B=6; A=2,B=5; A=3,B=4; A=4,B=3; A=5,B=2; A=6,B=1 概率为6/36=1/6，所以信息量-log(1/6)=1+log3≈2.58 bit(b) 骰子A 和B ，掷出12点只有1种可能： A=6,B=6概率为1/36，所以信息量-log(1/36)=2+log9≈5.17 bit2.5解：出现各点数的概率和信息量：1点：1/21，log21≈4.39 bit ； 2点：2/21，log21-1≈3.39 bit ； 3点：1/7，log7≈2.81bit ； 4点：4/21，log21-2≈2.39bit ； 5点：5/21，log （21/5）≈2.07bit ； 6点：2/7，log(7/2)≈1.81bit 平均信息量：(1/21)×4.39+(2/21)×3.39+(1/7)×2.81+(4/21)×2.39+(5/21)×2.07+(2/7)×1.81≈2.4bit2.7解：X=1:考生被录取； X=0:考生未被录取； Y=1:考生来自本市；Y=0:考生来自外地； Z=1: 考生学过英语；Z=0：考生未学过英语P(X=1)=1/4, P(X=0)=3/4; P(Y=1/ X=1)=1/2； P(Y=1/ X=0)=1/10；P(Z=1/ Y=1)=1, P(Z=1 / X=0, Y=0)=0.4, P(Z=1/ X=1, Y=0)=0.4, P(Z=1/Y=0)=0.4 (a) P(X=0,Y=1)=P(Y=1/X=0)P(X=0)=0.075, P(X=1,Y=1)= P(Y=1/X=1)P(X=1)=0.125P(Y=1)= P(X=0,Y=1)+ P(X=1,Y=1)=0.2P(X=0/Y=1)=P(X=0,Y=1)/P(Y=1)=0.375, P(X=1/Y=1)=P(X=1,Y=1)/P(Y=1)=0.625 I (X ;Y=1)=∑∑=====xx)P()1Y /(P log)1Y /(P )1Y (I )1Y /(P x x x x;x=1)P(X )1Y /1X (P log)1Y /1X (P 0)P(X )1Y /0X (P log)1Y /0X (P =====+======0.375log(0.375/0.75)+0.625log(0.625/0.25)=(5/8)log5-1≈0.45bit(b) 由于P(Z=1/ Y=1)=1, 所以 P （Y=1，Z=1/X=1）= P （Y=1/X=1）=0.5 P （Y=1，Z=1/X=0）= P （Y=1/X=0）=0.1那么P （Z=1/X=1）= P （Z=1,Y=1/X=1）+ P （Z=1,Y=0/X=1）=0.5+ P （Z=1/Y=0，X=1）P （Y=0/X=1）=0.5+0.5*0.4=0.7P(Z=1/X=0)= P （Z=1,Y=1/X=0）+ P （Z=1,Y=0/X=0）=0.1+P(Z=1/Y=0，X=0)P(Y=0/X=0)=0.1+0.9*0.4=0.46P （Z=1,X=1）= P （Z=1/X=1）*P(X=1)=0.7*0.25=0.175 P （Z=1,X=0）= P （Z=1/X=0）*P(X=0)= 0.46*0.75=0.345 P(Z=1) = P(Z=1,X=1)+ P(Z=1,X=0) = 0.52 P(X=0/Z=1)=0.345/0.52=69/104 P(X=1/Z=1)=35/104I (X ;Z=1)=∑∑=====xx )P()1Z /(P log )1Z /(P )1Z (I )1Z /(P x x x x;x=1)P(X )1Z /1X (P log )1Z /1X (P 0)P(X )1Z /0X (P log )1Z /0X (P =====+======(69/104)log(23/26)+( 35/104)log(35/26) ≈0.027bit(c)H （X ）=0.25*log(1/0.25)+0.75*log(1/0.75)=2-(3/4)log3=0.811bit H(Y/X)=-P(X=1,Y=1)logP(Y=1/X=1) -P(X=1,Y=0)logP(Y=0/X=1)-P(X=0,Y=1)logP(Y=1/X=0) -P(X=0,Y=0)logP(Y=0/X=0)=-0.125*log0.5-0.125*log0.5-0.075*log0.1-0.675*log0.9=1/4+(3/40)log10-(27/40)log(9/10)≈0.603bitH(XY)=H(X)+H(Y/X)=9/4+(3/4)log10-(21/10)log3=1.414bitP(X=0,Y=0,Z=0)= P(Z=0 / X=0, Y=0)* P( X=0, Y=0)=(1-0.4)*(0.75-0.075)=0.405 P(X=0,Y=0,Z=1)= P(Z=1 / X=0, Y=0)* P( X=0, Y=0)=0.4*0.675=0.27P(X=1,Y=0,Z=1)= P(Z=1/ X=1,Y=0)* P(X=1,Y=0)=0.4*(0.25-0.125)=0.05 P(X=1,Y=0,Z=0)= P(Z=0/ X=1,Y=0)* P(X=1,Y=0)=0.6*0.125=0.075 P(X=1,Y=1,Z=1)=P(X=1,Z=1)- P(X=1,Y=0,Z=1)=0.175-0.05=0.125 P(X=1,Y=1,Z=0)=0 P(X=0,Y=1,Z=0)=0P(X=0,Y=1,Z=1)= P(X=0,Z=1)- P(X=0,Y=0,Z=1)= 0.345-0.27=0.075H(XYZ)=-0.405*log0.405-0.27*log0.27-0.05*log0.05-0.075*log0.075-0.125*log0.125-0.075*log 0.075=(113/100)+(31/20)log10-(129/50)log3 =0.528+0.51+0.216+0.28+0.375+0.28=2.189 bitH(Z/XY)=H(XYZ)-H(XY)= -28/25+(4/5)log10-12/25log3 =0.775bit2.9 解：A ，B ，C 分别表示三个筛子掷的点数。

2.1 同时掷两个正常的骰子，也就是各面呈现的概率都是1/6，求： （1）“3和5同时出现”事件的自信息量； （2）“两个1同时出现”事件的自信息量；（3）两个点数的各种组合（无序对）的熵或平均信息量； （4）两个点数之和（即2，3，…，12构成的子集）的熵；（5）两个点数中至少有一个是1的自信息。

解：（1）一个骰子点数记为X ，另一个骰子的点数记做Y ，X 、Y 之间相互独立，且都服从等概率分布，即同理一个骰子点数为3，另一个骰子点数为5属于组合问题，对应的概率为181616161613Y Py 5X Px 5Y Py 3X Px P 1=⨯+⨯===+===）（）（）（）（对应的信息量为比特）（）（17.4181-lb P -I 11===lb（2）两个骰子点数同时为1的概率为）（）（3611Y Py 1X Px P 2==== 对应的信息量为比特）（）（17.5361-lb P -I 22===lb（3）各种组合及其对应的概率如下,6,5,4,3,2,1Y X 3616161Y X P ===⨯==）（共6种可能18161612Y X P =⨯⨯=≠）（ 共有15种可能因此对应的熵或者平均自信息量为34.418118115-3613616-H 1=⨯⨯⨯⨯=）（）（lb lb 比特/符号 （4）令Z=X+Y ，可以计算出Z 对应的概率分布如下对应的熵为符号比特）（）（）（）（）（）（）（/1.914366366-3653652-3643642-3633632-3633632-3623622-361361-2H 1=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=lb lb lb lb lb lb lb （5）X 、Y 相互独立，所以联合熵为比特）（）（597.06162Y X,I =⨯=lb2.2 设在一只布袋中装有100个大小、手感完全相同的球，每个球上涂有一种颜色。

100个球的颜色有下列3种情况：（1）红色球和白色球各50个； （2）红色球99个，白色球1个； （3）红、黄、蓝、白色球各25个。

第二章信息的度量2.1信源在何种分布时，熵值最大？又在何种分布时，熵值最小？答：信源在等概率分布时熵值最大；信源有一个为1，其余为0时熵值最小。

2.2平均互信息量I(X;Y)与信源概率分布q(x)有何关系？与p(y|x)又是什么关系？答：若信道给定，I(X;Y)是q(x)的上凸形函数；若信源给定，I(X;Y)是q(y|x)的下凸形函数。

2.3熵是对信源什么物理量的度量？答：平均信息量2.4设信道输入符号集为{x1,x2,……xk}，则平均每个信道输入符号所能携带的最大信息量是多少？答：kk k xi q xi q X H i log 1log 1)(log )()(2.5根据平均互信息量的链规则，写出I(X;YZ)的表达式。

答：)|;();();(Y Z X I Y X I YZ X I 2.6互信息量I(x;y)有时候取负值，是由于信道存在干扰或噪声的原因，这种说法对吗？答：互信息量)()|(log );(xi q yj xi Q y x I ，若互信息量取负值，即Q(xi|yj)<q(xi)，说明事件yi 的出现告知的是xi 出现的可能性更小了。

从通信角度看，视xi 为发送符号，yi 为接收符号，Q(xi|yj)<q(xi)，说明收到yi 后使发送是否为xi 的不确定性更大，这是由于信道干扰所引起的。

2.7一个马尔可夫信源如图所示，求稳态下各状态的概率分布和信源熵。

答：由图示可知：43)|(41)|(32)|(31)|(41)|(43)|(222111110201s x p s x p s x p s x p s x p s x p 即：43)|(0)|(41)|(31)|(32)|(0)|(0)|(41)|(43)|(222120121110020100s s p s s p s s p s s p s s p s s p s s p s s p s s p 可得：1)()()()(43)(31)()(31)(41)()(41)(43)(210212101200s p s p s p s p s p s p s p s p s p s p s p s p得：114)(113)(114)(210s p s p s p )]|(log )|()|(log )|()[()]|(log )|()|(log )|()[()]|(log )|()|(log )|()[(222220202121211111010100000s s p s s p s s p s s p s p s s p s s p s s p s s p s p s s p s s p s s p s s p s p H 0.25（bit/符号）2.8一个马尔可夫信源，已知：0)2|2(,1)2|1(,31)1|2(,32)1|1(x x p x x p x x p x x p 试画出它的香农线图，并求出信源熵。

1第2章 信息的度量2.1 同时扔一对质地均匀的骰子，当得知“两骰子面朝上点数之和为5”或“面朝上点数之和为8”或“两骰子面朝上点数是3和6”时，试问这三种情况分别获得多少信息量？解：某一骰子扔得某一点数面朝上的概率是相等的，均为1/6，两骰子面朝上点数的状态共有36种,其中任一状态出现都是等概率的,出现概率为1/36。

设两骰子面朝上点数之和为事件a ，有：⑴ a=5时，有1+4，4+1，2+3，3+2，共4种，则该事件发生概率为4/36=1/9，则信息量为I(a)=-logp(a=5)=-log1/9≈3.17(bit)⑵ a=8时，有2+6，6+2，4+4，3+5，5+3，共5种，则p(a)=5/36,则I(a)= -log5/36≈2.85(bit) ⑶ p(a)=2/36=1/18,则I(a)=-log1/18≈4.17(bit)2.2 如果你在不知道今天是星期几的情况下问你的朋友“明天是星期几”，则答案中含有多少信息量？如果你在已知今天是星期三的情况下提出同样的问题，则答案中你能获得多少信息量（假设已知星期一至星期日的排序）？解：设“明天是星期几”为事件a ：⑴ 不知道今天是星期几：I(a)=-log1/7≈2.81(bit) ⑵ 知道今天是星期几：I(a)=-log1=0 (bit)2.3 居住某地区的女孩中有20%是大学生，在女大学生中有80%是身高1米6以上的，而女孩中身高1米6以上的占总数的一半。

假如我们得知“身高1米6以上的某女孩是大学生”的消息，求获得多少信息量？解：设“居住某地区的女孩是大学生”为事件a ，“身高1米6以上的女孩”为事件b ，则有： p(a)= 0.2，p(b|a)=0.8，p(b)=0.5，则“身高1米6以上的某女孩是大学生”的概率为：32.05.08.02.0)()|()()|(=⨯==b p a b p a p b a p信息量为：I=-logp(a|b)=-log0.32≈1.64(bit)2.4 从大量统计资料知道，男性中红绿色盲的发病率为7%，女性发病率为0.5%，如果你问一位男同志：“你是否是红绿色盲？”，他回答“是”或“否”，问这两个回答中各含有多少信息量？平均每个回答中含有多少信息量？如果你问一位女同志，则答案中含有的平均自信息量是多少？解：⑴ 男同志回答“是”的概率为7%=0.07，则信息量I=-log0.07≈3.84(bit) 男同志回答“否”的概率为1-7%=0.93，则信息量I=-log0.93≈0.10(bit) 平均信息量为：H 1=-(0.07×log0.07+0.93×log0.93) ≈0.37(bit/符号) ⑵ 问女同志的平均自信息量：H 2=-[0.05×log0.05+(1-0.05) ×log(1-0.05)] ≈0.045(bit/符号)2.5 如有7行9列的棋型方格，若有两个质点A 和B ，分别以等概率落入任一方格内，2且它们的坐标分别为（X A ，Y A ）、（X B ，Y B ），但A 、B 不能落入同一方格内。