
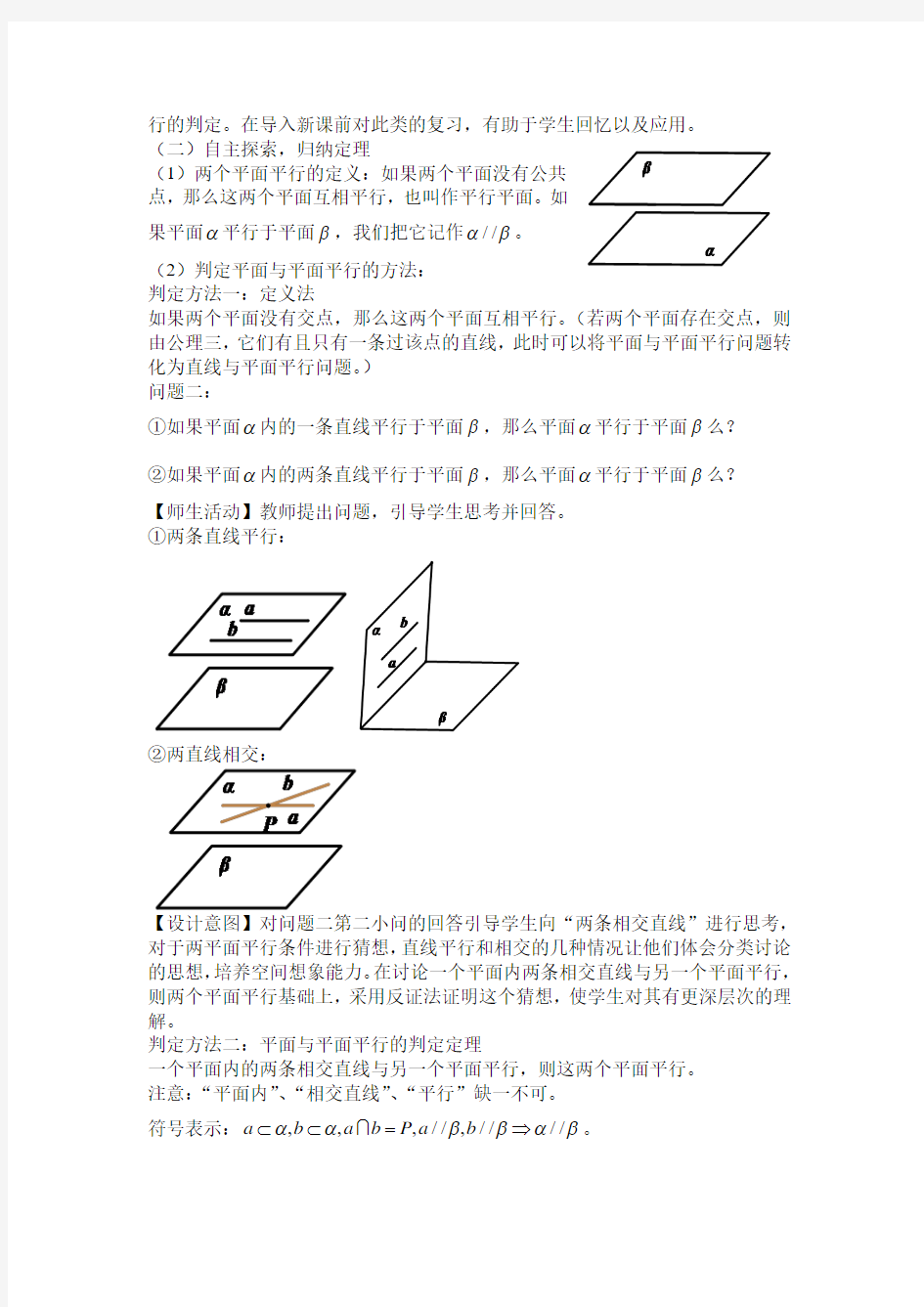
平面与平面平行的判定
一、学习内容分析
本节课选自《普通高中标准实验教科书—数学必修二》(人教版)第二章点、直线、平面之间的位置关系第二节直线、平面平行的判定及其性质,主要研究平面与平面平行的判定方法。根据课标要求和学生情况,本节课分为四个课时,今天学习第二课时。本节课是建立在学习空间中直线与直线、直线与平面位置关系基础上的一节课,并为后续学习平面与平面平行性质奠定基础。
教材首先通过观察三角板所在平面与桌面位置关系引入课题,然后将两个平面平行的问题转化为一个平面内的直线与另一个平面平行的问题,体现数学中的转化思想。接着根据两个平面中直线的关系探究两个平面的位置关系,体现分类讨论思想,培养了学生自主探究的能力。
二、学习者分析
(1)从已有知识来看,学生已经学习了空间点、直线、平面之间的位置关系,掌握了直线与平面平行的判定定理;
(2)从已有经验来看,学生已经掌握了分类讨论、转化的思想;
(3)从已有能力来看,学生已经具有了自主探索、简单的空间想象能力。
但对于高二学生来说,他们初次接触空间立体几何,对于空间的部分问题仍有较大困惑,空间想象能力还不是很强。
三、教学目标
(1)知识与技能目标:
①通过直观感知,操作确认,归纳出平面与平面平行的判定定理;
②理解并掌握两平面平行的判定方法;
③能够运用两个平面平行的判定方法解决相关问题。
(2)过程与方法目标:
①通过观察相关模型以及实物,培养分析、归纳的能力;
②在探究平面与平面平行判定定理的过程中,体会分类讨论、转化的思想。(3)情感、态度与价值观目标:
在发现中学习,提高学习数学的积极性,培养主动探究、合作交流的意识
四、教学重难点
(1)教学重点:两个平面平行的判定;
(2)教学难点:探究平面与平面平行的判定定理以及应用判定定理解决相关问题。
五、教学过程
(一)复习旧知,导入新课
问题一:
①平面几何中,判定两直线平行有哪几种方法?
②直线与平面平行有哪些方法?
③平面与平面有哪些位置关系?
师生活动:教师提出问题,引导学生进行回答。
【设计意图】通过回顾两直线平行、直线与平面平行的判定方法引出平面与平面之间的关系,从而引入课题:平面与平面平行的判定。在探索平面与平面平行的判定定理以及应用定理进行证明过程中,仍然要用到直线平行以及直线与平面平
行的判定。在导入新课前对此类的复习,有助于学生回忆以及应用。
(二)自主探索,归纳定理
(1)两个平面平行的定义:如果两个平面没有公共
点,那么这两个平面互相平行,也叫作平行平面。如
果平面α平行于平面β,我们把它记作//αβ。
(2)判定平面与平面平行的方法:
判定方法一:定义法
如果两个平面没有交点,那么这两个平面互相平行。(若两个平面存在交点,则由公理三,它们有且只有一条过该点的直线,此时可以将平面与平面平行问题转化为直线与平面平行问题。)
问题二:
①如果平面α内的一条直线平行于平面β,那么平面α平行于平面β么? ②如果平面α内的两条直线平行于平面β,那么平面α平行于平面β么?
【师生活动】教师提出问题,引导学生思考并回答。
①两条直线平行:
②两直线相交:
【设计意图】对问题二第二小问的回答引导学生向“两条相交直线”进行思考,对于两平面平行条件进行猜想,直线平行和相交的几种情况让他们体会分类讨论的思想,培养空间想象能力。在讨论一个平面内两条相交直线与另一个平面平行,则两个平面平行基础上,采用反证法证明这个猜想,使学生对其有更深层次的理解。
判定方法二:平面与平面平行的判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。 注意:“平面内”、“相交直线”、“平行”缺一不可。
符号表示:,,,//,////a b a b P a b ααββαβ??=? 。
利用反证法证明定理:,,,//,////a b a b P a b ααββαβ??=?
假设平面=l αβ
判定方法三:一个平面内的两条相交直线分别与另一个平面内的两条相交直线平行,则这两个平面平行。
(三)巩固练习,加深理解
例1:判断下列命题是否正确,请说明理由。
①若平面α内的两条直线分别与平面β平行,则α与β平行;
②若平面α内有无数条直线分别与平面平行,则α与β平行;
③一个平面α内两条不平行的直线都平行于β平面,则α与β平行;
④如果一个平面内的任何直线都平行于另一个平面,那么这两个平面平行; ⑤如果一个平面内的一条直线平行于另一个平面,那么这两个平面平行。 例2:1111
111//ABCD A BC D AB D C BD -已知正方体,求证:平面平面。
例3:111111111111,,,,,,//ABCD A B C D M N E F A B A D B C C D AMN EFDB
-已知中,分别是棱的中点,求证:平面平面
例4:11111111,,//ABCD A B C D E F CC AA BDE B D F
-已知正方体中,分别是的中点,求证:平面平面
(四)复习小结,深化内涵
1、平面与平面平行的判定:
(1)定义法;
(2)判定定理:如果一个平面内的两条相交直线平行于另一个平面,那么这两个平面平行。
(3)定理:如果一个平面内的两条相交直线分别与另一个平面内的两条相交直线平行,那么这两个平面平行。
(4)平面平行的传递性。
2、思想方法:
面面平行——线面平行——线线平行
(五)布置作业
六、板书设计
2.2.2平面与平面平行的判定
判定定理:如果一个平面内的两条相交直线平行于另一个平面,那么这两个平面平行。(1)反证法:(2)例1:
两个平面平行的判定和性质(一) ●教学目标 (一)教学知识点 1.两个平面的位置关系. 2.两个平面平行的判定方法. (二)能力训练要求 1.等价转化思想在解决问题中的运用. 2.通过问题解决提高空间想象能力. (三)德育渗透目标 1.渗透问题相对论观点. 2.通过问题的证明寻求事物的统一性. ●教学重点 两个平面的位置关系;两个平面平行的判定. ●教学难点 判定定理、例题的证明. ●教学方法 启发式 在启发、诱思下逐步完成定理的证明过程. 平面的位置关系也需以实物(教室)为例,启发诱思完成.通过师生互议,解决例1问题. ●教具准备 投影片两张 第一张:(记作§9.5.1 A) 第二张:(记作§9.5.1 B)
●教学过程 Ⅰ.复习回顾 师生共同复习回顾,线面垂直定义,判定定理. 性质定理:归纳小结线面距离问题求解方法,以及利用三垂线定理及其逆定理解决问题. 立体几何的问题解决:一是如何将立体几何问题转化成平面几何问题;二是数学思想方法怎样得到充分利用、渗透,这些都需在实践中进一步体会. 下面继续研究面面位置关系. Ⅱ.讲授新课 1.两个平面的位置关系 除教材上例子外,我们以所在教室为例,观察面与面之间关系. [师]观察教室前、后两个面,左、右两个面及上、下两个面都是平行的,而其相邻两个面是相交的.[师]打开教材竖直放在桌上,其间有许多个面,它们共同点是都经过一条直线.观察教室的门与其所在墙面关系,随着门的开启,门所在面与墙面始终有一条公共线.结合生观察教室的结论,引导其寻找平面公共点,然后给出定义. 定义:如果两个平面没有公共点,我们就说这两个平面互相平行. 如果两个平面有公共点,它们相交于一条公共直线. 两个平面的位置关系只有两种: (1)两个平面平行——没有公共点; (2)两个平面相交——有一条公共直线. [师]两个平面平行,如平面α和平面β平行,记作α∥β. 下面给出两个示意图,同学们考虑哪个较直观? [生]图(1)较直观,图(2)不直观. [师]从以上两种画法,告诉我们画图过程中应注意什么?图(2)为何不直观?
. 一.平面几何 1. 勾股定理(毕达哥拉斯定理)(广义勾股定理)(1)锐角对边 的平方,等于其他两边之平方和,减去这两边中的一边和另一边在这边上的射影乘积的两倍. (2)钝角对边的平方等于其他两边的平方和,加上这两边中的一边与另一边在这边上的射影乘积的两倍. 2. 射影定理(欧几里得定理) 3. 中线定理(巴布斯定理)设△ABC 的边BC 的中点为P ,则 有)(22222BP AP AC AB +=+; 中线长:2 222 22a c b m a -+= 4. 垂线定理:2 2 2 2 BD BC AD AC CD AB -=-?⊥ 高 线 长 : C b B c A a bc c p b p a p p a h a sin sin sin ))()((2===---= 5. 角平分线定理:三角形一个角的平分线分对边所成的两条线 段与这个角的两边对应成比例. 如△ABC 中,AD 平分∠BAC ,则AC AB DC BD =;(外角平分线定 理) 角平分线长:2 cos 2)(2A c b bc a p bcp c b t a +=-+= (其中 p 为周长一半) 6. 正弦定理: R C c B b A a 2sin sin sin ===, (其中R 为三角形外接圆半径) 7. 余弦定理:C ab b a c cos 2222 -+= 8. 张角定理:AB DAC AC BAD AD BAC ∠+∠=∠sin sin sin 9. 斯特瓦尔特(Stewart )定理:设已知△ABC 及其底边上B 、C 两点间的一点D ,则有AB 2 ·DC +AC 2 ·BD -AD 2 ·BC =BC ·DC ·BD 10. 圆周角定理:同弧所对的圆周角相等,等于圆心角的一 半.(圆外角如何转化?) 11. 弦切角定理:弦切角等于夹弧所对的圆周角 12. 圆幂定理:(相交弦定理:垂径定理:切割线定理(割线定 理):切线长定理:) 13. 布拉美古塔(Brahmagupta )定理: 在圆内接四边形ABCD 中,AC ⊥BD ,自对角线的交点P 向一边作垂线,其延长线必平分对边 14. 点到圆的幂:设P 为⊙O 所在平面上任意一点,PO =d ,⊙ O 的半径为r ,则d 2-r 2就是点P 对于⊙O 的幂.过P 任作 一直线与⊙O 交于点A 、B ,则PA ·PB = |d 2 -r 2 |.“到两圆等幂的点的轨迹是与此二圆的连心线垂直的一条直线,如果此二圆相交,则该轨迹是此二圆的公共弦所在直线”这个结论.这条直线称为两圆的“根轴”.三个圆两两的根轴如果不互相平行,则它们交于一点,这一点称为三圆的“根心”.三个圆的根心对于三个圆等幂.当三个圆两两相交时,三条公共弦(就是两两的根轴)所在直线交于一点. 15. 托勒密(Ptolemy )定理:圆内接四边形对角线之积等于两 组对边乘积之和,即AC ·BD =AB ·CD +AD ·BC ,(逆命题成立) .(广义托勒密定理)AB ·CD +AD ·BC ≥AC ·BD 16. 蝴蝶定理:AB 是⊙O 的弦,M 是其中点,弦CD 、EF 经过 点M ,CF 、DE 交AB 于P 、Q ,求证:MP =QM . 17. 费马点:定理1等边三角形外接圆上一点,到该三角形较近 两顶点距离之和等于到另一顶点的距离;不在等边三角形外接圆上的点,到该三角形两顶点距离之和大于到另一点的距 离.定理2 三角形每一内角都小于120°时,在三角形内必存在一点,它对三条边所张的角都是120°,该点到三顶点距离和达到最小,称为“费马点”,当三角形有一内角不小于120°时,此角的顶点即为费马点 18. 拿破仑三角形:在任意△ABC 的外侧,分别作等边△ABD 、 △BCE 、△CAF ,则AE 、AB 、CD 三线共点,并且AE =BF = CD ,这个命题称为拿破仑定理. 以△ABC 的三条边分别向 外作等边△ABD 、△BCE 、△CAF ,它们的外接圆⊙C 1 、⊙ A 1 、⊙ B 1的圆心构成的△——外拿破仑的三角形,⊙ C 1 、 ⊙A 1 、⊙B 1三圆共点,外拿破仑三角形是一个等边三角形;△ABC 的三条边分别向△ABC 的内侧作等边△ABD 、△BCE 、△CAF ,它们的外接圆⊙C 2 、⊙A 2 、⊙B 2的圆心构成的△——内拿破仑三角形,⊙C 2 、⊙A 2 、⊙B 2三圆共点,内拿破仑三角形也是一个等边三角形.这两个拿破仑三角形还具有相同的中心 19. 九点圆(Nine point round 或欧拉圆或费尔巴赫圆):三角形 中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,九点圆具有许多有趣的性质,例如: (1)三角形的九点圆的半径是三角形的外接圆半径之半 (2)九点圆的圆心在欧拉线上,且恰为垂心与外心连线的中点 (3)三角形的九点圆与三角形的内切圆,三个旁切圆均相切〔费尔巴哈定理〕 20. 欧拉(Euler )线:三角形的外心、重心、九点圆圆心、垂心 依次位于同一直线(欧拉线)上. 21. 欧拉(Euler )公式:设三角形的外接圆半径为R ,内切圆半 径为r ,外心与内心的距离为d ,则d 2 =R 2 -2Rr . 22. 锐角三角形的外接圆半径与内切圆半径的和等于外心到各 边距离的和. 23. 重心:三角形的三条中线交于一点,并且各中线被这个点分 成2:1的两部分;)3 ,3(C B A C B A y y y x x x G ++++ 重心性质:(1)设G 为△ABC 的重心,连结AG 并延长交BC
两个平面平行的判定和性质 一.选择题 1.α,β是两个不重合的平面,b a ,是两条不同的直线,在下列条件下,可判断βα//的是 A.α,β都平行于直线b a , B.α内有三个不共线的点到β的距离相等 C.b a ,是α内两条直线,且ββ//,//b a D.b a ,是异面直线,且ββαα//,//,//,//b a b a 2. 已知:n m ,表示两条直线,γβα,,表示平面,下列命题中正确的个数是 ( ) ①若βαγβγα//,//,,则且n m n m =?=? ②若n m ,相交且都在α,β外,βαβα//,//,//,//n n m m ,则βα// ③若,//,//βαm m 则βα// ④若,//,//,//n m n m 且βα则βα// A.1 个 B.2个 C.3个 D.4个 3. 在正方体ABCD -A 1B 1C 1D 1中,点P 在线段AD 1上运动,则异面直线CP 与BA 1所成角θ的取值范围是( ) A.2 0π θ< < B.2 0π θ≤ < C.3 0π θ≤ ≤ D.3 0π θ≤ < 4. 给出下列四个命题: ①夹在两个平行平面间的线段中,较长的线段与平面所成的角较小; ②夹在两个平行平面间的线段相等,则它们与两个平面所成的角相等; ③夹在两个平行平面间的线段相等,则这两线段必平行; ④夹在两个平行平面间的平行线段必相等.其中正确的命题有( ) A.①②④ B.②③④ C.①③ D.④ 二.填空 5.如果平面α内的两条相交直线与平面β所成的角相等,那么这两个平面的位置关系是 6.如果βα//,AB 和AC 是夹在平面α与β之间的两条线段,AC AB ⊥,且2=AB ,直线AB 与平面α所成的角为?30,则线段AC 长的取值范围为 . 7.(1)直线b a //,α平面//a ,则b 与平面α的位置关系是_____________. (2)A 是两异面直线a 、b 外的一点,过A 最多可作___________个平面同时与a 、b 平行. 三、解答题 8.如图,βα//,AB βα,交于A 、B ,CD βα,交 于C 、D ,AB ?CD =O ,O 在两平面之间,
直线与平面、平面与平面平行的判定 [学习目标] 1.理解直线与平面平行、平面与平面平行判定定理的含义.2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的判定定理,并知道其地位和作用.3.能运用直线与平面平行的判定定理、平面与平面平行的判定定理证明一些空间线面关系的简单问题. 知识点一直线与平面平行的判定定理 语言叙述符号表示图形表示 平面外一条直线与此平面内的一条直线平 行,则该直线与此平面平行 ?? ? ?? a?α b?α a∥b ?a∥α 思考若一条直线平行于一个平面内的一条直线,则这条直线和这个平面平行吗? 答根据直线与平面平行的判定定理可知该结论错误. 知识点二平面与平面平行的判定定理 语言叙述符号表示图形表示 一个平面内的两条相交直线与另一个平 面平行,则这两个平面平行 ?? ? ?? a?α,b?α a∩b=A a∥β,b∥β ?α∥β 思考如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面也平行吗?答不一定.这条直线与另一个平面平行或在另一个平面内. 题型一直线与平面平行的判定定理的应用 例1如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、 DA的中点. 求证:(1)EH∥平面BCD; (2)BD∥平面EFGH. 证明(1)∵EH为△ABD的中位线, ∴EH∥BD.
∵EH?平面BCD,BD?平面BCD, ∴EH∥平面BCD. (2)∵BD∥EH,BD?平面EFGH, EH?平面EFGH, ∴BD∥平面EFGH. 跟踪训练1在四面体A-BCD中,M,N分别是△ABD和△BCD的重心,求证:MN∥平面ADC. 证明如图所示,连接BM,BN并延长,分别交AD,DC于P,Q两 点,连接PQ. 因为M,N分别是△ABD和△BCD的重心, 所以BM∶MP=BN∶NQ=2∶1. 所以MN∥PQ. 又因为MN?平面ADC,PQ?平面ADC, 所以MN∥平面ADC. 题型二面面平行判定定理的应用 例2如图所示,在三棱柱ABC-A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1. 证明由棱柱性质知, B1C1∥BC,B1C1=BC, 又D,E分别为BC,B1C1的中点, 所以C1E綊DB,则四边形C1DBE为平行四边形, 因此EB∥C1D, 又C1D?平面ADC1, EB?平面ADC1, 所以EB∥平面ADC1. 连接DE,同理,EB綊BD,
线面平行的判定定理和性质定理 教学目的: 1. 掌握空间直线和平面的位置关系; 2. 直线和平面平行的判定定理和性质定理,灵活运用线面平行的判定定理和性质定 掌握理实现“线线”“线面”平行的转化 教学重点:线面平行的判定定理和性质定理的证明及运用 教学难点:线面平行的判定定理和性质定理的证明及运用 授课类型:新授课 课时安排: 1 课时 教具:多媒体、实物投影仪 内容分析: 本节有两个知识点,直线与平面和平面与平面平行,直线与平面、平面与平面 平行特征性质这也可看作平行公理和平行线传递性质的推广直线与平面、平面与平面平行判定的依据是线、线平行这些平行关系有着本质上的联系 通过教学要求学生掌握线、面和面、面平行的判定与性质这两个平行关系是下一大节学习共面向量的基础 前面3 节主要讨论空间的平行关系,其中平行线的传递性和平行平面的性质是 这三小节的重点 教学过程: 一、复习引入:
1 空间两直线的位置关系 ( 1 )相交;( 2 )平行;( 3)异面 2. 公理 4 :平行于同一条直线的两条直线互相平行 推理模式: a // b,b // c a // c . 3. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等 4. 等角定理的推论 : 如果两条相交直线和另两条相交直线分别平行 ,那么这两条直线 所成的锐角 (或直角 )相等 . 5. 空间两条异面直线的画法 a b b D 1 C 1 b a a A 1 B 1 D C A B 6. .异面直线定理: 连结平面内一点与平面外一点的直线, 和这个平面内不经过此点的直线是异面直线 推理模式: A , B ,l , B l AB 与 l 是异面直线 7. .异面直线所成的角: 已知两条异面直线 a, b ,经过空间任一点 O a b ′ 作直线 a // a, b // b , a , b 所成的角的大小与点 O 的选择无关,把 b O a , b 所成的锐角 (或直角) 叫异面直线 a, b 所成的角 (或夹角).为 了简便,点 O 通常取在异面直线的一条上 异面直线所成的角的范围: (0, ] 2 8. .异面直线垂直: 如果两条异面直线所成的角是直角, 则叫两条异面直线垂直. 两
专题平面几何的四个重 要定理 SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#
竞赛专题讲座06 -平面几何四个重要定理 四个重要定理: 梅涅劳斯(Menelaus)定理(梅氏线) △ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、 Q、R共线的充要条件是。 塞瓦(Ceva)定理(塞瓦点) △ABC的三边BC、CA、AB上有点P、Q、R,则AP、BQ、CR共点 的充要条件是。 托勒密(Ptolemy)定理 四边形的两对边乘积之和等于其对角线乘积的充要条件是该 四边形内接于一圆。 西姆松(Simson)定理(西姆松线) 从一点向三角形的三边所引垂线的垂足共线的充要条件是 该点落在三角形的外接圆上。 例题: 1.设AD是△ABC的边BC上的中线,直线CF交AD于F。求 证:。
【分析】CEF截△ABD→(梅氏定理) 【评注】也可以添加辅助线证明:过A、B、D之一作CF的平行线。 2.过△ABC的重心G的直线分别交AB、AC于E、F, 交CB于D。 求证:。 【分析】连结并延长AG交BC于M,则M为BC的 中点。 DEG截△ABM→(梅氏定理) DGF截△ACM→(梅氏定理) ∴===1 【评注】梅氏定理 3. D、E、F分别在△ABC的BC、CA、AB边上, ,AD、BE、CF交成△LMN。 求S△LMN。 【分析】 【评注】梅氏定理 4.以△ABC各边为底边向外作相似的 等腰△BCE、△CAF、△ABG。求证:AE、 BF、CG相交于一点。
【分析】 【评注】塞瓦定理 5.已知△ABC中,∠B=2∠C。求证:AC2=AB2+AB·BC。 【分析】过A作BC的平行线交△ABC的外接圆于D,连结BD。则 CD=DA=AB,AC=BD。 由托勒密定理, AC·BD=AD·BC+CD·AB。 【评注】托勒密定理 6.已知正七边形A 1A2A3A4A5A6A7。 求证:。(第21届全苏数学竞赛) 【分析】 【评注】托勒密定理 7.△ABC的BC边上的高AD的延长线交 外接圆于P,作PE⊥AB于E,延长ED交 AC延长线于F。 求证:BC·EF=BF·CE+BE·CF。 【分析】 【评注】西姆松定理(西姆松线) 8.正六边形ABCDEF的对角线AC、CE分别被内分点M、N分成的 比为AM:AC=CN:CE=k,且B、M、N共 线。求k。(23-IMO-5) 【分析】 【评注】面积法 9. O为△ABC内一点,分别以d a、d b、d c表示O到BC、CA、AB的距离,以R a、 R b、R c表示O到A、B、C的距离。
两个平面平行的判定和性质 年级__________ 班级_________ 学号_________ 姓名__________ 分数____ 一、选择题(共21题,题分合计105分) 1.夹在两平行平面之间的两条线段的长度相等的充要条件是 A.两条线段同时与平面垂直 B.两条线段互相平行 C.两条线段相交 D.两条线段与平面所成的角相等 2.平面α与平面β平行,它们之间的距离为d (d >0),直线a 在平面α内,则在平面β内与直线a 相距2d 的直线有 A.一条 B.二条 C.无数条 D.一条也没有 3.以下四个命题:①P A ?PB 是平面α的两条相等的斜线段,则它们在平面α内的射影必相等;②平面α内的两条直线l 1? l 2,若l 1?l 2均与平面β平行,则α//β;③若平面α内有无数个点到平面β的距离相等,则α//β;④α?β为两相交平面,且α不垂直于β,α内有一定直线a ,则在平面β内有无数条直线与a 垂直.其中正确命题的个数是 A.1个 B.2个 C.3个 D.4个 4.已知直线l ⊥平面α,直线m 平面β,有下列四个命题:(1) α∥β?l ⊥m ;(2) α⊥β?l ∥m ;(3)l ∥m ?α⊥β;(4)l ⊥ m ?α∥β,其中正确的两个命题是: A.(1)与 (2) B.(1)与(3) C.(2)与(4) D.(3)与(4)
5.两个平面平行的条件是 A.一个平面内一条直线平行于另一个平面 B.一个平面内两条直线平行于另一个平面 C.一个平面内的无数条直线平行于另一个平面 D.一个平面内的任一条直线平行于另一个平面 6.两平面α与β平行,α ? a,下列四个命题中 ①α与β内的所有直线平行 ②α与β内的无数条直线平行 ③α与β内的任何一条直线都不垂直 ④α与β无公共点 其中真命题的个数是 A.1 B.2 C.3 D.4 7.给出下列命题: ①平行于同一条直线的两平面平行;②垂直于同一平面的两平面平行;③一个平面内有无数条直线和另一个平面平行,则这两个平面平行④一条直线和两个平面所成的角相等,则这两个平面平行. 其中真命题的个数是 A.0 B.1 C.2 D.3 8.在下列条件中,可判断平面α与β平行的是 A.α?β都垂直于平面r. B.α内存在不共线的三点到β的距离相等. C.l,m是α内两条直线,且l∥β,m∥β. D.l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β. 9.给出下列命题: ①平行于同一条直线的两平面平行;②垂直于同一平面的两平面平行;③一个平面内有无数条直线和另一个平面平行,则这两个平面平行④一条直线和两个平面所成的角相等,则这两个平面平行. 其中真命题的个数是 A.0 B.1 C.2 D.3 10.给出以下命题: (1)平面α∩平面β=直线l,点P∈α,点P∈β,则P∈l (2)过平面的一条斜线作这个平面的垂面有且只有一个
第十九讲平面几何中的几个著名定理 几何学起源于土地测量,几千年来,人们对几何学进行了深入的研究,现已发展成为一门具有严密的逻辑体系的数学分支.人们从少量的公理出发,经过演绎推理得到不少结论,这些结论一般就称为定理.平面几何中有不少定理,除了教科书中所阐述的一些定理外,还有许多著名的定理,以这些定理为基础,可以推出不少几何事实,得到完美的结论,以至巧妙而简捷地解决不少问题.而这些定理的证明本身,给我们许多有价值的数学思想方法,对开阔眼界、活跃思维都颇为有益.有些定理的证明方法及其引伸出的结论体现了数学的美,使人们感到对这些定理的理解也可以看作是一种享受.下面我们来介绍一些著名的定理. 1.梅内劳斯定理 亚历山大里亚的梅内劳斯(Menelaus,约公元100年,他和斯巴达的Menelaus是两个人)曾著《球面论》,着重讨论球面三角形的几何性质.以他的名子命名的“梅内劳斯定理”现载在初等几何和射影几何的书中,是证明点共线的重要定理. 定理一直线与△ABC的三边AB,BC,CA或延长线分别相交于X,Y,Z,则 证过A,B,C分别作直线XZY的垂线,设垂足分别为Q,P,S,见图3-98.由△AXQ∽△BXP得
同理 将这三式相乘,得 说明(1)如果直线与△ABC的边都不相交,而相交在延长线上,同样可证得上述结论,但一定要有交点,且交点不在顶点上,否则定理的结论中的分母出现零,分子也出现零,这时定理的结论应改为 AX×BY×CZ=XB×YC×ZA, 仍然成立. (2)梅内劳斯定理的逆定理也成立,即“在△ABC 的边AB和AC上分别取点X,Z,在BC的延长线上取点Y,如果 那么X,Y,Z共线”.梅内劳斯定理的逆定理常被用来证明三点共线. 例1 已知△ABC的内角∠B和∠C的平分线分别为BE和CF,∠A的外角平分线与BC的延长线相交于D,求证:D,E,F共线. 证如图3-99有 相乘后得
§2.2.1 直线与平面平行的判定 一、学习目标: (1)理解并掌握直线与平面平行的判定定理; (2)进一步培养学生观察、发现的能力和空间想象能力; 二、学习重点与难点 重点:直线与平面平行的判定定理及应用。 难点:直线与平面平行的判定定理的探索及应用。 三、教学过程 (一)知识准备、新课引入 α 提问2:今天我们针对直线与平面平行的位置关系进行探究。根据直线与平面平行的定义(没有公共点)来判定直线与平面平行你认为方便吗?谈谈你的看法,并指出是否有别的判定途径。 (二)探求判定定理 1、直观感知 提问:根据同学们日常生活的观察,你们能感知到并举出直线与平面平行的具体事例吗? 2、动手实践 教师取出预先准备好的直角梯形泡沫板演示: 当把互相平行的一边放在讲台桌面上并转动,观察另一边与桌面的位置给人以的感觉, 当把直角腰放在桌面上并转动,观察另一边与桌面给人的印象是 3、探究思考 (1)上述演示的直线与平面位置关系为何有如此的不同?关键是什么因素起了作用呢? (2)如果平面外的直线a与平面α内的一条直线b平行,那么直线a与平面α平行吗?
4、归纳确认: 直线和平面平行的判定定理: 文字语言: 图形语言: 符号语言: 简单概括:(内外)线线平行 线面平行 温馨提示: 作用:判定或证明线面平行。 关键:在平面内找(或作)出一条直线与面外的直线平行。 思想:空间问题转化为平面问题 5、思考:你能否尝试证明一下线面平行判定定理? (三)应用定理,巩固与提高 例1:已知:空间四边形ABCD 中,E 、F 分别是AB 、AD 试判断EF 与平面BCD 的关系,并予以证明 变式:空间四边形ABCD 中,E 、F 分别是AB 、AD 上的点, 且AE= 31AB ,AF=3 1AD 求证:EF ∥平面BCD . A B C D E F
【认识平面几何的61个著名定理,自行画出图形来学习,★部分要求证明出来】 ★1、勾股定理(毕达哥拉斯定理) ★2、射影定理(欧几里得定理) ★3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分 4、四边形两边中心的连线和两条对角线中心的连线交于一点 5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。 ★6、三角形各边的垂直平分线交于一点。 ★7、从三角形的各顶点向其对边所作的三条垂线交于一点 8、设三角形ABC 的外心为O ,垂心为H ,从O 向BC 边引垂线,设垂足不L ,则AH=2OL 9、三角形的外心,垂心,重心在同一条直线上。 10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上, 11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上 12、库立奇大上定理:(圆内接四边形的九点圆) 圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。 ★13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式: ()()()s c s b s a s r ---=,s 为三角形周长的一半 ★14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点 15、中线定理:(巴布斯定理)设三角形ABC 的边BC 的中点为P ,则有AB 2+AC 2=2(AP 2+BP 2) 16、斯图尔特定理:P 将三角形ABC 的边BC 分成m 和n 两段,则有n×AB 2+m×AC 2=BC×(AP 2+mn ) 17、波罗摩及多定理:圆内接四边形ABCD 的对角线互相垂直时,连接AB 中点M 和对角线交点E 的直线垂直于CD 18、阿波罗尼斯定理:到两定点A 、B 的距离之比为定比m:n (值不为1)的点P ,位于将线段AB 分成m:n 的内分点C 和外分点D 为直径两端点的定圆周上 ★19、托勒密定理:设四边形ABCD 内接于圆,则有AB×CD+AD×BC=AC×BD
文字语言:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行. 符号语言:α?a ,α?b ,且b a //α//a ?. 图形语言: 定理二(平面与平面平行的判定定理) 文字语言:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行. 符号语言:β?a ,β?b ,P b a = ,α//a ,α//b αβ//?. 图形语言: 定理三(直线与平面平行的性质定理) 文字语言:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行. 符号语言:α//a ,β?a ,且b =βα b a //?. 图形语言: 证明:因为b =βα ,所以α?b . 又因为α//a ,所以a 与b 无公共点. 又因为β?a ,β?b ,所以b a //. 定理四(平面与平面平行的性质定理) 文字语言:如果两个平行平面同时和第三个平面相交,那么它们的交线平行. 符号语言:βα//,a =γα ,b =γβ b a //?. 图形语言: α b a P βα b a a α βa b αγ a b αβ
文字语言:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直. 符号语言:a c ⊥,b c ⊥,P b a = ,α?a ,α?b α//c ?. 图形语言: 定理六(平面与平面垂直的判定定理) 文字语言:一个平面过另一个平面的垂线,则这两个平面垂直. 符号语言:α⊥a ,β?a ,αβ⊥?. 图形语言: 定理七(直线与平面垂直的性质定理) 文字语言:垂直于同一平面的两条直线平行. 符号语言:α⊥a ,α⊥b b a //?. 图形语言: 定理八(平面与平面垂直的性质定理) 文字语言:对于两个相互垂直的平面,在一个平面内垂直交线的直线垂直另一平面. 符号语言:βα⊥,m =βα ,β?a ,m a ⊥α⊥?a . 图形语言: c a b αP αβa αb a βa m α
托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组 对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之 和). 即:ABCD AB CD AD BC AC BD ?+?≥? 定理:在四边形中,有: ABCD 并且当且仅当四边形内接于圆时,等式成立; () ABCD E BAE CAD ABE ACD AB BE ABE ACD AB CD AC BE AC CD AB AE BAC EAD ABC AED AC AD BC ED AD BC AC ED AC AD AB CD AD BC AC BE ED AB CD AD BC AC BD E BD A B C ∠=∠∠=∠ ??∴=??=? =∠=∠∴?? ∴=??=? ∴?+?=?+ ∴?+?≥? 证:在四边形内取点,使, 则:和相似 又且和相似 且等号当且仅当在上时成立,即当且仅当、、、 一、直接应用托勒密定理 例1如图2,P是正△ABC外接圆的劣弧上任一点(不与B、C重合), 求证:PA=PB+PC. 分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为 繁冗.若借助托勒密定理论证,则有PA·BC=PB·AC+PC·AB, ∵AB=BC=AC.∴PA=PB+PC. 二、完善图形借助托勒密定理 例2证明“勾股定理”:在Rt△ABC中,∠B=90°,求证:AC2=AB2+BC2 证明:如图,作以Rt△ABC的斜边AC为一对角线的矩形ABCD,显然ABCD是 圆内接四边形. 由托勒密定理,有AC·BD=AB·CD+AD·BC.① 又∵ABCD是矩形,∴AB=CD,AD=BC,AC=BD.② 把②代人①,得AC2=AB2+BC2. 例3如图,在△ABC中,∠A的平分线交外接∠圆于D,连结BD, 求证:AD·BC=BD(AB+AC). 证明:连结CD,依托勒密定理,有AD·BC=AB·CD+AC·BD. ∵∠1=∠2,∴BD=CD. 故AD·BC=AB·BD+AC·BD=BD(AB+AC). 三、构造图形借助托勒密定理 例4若a、b、x、y是实数,且a2+b2=1,x2+y2=1.求证:ax+by≤1. 证明:如图作直径AB=1的圆,在AB两边任作Rt△ACB和Rt△ADB, 使AC=a,BC=b,BD=x,AD=y. 由勾股定理知a、b、x、y是满足题设条件的. 据托勒密定理,有AC·BD+BC·AD=AB·CD. ∵CD≤AB=1,∴ax+by≤1. 四、巧变原式妙构图形,借助托勒密定理 例5已知a、b、c是△ABC的三边,且a2=b(b +c),求证:∠A=2∠B. 分析:将a2=b(b+c)变形为a·a=b·b+bc,从而联想到托勒密定理,进 而构造一个等腰梯形,使两腰为b,两对角线为a,一底边为c. 证明:如图,作△ABC 的外接圆,以A为圆心,BC为半径作弧交圆于 D,连结BD、DC、DA.∵AD=BC,ACD BDC =∴∠ABD=∠BAC. 又∵∠BDA=∠ACB(对同弧),∴∠1=∠2. 依托勒密定理,有BC·AD=AB·CD+BD·AC.① 而已知a2=b(b+c),即a·a=b·c+b2.② ∴∠BAC=2∠ABC. 五、巧变形妙引线 借肋托勒密定理 例6在△ABC中,已知∠A∶∠B∶∠C=1∶2∶4, 分析:将结论变形为AC·BC+AB·BC=AB·AC,把三角形和圆联系起 来,可联想到托勒密定理,进而构造圆内接四边形. 如图,作△ABC的外接圆,作弦BD=BC,边结AD、CD. 在圆内接四边形ADBC中,由托勒密定理, 有AC·BD+BC·AD=AB·CD 易证AB=AD,CD=AC,∴AC·BC+BC·AB=AB·AC, 1.已知△ ABC 中,∠ B=2∠ C。求证:AC2=AB2+AB·BC。 【分析】过A作BC的平行线交△ABC的外接圆于D,连结BD。 则CD=DA=AB,AC=BD。由托勒密定理,AC·BD=AD·BC+CD·AB。 2.ABC BC P BC AC AB PK PL PN BC AC AB PK PL PM ? =+ 由外接圆的弧上一点分别向边、与作垂线、和, 求证:
7.3平行线的判定 【知识沙盘】 【学习目标】 1.会根据基本事实“同位角相等,两直线平行”来规范证明“内错角相等,两直线平行”“同旁内角互补,两直线平行”. 2.能用平行线的判定解决一些简单的问题. 【重点】1. 能规范证明平行线的判定定理. 2.平行线判定定理的简单应用. 【难点】用数学语言和符号语言对文字命题的表述. 【学情分析】 经过前面的学习我们发现,我们得打的任何一个结论都要有依据。而我们根据这些“依据”推理、证明,从而得到结论的过程叫做证明。在“同位角相等,两直线平行”的基本事实下,我们将通过演绎推理得到“内错角相等,两直线平行”和“同旁内角互补,两直
线平行”,从而得到平行线的判定定理. 【教学过程】 一、导入 你能用折纸的方法折出两条平行线吗?你的依据是什么?通过前面的学习,我们知道了“同位角相等,两直线平行”的基本事实,那我们能利用它证明另外两个判定定理吗?让我们一起来探究吧! 二、自主学习 阅读并完成学习指导书的知识储备,完成【自主学习】A级和B级. 三、交流研讨 出示答案,自主订正 四、精讲部分 (一)不讲内容: ①知识储备、归类总结 ②A级1,2 (二)略讲内容: ①B级 3 3.蜂房的顶部由三个全等的四边形围成,每个四边形的形状如图所示,其中 o = B70 = ∠.试确定这个四边形对边的位置关系,并证明你的结论. D ∠ = C A110 = ∠ ∠,o
直线平行) (同旁内角互补,两BD(等式的性质) B(已知) B,直线平行) (同旁内角互补,两(等式的性质) (已知) ,理由:BD解:C A A A DC AB D A D A C A DC A B O O //18070110//18070110////o o o o ∴=∠+∠∴=∠=∠∴=∠+∠∴=∠=∠ (三)精讲内容: ① C 级 4 4.如图,点D,E分别在AB 和AC 上,.ABC BE ∠平分 (1)若DEB DBE ∠=∠,求证:BC DE //. (2)若BC DE //,求证:BDE ?为等腰三角形. (3)在(1)的条件下,若O EBC 25=∠,求BDE ∠的度数.
§9.2.2 直线、平面平行的判定(2) 3、直线与平面 时间:2018、12、7 (总第65课时) 一、教学目标: 1、知识与技能 理解并掌握两平面平行的判定定理。 2、过程与方法 让学生通过观察实物及模型,得出两平面平行的判定。 3、情感、态度与价值观 进一步培养学生空间问题平面化的思想。 二、教学重点、难点 重点:两个平面平行的判定。 难点:判定定理、例题的证明。 三、学法与教学用具 1、学法:学生借助实物,通过观察、类比、思考、探讨,教师予以启发,得出两平面平行的判定。 2、教学用具:投影仪、投影片、长方体模型 四、教学思想 (一)创设情景、引入课题 引导学生观察、思考教材第57页的观察题,导入本节课所学主题。 (二)研探新知 1、问题: (1)平面β内有一条直线与平面α平行,α、β平行吗? (2)平面β内有两条直线与平面α平行,α、β平行吗? 通过长方体模型,引导学生观察、思考、交流,得出结论。 两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。 符号表示: a β b β
a∩b = P β∥α a∥α b∥α 教师指出:判断两平面平行的方法有三种: (1)用定义; (2)判定定理; (3)垂直于同一条直线的两个平面平行。 2、例2 引导学生思考后,教师讲授。 例子的给出,有利于学生掌握该定理的应用。 (三)自主学习、加深认识 练习:教材第59页1、2、3题。 学生先独立完成后,教师指导讲评。 (四)归纳整理、整体认识 1、判定定理中的线与线、线与面应具备什么条件? 2、在本节课的学习过程中,还有哪些不明白的地方,请向老师提出。(五)作业布置 第65页习题2.2 A组第7题。 板书设计: 1、定义 2、判定 3、性质
平面几何的几个重要的定理 一、梅涅劳斯定理: 1=??=??B A A C C B C B A h h h h h h RB AR QA CQ PC BP l C B A h h h 的垂线的长度,则:到直线 、、分别是、、证:设 注:此定理常运用求证三角形相似的过程中的 线段成比例的条件; 。 的交点,证明:与是的中点,是上,在点 的平分线,是是斜边上的高,中,:若直角例CE //BF CK DE F AC D AK E ACK CE CK ABC ∠?11PC BP R Q P AB CA BC ABC ABC l 1=??RB AR QA CQ ,则 、、的延长线分别交于或它们、、的三边的顶点,并且与不经过:若直线定理??CE //BF CKE FKB KE BK KC KF BE BK FC KF BE BK BC BP AC EP AC CK AE EK FC KF 1FC KF EK AE DA CD F E D ACK EP CK EP BC EBC CE BH 90HCB ACE HCB HBC ACE HBC ACK EBC BH B EBC ∴?∴= ====??=∴⊥?=∠+∠=∠+∠∠=∠∠=∠∠?????= 依分比定理有:=即:=于是依梅涅劳斯定理有:、、和三点对于,则:上的高作为等腰三角形 即:则:的平分线中,作在证:Θ
1 11 111111111D B D A : C B C A B D AD :BC AC D C B A D C B A K 1=,试证:、、、和、、、线分别交这四条直线于引四条直线,另两条直】从点【练习 注:此定理常用于证明三点共线的问题,且常需要多次使用 再相乘; 共线; 、、证明点引的垂线的垂足, 、、向是从点、、的外接圆上;位于点例111111C B A AB CA BC P C B A ABC P .2? 三点共线; 、、综上可得:也重合与的延长线上时,同在与类似地可证得当矛盾=这与于是可得即这时设必定重合,不然的话,与线段上,则同在与若的延长线上; 线段上,或者同在或者同在与因此,或边上的点的个数也为三点中,位于、、由于在同一直线上的= ,则:又得: ,于是由定理交于与直线证:设直线R Q P R R AB R R BR AR BR AR BR AR BR AR ,BR BR ,AR AB AR AB ,AR AR R R AB R R AB AB R R 20ABC R Q P RB AR B R AR 1RB AR QA CQ 1B R AR QA CQ 1R AB PQ ''' ' ' ' ' ' ''''''''' '> <-<->=??=???PC BP PC BP Θ三点共线; 、、求证:, ,这时若或边上的点的个数为三点中,位于、、三点,并且 上或它们的延长线上的、、的三边分别是、、:设定理R Q P PC BP 20ABC R Q P AB CA BC ABC R Q P 21RB AR QA CQ =???? C B A 1 A 1 B 1 C 三点共线; 、、依梅涅劳斯定理可知,=可得 且将上面三条式子相乘, 证:易得:1111 1 1111111111C B A 1BC AC AB CB CA BA 180PBA PCA ,PCB PAB ,PBC PAC PBA cos PB PAB cos AP BC AC PAC cos AP PCA cos CP AB CB , PCB cos CP PBC cos BP CA BA ???=∠+∠∠=∠∠=∠∠?∠?-=∠?∠?-=∠?∠?-=Θ
平行线的判定定理和性质定理 [一]、平行线的判定 一、填空 1.如图1,若∠A=∠3,则 ∥ ; 若∠2=∠E ,则 ∥ ; 若∠ +∠ = 180°,则 ∥ . 2.若a⊥c,b⊥c,则a b . 3.如图2,写出一个能判定直线a ∥b 的条件: . 4.在四边形ABCD 中,∠A +∠B = 180°,则 ∥ ( ). 5.如图3,若∠1 +∠2 = 180°,则 ∥ 。 6.如图4,∠1、∠2、∠3、∠4、∠5中, 同位角有 ; 内错角有 ;同旁内角有 . 7.如图5,填空并在括号中填理由: (1)由∠ABD =∠CDB 得 ∥ ( ); (2)由∠CAD =∠ACB 得 ∥ ( ); (3)由∠CBA +∠BAD = 180°得 ∥ ( ) 8.如图6,尽可能多地写出直线l 1∥l 2的条件: . 9.如图7,尽可能地写出能判定AB∥CD 的条件来: . 10.如图8,推理填空: (1)∵∠A =∠ (已知), ∴AC∥ED( ); (2)∵∠2 =∠ (已知), ∴AC∥ED( ); (3)∵∠A +∠ = 180°(已知), ∴AB∥FD( ); (4)∵∠2 +∠ = 180°(已知), ∴AC∥ED( ); 二、解答下列各题 11.如图9,∠D =∠A,∠B =∠FCB,求证:ED∥C F . A C B 4 1 2 3 5 图4 a b c d 1 2 3 图3 A B C E D 1 2 3 图1 图2 4 3 2 1 5 a b 1 2 3 A F C D B E 图8 E B A F D C 图9 A D C B O 图5 图6 5 1 2 4 3 l 1 l 2 图7 5 4 3 2 1 A D C B
§2.2.1 直线与平面平行的判定 (选自人教A版必修②第二章第二节第一课时) 一、教材分析 本节教材选自人教A版数学必修②第二章第二节第一课时,主要内容是直线与平面平行的判定定理的探究与发现、归纳概括、练习与应用。它是在前面已学空间点、线、面的位置关系的基础上,结合有关的实物模型,通过直观感知、操作确认(合情推理,不要求证明)归纳出直线与平面平行的判定定理。学线面平行判定是三大平行判定(线线平行、线面平行、面面平行)的核心,也是高考的高频考点之一,学好线面平行对后续学习面面平行及三大垂直的判定与性质等内容,具有良好的示范作用,同时,它在立体几何学习中起着承上启下的作用,具有重要的意义与地位。本节课的学习对培养学生空间想象能力与逻辑推理能力起到重要作用。线面平行的判定蕴含的数学思想方法主要有数形结合与化归与转化思想。 二、学情分析 本节课的教学对象是高一的学生,他们具备一定的由形象思维转化为逻辑思维的能力。学生在此前已经学习了直线与直线平行的性质及判定、直线与平面平行的定义,对直线与平面平行有了一定的认识,这些都为学生学习本节课做了准备。同时,由于本节课与生活实际相结合,学生的学习兴趣、参与度会比较大。但是由于学生处于学习空间立体几何的初始阶段,学习立体几何所具备的语言表达及空间感与空间想象能力不够,特别是对线面平行(空间立体)转化为线线平行(平面)的化归与转化思想,这是学生首次接触的思想方法,应加以必要的强化与引导。 三、教学目标 (一)知识技能目标 (1)理解直线与平面平行的判定定理并能进行简单应用; (2)培养学生观察、发现问题的能力和空间想象能力。 (二)过程方法目标 (1)启发式:以实物(门、书、直角梯形卡纸)为媒介,启发、诱导学生逐步经历定理的直观感知过程;