北航数据结构课件第一章
- 格式:pps
- 大小:484.50 KB
- 文档页数:27










祝同学们
新学期愉快
学习进步!
课程名称:数据结构
教材名称:《数据结构教程》
唐发根刘又诚编著
北京航空航天大学出版社1996
《数据结构》
唐发根编著
科学出版社1998
开设本课程的必要性以及课程的特点:
1. 计算机专业重要的专业基础课之一.
2. 需要有关“程序设计语言”和“离散数学
”
的知识作为课程的基础.
3. 实践性较强.
第一章绪论
1.1 什么是数据结构
描述客观事物的数字、字符以及一切能够输入到计算机中,并且能够被计算机程序处理的符号的集合。
数据这个集合中的一个一个元素。
具有相同特性的数据元素的集合。
数据元素之间具有的关系(联系)。
数据
数据元素数据对象结构
一. 名词术语
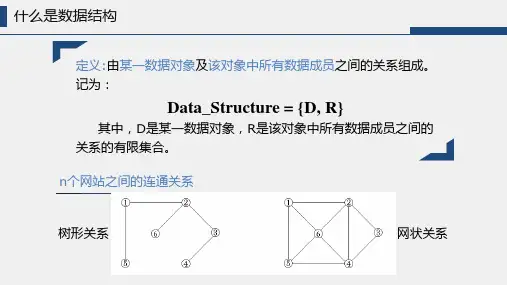
二. 数据结构的定义
1.数据元素之间的联系称之为结构,数据结构就是具有结构的数据元素的集合。
2. 数据结构是一个二元组
Data-Structure=(D,R)
其中,D是数据元素的有限集合,R是D上的关系的集合。
数据元素之间具有的逻辑关系(结构)。
线性关系(线性结构)
如线性表、数组、堆栈、队列、串、文件等
具有某种逻辑结构的数据在计算机存储器中的
存储方式(存储映象)。
物理结构也被称为存储结构。
顺序存储结构
链式存储结构
用一组地址连续的存储单元依次存放数据元素,数据元素之间的逻辑关系通过元素的地址直接反映。
用一组地址任意的存储单元依次存放数据元素,数据元素之间的逻辑关系通过指针间接地反映。
非线性关系(非线性结构)
如树、二叉树、图等
物理结构逻辑结构
例
刘晓光马广生
王民…
张玉华
男
男…
女
男汉回
壮
…
汉
1617
21
…
25
…
…………姓名
性别
民族
年龄
其他逻辑结构:线性结构(线性表)a 1a 2a 3 a 30
…
d 1
d 2 d 3
d 4
…
d 30
a 2
a 1
a 3
a 4
a 30
存储结构:
1. 顺序存储结构
:
2. 链式存储结构:
…
d 1
d 2 d 3
d 4
a 1
a 2
a 3
a 30
∧
list
…
a 2
a 1
a 4
a 3
d 4
d 1
d 5
d
3
1.研究数据元素之间的客观联系。
2. 研究具有某种逻辑关系的数据在计算机存储器内的存储方式。
3. 研究如何在数据的各种结构(逻辑的和物理的)的基础上对数据实施一系列有效的基本操作。
三. 数据结构课程研究的主要内容
(算法)
(逻辑结构)(存储结构)
1.2 算法及其描述
输入一个完整的算法应该满足下面五个基本标准:确定性有穷性输出一. 算法及其性质
(2).算法是由人们组织起来准备加以实施的一系
列有限的基本步骤。
1.算法的定义
2.算法的性质
(1).算法
是用来解决某个特定课题的指令的集合。
二. 算法的描述
1. 采用自然语言来描述
问题:求两个正整数M与N的最大公因子。
(1) M除以N,将余数送中间变量R;
(2) 测试余数R是否等于零?
a) 若R等于零,求得的最大公因子为当前N
的值, 算法到此结束。
b) 若R不等于零,将N送入M,将R送N,重
复算法的(1)和(2)。
2. 采用程序流程图的形式来描述
M 除以N 的余数送R
余数R 为0否?
将N 送M 将R 送N
输出N 的值
结束
开始
yes
no
采用某种具体程序语言来描述3.
COMFACTOR( M, N )
int M, N;
{
int R;
while( 1 )
{
R=M % N;
if (R==0)
return N;
M=N;
N=R;
}
}
4. 设计一种既脱离某种具体的程序设计语言,
又具有各种程序设计语言的共同特点的形
式化语言来描述
SPARKS语言,一种类Pascal
一. 算法格式
一个完整的用SPARKS语言编写的算法必须具有以下两种格式之一。
procedure算法名(参数表)语句串
end function算法名(参数表)语句串
end
1.3 SPARKS
语言简介
二. 语句
1.赋值语句:(1) if 条件then [ 语句串](2) if
条件then [ 语句串1 ]
else
[ 语句串2 ]
V←E
2. 条件语句(两种)
3.循环语句(四种)
while 循环条件do
语句串
end
repeat
语句串
until 循环结束条件for v←e
1
to/downto e2 by e3do 语句串
end
loop
语句串
forever
return
return (表达式)
call 算法名(参数表)变量名←算法名(参数表)
case
:条件1:语句串1:条件2:语句串2
... ...... ...:条件n :语句串n :else :语句串n+1end
4. 分情况语句
5. 算法调用语句
6.返回语句
goto 语句标号
stop
// 注释内容//
exit
read(参数表)print(参数表)
7. 转移语句
8. 出口语句
9. 输入/输出语句
10. 停止语句
11.
注释
三. 常用的符号和函数
1. ⎣X⎦表示取不大于x的最大整数,如⎣
2.8⎦= 2。
2. ⎡X⎤表示取不小于x的最小整数,如⎡2.1⎤= 3。
3.MAX与MIN分别表示取最大值和最小值;
4.m MOD n表示m对n取模。
5. 算术运算符有+、-、⨯、/、↑(幂);
6. 关系运算符有=、≠、<、>、≤、≥;
7. 逻辑运算符有and、or、not。
例
求两个n阶矩阵的乘积:
procedure MATRIX( A, B, C, n )
for i←1 to n do
for j←1 to n do
C[i, j]←0
for k←1 to n do
C[i, j]←C[i, j]+A[i, k] B[k, j]
end
end
end
end
1.4 算法分析
算法分析是指对算法质量优劣的评价。
除正确性外,应从三个方面分析一个算法:1.依据算法编写的程序在计算机中运行时间多少的度量,称之为时间复杂度。
2.依据算法编写的程序在计算机中占存储空间多少的度量,称之为空间复杂度。
3.其他方面。
如算法的可读性、可移植性以及易测试性的好坏。
一. 时间复杂度
一个程序在计算机中运行时间的多少与诸多因素有关,其中主要有:
1. 问题的规模。
2. 源程序编译的强弱以及所产生的机器
代码质量的优劣。
3. 机器执行一条指令的时间长短。
4. 程序中语句的执行次数。
频度统计法
以语句执行的次数的多少作为算法的时间量度的分析方法称为频度统计法。
一条语句的频度是指该语句被执行的次数,而整个算法的频度是指算法中所有语句的频度之和。
procedure MATRIX( A, B, C, n )
for i ←1 to n do for j ←1 to n do C[i, j]←0for k ←1 to n do C[i, j]←C[i, j]+A[i, k] B[k, j]end
end
end
end
--------------------------n+1-------------------n(n+1)----------------------------------n 2-----------n 2(n+1)----n 3算法的频度:
f(n)= n+1 + n(n+1) + n 2+ n 2(n+1) + n
3= 2n 3+ 3n 2
+ 2n + 1
当n →∞时,有f(n)/g(n)=常数≠0,
则称函数f(n)与g(n)同阶,或者说,f(n)与g(n)同一个数量级,记作
f(n)=O(g(n))
称上式为算法的时间复杂度,或称该算法的时间复杂度为O(g(n))。
其中,n 为问题的规模(大小)的量度。
算法的时间复杂度为O(n 3)lim(f(n)/g(n)) =lim((2n 3+ 3n 2+ 2n + 1)/n 3)=2n →∞n
→∞
符号O 的的数学定义。