
线段的垂直平分线和角平分线讲义
教学重点:掌握线段垂直平分线和角平分线的性质与判定,并能够正确叙述结论
及正确书写证明过程,熟悉作为证明基础的几条公理的内容,通过学习掌握证明学习目标的基本步骤和书写格式
教学难点:熟练应用垂直平分线、角平分线的性质定理在实际问题中的运用
教学内容
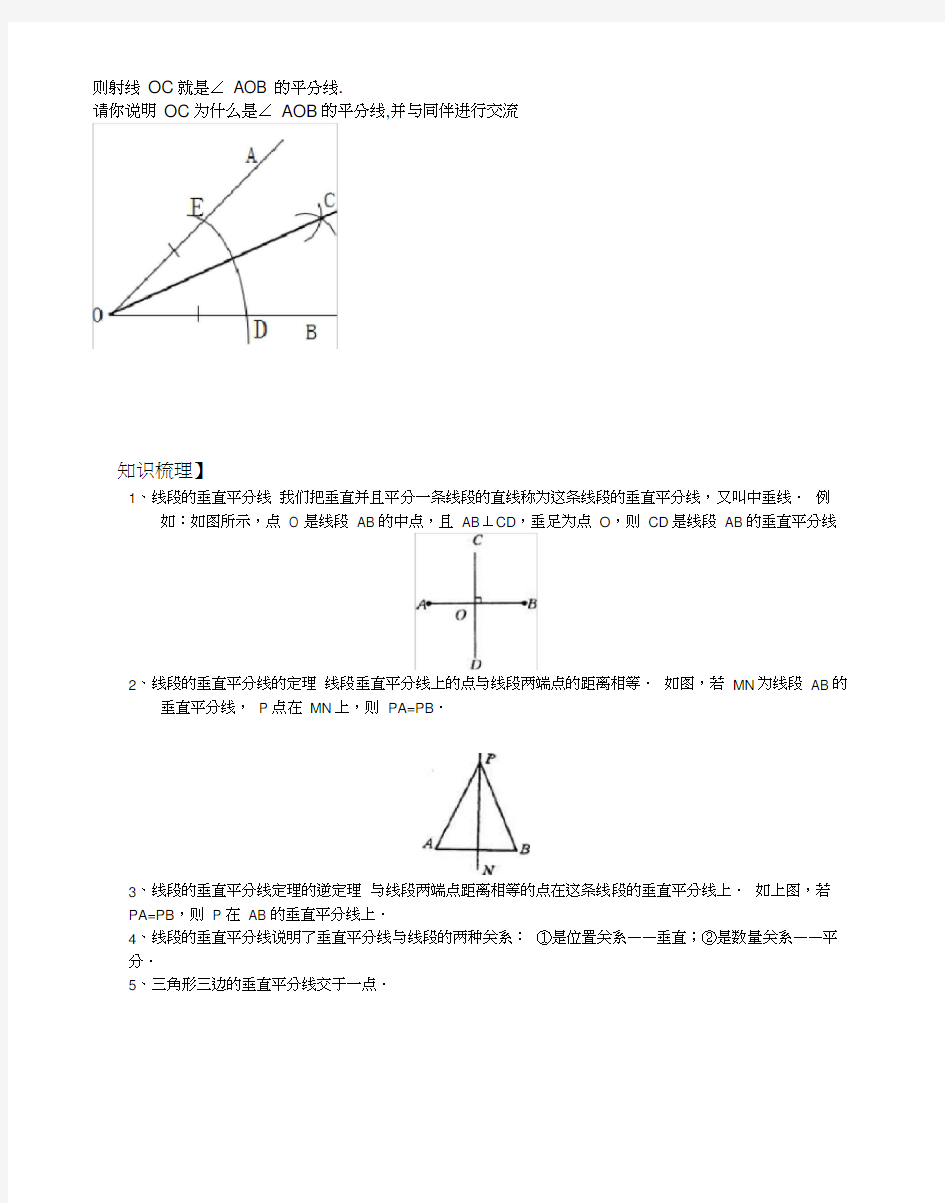
如何作角的平分线?
1. 动手用尺规画出一个角的平分线;
2. 说明为什么是角平分线的理由。用尺规作角的平分线.
已知:∠AOB,如图. 求作:射线OC,使∠ AOC=∠BOC.
1.在OA 和OB上分别截取OD,OE,使OD=
2.分别以点D 和E为圆心,以大于长为半径作弧,两弧在∠AOB 内交于点C.
3. 作射线OC.
则射线OC就是∠ AOB 的平分线.
请你说明OC为什么是∠ AOB的平分线,并与同伴进行交流
知识梳理】
1、线段的垂直平分线我们把垂直并且平分一条线段的直线称为这条线段的垂直平分线,又叫中垂线.例
如:如图所示,点O 是线段AB的中点,且AB⊥CD,垂足为点O,则CD是线段AB的垂直平分线
2、线段的垂直平分线的定理线段垂直平分线上的点与线段两端点的距离相等.如图,若MN为线段AB的
垂直平分线,P 点在MN上,则PA=PB.
3、线段的垂直平分线定理的逆定理与线段两端点距离相等的点在这条线段的垂直平分线上.如上图,若
PA=PB,则P 在AB的垂直平分线上.
4、线段的垂直平分线说明了垂直平分线与线段的两种关系:①是位置关系——垂直;②是数量关系——平
分.
5、三角形三边的垂直平分线交于一点.
从图中可以看出,要证明三条垂直平分线交于一点,只需证明其中的两条垂直平分线的交点一定在第三条垂直平分线上就可以了
6、角的平分线的作法
(1)在∠ AOB的两边OA、OB上分别截取OD、OE,使OD=OE.
(2)分别以D、E 为圆心,以大于DE长为半径画弧,两弧交于∠ AOB内一点C. (3)作射线
OC,则OC为∠ AOB的平分线(如图)
指出:(1)作角的平分线的依据是三角形全等的条件——“ SSS”.
(2)角的平分线是一条射线,不能简单地叙述为连接.
7、角平分线的性质在角的平分线上的点到角的两边的距离相等.
指出:(1)这里的距离是指点到角两边垂线段的长.
(2)该结论的证明是通过三角形全等得到的,它可以独立作为证明两条线段相等的依据
(3)使用该结论的前提条件是有角的平分线,关键是图中有“垂直”.
8、角平分线的判定到角的两边的距离相等的点在角的平分线上.
指出:(1)此结论是角平分线的判定,它与角平分线的性质是互逆的.
(2)此结论的条件是指在角的内部有点满足到角的两边的距离相等,那么过角的顶点和该点的射线必平分这个角.
9、三角形的角平分线的性质三角形的三条角平分线相交于一点,且这点到三角形三边的距离相等.
指出:(1)该结论的证明揭示了证明三线共点的证明思路:先设其中的两线交于一点,再证明该交点在第三线上.
(2)该结论多应用于几何作图,特别是涉及到实际问题的作图题.
典型例题】
知识点一:线段的垂直平分线
考点一:利用线段垂直平分线求角的度数
例1、在△ABC中,AB=AC,AB的中垂线与AC所在直线相交所得的锐角为50°,求底角B的大小. 分析:
AB的中垂线与AC所在直线的交点可能在AC上,也可能在CA的延长线上,故应分类讨论解:若∠A 为锐角,如图
∵∠AED=50°,∴∠ A=40° ∵AB=AC,∴∠ B=∠C=70° 若∠A为钝角,如图:
∵∠AED=50°,∴∠ EAD=40°,
∵AB=AC,∴∠ B=∠C=20°.
例2、如图,DE是△ABC的AB边的垂直平分线,分别交AB、BC于D、E两点,AE平分∠ BAC,若∠B=30°,求∠C 的度数.
解:此题考查“线段垂直平分线的性质”.
因为DE垂直平分AB,所以BE=AE.所以∠ 1=∠B=30° 又因为∠ 1=∠2,所以∠ 1=∠2=30°.
所以∠ C=180°-∠ BAC-∠ B=90°.
考点二:利用线段垂直平分线求长度
例3、如图,AB=AC,DE垂直平分AB交AB于D,交AC于E.若△ ABC的周长为28,BC=8,求△ BCE的周
长.
解:∵等腰△ ABC 的周长为28,BC=8,
∴2AC+BC=28.∴ AC=10.
∵DE 垂直平分AB,
∴BE=AE线(段垂直平分线上的点到线段两端点的距离相等).
∴△BCE周长=BE+EC+BC=AE+EC+BC
=AC+BC =10 +8=18 .点拨:这里是将△ BCE 的周长转化为等腰△ ABC 的腰和底,再由已
知条件求得.例4、如图所示,在△ ABC 中,AC的垂直平分线交AC于E,交BC于D,且
△ BAD的周长为16cm,AE=7cm,求△ ABC的周长.
因为DE是AC的垂直平分线,所以EA=EC,DA=DC.又因为AE=7cm,所以AC=2AE=2×7=14(cm).因为△ BAD的周长为16cm,即AB+BD+AD=AB+BC=16cm,所以△ ABC的周长为AB+BC+
AC=16+14=30(cm) .
例5、直角ΔABC中, ∠ACB=90°, ∠A=15°,将顶点A翻折使它与顶点B重合,折痕为MH,已知AH=2,求BC 的长.
分析:折叠问题可以看成轴对称问题.由外角定理得到直角三角形中有30°角,利用30°角所对的直角
边等于斜边的一半可得.
解:由于轴对称,得∠ MA′H=∠A=15°,
所以∠ BHC=3°0 ,BH=AH,
又△ BHC为直角三角形,因为直角三角形中30°角所对的直角边等于斜边的一半,
所以BC= BH= ×2=1.
变式训练
1.如图,AB=AC,AC的垂直平分线MN 交AB 于D,交AC于E. (1)若∠ A=40°,求∠ BCD 的度数;
(2)若AE=5,△BCD 的周长17,求△ ABC的周长.
2.在Rt△ABC中,∠ A=90°,AB=3,AC=4,∠ABC,∠ACB 的平分线交于P 点,PE⊥BC于E 点,求PE 的长.
考点三:线段垂直平分线与证明题
例6、如图,点 D 、 E 在△ABC 的边 证明:过点 A 作AF ⊥BC 于 F . ∵AB=AC ,AF ⊥BC ,∴BF=CF . ∵BD=C ,E ∴ BF -BD=CF-CE . ∴DF=EF .
∴AF 是 DE 的垂直平分线. AD=AE .
分析:由线段的垂直平分线性质知联结 AF ,证线段二倍关系,通常考虑是否有直角三角形,且直角三 角形中是否有 30°角 .
证明:如图所示,联结 AF , ∵AB=AC ,∠ BAC=12°0 (已知),
∴∠ B=∠C= =30°(等腰三角形性质) .
又∵EF 是 AC 的垂直平分线(已知), ∴FA=FC (线段垂直平分线性质) .
∴∠C=∠FAC=30°(等边对等角),
∴∠ BAF=∠BAC -∠ FAC=120°- 30°=90°(等式性质) .
在 Rt △BAF 中,∠ BAF=90°,∠ B=30°( 已证 ) ,
例 7、如图所示,在△ ABC 中, 证 BF=2CF.
AB=AC ,∠ BAC=12°0 , AC 的垂直平分线 EF 交AC 于点 E ,交 BC 于点 F.
求
答案: 1.(1) 30°(2)27 2.1
BC 上, BD=CE ,AB=AC ,求证:
AD=AE .
∴AF= BF(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)
∴CF= BF(等量代换).
∴BF=2CF(等式性质).
△ ABC 中,∠ B=22.5°,AB的垂直平分线交AB于Q点,交BC于P 点,PE⊥AC 于 E 点,AD 交PE于 F
点.求证:DF=DC.
连接PA,再证△
PDF≌△ADC
(ASA),即可得证. 考点四:线段垂直平分线的实际应用例9、如图所示,牧童在 A 处放牛,他的家在B
处,晚上回家时要到河边让牛饮一次水,则饮水的地点选在何处,牧童所走的路最短?
直接确定牛饮水的位置并不容易,但若A,B 在河的两侧就容易了.将
,直线是AA′的垂直平分线,不论饮水处在什么位置, A 点与它的对称
最小时,饮水处到A,B 的距离和最小.
例10、在沪宁高速公路L 的同侧,有两个化工厂A、B,为了便于两
厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工
人都没意见,问医院的院址应选在何处?院址应同时满足两个条件:
(1)在公路L 上;
(2)到A、B 两厂的距离相等。
解决问题的关键在于满足条件(2).同时医院在公路上,所以AB的垂直平分线与公路L 的交点就是医院的院址.例8、如图,
AD⊥BC 于D
点,
则PA=PB,可求∠ APD=45°,从而可得出AD=PD,
分析:
本题A,B 两点在河的同侧, A 点
转化到河流的另一侧,设为A′ 点
到饮水处的距离都相等.当A′B
解:如图所示,点C即为所求.