BCD编码

bcd码标准
BCD码，也称二-十进制编码，是一种数字编码方式，用4位二进制码的组合代表十进制数的0，1，2，3，4，5，6，7，8，9十个数符。

最常用的BCD码称为8421BCD 码，8、4、2、1分别是4位二进数的位取值。

BCD码的转换方式如下：
BCD码与十进制数的转换：若将BCD码1000 0101.0101转换为十进制数如：(1000 0101.0101)BCD＝85.5。

BCD码的加法运算：以8421BCD码为例，若要计算38+49，首先将38和49分别转换为二进制码(0010 0100 1000)和(0010 0100 1001)，然后进行加法运算，(0010 0100 1000) + (0010 0100 1001) = (0100 1001 0001)，这就是38+49的8421BCD码结果。

另外，BCD码也广泛应用于计算机科学、通信工程、电子工程等领域。

在计算机科学中，BCD码被用于表示和存储十进制数，以提高数据的可读性和精度。

在通信工程中，BCD码被用于数据的传输和编码，以确保数据的准确性和可靠性。

在电子工程中，BCD 码被用于数字电路的设计和实现，以提高电路的可靠性和稳定性。

BCD码（Binary-Coded Decimal‎）亦称二进码十进数或二-十进制代码。

用4位二进制数来表示1位十进制数中的0~9这10个数码。

是一种二进制的数字编码形式，用二进制编码的十进制代码。

BCD码这种编码形式利用了四个位元来储存一个十进制的数码，使二进制和十进制之间的转换得以快捷的进行。

这种编码技巧最常用于会计系统的设计里，因为会计制度经常需要对很长的数字串作准确的计算。

相对于一般的浮点式记数法，采用BCD码，既可保存数值的精确度，又可免却使电脑作浮点运算时所耗费的时间。

此外，对于其他需要高精确度的计算，BCD编码亦很常用。

即BCD代码。

Binary-Coded Decimal?，简称BCD，称BCD码或二-十进制代码，亦称二进码十进数。

是一种二进制的数字编码形式，用二进制编码的十进制代码。

这种编码形式利用了四个位元来储存一个十进制的数码，使二进制和十进制之间的转换得以快捷的进行。

这种编码技巧，最常用于会计系统的设计里，因为会计制度经常需要对很长的数字串作准确的计算。

相对于一般的浮点式记数法，采用BCD码，既可保存数值的精确度，又可免却使电脑作浮点运算时所耗费的时间。

此外，对于其他需要高精确度的计算，BCD编码亦很常用。

由于十进制数共有0、1、2、……、9十个数码，因此，至少需要4位二进制码来表示1位十进制数。

4位二进制码共有2^4=16种码组，在这16种代码中，可以任选10种来表示10个十进制数码，共有N=16！/（16-10）！约等于2.9乘以10的10次方种方案。

常用的BCD代码列于末。

常用BCD编码方式最常用的BCD编码，就是使用"0"至"9"这十个数值的二进码来表示。

这种编码方式，在中国大陆称之为“8421码”。

除此以外，对应不同需求，各人亦开发了不同的编码方法，以适应不同的需求。

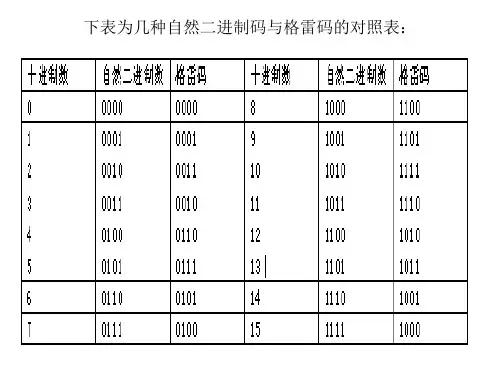
这些编码，大致可以分成有权码和无权码两种：有权BCD码，如：8421(最常用)、2421、5421…无权BCD码，如：余3码、格雷码…以下为三种常见的BCD编码的比较。

BCD码和十六进制数的区别BCD 码（Binary-Coded Decimal）是二进制编码的十进制数的缩写，BCD码用4位二进制数表示一位十进制数。

BCD码各位的数值范围为2#0000～2#1001，对应于十进制数0～9。

BCD码不能使用十六进制的A~F（2#1010～2#1111）这6个数字。

BCD码本质上是十进制数，因此相邻两位逢十进一。

BCD码的最高位二进制数是符号位，负数的符号位为1，正数为0。

16位BCD码的范围为–999～＋999。

下图的拨码开关将显示的数字转换为4位二进制数。

PLC用12个数字量输入点读取的是3位BCD码，它的值为2#1000 0010 1001，即十六进制数16#829。

BCD码没有单独的表示方法，而是借用了十六进制的表示方法，因此二者很容易混淆。

下图是S7-300/400的BCD码和整数的相互转换指令，可以看到在指令中BCD码均用十六进制的形式表示。

在程序中，怎么知道一个数字是BCD码还是十六进制数呢？1）看数据的来源和用途。

BCD码一般用于输入和输出，例如来自拨码开关的数据是BCD码，送给显示电梯楼层的译码器芯片的是BCD码。

2）看手册的规定，例如数据类型DATE_AND_TIME中的日期和时间值是BCD码，计数器的预设值PV和当前计数值CV_BCD 为BCD码。

怎样监视BCD码？在变量表和程序状态监控中，用十六进制格式监视BCD码。

怎样输入BCD码？从上图可以看出，BCD码用十六进制格式输入，其最高位（符号位）为16#F（2#1111）。

BCD码的低3位各位只能是0~9，如果是16#A~16#F则会出错。

计数器的预设值PV是0~999的BCD码，可以用格式为C#的常数（C#1~C#999）作为计数器的预设值。

下图用MW42提供计数器的预设值PV，如果用MOVE指令将十进制数348（对应的十六进制数为16#15C）传送给MW42，进入RUN模式时，操作系统将它转换为BCD码时出错（16#15C不是BCD码），不能切换到RUN模式。

几种自然二进制码与格雷码的对照表：
二进制码与格雷码互相转换方法
二进制码->格雷码（编码）：从最右边一位起，依次将每一位与左边一位异或 (XOR)(/lemma-php/dispose/view.php/379209.htm)，作为 对应格雷码该位的值，最左边一位不变(相当于左边是0)； 格雷码-〉二进制码（解码）：从左边第二位起，将每位与左边一位解码后的值 异或，作为该位解码后的值（最左边一位依然不变）. 数学(计算机)描述： 原码：p[0~n]；格雷码：c[0~n](n∈N)；编码：c=G(p)；解码：p=F(c)；书写时 从左向右标号依次减小. 编码：c=p XOR p[i+1](i∈N,0≤i≤n-1)，c[n]=p[n]； 解码：p[n]=c[n]，p=c XOR p[i+1](i∈N,0≤i≤n-1). Gray Code是由贝尔实验室的Frank Gray在20世纪40年代提出的（是1880年由法 国工程师Jean-Maurice-Emlle Baudot发明的），用来在使用PCM（Pusle Code Modulation）方法传送讯号时避免出错，并于1953年3月17日取得美国专利。 由定义可知，Gray Code的编码方式不是唯一的，这里讨论的是最常用的一 种。
格雷码
格雷码(Gray code),又叫循环二进制码或反射二进制码 在数字系统中只能识别0和1，各种数据要转换为二进制代码才 能进行处理，格雷码是一种无权码，采用绝对编码方式，典型格 雷码是一种具有反射特性和循环特性的单步自补码，它的循环、 单步特性消除了随机取数时出现重大误差的可能，它的反射、自 补特性使得求反非常方便。格雷码属于可靠性编码，是一种错误 最小化的编码方式，因为，自然二进制码可以直接由数/模转换器 转换成模拟信号，但某些情况，例如从十进制的3转换成4时二进 制码的每一位都要变，使数字电路产生很大的尖峰电流脉冲。而 格雷码则没有这一缺点，它是一种数字排序系统，其中的所有相 邻整数在它们的数字表示中只有一个数字不同。它在任意两个相 邻的数之间转换时，只有一个数位发生变化。它大大地减少了由 一个状态到下一个状态时逻辑的混淆。另外由于最大数与最小数 之间也仅一个数不同，故通常又叫格雷反射码或循环码。

微机原理与接口技术──BCD 码和 BCD 调整指令一、 BCD码BCD 码是一种用 4 位二进制数字来表示一位十进制数字的编码，也称为二进制编码表示的十进制数（ Binary Coded Decimal），简称 BCD 码。

二、 BCD码两种格式1、压缩 BCD 码格式（ Packed BCD Format）。

1 个字节的高低 4 位各表示 1 位十进制数。

比方：十进制数 4256 的压缩 BCD 码表示为 2 个字节： 0100 0010B、 0101 0110 B2、非压缩 BCD 码格式（ Unpacked BCD Format）。

1 个字节的高 4 位悠闲不用，仅用低4位表示 1 位十进制数。

比方：十进制数4256 的非压缩 BCD 码表示为 4 个字节：xxxx0100B 、xxxx0010B 、 xxxx0101B 、 xxxx0110 B三、 BCD码的运算和调整BCD 码使用频率不高，因此任何CPU 都不会设置特地的BCD 运算指令。

遇到BCD 码的运算，只好利用一般 2 进制运算指令来进行。

但是，运用 2 进制的运算指令获得的结果就会失掉BCD 码的特色。

例 1：BCD 码35 + 35 ，我们希望获得BCD 码 70（0111 0000B）。

但是依据 2 进制规律， 0011 0101B + 0011 0101B实质等于 0110 1010B。

也就是说低 4 位依据 2 进制可以表达 10 而不会进位。

此时，若对结果加 6（0110 1010 + 0000 0110），就可以获得正确 BCD 结果 0111 0000B。

例 2：BCD 码 38 + 38，我们希望获得 BCD 码 76（0111 0110B）。

但是依据 2 进制规律， 0011 1000B +0011 1000B 实质等于 0111 0000B（BCD 码 70）。

也就是说低4 位依据2 进制规律产生了进位，而这个进位带走了16，而不是10，因此结果依据BCD 理解少了 6。

bcd转换成十六进制BCD是二进制编码的十进制数码的缩写，全称Binary Coded Decimal。

BCD码是一种十进制数的二进制表示方法，将十进制数的每一位数码转换成二进制数码，然后将每个二进制数码存储在一个四位二进制数中。

BCD码的优点是易于人类阅读和理解，但其缺点是占用的存储空间较大。

而十六进制是一种数制，基数为16，使用0-9和A-F表示数码，其中A-F分别表示十进制数10-15。

在计算机领域，十六进制常用于表示二进制数，因为十六进制可以很方便地表示四位二进制数。

BCD码转换成十六进制有两种方法，一种是直接将BCD码转换成十进制数，然后再将十进制数转换成十六进制数；另一种是将BCD码直接转换成十六进制数。

一、BCD码转换成十进制数将BCD码转换成十进制数的方法是将每个四位二进制数转换成十进制数，然后将各位数相加。

例如，将BCD码1101 1010 0011 0110转换成十进制数的过程如下：第一位数：1101 = 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0 = 13第二位数：1010 = 1*2^3 + 0*2^2 + 1*2^1 + 0*2^0 = 10第三位数：0011 = 0*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = 3第四位数：0110 = 0*2^3 + 1*2^2 + 1*2^1 + 0*2^0 = 6将各位数相加得到十进制数：13 + 10 + 3 + 6 = 32因此，BCD码1101 1010 0011 0110转换成十进制数为32。

二、十进制数转换成十六进制数将十进制数转换成十六进制数的方法是不断地将十进制数除以16，直到商为0为止。

每次将余数转换成十六进制数，并将其保存在一个数组中。

最后将数组中的数倒序排列就得到了十六进制数。

例如，将十进制数32转换成十六进制数的过程如下：32 ÷ 16 = 2 02 ÷ 16 = 0 (2)因此，32转换成十六进制数为20。

十进制数的二进制编码（BCD）BCD码不是二进制数，而是用4位二进制码对十进制数字符号进行编码后的十进制数，即二进制编码的十进制数，简称BCD（Binary Coded Decimal）码。

BCD码与十进制数之间的转换是按4位二进制码对应1位十进制数，直接进行转换的，即1个n位十进制数对应的BCD码肯定为4n位二进制码。

数字系统中常用的BCD码有8421码、2421码和余3码，3种编码的特点可归纳如下。

1．8421码8421码是一种用4位二进制码表示1位十进制数字符号的有权码，其4位二进制码从高位至低位的权依次为8、4、2、1，故称为8421码。

例如，（369）10＝（0011 0110 1001）84218421码的位权与4位二进制数的位权完全相同，但8421码不允许消失1010～1111六种组合。

其次，8421码与ASCII码的低4位相同，两者转换特别便利。

2．2421码2421码是一种用4位二进制码表示1位十进制数字符号的有权码，其4位二进制码从高位至低位的权依次为2、4、2、1，故称为2421码。

例如，（369）10＝（0011 1100 1111）24212421码不允许消失0101～1010六种组合。

其次，2421码是一种“对9的自补代码”，可给运算带来便利。

3．余3码余3码是由8421码加上0011形成的一种无权码，由于它的每个字符编码比相应8421码多3，故称为余3码。

例如，（369）10＝（0110 1001 1100）余3码余3码不允许消失0000、0001、0010、1101、1110和1111六种组合。

其次，余3码是一种“对9的自补代码”，可给运算带来便利。

java bcd码解析BCD码是一种二进制编码方式，它用四位二进制数来表示一个十进制数的每一位。

在Java中，我们可以使用一些算法和方法来解析BCD码。

我们需要了解BCD码的基本原理。

BCD码的全称为Binary-Coded Decimal，即二进制编码的十进制数。

它是一种直观的表示十进制数的方法，通过将每个十进制位数转换为四位二进制数来实现。

在Java中，我们可以使用字符串来表示BCD码。

假设我们有一个BCD码为"0011 0101 1000"，我们可以通过以下步骤来解析它：1. 去掉空格，得到"001101011000"；2. 将字符串转换为字符数组，方便后续处理；3. 创建一个int类型的变量result，用于保存解析后的十进制数；4. 从左到右遍历字符数组，对于每个字符，将其转换为对应的十进制数并累加到result中；5. 最后得到的result即为解析后的十进制数。

下面我们来具体实现一下：```javapublic class BCDParser {public static int parseBCD(String bcd) {// 去掉空格bcd = bcd.replaceAll(" ", "");// 转换为字符数组char[] bcdArray = bcd.toCharArray();// 解析BCD码int result = 0;for (int i = 0; i < bcdArray.length; i++) {int digit = bcdArray[i] - '0'; // 将字符转换为对应的十进制数result = result * 10 + digit; // 累加到result 中}return result;}public static void main(String[] args) {String bcd = "0011 0101 1000";int decimal = parseBCD(bcd);System.out.println("解析后的十进制数为：" + decimal);}}```以上代码中，我们通过定义一个静态方法parseBCD来实现BCD码的解析。

bcd原理
BCD编码是用4位二进制数来表示十进制数的一种编码方式。

BCD的全称是二进制编码十进制，也就是Binary Coded Decimal的缩写。

BCD编码使用4位二进制数来表示十进制数的每一位。

每一
位的取值范围是0~9，即0000~1001。

例如，十进制数25可
以表示为0010 0101，其中0010表示十位上的2，0101表示个位上的5。

BCD编码的优点是可以直接表示十进制数，不涉及二进制和
十进制之间的转换。

相比其他编码方式，BCD编码更直观、
易懂，且不需要进行数制转换。

然而，BCD编码也存在一些缺点。

首先，BCD编码使用的存
储空间较大，每位十进制数需要4位二进制数来表示，比纯二进制编码需要更多的存储空间。

其次，BCD编码的运算复杂
度较高，与二进制运算相比，BCD编码的运算速度较慢。

因此，在计算机系统中，通常使用二进制编码进行运算，而在人机接口中使用BCD编码进行显示和输入。

总结起来，BCD编码是一种直观、易懂的表示十进制数的方式，但在存储空间和运算速度方面存在一些不足。

8421的解法
8421是一种编码方法，也称为BCD编码。

它将十进制数转换为由四个数字组成的二进制数，每个数字的权值分别是1、4、16、64。

下面是8421编码的解法：
1. 将要转换的十进制数除以10，得到商和余数。

2. 将商作为第一位数字，余数作为第二位数字，用二进制表示，并将每个数字的权值表示为1、4、16、64。

3. 重复步骤2，直到商为0为止。

4. 得到的结果就是8421编码的表示形式。

例如，将十进制数23转换为8421编码：
1. 23除以10得到2余3。

2. 将2作为第一位数字，3作为第二位数字，用二进制表示为1010，表示权值为1、4、16、64的数字分别为0、1、0、1。

3. 重复步骤2，直到商为0为止，得到的8421编码为10101001。

因此，十进制数23的8421编码为10101001。

第1页/ 共1页。

bcd码是什么意思你知道bcd码是什么意思吗？说起这个，我们可能不太清楚。

但是，如果说它的作用的话，那你就肯定知道了！这是一个小女孩的故事，她今年七岁，生活在一个富裕的家庭里。

小女孩的爸爸是电脑公司的老板，妈妈是个钢琴家，爷爷也是著名的物理学家，从小就受到良好的教育。

她非常想拥有一台属于自己的计算机，她要求妈妈给她买一台。

但是，妈妈对这件事并不感兴趣，因为她认为家里已经有了三台计算机了，何必再买呢？但是小女孩不死心，一定要买。

这时，小女孩又来央求爷爷，可爷爷就是不答应。

小女孩没办法了，就开始行动了。

她回到自己房间，拿出剪刀、胶水等东西，“哗啦”一声，将房间的计算机都拆开了。

她把计算机都组装好之后，还向妈妈炫耀。

这时，妈妈回来了，看见女儿的杰作后大吃一惊，厉声问道：“你这是在干什么？”小女孩理直气壮地说：“这些是我组装的，我想怎样就怎样。

”妈妈听后很生气，立即让保安将她关进了房间。

妈妈把女儿软禁在房间里后，让管家把家里的所有计算机都拿走了。

只留下她一台。

在此之后，小女孩越来越孤僻，对外界失去了信心。

渐渐的，小女孩变成了一个“木头人”。

虽然爸爸给她找了许多心理医生，但她都不愿意去。

这时，小女孩发现每天晚上都有一台机器放在桌子上，原来是爷爷晚上偷偷放的。

他觉得孙女在受苦，就悄悄地把机器搬了过来，并设置了密码，自己就在门外睡觉，以免吵醒孙女。

于是，小女孩又重新开始了她的寻机之旅……bcd码到底有什么作用呢？ bcd码又称十六进制编码。

它是电子计算机中最基本的数据输入方式，也是由两种不同的数码组成的二进制编码，分别用a、 b、 c表示十六进制数的a、 b、 c三个字母。

如果一个数是8位的，它的bcd码就是在“ 0”和“ 7”之间加上“ 00”，也就是“ 23”。

我们知道，电脑是按照十六进制工作的，如果你要在电脑中输入一个大于十六的数，比如要输入1728，就会自动提示你用十六进制表示，这时你再把“ 00”改成“ 5”，这个数就会变成1728，数值完全一样。

bcd码转换成十进制摘要：一、引言二、BCD 码简介1.BCD 码的定义2.BCD 码的优势三、BCD 码转换成十进制数1.转换原理2.转换方法四、举例说明1.单个BCD 码转换2.多个BCD 码转换五、总结正文：一、引言在计算机科学中，BCD 码（二- 十进制编码）是一种将二进制数转换为十进制数的编码方式。

在很多实际应用中，需要将BCD 码转换为十进制数进行计算和处理。

本文将详细介绍BCD 码转换成十进制数的方法和原理。

二、BCD 码简介1.BCD 码的定义BCD 码是一种二进制编码方式，用4 位二进制数表示0~9 的十进制数。

通常，BCD 码中的每一位都代表一个十进制数的相应位，从低位到高位排列。

2.BCD 码的优势BCD 码相较于普通的二进制码，更容易被人眼识别和理解。

同时，BCD 码在某些情况下可以减少硬件设备的需求，如BCD 加法器和减法器等。

三、BCD 码转换成十进制数1.转换原理BCD 码转换成十进制数的原理是通过将每个BCD 码对应的权重与其数值相乘，再将结果相加得到相应的十进制数。

2.转换方法具体的转换方法是，将每个BCD 码乘以相应的权重（8、4、2、1），然后将这些乘积相加。

例如，对于BCD 码1001，其对应的权重分别是1000、100、10、1，计算方法为：1*1000 + 0*100 + 0*10 + 1*1 = 1001。

四、举例说明1.单个BCD 码转换以BCD 码1001 为例，根据转换方法，计算结果为1001，即十进制数11。

2.多个BCD 码转换假设有一个4 位BCD 码1001 和另一个4 位BCD 码1100，分别转换为十进制数11 和12。

五、总结BCD 码转换成十进制数的过程是通过将每个BCD 码乘以相应的权重，然后将这些乘积相加得到相应的十进制数。

bcd转换成十六进制BCD码是二进制编码的一种，其全称为Binary Coded Decimal，即二进制编码的十进制数。

BCD码是将十进制数码的0~9转化为4位二进制数码来表示的，通常用于数字显示、计算机内部数据处理等领域。

而十六进制是一种基数为16的进位制数，其由0~9和A~F共16个符号组成。

在计算机领域中，十六进制常用于表示内存地址、颜色代码等。

本文将介绍如何将BCD码转换为十六进制数。

一、BCD码的转换BCD码是将十进制数码的0~9转化为4位二进制数码来表示的，其中每一位都代表一个十进制数码。

例如，数字0可以表示为0000，数字1可以表示为0001，以此类推，数字9可以表示为1001。

以数字234为例，其BCD码的表示为0010 0011 0100。

其中，0010代表数字2，0011代表数字3，0100代表数字4。

二、将BCD码转换为十六进制数将BCD码转换为十六进制数的方法是将BCD码的每4位转换为一个十六进制数码。

例如，0010可以转换为数字2，0011可以转换为数字3，0100可以转换为数字4。

因此，数字234的BCD码可以转换为十六进制数码23 4。

需要注意的是，如果BCD码的位数不是4的倍数，则需要在最高位补0，使其成为4的倍数。

例如，数字7的BCD码为0111，需要在最高位补0，使其成为0000 0111，然后再将其转换为十六进制数码0 7。

三、实例分析下面通过一个实例来演示BCD码转换为十六进制数的方法。

假设有一个BCD码为1001 1100 0110 0011，需要将其转换为十六进制数。

首先，将BCD码的每4位转换为一个十六进制数码，得到91C3。

然后，将十六进制数码中的每个数字转换为二进制数，得到1001 0001 1100 0011。

最后，将二进制数转换为十进制数，得到23107。

因此，BCD码为1001 1100 0110 0011的数转换为十六进制数为91C3，对应的十进制数为23107。

十六进制转bcd码公式
BCD码（Binary-Coded Decimal）是一种二进制编码的十进制数表示方法，每一位十进制数由4位二进制数表示。

将十六进制数转换为BCD码的公式
如下：
假设十六进制数为 x，其每一位数字可以表示为 x1, x2, x3, x4。

BCD码为：
bcd_x1 = x1
bcd_x2 = x2
bcd_x3 = x3
bcd_x4 = x4
然后，将bcd_x1, bcd_x2, bcd_x3, bcd_x4 转换为二进制，并合并在一起，即为 BCD码。

注意，这个公式假设十六进制数的每一位数字都在0-9之间。

如果十六进制数的某一位数字超过9，那么需要将其拆分为多个数字，并分别应用上述公式。

例如，十六进制数 1A 可以拆分为 1 和 A，然后分别应用上述公式。

十进制40的bcd编码在计算机科学和电子工程领域，二进制编码十进制（BCD）是一种常用的数字编码方式。

它可以将十进制数字以二进制编码的形式表示，使得数字在数字电路和计算机中更容易处理和传输。

本文将介绍十进制40的BCD编码方法。

一、BCD编码的基本原理BCD编码将每一位十进制数字用四位二进制数表示，其中每四位二进制数对应一个特定的编码值。

因此，对于十进制数40，我们可以将其转换为二进制数10000，然后再将其转换为BCD编码值。

为了将十进制数40转换为BCD码，我们可以按照以下步骤进行操作：1.将十进制数40除以16，得到商和余数。

在这个例子中，商为2，余数为0。

2.将商的个位数保留并存储为结果的第一位，即BCD编码值中的最高位。

在这里，商的个位数是2，所以BCD编码值为0x2。

3.将余数继续除以16，得到新的商和余数。

在这个例子中，新的商为0，余数为0。

4.将第二个余数的个位数作为结果的第二位，即BCD编码值中的次高位。

在这里，第二个余数的个位数是0，所以BCD编码值的次高位是0x0。

5.重复上述步骤，直到所有位数都被处理完毕。

根据上述步骤，我们可以得到十进制数40的BCD编码值为：0x20。

因此，十进制数40的BCD编码就是0x20。

在实际应用中，BCD码常用于数字电路和计算机中表示和传输数字信息，因为它更易于电路中的逻辑运算和处理。

除了上述手动转换的方法，我们还可以使用专门的BCD编码器芯片来将十进制数转换为BCD码。

这些芯片通常具有与标准BCD码兼容的输出端口，可以直接连接计算机或其他数字设备。

此外，这些芯片还具有其他功能，如解码和校验，可以确保BCD码的正确性和可靠性。

总之，通过掌握十进制数40的BCD编码方法，我们可以更好地理解和应用数字电路和计算机技术。

在实际应用中，BCD码是一种常用的数字编码方式，它可以提高数字信息的处理和传输效率。

同时，使用专门的BCD编码器芯片可以简化数字电路的设计和实现过程。

java bcd码的算法Java BCD码的算法BCD码是二进制编码的十进制表示形式，即Binary-Coded Decimal的简称。

在计算机中，常用BCD码来表示数字，可以在计算和显示数字时提供高精度和可读性。

本文将介绍Java中BCD码的算法。

1. BCD码的原理BCD码使用4位二进制数来表示一个十进制数的每一位。

例如，数字5的BCD码是0101，数字9的BCD码是1001。

BCD码的优点是可以直接与十进制数进行转换和计算，而无需进行复杂的位运算。

2. Java中BCD码的转换在Java中，可以使用整数类型（如int）来表示BCD码。

将一个十进制数转换为BCD码的算法如下：- 将十进制数的每一位拆分出来，得到个位、十位、百位等数字。

- 将每一位数字转换为对应的BCD码，例如将数字5转换为0101。

- 将每一位的BCD码按位拼接起来，得到最终的BCD码。

例如，将数字259转换为BCD码的过程如下：- 个位数字为9，对应的BCD码为1001。

- 十位数字为5，对应的BCD码为0101。

- 百位数字为2，对应的BCD码为0010。

- 将个位、十位和百位的BCD码按位拼接起来，得到最终的BCD 码为0010 0101 1001。

3. Java中BCD码的计算在Java中，可以使用BCD码进行数字的加减乘除运算。

例如，将两个BCD码相加的算法如下：- 从最低位开始，将两个BCD码对应的每一位相加，得到一个新的BCD码的每一位和进位。

- 将新的BCD码的每一位和进位拼接起来，得到最终的和。

例如，将BCD码0010 0101 1001和BCD码0011 0110 0010相加的过程如下：- 个位相加得到和为11，进位为1。

- 十位相加得到和为11，进位为1。

- 百位相加得到和为10，进位为1。

- 将个位、十位和百位的和和进位拼接起来，得到最终的和为1101 1101 0111。

4. Java中BCD码的显示在Java中，可以将BCD码转换为十进制数进行显示。

事业单位备考—计算机专业知识：BCD码BCD码(Binary-Coded Decimal‎)亦称二进码十进数或二-十进制代码。

用4位二进制数来表示1位十进制数中的0~9这10个数码。

是一种二进制的数字编码形式，用二进制编码的十进制代码。

BCD码这种编码形式利用了四个位元来储存一个十进制的数码，使二进制和十进制之间的转换得以快捷的进行。

这种编码技巧最常用于会计系统的设计里，因为会计制度经常需要对很长的数字串作准确的计算。

相对于一般的浮点式记数法，采用BCD码，既可保存数值的精确度，又可免却使电脑作浮点运算时所耗费的时间。

此外，对于其他需要高精确度的计算，BCD编码亦很常用。

我们把每位十进制数转换二进制的编码，简称为BCD码(Binary Coded Decimal)。

BCD码是用4位二进制编码来表示1位十进制数。

这种编码方法有多种，但常用的编码是8421BCD编码，如表1.2所示。

这种BCD编码实际上就是0~9的“等值”二进制数。

表1.2 8421BCD编码列表十进制数字8421BCD码十进制数字8421BCD码0 0 5 1011 1 6 1102 10 7 1113 11 8 10004 100 9 1001用BCD码进行进制的转换时，是要求在二种进制的表现形式上快速转换，而不是要求在“数值相等”的含义快速转换。

例：求十进制数2000的BCD编码和其二进制数。

解：2000的BCD编码是把每位上的数2、0、0、0分别转换为其对应的BCD编码：0010、0000、0000和0000，把它们合在一起就是2000的BCD编码：0010 0000 0000 0000。

十进制数2000的二进制数是：11111010000，它们在数值上是相等的。

汉字机内码(内码)(汉字存储码)的作用是统一了各种不同的汉字输入码在计算机内部的表示。

汉字字形码(输出码)用于汉字的显示和打印，是汉字字形的数字化信息。

在汉字系统中，一般采用点阵来表示字形。