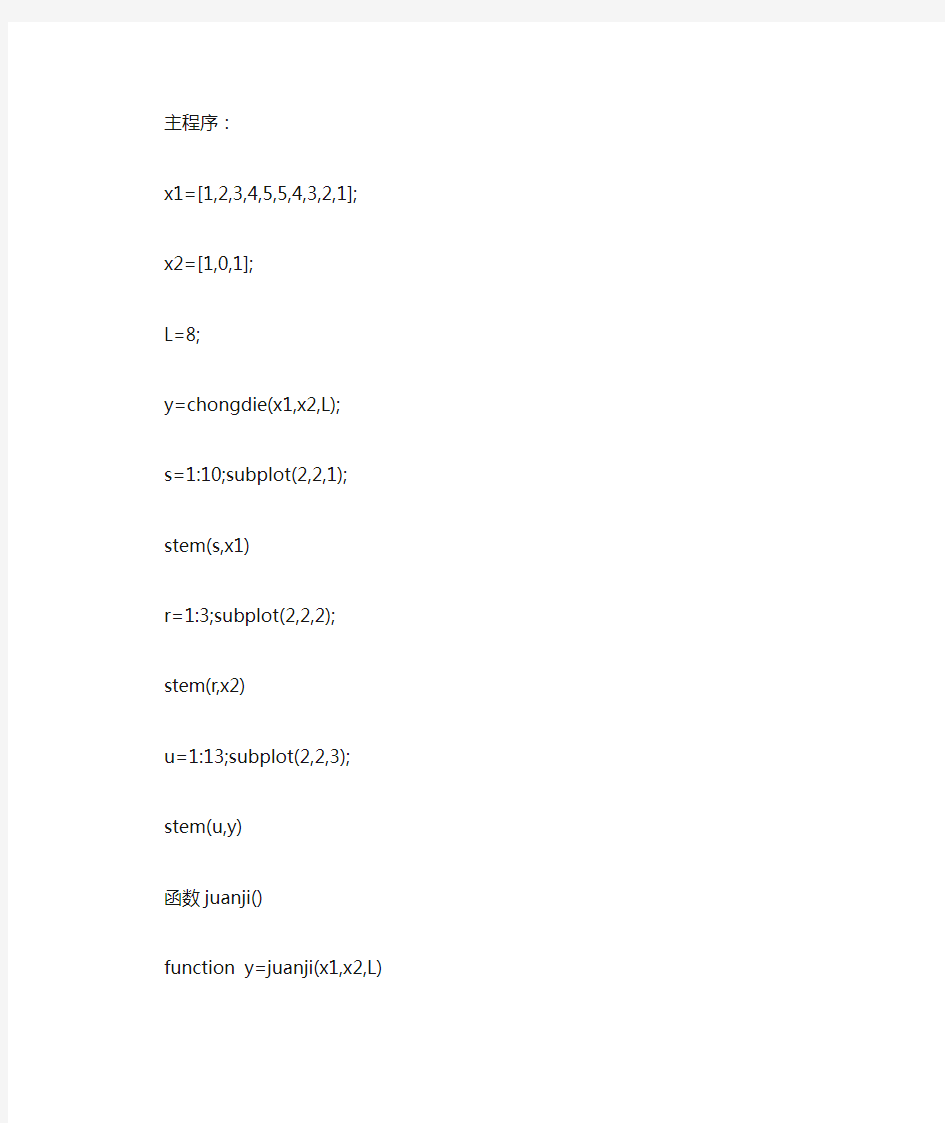

主程序:
x1=[1,2,3,4,5,5,4,3,2,1];
x2=[1,0,1];
L=8;
y=chongdie(x1,x2,L);
s=1:10;subplot(2,2,1);
stem(s,x1)
r=1:3;subplot(2,2,2);
stem(r,x2)
u=1:13;subplot(2,2,3);
stem(u,y)
函数juanji()
function y=juanji(x1,x2,L)
if length(x1)>L %如果x1长度大于L则产生错误error('L must not be less than length of x1');
end
if length(x2)>N %如果x2长度大于L则产生错误error('L must not be less than length of x2');
end
X1k=fft(x1,L); %对x1进行L点FFT计算
X2k=fft(x2,L); %对x2进行L点FFT计算
Yk=X1k.*X2k; %频域相乘
y=ifft(Yk); %反变换得卷积结果
if (all(imag(x1)==0))&(all(imag(x2)==0))
y=real(y);
end
函数chongdie()
方案1:
function[y]=chongdie(x,h,N)
Lenx=length(x); %取x(n)的长度
M=length(h); %取h(n)的长度
L=N+M-1; %计算圆周卷积的周期L使其不发生混叠
x=(x,zero(1,N-1)); %填充序列使得循环中对序列的索引不会超出围K=floor(Lenx/N);
y=zeros(1,Lenx+L-1); %确定分段数K
for i=0:1:K
ix=i*N;
x_seg=x(ix+1:ix+N); %将x(n)分段
y_seg=juanji(x_seg,h,L); %调用函数juanji()计算圆周卷积
y(ix+1:ix+L)=y(ix+1:ix+L)+y_seg(1:L); %各段重叠相加
end
y=y(1:Lenx+M-1); %取出实际的输出序列
方案2:
function[y]=chongdie(x,h,L)
Lenx=length(x); %取x(n)的长度
M=length(h); %取h(n)的长度
N=L-M+1; %计算分段大小N
x=[x,zeros(1,N-1)]; %填充序列使得循环中对序列的索引不会超出围K=floor(Lenx/N); %确定分段数K
y=zeros(1,Lenx+L-1);
for i=0:1:K
ix=i*N;
x_seg=x(ix+1:ix+N); %将x(n)分段
y_seg=juanji(x_seg,h,L); %调用函数juanji()计算圆周卷积y(ix+1:ix+L)=y(ix+1:ix+L)+y_seg(1:L); %各段重叠相加
end
y=y(1:Lenx+M); %取出实际的输出序列
循环卷积与线性卷积的实现 1、实验目的:(1)进一步理解并掌握循环卷积与线性卷积的概 念。 (2)理解掌握二者的关系。 三、实验原理 两个序列的N点循环卷积定义为 从定义中可以看到,循环卷积和线性卷积的不同之处在于:两个N 点序列的N点循环卷积的结果仍为N点序列,而他们的线性卷积的结果的长度则为2N-1;循环卷积对序列的移位采取循环移位,而线性卷积对序列采取线性位移。正式这些不同,导致了线性卷积和循环卷积有不同的结果和性质。 循环卷积和线性卷积虽然是不用的概念,但是它们之间有一个有意义的公式联系在一起 其中 也就是说,两个序列的N点循环卷积是他们的线性卷积以N为周期的周期延阔。设序列的长度为,序列的长度为,此时,线性卷积结果的序列的点数为;因此如果循环卷积的点数N小于,那么上述周期性延阔的结果就会产生混叠,从而两种卷积会有不同的结果。而如果N满足的条件,就会有 这就会意味着在时域不会产生混叠。因此,我们得出结论:若通过在序列的末尾填充适当的零值,使得和成为店序列,并作出这两个序列的循环卷积与线性卷积的结果在范围内相同。 根据DFT循环卷积性质中的卷积定理 便可通过两种方法求两个序列的循环卷积:一是直接根据定义计算;二是根据性质先分别求两个序列的N点DFT,并相乘,然后取IDFT以得到循环卷积。第二种方法看起来要经过若干个步骤,但由于求序列的DFT和IDFT都有快速算法,因此它的效率比第一种方法要高得多。 同样,根据线性卷积和循环卷积的关系,可以通过计算循环卷积以求得线性卷积,提高计算序列线性卷积的效率。 4、实验内容 输入程序序列如下: n=[0:1:4];m=[0:1:3]; x1=1+n;x2=4-m; %生成函数x1和x2 L1=length(x1)-1;L2=length(x2)-1; %取函数的长度
圆周卷积与周期卷积、线性卷积的关系及计算 一、三者关系 设: 1122()01()01 x n n N x n n N ≤≤-≤≤-N :圆周卷积的点数 ? 圆周卷积是周期卷积的主值序列。 周期卷积:1 120()()()N m y n x m x n m -==-∑ (1) 圆周卷积:1 120 ()()()[()(())]()N c N N N m y n y n R n x m x n m R n -===-∑ 1 210 [()(())]()N N N m x m x n m R n -==-∑ (2) 注意:(2)式直接使用的前提是圆周卷积的点数N 应满足: 12max[,]N N N ≥(一般题目均符合此种情况) ? 周期卷积是线性卷积的周期延拓。 线性卷积:11 12120()()*()()()N l m y n x n x n x m x n m -===-∑ 212 1 2 1 ()()()*()N m x m x n m x n x n -== -=∑ (4) 圆周卷积与线性卷积的关系:()[()]()c l N r y n y n rN R n ∞ =-∞ =+∑ (5) 注意:上述关系式对任意长度的圆周卷积均适合。 二、举例说明 1、对于12max[,]N N N ≥的情况,各教材例题很多,不再举例。 2、12N N N N <<或的情况。 习题8.已知序列()()2(1)(4)3(5)x n n n n n δδδδ=+-+-+-, 4()()y n R n =,求:
(1)()()*()z n x n y n = (2)()()f n x n =○5()y n (5点圆周卷积)。 解:(){1,2,0,0,4,3}, (){1,1,1,1}x n y n == (1)()()(){1,3,3,3,3,4,4,4,3}z n x n y n =*=(过程略) (2)()()f n x n =○5()y n (5点圆周卷积),N =5。 *利用圆周卷积与线性卷积的关系计算* ()[()]()[...(5)()(5)...]() N N r f n z n rN R n z n z n z n R n ∞ =-∞ =+=+-++++∑ 所以:()()f n x n =○5()y n ={5,7,7,6,3} 这种方法计算过程比较简单,但前提是先计算出线性卷积的结果。 三、结论 ? 圆周卷积的计算始终要记住一点:圆周卷积虽然是针对有限长序列的卷积运算,但它是由周期卷积推导而来的,故隐含了周期性。 ? (2)式虽然是圆周卷积的定义式,但要正确理解,灵活应用。它是在满足12max[,]N N N ≥的前提下由周期卷积推导而来的,其适用场合仅限于12max[,]N N N ≥的情况。
Matlab编程实现主成分分析 .程序结构及函数作用 在软件Matlab中实现主成分分析可以采取两种方式实现:一是通过编程来实现;二是直接调用Matlab种自带程序实现。下面主要主要介绍利用Matlab的矩阵计算功能编程实现主成分分析。 1程序结构 2函数作用 Cwstd.m——用总和标准化法标准化矩阵 Cwfac.m——计算相关系数矩阵;计算特征值和特征向量;对主成分进行排序;计算各特征值贡献率;挑选主成分(累计贡献率大于85%),输出主成分个数;计算主成分载荷 Cwscore.m——计算各主成分得分、综合得分并排序 Cwprint.m——读入数据文件;调用以上三个函数并输出结果
3.源程序 3.1 cwstd.m总和标准化法标准化矩阵 %cwstd.m,用总和标准化法标准化矩阵 function std=cwstd(vector) cwsum=sum(vector,1); %对列求和 [a,b]=size(vector); %矩阵大小,a为行数,b为列数 for i=1:a for j=1:b std(i,j)= vector(i,j)/cwsum(j); end end 3.2 cwfac.m计算相关系数矩阵 %cwfac.m function result=cwfac(vector); fprintf('相关系数矩阵:\n') std=CORRCOEF(vector) %计算相关系数矩阵 fprintf('特征向量(vec)及特征值(val):\n') [vec,val]=eig(std) %求特征值(val)及特征向量(vec) newval=diag(val) ; [y,i]=sort(newval) ; %对特征根进行排序,y为排序结果,i为索引fprintf('特征根排序:\n') for z=1:length(y) newy(z)=y(length(y)+1-z); end fprintf('%g\n',newy) rate=y/sum(y); fprintf('\n贡献率:\n') newrate=newy/sum(newy) sumrate=0; newi=[]; for k=length(y):-1:1 sumrate=sumrate+rate(k); newi(length(y)+1-k)=i(k); if sumrate>0.85 break; end end %记下累积贡献率大85%的特征值的序号放入newi中fprintf('主成分数:%g\n\n',length(newi)); fprintf('主成分载荷:\n') for p=1:length(newi)
数字信号处理实验报告 黎美琪 201300800610 13通信2 实验一名称:周期卷积、循环卷积和线性卷积比较 一、实验目的 1.理解周期卷积、循环卷积、线性卷积的定义 2.用图像显示上述几种卷积并对其进行直观的比较 二、实验步骤 自行设定: )它们的线性卷积()求它们的循环卷积(求它们的周期卷积(两个有限长序列 3)8(2)8)1(20 12,81,1129,1)(,2012,81,0129,8)(21==?? ?≤≤≤≤-≤≤=???≤≤≤≤≤≤-=N N n n n n x n n n n n x 实验代码:(大部分语句为图像显示处理) %循环卷积&线性卷积&周期卷积 %%线性卷积 figure(1); set(gcf, 'color', 'w')%将图的背景设置为白色 x1=[zeros(1,8),[1:4],zeros(1,4),zeros(1,8)];%原有限长序列x1(n ) x2=[zeros(1,8),ones(1,4),zeros(1,4),zeros(1,8)] ; %原有限长序列x2(n ) L=length(x1)%长度L M=length(x2)%长度M y1=conv(x1,x2) %线性卷积 subplot(311) stem(x1); title('有限长序列x1(n )') axis([1 L 0 5]) subplot(312) stem(x2); title('有限长序列x2(n )') axis([1 M 0 1]) subplot(313) stem(y1);grid on ; title('线性卷积') axis([1 L+M-1 0 11]) %%循环卷积(圆周卷积) figure(2); set(gcf, 'color', 'w')%将图的背景设置为白色 %x11=[[1:4],zeros(1,4),[1:4],zeros(1,4),[1:4],zeros(1,4)]; x11=[[1:4],zeros(1,2),[1:4],zeros(1,2),[1:4],zeros(1,2),[1:4],zeros(1
层次分析法建模 层次分析法(AHP-Analytic Hierachy process)---- 多目标决策方法 70 年代由美国运筹学家T·L·Satty提出的,是一种定性与定量分析相结合的多目标决策分析方法论。吸收利用行为科学的特点,是将决策者的经验判断给予量化,对目标(因素)结构复杂而且缺乏必要的数据情况下,採用此方法较为实用,是一种系统科学中,常用的一种系统分析方法,因而成为系统分析的数学工具之一。 传统的常用的研究自然科学和社会科学的方法有: 机理分析方法:利用经典的数学工具分析观察的因果关系; 统计分析方法:利用大量观测数据寻求统计规律,用随机数学方法描述(自然现象、 社会现象)现象的规律。 基本内容:(1)多目标决策问题举例AHP建模方法 (2)AHP建模方法基本步骤 (3)AHP建模方法基本算法 (3)AHP建模方法理论算法应用的若干问题。 参考书:1、姜启源,数学模型(第二版,第9章;第三版,第8章),高等教育出版社 2、程理民等,运筹学模型与方法教程,(第10章),清华大学出版社 3、《运筹学》编写组,运筹学(修订版),第11章,第7节,清华大学出版社 一、问题举例: A.大学毕业生就业选择问题 获得大学毕业学位的毕业生,“双向选择”时,用人单位与毕业生都有各自的选择标准和要求。就毕业生来说选择单位的标准和要求是多方面的,例如: ①能发挥自己的才干为国家作出较好贡献(即工作岗位适合发挥专长); ②工作收入较好(待遇好); ③生活环境好(大城市、气候等工作条件等); ④单位名声好(声誉-Reputation); ⑤工作环境好(人际关系和谐等) ⑥发展晋升(promote, promotion)机会多(如新单位或单位发展有后劲)等。 问题:现在有多个用人单位可供他选择,因此,他面临多种选择和决策,问题是他将如何作出决策和选择?——或者说他将用什么方法将可供选择的工作单位排序?
实验三 线性卷积与圆周卷积的计算 一、 实验目的 1、掌握计算机的使用方法和常用系统软件及应用软件的使用。 2、通过编程,上机调试程序,进一步增强使用计算机解决问题的能力。 3、掌握线性卷积与循环卷积软件实现的方法,并验证二者之间的关系。 二、实验原理 1、线性卷积: 线性时不变系统(Linear Time-Invariant System, or L. T. I 系统)输入、输出间的关系为:当系统输入序列为)(n x ,系统的单位脉冲响应为)(n h ,输出序列为)(n y ,则系统输出为: ∑∞ -∞ ==-= m n h n x m n h m x n y ) (*)()()()( 或 ∑+∞ -∞ ==-= m n x n h m n x m h n y ) (*)()()()( 上式称为离散卷积或线性卷积。 图1.1示出线性时不变系统的输入、输出关系。 )(n δ→ L. T. I —→)(n h —→ —→ 图1.1 线性时不变系统的输入、输出关系 2、圆周卷积 设两个有限长序列)(1n x 和)(2n x ,均为N 点长 )(1n x )(1k X )(2n x )(2k X 如果)()()(213k X k X k X ?= )(n x 0 L. T. I ∑+∞ -∞ =-= m m n h m x n y ) ()()( D F T D F T
则) ()(~)(~)(10213n R m n x m x n x N N m ??? ???-=∑-= [] ∑---=1 021)()(N m N m n x m x )(1n x =N 10)(2-≤≤N n n x 上式称为圆周卷积。 注:)(~1n x 为)(1n x 序列的周期化序列;)()(~1n R n x N 为)(~1n x 的主值序列。 上机编程计算时,)(3n x 可表示如下: ∑∑-+==-++ -=1 1 2 1 0213) ()()()()(N n m n m m n N x m x m n x m x n x 3、两个有限长序列的线性卷积 序列)(1n x 为L 点长,序列)(2n x 为P 点长,)(3n x 为这两个序列的线性卷积,则)(3n x 为 ∑+∞ -∞ =-= m m n x m x n x ) ()()(2 1 3 且线性卷积)(3n x 的最大长1-+P L ,也就是说当1-≤n 和1-+≥P L n 时 0)(3=n x 。 4、圆周卷积与线性卷积的关系 序列)(1n x 为L 点长,序列)(2n x 为P 点长,若序列)(1n x 和)(2n x 进行N 点的圆周卷积,其结果是否等于该两序列的线性卷积,完全取决于圆周卷积的长度: 当1-+≥P L N 时圆周卷积等于线性卷积,即 )(1n x N )(*)()(212n x n x n x = 当1-+
实验一线性卷积与圆周卷积演示程序的设计 实验报告 学号 专业班级 指导老师 分数
《数字信号处理课程设计》任务书
实验一 线性卷积与圆周卷积演示程序的设计 一、 实验目的 目的:① 熟练掌握MATLAB 工具软件在工程设计中的使用; ② 熟练掌握线性卷积与圆周卷积的关系及LSI 离散时间系统系统响应的求解方法。 要求:① 动态演示线性卷积的完整过程; ② 动态演示圆周卷积的完整过程; ③ 对比分析线性卷积与圆周卷积的结果。 步骤:① 可输入任意2待卷积序列x1(n)、x2(n),长度不做限定。测试数据为: x1(n)={1,1,1,1,0,0,1,1,1,1,0,0},x2(n)={0,1,2,1,0,0,0,1,2,1,0,0}; ② 分别动态演示两序列进行线性卷积x1(n)﹡x2(n)和圆周卷积x1(n)⊙x2 (n)的 过程;要求分别动态演示翻转、移位、乘积、求和的过程; ③ 圆周卷积默认使用2序列中的最大长度,但卷积前可以指定卷积长度N 用以进行混叠分析; ④ 根据实验结果分析两类卷积的关系。 ⑤ 假定时域序列x1(n)、x2(n)的长度不小于10000,序列容自定义。利用 FFT 实现快速卷积,验证时域卷积定理,并与直接卷积进行效率对比。 二、实验原理 1、线性卷积: 线性时不变系统(Linear Time-Invariant System, or L. T. I 系统)输入、输出间的关系为:当系统输入序列为)(n x ,系统的单位脉冲响应为)(n h ,输出序列为)(n y ,则系统输出为: ∑∞ -∞ ==-= m n h n x m n h m x n y ) (*)()()()( 或 ∑+∞ -∞ ==-= m n x n h m n x m h n y ) (*)()()()(
1 1.微分方程的定义 对于duffing 方程03 2 =++x x x ω ,先将方程写作??? --==3 1122 21x x x x x ω function dy=duffing(t,x) omega=1;%定义参数 f1=x(2); f2=-omega^2*x(1)-x(1)^3; dy=[f1;f2]; 2.微分方程的求解 function solve (tstop) tstop=500;%定义时间长度 y0=[0.01;0];%定义初始条件 [t,y]=ode45('duffing',tstop,y0,[]); function solve (tstop) step=0.01;%定义步长 y0=rand(1,2);%随机初始条件 tspan=[0:step:500];%定义时间范围 [t,y]=ode45('duffing',tspan,y0); 3.时间历程的绘制 时间历程横轴为t ,纵轴为y ,绘制时只取稳态部分。 plot(t,y(:,1));%绘制y 的时间历程 xlabel('t')%横轴为t ylabel('y')%纵轴为y grid;%显示网格线
2 axis([460 500 -Inf Inf])%图形显示范围设置 4.相图的绘制 相图的横轴为y ,纵轴为dy/dt ,绘制时也只取稳态部分。红色部分表示只取最后1000个点。 plot(y(end-1000:end ,1),y(end-1000:end ,2));%绘制y 的时间历程 xlabel('y')%横轴为y ylabel('dy/dt')%纵轴为dy/dt grid;%显示网格线 5.Poincare 映射的绘制 对于不同的系统,Poincare 截面的选取方法也不同 对于自治系统一般每过其对应线性系统的固有周期,截取一次 对于非自治系统,一般每过其激励的周期,截取一次 例程:duffing 方程03 2=++x x x ω 的poincare 映射 function poincare(tstop) global omega; omega=1; T=2*pi/omega;%线性系统的周期或激励的周期 step=T/100;%定义步长为T/100 y0=[0.01;0];%初始条件 tspan=[0:step:100*T];%定义时间范围 [t,y]=ode45('duffing',tspan,y0); for i=5000:100:10000%稳态过程每个周期取一个点 plot(y(i,1),y(i,2),'b.'); hold on;% 保留上一次的图形 end xlabel('y');ylabel('dy/dt');
实验五 循环卷积与线性卷积的实现 一、实验目的 (1) 进一步理解并掌握循环卷积与线性卷积的概念; (2) 理解掌握二者的关系。 二、实验原理 两个序列的N 点的循环卷积定义为 1 0[()()]()(())N N N k h n x n h m x n m -=?=-∑ (0) n N ≤< 从定义中可以看到,循环卷积和线性卷积的不同之处在于:两个N 点序列的N 点循环 卷积结果仍为N 点序列,而它们的线性卷积的结果长度则为2N -1;循环卷积对序列的移位采取循环移位,而线性卷积对序列采取线性移位。正是这些不同,导致了线性卷积和循环卷积有不同的结果和性质。 两个序列的N 点循环卷积是它们的线性卷积以N 为周期的周期延拓。设序列()h n 的长度为1N ,序列()x n 的长度为2N ,此时线性卷积结果的序列点数为'121N N N =+-;因此如果循环卷积的点数N 小于121N N +-,那么上述周期性延拓的结果就会产生混叠,从而两种卷积会有不同的结果。而如果满足'N N =的条件,就有循环卷积与线性卷积的结果在0n N ≤<范围内相同。 根据DFT 循环卷积性质中的卷积定理 {[()()]}[()][()]N DFT h n x n DFT x n DFT h n ?=? 因此可以根据性质先分别求两个序列的N 点DFT ,并相乘,然后取IDFT 以得到循环卷积。 三、实验分析 例题:已知有限长序列()x n 与()h n 如下图所示, (1) 画出两者之间的线性卷积 (2) 8点圆卷积。 (3) 5点圆卷积。
解析如下: (1)()x n 与()h n 的线性卷积,由公式可知: ()*()()()m h n x n x m h n m ∞ =-∞ = -∑ ()x m 与()h m -的图形如下: 利用方格平移法: 由方格平移法可知: 当0n =时,()*()0h n x n = 当1n =时,()*()0h n x n = 当2n =时,()*()0*11*11h n x n =+= 当3n =时,()*()2*11*10*13h n x n =++= 当4n =时,()*()3*12*11*10*16h n x n =+++= 当5n =时,()*()3*12*11*10*16h n x n =+++= 当6n =时,()*()3*12*11*16h n x n =++= 当7n =时,()*()3*12*15h n x n =+= 当8n =时,()*()3*13h n x n ==
信号、系统与信号处理实验Ⅱ 实验报告
实验名称:线性卷积与圆周卷积的计算 一、 实验目的 (1) 通过编程、上机调试程序,进一步掌握使用计算机解决问题的能力 (2) 掌握线性卷积和圆周卷积软件实现的方法,并验证二者之间的关系 二、 实验内容与要求 1. 线性卷积 当系统输入序列为x(n),系统的单位冲击响应为h(n),输出序列为y (n ),则线性时不变系统输入、输出间的关系为: Y (n )=h (n )*x (n ) 2. 圆周卷积 设两个有限长序列1()x n 和2()x n ,均为N 点,其N 点的DFT 分别为1()X k 和2()X k ,如果312()()()X k X k X k =?,则 1 3120()[()()]()N N m x n x m x n m R n -==-∑ 1 120()(())N N m x m x n m -==-∑ 1()x n =○ N 2()x n 01n N ≤≤- 已知两个有限长序列: ()()2(1)3(2)4(3)5(4)x n n n n n n δδδδδ=+-+-+-+- ()()2(1)(2)2(3)h n n n n n δδδδ=+-+-+- (1) 实验前,预先笔算好这两个序列的线性卷积及下列几种情况的圆周卷积 ①()x n ⑤()h n ②()x n ⑥()h n ③()x n ⑨()h n ④()x n ⑩()h n (2)编制一个计算两个序列线性卷积的通用程序,计算()()x n h n *。 (3)编制一个计算圆周卷积的通用程序,计算上述4种情况下的两个序列的圆周卷积。 (4)上机调试并记录实验结果 (5)将实验结果和预先笔算的结果比较,验证其正确性。
Matlab 信号处理工具箱 谱估计专题 频谱分析 Spectral estimation (谱估计)的目标是基于一个有限的数据集合描述一个信号的功率(在频率上的)分布。功率谱估计在很多场合下都是有用的,包括对宽带噪声湮没下的信号的检测。 从数学上看,一个平稳随机过程n x 的power spectrum (功率谱)和correlation sequence (相关序列)通过discrete-time Fourier transform (离散时间傅立叶变换)构成联系。从normalized frequency (归一化角频率)角度看,有下式 ()()j m xx xx m S R m e ωω∞ -=-∞ = ∑ 注:()() 2 xx S X ωω=,其中()/2 /2 1 lim N j n n N n N X x e N ωω→∞=-=∑ πωπ-<≤。其matlab 近似为X=fft(x,N)/sqrt(N),在下文中()L X f 就是指matlab fft 函数的计算结果了 使用关系2/s f f ωπ=可以写成物理频率f 的函数,其中s f 是采样频率 ()()2/s jfm f xx xx m S f R m e π∞ -=-∞ = ∑ 相关序列可以从功率谱用IDFT 变换求得: ()()()/2 2//2 2s s s f jfm f j m xx xx xx s f S e S f e R m d df f πωπ π ωωπ--= =? ? 序列n x 在整个Nyquist 间隔上的平均功率可以表示为 ()()() /2 /2 02s s f xx xx xx s f S S f R d df f π π ωωπ- -= =?? 上式中的
题目:已知两个有限长序列 x(n>=δ(n>+2δ(n-1>+3δ(n-2>+4δ(n-3>+5δ(n-4> h(n>=δ(n>+2δ(n-1>+δ(n-2>+2δ(n-3> 计算以下两个序列的线性卷积和圆周卷积 <1)x(n>⑤y(n> (2>x(n>⑥y(n> (3>x(n>⑨y(n> (4>x(n>⑩y(n>b5E2RGbCAP ●调用函数circonv function yc=circonv(x1,x2,N> %用直接法实现圆周卷积 %y=circonv(x1,x2,N> %y:输出序列 %x1,x2:输入序列 %N:圆周卷积的长度 if length(x1>>N error。 end if length(x2>>N error。 end %以上语句判断两个序列的长度是否小于N x1=[x1,zeros(1,N-length(x1>>]。%填充序列x1(n>使其长度为N,序列h(n>的长度为N1,序列x(n>的长度为N2p1EanqFDPw x2=[x2,zeros(1,N-length(x2>>]。
%填充序列x2(n>使其长度为N n=[0:1:N-1]。 x2=x2(mod(-n,N>+1>。 %生成序列x2((-n>>N,镜像,可实现对x(n>以N为周期的周期延拓,加1是因为MATLAB向量下标只能从1开始。DXDiTa9E3d H=zeros(N,N>。%生成N行N列的零矩阵 for n=1:1:N H(n,:>=cirshiftd(x2,n-1,N>。%该矩阵的k行为x2((k-1-n>>N end yc=x1*H'。%计算圆周卷积 ●调用函数cirshiftd function y=cirshiftd(x,m,N> %直接实现序列x的圆周移位 %y=cirshiftd(x,m,N> %x:输入序列,且它的长度小于N %m:移位位数 %N:圆周卷积的长度 %y:输出的移位序列 if length(x>>N error('x的长度必须小于N'>。 end x=[x,zeros(1,N-length(x>>]。
上海电力学院 信号与系统实验报告 题目:循环卷积与线性卷积的实现 班级:2011023 专业:电气工程及其自动化 学号:20111257 2013年12月17日
循环卷积与线性卷积的实现 一、实验目的 1、进一步理解并掌握循环卷积与线性卷积的概念; 2、理解掌握二者的关系; 二、实验原理 两个序列的N 点循环卷积的定义为: ()()[]()()()N N k N m n x m h n x n h -=?∑-=10() N N <≤0从定义中可以看到,循环卷积和线性卷积的不同之处在于:两个N 点序列的N 点循环卷积的结果仍为N 点序列,而它们的线性卷积的结果的长度则为2N-1;循环卷积对序列的位移采取循环位移,而线性卷积对序列采取线性位移。正是这些不同,导致了线性卷积和循环卷积有不同的结果和性质。 循环卷积和线性卷积虽然是不同的概念,但它们之间由一个有意义的公式联系在一起:()()()[]()()n G rN n y n x n h n y N r N ??? ??-'=?=∑∞-∞=其中()()()n x n h n y *='。 也就是说,两个序列的N 点循环卷积是他们的线性卷积以N 为周期延拓。设序列()n h 的长度为N1,序列()n x 的长度为N2,此时,线性卷积结果的序列的点数为121-+='N N N ;因此如果循环卷积的点数N 小于121-+N N ,那么上述周期性延拓的结果就会产生混叠,从而两种卷积会有不同的结果。而如果N 满足N N '=的条件,就会有()()n y n y '=() N n <≤0这就意味着在时域不会产生混叠。因此,我们得出结论:若通过在序列的末尾填充适当的零值,使得()n x 和()n h 成为121-+N N 点序列,并作出这两个序列的121-+N N 循环卷积,那么循环卷积与线性卷积的结果在N n <≤0范围内相同。 根据DFT 循环卷积性质中的卷积定理
1.实验目的 1) 通过编程,上机调试程序,进一步增强使用计算机解决问题的能力。 2) 掌握线性卷积与圆周卷积软件实现的方法,并验证两者之间的关系。 2.基本原理 线性卷积;圆周卷积;两个有限长序列的线性卷积;圆周卷积与线性卷积的关系。 3.实验内容及要求 已知两个有限长序列 X(n)= S (n)+2 -?+3 S -2)+4 S -3)+5 S (rt) h(n)= S (n)+2-1S+(n S -2)+2 S (3) 1.编制一个计算两个线性卷积的通用程序,计算x(n)*h(n) 。 2?编制一个计算圆周卷积的通用程序,计算上述4种情况下两个序列x(n)与h(n)的圆周卷积。 3.上机调试并打印或记录实验结果。 4.将实验结果与预先笔算的结果比较,验证真确性。 4.相应程序及图像 1 )编制一个计算两个序列线性卷积的通用程序,计算x(n)*h(n). clear all; xn=[1 2 3 4 5]; hn=[1 2 1 2]; yln=conv(xn,hn); ny=[0:1:length(yln)-1]; stem(ny,yln); xlabel('时间序号n'); ylabel('信号幅度'); title('线性卷积');
线性卷积 1 1 T — 2)编制一个计算圆周卷积的通用程序,计算上述4种情况下两个序列x(n)与h(n)的圆周卷 积。 主程序: clear all clc N=[5 6 9 10];%圆周卷积的长度向量 xn=[1 2 3 4 5]; hn=[1 2 1 2]; y1n=conv(xn,hn)%计算线性卷积 ny仁0:length(y1 n)-1;%分别计算x (n)和h ( n)的5点,6点,9点和10点圆周卷积 yc1=circ onv(xn,hn,N ⑴) yc2=circo nv(x n,h n,N(2)) yc3=circo nv(x n,h n,N(3)) yc4=circonv(xn,hn,N(4))%分别作出线性卷积和取不同点数的圆周卷积的图像比较 subplot(1,2,1) stem (n y1,y1 n); xlabel('时间序号n'); ylabel('信号幅度'); title('线性卷积'); subplot(1,2,2) stem(0:N(1)-1,yc1); xlabel('时间序号n'); ylabel('信号幅度'); title('5点圆周卷积'); figure subplot(1,2,1) stem(ny1,y1n); xlabel(' 时间序号n'); ylabel(' 信号幅度');
clc clear all; format long; Ns=1000; order=13; ! %**********************read the position and flux density************************ fid=fopen('','r'); %open the original file fidnew = fopen('','w'); %write the new file while feof(fid)==0 > tline = fgetl(fid); %tline if ~ischar(tline), break, end temp=abs(tline); Nlength=length(tline); isemptyline=0; % { if Nlength==0 isemptyline=1; end allspace=0; % 、 isspace=0; for i=1:Nlength T=temp(i); if T==32 isspace=isspace+1; % end if isspace==Nlength allspace=1; break end < end findalpha=0; % for j=1:Nlength T=temp(j); ! if ((T>=65)&(T>=90))|((T>=97)&(T>=122)) findalpha=1;
break; end end ) if (~findalpha)&(~allspace)&(isemptyline==0) % fprintf(fidnew,tline); fprintf(fidnew,'\n'); end - end fclose(fid); fclose(fidnew); fid1=fopen('','r'); · flux_position =fscanf(fid1,'%f',[2,Ns]); fclose(fid1); %********************************read file finish***************************************** flux_position=flux_position'; pos1=flux_position(:,1); { pos_delta=pos1(2); pos_length=length(pos1); pos_last=pos1(pos_length); for i=1:1:pos_length %copy and get another part of position pos2(i)=pos_last+i*pos_delta; ( end pos1=pos1'; flux1=flux_position(:,2); flux2=-flux_position(:,2); pos=[pos1,pos2];%combine and get all part of position > flux1=flux1'; flux2=flux2'; flux=[flux1,flux2];%combine and get all part of flux density value figure; plot(pos1,flux1,'r');%plot origional waveform " hold on; grid on; fft1=fft(flux,Ns);
写在前面: 本文主要讨论圆周卷积的一种特殊情况:圆周卷积的点数小于参与卷积的序列的长度的情况。这种情况在大多数《数字信号处理》教材和习题中都没有专门提及或涉及,所以在计算过程中给很多同学带来了困惑。结课后这两天终于能轻松一点,重新把这个问题思考了一下,整理成文,供大家学习讨论。 从信号与系统的角度来考虑,“圆周卷积的点数小于参与卷积的序列的长度的情况”不具有太多的实际意义,因为在这种情况下信号周期化的过程中存在混叠,运算前信号已经产生失真。但从理论的角度来看,作为圆周卷积的一种特殊情况还是值得讨论的,通过讨论可以更好的理解圆周卷积与周期卷积、线性卷积的关系及计算方法。 另外,本文与考试无关,仅希望通过本文让大家更好的理解三种卷积之间的关系。如有疑问,可继续讨论。 黄勇坚 2011年7月3日
圆周卷积与周期卷积、线性卷积的关系及计算 一、三者关系 设: 1122()01()01 x n n N x n n N ≤≤-≤≤-N :圆周卷积的点数 ? 圆周卷积是周期卷积的主值序列。 周期卷积:1 120()()()N m y n x m x n m -==-∑ (1) 圆周卷积:1 120 ()()()[()(())]()N c N N N m y n y n R n x m x n m R n -===-∑ 1 210 [()(())]()N N N m x m x n m R n -==-∑ (2) 注意: (2)式直接使用的前提是圆周卷积的点数N 应满足: 12max[,]N N N ≥(一般题目均符合此种情况) 若12N N N N <<或时,则不能直接用(2)式计算,否则分别用(2)式中的两个公式计算,即在12()()x n x n 、卷积顺序不同时,会出现计算结果不一致的问题。这种情况下应从圆周卷积与周期卷积的关系出发,将(2)式改为: 1 120 ()()()[(())(())]()N c N N N N m y n y n R n x m x n m R n -===-∑ 1 210 [(())(())]()N N N N m x m x n m R n -==-∑(3) 即在此种情况下,首先需对12()()x n x n 、都进行周期为N 的延拓,然后再取主值序列进行计算。
·· 1.微分方程的定义 对于duffing 方程03 2 =++x x x ω ,先将方程写作??? --==3 1122 21x x x x x ω function dy=duffing(t,x) omega=1;%定义参数 f1=x(2); f2=-omega^2*x(1)-x(1)^3; dy=[f1;f2]; 2.微分方程的求解 function solve (tstop) tstop=500;%定义时间长度 y0=[0.01;0];%定义初始条件 [t,y]=ode45('duffing',tstop,y0,[]); function solve (tstop) step=0.01;%定义步长 y0=rand(1,2);%随机初始条件 tspan=[0:step:500];%定义时间范围 [t,y]=ode45('duffing',tspan,y0); 3.时间历程的绘制 时间历程横轴为t ,纵轴为y ,绘制时只取稳态部分。 plot(t,y(:,1));%绘制y 的时间历程 xlabel('t')%横轴为t ylabel('y')%纵轴为y grid;%显示网格线 axis([460 500 -Inf Inf])%图形显示范围设置 4.相图的绘制 相图的横轴为y ,纵轴为dy/dt ,绘制时也只取稳态部分。红色部
·· 分表示只取最后1000个点。 plot(y(end-1000:end,1),y(end-1000:end,2));%绘制y 的时间历程 xlabel('y')%横轴为y ylabel('dy/dt')%纵轴为dy/dt grid;%显示网格线 5.Poincare 映射的绘制 对于不同的系统,Poincare 截面的选取方法也不同 对于自治系统一般每过其对应线性系统的固有周期,截取一次 对于非自治系统,一般每过其激励的周期,截取一次 例程:duffing 方程03 2=++x x x ω 的poincare 映射 function poincare(tstop) global omega; omega=1; T=2*pi/omega;%线性系统的周期或激励的周期 step=T/100;%定义步长为T/100 y0=[0.01;0];%初始条件 tspan=[0:step:100*T];%定义时间范围 [t,y]=ode45('duffing',tspan,y0); for i=5000:100:10000%稳态过程每个周期取一个点 plot(y(i,1),y(i,2),'b.'); hold on;% 保留上一次的图形 end xlabel('y');ylabel('dy/dt'); Poincare 映射也可以通过取极值点得到 function poincare(tstop) y0=[0.01;0]; tspan=[0:0.01:500]; [t,y]=ode45('duffing',tspan,y0); count=find(t>100);%截取稳态过程 y=y(count,:); n=length(y(:,1));%计算点的总数
循环卷积与线性卷积的实现 一、 实验目的:(1)进一步理解并掌握循环卷积与线性卷积的概念。 (2)理解掌握二者的关系。 三、实验原理 两个序列的N 点循环卷积定义为 ()()[]()()()()N n m n x m h n x n h N k N N <≤-= ?∑-=01 从定义中可以看到,循环卷积和线性卷积的不同之处在于:两个N 点序列的N 点循环卷积的结果仍为N 点序列,而他们的线性卷积的结果的长度则为2N-1;循环卷积对序列的移位采取循环移位,而线性卷积对序列采取线性位移。正式这些不同,导致了线性卷积和循环卷积有不同的结果和性质。 循环卷积和线性卷积虽然是不用的概念,但是它们之间有一个有意义的公式联系在一起 ()()()[]()()n G rN n y n x n h n y N r N ?? ? ??-'=?=∑∞-∞= 其中()()()n x n h n y *=' 也就是说,两个序列的N 点循环卷积是他们的线性卷积以N 为周期的周期延阔。设序列()n h 的长度为1N ,序列()n x 的长度为2N ,此时,线性卷积结果的序列的点数为121-+='N N N ;因此如果循环卷积的点 数N 小于12 1-+N N ,那么上述周期性延阔的结果就会产生混叠,从 而两种卷积会有不同的结果。而如果N 满足N N '=的条件,就会有 ()()()N n n y n y <≤'=0
这就会意味着在时域不会产生混叠。因此,我们得出结论:若通过在序列的末尾填充适当的零值,使得()n x 和()n h 成为121-+N N 店序 列,并作出这两个序列的12 1-+N N 循环卷积与线性卷积的结果在 N n <≤0范围内相同。 根据DFT 循环卷积性质中的卷积定理 ()()[]{}()[]()[]n h DFT n x DFT n x n h DFT N ?= ? 便可通过两种方法求两个序列的循环卷积:一是直接根据定义计算;二是根据性质先分别求两个序列的N 点DFT ,并相乘,然后取IDFT 以得到循环卷积。第二种方法看起来要经过若干个步骤,但由于求序列的DFT 和IDFT 都有快速算法,因此它的效率比第一种方法要高得多。 同样,根据线性卷积和循环卷积的关系,可以通过计算循环卷积以求得线性卷积,提高计算序列线性卷积的效率。 四、 实验内容 输入程序序列如下: n=[0:1:4];m=[0:1:3]; x1=1+n;x2=4-m; %生成函数x1和x2 L1=length(x1)-1;L2=length(x2)-1; %取函数的长度 y1=conv(x1,x2); %直接用函数conv 计算线性卷积 n1=[0:1:L1+L2]; subplot(3,1,1);stem(n1,y1) %绘制线性卷积图形