当前位置：文档之家› 分治算法实验(用分治法查找数组元素的最大值和最小值)

分治算法实验(用分治法查找数组元素的最大值和最小值)

算法分析与设计实验报告第一次实验

else

Max=max2; //分别保存在Max与Min

if(min1<=min2)

Min=min1;

else

Min=min2;

}

else //当数组中元素个数少于2时，直接赋值处理

{

Max=compmax(a,left,right);

Min=compmin(a,left,right);

}

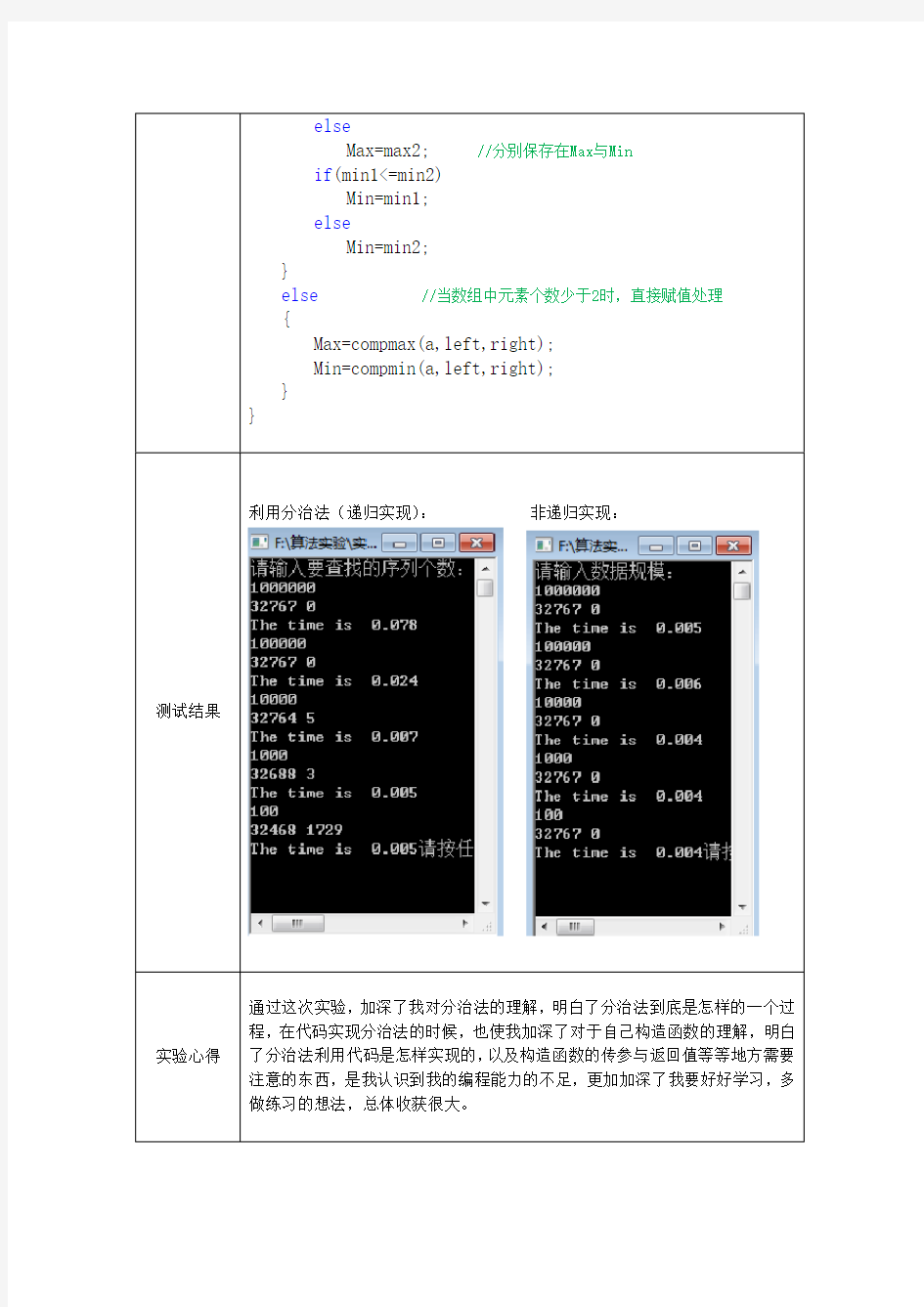
测试结果

利用分治法（递归实现）：非递归实现：

实验心得通过这次实验，加深了我对分治法的理解，明白了分治法到底是怎样的一个过程，在代码实现分治法的时候，也使我加深了对于自己构造函数的理解，明白了分治法利用代码是怎样实现的，以及构造函数的传参与返回值等等地方需要注意的东西，是我认识到我的编程能力的不足，更加加深了我要好好学习，多做练习的想法，总体收获很大。

附录：

完整代码（分治法）

#include

using namespace std;

//当数组中的元素个数小于3时，处理最大值

int compmax(int A[],int start,int end) {

int max;

if(start

if(A[start]<=A[end])

max=A[end];

else

max=A[start];

}

else//有一个元素max=A[start];

return max;

}

//当数组中元素的个数小于2时，处理最小值

int compmin(int A[],int start,int end) {

int min;

if(start

if(A[start]<=A[end])

min=A[start];

else

min=A[end];

}

else//有一个元素

min=A[start];

return min;

}

//分治法处理整个数组，求最大值与最小值

void merge(int a[],int left,int right,int &Max,int &Min) //Max,Min 用来保存最大值与最小值

//之所以使用&引用，是由于如果只是简单的使用变量，并不会改变Max与Min的值，使用指针也可以

{

int max1=0,min1=0,max2=0,min2=0;

if(right-left>2) //当数组中元素个数大于等于3时，进行分治

{

int mid=(right+left)/2;

merge(a,left,mid,max1,min1); //左半边递归调用自身，求出最大值最小值，分别保存在max1,min1中

merge(a,mid+1,right,max2,min2); //右半边递归调用自身，求出最大值最小值，分别保存在max2,min2中

if(max1>=max2) //子序列两两合并，求出最大值与最小值，保存在Max与Min中

Max=max1;

else

Max=max2;

if(min1<=min2)

Min=min1;

else

Min=min2;

}

else//数组中元素个数小于3时的情况，直接赋值

{

Max=compmax(a,left,right);

Min=compmin(a,left,right);

}

void ran(int *input,int n) //随机生成数组元素函数

{

int i;

srand(time(0));

for(i=0;i

input[i]=rand();

input[i]='\0';

}

int a[1000000]; //定义全局变量用来存放要查找的数组

int main()

{

int n;

int i;

int max;

int min;

cout<<"请输入要查找的序列个数："<

for(i=0;i<5;i++)

{

cin>>n;

ran(a,n);

clock_t start,end,over; //计算程序运行时间的算法

start=clock();

end=clock();

over=end-start;

start=clock();

merge(a,0,n-1,max,min); //调用分治法算法

cout<

end=clock();

printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); //显示运行时间

}

system("pause"); //停止运行窗口

return 0;

}

完整代码（非递归方法）

#include

using namespace std;

void ran(int *input,int n) //随机生成数组元素函数

{

int i;

srand(time(0));

for(i=0;i

input[i]=rand();

input[i]='\0';

}

int a[1000000];

int main()

{

int max=a[0],min=a[0];

int i,j,n;

cout<<"请输入数据规模："<

for(j=0;j<5;j++)

{

cin>>n;

ran(a,n);

clock_t start,end,over; //计算程序运行时间的算法

start=clock();

end=clock();

over=end-start;

start=clock();

for(i=1;i

{

if(a[i]>max)

max=a[i];

if(a[i]

min=a[i];

}

cout<

end=clock();

printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); //显示运行时间

}

system("pause");

return 0;

}

分治算法求最大值与最小值

实践题目：给定一个顺序表，编写一个求出其最大值和最小值的分治算法。分析：由于顺序表的结构没有给出，作为演示分治法这里从简顺序表取一整形数组数组大小由用户定义，数据随机生成。我们知道如果数组大小为 1 则可以直接给出结果，如果大小为 2则一次比较即可得出结果，于是我们找到求解该问题的子问题即: 数组大小 <= 2。到此我们就可以进行分治运算了，只要求解的问题数组长度比 2 大就继续分治，否则求解子问题的解并更新全局解以下是代码。 */ /*** 编译环境TC ***/ #include #include #include #define M 40 /* 分治法获取最优解 */ void PartionGet(int s,int e,int *meter,int *max,int *min){ /* 参数: * s 当前分治段的开始下标 * e 当前分治段的结束下标 * meter 表的地址 * max 存储当前搜索到的最大值 * min 存储当前搜索到的最小值 */ int i; if(e-s <= 1){ /* 获取局部解，并更新全局解 */ if(meter[s] > meter[e]){ if(meter[s] > *max)

*max = meter[s]; if(meter[e] < *min) *min = meter[e]; } else{ if(meter[e] > *max) *max = meter[s]; if(meter[s] < *min) *min = meter[s]; } return ; } i = s + (e-s)/2; /* 不是子问题继续分治,这里使用了二分，也可以是其它 */ PartionGet(s,i,meter,max,min); PartionGet(i+1,e,meter,max,min); } int main(){ int i,meter[M]; int max = INT_MIN; /* 用最小值初始化 */ int min = INT_MAX; /* 用最大值初始化 */ printf("The array's element as followed:\n\n"); randomize(); /* 初始化随机数发生器 */ for(i = 0; i < M; i ++){ /* 随机数据填充数组 */ meter[i] = rand()%10000; if(!((i+1)%10)) /* 输出表的随机数据 */ printf("%-6d\n",meter[i]);

例说求函数的最大值和最小值的方法

例说求函数的最大值和最小值的方法例1.设x 是正实数，求函数x x x y 32+ +=的最小值。解：先估计y 的下界。 55)1(3)1(5)21(3)12(222≥+- +-=+-+ ++-=x x x x x x x y 又当x =1时，y =5，所以y 的最小值为5。说明本题是利用“配方法”先求出y 的下界，然后再“举例”说明这个下界是可以限到的。“举例”是必不可少的，否则就不一定对了。例如，本题我们也可以这样估计： 77)1(3)1(7)21(3)12(222-≥-+ +-=-++ ++-=x x x x x x x y 但y 是取不到-7的。即-7不能作为y 的最小值。例2. 求函数1 223222++--=x x x x y 的最大值和最小值。解去分母、整理得：(2y -1)x 2+2(y +1)x +(y +3)=0. 当2 1≠y 时，这是一个关于x 的二次方程，因为x 、y 均为实数，所以 ?=[2(y +1)]2-4(2y -1)(y +3)≥0, y 2+3y --4≤0, 所以 -4≤y ≤1 又当3 1-=x 时，y =-4;x =-2时，y =1.所以y min =-4，y max =1.

说明本题求是最值的方法叫做判别式法。例3.求函数152++-=x x y ，x ∈[0,1]的最大值解：设]2,1[1∈=+t t x ，则x =t 2-1 y = -2(t 2-1)+5t = -2t 2+5t +1 原函数当t =169,45=x 即时取最大值8 33 例4求函数22 3,5212≤≤+--=x x x x y 的最小值和最大值解：令x -1=t ( 121≤≤t ) 则t t t t y 4142+=+= y min =5 1,172max =y 例5.已知实数x ,y 满足1≤x 2+y 2≤4,求f (x )=x 2+xy +y 2的最小值和最大值解：∵)(2 122y x xy +≤ ∴6)(23 ),(2222≤+≤++=y x xy y x y x f 又当2==y x 时f (x ,y )=6，故f (x ,y )max =6 又因为)(2122y x xy +- ≥

利用导数求函数值域

利用导数求函数最值高二苏庭导数是对函数的图像与性质的总结与拓展，导数是研究函数单调性极佳、最佳的重要工具，在掌握求函数的极值和最值的基础上学习用导数解决生产生活中的有关最大最小最有效等类似的应用问题广泛运用在讨论函数图像的变化趋势及证明不等式等方面。导数是初等数学与高等数学的重要衔接点，是高考的热点，高考对导数的考查定位于作为解决初等数学问题的工具出现，高考对这部分内容的考查将仍会以导数的应用题为主，如利用导数处理函数的极值、最值和单调性问题和曲线的问题等，考题不难，侧重知识之意。导数应用主要有以下三个方面： ①运用导数的有关知识研究函数的单调性和最值问题， ②利用导数的几何意义，研究曲线的切线斜率。函数y=f(x)在x=x0处的导数，表示曲线在点P（x0 , y0）处的切线斜率。由导数来求最值问题的方法可知，解这类实际问题需先建立函数关系，再求极值点，确定最值点及最值．在设变量时可采用直接法也可采用间接法．

求函数极值时，导数值为0的点是该点为极值点的必要条件，但不是充分条件。运用导数确定函数单调区间的一般步骤为：（1）求出函数y=f(x)的导函数；（2）在函数定义域内解不等式得函数y=f(x)的单调增区间；解不等式得函数y=f(x)的单调减区间。例题剖析例1、求函数的值域. 分析：求函数的值域以前学过一些方法，也可利用求导的方法，根据函数的单调性求解. 解答：函数的定义域由求得，即x≥－2.

当x>－2时，y′>0，即函数，在（－2，＋∞）上是增函数，又f(－2)=－1，∴所求函数的值域为[－1，＋∞）. 点评：（1）从本题的解答过程可以看到，当单调区间与函数的值域相同时，才可使用此法，否则会产生错误. （2）求值域时，当x=－2，函数不可导，但函数在[－2，＋∞）上是连续的，函数图象是连续变化的，因此在x=－2时，取得最小值. 例2、把长度为16cm的线段分成两段，各围成一个正方形，它们的面积之和的最小值为多少？分析：建立面积和与一正方形的周长的函数关系，再求最小值．解答：设一段长为xcm，则另一段长(16－x)cm． ∴面积和 ∴S′＝－2，令S′＝0有x＝8．列表：

导数运用最大值与最小值(含答案)

最大值与最小值一、基础过关 1．函数f (x )＝－x 2＋4x ＋7，在x ∈[3,5]上的最大值和最小值分别是________，________. 2．f (x )＝x 3－3x 2＋2在区间[－1,1]上的最大值是________． 3．函数y ＝ln x x 的最大值为________． 4．函数f (x )＝x e x 的最小值为________． 5．已知函数y ＝－x 2－2x ＋3在区间[a ,2]上的最大值为15 4 ，则a 等于________． 6．已知f (x )＝－x 2＋mx ＋1在区间[－2，－1]上最大值就是函数f (x )的极大值，则m 的取值范围是________． 7．求函数f (x )＝1 3x 3－4x ＋4在[0,3]上的最大值与最小值．二、能力提升 8．函数y ＝4x x 2＋1 的值域为________． 9．设直线x ＝t 与函数f (x )＝x 2，g (x )＝ln x 的图象分别交于点M ，N ，则当MN 达到最小时t 的值为________． 10．已知函数f (x )＝e x －2x ＋a 有零点，则a 的取值范围是________． 11．已知函数f (x )＝2x 3－6x 2＋a 在[－2,2]上有最小值－37，求a 的值及f (x )在[－2,2]上的最大值． 12．已知函数f (x )＝x 3－ax 2＋bx ＋c (a ，b ，c ∈R )． (1)若函数f (x )在x ＝－1和x ＝3处取得极值，试求a ，b 的值； (2)在(1)的条件下，当x ∈[－2,6]时，f (x )<2|c |恒成立，求c 的取值范围．三、探究与拓展 13．已知函数f (x )＝(x －k )e x . (1)求f (x )的单调区间； (2)求f (x )在区间[0,1]上的最小值．

高中数学第四章导数应用2.2最大值最小值问题二学案北师大版选修

2.2最大值、最小值问题(二) 学习目标1.了解导数在解决实际问题中的作用.2.会利用导数解决简单的实际生活中的优化问题．知识点生活中的优化问题 1．生活中经常遇到求利润最大、用料最省、效率最高等问题，这些问题通常称为____________． 2．利用导数解决优化问题的实质是求函数最值． 3．解决优化问题的基本思路：上述解决优化问题的过程是一个典型的______________过程．类型一几何中的最值问题命题角度1平面几何中的最值问题例1如图，要设计一张矩形广告，该广告含有大小相等的左右两个矩形栏目(即图中阴影部分)，这两栏的面积之和为18 000 cm2，四周空白的宽度为10 cm，两栏之间的中缝空白的宽度为5 cm.怎样确定广告的高与宽的尺寸(单位：cm)，能使矩形广告面积最小？

反思与感悟平面图形中的最值问题一般涉及线段、三角形、四边形等图形，主要研究与面积相关的最值问题，一般将面积用变量表示出来后求导数，求极值，从而求最值．跟踪训练1如图所示，在二次函数f(x)＝4x－x2的图像与x轴所围成图形中有一个内接矩形ABCD，求这个矩形面积的最大值．命题角度2立体几何中的最值问题例2请你设计一个包装盒如图所示，ABCD是边长为60 cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得ABCD四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E，F在AB上是被切去的等腰直角三角形斜边的两个端点，设AE＝FB＝x cm. (1)若广告商要求包装盒侧面积S最大，则x应取何值？ (2)若广告商要求包装盒容积V最大，则x应取何值？并求出此时包装盒的高与底面边长的比值．

(完整版)导数与函数的极值、最值问题(解析版)

【高考地位】导数在研究函数的极值与最值问题是高考的必考的重点内容，已由解决函数、数列、不等式问题的辅助工具上升为解决问题的必不可少的工具，特别是利用导数来解决函数的极值与最值、零点的个数等问题，在高考中以各种题型中均出现，对于导数问题中求参数的取值范围是近几年高考中出现频率较高的一类问题，其试题难度考查较大. 【方法点评】类型一利用导数研究函数的极值使用情景：一般函数类型解题模板：第一步计算函数()f x 的定义域并求出函数()f x 的导函数'()f x ；第二步求方程'()0f x =的根；第三步判断'()f x 在方程的根的左、右两侧值的符号；第四步利用结论写出极值. 例1 已知函数x x x f ln 1 )(+= ，求函数()f x 的极值. 【答案】极小值为1，无极大值. 【点评】求函数的极值的一般步骤如下：首先令'()0f x =，可解出其极值点，然后根据导函数大于0、小于0即可判断函数()f x 的增减性，进而求出函数()f x 的极大值和极小值．【变式演练1】已知函数322()f x x ax bx a =+++在1x =处有极值10，则(2)f 等于（） A ．11或18 B ．11 C ．18 D ．17或18 【答案】C 【解析】

试题分析：b ax x x f ++='23)(2,???=+++=++∴1010232 a b a b a ???-==????=----=?114012232b a a a a b 或???=-=33 b a ．当???=-=3 3 b a 时,∴≥-=',0)1(3)(2x x f 在1=x 处不存在极值．当???-==11 4b a 时， )1)(113(1183)(2-+=-+='x x x x x f ，0)(),1,3 11 (<'- ∈∴x f x ；0)(),,1(>'+∞∈x f x ,符合题意．所以???-==114b a ．181622168)2(=+-+=∴f ．故选C ．考点：函数的单调性与极值．【变式演练2】设函数()21 ln 2 f x x ax bx =--，若1x =是()f x 的极大值点，则a 的取值范围为（） A ．()1,0- B ．()1,-+∞ C ．()0,+∞ D ．()(),10,-∞-+∞U 【答案】B 【解析】考点：函数的极值．【变式演练3】函数x m x m x x f )1(2)1(2 1 31)(23-++-=在)4,0(上无极值，则=m _____. 【答案】3 【解析】试题分析：因为x m x m x x f )1(2)1(2 1 31)(23-++-= ，所以()()2'()(1)2(1)21f x x m x m x x m =-++-=--+，由()'0f x =得2x =或1x m =-，又因为