山东省实验中学2013-2014学年高一上学期期中考试 地理

山东省实验中学2025届高三第二次诊断考试地理试题2024.11说明：本试卷满分100分，分为第I 卷(选择题)和第Ⅱ卷(非选择题)两部分，第I 卷为第1页至第5页，第Ⅱ卷为第5页至第8页。

试题答案请用2B 铅笔或0.5 mm 签字笔填涂到答题卡规定位置上，书写在试题上的答案无效。

考试时间90分钟。

第I 卷(选择题，共45分)一、选择题(本题包括15小题，每小题3分，共45分。

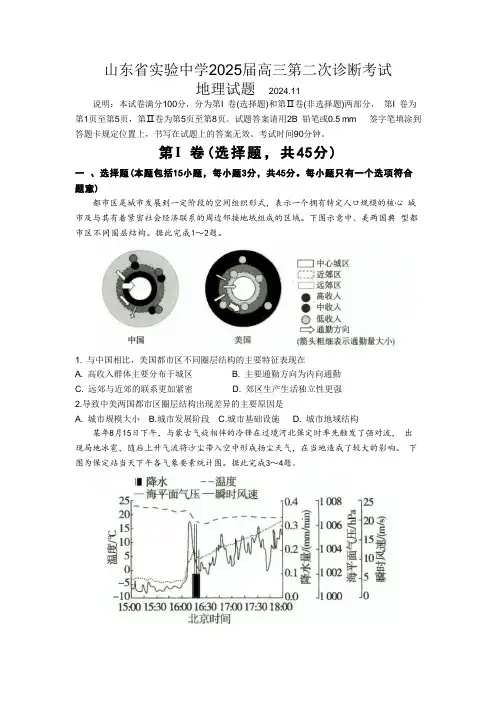
每小题只有一个选项符合题意)都市区是城市发展到一定阶段的空间组织形式，表示一个拥有特定人口规模的核心城市及与其有着紧密社会经济联系的周边邻接地域组成的区域。

下图示意中、美两国典型都市区不同圈层结构。

据此完成1～2题。

1. 与中国相比，美国都市区不同圈层结构的主要特征表现在A. 高收入群体主要分布于城区B. 主要通勤方向为内向通勤C. 远郊与近郊的联系更加紧密D. 郊区生产生活独立性更强2.导致中美两国都市区圈层结构出现差异的主要原因是A. 城市规模大小B.城市发展阶段C.城市基础设施D. 城市地域结构某年8月15日下午，与蒙古气旋相伴的冷锋在过境河北保定时率先触发了强对流，出现局地冰雹，随后上升气流将沙尘带入空中形成扬尘天气，在当地造成了较大的影响。

下图为保定站当天下午各气象要素统计图。

据此完成3～4题。

3. 此次保定市冷锋过境触发了锋前强对流天气的原因是A. 暖气团控制下气压低B.空气湿度大温度高C. 天气晴朗地面升温快D. 锋前空气挤压抬升4. 15日16:15到16:20期间，保定市可能出现的天气现象是A. 暴雨B.泥雨C.沙尘暴D.大雾卡里马塔海峡是南海和爪哇海及印度洋水体和热量交换的通道。

科学家在数值诊断实验中用拦水坝关闭卡里马塔海峡，以研究卡里马塔海峡不同季节对爪哇海的影响及对望加锡海峡南下洋流流速的影响。

下图示意卡里马塔海峡及周边区域自然地理环境。

据此完成5～6题。

5.卡里马塔海峡表层洋流A. 全年向南流B.7 月向南流，1月向北流C. 全年向北流D.7 月向北流，1月向南流6.若在1月用拦水坝关闭卡里马塔海峡，则可能出现的现象是A. 爪哇海水温上升，水位下降B. 望加锡海峡南下洋流流速减慢C. 爪哇海水温下降，水位上升D. 望加锡海峡北上洋流流速加快省会“首位度”指的是省会城市的经济总量占全省经济总量的比例。

山东省滕州实验高级中学2014-2015学年高一上学期第一次模块检测地理试题2014年9月本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

考试时间：90分钟。

满分：100分。

第Ⅰ卷注意事项：1..每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

在试题卷上作答无效．．．．．．．．．。

2.本试卷共30小题，每小题2分，共60分。

在每题给出的四个选项中，只有一项是符合题目要求。

“太阳大，地球小，太阳带着地球跑；地球大，月亮小，地球带着月亮跑。

”根据童谣，回答1～2题。

1.童谣中出现的所有天体都属于①太阳系②地月系③银河系④河外星系⑤总星系A.①③⑤B.①②③④⑤C.①②④⑤D.①③④⑤2.童谣中涉及的最低一级天体系统的中心天体是A.太阳B.地球C.月球D.恒星3. 下列各图中的大中小圆分别表示河外星系、太阳系、地月系，其中能正确表示它们三者之间关系的是4．我们在夜空中看到的点点繁星大多数是A恒星 B行星 C卫星 D星云据美国《科学日报》报道，日前，天文学家发现了早期宇宙的“残骸”——一颗宇宙大爆炸之后形成的第二代恒星。

它位于距离地球29万光年之遥的矮星系玉夫星座。

据此回答5～6题。

5．下列对于该二代恒星的判断，正确的是A．由炽热气体组成，能发光发热B．自身不发光，但能反射太阳光而明亮C．由气体和尘埃组成，呈云雾状外表D．该恒星所在天体系统内有生命存在6．该恒星所处的天体系统是A．银河系 B．河外星系 C．太阳系D．地月系7. 下列不属于天体的是A．太阳 B．哈雷彗星 C．运行中的“嫦娥一号” D．陨石图中的“蓝月亮”为科学家用计算机模拟出的银河系中一个可能孕育生命的外星天体，据推测它本身不发光，但该天体上光照良好。

据此回答下列问题。

8．“蓝月亮”应属于A．行星 B．恒星 C．彗星 D．卫星9．“蓝月亮”上的光照可能来自A．地球 B．行星 C．恒星 D．太阳10．在类地行星中，距离太阳最近的是：A、地球B、水星C、火星D、海王星11．不包括地球在内的天体系统是A．河外星系 B．总星系 C．银河系 D．太阳系读图，回答下列问题。

高一学分认定考试地理试卷 2014.11注意事项：1.本次考试分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共8页。

2.请把第Ⅰ卷的答案连同自己的学校、姓名、班级、考号图写在答题卡上。

3.请把第Ⅱ卷所有题目的答案用黑色签字笔答在答题卡上，在试题卷上答题无效。

4.满分100分，时间：100分钟。

第Ⅰ卷 （选择题 共50分）本试卷共25小题，每小题2分，共50分。

每小题给出的四个选项中，只有一个是最符合题目要求的。

北京时间2012年8月6日13时31分，美国航天局发射的好奇号探测车登陆火星表面。

据此回答1~2题。

1.好奇号探测车勇于研究火星上是否存在适合生物生存的环境，其主要目标是探测火星上是否存在（ ）A.液态水和有机物B.山脉和平原C.大气和云雾D.太阳辐射和火星引力2.当好奇号探测车登陆火星层表面时，肯尼迪航天中心（N 0328' 、W 2480'）的区时是 A.8月5日11时31分 B.8月6日0时31分C.8月7日1时31分D.8月7日5时31分太阳黑子活动的变化会对地球的气候产生明显影响。

下图显示北半球部分高纬度地区太阳黑子活动与年均降水量的关系。

读图回答3~4题。

3.材料中提到的“太阳黑子”出现在太阳大气层的（ ）A.光球层B.色球层C.日冕层D.太阳内部4.观测现实，所观测地区年平均降水量（ ）A.随太阳黑子活动的增强而增大B.随太阳黑子活动的增强而减小C.变化周期与太阳黑子活动周期吻合D.变化周期与太阳黑子活动周期无关下图是以极地为中心的地球示意图，读图回答5~6题。

5.关于图中甲、丙两地的叙述，正确的是（ ）A.自转线速度相等，甲地自转角速度大于丙地B.自转线速度相等，甲地自转角速度小于丙地C.自转角速度相等，甲地自转角速度大于丙地D.自转角速度相等，甲地自转角速度小于丙地6.图中丁地位与乙地的（ ）A.西南方向B.东南方向C.东北方向D.西北方向下图是北京时间2014年11月12日甲、乙、丙、丁四地的昼夜长短分布示意图，途中阴影部分表示黑夜。

山东省实验中学2024～2025学年第一学期期中高二数学试题 2024.11（选择性必修—检测）说明：本试卷满分150分，分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷为第1页至第2页，第Ⅱ卷为第3页至第4页.试题答案请用2B 铅笔或0.5mm 签字笔填涂到答题卡规定位置上，书写在试题上的答案无效。

考试时间120分钟。

第Ⅰ卷（共58分）一、单选题（本题包括8小题，每小题5分，共40分。

每小题只有一个选项符合题意）1.已知空间向量，，，若，，共面，则实数（ ）A.1B.2C.3D.42.“”是“直线与直线平行”的（ ）A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件3.给出下列说法，其中不正确的是（）A.若，则，与空间中其它任何向量都不能构成空间的一个基底向量B.若，则点是线段的中点C.若，则，，，四点共面D.若平面，的法向量分别为，，且，则3.若三条直线，，不能围成三角形，则实数的取值最多有（ ）A.2个B.3个C.4个D.5个4.实数，满足，则的最小值为（ ）A. B.7C. D.36.若直线与曲线有两个不同的交点，则实数的取值范围是（ ）A.()1,2,0a = ()0,1,1b =- ()2,3,c m = a b cm =1m =-()1:2310l mx m y +++=2:30l x my ++=a b ∥a b c2PM PA PB =+M AB 2OA OB OC OD =+-A B C D αβ()12,1,1n =- ()21,,1n t =-αβ⊥3t =1:43l x y +=2:0l x y +=3:2l x my -=m x y 2222x y x y +=-3x y -+3+:20l kx y --=:1C x =-k k >5k <≤k <<1k <≤7.在三棱锥中，为的重心，，，，，，若交平面于点，且，则的最小值为（ ）A.B.C.1D.8.已知椭圆的左、右焦点分别为，，点在上且位于第一象限，圆与线段的延长线，线段以及轴均相切，的内切圆为圆.若圆与圆外切，且圆与圆的面积之比为4，则的离心率为（ ）A.C.二.多选题（本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，有选错的得0分，部分选对的得部分分.）9.下列说法正确的是（）A.若直线的倾斜角越大，则直线的斜率就越大B.圆与直线必有两个交点C.在轴、轴上的截距分别为，的直线方程为D.设，，若直线与线段有交点，则实数的取值范围是10.已知椭圆的离心率为，长轴长为6，，分别是椭圆的左、右焦点，是一个定点，是椭圆上的动点，则下列说法正确的是（ ）A.焦距为2B.椭圆的标准方程为P ABC -G ABC △PD PA λ= PE PB μ= 12PF PC =λ()0,1μ∈PG DEF M 12PM PG =λμ+122343()2222:10x y C a b a b+=>>1F 2F P C 1O 1F P 2PF x 12PF F △2O 1O 2O 1O 2O C 123522:4O x y +=10mx y m +--=x y a b 1x y a b+=()2,2A -()1,1B :10l ax y ++=AB a (]322⎡⎫-∞-+∞⎪⎢⎣⎭，，()2222:10x y E a b a b +=>>23F F '()1,1A P E E 22195x y +=C.D.的最大值为11.立体几何中有很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体.如图，这是一个棱数24，棱长为的半正多面体，它所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得的，下列结论正确的有（）A.平面B.，，，四点共面C.点到平面的距离为D.若为线段上的动点，则直线与直线所成角的余弦值范围为第Ⅱ卷（非选择题，共92分）三、填空题（本题共3小题，每小题5分，共15分，其中14题第一空2分，第二空3分.）12.已知直线的倾斜角，则直线的斜率的取值范围为______.13.如图，已知点，，从点射出的光线经直线反射后再射到直线上，最后经直线反射后又回到点，则光线所经过的路程是______.14.杭州第19届亚运会的主会场——杭州奥体中心体育场，又称“大莲花”（如图1所示）.会场造型取意于杭州丝绸纹理与纺织体系，建筑体态源于钱塘江水的动态，其简笔画如图2所示.一同学初学简笔画，先AF '=PA PF +6AG ⊥BCDG A F C D B ACD E BC DE AF 12⎡⎢⎣l 2,43ππθ⎛⎫∈⎪⎝⎭l ()8,0A ()0,4B -()3,0P AB OB OB P画了一个椭圆与圆弧的线稿，如图3所示.若椭圆的方程为，下顶点为，为坐标原点，为圆上任意一点，满足，则点的坐标为______；若为椭圆上一动点，当取最大值时，点恰好有两个，则的取值范围为______.图1 图2 图3四、解答题（本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.）15.（13分）已知两直线和的交点为.（1）直线过点且与直线平行，求直线的一般式方程；（2）圆过点且与相切于点，求圆的一般方程.16.（15分）已知椭圆，且过点.（1）求椭圆的方程；（2）若斜率为的直线与椭圆交于，两点，且点在第一象限，点，分别为椭圆的右顶点和上顶点，求四边形面积的最大值.17.（15分）在梯形中，，，，为的中点，线段与交于点（如图1）.将沿折起到位置，使得（如图2）.图1 图2（1）求证：平面平面；（2）线段上是否存在点，使得与平面的值；若不存在，请说明理由.E()222210x ya ba b+=>>10,2A⎛⎫-⎪⎝⎭O P C2PO PA=C Q QC Q a1:20l x y++=2:3210l x y-+=Pl P310x y++=lC()1,01l P C()2222:10x yC a ba b+=>>⎛⎝C12l C M N M A B CAMBN SABCD AB CD∥3BADπ∠=224AB AD CD===P AB AC DP O ACD△AC ACD'△D O OP'⊥D AC'⊥ABCPD'Q CQ BCD'PQPD'18.（17分）已知直线，半径为2的圆与相切，圆心在轴上且在直线的右上方.（1）求圆的方程；（2）直线与圆交于不同的，两点，且，求直线的斜率；（3）过点的直线与圆交于，两点（在轴上方），问在轴正半轴上是否存在定点，使得轴平分？若存在，请求出点的坐标：若不存在，请说明理由.19.（17分）已知点，是平面内不同的两点，若点满足（，且），则点的轨迹是以有序点对为“稳点”的-阿波罗尼斯圆.若点满足，则点的轨迹是以为“稳点”的-卡西尼卵形线.已知在平面直角坐标系中，，.（1）若以为“稳点”的-阿波罗尼斯圆的方程为，求，，的值；（2）在（1）的条件下，若点在以为“稳点”的5-卡西尼卵形线上，求（为原点）的取值范围；（3）卡西尼卵形线是中心对称图形，且只有1个对称中心，若，，求证：不存在实数，，使得以—阿波罗尼斯圆与—卡西尼卵形线都关于同一个点对称.:40l x ++=C l C x l C 2y kx =-C M N 120MCN ︒∠=2y kx =-()0,1M C A B A x y N y ANB ∠N A B P PAPBλ=0λ>1λ≠P (),A B λQ ()0QA QB μμ⋅=>Q (),A B μ()2,0A -()(),2B a b a ≠-(),A B λ221240x y x +-+=a b λQ (),A B OQ O 0b =λ=a μ(),A B μ山东省实验中学2024～2025学年第一学期期中高二数学试题参考答案 2024.11选择题1234567891011ABCBDDCCBDBCDABD填空题12..13.，.解答题15.【答案】（1）（2）.【详解】（1）直线与直线平行，故设直线为，……1分联立方程组，解得.直线和的交点.……3分又直线过点，则，解得，即直线的方程为.……5分（2）设所求圆的标准方程为，的斜率为，故直线的斜率为1，由题意可得，……8分解得，……11分故所求圆的方程为.(()1,-∞-+∞ ,20,3⎛⎫-⎪⎝⎭a >340x y ++=221140333x y x y +++-=l 310x y ++=l 130x y C ++=203210x y x y ++=⎧⎨-+=⎩11x y =-⎧⎨=-⎩∴1:20l x y ++=2:3210l x y -+=()1,1P --l P 1130C --+=14C =l 340x y ++=()()222x a y b r -+-=1:20l x y ++=1-CP ()()()()2222221110111a b r a b r b a ⎧--+--=⎪⎪-+-=⎨⎪+⎪=+⎩216162518a b r ⎧=-⎪⎪⎪=-⎨⎪⎪=⎪⎩2211256618x y ⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭化为一般式：.……13分16.【答案】（1）（2）【详解】（1）由椭圆，解得，……2分由椭圆过点，得，联立解得，，……4分所以椭圆的方程为.……5分（2）由题意可设，点在第一象限，，……6分设，，点，到直线的距离分别为，，由，消可得，，，……8分10分，，直线的一般式方程：，，，，……12分14分当时，有最大值为……15分17.【答案】（1）证明见解析（2）存在，【详解】（1）证明：在梯形中，，22114333x y x y+++-=2214xy+=2222:1x yCa b+==2a b= C⎛⎝221314a b+=2a=1b=C2214xy+=1:2l y x m=+M11m∴-<<()11,M x y()22,N x y A B l1d2d221412xyy x m⎧+=⎪⎪⎨⎪=+⎪⎩y222220x mx m++-=122x x m∴+=-21222x x m=-MN∴===()2,0A()0,1B l220x y m-+=1d∴=2d=12d d∴+=()121122AMN BMNS S S MN d d∴=+=⋅+==△△m=S13ABCD AB CD∥，，为的中点，，，，……1分是正三角形，四边形为菱形，，，……3分，，又，，平面，平面，……5分平面，平面平面.……6分（2）存在，，理由如下：……8分平面，，，，两两互相垂直，如图，以点为坐标原点，，，所在直线为，，轴建立空间直角坐标系.则，，，，，，设平面的一个法向量为，则，即，令，则，，，……11分设，，，， (12)分设与平面所成角为，则，即，，解得，224AB AD CD ===3BAD π∠=P AB CD PB ∴∥CD PB =BC DP =ADP ∴△DPBC AC BC ∴⊥AC DP ⊥AC D O ⊥' D O OP '⊥AC OP O = AC OP ⊂ABC D O ∴'⊥ABC D O ⊂' D AC '∴D AC '⊥ABC 13PQ PD '=D O ⊥' BAC OP AC ⊥OA ∴OP OD 'O OA OP OD 'x y z ()C ()2,0B ()0,0,1D '()0,1,0P )2,1BD ∴'=- )CD '=CBD '(),,n x y z =00n BD n CD ⎧⋅=⎪⎨⋅=⎪⎩'' 200y z z -+=+=⎪⎩1x =0y =z =(1,0,n ∴=()01PQ PD λλ'=≤≤)CP =()0,1,1PD =-'),CQ CP PQ CP PD λλλ∴=+=+=- CQ BCD 'θsin cos ,CQ n CQ n CQ n θ⋅====23720λλ-+=01λ≤≤ 13λ=线段上存在点，且，使得与平面……15分18.【答案】（1）（2）（3）【详解】（1）设圆心，则，……2分解得或（舍），故圆的方程为.……4分（2）由题意可知圆心到直线的距离为，……6分，解得.……8分（3）当直线的斜率存在时，设直线的方程为，，，，由得，……10分，……12分若轴平分，则，即，即，即，即，即，……14分当时，上式恒成立，即；……15分当直线的斜率不存在或斜率为0时，易知满足题意；综上，当点的坐标为时，轴平分.……17分19.【答案】（1），，（2）（3）证明见解析【详解】（1）因为以为“稳点”的—阿波罗尼斯圆的方程为，设是该圆上任意一点，则，……1分所以，……3分∴PD 'Q 13PQ PD '=CQ BCD '224x y +=k =()0,4N ()(),04C a a >-422a +=0a =8a =-C 224x y +=C 2y kx =-2sin 301︒=1=k =AB AB ()10y kx k =+≠()()0,0N t t >()11,A x y ()22,B x y 224,1x y y kx ⎧+=⎨=+⎩()221230k x kx ++-=12221k x x k -∴+=+12231x x k -=+y ANB ∠AN BN k k =-12120y t y t x x --+=1212110kx t kx tx x +-+-+=()()1212210kx x t x x +-+=()()22126011t k k k k -⨯--+=++40k kt -+=4t =()0,4N AB ()0,4N N ()0,4y ANB ∠2a =0b =λ=[]1,3(),A B λ221240x y x +-+=(),P x y 22124x y x +=-()()()()22222222222222244162212224PA x y x y x x x y ax by a b a x by a bx a y b PB+++++===+--++--+-+-+-因为为常数，所以，，且，……5分所以，，.……6分（2）解：由（1）知，，设，由，所以，……7分，整理得，即，所以，……9分，……10分由，得，即的取值范围是.……12分（3）证明：若，则以—阿波罗尼斯圆的方程为，整理得，该圆关于点对称.……15分由点，关于点对称及，可得—卡西尼卵形线关于点对称，令，解得，与矛盾，所以不存在实数，，使得以—阿波罗尼斯圆与—卡西尼卵形线都关于同一个点对称……17分22PA PB2λ2240a b -+=0b =2a ≠-2a =0b =λ==()2,0A -()2,0B (),Q x y 5QA QB ⋅=5=()222242516x y x ++=+2240y x =--≥42890x x --≤()()22190x x +-≤209x ≤≤OQ ==209x ≤≤13OQ ≤≤OQ []1,30b =(),A B ()()222222x y x a y ⎡⎤++=-+⎣⎦()22244240x y a x a +-++-=()22,0a +()2,0A -(),0B a 2,02a -⎛⎫⎪⎝⎭QA QB μ⋅=μ2,02a -⎛⎫⎪⎝⎭2222a a -+=2a =-2a ≠=-a μ(),A B μ。

山东省实验中学2023 级十月测试地理试题（2024.10）说明：试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷为第1 页至第7 页，第Ⅱ卷为第8 页。

考试时间90 分钟。

第Ⅰ卷（选择题70 分）一、选择题：本大题共35 小题，每小题2 分，共70 分。

在每小题列出的四个选项中，选出符合题目要求的一项。

日晷由晷盘和晷针组成。

北京故宫太和殿外广场（40 °N，116 °E）所立日晷属于赤道式日晷，其晷盘与地球赤道面平行，晷针垂直穿过晷盘中心并指向北极星。

图 1 为北半球夏半年某日拍摄的太和殿外广场日晷照片。

据此完成1～3题。

图11 ．太和殿外广场所立日晷，摆放正确的示意图是A B C D2 ．图1 所示时刻，太阳位于当地的A ．西北方天空B ．西南方天空C ．东北方天空D ．东南方天空3 ．该日，随白昼时间的推移，晷针的日影在晷盘上的移动方向是A ．顺时针B ．逆时针C ．先逆时针后顺时针D ．先顺时针后逆时针2024 年5 月3 日17 时27 分，搭载嫦娥六号探测器的运载火箭在文昌航天发射场成功发射。

37 分钟后，器箭分离，嫦娥六号准确进入预定轨道。

嫦娥六号探测器开启世界首次月球背面采样并返回之旅，从发射至采样返回全过程约53 天。

据此完成4～6 题。

4 ．正在德国柏林（13.2°E）留学的小明在学校观看嫦娥六号发射实况直播，器箭分离时当地时间为A ．2 日11 时4 分B ．3 日10 时27 分C ．3 日11 时4 分D ．2 日1 时4 分5 ．嫦娥六号发射时，与北京处于同一天的日期范围约占全球的比例是A ．90%B ．70%C ．50%D ．30%6 ．嫦娥六号发射至采样返回期间，济南某中学操场旗杆正午影子长度变化为A ．先变长后变短B ．先变短后变长C ．一直变短D ．一直变长对日影和太阳高度变化的观测可以判断地理位置、地方时等要素。

图 2 为甲地某日日出至日落期间标杆的日影变化示意图，当日影朝正北方向时，标杆长度与其日影长度相等。

山东省实验中学2013～2014学年第一学期高一历史试题 2013．11（必修1阶段检测）说明：本试卷为发展卷，采用长卷出题、自主选择、分层记分的方式，试卷满分120分，考生每一专题的题目都要有所选择，至少选做100分的题目，多选不限。

试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷为第1页至第4页，第Ⅱ卷为第5页至第6页。

试题全部答案请用2B铅笔或0.5mm签字笔填涂到答题纸规定位置上，书写在试题上的答案无效。

考试时间60分钟。

第Ⅰ卷．．．．80．．分）．．．（共一、选择题（本题包括20小题，每小题2分，共80分。

每小题只有一个选项．．．．．．符合题意，基础题70分，发展题10分）1.“每逢佳节倍思亲”，追根溯源，下列制度中与这种珍惜亲情、渴望相聚情结的形成有密切关系的是A.分封制B.宗法制C.郡县制D.科举制2.山东自古就有“齐鲁”之称。

这个称呼依据的史实最早可追溯至A.夏B.商C.西周D.春秋时期3.“昔武王克殷，成王靖四方，康王息民，并建母弟，以藩屏周”。

这里的“并建母弟，以藩屏周”指的是A.分封制B.宗法制C.礼制D.等级制度4.秦朝开创的中央集权政治制度对后代影响深远。

为加强皇权，秦朝在中央实行的政治制度是A.三公九卿制B.郡县制C.内阁制D.科举制5.唐太宗看见新进士络绎而出，大笑说：“天下英雄，尽入我彀中矣！”由此，唐人也有诗曰：“太宗皇帝真长策，赚得英雄尽白头”。

这反映的是科举制度A.成功地将人才选拔与仕途联系在一起B.选拔了大量年轻有为的人才C.提高了庶族地主地位D.阻碍了学术和时代的进步6.司马迁在《史记·秦始皇本纪》曾经描述秦代的政治制度：“法令出一”“天下之事无小大皆决于上”。

这反映了A.皇权至高无上B.中央官职互相制约C.秦律严苛细密D.丞相大权独揽7.秦朝推行的地方行政制度是A.分封制B.郡县制C.宗法制D.行省制度8.“三司之职，国初沿五代之制置使，以总国计，应四方贡赋之入，朝廷不预，一归三司，通管盐铁、度支、户部……。

山东省实验中学2013～2014学年第一学期高一政治试题 2013．11（必修1阶段检测）说明：本试卷为发展卷，采用长卷出题、自主选择、分层记分的方式，试卷满分120分，考生每一专题的题目都要有所选择，至少选做100分的题目，多选不限。

试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷为第1页至第8页，第Ⅱ卷为第9页至第10页。

试题全部答案请用2B铅笔或0.5mm签字笔填涂到答题纸规定位置上，书写在试题上的答案无效。

考试时间60分钟。

第Ⅰ卷（共80分）一、选择题（本题包括40小题，每小题2分，共80分。

每小题只有一个选项．．．．．．符合题意，基础题68分，发展题12分）（一）基础知识全知道。

1.成为商品必须具备的条件有①劳动产品②自然物③自己生产自己享用④用于交换A．①② B. ①④ C. ③④ D. ①③④2.下列说法正确的是A．商品货币同时存在，同时产生 B．先有商品后有货币C．先有货币后有商品 D．有了商品就有了货币3.在一定意义上，货币是财富的象征，是因为①货币的本质是一般等价物②货币是唯一充当过一般等价物的商品③金银天然是货币④货币具有价值尺度和流通手段两种基本职能A．①③④ B．①②④ C．①④ D．①②③④4.下列对纸币的认识正确的有A．纸币是国家发行的，国家可随意决定发行数量B．纸币发行量过少会引起物价上涨C．制造假币是违法的，持有、使用假币不受法律制裁D．纸币在流通中可代替货币执行价值尺度和流通手段等职能5.消费者使用信用卡①可以提高支付结算效率②可以减少现金流通，增强消费安全③方便购物消费④能集存款、取款、借款、消费、结算、查询为一体A．①② B．③④ C．①③④ D．①②③④6．决定价格，影响价格。

A．生产、消费 B．供求、消费C．价值、供求 D．消费、生产7.不同商品的需求量对价格变动的反应程度是不同的，下列说法正确的A．奢侈品反应大，生活必需品反应小 B．替代品反应大，互补品反应小C．替代品反应小，互补品反应大 D．生活必需品反应小，高档耐用品反应大8. 按照消费的目的，生活消费可以分为A. 钱货两清的消费、租赁消费、贷款消费B. 生存资料的消费、发展资料的消费和享受资料的消费C. 从众消费、求异消费和求实消费D. 物质消费和精神消费9. 社会再生产过程包括生产、分配、交换、消费这样互相联系的四个环节，其中直接起决定作用的环节是，中间的桥梁和纽带是，物质资料生产总过程的最终目的和动力是。

天津市部分区2024～2025学年度第一学期期中练习高一地理本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共100分，练习用时60分钟。

使用答题卡的地区，将答案写在答题卡上；不使用答题卡的地区，将答案写在练习卷上。

第Ⅰ卷一、选择题（共20小题，每小题3分，共60分）在每题给出的四个选项中，只有一项是最符合题目要求的。

2024年6月2日6时23分，嫦娥六号成功着陆在月球背面南极-艾特肯盆地预选着陆区（图1），回答1-2题。

图11．包含月球及嫦娥六号和地球的最低等级天体系统是（）A．地月系B．太阳系C．银河系D．河外星系2．月球上不存在生命物质的原因有（）A．与太阳距离太远B．没有稳定的太阳光照C．没有适宜生物呼吸的大气D．没有昼夜更替现象图2为我国新疆和田的大型光伏发电项目景观，读图回答3-4题。

图23．该地建设大型光伏发电项目的主要自然原因是（）A．技术先进，能源需求量大B．资金雄厚，能源供应短缺C．太阳能丰富，土地储备充足D．太阳能稳定，不受天气影响4．太阳辐射对地球的影响是（）A．人类生产、生活的唯一能量来源B．为生物生长、水体运动等提供能量和动力C．扰动电离层，影响无线短波通信D．造成地球各地降水增多，洪灾多发2024年初科学家预测：2024年是太阳黑子“大年”，1月至10月之间可能出现太阳黑子活动极大期，即达到本周期的峰值，最大太阳黑子数为137至173之间。

据此回答5-6题。

5．太阳黑子出现的位置是（）A．太阳内部B．光球层C．色球层D．日冕层6．太阳黑子数量增多时（）A．太阳活动的周期变长B．太阳表面的温度会大幅度升高C．太阳耀斑的强度增强D．到达地球的光热资源瞬时增多北京时间2024年1月23日2时09分，新疆阿克苏地区乌什县（41.26°N，78.63°E）发生7.1级地震，震源深度为22千米。

图3为某同学绘制的地球内部地震波传播速度与圈层结构示意图，读图回答7-8题。

山东省滕州市实验中学2014-2015学年度高一上学期期中考试地理试题考试时间：90分钟试卷满分：100分第Ⅰ卷（选择题共60分）一、选择题（本卷共40个小题，每小题1．5分，共60分。

在每小题给出的四个选项中，只有一个是符合题目要求的）电影《2012》讲述在2012年，地球因为异常的太阳活动而面临毁灭，到处都是天崩地裂、岩浆喷发。

据此回答1～2题。

1．下列关于太阳活动的说法中正确的是A．一定会引发地震、火山喷发B．可能引发干旱、洪涝等灾害C．使青藏高原海拔升高D．一定使人类遭受灭顶之灾2．下列属于地球上存在生命的条件的是A．黄赤交角的存在B．地球自转和公转周期较长C．适宜的温度、液态水和大气D．地球不透明、不发光2014年4月18日，美国天文学家宣布发现了迄今为止人类寻找到的最像地球的宜居行星，该行星大小约为地球的1.1倍，距离地球约500光年。

据此完成3-4题。

3．该行星所在天体系统的中心天体为A．彗星B．卫星C．恒星D．银河系4．科学家认定该行星为“最像地球的宜居行星”，最主要依据可能为该行星A．体积与地球相当B．与地球围绕同一中心天体运转C．可能有液态水存在D．上面找到了生物化石太阳源源不断地向外辐射能量，虽然到达地球的能量只占二十二亿分之一，但对地球和人类的影响却是巨大的。

据此完成5—6题。

5．关于太阳辐射及其对地球的影响，正确的说法是A．太阳源源不断地以电滋波的形式向四周放射能量，这种现象即太阳辐射B．太阳能量来源于太阳内部的核裂变反应C．由于日地距离适中，单位面积所获得的太阳辐射能地球比其他行星多D．太阳辐射能量巨大，是目前人们生产、生活所使用的唯一能源6．下列能源来自太阳能的有①煤②石油③核能④风能⑤水能A．①②③④B．①②③⑤C．①②④⑤D．①③④⑤受玛雅预言的启示，天文物理学家与计算机专家共同进行的一项电脑模拟预测显示，地球与太阳的磁极将于2012年发生颠倒，所引发的地球磁力混乱可能对人类社会造成一定的影响。

2023-2024学年山东省实验中学高一（上）期中数学试卷一、单选题（本题包括8小题，每小题5分，共40分.每小题只有一个选项符合题意） 1．集合A ＝{﹣1，0，1，2，3}，B ＝{0，2，4}，则图中阴影部分所表示的集合为（ ）A ．{0，2}B ．{﹣1，1，3，4}C ．{﹣1，0，2，4}D ．{﹣1，0，1，2，3，4}2．命题“∀x ∈R 都有x 2+x +1＞0”的否定是（ ） A ．不存在x ∈R ，x 2+x +1＞0B ．存在x 0∈R ，x 02+x 0+1≤0C ．存在x 0∈R ，x 02+x 0+1＞0D ．对任意的x ∈R ，x 2+x +1≤03．下列图象中，以M ＝{x |0≤x ≤1}为定义域，N ＝{x |0≤x ≤1}为值域的函数是（ ）A ．B ．C ．D ．4．“x ＞12”是“1x＜2”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件5．已知函数f （2x +1）＝3x +2，则f （3）的值等于（ ） A ．11B ．2C ．5D ．﹣16．函数f(x)=√3+2x −x 2的单调递增区间是（ ） A ．（﹣∞，1]B ．[1，+∞）C ．[1，3]D ．[﹣1，1]7．已知实数a ≠0，函数f(x)={2x +a ，x ＜1−x −2a ，x ≥1，若f （1﹣a ）＝f （1+2a ），则a 的值为（ ）A ．1B ．−12C ．﹣1D ．28．已知函数y =√ax 2+bx +c 的定义域与值域均为[0，1]，则实数a 的取值为（ ） A ．﹣4B ．﹣2C ．1D ．11二、多选题（本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分.） 9．若a ＞b ＞0＞c 则以下结论正确的是（ ） A ．ca＞cbB ．ac 2＞bc 2C ．a ﹣b ＞b ﹣cD ．b+ca+c＞ba10．设正实数a 、b 满足a +b ＝1，则（ ） A ．√ab 有最大值12B ．1a+2b+12a+b有最小值3C ．a 2+b 2有最小值12D ．√a +√b 有最大值√211．若定义域为R 的函数f （x ）满足f （x +2）为奇函数，且对任意x 1，x 2∈[2，+∞），x 1≠x 2已知[f （x 1）﹣f （x 2）]（x 1﹣x 2）＞0恒成立，则下列正确的是（ ） A ．f （x ）的图像关于点（﹣2，0）对称B ．f （x ）在R 上是增函数C ．f （x ）+f （4﹣x ）＝4D ．关于x 的不等式f （x ）＜0的解集为（﹣∞，2）12．设函数y ＝f （x ）的定义域为R ，对于任意给定的正数p ，定义函数f p (x)={f(x)，f(x)≤p p ，f(x)＞p，则称f p（x ）为f （x ）的“p 界函数”．若函数f （x ）＝x 2﹣2x +1，则下列结论正确的是（ ） A ．f 4（2）＝4B ．f 4（x ）的值域为[0，4]C ．f 4（x ）在[﹣1.1]上单调递减D ．函数y ＝f 4（x +1）为偶函数三、填空题（本题共4小题，每小题5分，共20分.）13．已知集合M ＝{﹣1，m +2，m 2+4}，且5∈M ，则m 的值为 ． 14．函数f(x)=√1−x2x+1的定义域为 ． 15．函数f(x)={(a −5)x −2，x ≥2x 2−2(a +1)x +3a ，x ＜2是R 上的单调减函数，则实数a 的取值范围为 ．16．设f （x ）是定义在R 上的奇函数，对任意的x 1，x 2∈（0，+∞），x 1≠x 2，满足：x 1f(x 1)−x 2f(x 2)x 1−x 2＞0，若f（2）＝4，则不等式f(x)−8x＞0的解集为．四、解答题（本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.）17．（10分）已知集合A＝{x|﹣2≤x≤7}，B＝{x|m+1＜x＜2m﹣1}．（1）m＝3时，求A∩B；（2）若A∩B＝B，求实数m的取值范围．18．（12分）已知幂函数f（x）＝（m2﹣m﹣5）x m+1，且函数在（0，+∞）上单调递增．（1）函数f（x）的解析式；（2）若f（1﹣2a）＜f（2），求实数a的取值范围．19．（12分）已知函数f(x)=ax2−bx，且f（﹣1）＝﹣1，f（1）＝3．（1）求f（x）解析式；（2）判断并证明函数f（x）在区间（1，+∞）的单调性．20．（12分）一家商店使用一架两臂不等长的天平称黄金，其中左臂长和右臂长之比为λ．一位顾客到店里购买10克黄金，售货员先将5g的砝码放在天平左盘中，取出一些黄金放在天平右盘中使天平平衡；再将5g砝码放在天平右盘中，然后取出一些黄金放在天平左盘中使天平平衡．最后将两次称得的黄金交给顾客，（1）试分析顾客购得的黄金是小于10g，等于10g，还是大于10g？为什么？（2）如果售货员又将5g的砝码放在天平左盘中，然后取出一些黄金放在天平右盘中使天平平衡，请问要使得三次黄金质量总和最小，商家应该将左臂长和右臂长之比λ设置为多少？请说明理由．21．（12分）已知命题：“∀x∈[﹣1，3]，都有不等式x2﹣4x﹣m＜0成立”是真命题．（1）求实数m的取值集合A；（2）设不等式x2﹣3ax+2a2≥0（a≠0）的解集为B，若x∈A是x∈B的充分条件，求实数a的取值范围．22．（12分）已知函数f（x）是定义域在R上的奇函数，当x≥0时，f（x）＝﹣x2+ax．（1）当a＝1时，求函数f（x）的解析式；（2）若函数f（x）为R上的单调函数．且对任意的m∈[1，+∞），f(2mt−4m2)+f(tm−1m2)＞0恒成立，求实数t的范围．2023-2024学年山东省实验中学高一（上）期中数学试卷参考答案与试题解析一、单选题（本题包括8小题，每小题5分，共40分.每小题只有一个选项符合题意）1．集合A＝{﹣1，0，1，2，3}，B＝{0，2，4}，则图中阴影部分所表示的集合为（）A．{0，2}B．{﹣1，1，3，4}C．{﹣1，0，2，4}D．{﹣1，0，1，2，3，4}解：∵A＝{﹣1，0，1，2，3}，B＝{0，2，4}，则A∩B＝{0，2}，A∪B＝{﹣1，0，1，2，3，4}，∴阴影部分表示集合为{﹣1，1，3，4}．故选：B．2．命题“∀x∈R都有x2+x+1＞0”的否定是（）A．不存在x∈R，x2+x+1＞0B．存在x0∈R，x02+x0+1≤0C．存在x0∈R，x02+x0+1＞0D．对任意的x∈R，x2+x+1≤0解：命题为全称命题，则命题的否定为∃x0∈R，x02+x0+1≤0．故选：B．3．下列图象中，以M＝{x|0≤x≤1}为定义域，N＝{x|0≤x≤1}为值域的函数是（）A．B．C．D．解：根据题意，依次分析选项：对于A，该函数的定义域为M＝{x|0≤x≤1}，值域不是N＝{x|0≤x≤1}，不符合题意；对于B ，该函数的定义域不是M ＝{x |0≤x ≤1}，值域是N ＝{x |0≤x ≤1}，不符合题意； 对于C ，该函数的定义域为M ＝{x |0≤x ≤1}，值域为N ＝{x |0≤x ≤1}，符合题意； 对于D ，该函数的图象中存在一个x 对应两个y 的情形，不符合函数的定义，不符合题意． 故选：C ．4．“x ＞12”是“1x＜2”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解：当x ＞12时1x＜2成立，1x＜2时如1x=−1＜2，则x ＝﹣1＜12， 因此只能是充分不必要条件， 故选：A ．5．已知函数f （2x +1）＝3x +2，则f （3）的值等于（ ） A ．11B ．2C ．5D ．﹣1解：因为f （2x +1）＝3x +2， 令2x +1＝3可得x ＝1， 则f （3）＝3+2＝5． 故选：C ．6．函数f(x)=√3+2x −x 2的单调递增区间是（ ） A ．（﹣∞，1]B ．[1，+∞）C ．[1，3]D ．[﹣1，1]解：设z ＝3+2x ﹣x 2，则y =√z ， 由3+2x ﹣x 2≥0，解得﹣1≤x ≤3，由于z ＝3+2x ﹣x 2在[﹣1，1]递增，在[1，3]递减， 又y =√z 在z ∈[0，+∞）递增，可得f(x)=√3+2x −x 2的单调递增区间为[﹣1，1]． 故选：D ．7．已知实数a ≠0，函数f(x)={2x +a ，x ＜1−x −2a ，x ≥1，若f （1﹣a ）＝f （1+2a ），则a 的值为（ ）A ．1B ．−12C ．﹣1D ．2解：当a ＞0时，1﹣a ＜1，1+2a ＞1， f （1﹣a ）＝f （1+2a ），则2（1﹣a ）+a ＝﹣（1+2a ）﹣2a ，解得a ＝﹣1，不符合a ＞0，舍去， 当a ＜0时，1﹣a ＞1，1+2a ＜1， f （1﹣a ）＝f （1+2a ），则﹣（1﹣a ）﹣2a ＝2（1+2a ）+a ，解得a =−12， 综上所述，a 的值为−12． 故选：B ．8．已知函数y =√ax 2+bx +c 的定义域与值域均为[0，1]，则实数a 的取值为（ ） A ．﹣4B ．﹣2C ．1D ．11解：依题意，y ＝ax 2+bx +c 的值域为[0，1]，且ax 2+bx +c ≥0 的解集为[0，1]，故函数的开口向下，a ＜0，则方程ax 2+bx +c ＝0 的两根为x ＝0或1，则c ＝0，−b2a =0+12， 即a ＝﹣b ，则y =ax 2+bx +c =ax 2−ax =a(x −12)2−a 4，当x =12 时，y =a(x −12)2−a4取得最大值为1，即−a 4=1，解得a ＝﹣4． 故选：A ．二、多选题（本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分.） 9．若a ＞b ＞0＞c 则以下结论正确的是（ ） A ．ca＞c bB ．ac 2＞bc 2C ．a ﹣b ＞b ﹣cD ．b+ca+c＞ba解：对于A ，因为a ＞b ＞0，所以1a＜1b，又因为c ＜0，所以ca＞cb，故A 正确；对于B ，因为a ＞b ＞0＞c ，则有c 2＞0，所以ac 2＞bc 2，故B 正确；对于C ，因为a ＞b ＞0＞c ，若a ＝2，b ＝1，c ＝﹣1，则a ﹣b ＝2﹣1＝1，b ﹣c ＝1﹣（﹣1）＝2，此时a ﹣b ＜b ﹣c ，故C 错误；对于D ，因为a ＞b ＞0＞c ，若a ＝2，b ＝1，c ＝﹣1，则b+c a+c=1−12−1=0，b a=12，此时b+ca+c＜ba，故D 错误．故选：AB ．10．设正实数a 、b 满足a +b ＝1，则（ ） A ．√ab 有最大值12B ．1a+2b+12a+b有最小值3C ．a 2+b 2有最小值12D ．√a +√b 有最大值√2解：因为正实数a 、b 满足a +b ＝1． 对于A 选项，由基本不等式可得√ab ≤a+b 2=12，当且仅当a =b =12时，等号成立，A 选项正确； 对于B 选项，由基本不等式可得1a+2b+12a+b=13(3a +3b)(1a+2b+12a+b)，=13[(a +2b)+(2a +b)](1a+2b +12a+b )=13(2+2a+b a+2b +a+2b 2a+b )≥13(2+2√a+2b 2a+b ⋅2a+b a+2b )=43， 当且仅当a =b =12时，等号成立，B 选项错误；对于C 选项，a 2+b 2=(a +b)2−2ab ≥(a +b)2−2×(a+b 2)2=(a+b)22=12， 当且仅当a =b =12时，等号成立，C 选项正确；对于D 选项，∵(√a +√b)2=a +b +2√ab ≤2(a +b)=2，则√a +√b ≤√2， 当且仅当a =b =12时，等号成立，D 选项正确． 故选：ACD ．11．若定义域为R 的函数f （x ）满足f （x +2）为奇函数，且对任意x 1，x 2∈[2，+∞），x 1≠x 2已知[f （x 1）﹣f （x 2）]（x 1﹣x 2）＞0恒成立，则下列正确的是（ ） A ．f （x ）的图像关于点（﹣2，0）对称B ．f （x ）在R 上是增函数C ．f （x ）+f （4﹣x ）＝4D ．关于x 的不等式f （x ）＜0的解集为（﹣∞，2） 解：∵定义域为R 的函数f （x ）满足f （x +2）为奇函数， ∴f （0+2）＝f （2）＝0①，f （﹣x +2）+f （x +2）＝0，② ∴f （x ）的图像关于点（2，0）对称③，故A 错误；对任意x 1，x 2∈[2，+∞），x 1≠x 2已知[f （x 1）﹣f （x 2）]（x 1﹣x 2）＞0恒成立⇒f （x ）在[2，+∞）上是增函数，∴f （x ）在R 上是增函数④，故B 正确；在②中，令2﹣x 替换x ，得f （x ）+f （4﹣x ）＝0，故C 错误； 由①④得关于x 的不等式f （x ）＜0的解集为（﹣∞，2），故D 正确． 故选：BD ．12．设函数y＝f（x）的定义域为R，对于任意给定的正数p，定义函数f p(x)={f(x)，f(x)≤pp，f(x)＞p，则称f p（x）为f（x）的“p界函数”．若函数f（x）＝x2﹣2x+1，则下列结论正确的是（）A．f4（2）＝4B．f4（x）的值域为[0，4]C．f4（x）在[﹣1.1]上单调递减D．函数y＝f4（x+1）为偶函数解：根据题意，由x2﹣2x+1≤4，解得﹣1≤x≤3，∴f4（x）={x2−2x+1，−1≤x≤3 4，x＜−14，x＞3，所以f4(2)=22−2×2+1=1，故A错误；当﹣1≤x≤3时，f4（x）＝x2﹣2x+1＝（x﹣1）2，且f4（x）在[﹣1，1]上单调递减，在[1，3]上单调递增，f4（1）＝0，f4（﹣1）＝f4（3）＝4，所以0≤f4（x）≤4，即f4（x）的值域为[0，4]，故B、C正确；因为y＝f4（x+1）={x2−2x+1，−1≤x≤34，x＜−14，x＞3，则y＝f4（x+1）的图象如下所示：由图可知y＝f4（x+1）的图象关于y轴对称，所以函数y＝f4（x+1）为偶函数，故D正确．故选：BCD．三、填空题（本题共4小题，每小题5分，共20分.）13．已知集合M＝{﹣1，m+2，m2+4}，且5∈M，则m的值为±1或3．解：集合M＝{﹣1，m+2，m2+4}，且5∈M，当m+2＝5，∴m＝3，满足题意；当m2+4＝5，∴m＝±1，满足题意．故答案为：﹣1，1，3．14．函数f(x)=√1−x 2x+1的定义域为 (−12，1] ．解：对于函数f(x)=√1−x 2x+1，则{1−x 2x+1≥02x +1≠0等价于{(1−x)(2x +1)≥02x +1≠0，解得−12＜x ≤1，所以函数f(x)=√1−x 2x+1的定义域为(−12，1]． 故答案为：(−12，1]．15．函数f(x)={(a −5)x −2，x ≥2x 2−2(a +1)x +3a ，x ＜2是R 上的单调减函数，则实数a 的取值范围为 [1，4] ．解：根据题意，函数f(x)={(a −5)x −2，x ≥2x 2−2(a +1)x +3a ，x ＜2是R 上的单调减函数，则有{a −5＜0a +1≥24−4(a +1)+3a ≥2(a −5)−2，解可得1≤a ≤4，即a 的取值范围为[1，4]．故答案为：[1，4]．16．设f （x ）是定义在R 上的奇函数，对任意的x 1，x 2∈（0，+∞），x 1≠x 2，满足：x 1f(x 1)−x 2f(x 2)x 1−x 2＞0，若f （2）＝4，则不等式f(x)−8x ＞0的解集为 （﹣2，0）∪（2，+∞） ． 解：令g （x ）＝xf （x ），∵f （x ）是定义在R 上的奇函数，∴g （x ）＝xf （x ）是定义在R 上的偶函数， 又对任意的x 1，x 2∈（0，+∞），x 1≠x 2，满足：x 1f(x 1)−x 2f(x 2)x 1−x 2＞0，∴g （x ）在（0，+∞）上单调递增，又f （2）＝4， ∴g （2）＝2f （2）＝8， ∴f(x)−8x ＞0可化为：xf(x)−8x=g(x)−g(2)x＞0，当x ＞0时，g （x ）＞g （2）⇒x ＞2； 当x ＜0时，g （x ）＜g （﹣2）⇒﹣2＜x ＜0；综上，不等式f(x)−8x ＞0的解集为（﹣2，0）∪（2，+∞）． 故答案为：（﹣2，0）∪（2，+∞）．四、解答题（本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.） 17．（10分）已知集合A ＝{x |﹣2≤x ≤7}，B ＝{x |m +1＜x ＜2m ﹣1}． （1）m ＝3时，求A ∩B ；（2）若A ∩B ＝B ，求实数m 的取值范围．解：（1）m ＝3时，集合A ＝{x |﹣2≤x ≤7}，B ＝{x |4＜x ＜5}， ∴A ∩B ＝{x |4＜x ＜5}； （2）若A ∩B ＝B ，则B ⊆A ，当B ＝∅时，m +1≥2m ﹣1，解得m ≤2， 当B ≠∅时，{m +1＜2m −1m +1≥−22m −1≤7，解得2＜x ≤4．综上，实数m 的取值范围是（﹣∞，4]．18．（12分）已知幂函数f （x ）＝（m 2﹣m ﹣5）x m +1，且函数在（0，+∞）上单调递增． （1）函数f （x ）的解析式；（2）若f （1﹣2a ）＜f （2），求实数a 的取值范围． 解：（1）函数f （x ）为幂函数， 则m 2﹣m ﹣5＝1，解得m ＝﹣2或3，当m ＝﹣2时，f （x ）＝x ﹣1，函数在（0，+∞）上单调递减，不符合题意，舍去，当m ＝3时，f （x ）＝x 4，函数在（0，+∞）上单调递增，符合题意， 综上所述，f （x ）＝x 4，（2）f （x ）＝x 4，函数定义域为R ， 在（0，+∞）上单调递增，f （1﹣2a ）＜f （2），函数f （x ）为偶函数， 则f （|1﹣2a |）＜f （2）， 故|1﹣2a |＜2，解得−12＜a ＜32， 故实数a 的取值范围为（−12，32）．19．（12分）已知函数f(x)=ax 2−b x，且f （﹣1）＝﹣1，f （1）＝3． （1）求f （x ）解析式；（2）判断并证明函数f （x ）在区间（1，+∞）的单调性．解：（1）根据题意，函数f(x)=ax 2−b x，且f （﹣1）＝﹣1，f （1）＝3， 则有{a +b =−1a −b =3，解可得a ＝1，b ＝﹣2，则f （x ）＝x 2+2x ；（2）f （x ）在区间（1，+∞）上递增，证明：设1＜x 1＜x 2，则f （x 1）﹣f （x 2）＝（x 12+2x 1）﹣（x 22+2x 2）＝（x 1﹣x 2）（x 1+x 2−2x 1x 2）， 由于1＜x 1＜x 2，则x 1﹣x 2＜0，x 1+x 2＞2，x 1x 2＞1，2x 1x 2＜2， 则有f （x 1）﹣f （x 2）＜0，故f （x ）在区间（1，+∞）上递增．20．（12分）一家商店使用一架两臂不等长的天平称黄金，其中左臂长和右臂长之比为λ．一位顾客到店里购买10克黄金，售货员先将5g 的砝码放在天平左盘中，取出一些黄金放在天平右盘中使天平平衡；再将5g 砝码放在天平右盘中，然后取出一些黄金放在天平左盘中使天平平衡．最后将两次称得的黄金交给顾客，（1）试分析顾客购得的黄金是小于10g ，等于10g ，还是大于10g ？为什么？（2）如果售货员又将5g 的砝码放在天平左盘中，然后取出一些黄金放在天平右盘中使天平平衡，请问要使得三次黄金质量总和最小，商家应该将左臂长和右臂长之比λ设置为多少？请说明理由． 解：（1）由于天平两臂不等长，设天平左臂长为a ，右臂长为b ，且a ≠b ，先称得黄金为xg ，后称得黄金为yg ，则bx ＝5a ，ay ＝5b ，则x =5a b ，y =5b a ，所以x +y =5a b +5b a ≥2√5a b ⋅5b a =10， 当且仅当5a b =5b a ，即a ＝b 时取等号，由a ≠b ，所以x +y ＞10，顾客购得的黄金是大于10g ；（2）由（1）再一次将5g 的砝码放在天平左盘，再取黄金mg 放在右盘使之平衡，则此时有5a ＝bm ，此时有m =5a b ， 所以三次黄金质量总和为：x +y +m =5a b +5b a +5a b =10a b +5b a ≥2√10a b ⋅5b a =10√2，当且仅当10a b =5b a ，即b =√2a 时取等号， ∴a b =√22=λ，所以三次黄金质量总和要最小，则左臂长和右臂长之比λ=√22．21．（12分）已知命题：“∀x ∈[﹣1，3]，都有不等式x 2﹣4x ﹣m ＜0成立”是真命题．（1）求实数m 的取值集合A ；（2）设不等式x 2﹣3ax +2a 2≥0（a ≠0）的解集为B ，若x ∈A 是x ∈B 的充分条件，求实数a 的取值范围． 解：（1）由∀x ∈[﹣1，3]，都有不等式x 2﹣4x ﹣m ＜0成立，得x 2﹣4x ﹣m ＜0在x ∈[﹣1，3]时恒成立，所以m ＞（x 2﹣4x ）max ，因为二次函数y ＝x 2﹣4x 在[﹣1，2]上单调递减，在[2，3]上单调递增，且f （﹣1）＝5，f （3）＝﹣3，当x ∈[﹣1，3]时，y max ＝5，可得m ＞5，所以A ＝{m |m ＞5}．（2）由x 2﹣3ax +2a 2≥0可得（x ﹣a ）（x ﹣2a ）≥0．①当a ＜0时，可得B ＝{x |x ≤2a 或x ≥a }，因为x ∈A 是x ∈B 的充分条件，则A ⊆B ，则a ≤5，此时，a ＜0；②当a ＞0时，可得B ＝{x |x ≤a 或x ≥2a }，因为x ∈A 是x ∈B 的充分条件，则A ⊆B ，则2a ≤5，解得a ≤52，此时0＜a ≤52．综上所述，实数a 的取值范围是{a|a ＜0或0＜a ≤52}．22．（12分）已知函数f （x ）是定义域在R 上的奇函数，当x ≥0时，f （x ）＝﹣x 2+ax ．（1）当a ＝1时，求函数f （x ）的解析式；（2）若函数f （x ）为R 上的单调函数．且对任意的m ∈[1，+∞），f(2mt −4m 2)+f(t m −1m 2)＞0恒成立，求实数t 的范围．解：（1）当a ＝1时，当x ≥0时，f （x ）＝﹣x 2+x ，设x ＜0，则﹣x ＞0，所以f （x ）＝﹣f （﹣x ）＝﹣（﹣x 2﹣x ）＝x 2+x ，所以f （x ）={−x 2+x ，(x ≥0)x 2+x ，(x ＜0)． （2）因为函数f （x ）为奇函数，所以函数f （x ）在关于原点对称的区间上有相同的单调性，①当函数f （x ）单调递减时，f （x ）＝﹣x 2+ax 在[0，+∞）上单调递减，又函数f （x ）的对称轴为x =a 2，所以a 2≤0，即a ≤0，因为函数f（x）为奇函数，所以f（2mt﹣4m2）+f（tm −1m2）＞0，所以f（2mt﹣4m2）＞﹣f（tm−1m2）＝f（−tm+1m2），又当a≤0时，函数f（x）单调递减，所以2mt﹣4m2＜−tm+1m2，所以（2m+1m）t＜4m2+1m2=（2m+1m）2﹣4，又m≥1，所以2m+1m＞0，所以t＜（2m+1m）−4(2m+1m)，令g（x）＝2x+1x，x≥1，任取x1，x2∈[1，+∞），且x1＜x2，所以g（x1）﹣g（x2）＝2x1+1x1−2x2−1x2=2（x1﹣x2）+x2−x1x1x2＝（x1﹣x2）（2−1x1x2），因为x1＜x2，x1，x2∈[1，+∞），所以x1﹣x2＜0，2−1x1x2＞0，所以（x1﹣x2）（2−1x1x2）＜0，即g（x1）＜g（x2），所以g（x）在[1，+∞）上单调递增，所以g（x）≥g（1）＝3，又令2m+1m=n，则t＜（2m+1m）−4(2m+1m)，转化为t＜n−4n，其中n≥3，所以只需t＜（n−4n）min，又注意到函数y＝x与函数y=−4x在[3，+∞）上单调递增，则函数y＝x−4x在[3，+∞）上单调递增，所以n −4n ≥3−43=53，所以t ＜53，所以t 的取值范围为（﹣∞，53）， ②当函数f （x ）单调递增时，f （x ）＝﹣x 2+ax 在[0，+∞）上单调递增， 又函数f （x ）的对称轴为x =a 2， 所以a 2＞0，即a ＞0， 因为函数f （x ）为奇函数，所以f （2mt ﹣4m 2）+f （t m −1m 2）＞0， 所以f （2mt ﹣4m 2）＞﹣f （t m −1m 2）＝f （−t m +1m 2）， 又当a ＞0时，函数f （x ）单调递增， 所以2mt ﹣4m 2＞−t m +1m 2， 所以（2m +1m ）t ＞4m 2+1m 2=（2m +1m ）2﹣4， 又m ≥1，所以2m +1m＞0， 所以t ＞（2m +1m ）−4(2m+1m )， 令g （x ）＝2x +1x ，x ≥1，任取x 1，x 2∈[1，+∞），且x 1＜x 2，所以g （x 1）﹣g （x 2）＝2x 1+1x 1−2x 2−1x 2=2（x 1﹣x 2）+x 2−x1x 1x 2 ＝（x 1﹣x 2）（2−1x 1x 2）， 因为x 1＜x 2，x 1，x 2∈[1，+∞）， 所以x 1﹣x 2＜0，2−1x 1x 2＞0， 所以（x 1﹣x 2）（2−1x 1x 2）＜0， 即g （x 1）＜g （x 2），所以g （x ）在[1，+∞）上单调递增，所以g （x ）≥g （1）＝3， 又令2m +1m =n ，则t ＞（2m +1m ）−4(2m+1m )，转化为t ＞n −4n，其中n ≥3， 所以只需t ＞（n −4n ）max ，但是n −4n 无最大值，无解，综上所述，t 的取值范围为（﹣∞，53）．。