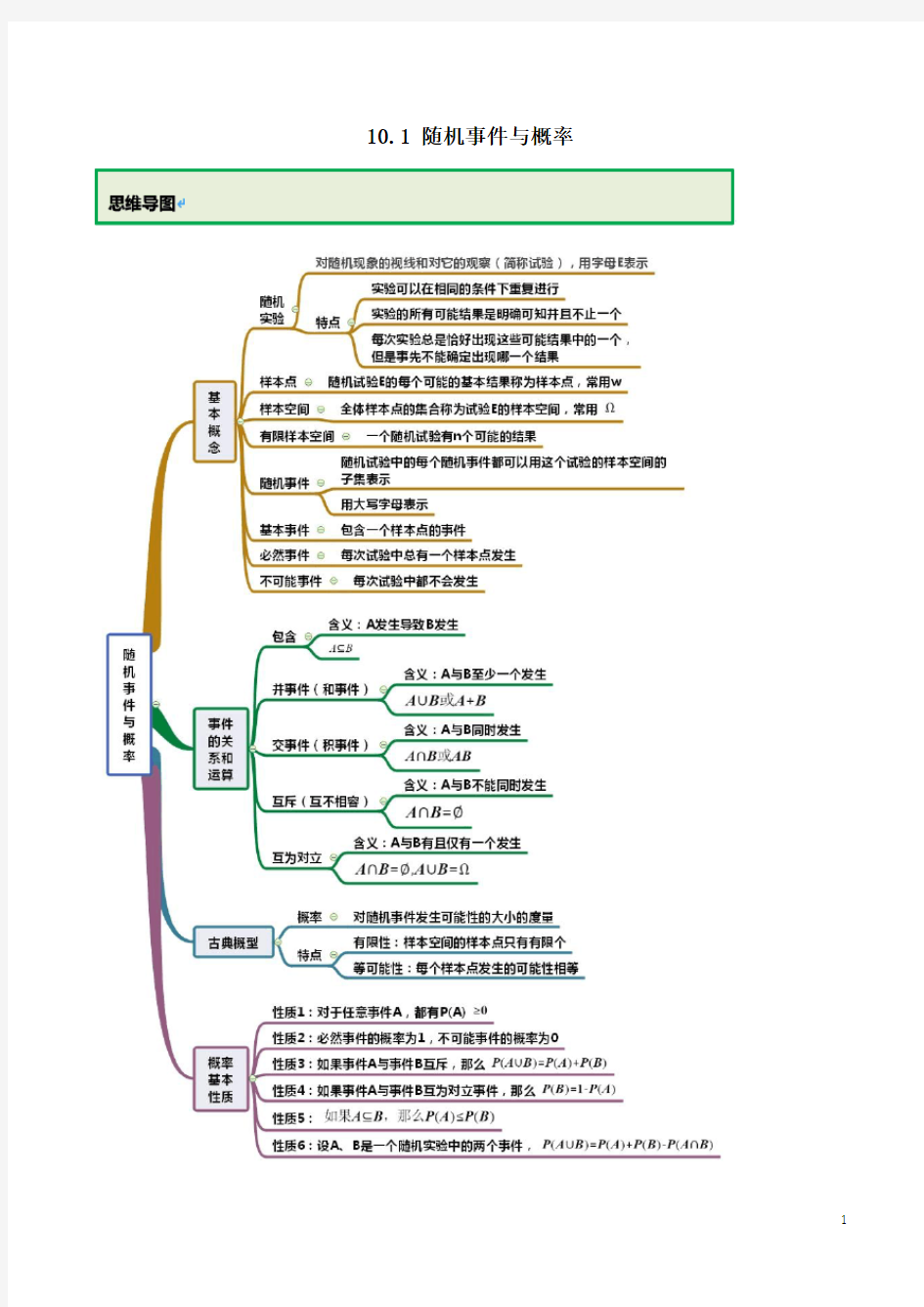

10.1 随机事件与概率
运用一随机事件判断
【例1-1】(2019·河南高一期中)下列事件中是随机事件的个数有
①连续两次抛掷两个骰子,两次都出现2点;
②在地球上,树上掉下的雪梨不抓住就往下掉;
③某人买彩票中奖;
④已经有一个女儿,那么第二次生男孩;
⑤在标准大气压下,水加热到90℃是会沸腾。
A.1 B.2 C.3 D.4
【答案】C
【解析】由题意,随机事件就是在指定条件下,可能发生,也可能不发生的事件,
①连续两次抛掷两个骰子,两次都出现2点可能发生,也可能不发生,所以是随机事件,
②在地球上,树上掉下的雪梨不抓住就往下掉,这是一定发生的事件,不是随机事件;
③某人买彩票中奖,此事可能发生,也可能不发生,所以是随机事件;
④已经有一个女儿,那么第二次生男孩,此事可能发生,也可能不发生,所以是随机事件;
⑤在标准大气压下,水加热到90℃是会沸腾,此事一定不发生,不是随机事件.故选C.
【例1-2】(2020·全国高三专题练习)某小组有5名男生和4名女生,从中任选4名同学参加“教师节”演讲比赛,则下列每对事件是对立事件的是()
A.恰有2名男生与恰有4名男生
B.至少有3名男生与全是男生
C.至少有1名男生与全是女生
D.至少有1名男生与至少有1名女生
【答案】C
【解析】“恰有2名男生”与“恰有4名男生”是互斥事件,但不是对立事件,排除A项;“至少有3名男生”与“全是男生”可以同时发生,不是互斥事件,排除B项;“至少有1名男生”与“全是女生”不可能同时发生,且必有一个发生,是对立事件,C项正确;“至少有1名男生”与“至少有1名女生”可以同时发生,不互斥,排除D项.
故选:C.
【例1-3】.(2020·全国高三专题练习)设事件A ,B ,已知()15P A =, ()13
P B =,()8
15P A B =U ,
则A ,B 之间的关系一定为( ) A .两个任意事件 B .互斥事件
C .非互斥事件
D .对立事件
【答案】B 【解析】()1
5P A =
Q ,()13
P B =, ()()118
3515P A P B ∴+=+=
又()815
P A B =
U ()()()P A B P A P B ∴=+U
A ∴.
B 为互相斥事件
故选:B . 【举一反三】
1.(2019·全国高二单元测试)下列事件中,随机事件的个数为( ) ①在学校明年召开的田径运动会上,学生张涛获得100米短跑冠军; ②在体育课上,体育老师随机抽取一名学生去拿体育器材,抽到李凯; ③从标有1,2,3,4的4张号签中任取一张,恰为1号签; ④在标准大气压下,水在4°C 时结冰. A .1 B .2C .3 D .4 【答案】C
【解析】①张涛获得冠军有可能发生也有可能不发生,所以为随机事件; ②抽到的学生有可能是李凯,也有可能不是,所以为随机事件; ③有可能抽到1号签也有可能抽不到,所以为随机事件;
④标准大气压下,水在4°C 时不会结冰,所以是不可能事件,不是随机事件. 故选C.
2.(2019·全国高二单元测试)下列说法正确的有( ) ①随机事件A 的概率是频率的稳定值,频率是概率的近似值. ②一次试验中不同的基本事件不可能同时发生. ③任意事件A 发生的概率()P A 总满足()01P A <<.
④若事件A 的概率为0,则A 是不可能事件. A .0个 B .1个
C .2个
D .3个
【答案】C
【解析】不可能事件的概率为0,但概率为0的事件不一定是不可能事件,如几何概率中“单点”的长度、面积、体积都是0,但不是不可能事件,∴④不对;抛掷一枚骰子出现1点和出现2点是不同的基本事件,
在同一次试验中,不可能同时发生,故②正确;任意事件A 发生的概率P (A )满足()01P A 剟
,∴③错误;又①正确.∴选C.
3.(2020·全国高三专题练习)若随机事件A 、B 互斥,A 、B 发生的概率均不等于0,且分别为()2P A a =-,()45P B a =-,则实数a 的取值范围是( )
A .5,24??
???
B .53,42??
???
C .53,42
??????
D .54,43??
???
【答案】D
【解析】Q 随机事件A 、B 互斥,A 、B 发生的概率均不等于0, 且分别为()2P A a =-,()45P B a =-,
∴0()10()1()()1
P A P B P A P B <
<
?,即021
0451331a a a <-
解得
544
3a
. 故选:D .
4(2020·浙江高三专题练习)袋中装有白球3个,黑球4个,从中任取3个,下列各对事件中互为对立事件的是( )
A .恰有1个白球和全是白球
B .至少有1个白球和全是黑球
C .至少有1个白球和至少有2个白球
D .至少有1个白球和至少有1个黑球
【答案】B
【解析】从白球3个,黑球4个中任取3个,共有四种可能,全是白球,两白一黑,一白两黑和全是黑球,故
①恰有1个白球和全是白球,是互斥事件,但不是对立事件,
②至少有1个白球和全是黑球是对立事件; ③至少有1个白球和至少有2个白球不是互斥事件, ④至少有1个白球和至少有1个黑球不是互斥事件, 故选:B .
运用二 事件的关系和运算
【例2】(1)(2019·辽宁高一期末)已知随机事件A 和B 互斥,且()0.5P AUB =,()0.3P B =.则()
P A =( ) A .0.5
B .0.2
C .0.7
D .0.8
(2)(2020·浙江高三专题练习)某电视台的夏日水上闯关节目中的前四关的过关率分别为
56,45,35,1
2
,只有通过前一关才能进入下一关,其中,第三关有两次闯关机会,且通过每关相互独立.一选手参加该节目,则该选手能进入第四关的概率为() A .
7
25
B .
25
C .
1225
D .
1425
【答案】(1)D (2)D
【解析】(1)A Q 与B 互斥 ()()()P A B P A P B ∴=+U
()0.50.30.2P A ∴=-= ()()110.20.8P A P A ∴=-=-=
本题正确选项:D
(2)第一种情况:该选手通过前三关,进入第四关,所以15432
6555
P =
??=, 第二种情况:该选手通过前两关,第三关没有通过,再来一次通过,进入第四关, 所以154334
1)655525
P =
??-?=(. 所以该选手能进入第四关的概率为543543314
1655655525
????+??-?= ???. 故选:D 【举一反三】
1.(2019·重庆高二期末(文))在一次随机试验中,已知A , B , C 三个事件发生的概率分别为0.2, 0.3, 0.5,则下列说法一定正确的是( ) A .B 与C 是互斥事件
B .A +B 与
C 是对立事件
C .A +B +C 是必然事件
D .()0.3P A B 0.5≤+≤
【答案】D
【解析】A,B , C 三个事件发生的概率分别为0.2, 0.3, 0.5,不能确定它们之间有任何关系,故选项A 、B 、C 均错,而()()()0.20.30.5P A B P A P B +≤+=+=,()max{(),()}0.3P A B P A P B +≥=,D 正确. 故选D .
2.(2019·全国高三专题练习(理))甲、乙两人下棋,结果是一人获胜或下成和棋.已知甲不输的概率为0.8,乙不输的概率为0.7,则两人下成和棋的概率为______. 【答案】0.5
【解析】设甲、乙两人下成和棋P ,甲获胜的概率为()P A ,则乙不输的概率为()1P A -,
Q 甲不输的概率为0.8,乙不输的概率为0.7,
()0.8P A P ∴+=,()10.7P A -=,
1 1.5P ∴+=,
解得0.5P =.
∴两人下成和棋的概率为0.5.
故答案为:0.5
3.(2020·浙江高三专题练习)眉山市位于四川西南,有“千载诗书城,人文第一州”的美誉,这里是大文豪苏轼、苏洵、苏辙的故乡,也是人们旅游的好地方.在今年的国庆黄金周,为了丰富游客的文化生活,每天在东坡故里三苏祠举行“三苏文化”知识竞赛.已知甲、乙两队参赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为
23,乙队中3人答对的概率分别为2
3
,23,1
2
,且各人回答正确与否相互之间没有影响. (1)分别求甲队总得分为0分;2分的概率; (2)求甲队得2分乙队得1分的概率. 【答案】(1)0分概率
127;2分概率49
;(2) 1081 【解析】(1)记“甲队总得分为0分”为事件A ,“甲队总得分为2分”为事件B ,
甲队总得分为0分,即甲队三人都回答错误,其概率()3
211327
P A ??=-= ???;
甲队总得分为2分,即甲队三人中有1人答错,其余两人答对,其概率()2
22431339
P B ????=?-= ? ???
??;
(2)记“乙队得1分”为事件C ,“甲队得2分乙队得1分”为事件D ; 事件C 即乙队三人中有2人答错,其余1人答对, 则()2212211(1)1(1)332332P C ????????=-
??-+?-?- ? ? ? ?????????22151133218
??????+-?-?= ? ? ???????, 甲队得2分乙队得1分即事件B 、C 同时发生, 则()()()4510
91881
P D P B P C ==
?=. 运用三 古典概型
【例3】(1)(2020·浙江高三专题练习)从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( ) A .
1
10
B .
35
C .
310
D .
25
(2)(2020·浙江高三专题练习)生物实验室有5只兔子,其中只有3只测量过某项指标,若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为
A .
2
3 B .
3
5 C .25
D .15
【答案】(1)D (2)B
【解析】从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张, 基本事件总数n=5×5=25,
抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有:
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4), 共有m=10个基本事件,
∴抽得的第一张卡片上的数大于第二张卡片上的数的概率p=42
.105
= 故答案为D .
(2)设其中做过测试的3只兔子为,,a b c ,剩余的2只为,A B ,则从这5只中任取3只的所有取法有
{,,},{,,},{,,},{,,},{,,},{,,}a b c a b A a b B a c A a c B a A B ,{,c,},{,c,},{b,,},{c,,}b A b B A B A B 共10种.其
中恰有2只做过测试的取法有{,,},{,,},{,,},{,,},a b A a b B a c A a c B {,c,},{,c,}b A b B 共6种,
所以恰有2只做过测试的概率为
63
105
,选B.
【举一反三】
1.(2020·全国高三专题练习)一盒中装有12个球,其中5个红球,4个黑球,2个白球,1个绿球.从中随机取出1球,求:
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球的概率.
【答案】(1)取出1球为红球或黑球的概率为3
.
4
(2)取出1球为红球或黑球或白球的概率为
11
.
12
【解析】(1)由题意知本题是一个古典概型,
试验包含的基本事件是从12个球中任取一球共有12种结果;
满足条件的事件是取出的球是红球或黑球共有9种结果,
∴概率为.
(2)由题意知本题是一个古典概型,
试验包含的基本事件是从12个球中任取一球共有12种结果;
满足条件的事件是取出的一球是红球或黑球或白球共有11种结果,
∴概率为.
即取出的1球是红球或黑球的概率为;
取出的1球是红球或黑球或白球的概率为.
运用四综合运用
【例4】(2020·全国高三专题练习)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(Ⅱ)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
【答案】(1)3,2,2(2)(i)见解析(ii)5 21
【解析】(Ⅰ)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法
从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人. (Ⅱ)(i )从抽出的7名同学中随机抽取2名同学的所有可能结果为
{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,
D },{C ,
E },{C ,
F },{C ,
G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种.
(ii )由(Ⅰ),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种. 所以,事件M 发生的概率为P (M )=5
21
. 【举一反三】
1.(2020·江西高二期末(文))智能手机的出现,改变了我们的生活,同时也占用了我们大量的学习时间.某市教育机构从500名手机使用者中随机抽取100名,得到每天使用手机时间(单位:分钟)的频率分布直方图(如图所示),其分组是: [](]0,20,20,40,(]]]
40,60,(60,80,(80,100.
(1)根据频率分布直方图,估计这500名手机使用者中使用时间的中位数是多少分钟? (精确到整数) (2)估计手机使用者平均每天使用手机多少分钟? (同一组中的数据以这组数据所在区间中点的值作代表) (3)在抽取的100名手机使用者中在(]20,40和(]40,60中按比例分别抽取2人和3人组成研究小组,然后再从研究小组中选出2名组长.求这2名组长分别选自(]20,40和(]40,60的概率是多少? 【答案】(1) 57分钟. (2)58分钟;(3)
35
【解析】(1)设中位数为x ,则()0.0023200.01200.015400.5x ?+?+?-= 解得:170
573
x =
≈(分钟) ∴这500名手机使用者中使用时间的中位数是57分钟
(2)平均每天使用手机时间为:0.05100.230+0.350+0.270+0.259058?+????=(分钟)
即手机使用者平均每天使用手机时间为58分钟
(3)设在(]20,40内抽取的两人分别为,a b ,在(]40,60内抽取的三人分别为,,x y z , 则从五人中选出两人共有以下10种情况:
()()()()()()()()()(),,,,,,,,,,,,,,,,,,,a b a x a y a z b x b y b z x y x z y z
两名组长分别选自(]20,40和(]40,60的共有以下6种情况:()()()()()(),,,,,,,,,,,a x a y a z b x b y b z
∴所求概率63105
p =
= 2.(2020·黑龙江哈尔滨市第六中学校高二期末(理))40名学生某次数学考试成绩(单位:分)的频率分布直方图如下:
(1)求频率分布直方图中a 的值;
(2)根据频率分布直方图求出样本数据的中位数 (保留小数点后两位数字)和众数; (3)从成绩在[)50,70的学生中任选3人,求这3人的成绩都在[)60,70中的概率. 【答案】(1)0.005a =;(2)77.14,75;(3)
1
6
【解析】(1)依题意()23762101a a a a a ++++?=,解得0.005a =.
(2)最高的小长方形的中点为75,故众数的估计值为75.由于()2310500.25a a a +?==,
()23710700.6a a a a ++?==,设中位数为70x +,则0.2570.5a x +?=,解得7.14x ≈,故中位数为
7077.14x +=.
(3)[)50,70的人数为()40231010a a ?+?=人,[)50,60与[)60,70人数的比例为2:32:3a a =,即
[)50,60中有4人,[)60,70中有6人,从中任选3人,这3人的成绩都在[)60,70中的概率为
363
10
201
1206
C C ==.
1.(2020·全国高三专题练习)甲:1A 、2A 是互斥事件;乙:1A 、2A 是对立事件,那么( ) A .甲是乙的充要条件
B .甲是乙的充分但不必要条件
C .甲是乙的必要但不充分条件
D .甲既不是乙的充分条件,也不是乙的必要条件 【答案】C 【解析】
当1A 、2A 是互斥事件时,1A 、2A 不一定是对立事件,所以甲是乙的非充分条件. 当1A 、2A 是对立事件时,1A 、2A 一定是互斥事件,所以甲是乙的必要条件. 所以甲是乙的必要非充分条件.故选C.
2.(2020·浙江高三专题练习)学校将5个不同颜色的奖牌分给5个班,每班分得1个,则事件“1班分得黄色的奖牌”与“2班分得黄色的奖牌”是( ) A .对立事件 B .不可能事件
C .互斥但不对立事件
D .不是互斥事件
【答案】C
【解析】由题意,1班和2班不可能同时分得黄色的奖牌,因而这两个事件是互斥事件;又1班和2班可能都得不到黄色的奖牌,故这两个事件不是对立事件,所以事件“1班分得黄色的奖牌”与“2班分得黄色的奖牌”是互斥但不对立事件.故选:C
3.(2019·福建高一期末)已知随机事件,,A B C 中,A 与B 互斥,B 与C 对立,且()()0.3,0.6P A P C ==,则()P A B +=( ) A .0.3 B .0.6
C .0.7
D .0.9
【答案】C
【解析】因为()0.6P C =,事件B 与C 对立,所以()0.4P B =,又()0.3P A =,A 与B 互斥,所以
()()()0.30.40.7P A B P A P B +=+=+=,故选C .
4.(2019·贵州高二月考)从装有5个红球和3个白球的口袋内任取3个球,那么互斥而不对立的事件是( )
A.至少有一个红球与都是红球
B.至少有一个红球与都是白球
C.恰有一个红球与恰有二个红球
D.至少有一个红球与至少有一个白球
【答案】C
【解析】从装有5个红球和3个白球的口袋内任取3个球,不同的取球情况共有以下几种:
3个球全是红球;2个红球和1个白球;1个红球2个白球;3个全是白球.
选项A中,事件“都是红球”是事件“至少有一个红球”的子事件;
选项B中,事件“至少有一个红球”与事件“都是白球”是对立事件;
选项D中,事件“至少有一个红球”与事件“至少有一个白球”的事件为“2个红球1个白球”与“1个红球2个白球”;
选项C中,事件“恰有一个红球”与事件“恰有2个红球”互斥不对立,故选C.
5.(2019·北京八中高一期末)从装有两个红球和两个黑球的口袋里任取两个球,那么对立的两个事件是()
A.“至少有一个黑球”与“都是黑球”
B.“至少有一个黑球”与“至少有一个红球”
C.“恰好有一个黑球”与“恰好有两个黑球”
D.“至少有一个黑球”与“都是红球”
【答案】D
【解析】记两个黑球为,A B,两个红球为1,2,则任取两球的所有等可能结果为:
1,2,1,2,,12,
A A
B B AB,记事件A为“至少有一个黑球”,事件B为:“都是红球”,
则
51
(),()
66
P A P B
==,因为()()1
P A P B
+=,所以事件A与事件B互为对立事件.
6.(2019·河北鹿泉区第一中学高二开学考试)从含有10件正品、2件次品的12件产品中,任意抽取3件,则必然事件是()
A.3件都是正品B.3件都是次品
C.至少有1件次品D.至少有1件正品
【答案】D
【解析】从10件正品, 2件次品,从中任意抽取3件
A:3件都是正品是随机事件,
B:3件都是次品不可能事件,
C:至少有1件次品是随机事件,
D:因为只有两件次品,所以从中任意抽取3件必然会抽到正品,即至少有一件是正品是必然事件,故选D . 7.(2019·黄陵中学高新部高二期末(文))一个射手进行一次射击,则事件“命中环数小于6环”的对立事件是()
A.命中环数为7、8、9、10环
B.命中环数为1、2、3、4、5、6环
C.命中环数至少为6环
D.命中环数至多为6环
【答案】C
【解析】根据对立事件的定义,可得一个射手进行一次射击,则事件:“命中环数小于6环”的对立事件是“命中环数至少是6环”,故选C.
8.(2019·陕西高考模拟(文))口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.38,摸出白球的概率是0.32,那么摸出黑球的概率是()
A.0.42B.0.28
C.0.3D.0.7
【答案】C
【解析】∵口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,
在口袋中摸球,摸到红球,摸到黑球,摸到白球这三个事件是互斥的,
摸出红球的概率是0.38,摸出白球的概率是0.32,
∵摸出黑球是摸出红球或摸出白球的对立事件,
--=.
∴摸出黑球的概率是10.380.320.3
故应选C.
9.(2019·湖南高一期中)从6个篮球、2个排球中任选3个球,则下列事件中,是必然事件的是(). A.3个都是篮球B.至少有1个是排球
C.3个都是排球D.至少有1个是篮球
【答案】D
【解析】从6个篮球、2个排球中任选3个球,A,B是随机事件,C是不可能事件,D是必然事件,故选D.
10.(2018·湖南省茶陵县第二中学高一单元测试)下列事件中,随机事件的个数是( )
①2020年8月18日,北京市不下雨;
②在标准大气压下,水在4℃时结冰;
③从标有1,2,3,4的4张号签中任取一张,恰为1号签;
④向量的模不小于0.
A.1 B.2 C.3 D.4
【答案】B
【解析】①③为随机事件,②为不可能事件,④为必然事件.故选B.
11.(2019·海南高二期末)甲、乙两人进行象棋比赛,已知甲胜乙的概率为0.5,乙胜甲的概率为0.3,甲乙两人平局的概率为0.2.若甲乙两人比赛两局,且两局比赛的结果互不影响,则乙至少赢甲一局的概率为()
A.0. 36 B.0. 49 C.0. 51 D.0. 75
【答案】C
P=-?=.
【解析】乙至少赢甲—局的概率为10.70.70.51
故选C
12.(2019·安徽高一期末(理))某人射击一次,设事件A:“击中环数小于4”;事件B:“击中环数大于4”;事件C:“击中环数不小于4”;事件D:“击中环数大于0且小于4”,则正确的关系是
A.A和B为对立事件B.B和C为互斥事件
C.C与D是对立事件D.B与D为互斥事件
【答案】D
【解析】由题意,A项中,事件“击中环数等于4环”可能发生,所以事件A和B为不是对立事件;
B项中,事件B和C可能同时发生,所以事件B和C不是互斥事件;
C项中,事件“击中环数等于0环”可能发生,所以事件C和D为不是对立事件;
D项中,事件B:“击中环数大于4”与事件D:“击中环数大于0且小于4”,不可能同时发生,所以B与D 为互斥事件,故选D.
13(2020·全国高三专题练习)某产品分甲、乙、丙三级,其中乙、丙两级均属次品,在正常生产情况下,出现乙级品和丙级品的概率分别是5%和3%,则抽验一只是正品(甲级)的概率为( )
A.0.95 B.0.97 C.0.92 D.0.08
【答案】C
【解析】因为抽验一件产品只有三种结果,甲、乙、丙三级.利用对立事件的概率公式可知1-5%-3%=92%,即选择C
14.(2020·全国高三专题练习)围棋盒子中有多粒黑子和白子,已知从中取出2粒都是黑子的概率为1
7
,
从中取出2粒都是白子的概率是12
35
,则从中任意取出2粒恰好是同一色的概率是( )
A.1
7
B.
12
35
C.
17
35
D.1
【答案】C
【解析】设“从中取出2粒都是黑子”为事件A,“从中取出2粒都是白子”为事件B,“任意取出2粒恰好
是同一色”为事件C,则C=A∪B,且事件A与B互斥,所以P(C)=P(A)+P(B)=1
7
+
12
35
=
17
35
,即任意
取出2粒恰好是同一色的概率为17 35
.
15.(2020·浙江高三专题练习)一个盒子内装有大小相同的红球、白球和黑球若干个,从中摸出1个球,若摸出红球的概率是0.45,摸出白球的概率是0.25,那么摸出黑球或红球的概率是()
A.0.3 B.0.55 C.0.7 D.0.75
【答案】D
【解析】因为从中摸出1个球,若摸出红球的概率是0.45,摸出白球的概率是0.25,
所以摸出黑球的概率是1(0.450.25)0.3
-+=,
因为从盒子中摸出1个球为黑球或红球为互斥事件,
所以摸出黑球或红球的概率0.30.450.75
P=+=,故选D.
16.(2020·全国高三专题练习)把红、黄、蓝、白4张纸牌随机地分发给甲、乙、丙、丁四人,每个人分得一张,事件“甲分得红牌”与“乙分得红牌”()
A.是对立事件B.是不可能事件
C.是互斥但不对立事件D.不是互斥事件
【答案】C
【解析】显然两个事件不可能同时发生,但两者可能同时不发生,因为红牌可以分给丙、丁两人,综上,这两个事件为互斥但不对立事件.故选:C.
17.(2020·浙江高三专题练习)从装有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概率是( )
A.
1
10
B.
3
10
C.
3
5
D.
9
10
【答案】D
【解析】从装有3个红球,2个白球的袋中任取3个球,共有基本事件3510C =种,则全取红球的基本事件只有一种,所以所取3个球中至少有1个白球的概率为19
11010
-
=,故选D. 18.(2019·北京高一期末)如果事件A 与事件B 互斥,且()0.2P A =,()0.3P B =,则()P A B U = . 【答案】0.5
【解析】()()0.20.3)0.5(P A P B P A B =+=+=U
19.(2020·全国高三专题练习)经统计,在某储蓄所一个营业窗口排队等候的人数及相应概率如下:
(1)至多有2人排队等候的概率是多少? (2)至少有3人排队等候的概率是多少? 【答案】(1)0.56;(2)0.44
【解析】记“无人排队等候”为事件A ,“1人排队等候”为事件B ,“2人排队等候”为事件C ,“3人排队等候”为事件D ,“4人排队等候”为事件E ,“5人及5人以上排队等候”为事件F ,则事件A ,B ,C ,D ,E ,F 互斥.
(1)记“至多2人排队等候”为事件G ,则G =A ∪B ∪C ,所以P(G)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
(2) 记“至少3人排队等候”为事件H ,则H =D ∪E ∪F ,所以P(H)=P(D)+P(E)+P(F)=0.3+0.1+0.04=0.44.
20.(2020·浙江高三专题练习)某旅游爱好者计划从3个亚洲国家A 1,A 2,A 3和3个欧洲国家B 1,B 2,B 3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A 1,但不包括B 1的概率. 【答案】(1)1
5
P =
;(2)29P =
【解析】(Ⅰ)由题意知,从6个国家中任选两个国家,其一切可能的结果组成的基本事件有:
{}{}{}{}{}{}{}{}{}{}{}{}121323111213212223313233,,,,,,,,,,,,,,,,,,,,,,,,A A A A A A A B A B A B A B A B A B A B A B A B
{}{}{}121323,,,,,B B B B B B ,共15个.
所选两个国家都是亚洲国家的事件所包含的基本事件有:
{}{}{}121323,,,,,A A A A A A ,共3个,则所求事件的概率为:31155
P =
=. (Ⅱ)从亚洲国家和欧洲国家中各任选一个,其一切可能的结果组成的基本事件有:
{}{}{}{}{}{}{}{}111213212223313233,,{,},,,,,,,,,,,,,,A B A B A B A B A B A B A B A B A B ,共9个,
包含1A 但不包括1B 的事件所包含的基本事件有:{}{}1213,,,A B A B ,共2个, 所以所求事件的概率为:2
9
P =
. 21.(2020·全国高三专题练习)某商场有奖销售活动中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为,求: (1);
(2)1张奖券的中奖概率;
(3)1张奖券不中特等奖且不中一等奖的概率. 【答案】(1);(2);(3).
【解析】(1)∵每1 000张奖券中设特等奖1个,一等奖10个,二等奖50个,∴. (2)设“抽取1张奖券中奖”为事件D ,则P (D )=P (A )+P (B )+P (C )= .
(3)设“抽取1张奖券不中特等奖和一等奖”为事件E ,则P (E )=1-P (A )-P (B )=1-.
22.(2020·北京高一期末)某校高一新生共有320人,其中男生192人,女生128人.为了解高一新生对数学选修课程的看法,采用分层抽样的方法从高一新生中抽取5人进行访谈. (Ⅰ)这5人中男生、女生各多少名?
(Ⅱ)从这5人中随即抽取2人完成访谈问卷,求2人中恰有1名女生的概率. 【答案】(Ⅰ)男生3人,女生2人;(Ⅱ)3
5
【解析】(Ⅰ)这5人中男生人数为
19253320?=,女生人数为128
52320
?=. (Ⅱ)记这5人中的3名男生为B 1,B 2,B 3,2名女生为G 1,G 2, 则样本空间为:
Ω={ (B1,B2), (B1,B3), (B1,G1), (B1,G2), (B2,B3), (B2,G1), (B2,G2), (B3,G1), (B3,G2),(G1,G2)},
样本空间中,共包含10个样本点.
设事件A为“抽取的2人中恰有1名女生”,
则A={ (B1,G1), (B1,G2), (B2,G1), (B2,G2), (B3,G1), (B3,G2)},
事件A共包含6个样本点.从而()
63 105
P A==
所以抽取的2人中恰有1名女生的概率为3
5
.
解析几何大量精选 1.在直角坐标系xOy 中,点M 到点()1,0F ,) 2 ,0F 的距离之和是4,点M 的轨迹 是C 与x 轴的负半轴交于点A ,不过点A 的直线:l y kx b =+与轨迹C 交于不同的两点P 和Q . ⑴求轨迹C 的方程; ⑴当0AP AQ ?=u u u r u u u r 时,求k 与b 的关系,并证明直线l 过定点. 【解析】 ⑴ 2 214 x y +=. ⑴将y kx b =+代入曲线C 的方程, 整理得2 2 2 (14)8440k x kbx b +++-=, 因为直线l 与曲线C 交于不同的两点P 和Q , 所以222222644(14)(44)16(41)0k b k b k b ?=-+-=-+> ① 设()11,P x y ,()22,Q x y ,则122 814kb x x k +=-+,21224414b x x k -= + ② 且2222 121212122 4()()()14b k y y kx b kx b k x x kb x x b k -?=++=+++=+, 显然,曲线C 与x 轴的负半轴交于点()2,0A -, 所以()112,AP x y =+u u u r ,()222,AQ x y =+u u u r . 由0AP AQ ?=u u u r u u u r ,得1212(2)(2)0x x y y +++=. 将②、③代入上式,整理得22121650k kb b -+=. 所以(2)(65)0k b k b -?-=,即2b k =或6 5 b k =.经检验,都符合条件① 当2b k =时,直线l 的方程为2y kx k =+.显然,此时直线l 经过定点()2,0-点. 即直线l 经过点A ,与题意不符. 当65b k =时,直线l 的方程为6655y kx k k x ? ?=+=+ ?? ?. 显然,此时直线l 经过定点6,05?? - ??? 点,满足题意. 综上,k 与b 的关系是65b k =,且直线l 经过定点6,05?? - ??? 2. 已知椭圆2222:1x y C a b +=(0)a b >>的离心率为1 2 ,以原点为圆心,椭圆的短半轴为半径的 圆与直线0x y -=相切. ⑴ 求椭圆C 的方程; ⑴ 设(4,0)P ,A ,B 是椭圆C 上关于x 轴对称的任意两个不同的点,连结PB 交椭圆C 于另一点E ,证明直线AE 与x 轴相交于定点Q ; ⑴ 在⑴的条件下,过点Q 的直线与椭圆C 交于M ,N 两点,求OM ON ?u u u u r u u u r 的取值范围. 【解析】 ⑴22 143 x y +=. ⑴ 由题意知直线PB 的斜率存在,设直线PB 的方程为(4)y k x =-.
专题四 解析几何专题 【命题趋向】解析几何是高中数学的一个重要内容,其核心内容是直线和圆以及圆锥曲线.由于平面向量可以用坐标表示,因此以坐标为桥梁,可以使向量的有关运算与解析几何中的坐标运算产生联系,平面向量的引入为高考中解析几何试题的命制开拓了新的思路,为实现在知识网络交汇处设计试题提供了良好的素材.解析几何问题着重考查解析几何的基本思想,利用代数的方法研究几何问题的基本特点和性质.解析几何试题对运算求解能力有较高的要求.解析几何试题的基本特点是淡化对图形性质的技巧性处理,关注解题方向的选择及计算方法的合理性,适当关注与向量、解三角形、函数等知识的交汇,关注对数形结合、函数与方程、化归与转化、特殊与一般思想的考查,关注对整体处理问题的策略以及待定系数法、换元法等的考查.在高考试卷中该部分一般有1至2道小题有针对性地考查直线与圆、圆锥曲线中的重要知识和方法;一道综合解答题,以圆或圆锥曲线为依托,综合平面向量、解三角形、函数等综合考查解析几何的基础知识、基本方法和基本的数学思想方法在解题中的应用,这道解答题往往是试卷的把关题之一. 【考点透析】解析几何的主要考点是:(1)直线与方程,重点是直线的斜率、直线方程的各种形式、两直线的交点坐标、两点间的距离公式、点到直线的距离公式等;(2)圆与方程,重点是确定圆的几何要素、圆的标准方程与一般方程、直线与圆和圆与圆的位置关系,以及坐标法思想的初步应用;(3)圆锥曲线与方程,重点是椭圆、双曲线、抛物线的定义、标准方程和简单几何性质,圆锥曲线的简单应用,曲线与方程的关系,以及数形结合的思想方法等. 【例题解析】 题型1 直线与方程 例1 (2008高考安徽理8)若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为( ) A .[ B .( C .[33 D .(33 - 分析:利用圆心到直线的距离不大于其半径布列关于直线的斜率k 的不等式,通过解不等式解决. 解析:C 设直线方程为(4)y k x =-,即40kx y k --=,直线l 与曲线22(2)1 x y -+= 有公共点,圆心到直线的距离小于等于半径 1d =≤,得222141,3 k k k ≤+≤,选择C 点评:本题利用直线和圆的位置关系考查运算能力和数形结合的思想意识.高考试卷中一般不单独考查直线与方程,而是把直线与方程与圆、圆锥曲线或其他知识交汇考查. 例2.(2009江苏泰州期末第10题)已知04,k <<直线1:2280l kx y k --+=和直线
1.【2015·新课标II】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下: A地区:62 73 81 92 95 85 74 64 53 76 78 86 95 66 97 78 88 82 76 89 B地区:73 83 62 51 91 46 53 73 64 82 93 48 65 81 74 56 54 76 65 79 (Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可); 价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率. 2.【2015·福建】某银行规定,一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定,小王到银行取钱时,发现自己忘记了银行卡的密码,但是可以确定该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定. (Ⅰ)求当天小王的该银行卡被锁定的概率; (Ⅱ)设当天小王用该银行卡尝试密码次数为X,求X的分布列和数学期望.
3.【2015·山东】若n是一个三位正整数,且n的个位数字大于十位数字,十位数字大于百位数字,则称n为“三位递增数”(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10 分;若能被10整除,得1分. 整除,得1 (I)写出所有个位数字是5的“三位递增数” ; (II)若甲参加活动,求甲得分X的分布列和数学期望EX. 4.【2015·安徽】已知2件次品和3件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束. (Ⅰ)求第一次检测出的是次品且第二次检测出的是正品的概率; (Ⅱ)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所 需要的检测费用(单位:元),求X的分布列和均值(数学期望).
1(本小题满分12分)某赛季, 甲、乙两名篮球运动员都参加了7场比赛, 他们所有比赛得分的情况用如图所示的茎叶图表示 (1)求甲、乙两名运动员得分的中位数; (2)你认为哪位运动员的成绩更稳定? (3)如果从甲、乙两位运动员的7场得分中各随 机抽取一场的得分, 求甲的得分大于乙的得分的概率. (参考数据:2222222981026109466++++++=, 236112136472222222=++++++) 2在学校开展的综合实践活动中, 某班进行了小制作评比, 作品上交时间为5月1日至30日, 评委会把同学们上交作品的件数按5天一组分组统计, 绘制了频率分布直方图(如图), 已知从左到右各长方形的高的比为2:3:4:6:4:1, 第三组的频数为12, 请解答下列问 题: (1)本次活动共有多少件作品参加评比? (2)哪组上交的作品数量最多?共有多少件? (3)经过评比, 第四组和第六组分别有10件、2件作品获奖, 问这两组哪组获奖率高? 3已知向量()1,2a =-r , (),b x y =r . (1)若x , y 分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1, 2, 3, 4, 5, 6)先后抛掷两次时第一次、第二次出现的点数, 求满足1a b =-r r g 的概率; (2)若实数,x y ∈[]1,6, 求满足0a b >r r g 的概率.
4某公司在过去几年内使用某种型号的灯管1000支, 该公司对这些灯管的使用寿命(单位:小时)进行了统计, 统计结果如下表所示: (1)将各组的频率填入表中; (2)根据上述统计结果, 计算灯管使用寿命不足1500小时的频率; (3)该公司某办公室新安装了这种型号的灯管2支, 若将上述频率作为概率, 试求恰有1支灯管的使用寿命不足1500小时的概率. 5为研究气候的变化趋势, 某市气象部门统计了共100个星期中每个星期气温的最高温度和最低温度, 如下表: (1)若第六、七、八组的频数t 、m 、 n 为递减的等差数列, 且第一组与第八组 的频数相同, 求出x 、t 、m 、n 的值; (2)若从第一组和第八组的所有星期 中随机抽取两个星期, 分别记它们的平均 温度为x , y , 求事件“||5x y ->”的概率. 6某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5 所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人. (1)问各班被抽取的学生人数各为多少人? (2)在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率. 频率 分数 90100110120130 0.05 0.100.150.200.250.300.350.4080 70
高考数学解析几何专题练习解析版82页 1.一个顶点的坐标()2,0 ,焦距的一半为3的椭圆的标准方程是( ) A. 19422=+y x B. 14922=+y x C. 113422=+y x D. 14132 2=+y x 2.已知双曲线的方程为22 221(0,0)x y a b a b -=>>,过左焦点F 1的直线交 双曲线的右支于点P ,且y 轴平分线段F 1P ,则双曲线的离心率是( ) A . 3 B .32+ C . 31+ D . 32 3.已知过抛物线y 2 =2px (p>0)的焦点F 的直线x -my+m=0与抛物线交于A ,B 两点, 且△OAB (O 为坐标原点)的面积为,则m 6+ m 4的值为( ) A .1 B . 2 C .3 D .4 4.若直线经过(0,1),(3,4)A B 两点,则直线AB 的倾斜角为 A .30o B . 45o C .60o D .120o 5.已知曲线C 的极坐标方程ρ=2θ2cos ,给定两点P(0,π/2),Q (-2,π),则有 ( ) (A)P 在曲线C 上,Q 不在曲线C 上 (B)P 、Q 都不在曲线C 上 (C)P 不在曲线C 上,Q 在曲线C 上 (D)P 、Q 都在曲线C 上 6.点M 的直角坐标为)1,3(--化为极坐标为( ) A .)65, 2(π B .)6 ,2(π C .)611,2(π D .)67,2(π 7.曲线的参数方程为???-=+=1 232 2t y t x (t 是参数),则曲线是( ) A 、线段 B 、直线 C 、圆 D 、射线 8.点(2,1)到直线3x-4y+2=0的距离是( ) A . 54 B .4 5 C . 254 D .4 25 9. 圆0642 2 =+-+y x y x 的圆心坐标和半径分别为( ) A.)3,2(-、13 B.)3,2(-、13 C.)3,2(--、13 D.)3,2(-、13 10.椭圆 122 2 2=+b y x 的焦点为21,F F ,两条准线与x 轴的交点分别为M 、N ,若212F F MN ≤,则该椭圆离心率取得最小值时的椭圆方程为 ( )
《曲线的方程和性质》专题 一、《考试大纲》要求 ⒈直线和圆的方程 (1)理解直线的倾斜角和斜率的概念,掌握过两点的直线的斜率公式.掌握直线方 程的点斜式、两点式、一般式,并能根据条件熟练地求出直线方程. (2)掌握两条直线平行与垂直的条件,两条直线所成的角和点到直线的距离公式.能够根据直线的方程判断两条直线的位置关系. (3)了解二元一次不等式表示平面区域. (4)了解线性规划的意义,并会简单的应用. (5)了解解析几何的基本思想,了解坐标法. (6)掌握圆的标准方程和一般方程,了解参数方程的概念,理解圆的参数方程. ⒉圆锥曲线方程 (1)掌握椭圆的定义、标准方程和椭圆的简单几何性质,理解椭圆的参数方程. (2)掌握双曲线的定义、标准方程和双曲线的简单几何性质. (3)掌握抛物线的定义、标准方程和抛物线的简单几何性质. (4)了解圆锥曲线的初步应用. 二、高考试题回放 1.(福建)已知F 1、F 2是椭圆的两个焦点,过F 1且与椭圆长轴垂直 的直线交椭圆于A 、B 两点,若△ABF 2是正三角形,则这个椭圆的离心率是 ( ) A . 33 B .32 C .2 2 D .23
2.(福建)直线x +2y=0被曲线x 2+y 2-6x -2y -15=0所截得的弦长等于 . 3.(福建)如图,P 是抛物线C :y=2 1x 2上一点,直线l 过点P 且与抛物线C 交于另一点Q.(Ⅰ)若直线l 与过点P 的切线垂直,求线段PQ 中点M 的轨迹方程; (Ⅱ)若直线l 不过原点且与x 轴交于点S ,与y 轴交于点T ,试求 | || |||||SQ ST SP ST +的取值范围. 4.(湖北)已知点M (6,2)和M 2(1,7).直线y=mx —7与线段M 1M 2的交点M 分有向线段M 1M 2的比为3:2,则m 的值为 ( ) A .2 3 - B .3 2- C .4 1 D .4 5.(湖北)两个圆0124:0222:222221=+--+=-+++y x y x C y x y x C 与的 公切线有且仅有 ( ) A .1条 B .2条 C .3条 D .4条 6.(湖北)直线12:1:22=-+=y x C kx y l 与双曲线的右支交于不同的两 点A 、B. (Ⅰ)求实数k 的取值范围; (Ⅱ)是否存在实数k ,使得以线段AB 为直径的圆经过双曲线C 的右焦点F ?若存在,求出k 的值;若不存在,说明理由. 7.(湖南)如果双曲线112 132 2 =-y x 上一点P 到右焦点的距离为13, 那么 点 P 到右准线 的 距 离 是 ( )
全国一卷真题分析---概率统计 1.(2011年)根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的 概率为0.3,设各车主购买保险相互独立. (Ⅰ)求该地1位车主至少购买甲、乙两种保险中的l种的概率; (Ⅱ)X表示该地的l00位车主中,甲、乙两种保险都不购买的车主数.求X的期望. 2.(2012年)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果 当天卖不完,剩下的玫瑰花作垃圾处理.(Ⅰ)若花店一天购进16朵玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,N n )的函数解析式;(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表: 以100天记录的各需求量的频率作为 各需求量发生的概率. (ⅰ)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列、数学期望及方差; (ⅱ)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由. 3.(2013年)一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中 优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下, 这批产品都不能通过检验.假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为1 2, 且各件产品是否为优质品相互独立. (1)求这批产品通过检验的概率; (2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望. 1
高考数学一轮复习: 概率与统计 高考大题专项(六) 概率与统计 考情分析 一、考查范围全面 概率与统计解答题对知识点的考查较为全面,近五年的试题考点覆盖了概率与统计必修与选修的各个章节内容,考查了抽样方法、统计图表、数据的数字特征、用样本估计总体、回归分析、相关系数的计算、独立性检验、古典概型、条件概率、相互独立事件的概率、独立重复试验的概率、离散型随机变量的分布列、数学期望与方差、超几何分布、二项分布、正态分布等基础知识和基本方法. 二、考查方向分散 从近五年的高考试题来看,对概率与统计的考查主要有四个方面:一是统计与统计案例,其中回归分析、相关系数的计算、独立性检验、用样本的数字特征估计总体的数字特征是考查重点,常与抽样方法、茎叶图、频率分布直方图、概率等知识交汇考查;二是统计与概率分布的综合,常与抽样方法、茎叶图、频率分布直方图、频率、概率以及函数知识、概率分布列等知识交汇考查;三是期望与方差的综合应用,常与离散型随机变量、概率、相互独立事件、二项分布等知识交汇考查;四是以生活中的实际问题为背景将正态分布与随机变量的期望和方差相结合综合考查. 三、考查难度稳定 高考对概率与统计解答题的考查难度稳定,多年来都控制在中等或中等偏上一点的程度,解答题一般位于试卷的第18题或第19题的位置.近两年有难度提升的趋势,位置有所后调. 典例剖析 题型一相关关系的判断及回归分析 【例1】近年来,随着互联网技术的快速发展,共享经济覆盖的范围迅速扩张,继共享单车、共享汽车之后,共享房屋以“民宿”“农家乐”等形式开始在很多平台上线.某创业者计划在某景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向,此创业者对该景区附近六家“农家乐”跟踪调查了100天.得到的统计数据如下表,x为收费标准(单位:元/日),t为入住天数(单位:天),以频率作为各自的“入住率”,收费标准x与“入住率”y的散点图如图. x50100150200300400 t906545302020
统计概率大题题型总结 题型一 频率分布直方图与茎叶图 例1.(2013广东理17)某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如 图所示,其中茎为十位数,叶为个位数. (Ⅰ) 根据茎叶图计算样本均值; (Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间12名工人中有几名优秀工人; (Ⅲ) 从该车间12名工人中,任取2人,求恰有名优秀工人的概率. 例2.(2013新课标Ⅱ理)经销商经销某种农产品,在一个销售季度内,每售出t 该产品获利润500 元,未售出的产品,每t 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t 该农产品,以X (单位:t,150100≤≤X )表示下一个销售季度内的市场需求量,T (单位:元)表示下一个销售季度内销商该农产品的利润. (Ⅰ)将T 表示为X 的函数; (Ⅱ)根据直方图估计利润T 不少于57000元的概率; 1 7 9 2 0 1 5 3 0 第17题图
(Ⅲ)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若[100,110)X ∈,则取105X =,且105X =的概率等于需求量落入[100,110)的概率),求利润T 的数学期望. 变式1. 【2015高考重庆,理3】重庆市2013年各月的平均气温(o C )数据的茎叶图如下: 08912 58 200338312 则这组数据的中位数是( ) A 、19 B 、20 C 、21.5 D 、23 /频率组距0.010 0.0150.0200.0250.030100110120130140150需求量/x t
高中数学概率大题(经典一) 一.解答题(共10小题) 1.在一次运动会上,某单位派出了有6名主力队员和5名替补队员组成的代表队参加比赛.(1)如果随机抽派5名队员上场比赛,将主力队员参加比赛的人数记为X,求随机变量X 的数学期望; (2)若主力队员中有2名队员在练习比赛中受轻伤,不宜同时上场;替补队员中有2名队员身材相对矮小,也不宜同时上场;那么为了场上参加比赛的5名队员中至少有3名主力队员,教练员有多少种组队方案? 2.某银行柜台设有一个服务窗口,假设顾客办理业务所需的时间互相独立,且都是整数分 (1)估计第三个顾客恰好等待4分钟开始办理业务的概率; (2)X表示至第2分钟末已办理完业务的顾客人数,求X的分布列及数学期望. 3.某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖,否则,均为不获奖.卡片用后放回盒子,下一位参加者继续重复进行. (1)有三人参加抽奖,要使至少一人获奖的概率不低于,则“海宝”卡至少多少张? (2)现有甲乙丙丁四人依次抽奖,用ξ表示获奖的人数,求ξ的分布列及Eξ的值. 4.一袋中有m(m∈N*)个红球,3个黑球和2个白球,现从中任取2个球. (1)当m=4时,求取出的2个球颜色相同的概率; (2)当m=3时,设ξ表示取出的2个球中黑球的个数,求ξ的概率分布及数学期望; (3)如果取出的2个球颜色不相同的概率小于,求m的最小值. 5.某商场为促销设计了一个抽奖模型,一定数额的消费可以获得一张抽奖券,每张抽奖券可以从一个装有大小相同的4个白球和2个红球的口袋中一次性摸出3个球,至少摸到一个红球则中奖. (Ⅰ)求一次抽奖中奖的概率; (Ⅱ)若每次中奖可获得10元的奖金,一位顾客获得两张抽奖券,求两次抽奖所得的奖金额之和X(元)的概率分布和期望E(X). 6.将一枚硬币连续抛掷15次,每次抛掷互不影响.记正面向上的次数为奇数的概率为P1,正面向上的次数为偶数的概率为P2. (Ⅰ)若该硬币均匀,试求P1与P2; (Ⅱ)若该硬币有暇疵,且每次正面向上的概率为,试比较P1与P2的大小. 7.某地位于甲、乙两条河流的交汇处,根据统计资料预测,今年汛期甲河流发生洪水的概率为0.25,乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响).现有一台大型设备正在该地工作,为了保护设备,施工部门提出以下三种方案:
高考数学专题复习:解析几何专题 【命题趋向】 1.注意考查直线的基本概念,求在不同条件下的直线方程,直线的位置关系,此类题大多都属中、低档题,以选择、填空题的形式出现,每年必考 2.考查直线与二次曲线的普通方程,属低档题,对称问题常以选择题、填空题出现 3.考查圆锥曲线的基础知识和基本方法的题多以选择题和填空题的形式出现,与求轨迹有关、与向量结合、与求最值结合的往往是一个灵活性、综合性较强的大题,属中、高档题, 4.解析几何的才查,分值一般在17---22分之间,题型一般为1个选择题,1个填空题,1个解答题. 【考题解析与考点分析】 考点1.求参数的值 求参数的值是高考题中的常见题型之一,其解法为从曲线的性质入手,构造方程解之. 例1.若抛物线22y px =的焦点与椭圆22162 x y +=的右焦点重合,则p 的值为( ) A .2- B .2 C .4- D .4 考查意图: 本题主要考查抛物线、椭圆的标准方程和抛物线、椭圆的基本几何性质. 解答过程:椭圆22162 x y +=的右焦点为(2,0),所以抛物线22y px =的焦点为(2,0),则4p =,故选D. 考点2. 求线段的长 求线段的长也是高考题中的常见题型之一,其解法为从曲线的性质入手,找出点的坐标,利用距离公式解之. 例2.已知抛物线y-x 2+3上存在关于直线x+y=0对称的相异两点A 、B ,则|AB|等于 A.3 B.4 C.32 D.42 考查意图: 本题主要考查直线与圆锥曲线的位置关系和距离公式的应用. 解:设直线AB 的方程为y x b =+,由22123301y x x x b x x y x b ?=-+?++-=?+=-?=+?,进而可求出AB 的中点1 1(,)22M b --+,又由11(,)22 M b --+在直线0x y +=上可求出1b =, ∴220x x +-=,由弦长公式可求出AB ==. 故选C 例3.如图,把椭圆2212516x y +=的长轴 AB 分成8等份,过每个分点作x 轴的垂线交椭圆的上半部 分于1234567 ,,,,,,P P P P P P P 七个点,F 是椭圆的一个焦点, 则1234567PF P F P F P F P F P F P F ++++++= ____________. 考查意图: 本题主要考查椭圆的性质和距离公式的灵活应用.
【精品】2007——2017年高考数学全国卷概率统计大题 2007某商场经销某商品,顾客可采用一次性付款或分期付款购买.根据以往资料统计,顾客采用一次性付款的概率是0.6.经销一件该商品,若顾客采用一次性付款,商场获得利润200元;若顾客采用分期付款,商场获得利润250元. (Ⅰ)求3位购买该商品的顾客中至少有1位采用一次性付款的概率; (Ⅱ)求3位顾客每人购买1件该商品,商场获得利润不超过650元的概率. 记A 表示事件:“3位顾客中至少1位采用一次性付款”,则A 表示事件:“3位顾客中无人采用一次性付款”. 2 ()(10.6) 0.064 P A =-=,()1()10.0640.936P A P A =-=-=. (Ⅱ)记B 表示事件:“3位顾客每人购买1件该商品,商场获得利润不超过650元”. 0B 表示事件:“购买该商品的3位顾客中无人采用分期付款”. 1B 表示事件:“购买该商品的3位顾客中恰有1位采用分期付款”. 则01B B B =+.30()0.60.216P B ==,12 13()0.60.40.432P B C =??=. 01()()P B P B B =+01()()P B P B =+0.2160.432=+0.648=. 2008 已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方案: 方案甲:逐个化验,直到能确定患病动物为止. 方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验. 求依方案甲所需化验次数不少于依方案乙所需化验次数的概率. (20)解:记A 1、A 2分别表示依方案甲需化验1次、2次,B 表示依方案乙需化验3次,A 表示依方案甲所需化验次数不少于依方案乙所需化验次数。依题意知A 2与B 独立,且 B A A A 21+=, 5 1C 1)A (P 15 1= = ,5 1A A )A (P 25 142= = ,5 2) (1 3 3 51224= ??= C C C C B P 。 P(A )=P(A 1+A 2·B) =P(A 1)+P(A 2·B)=P(A 1)+P(A 2)·P(B) =5 25 15 1? += 25 7 所以 P(A)=1-P(A )= 25 18=0.72 2009 甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束。假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立。已知前2局中,甲、乙各胜1局。 (Ⅰ)求再赛2局结束这次比赛的概率;
解析几何大量精选 1 2 1.在直角坐标系xOy 中,点M 到点()1,0F ,)2,0F 的距离之和是4,点M 3 的轨迹是C 与x 轴的负半轴交于点A ,不过点A 的直线:l y kx b =+与轨迹C 交于4 不同的两点P 和Q . 5 ⑴求轨迹C 的方程; 6 ⑵当0AP AQ ?=时,求k 与b 的关系,并证明直线l 过定点. 7 【解析】 ⑴ 2214 x y +=. 8 ⑵将y kx b =+代入曲线C 的方程, 9 整理得222(14)8440k x kbx b +++-=, 10 因为直线l 与曲线C 交于不同的两点P 和Q , 11 所以222222644(14)(44)16(41)0k b k b k b ?=-+-=-+> ① 12 设()11,P x y ,()22,Q x y ,则122814kb x x k +=-+,21224414b x x k -=+ ② 13 且22 2 2 121212122 4()()()14b k y y kx b kx b k x x kb x x b k -?=++=+++=+, 14 显然,曲线C 与x 轴的负半轴交于点()2,0A -, 15 所以()112,AP x y =+,()222,AQ x y =+. 16 由0AP AQ ?=,得1212(2)(2)0x x y y +++=. 17
将②、③代入上式,整理得22121650k kb b -+=. 18 所以(2)(65)0k b k b -?-=,即2b k =或65 b k =.经检验,都符合条件① 19 当2b k =时,直线l 的方程为2y kx k =+.显然,此时直线l 经过定点()2,0-20 点. 21 即直线l 经过点A ,与题意不符. 22 当6 5b k =时,直线l 的方程为665 5y kx k k x ??=+=+ ?? ? . 23 显然,此时直线l 经过定点6 ,05 ??- ?? ? 点,满足题意. 24 综上,k 与b 的关系是65 b k =,且直线l 经过定点6 ,05?? - ??? 25 26 2. 已知椭圆2222:1x y C a b +=(0)a b >>的离心率为1 2 ,以原点为圆心,椭圆的短半 27 轴为半径的圆与直线0x y -+相切. 28 ⑴ 求椭圆C 的方程; 29 ⑵ 设(4,0)P ,A ,B 是椭圆C 上关于x 轴对称的任意两个不同的点,连结PB 30 交椭圆C 于另一点E ,证明直线AE 与x 轴相交于定点Q ; 31 ⑶ 在⑵的条件下,过点Q 的直线与椭圆C 交于M ,N 两点,求OM ON ?的取32 值范围. 33 【解析】 ⑴22 143 x y +=. 34
高中数学概率大题(经典二) 一.解答题(共10小题) 1.某会议室用5盏灯照明,每盏灯各使用灯泡一只,且型号相同.假定每盏灯能否正常照明只与灯泡的寿命有关,该型号的灯泡寿命为1年以上的概率为p1,寿命为2年以上的概率为p2.从使用之日起每满1年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换.(Ⅰ)在第一次灯泡更换工作中,求不需要换灯泡的概率和更换2只灯泡的概率; (Ⅱ)在第二次灯泡更换工作中,对其中的某一盏灯来说,求该盏灯需要更换灯泡的概率;(Ⅲ)当p1=0.8,p2=0.3时,求在第二次灯泡更换工作,至少需要更换4只灯泡的概率(结果保留两个有效数字). 2.已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止.设ξ为取出的次数,求ξ的分布列及Eξ.3.某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有n位学生,每次活动均需该系k位学生参加(n和k都是固定的正整数),假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系k位学生,且所发信息都能收到,记该系收到李老师或张老师所发活动通知信息的学生人数为X.(I)求该系学生甲收到李老师或张老师所发活动通知信息的概率; (II)求使P(X=m)取得最大值的整数m. 4.在医学生物学试验中,经常以果蝇作为试验对象,一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.以ξ表示笼内还剩下的果蝇的只数. (Ⅰ)写出ξ的分布列(不要求写出计算过程)和数学期望Eξ; (Ⅱ)求概率P(ξ≥Eξ). 5.A,B,C三个班共有100名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如表(单位:小时): A班 6 6.5 7 7.5 8 B班 6 7 8 9 10 11 12 C班 3 4.5 6 7.5 9 10.5 12 13.5 (Ⅰ)试估计C班的学生人数; (Ⅱ)从A班和C班抽出的学生中,各随机选取一个人,A班选出的人记为甲,C班选出的人记为乙.假设所有学生的锻炼时间相对独立,求该周甲的锻炼时间比乙的锻炼时间长的概率; (Ⅲ)再从A,B,C三班中各随机抽取一名学生,他们该周锻炼时间分别是7,9,8.25(单位:小时),这3个新数据与表格中的数据构成的新样本的平均数记为μ1,表格中数据的平均数记为μ0,试判断μ0和μ1的大小.(结论不要求证明) 6.某商场经销某商品,根据以往资料统计,顾客采用的付款期数ξ的分布列为ξ 1 2 3 4 5 P 0.4 0.2 0.2 0.1 0.1 商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元,η表示经销一件该商品的利润. (Ⅰ)求事件A:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率P(A);
解析几何解答题 1、椭圆G :)0(122 22>>=+b a b y a x 的两个焦点为F 1、F 2,短轴两端点B 1、B 2,已知 F 1、F 2、B 1、B 2四点共圆,且点N (0,3)到椭圆上的点最远距离为.25 (1)求此时椭圆G 的方程; (2)设斜率为k (k ≠0)的直线m 与椭圆G 相交于不同的两点E 、F ,Q 为EF 的中点,问E 、F 两点能否关于 过点P (0, 3 3)、Q 的直线对称若能,求出k 的取值范围;若不能,请说明理由. ; 2、已知双曲线221x y -=的左、右顶点分别为12A A 、,动直线:l y kx m =+与圆22 1x y +=相切,且与双曲线左、右两支的交点分别为111222(,),(,)P x y P x y . (Ⅰ)求k 的取值范围,并求21x x -的最小值; (Ⅱ)记直线11P A 的斜率为1k ,直线22P A 的斜率为2k ,那么,12k k ?是定值吗证明你的结论. @ [
3、已知抛物线2 :C y ax =的焦点为F ,点(1,0)K -为直线l 与抛物线C 准线的交点,直线l 与抛物线C 相交于A 、 B 两点,点A 关于x 轴的对称点为D . (1)求抛物线 C 的方程。 ~ (2)证明:点F 在直线BD 上; (3)设8 9 FA FB ?=,求BDK ?的面积。. { — 4、已知椭圆的中心在坐标原点O ,焦点在x 轴上,离心率为1 2 ,点P (2,3)、A B 、在该椭圆上,线段AB 的中点T 在直线OP 上,且A O B 、、三点不共线. (I)求椭圆的方程及直线AB 的斜率; (Ⅱ)求PAB ?面积的最大值. - 、
解析几何(4) 23.(本大题满分18分,第1小题满分4分,第二小题满分6分,第3小题满分8分) 已知平面上的线段l 及点P ,任取l 上一点Q ,线段PQ 长度的最小值称为点P 到线段 l 的距离,记作(,)d P l (1)求点(1,1)P 到线段:30(35)l x y x --=≤≤的距离(,)d P l ; (2)设l 是长为2的线段,求点的集合{(,)1}D P d P l =≤所表示的图形面积; (3)写出到两条线段12,l l 距离相等的点的集合12{(,)(,)}P d P l d P l Ω==,其中 12,l AB l CD ==,,,,A B C D 是下列三组点中的一组. 对于下列三种情形,只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种情形,则按照序号较小的解答计分. ①(1,3),(1,0),(1,3),(1,0)A B C D --. ②(1,3),(1,0),(1,3),(1,2)A B C D ---. ③(0,1),(0,0),(0,0),(2,0)A B C D . 23、解:⑴ 设(,3)Q x x -是线段:30(35)l x y x --=≤≤上一点,则 ||5) PQ x ==≤≤,当 3 x =时 , min (,)||d P l PQ == ⑵ 设线段l 的端点分别为,A B ,以直线AB 为x 轴,AB 的中点为原点建立直角坐标系, 则(1,0),(1,0)A B -,点集D 由如下曲线围成 12:1(||1),:1(||1) l y x l y x =≤=-≤, 222212:(1)1(1),:(1)1(1)C x y x C x y x ++=≤--+=≥ 其面积为4S π=+。 ⑶① 选择(1,3),(1,0),(1,3),(1,0)A B C D --,{(,)|0}x y x Ω== ② 选择(1,3),(1,0),(1,3),(1,2)A B C D ---。 2{(,)|0,0}{(,)|4,20}{(,)|10,1}x y x y x y y x y x y x y x Ω==≥=-≤<++=> ③ 选择(0,1),(0,0),(0,0),(2,0)A B C D 。
大题专项:统计与概率问题 一、解答题 1.为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛. (1)设A 为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”,求事件A 发生的概率; (2)设X 为选出的4人中种子选手的人数,求随机变量X 的分布列和数学期望. 解:(1)由已知,有P (A )= C 22C 32+C 32C 3 2C 8 4=6 35. 所以,事件A 发生的概率为6 35. (2)随机变量X 的所有可能取值为1,2,3,4. P (X=k )= C 5k C 3 4-k C 8 4(k=1,2,3,4). 所以,随机变量X 的分布列为 随机变量X 的数学期望E (X )=1×1 14+2×3 7+3×3 7+4×1 14=5 2. 好评率是指:一类电影中获得好评的部数与该类电影的部数的比值. 假设所有电影是否获得好评相互独立. (1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率; (2)从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率; (3)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等.用“ξk =1”表示第k 类电影得到人们喜欢,用“ξk =0”表示第k 类电影没有得到人们喜欢(k=1,2,3,4,5,6).写出方差D (ξ1),D (ξ2),D (ξ3),D (ξ4),D (ξ5),D (ξ6)的大小关系. 解:(1)设“从电影公司收集的电影中随机选取1部,这部电影是获得好评的第四类电影”为事件A , 第四类电影中获得好评的电影为200×0.25=50(部). P (A )=50 140+50+300+200+800+510=50 2 000=0.025.
专题09 解析几何 第二十四讲 抛物线 2019年 1.(2019全国II 文9)若抛物线y 2 =2px (p >0)的焦点是椭圆 22 13x y p p +=的一个焦点,则p = A .2 B .3 C .4 D .8 2.(2019浙江21)如图,已知点(10)F ,为抛物线2 2(0)y px p =>的焦点,过点F 的直线交抛物线于A 、B 两点,点C 在抛物线上,使得ABC △的重心G 在x 轴上,直线AC 交x 轴于点Q ,且Q 在点F 右侧.记,AFG CQG △△的面积为12,S S . (1)求p 的值及抛物线的准线方程; (2)求 1 2 S S 的最小值及此时点G 的坐标. 3.(2019全国III 文21)已知曲线C :y =2 2 x ,D 为直线y =12-上的动点,过D 作C 的两条 切线,切点分别为A ,B . (1)证明:直线AB 过定点: (2)若以E (0,5 2 )为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求该圆的方程. 2015-2018年 一、选择题 1.(2017新课标Ⅱ)过抛物线C :2 4y x =的焦点F ,3的直线交C 于点M (M
在x 轴上方),l 为C 的准线,点N 在l 上且MN ⊥l ,则M 到直线NF 的距离为 A B . C . D .2.(2016年全国II 卷)设F 为抛物线C :y 2=4x 的焦点,曲线y = k x (k >0)与C 交于点P ,PF ⊥x 轴,则k = A . 12 B .1 C .3 2 D .2 3.(2015陕西)已知抛物线2 2y px =(0p >)的准线经过点(1,1)-,则该抛物线的焦点坐 标为 A .(-1,0) B .(1,0) C .(0,-1) D .(0,1) 4.(2015四川)设直线l 与抛物线2 4y x =相交于,A B 两点,与圆2 2 2 (5)(0)x y r r -+=>相切于点M ,且M 为线段AB 的中点.若这样的直线l 恰有4条,则r 的取值范围是 A .()13, B .()14, C .()23, D .()24, 二、填空题 5.(2018北京)已知直线l 过点(1,0)且垂直于x 轴,若l 被抛物线2 4y ax =截得的线段长为 4,则抛物线的焦点坐标为_________. 6.(2015陕西)若抛物线2 2(0)y px p =>的准线经过双曲线2 2 1x y -=的一个焦点,则p = 三、解答题 7.(2018全国卷Ⅱ)设抛物线2 4=:C y x 的焦点为F ,过F 且斜率为(0)>k k 的直线l 与 C 交于A ,B 两点,||8=AB . (1)求l 的方程; (2)求过点A ,B 且与C 的准线相切的圆的方程. 8.(2018浙江)如图,已知点P 是y 轴左侧(不含y 轴)一点,抛物线C :2 4y x =上存在 不同的两点A ,B 满足PA ,PB 的中点均在C 上.