当前位置：文档之家› 多元函数泰勒公式的张量表示

多元函数泰勒公式的张量表示

第21卷第3期2018年5月

西安文理学院学报（自然科学版）

Journal of Xi?an University (Natural Science Edition)

Vol.21 No3

May2018

文章编号:1008-5564 (2018 )03-0001-03

多元函数泰勒公式的张量表示

曹文飞，韩国栋

(陕西师范大学数学与信息科学学院，西安710119)

摘要:泰勒公式在多元微分学中占据着十分重要的地位，在多元函数逼近、计算机图形学以及工程近似计算等分支中有成功的应用.在高等数学教材中，多元函数泰勒展开式中的高阶项通常是借助于

多项展开式进行表达，这种抽象的表达形式导致本知识点艰涩难懂.为了克服此授课难点，基于张量与

张量积运算为泰勒公式引人一种直观且简洁的新表达形式.该新形式有利于学生对泰勒公式的理解与

记忆，从而激发起他们运用数学工具解决实际问题的兴趣.

关键词:泰勒公式;矩阵;张量;教学研究

中图分类号:〇172.1 文献标志码:A

Tensor Representation for Taylor Formula of

the Multivariate Function

C A O W en-f e i,H A N G u o-d on g

(School of Mathematics and Information Science，Shaanxi Normal University，Xi’an710119，China) Abstract! Taylor’s formula occupies a very important position in multivariate differential calcu-

lus.It has been applied successfi^lly to many branches such as multivariate function approxima-

tion，computer graphics and engineering approximate calculation.In the teaching materials of

higher mathematics，the high order term in the Taylor expansion of multiple functions is usually

expressed by multiple expansion，and this abstract expression form leads to th edge.In order to overcome the diiculty of teaching，a new and co Taylors formula based o n the tensor and tensor product operation is introduced in this paper.

This new form is b eneficial to students7understanding and memory of Taylors formula，thus a-

rousing their interest in solving practical problems by using mathematical tools.

Key words ：Taylor formu l a$matrix$tensor$teaching research

我们正处在一个高新技术蓬勃发展的时代，数学对高新技术的发展发挥巨大的推动作用.正如应用数学家D avd[1]指出:很少有人认识到，被如此称颂的高新技术本质上是一种数学技术.因此，良好的数学教育在这个年代显得尤为迫切.高等数学教育是数学教育中不可缺少的重要环节，因而如何讲授好高

收稿日期：2018-01-09

基金项目：国家自然科学基金项目（61603235 )$陕西师范大学科研启动基金

作者简介:曹文飞（1985%)，男，安徽怀宁人，陕西师范大学数学与信息科学学院讲师，博士，主要从事机器学习、图像处理研究；

韩国栋（1978%)，男，山西祁县人，陕西师范大学数学与信息科学学院副教授，博士，主要从事非线性泛函

分析及其应用研究.

常用泰勒公式

简介在数学上, 一个定义在开区间(a-r, a+r)上的无穷可微的实变函数或复变函数f的泰勒级数是如下的幂级数这里，n!表示n的阶乘而f(n)(a) 表示函数f在点a处的n阶导数。如果泰勒级数对于区间(a-r, a+r)中的所有x都收敛并且级数的和等于f(x)，那么我们就称函数f(x)为解析的。当且仅当一个函数可以表示成为幂级数的形式时，它才是解析的。为了检查级数是否收敛于f(x)，我们通常采用泰勒定理估计级数的余项。上面给出的幂级数展开式中的系数正好是泰勒级数中的系数。如果a = 0, 那么这个级数也可以被称为麦克劳伦级数。泰勒级数的重要性体现在以下三个方面：首先，幂级数的求导和积分可以逐项进行，因此求和函数相对比较容易。第二，一个解析函数可被延伸为一个定义在复平面上的一个开片上的解析函数，并使得复分析这种手法可行。第三，泰勒级数可以用来近似计算函数的值。对于一些无穷可微函数f(x) 虽然它们的展开式收敛，但是并不等于f(x)。例如，分段函数f(x) = exp(?1/x2) 当x≠ 0 且f(0) = 0 ，则当x = 0所有的导数都为零，所以这个f(x)的泰勒级数为零，且其收敛半径为无穷大，虽然这个函数f仅在x = 0 处为零。而这个问题在复变函数内并不成立，因为当z沿虚轴趋于零时 exp(?1/z2) 并不趋于零。一些函数无法被展开为泰勒级数因为那里存在一些奇点。但是如果变量x是负指数幂的话，我们仍然可以将其展开为一个级数。例如，f(x) = exp(?1/x2) 就可以被展开为一个洛朗级数。 Parker-Sockacki theorem是最近发现的一种用泰勒级数来求解微分方程的定理。这个定理是对Picard iterati on一个推广。 [编辑]

第九节多元函数的泰勒公式

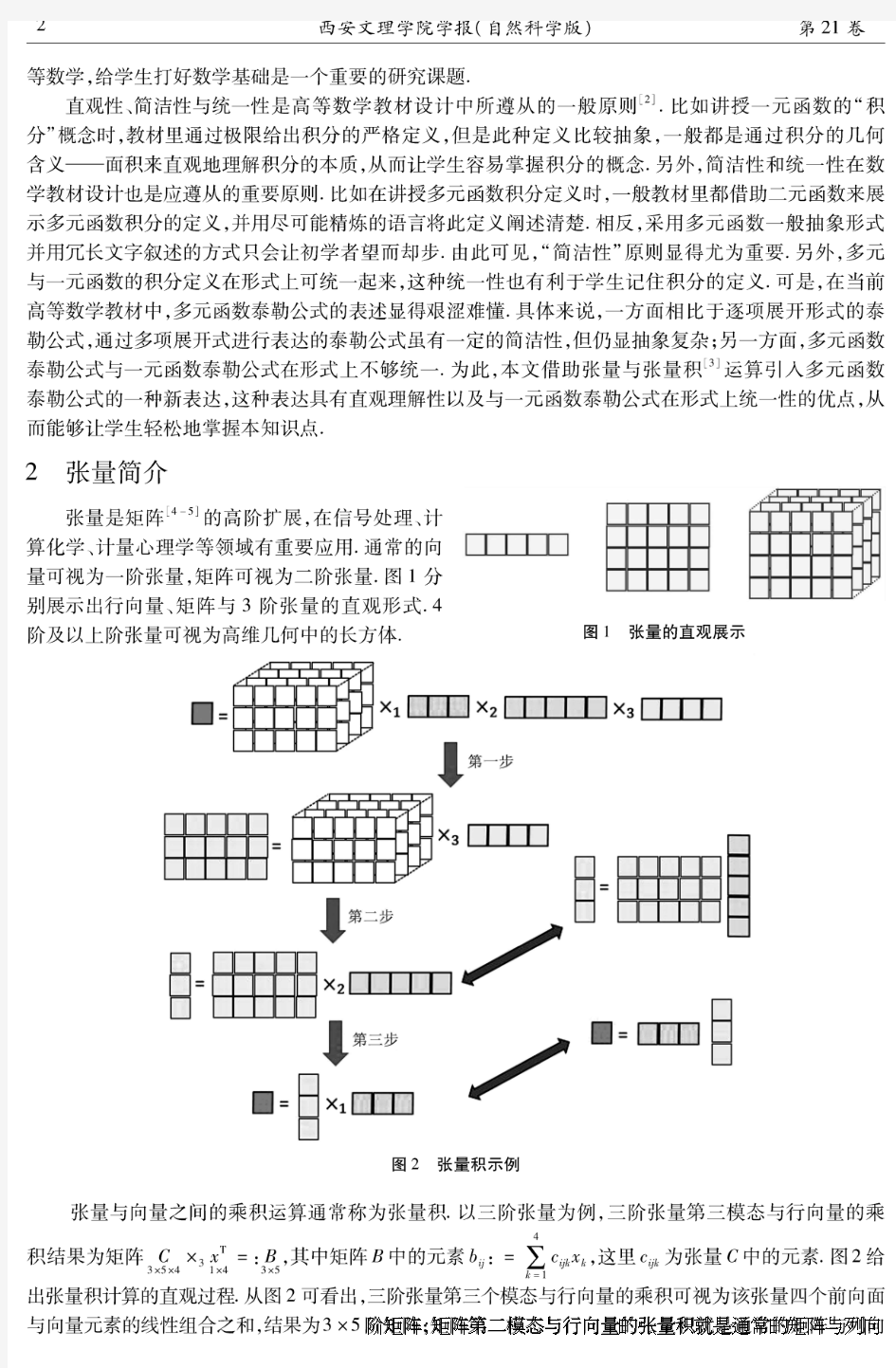
第九节多元函数的泰勒公式分布图示 ★ 二元函数的泰勒公式 ★ 例1 ★ 关于极值充分条件的证明 ★ 内容小结 ★ 习题8—9 ★ 返回内容要点一、二元函数的泰勒公式我们知道用一个一元函数的泰勒公式可以按任意给定的精度要求来近似表达这个函数. 对多元函数也有类似的结果，即可以用一个多元多项式按任意给定的精度要求来近似表达一个多元函数. 现以二元函数为例叙述如下：定理1 设),(y x f z =在点),(00y x 的某一邻域内连续且有直到1+n 阶的连续偏导数, ),(00k y h x ++为此邻域内任一点, 则有 ),(),(),(000000y x f y k x h y x f h y h x f ???? ????+??+=++),(!21002 y x f y k x h ???? ????+??+ ),(!100y x f y k x h n n ???? ????+??++ ),()!1(1001k y h x f y k x h n n θθ++???? ????+??+++ ).10(<<θ 这个公式称为二元函数),(y x f 在点),(00y x 的n 阶泰勒公式. 推论1 设函数),(y x f 在区域D 上具有连续的一阶偏导数，且在区域D 内，有,0),(≡y x f x 0),(≡y x f y ，则函数),(y x f 在区域D 内为一常数. 二、极值充分条件的证明例题选讲例1（E01）求函数)1ln(),(y x y x f ++=的三阶麦克劳林公式. 解 ,11),(y x y x f x ++=,11),(y x y x f y ++= ),(y x f xx 2)1(1y x ++- =),(y x f xy =),,(y x f yy =

一些常用函数及其泰勒(Taylor)展开式的图像

其中，。 ! 4!3!21)(; ! 3!21)(; ! 21)(; 1)(;)exp(4 32443 23322211x x x x x P y x x x x P y x x x P y x x P y e x y x ++++==+++==++==+==== -3 -2-1 0123 -50 5 10 15 20 25 Figure 1 y=exp(x) and its Taylor expansion equation X Y

其中，。 ! 7!5!3)(; !5!3)(; ! 3)(; )();sin(7 53775 35533311x x x x x P y x x x x P y x x x P y x x P y x y -+-==+-==-===== -4 -3-2-1 01234 -8-6-4-202468Figure 2 y=sin(x) and its Taylor expansion equation X Y

其中，。 ! 8!6!4!21)(; !6!4!21)(; ! 4!21)(; !21)(); cos(8 642886 42664 2442 22x x x x x P y x x x x P y x x x P y x x P y x y +-+-==-+-==+-==-=== -4 -3-2-1 01234 -8-6 -4 -2 2 4 Figure 3 y=cos(x) and its Taylor expansion equation X Y

其中，。 4 32)(; 3 2)(; 2 )(; )();1ln(4 32443 23322211x x x x x P y x x x x P y x x x P y x x P y x y -+-==+-==-====+= -1 -0.50 0.51 1.52 -3-2 -1 1 2 3 Figure 4 y=ln(x) and its Taylor expansion equation X Y

常见泰勒公式展开式

泰勒公式泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数满足一定的条件，泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数。泰勒公式得名于英国数学家布鲁克·泰勒，他在1712年的一封信里首次叙述了这个公式。泰勒公式是为了研究复杂函数性质时经常使用的近似方法之一，也是函数微分学的一项重要应用内容历史发展泰勒公式是高等数学中的一个非常重要的内容，它将一些复杂的函数逼近近似地表示为简单的多项式函数，泰勒公式这种化繁为简的功能，使得它成为分析和研究许多数学问题的有力工具。 18世纪早期英国牛顿学派最优秀的代表人物之一的数学家泰勒( Brook T aylor)，其主要著作是1715年出版的《正的和反的增量方法》，书中陈述了他于1712年7月给他老师梅钦信中提出的著名定理——泰勒定理。1717年,泰勒用泰勒定理求解了数值方程。泰勒公式是从格雷戈里——牛顿差值公式发展而来，它是一个用函数在某点的信息描述其附近取值的公式。如果函数足够光滑,在已知函数某一点各阶导数的前提下,泰勒公式可以利用这些导数值作为系数构建一个多项式来近似该函数在这一点的邻域中的值。1772年，拉格朗日强调了泰勒公式的重要性，称其为微分学基本定理，但是泰勒定理的证明中并没有考虑级数的收敛性，这个工作直到19世纪20年代，才由柯西完成。泰勒定理开创了有限差分理论，使任何单变量函数都

可以展开成幂级数，因此，人们称泰勒为有限差分理论的奠基者。泰勒公式是数学分析中重要的内容，也是研究函数极限和估计误差等方面不可或缺的数学工具，泰勒公式集中体现了微积分“逼近法”的精髓，在近似计算上有独特的优势。利用泰勒公式可以将非线性问题化为线性问题，且具有很高的精确度，因此其在微积分的各个方面都有重要的应用。泰勒公式可以应用于求极限、判断函数极值、求高阶导数在某点的数值、判断广义积分收敛性、近似计算、不等式证明等方面。

一些常用函数及其泰勒(Taylor)展开式的图像

图 1 )exp(x y =及其 Taylor 展开式其中，。 ! 4!3!21)(; ! 3!21)(; ! 21)(; 1)(;)exp(4 32443 23322211x x x x x P y x x x x P y x x x P y x x P y e x y x ++++==+++==++==+==== -3 -2-1 0123 -50 5 10 15 20 25 Figure 1 y=exp(x) and its Taylor expansion equation X Y

图 2 )sin(x y =及其 Taylor 展开式其中，。 ! 7!5!3)(; !5!3)(; ! 3)(; )();sin(7 53775 35533311x x x x x P y x x x x P y x x x P y x x P y x y -+-==+-==-===== -4 -3-2-1 01234 -8-6-4-202468Figure 2 y=sin(x) and its Taylor expansion equation X Y

图 3 )cos(x y =及其 Taylor 展开式其中，。 ! 8!6!4!21)(; !6!4!21)(; ! 4!21)(; !21)(); cos(8 642886 42664 2442 22x x x x x P y x x x x P y x x x P y x x P y x y +-+-==-+-==+-==-=== -4 -3-2-1 01234 -8-6 -4 -2 2 4 Figure 3 y=cos(x) and its Taylor expansion equation X Y

对于多元函数泰勒展开

… 电动力学中的泰勒展开问题物理系同学们在学习电动力学和量子力学的过程中会碰到对类似()f x y -展开的问题，初学者可能会对此类函数的展开感到困惑，对此，自己课下之余整理了一下，希望能对同学们的学习带来帮助。以下讨论主要针对的是电动力学中的极矩问题，源点与场点统一规定为用x '和x 来表示。对于多元函数泰勒展开，例如(),f x y ，有 (),f x y ()00,f x y =()()()0000,x x y y f x y x y ????+-+-????? ? ()()()200001,2!x x y y f x y x y ????+-+-+?????? （1）其中展开中心为()00,x y .对于函数()f x x '-，它是x x '-的函数，展开时需要指出其展开中心是源点x '还是场点x . 1 若在0x x '=处展开，则 ()f x x '- } ()()()()()(){}()20000012!f x x x x x x f x x x x x x f x x ''=-+---??-+---??-+???????? =()()()()()20000012!f x x x x f x x x x f x x ''-+-??-+ -??-+???? (2) 其中，()()() ???i j k x x y y z z ????=++'''?-?-?-，下同. 由于()f x x '-是在x '为小量的情况下展开的，为了计算方便，(2)式的0x 可取为原点，即x '=0，此时，(2)式便成为电势多级展开中常见的形式，即 ()()()()()()212!f x x f x x f x x f x '''-=+-??+-??+ (3) 2 若在0x x =处展开，则同理可得 ()f x x '- ()()()()()(){}()20000012!f x x x x x x f x x x x x x f x x '''''''=-+---??-+ ---??-+???????? ； =()()()()()2 0000012!f x x x x f x x x x f x x '''-+-??-+ -??-+???? (4)

常用十个泰勒展开公式

常用bai泰勒展开公式如下： 1、due^x = 1+x+x^2/2!+x^3/3!+……zhi+x^n/n!+…… 2、daoln(1+x)=x-x^2/2+x^3/3-……+(-1)^(k-1)*(x^k)/k(|x|<1) 3、sin x = x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k-1)!+……。(-∞

9、cosh x = 1+x^2/2!+x^4/4!+……+(-1)k*(x^2k)/(2k)!+……(-∞

二元函数的泰勒公式

§10.4. 二元函数的泰勒公式一、高阶偏导数二元函数),(y x f z =的两个（一阶）偏导数y z x z ????,仍是x 与y 的二元函数.若它们存在关于x 和y 的偏导数，即 .,;,??? ? ?????????? ???????? ? ????????? ??????y z y z y z x z x z y z x z x z 称它们是二元函数),(y x f z =的二阶偏导（函）数.二阶偏导数至多有22个.通常将它们表为： ??? ??????x z x z 表为 22x z ?? 或 ).,(y x f xx '' ?? ? ??????x z y z 表为 y x z ???2 或 ).,(y x f xy '' （混合偏导数） ??? ? ??????y z x z 表为 x y z ???2 或 ).,(y x f yx '' （混合偏导数） ???? ??????y z y z 表为 22y z ?? 或 ).,(y x f yy '' 一般地，二元函数),(y x f z =的1-n 阶偏导函数的偏导数称为二元函数的n 阶偏导数.二元函数的n 阶偏导数至多有n 2个.二元函数),(y x f z =的n 阶偏导数的符号与二阶偏导数类似.例如，符号 k k n n y x z ???- 或 ),()(y x f n y x k k n - 表示二元函数),(y x f z =的n 阶偏导数，首先对x 求k n -阶偏导数，其次接着对 y 求k 阶偏导数. 二阶与二阶以上的偏导数统称为高阶偏导数. 类似可定义三元函数、一般n 元函数的高阶偏导数. 例1. 求函数 332233++-=xy y x y x z 的二阶偏导数.

麦克劳林公式展开式

麦克劳林公式展开式麦克劳林公式是泰勒公式的一种特殊形式。麦克劳林简介麦克劳林,Maclaurin(1698-1746), 是18世纪英国最具有影响的数学家之一。 1719年Maclaurin在访问伦敦时见到了Newton，从此便成为了Newton的门生。 1742年撰写名著《流数论》,是最早为Newton流数方法做出了系统逻辑阐述的著作。他以熟练的几何方法和穷竭法论证了流数学说，还把级数作为求积分的方法，并独立于Cauchy以几何形式给出了无穷级数收敛的积分判别法。他得到数学分析中著名的Maclaurin级数展开式，并用待定系数法给予证明。他在代数学中的主要贡献是在《代数论》（1748，遗著）中，创立了用行列式的方法求解多个未知数联立线性方程组。但书中记叙法不太好，后来由另一位数学家Cramer又重新发现了这个法则，所以被称为Cramer法则。 Maclaurin的其他论述涉及到天文学，地图测绘学以及保险统计等学科，都取得了很多创造性的成果。 Maclaurin终生不忘牛顿Newton对他的栽培，死后在他的墓碑上刻有“曾蒙Newton的推荐”以表达他对Newton的感激之情。麦克劳林bai级数”是“泰勒级数”的du特殊形式，是展开zhi 位置为0的泰勒dao级数）。

一阶导数，系数=1/(x+1)=1/(1+x0)。二阶导数，系数=-1/(1+x)^2=-1/(1+x0)^2 数学中，泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数足够平滑的话，在已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还给出了这个多项式和实际的函数值之间的偏差。

常用十个泰勒展开公式

常用十个泰勒展开公式常用泰勒展开公式如下:1、e^x=1+x+x^2/2!+x^3/3!+……+x^n/n!+……2、ln(1+x)=x-x^2/2+x^3/3-……+(-1)^(k-1)*(x^k)/k(|x|<1)3、sinx=x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k-1)!+…….(- ∞

阶导数)泰勒定理开创了有限差分理论，使任何单变量函数都可展成幂级数。在数学中，泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数足够光滑的话，在已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还对于此处，这里o(x^5)和o(x^6)都是可以的∵sinx继续往后展开的次数为x^7∴可以写o(x^5)，也可以写o(x^6)但是写o(x^6)对这个无穷小的阶更准确通常的展开是分别按x，x，x，..展开的∴如果展开到x^n，那么后面一般就写o(x^n)就可以了

对于多元函数泰勒展开

电动力学中的泰勒展开问题物理系同学们在学习电动力学和量子力学的过程中会碰到对类似()f x y -展开的问题，初学者可能会对此类函数的展开感到困惑，对此，自己课下之余整理了一下，希望能对同学们的学习带来帮助。以下讨论主要针对的是电动力学中的极矩问题，源点与场点统一规定为用x ' 和x 来表示。对于多元函数泰勒展开，例如(),f x y ，有 (),f x y ()00,f x y =()()()0000,x x y y f x y x y ????+-+-????? ? ()()()2 00001,2!x x y y f x y x y ????+-+-+?????? （1）其中展开中心为()00,x y .对于函数()f x x '- ，它是x x '- 的函数，展开时需要指出其展开中心是源点x ' 还是场点x . 1 若在0x x '= 处展开，则 ()f x x '- ()()()()()(){}()20000012!f x x x x x x f x x x x x x f x x ''=-+---??-+---??-+??????? ? =()()()()()20000012!f x x x x f x x x x f x x ''-+-??-+-??-+???? (2) 其中，()()() ???i j k x x y y z z ????=++'''?-?-?-，下同. 由于()f x x '- 是在x ' 为小量的情况下展开的，为了计算方便，(2)式的0x 可取为原点，即x ' =0，此时，(2)式便成为电势多级展开中常见的形式，即 ()()()()()()212! f x x f x x f x x f x '''-=+-??+-??+ (3) 2 若在0x x = 处展开，则同理可得 ()f x x '- ()()()()()(){}()20000012!f x x x x x x f x x x x x x f x x '''''''=-+---??-+---??-+???????? =()()()()()20000012!f x x x x f x x x x f x x '''-+-??-+-??-+??? ? (4) 对在0x x = 处展开时， x ' 此时是变化的， ?算符可换为对源点的'?算符.

一些常用函数及其泰勒Taylor展开式的图像

一些常用函数及其泰勒 T a y l o r展开式的图像 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】